On the measurements of genetic differentiation among populations

Summary

F_ST, a measurement of the genetic differentiation among subpopulations, is a fundamental parameter in population genetics, with many valuable applications in molecular biology, evolutionary biology, conservation and forensics. One of its close relatives, G_ST, has been widely used to measure differentiation from highly polymorphic markers such as microsatellites. However, because of the high mutation rate of such markers, G_ST may underestimate the genomic differentiation due to demographic causes such as migration rate and subpopulation size. A new statistic proposed recently, Jost's D, was claimed to have better properties than G_ST and was advocated to replace G_ST as a measure of differentiation. This paper shows that D is not a proper measure of differentiation because it fails to meet some fundamental requirements as a differentiation statistic, and is hardly estimable without bias in practice. D is highly dependent on the gene diversity of a marker and on the unknown parameter of the number of subpopulations, is highly sensitive to how alleles and loci are defined and how data are analysed, does not increase monotonically with either divergence time or drift, and does not always have a maximal value of 1. The maximal D value can be zero or close to zero, depending on the number of alleles at a locus relative to the number of subpopulations. I suggest continuing the use of G_ST, with caution in its interpretation when highly polymorphic markers are used, before a better estimator of F_ST that explicitly accounts for mutations is developed.

1. Introduction

Wright (1943) first proposed a statistic, F _ST, to measure the extent of genetic differentiation among demes or subpopulations of a population. It has become a fundamental parameter in population genetics, with numerous valuable applications in molecular ecology, evolutionary biology and conservation biology. It has been used to model the allele frequency distribution (e.g. Weir, 2003) and genotype frequency distribution (e.g. Anderson & Weir, 2007) within and between subpopulations. Under certain demographic models (e.g. island and stepping stone models) without mutation and selection, F _ST is a function of migration rate (m) and subpopulation size (N), and can be used to estimate gene flow (mN). The F _ST value between a subpopulation and the others indicates its genetic uniqueness and thus can be used to prioritize subpopulations for conservation.

Since Wright (1943), many more differentiation statistics conceptually similar to F _ST have been proposed to deal with highly polymorphic markers such as microsatellites (e.g. G _ST and R _ST) and DNA sequences (e.g. Φ_ST and R _ST). The most widely applied statistic is G _ST, proposed by Nei (1973) for measuring differentiation from multiallelic markers. The development and wide application of microsatellites have made G _ST ever more popular, but also its weakness more prominent. The high mutation rate and thus high polymorphism of microsatellites lead to a high within subpopulation heterozygosity (H _S), and thus a low G _ST because it is upper bounded by the average within subpopulation homozygosity, 1−H _S (Jin & Chakraborty, 1995; Charlesworth, 1998; Nagylaki, 1998; Hedrick, 1999). This is not a problem as long as the differentiation at the focal microsatellite loci is concerned; G _ST provides an unbiased measurement of the actual level of differentiation in allele frequency at these particular loci due to all evolutionary forces, including migration, drift, mutation and selection. However, in almost all applications, we are interested in the differentiation at a random neutral locus in the genome caused solely by the demographic history of the population. For this general purpose, G _ST estimated from microsatellites could provide a serious underestimation of differentiation, and thus an overestimation of gene flow or connectivity among subpopulations. This is confirmed by many empirical studies (e.g. Balloux et al., 2000; Carreras-Carbonell et al., 2006) which obtained unexpectedly low microsatellite-based G _ST values among highly differentiated subspecies supported by morphological and other information.

To overcome the limitations of G _ST, Jost (2008) proposed a new differentiation statistic, D, based on measuring genetic diversity by the effective number of alleles and partitioning it multiplicatively into within – and between – subpopulation components. He claimed that G _ST does not measure differentiation, while his D does and measures differentiation independently of the heterozygosity (H _S) of markers. He suggested that G _ST should be replaced by D as a measure of differentiation. Tremendous controversies now exist as to which statistic, G _ST or D, is a better measure of differentiation, which has caused much confusion among empirical biologists. Ryman & Leimar (2009) and Whitlock (2011) criticized D on the ground that it depends heavily on the mutation rates that are specific to the marker loci used in the estimation, but is insensitive to the demographic factors such as population size and migration rate that are general to the whole genome. As a result, D estimated from a given set of loci cannot be extrapolated to other loci in the genome, and cannot be used to infer population demography without information on mutations. However, more researchers have advocated the use of D, either as a complete replacement (e.g. Gerlach et al., 2010) or a supplement of G _ST (e.g. Heller & Siegismund, 2009; Leng & Zhang, 2011; Meirmans & Hedrick, 2011). Some editors of peer-reviewed journals also support the use of D, asking the authors to calculate D as a differentiation measurement when microsatellites are used. The development of the software for calculating D (Crawford, 2010) facilitated the use of D by empirical biologists. As a result, many papers adopting D to measure differentiation have been published in prestigious journals, such as Molecular Ecology, since Jost's (2008) work.

In this study, I show by simulations and model analyses that D is not a proper measure of differentiation, and is difficult or impossible to estimate without bias from marker data in practice. I demonstrate that, even under some simple demographic models, D fails to meet the fundamental requirements as a measure of differentiation. G _ST, although having limitations when applied to highly polymorphic markers, should continue to be used before a better differentiation statistics, or a better F _ST estimator that accounts for mutations, is developed.

2. Measurements of differentiation

Wright (1943, 1951, 1965) first proposed a set of parameters (F _ST, F _IT and F _IS), called F statistics, for describing the properties of a hierarchically subdivided population. These parameters were originally defined either as inbreeding coefficients or in a broader context as fixation indexes (Wright, 1951). Inbreeding coefficient (Wright, 1921, 1922) was defined as the correlation between, or equally the probability of identity by descent (PIBD; Malécot, 1948) of, homologous genes of uniting gametes due to the relationship of the parents (Wright, 1965, p. 396, p. 399). As inbreeding coefficients, F _IS, F _ST and F _IT describe the relative extent of inbreeding at the individual (within a subpopulation), subpopulation (within a population) and population levels, respectively, with a relation (1−F _IT) = (1−F _IS)(1−F _ST) (Wright, 1951). As an example, Wright (1951, Fig. 3; 1965, Fig. 6) calculated F _IS, F _ST and F _IT as relative inbreeding coefficients of the cows of Bates's Duchess strain and of the Shorthorn breed using his path analysis on the pedigrees. According to Wright, the statistic F _ST measures the extent of inbreeding of a subpopulation that would result if the subpopulation were at random mating (random union of gametes; Wright 1951, p. 327), and was used by Wright (1943, 1951, 1965, 1978) to measure differentiation among subpopulations. It is caused by subdivision, and disappears at once with random mating among subpopulations. Formally, the inbreeding definition of F _ST is

(1)$$F_{{\rm ST}} \equals {{r_{\rm S} \minus r_{\rm T} } \over {1 \minus r_{\rm T} }}\comma $$

where r _S and r _T are the correlations between, or PIBD of, two homologous genes drawn at random from within a subpopulation and from the total population, respectively. Thus, F _ST can be regarded as the correlation due to common ancestry between random gametes from the same subpopulation relative to random gametes from the total population. Following Wright, F _ST was defined as ‘the probability that two homologous genes, chosen at random from the subpopulation, are both descended from a gene in the subpopulation’ by Crow & Kimura (1970, p. 105), and as ‘the average inbreeding of the subpopulation relative to the whole population’ by Falconer & Mackay (1996, p. 96).

According to Wright's definition of F _ST in terms of relative inbreeding or fixation index, F _ST is a population parameter dependent on the demographic history of the population only. It is not affected by mutations, because mutations do not alter inbreeding and population genealogy. All neutral loci in the genome are expected to have the same F _ST value, regardless of their mutation rates and polymorphisms. In other words, F _ST is a population property, not a locus-specific property.

In addition to the above original and fundamental definition of F _ST, Wright (1965) also offered several alternative interpretations. In particular, F _ST can be interpreted as the proportional decrease in heterozygosity of subpopulations relative to that of the total population, both being calculated assuming Hardy–Weinberg equilibrium. It is also ‘the ratio of the actual variance of gene frequencies of subdivisions to its limiting value, irrespective of their own structures’ (Wright, 1943, 1965),

(2)$$F_{{\rm ST}} \equals {{\sigma _{p}^{\setnum{2}} } \over {\bar{p}\lpar 1 \minus \bar{p}\rpar }}\comma $$

where $\bar{p}$ and σ_p ² are the mean and variance of allele frequencies in subpopulations. The denominator in (2) is the total variance in allele frequency in the population, including the within and between subpopulation components. It is equal to the maximal (or limiting) variance of allele frequencies between subpopulations (σ_p ²) when differentiation is complete, i.e., when an allele is either fixed in or lost from a subpopulation. Therefore, F _ST can also be interpreted as the proportion of genetic variation found between subpopulations at a locus.

Note the two alternative interpretations in terms of allele frequency variance and heterozygosity are both based on homologous genes that are identical in state (IIS), not identical by descent (IBD) or relative inbreeding (or correlation with regard to relationship). When evolutionary forces (e.g. mutation) additional to drift and migration also act on a locus, F _ST given by (2) will no longer be equivalent to that by (1). Wright recognized the difference between definitions (1) and (2), stating (Wright 1965, p. 403) that ‘More generally F _ST in the broad sense can always be obtained, at least empirically, from the variance of distribution of gene frequencies even in cases involving selection, … The results, of course, apply only to the particular loci in question’. Analogously, when mutations are important (compared with drift and migration) for a marker, it can still be used to estimate F _ST as defined by (2). The estimate is, however, applies to this locus only, and may not represent the genome-wide differentiation determined solely by the demography of the population.

Even when selections and mutations are absent, eqns (1) and (2) may also be different in some situations. For example, each subpopulation may have a lot of relatives moving to distinctive subpopulations (for whatever reason, such as avoiding inbreeding) so that relatives are predominantly found between rather than within subpopulations. In such a case, F _ST in terms of relative inbreeding (or IBD) defined by (1) or in terms of relative heterozygosity will be negative, because the PIBD of homologous genes within subpopulations (r _S) is smaller than that within the total population (r _T). In contrast, F _ST in terms of allele frequency variance defined by (2) will never be negative.

Despite the limitations, however, the IIS-based heterozygosity or variance definitions of F _ST do allow the estimation of F _ST conveniently from marker data in natural populations in which pedigrees are usually unavailable. In fact, the most widely applied F _ST estimator (Weir & Cockerham, 1984) and its relatives (e.g. Nei's G _ST, below) are based on either allele frequency variance or heterozygosity, and have gained high popularity thanks to the rapid development and applications of various genetic markers. However, it is important to remember the conceptual differences between the IIS-based heterozygosity or variance definitions on which most estimators are based, and the inbreeding (or IBD, correlation) definitions which were originally proposed by Wright. Hereafter in this paper, F _ST refers to that defined by (1) in terms of inbreeding except when explicitly stated.

Slatkin (1991, 1995) gave yet another definition of F _ST in terms of coalescence times. His derivation was based on (1), but r _S and r _T are the probabilities of homologous genes within subpopulations and within the total population that are IIS (not IBD). However, when mutation rate u is very small as he finally assumed, IIS and IBD are equivalent. Under the symmetric K alleles mutation model (the infinite allele model (IAM) is a special case where K → ∞), he derived r _S ≈ 1 − (1 − 1/K)ut _S and r _T ≈ 1 − (1 − 1/K)ut _T in the limit of small values of u, where t _S and t _T are the average coalescence times of two gene copies drawn at random from the same subpopulation and from the total population, respectively. Inserting r _S and r _T into (1) yields

(3)$$F_{{\rm ST}} \equals {{t_{\rm T} \minus t_{\rm S} } \over {t_{\rm T} }}.$$

Thus, F _ST can also be interpreted as the increase in coalescence time between genes in the total population relative to genes in the same subpopulation. In other words, F _ST measures the proportion of recent evolutionary history that is shared by genes from the same subpopulation (Whitlock, 2011).

Nei (1973) proposed his coefficient of gene differentiation, G _ST, to measure genetic differentiation in the case of multiallelic markers. G _ST is defined as

(4)$$G_{{\rm ST}} \equals {{H_{\rm T} \minus H_{\rm S} } \over {H_{\rm T} }}\comma $$

where H _T and H _S are the heterozygosity of the total population and the average heterozygosity of subpopulations expected under Hardy–Weinberg equilibrium. H _T and H _S are also known as gene diversity (Nei, 1973), and apply to haploid and multiploid species. Therefore, G _ST can be interpreted as the proportional reduction in heterozygosity or gene diversity due to subdivision, and is similar to Wright's alternative interpretation of F _ST in terms of heterozygosity or gene frequency variance. In other words, the heterozygosity at a locus is reduced by a factor G _ST due to subdivision relative to what would be expected for a panmictic population with the same allele frequencies. In the special case of a biallelic locus, Nei (1973) showed that $H_{\rm T} \equals 2\bar{p}\lpar 1 \minus \bar{p}\rpar $ and $H_{\rm T} \minus H_{\rm S} \equals 2\sigma _{p}^{\setnum{2}} $, and thus G _ST in (4) is identical to F _ST in (2). For a locus with k > 2 alleles, G _ST is equal to the weighted average of F _ST for all alleles (Nei, 1973),

(5)$$G_{{\rm ST}} \equals {1 \over k}\mathop\sum\limits_{i \equals \setnum{1}}^{k} {F_{{\rm ST}\lpar i\rpar } \equals {\left( \mathop\sum\limits_{i \equals \setnum{1}}^{k} \sigma _{p\lpar i\rpar }^{\setnum{2}} \right)\left\sol}\left( {\mathop\sum\limits_{i \equals \setnum{1}}^{k} {\bar{p}_{i} \lpar 1 \minus \bar{p}_{i} \rpar}} \right)}.}$$

In the above, F _ST and G _ST are defined as a quantity of a subpopulation (r _S, t _S, H _S) relative to that of the total population (r _T, t _T, H _T). These definitions introduce some difficulties in both interpretations and estimations. As an example, consider (1) in the case of a population subdivided into s subpopulations of effective size N_i (i = 1, 2, …, s). By definition, $r_{S} \equals \sum\nolimits_{i \equals \setnum{1}}^{s} {\sum\nolimits_{j \equals \setnum{1}}^{N_{i} } {\sum\nolimits_{k \equals \setnum{1}}^{N_{i} } {r_{ij\comma ik} } } } \sol \sum\nolimits_{i \equals \setnum{1}}^{s} {N_{i}^{\setnum{2}} } $ and $r_{T} \equals \sum\nolimits_{i \equals \setnum{1}}^{s} {\sum\nolimits_{j \equals \setnum{1}}^{s} {\sum\nolimits_{k \equals \setnum{1}}^{N_{i} } {\sum\nolimits_{l \equals \setnum{1}}^{N_{j} } {r_{ik\comma jl} } } } } \sol \sum\nolimits_{i \equals \setnum{1}}^{s} {\sum\nolimits_{j \equals \setnum{1}}^{s} {N_{i} N_{j} } } $, where r_ik,_jl is the PIBD between gamete k in subpopulation i and gamete l in subpopulation j. The first to notice is that r _S is a component of r _T, which consists of PIBD of gametes within and between subpopulations. As a result, F _ST will be partially determined by the relative subpopulation sizes due to their effects on both genetic drift and weightings in r _T. In the case of a large mainland subpopulation and a small island subpopulation, F _ST will always be small irrespective of the divergence time and migration rate, because both r _T and r _S are predominantly determined by the PIBD between gametes within the mainland subpopulation and thus always similar in values. In practice, N_i is usually unknown but assumed to be equal for all subpopulations (e.g. Nei, 1973). This treatment effectively removes the effect of different subpopulation sizes as weighting factors on the measurement of differentiation. The second to notice is that r _T and thus F _ST depend on s, the number of subpopulations. In reality, s is rarely known which makes the estimation of F _ST from a sample of subpopulations problematic.

Cockerham (1969, 1973) introduced an analogous measure of differentiation, coancestry θ, which does not rely on s. It is defined by (1) with r _T replaced by r _B, the PIBD or correlation between two gametes drawn at random from different subpopulations. Without knowing s, we can still estimate r _B and thus θ from a sample of subpopulations, as exemplified by the estimator of θ developed by Weir & Cockerham (1984). Although conceptually different, Cockerham's θ and Wright's F _ST give very similar results in practice except when s is very small, because the contribution of r _S to r _T decreases rapidly with an increasing value of s. Similarly, Nei (1986) redefined his G _ST and obtained a differentiation statistic, $G_{{\rm ST}}^{\prime} $, which is independent of s.

Based on a multiplicative partition of the effective number of alleles as a measure of genetic diversity, Jost (2008) proposed a new differentiation statistic,

(6)$$D \equals {{H_{\rm T} \minus H_{\rm S} } \over {1 \minus H_{\rm S} }}{s \over {s \minus 1}}\comma $$

where H _T and H _S are as defined in (4), and s is the number of subpopulations. He claims that D is a better measurement of differentiation than F _ST and G _ST, especially for highly polymorphic markers that could have a high within subpopulation heterozygosity (H _S).

3. General properties and comparisons of differentiation statistics

(i) Wright's F _ST is more general than G _ST and D

First, no matter is defined in terms of IBD, correlation (1) or coalescence time (3), F _ST is independent of mutations or gene diversities at a locus. In other words, F _ST has the same expected value for a given population at different neutral loci with varying mutational patterns (models, e.g. the IAM and a stepwise model) and rates, and thus with different levels of allelic or genetic diversity. This is because mutations do not alter the IBD status, coalescence times or the genealogy of genes, although they do change allele states (IIS) and thus obscure the genealogical history of genes. With the help of certain information such as pedigrees, mutations can be identified and thus the erased genealogical history recovered from genotype data (Wang, 2011). Furthermore, under certain mutation models in which mutations do not erase completely the ancestry of genes, the PIBD or coalescence time can still be inferred from genotype data alone, allowing for unbiased estimates of F _ST that reflect the demographic history of the population. For example, a point mutation just changes a single nucleotide in a DNA sequence and does not erase all evidence of ancestry when the infinite sites model holds (i.e. when no mutations hit the same site more than once during the interested period). Therefore, two genes that differ by more mutations are likely to have been evolving independently for longer and share less evolutionary history. For microsatellites under the stepwise mutation model, alleles of more similar sizes are more related in ancestry and have a more recent common ancestor. Based on this idea, Slatkin (1995) derived an F _ST estimator, R _ST, for DNA sequence and microsatellite marker data. He showed that R _ST gives unbiased estimates of differentiation due to demography (migration and population size), irrespective of the mutation rates. In fact, R _ST becomes more accurate with an increase in mutation rate, because more mutations allow a more accurate estimate of coalescent times.

In contrast, G _ST and D are defined in terms of IIS (heterozygosity and gene diversity) which is affected directly by mutations, and are thus variable among loci with different mutation patterns and rates. For the same population, differentiation calculated for one set of markers (e.g. microsatellites) can be dramatically different from that calculated for another set of markers (e.g. Single Nucleotide Polymorphism [SNPs]) simply because the two sets of markers have different mutational properties. When mutations are important compared with demography in shaping the genetic variation and its distribution in a population, G _ST and D are better regarded as ‘marker differentiation’ rather than ‘population differentiation’ measures because they apply only to the marker loci used in the estimation, and do not purely reflect the demographic history of populations. As G _ST and D are marker dependent and different studies may use different markers; it is also difficult to compare these statistics among studies.

Many of the misunderstandings and criticisms of F _ST stem from the confusion between IBD and IIS, between Wright's original definition in terms of inbreeding (1) and his alternative interpretations in terms of heterozygosity or allele frequency variance (2), and between F _ST and G _ST.

Second, F _ST can also be calculated from non-marker data, such as pedigrees. In fact, Wright (1943, 1951, 1965) calculated his F _ST in a number of numerical examples involving empirical (e.g. different cattle breeds) and hypothetical pedigrees. Indeed, when pedigree records are complete and reliable, they provide much more accurate estimates of F _ST than genotype data at a typical number of marker loci published in the literature. This is because a marker reflects just a single realization of the random genetic process experienced by a population, and it may be affected by mutations such that IIS does not truly reflect IBD. Although F _ST estimated from a marker should be unbiased under ideal conditions, it could suffer from substantial sampling errors, depending on the demographic history of the population (e.g. N _e and m), the property of the marker (e.g. diversity) and the sampling properties (e.g. sample size). The mean F _ST calculated from several independent markers has a reduced sampling variance, but is still less accurate than that calculated from a pedigree and can still be biased due to mutations.

In contrast, G _ST and D are defined in terms of population and subpopulation heterozygosities and thus rely solely on marker data for the estimation.

(ii) All differentiation statistics are defined independent of the demographic model of a subdivided population

In other words, these are descriptive statistics that measure how much the subpopulations are differentiated, but do not imply directly how and why the subpopulations become differentiated. In principle, therefore, they are applicable to any population regardless of the underlying models and mechanisms leading to the genetic structure of the population. Jost (2009, p. 2088) stated that ‘The task of measuring genetic differentiation answers a concrete question, “How different are the allele frequencies of the subpopulations?” This is a purely descriptive task which does not depend on the validity of a particular genetic model, or on the achievement of any kind of equilibrium.’ I would argue that, although all differentiation statistics are defined without any predefined demographic model and can thus be regarded as descriptive, they are not purely descriptive in the senses that their estimations, interpretations and applications require an explicit and valid genetic model.

First, all differentiation statistics require an explicit genetic model under which a statistical estimator can be developed. This is especially true for likelihood or Bayesian estimators (see e.g. Holsinger & Weir, 2009). Even simple moment estimators of G _ST and D may have to assume a model in which all subpopulations have the same and constant effective size. Coalescence time-based F _ST estimators, such as Slatkin's (1995)R _ST, require specific mutation models (e.g. stepwise model for microsatellites and infinite sites model for DNA sequence).

Second, a demographic model of the population and a genetic model of mutations for the cases of G _ST and D are required to explain the differentiation in terms of causal factors such as subpopulation size, migration pattern and rate. Rarely anybody is interested purely in the value of a differentiation statistic. Instead, given the value of a differentiation statistic, one asks what the value means biologically and why that particular value occurs rather than any value else. To interpret any differentiation measurement, one must specify (assume) a genetic model.

Third, demographic and mutational models are necessary for the applications of a differentiation statistic. For example, the inferences of gene flow from F _ST or G _ST are usually based on the island model (Whitlock & McCauley, 1999). The detection of loci under selection from the distribution of G _ST estimates requires the use of gene diversity as a control, because G _ST is expected to depend on gene diversity when mutations are important and unaccounted for in the estimation (Beaumont & Nichols, 1996).

The simplest and most widely used demographic model in studying population structures is Wright's (1931, 1943) island model. It assumes that a population consists of an infinite number of subpopulations of an equal and constant (effective) size N, and in each subpopulation a proportion m of the total gene pool is derived from immigrants that may be considered a random sample of the total population. In this model, genetic drift increases and migration decreases differentiation. At equilibrium between the two forces and irrespective of mutations, F _ST is (Wright, 1951; Takahata & Nei, 1984)

(7)$$F_{{\rm ST}} \equals 1\left\sol \left[ {1 \plus 2N\left( {{1 \over {\lpar 1 \minus m\rpar ^{\setnum{2}} }} \minus 1} \right)} \right] \approx {1 \over {4Nm \plus 1}}.}}}$$

When mutations occur at rate u under IAM, the equilibrium G _ST is (Wright, 1943; Takahata & Nei, 1984)

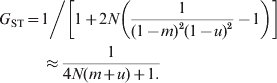(8)$$\eqalign{G_{{\rm ST}} \equals\tab {1 \mathord{\left/ {\vphantom {1 {\left[ {1 \plus 2N\left( {{1 \over {\lpar 1 \minus m\rpar ^{\setnum{2}} \lpar 1 \minus u\rpar ^{\setnum{2}} }} \minus 1} \right)} \right] \approx {1 \over {4N\lpar m \plus u\rpar \plus 1}}}}} \right. \kern-\nulldelimiterspace} {\left[ {1 \plus 2N\left( {{1 \over {\lpar 1 \minus m\rpar ^{\setnum{2}} \lpar 1 \minus u\rpar ^{\setnum{2}} }} \minus 1} \right)} \right]}}\cr\tab \approx {1 \over {4N\lpar m \plus u\rpar \plus 1.}}}}$$

In (7) and (8), the approximation applies when m,u≪1. For a finite island model with s subpopulations, (8) and (9) apply when N is replaced by Ns/(s−1) (Takahata & Nei, 1984). The difference between (7) and (8) stems from IBD and IIS which are used in defining F _ST and G _ST, respectively. Equation (8) shows that, at mutation–drift–migration equilibrium, mutations in the IAM have exactly the same effect on differentiation as migration in the island model. Migration and mutations have a large impact on harmonizing the population, and a migration or mutation rate of 1/N per generation would constrain G _ST to 0·2. When there are no mutations (u = 0), G _ST=F _ST, as shown by (7) and (8).

At the other extreme, Wright (1943) studied an isolation by distance model of population structure in which a population is distributed uniformly over a large habitat, but the parents of any given individual are drawn from a small surrounding region. As matings are restricted locally, individuals separated by a larger geographic distance are less related genetically, and any local population is differentiated from the total population. An intermediate between the two extreme models is the stepping stone model proposed by Kimura & Weiss (1964). In this mode, populations are discrete, like the island model, but migrations are restricted between neighbouring areas (stones, or subpopulations), like the isolation by distance model.

In reality, most populations may have much more complicated structures that do not fit into any of the three models. For example, subpopulations may have effective sizes that are different and variable over time with frequent local extinctions and recolonizations; migration patterns and rates may also vary among subpopulations and fluctuate over time. All these complications do not, however, prevent the calculation of the differentiation statistics, which still measure the extent of genetic differentiation. The estimation, interpretation and application of the statistics are, however, difficult or impossible without an appropriate demographic model.

(iii) All differentiation statistics have values in the range [0, 1]

All statistics yield the same value of 0 in the case of no differentiation. For F _ST, no differentiation means homologous genes taken at random from the same subpopulation have the same PIBD, correlation or coalescence time as those taken at random from the total population. For other statistics, no differentiation means all subpopulations have identical allele frequencies at a locus. At the other extreme, F _ST = 1 when all alleles within a subpopulation are IBD and G _ST = 1 when each subpopulation is fixed with one allele at a locus (H _S = 0). At G _ST = 1, some but not all subpopulations may have fixed the same allele. So long as the heterozygosity within all subpopulations is zero and the locus is polymorphic for the total population (H _T > 0), G _ST = 1. However, D is different from the other statistics in that its maximal value of 1 is realized whenever subpopulations have no alleles in common (a proof is available upon request). In other words, no matter how many alleles are segregating in each subpopulation or no matter how large the gene diversity within subpopulations is, D = 1 if no alleles are shared between any two or more subpopulations.

The magnitude of the statistics quantifies the genetic differentiation among subpopulations. As stated by Wright (1978, p. 85, where F refers to F _ST), ‘We will take F = 0·25 as an arbitrary value above which there is very great differentiation, the range 0·15–0·25 as indicating moderately great differentiation. Differentiation is, however, by no means negligible if F is as small as 0·05 or even less …’. When differentiation is mainly determined by demography rather than locus specifics such as mutation and selection, then F _ST and G _ST are expected to have the same value across the genome and can be compared among studies. However, D values can still be marker dependent (see below) and are thus incomparable among studies even in the absence of mutations.

(iv) Differentiation statistics could be affected by locus-specific selection and mutations

All statistics are affected by direct or indirect selection acting on the markers used in estimation. The extent of differentiation at marker loci under balancing selection (e.g. heterozygote advantage or allele frequency dependent selection) and directional selection will be decreased and increased, respectively, compared with that at neutral marker loci. By definitions of (1) and (3), F _ST is not affected by the mutation patterns and rates of markers. So long as selection is absent, all loci in the genome have the same expected value of F _ST, determined by the demographic history of the population only. However, both G _ST and D as well as F _ST defined in terms of IIS (2) are dependent on the mutation patterns and rates of markers. Consider the finite island model under IAM as an example. The equilibrium value of G _ST is given by (8), and that of D (Jost, 2008) is

(9)$$D \equals 1\sol \lcub 1 \plus \lpar 1 \minus g\rpar \sol \lsqb sg\lpar 2u \minus u^{\setnum{2}} \rpar \rsqb \rcub \approx u\lpar s \minus 1\rpar \sol m\comma $$

where g = [1−ms/(s−1)]². The approximation of (9) applies to the case of low migration (m≪1) and mutation (su≪m) rates. Striking differences emerge from the comparison between (8) and (9). First, mutations act to reduce G _ST but to increase D. Second, genetic drift acts to increase G _ST but has no effect on D. This property of D is peculiar, because, other things being equal, larger subpopulations are expected to experience weaker genetic drift and thus to differentiate less. Although no equilibrium D values are derived for other demographic models (e.g. stepping stone and isolation by distance), it is suspected that these striking differences between D and G _ST will persist.

Jost (2008) argues that ‘G _ST and its relatives do not measure differentiation’, while his D does. I would argue that the opposite is true (see also below), and believe that G _ST measures genetic differentiation correctly in all situations. When locus-specific effects (selection and mutations) are absent or negligible, G _ST measures the population differentiation due to demographic factors (migration and drift) and has the same expected value for any locus in the whole genome. In such a situation, G _ST is an unbiased estimator of F _ST. When locus-specific effects are present and stronger than migration and drift effects (e.g. u > m and u > 1/N), G _ST still faithfully measures marker differentiation. In this case, however, the differentiation as measured by G _ST reflects both the locus-specific effects and the general demographic effects. The value therefore applies only to the marker loci used in the estimation, and is no longer an unbiased estimate of F _ST. It thus has little relevance to the differentiation at other loci in the genome, and cannot be regarded as population differentiation that is interpretable in terms of the demography of the population (i.e. migration rate and subpopulation size). It is true that G _ST estimated from a locus with a higher mutation rate and thus higher heterozygosity within subpopulations is generally lower. This, however, is the truth, reflecting the fact that mutations have reduced the differentiation at the locus. Realizing and utilizing these locus-specific mutation and selection effects on G _ST, we can actually infer mutations and selection from estimates of G _ST (e.g. Beaumont & Nichols, 1996).

4. D does not measure differentiation

Contrary to the view of Jost (2008), I argue that D does not measure differentiation but G _ST and relatives do. The following analyses show that D fails to measure differentiation correctly even in some simple situations.

(i) D is highly dependent on initial genetic diversity

For analytical tractability, I assume Wright's (1943) island model of migration among s subpopulations of effective size N, and an IAM for mutations. For a neutral locus, the probabilities that two genes drawn at random from the same subpopulation and from different subpopulations are IIS are denoted by f and g, respectively. The heterozygosity expected at Hardy–Weinberg equilibrium is H _S = 1−f and H _T = (1−f)/s + (1−g)(s−1)/s for a subpopulation and the total population, respectively. Starting from the initial generation (0) when all subpopulations are identical at the locus (i.e. no differentiation), f and g change over generations due to genetic drift, mutation, and migration at rates d = 1/(2N), u and m, respectively. The recurrence equations are (Li, 1976)

(10)$$\openup3\eqalign{\tab f\lpar t \plus 1\rpar \equals c\lsqb a\lpar d \plus \lpar 1 \minus d\rpar f\lpar t\rpar \rpar \plus \lpar 1 \minus a\rpar g\lpar t\rpar \rsqb \comma \cr \tab g\lpar t \plus 1\rpar \equals c\lsqb b\lpar d \plus \lpar 1 \minus d\rpar f\lpar t\rpar \rpar \plus \lpar 1 \minus b\rpar g\lpar t\rpar \rsqb \comma \cr} $$

where c = (1−u)² is the probability that neither of two randomly drawn genes mutates in one generation, a = (1−m)²+m(2−m)/s and b=m(2−m)/s are the probabilities that two distinct genes, drawn at random from the same subpopulation and from different subpopulations, respectively, came from the same subpopulation in the previous generation. The initial probabilities of genes that are IIS are f(0)=g(0) = 1−H ₀, where H ₀ is the initial gene diversity at the locus.

Using (10) and the initial conditions, I can calculate the probabilities of IIS, f(t) and g(t), and thus the gene diversities for a subpopulation and the total population, H _S(t) = 1–f(t) and H _T(t) = 1–g(t), at any generation t. In the case of an infinite number of subpopulations (s → ∞), a closed form solution of f(t) and g(t) can be obtained from the recurrence equations, which leads to the expected values of G _ST and D at generation t

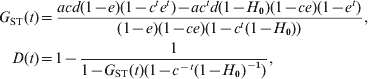(11)$$\eqalign{ G_{{\rm ST}} \lpar t\rpar \equals \tab {{acd\lpar 1 \minus e\rpar \lpar 1 \minus c^{t} e^{t} \rpar \minus ac^{t} d\lpar 1 \minus H_{\setnum{0}} \rpar \lpar 1 \minus ce\rpar \lpar 1 \minus e^{t} \rpar } \over {\lpar 1 \minus e\rpar \lpar 1 \minus ce\rpar \lpar 1 \minus c^{t} \lpar 1 \minus H_{\setnum{0}} \rpar \rpar }}\comma \cr D\lpar t\rpar \equals \tab 1 \minus {1 \over {1 \minus G_{{\rm ST}} \lpar t\rpar \lpar 1 \minus c^{ \minus t} \lpar 1 \minus H_{\setnum{0}} \rpar ^{ \minus \setnum{1}} \rpar }}\comma \cr} $$

where e=a(1−d). Equation (11) shows that D is a function of G _ST, corrected for initial gene diversity (H ₀) and mutations (c = (1−u)²). Some insights can be gained from (11) by further assuming that mutations are negligible because other forces (migration and drift) are much more important in determining differentiation. In such a case, (11) reduces to

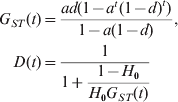(12)$$\eqalign{ G_{ST} \lpar t\rpar \equals \tab {{ad\lpar 1 \minus a^{t} \lpar 1 \minus d\rpar ^{t} \rpar } \over {1 \minus a\lpar 1 \minus d\rpar }}\comma \cr D\lpar t\rpar \equals \tab \displaystyle{1 \over {1 \plus \displaystyle{{1 \minus H_{\setnum{0}} } \over {H_{\setnum{0}} G_{ST} \lpar t\rpar }}}} \cr} $$

It is clear that, at any generation t, G _ST is independent of H ₀ (the initial gene diversity of a marker), while D increases monotonically with H ₀. D is always close to its maximal value of 1 and minimal value of 0 when H ₀ is close to 1 and 0, respectively, regardless of values of m, N and t. In other words, G _ST calculated from markers with different initial gene diversities would be expected to be the same at any time, if mutations are negligible (i.e. u≪m or u≪1/N). In contrast, D is highly dependent on the initial gene diversity of a marker. The value of D reflects the gene diversity more than the differentiation at a locus, let alone the differentiation at other loci of the genome. A given D value, say 0·01 or 0·99, can indicate low, moderate or high differentiation, depending on the gene diversity of the markers. Similarly, a population with a given level of differentiation, say F _ST = 0·25, may have different D values in the entire range of [0, 1], depending on the gene diversity of the markers. We always have D → 1 and D → 0 when H ₀ → 1 and H ₀ → 0, respectively, regardless of migration rate (m), subpopulation size (N) and divergence time (t). At any generation t, D is smaller than, equal to and larger than G _ST when the gene diversity of the marker (H ₀) used in the calculation is smaller than, equal to and larger than 1/(2−G _ST(t)), respectively.

In the absence of mutations, both G _ST and D will increase with t until an equilibrium and maximal value is reached. Their maximal values are $G_{{\rm ST}\lpar M\rpar } \equals {{ad} \over {1 \minus a\lpar 1 \minus d\rpar }}$ and $D_{\lpar M\rpar } \equals {{adH_{\setnum{0}} } \over {1 \minus H_{\setnum{0}} \minus a\lpar 1 \minus d \minus H_{\setnum{0}} \rpar }}$, respectively, when t → ∞ as can be obtained from (12). In the special case of m = 0 and thus a = 1, the G _ST(M) value for any locus with any initial gene diversity is always 1, achieved when the locus becomes fixed in all subpopulations and thus within subpopulation gene diversity drops to 0. In contrast, however, the expected maximal D value achievable for a locus is equal to its initial gene diversity H ₀. In other words, the maximal D value expected at a locus has an upper bound of H ₀, the initial gene diversity of the locus. Therefore, D values will be higher and lower when calculated from loci with higher (e.g. microsatellites) and lower (e.g. SNPs) gene diversity, respectively, for the same population. Although the above analysis and conclusions are based on the assumption of no mutations, they are good approximations when mutations are negligible compared with drift (1/(2N _e)≫u, see numerical example below).

To further understand the behaviours of G _ST and D, let us consider a numerical example. Figure 1 plots G _ST(t) and D(t) for t = 1, 10, 100 and 1000 as a function of H ₀, with N = 100 (d = 0·005). The results for the infinite island model (s = ∞) were obtained from (11), while those for the finite island model (s = 10) were obtained from recurrence eqn (10). Some parameter combinations involving a high genetic diversity (H ₀) but null or low mutation rate, as in this and some other examples of this study, seem to be paradoxical. However, they are realistic because we are dealing with non-equilibrium situations. For example, a large random mating population may be suddenly subdivided (due to habitat fragmentation or other causes) into small subpopulations in nature, or a number of inbred lines are established from a large outbred source population and are maintained in the laboratory. In both cases, H ₀ can be high because of the large ancestral population size, but mutations can be small and even negligible compared with drift and migration in the short time scale.

Fig. 1. Values of G _ST and D at generation t as a function of initial gene diversity H ₀. The parameters are s = ∞ and u = m = 0 for panel (a), s = ∞ and u = m = 0·001 for panel (b), s = 10 and u = m = 0·001 for panel (c) and s = 10, u = 0·01 and m = 0·001 for panel (d). In all four cases, the subpopulation size is N = 100.

As can be seen, at early generations (t < 10) when differentiation is low, D increases slowly with H ₀ when it is small but increases rapidly when it becomes large. At later generations (t > 100) when differentiation is close to complete, D increases almost linearly with H ₀. This is clear from an inspection of (12), which reduces to D(t)=H ₀ when t → ∞ and m = 0. In contrast, H ₀ has no effect on G _ST when u = 0. At intermediate differentiation (t = 100), G _ST increases slightly with an increase in H ₀ when u > 0. However, it should be pointed out that this slow change of G _ST with H ₀ is not a proof that G _ST depends on H ₀ per se, as believed by some researchers in their simulation studies (Leng & Zhang, 2011), but is the result of new mutations. Without mutations (u = 0), G _ST is always independent of H ₀. With an increase in mutation rate (see Figs 1(c) and (d)), G _ST decreases while D increases. The underestimation of differentiation (due to demographic factors only) by G _ST when mutations are important compared with drift and migration can be substantial, especially when t is large and the population is close to equilibrium.

(ii) D does not increase monotonically with differentiation

For a population subdivided into s subpopulations in the island model, everyone would agree that differentiation should increase monotonically with time, from no differentiation initially at the time of subdivision to an asymptotic maximum at equilibrium determined by parameters m, s, N and u. This is true when differentiation is measured by G _ST, but not always true when differentiation is measured by D. Figure 2(a) plots the changes in D and G _ST as a function of generations of differentiation for a population subdivided into s = 2 equal-sized (N = 100) subpopulations. Other parameters are m = 0·01, u = 0·001 and an initial frequency of 0·1 for each of 10 alleles at a locus in each subpopulation. The results for D and G _ST are obtained from both recurrence eqns (10) and simulations. While G _ST increases monotonically with t, D increases initially and then decreases with t to reach its asymptotic equilibrium value. Such results were also obtained when the initial allele frequencies were drawn from a uniform Dirichlet distribution. This peculiar behaviour of D is often true when m≫u, s is small and initial gene diversity is high.

Fig. 2. Simulated and theoretical D and G _ST values as a function of generations (a) and subpopulation size (b). The parameters used in generating the graphs are m = 0·01, u = 0·001, s = 2, N = 100 (a only), t = 200 (b only), and initially 10 alleles of an equal frequency for both subpopulations. Simulated values were obtained from 10 000 replicates, and theoretical values were obtained from recurrence eqn (10).

For a given set of parameters of m, s, t and u, D also does not decrease monotonically with an increasing subpopulation size N (Fig. 2(b)). Drift has been regarded as a force differentiating subpopulations at all loci in the genome. With an increasing subpopulation size, drift becomes weaker and as a result differentiation between subpopulations at any given time should become smaller. This is true, however, only when G _ST is used as the differentiation measurement (Fig. 2(b)), not D for some parameter combinations of m, N, s, u and H ₀.

(iii) D = 1 does not necessarily mean complete differentiation

Jost's (2008) criticisms of G _ST were almost exclusively based on a few numerical examples. His Figure 1 showed that, when two subpopulations are ‘completely differentiated’ because they have no shared alleles, D is always 1 while G _ST decreases with an increasing within-subpopulation heterozygosity. His Figure 2 plotted the changes in differentiation measured by G _ST and D between two initially identical subpopulations (sharing four equally common alleles) as unique alleles were added successively to each subpopulation. While D increases monotonically, G _ST first increases and then decreases with a successive addition of unique alleles to each subpopulation. In his Table 1, the two subpopulations for species B have allele frequencies {0·2, 0·8} and {0·8, 0·2}, respectively, at a biallelic locus, resulting in G _ST = 0·36 and D = 0·53. The two subpopulations for species C have allele frequencies {0·095, 0·08, 0·11, 0·08, 0·095, 0·06, 0·07, 0·096, 0·094, 0·08, 0·03, 0·06, 0·05, 0, 0, 0, 0, 0, 0, 0} and {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0·15, 0·16, 0·12, 0·13, 0·17, 0·14, 0·13}, respectively, at a 20-allele locus, with G _ST = 0·06 and D = 1. He concluded from the three examples that G _ST cannot be interpreted as a measure of differentiation, but his D can. I show below that his conclusion is incorrect because it is based on the misperceptions that subpopulations with no shared alleles should be 100% differentiated, and that the more unique (or private) alleles the subpopulations have, the more differentiated they will be.

First, subpopulations sharing no alleles among them are not necessarily completely differentiated. It can be shown (proof available upon request) that D = 1 when no alleles are shared between any two subpopulations, irrespective of the number and frequencies of segregating alleles (or the gene diversity) in each subpopulation and the number of subpopulations. It can also be shown that G _ST = 1 only when H _S = 0 and H _T > 0, and G _ST < 1 otherwise. The condition for G _ST = 1, H _S = 0 and H _T > 0, occurs when each of the s subpopulations has one allele fixed (i.e. frequency = 1) in and the others are lost (i.e. frequency = 0) from the subpopulation, no matter whether the fixed alleles are shared (except for the case that a single allele is fixed for all subpopulations such that H _T = 0) or not among subpopulations. In contrast, the gene diversities within subpopulations vary freely in the range (0, 1) when D = 1. I argue that G _ST = 1 means differentiation is complete, while D = 1 does not. Let us consider a simple example of a population subdivided into subpopulations of A and B, with each subpopulation having k private alleles and each allele having an equal frequency of 1/k in the subpopulation it occurs. Because A and B share no alleles, we always have D = 1, but the frequency difference for any allele between A and B can be very small if k becomes large. This property of D is thus in conflict with the statement of Jost (2009) that ‘The task of measuring genetic differentiation answers a concrete question, “How different are the allele frequencies of the subpopulations?”’ At D = 1, allele frequency difference among subpopulations can be very small for a highly polymorphic locus with many alleles.

Second, subpopulations that are completely differentiated do not necessarily have D = 1. Consider a locus with two initially equifrequent alleles A and B (k = 2) in a population subdivided into s = 3 subpopulations under the pure drift model. When the genetic composition is no longer changeable (H _S = 0, and thus G _ST = 1), either one allele (A or B) is fixed in all three subpopulations, or both alleles A and B are fixed in the three subpopulations (say, A and B are fixed in two and one subpopulations, respectively). The first and second events occur at a probability of 1/4 and 3/4, leading to H _S=H _T = 0, and H _S = 0 and H _T = 4/9, respectively. The two events lead to a D value of 0 and 2/3, respectively, and a G _ST value that is undefined (see below) and 1, respectively.

In general, whenever k < s, the maximal value of D must be smaller than 1, because some of the s subpopulations must share at least one allele no matter how long the subpopulations are separated and how strongly the drift occurs in each subpopulation. This conclusion contrasts with the claim that D always has a maximal value of 1 because it is not constrained by H _S (e.g. Jost, 2008; Ryman & Leimar, 2009).

When the effect of mutations is negligibly small compared with that of drift, a completely differentiated population (H _S = 0) will invariably have a G _ST value of 1, regardless of the parameters such as s and N. In contrast, a completely differentiated population will have an expected D value that is variable with the initial gene diversity (H ₀) at a locus, as shown above. Furthermore, the maximal D value for a population of s completely differentiated subpopulations follows a distribution, depending on the initial number and frequency distribution of alleles at a locus as well as s. For a locus with k alleles of an equal initial frequency of 1/k, the minimum D value in this distribution is always 0, which occurs when all subpopulations are fixed for the same allele (H _S=H _T = 0) with a probability 1/k^{s− 1}. The maximum D value in this distribution is variable. It is 1 with probability $\prod\nolimits_{i \equals \setnum{0}}^{s \minus \setnum{1}} {\lpar k \minus i\rpar \sol k} $ when k ⩾s, and is (s ²−q ²k − r(1 + 2q))/(s(s−1)) which is less than 1 when k < s, where q and r are the quotient and remainder of s divided by k. It should be noted that there could be many possible D values between the minimum (0) and maximum values of the distribution under complete differentiation. Even when k⩾s, the D value at complete differentiation may still be smaller than 1. Figure 3 shows the distributions of D values at complete differentiation for k = 2, 5, 10 and s = 10, generated by simulations. In summary, the above results show that, at complete differentiation (H _S = 0) when genetic variation within and between subpopulations are fixed, the D value varies depending on the number (k) and initial frequencies of alleles at a locus and the number of subpopulations (s). Even for a given combination of these parameters, the D value varies wildly between a lower limit of 0 and a higher limit variable depending on the parameters. These results are general and independent of the demographic models, the only assumption is that mutations are negligible compared with drift. This could happen, for example, when a large outbred population is subdivided into many isolated small populations, as in establishing inbred lines in plant and animal breeding and in some laboratory situations.

Fig. 3. Distributions of D values at complete differentiation (H _S = 0) of a population subdivided into s = 10 subpopulations under the pure drift model (no mutation, no migration and no selection). The distribution is obtained from 100 000 replicate simulations for a locus with k = 2, 5 and 10 alleles of an equal frequency initially. For all three cases, G _ST = 1 with frequency 1.

In contrast, the maximal value of G _ST is invariably 1 when differentiation is complete (H _S = 0), irrespective of k, the initial alleles frequencies at a locus and s. When each subpopulation is fixed for one allele, H _S = 0 and G _ST = 1, no matter how the fixed alleles are shared (or unshared) among subpopulations. The particular case of all subpopulations are fixed with a single allele, H _T=H _S = 0, needs some special attention. In this case, G _ST becomes undefined because both the denominator and the numerator of the ratio (H _T−H _S)/H _T are zero. This makes sense because in such a case the marker locus is monomorphic and thus uninformative, if considered in isolation of any other information, about differentiation. There are two possible explanations for H _T=H _S = 0. One is that the locus is monomorphic before the population is subdivided, and the other is that the locus is initially polymorphic when the population is subdivided but the same allele becomes fixed in all subpopulations due to drift. The marker is indeed uninformative about differentiation in the first scenario, but indicates complete differentiation in the second scenario. In contrast, D ≡ 0 for a monomorphic locus. Therefore, differentiation measured by D would be close to zero even between different species (e.g. humans and chimpanzees) if a random set of marker loci are assayed and used in the estimation, because most loci would be monomorphic even between species. If one chooses to use only polymorphic loci, D will be overestimated for the genome because the selected set of loci is not representative.

In the situation where one allele is fixed in a single subpopulation and another allele is fixed in all of the s − 1 subpopulations, we have D = 2/s and G _ST = 1 from definitions (6) and (4), respectively. When s is large, the small D value seems to be plausible and G _ST = 1 seems to be counterintuitive, as allele frequencies are the same across the vast majority of subpopulations. However, the opposite is true when one considers the possible genetic process (mechanism) leading to the observed pattern of genetic variation. The absence of variation within any subpopulation but the presence of variation in the total population implies both high genetic drift in and no migration among subpopulations, a condition that should lead to high differentiation. Otherwise, a low level of differentiation due to either weak drift or high migration will not in general lead to the observed pattern of genetic variation. In terms of allele frequency variance, although $\sigma _{p}^{\setnum{2}} \equals {\rm 1}\sol s$ (1 − 1/s) is small (indicating the high similarity in allele frequency among subpopulations) in (2) for a large s, it is equal to the maximal limiting value $\bar{p}{\rm \lpar 1} \minus \bar{p}\rpar $ where $\bar{p} \equals {\rm 1}\sol s$ (or $\bar{p} \equals {\rm 1} \minus {\rm 1}\sol s$ depending on the focal allele). As a result, F _ST = 1, in agreement with G _ST. In other words, F _ST or G _ST measures differentiation by putting allele frequency difference between subpopulations in context, relative to the total population. Although in the above situation the variance in allele frequencies across subpopulations is very small, it is also very small for the total population.

Let us now consider a practical example of a subdivided population. Suppose a number of s replicate inbred lines are established from the same large and outbred source population, and are maintained in the lab without crossing or immigration for many generations until they become pure inbred lines. If one assays a set of markers chosen at random, and uses the marker data in estimating differentiation, he/she would obtain very different results of D and G _ST. D values calculated for each of the loci will be highly variable between 0 and 1, depending on the initial number of alleles (k) of the marker relative to s. For a highly polymorphic microsatellite with k⩾s, D = 1 may be possible when each line is fixed for a distinctive allele. More generally, a whole distribution of D values between 0 and 1 is possible. For SNPs (k = 2), however, D is either 0 or 2/s, and will never reach a value of 1 except when s = 2. In contrast, G _ST is either undefined when a marker has a single allele fixed in all lines, or G _ST = 1 otherwise, irrespective of the initial polymorphisms of the markers in the source population. The results of G _ST obviously make sense.

Now let us consider the numerical examples in Jost's (2008) Table 1, outlined above. Although the two subpopulations of species B share both alleles, their allele frequencies are highly different (differentiated), with a frequency difference of 0·6. In contrast, although the two subpopulations of species C share none of the 20 alleles, they have very similar frequencies of each allele (not differentiated much) with a maximal difference of 0·17. I would argue that a measurement of differentiation based on allele frequency difference among subpopulations is more plausible and robust than that based on the number of unshared alleles among subpopulations. The behaviours of D and G _ST in Jost's (2008) Figures 1 and 2 and Jost's (2009) Figure 1 can be explained similarly, as adding more unique alleles to subpopulations effectively reduces frequency differences for each allele between subpopulations and thus reduces G _ST.

(iv) D is highly sensitive to how alleles and loci are defined and how data are analysed

For several types of markers, alleles are really arbitrary identities, depending on the technology used in differentiating and detecting them. For example, at the gene locus for the ABO blood-type carbohydrate antigens in humans, classical genetics recognizes three alleles, A, B and O that determine compatibility of blood transfusions. It is now known that each of the A, B and O alleles is actually a class of multiple alleles with different DNA sequences that produce proteins with identical properties. In total more than 70 alleles are now known at the ABO locus (Yip, 2002).

On the other hand, the same marker data can be and have been analysed differently for differentiation among populations. Suppose, for example, a segment of genomic or non-genomic DNA is sequenced for each of several individuals sampled from each of several subpopulations. The sequence data can be used to assess differentiation in two approaches. One approach treats each polymorphic site as a separate locus (i.e. as an SNP) and then estimates differentiation from the frequencies of alleles at each locus (e.g. Takahata & Palumbi, 1985; Lynch & Crease, 1990). The other approach treats the segment as a single locus, and then estimates differentiation from the haplotype frequencies (e.g. Φ_ST in analysis of molecular variance introduced by Excoffier et al., 1992) or from the gene trees reconstructed from the sequences (e.g. Slatkin & Maddison, 1989; Hudson et al., 1992). Therefore, the same DNA sequence data have operationally either many biallelic loci (SNPs) or a single highly polymorphic, many-allele locus.

In the above two situations, no matter how alleles and loci are pooled or split due to technological reasons or statistical treatments, differentiation would be expected to be the same if it is measured by F _ST, or G _ST when mutations are weak compared with drift and migration. G _ST is based on allele frequency difference and is thus robust to the changes in recognizable or operational alleles and loci, because each allele and each locus are expected to have the same G _ST value (Nei, 1973). Pooling several alleles (loci) to form a ‘super allele’ (‘super locus’) or splitting an allele (a locus) into two or more alleles (loci) has little effect on G _ST, when mutations are unimportant (e.g. when differentiation is dominated by drift because of a severe bottleneck in population size in the recent past). In contrast, D is highly sensitive to allele (locus) pooling or splitting, because it depends strongly on H _S which is always increased by allele splitting (locus pooling) and decreased by allele pooling (locus splitting).

Some simulations were conducted to check the effects of allele pooling on G _ST and D (the effect of allele splitting is just the opposite). Figure 4 shows the results from simulations assuming a population subdivided into s = 10 subpopulations at a locus with initially 10 equifrequent alleles in each subpopulation. Other parameters are m = 0·01, u = 0·001 and N = 100. Obviously, at any generation of differentiation, D is reduced substantially by pooling alleles. The more alleles are pooled, the smaller the D value becomes. In contrast, pooling (or splitting) of alleles does not bias G _ST estimates, it only reduces (increases) the estimation precision. This property of G _ST is true for other parameter combinations as long as drift or/and migration are the dominating (over mutations) forces in determining differentiation. Given the fact that alleles and loci are more or less arbitrary due to technological or operational reasons in many practical situations, D is also arbitrary and is hardly qualified as an objective measurement of differentiation.

Fig. 4. Effects of pooling alleles on D and G _ST values as a function of generations, since a population becomes subdivided. The simulations (10 000 replicates) assumed a population subdivided at t = 0 into s = 10 subpopulations, with m = 0·01, u = 0·001, N = 100 and initially 10 equifrequent alleles at a locus.

(v) D is highly dependent on the number of subpopulations

For mathematical tractability, consider the finite island model where the exact equilibrium values of F _ST, G _ST and D are given by (7)–(9). The equilibrium F _ST, G _ST and D as a function of the number of subpopulations are depicted in Fig. 5(a), assuming N = 100, m = 0·01 and u = 0·001. As is clear, D is much more dependent on s than G _ST and F _ST. While G _ST and F _ST become virtually constant when s reaches 5, D increases steadily with an increasing value of s with no sign of reaching an asymptotic value when s is 100. In fact, for this parameter combination, D does not asymptotes with an increasing s until it is close to 1. Its values are 0·088, 0·469, 0·907, 0·990 and 0·999 when s = 2, 10, 100, 1000 and 10 000, respectively. This much higher dependency of D on s than G _ST and F _ST is true when m>u, which is realistic even for markers with a high mutation rate (e.g. microsatellites).

Fig. 5. Effects of the number of subpopulations on D, G _ST and F _ST values. The results are obtained assuming a population subdivided into s subpopulations, with m = 0·01, u = 0·001, N = 100 in the island model and IAM. (a) Shows the equilibrium D, G _ST and F _ST values, and (b) shows the D and G _ST values at generations 10, 100 and 1000 since the subdivision.

D can also be highly dependent on s in non-equilibrium conditions. Figure 5(b) shows the values of G _ST and D as a function of s at different generations (t = 10, 100 and 1000) since the subdivision, obtained from recurrence eqn (10) with parameters N = 100, m = 0·01 and u = 0·001. Starting from initial IIS probabilities of f(0)=g(0) = 1−H ₀, where the initial gene diversity is H ₀ = 0·8, I calculated the IIS probabilities and G _ST and D values at each successive generation from (10). As is clear from Fig. 5(b), D is sensitive to s at different stages in the process towards the equilibrium differentiation. While D decreases with s at early stages, it increases with s at later stages or at equilibrium. In contrast, at all stages, G _ST changes little with s.

The high dependence of D on s means that it is impossible to estimate D reliably when the number of subpopulations s is unknown. Unfortunately, s is frequently unknown in practice. With frequent local extinctions and recolonizations in natural populations in the evolution scale relevant for measuring differentiation, it is actually difficult to define what s means. Is it the current, previous or average number of subpopulations? Obviously, the number of sampled subpopulations is an underestimate of s and could lead to serious under- or over-estimation of D if it is used in place of s in estimating D (Fig. 5(b)). This property of D makes it impossible to study the differentiation of a population by sampling a small number of subpopulations.

5. Conclusions

Wright's F _ST, no matter whether defined in terms of inbreeding (PIBD, correlation) or coalescence time, is a general measurement of population differentiation, independent of the type (e.g. SNPs and microsatellites) and properties (e.g. mutation rate) of the markers used in estimating it. It truly measures the differentiation due to demographic factors only (migration and subpopulation size), and can be interpreted as such and compared across studies. However, it is difficult to calculate from marker data when mutations are important. Better estimators of F _ST that can account for mutations (i.e. by distinguishing IBD and IIS) need to be developed. F _ST, when interpreted in terms of heterozygosity or variance of allele frequencies, becomes similar to G _ST as both are defined on IIS and are affected by mutations.

Nei's G _ST measures the differentiation at a locus due to all evolutionary forces, including genetic drift, migration, selection and mutation. As a result, G _ST should be interpreted in terms of demographic factors only when mutation and selection are unimportant. In situations where mutations are important in comparison with drift and migration, G _ST calculated from loci with high gene diversity is smaller than that calculated from loci with low gene diversity, and thus it measures marker differentiation rather than population differentiation. Although I suggest the continued use of G _ST in practice, caution should be exercised in its interpretation, especially for highly polymorphic markers. Mean within subpopulation diversity, H _S, should be reported together with G _ST to aid the interpretation.

Jost's D is not a proper measure of genetic differentiation. It is highly dependent on the initial gene diversity of the marker loci, is highly sensitive to how alleles and loci are defined and how data are analysed, does not always increase monotonically with divergence time and with drift, is highly dependent on the unknown parameter of the number of subpopulations and does not always have a maximal value of 1. The maximal D value when differentiation is complete can be zero, or close to zero, depending on the number of alleles at a locus relative to the number of subpopulations. Subpopulations that share no alleles at a locus are not completely differentiated. Rather, the extent of differentiation depends on the magnitude of difference in allele frequency, which is measured by F _ST and G _ST but not D.