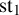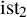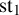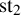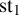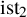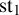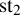1 Introduction
Let
![]() $\mathfrak {S}_{n}$
denote the symmetric group of permutations of the set
$\mathfrak {S}_{n}$
denote the symmetric group of permutations of the set ![]() . We call
. We call
![]() $i\in [n-1]$
a descent of
$i\in [n-1]$
a descent of
![]() $\pi \in \mathfrak {S}_{n}$
if
$\pi \in \mathfrak {S}_{n}$
if
![]() $\pi (i)>\pi (i+1)$
. Let
$\pi (i)>\pi (i+1)$
. Let
be the number of descents and the sum of descents of
![]() $\pi $
, respectively. The descent number
$\pi $
, respectively. The descent number
![]() $\operatorname {\mathrm {des}}$
and major index
$\operatorname {\mathrm {des}}$
and major index
![]() $\operatorname {\mathrm {maj}}$
are classical permutation statistics dating back to MacMahon [Reference MacMahon17].
$\operatorname {\mathrm {maj}}$
are classical permutation statistics dating back to MacMahon [Reference MacMahon17].
Given a permutation statistic
![]() $\operatorname {\mathrm {st}}$
, let us define its inverse statistic
$\operatorname {\mathrm {st}}$
, let us define its inverse statistic
![]() $\operatorname {\mathrm {ist}}$
by
$\operatorname {\mathrm {ist}}$
by ![]() . This paper is concerned with the general problem of finding the joint distribution of a permutation statistic
. This paper is concerned with the general problem of finding the joint distribution of a permutation statistic
![]() $\operatorname {\mathrm {st}}$
and its inverse statistic
$\operatorname {\mathrm {st}}$
and its inverse statistic
![]() $\operatorname {\mathrm {ist}}$
over the symmetric group
$\operatorname {\mathrm {ist}}$
over the symmetric group
![]() $\mathfrak {S}_{n}$
. This was first done by Carlitz, Roselle and Scoville [Reference Carlitz, Roselle and Scoville5] for
$\mathfrak {S}_{n}$
. This was first done by Carlitz, Roselle and Scoville [Reference Carlitz, Roselle and Scoville5] for
![]() $\operatorname {\mathrm {des}}$
and by Roselle [Reference Roselle20] for
$\operatorname {\mathrm {des}}$
and by Roselle [Reference Roselle20] for
![]() $\operatorname {\mathrm {maj}}$
. Among the results of Carlitz, Roselle and Scoville was the elegant generating function formula
$\operatorname {\mathrm {maj}}$
. Among the results of Carlitz, Roselle and Scoville was the elegant generating function formula
 $$ \begin{align} \sum_{n=0}^{\infty}\frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}=\sum_{i,j=0}^{\infty}\frac{s^{i}t^{j}}{(1-x)^{ij}} \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty}\frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}=\sum_{i,j=0}^{\infty}\frac{s^{i}t^{j}}{(1-x)^{ij}} \end{align} $$
for the two-sided Eulerian polynomials
![]() $A_{n}(s,t)$
defined by
$A_{n}(s,t)$
defined by
for
![]() $n\geq 1$
and
$n\geq 1$
and ![]() .Footnote
1
(Throughout this paper, all polynomials encoding distributions of permutation statistics will be defined to be 1 for
.Footnote
1
(Throughout this paper, all polynomials encoding distributions of permutation statistics will be defined to be 1 for
![]() $n=0$
.) Roselle gave a similar formula for the joint distribution of
$n=0$
.) Roselle gave a similar formula for the joint distribution of
![]() $\operatorname {\mathrm {maj}}$
and
$\operatorname {\mathrm {maj}}$
and
![]() $\operatorname {\mathrm {imaj}}$
over
$\operatorname {\mathrm {imaj}}$
over
![]() $\mathfrak {S}_{n}$
. Note that extracting coefficients of
$\mathfrak {S}_{n}$
. Note that extracting coefficients of
![]() $x^{n}$
from both sides of Equation (1.1) yields the formula
$x^{n}$
from both sides of Equation (1.1) yields the formula
 $$ \begin{align} \frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}}=\sum_{i,j=0}^{\infty}{ij+n-1 \choose n}s^{i}t^{j}, \end{align} $$
$$ \begin{align} \frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}}=\sum_{i,j=0}^{\infty}{ij+n-1 \choose n}s^{i}t^{j}, \end{align} $$
which Petersen [Reference Petersen19] later proved using the technology of putting balls in boxes. Equation (1.2) may be compared with the formula
 $$ \begin{align} \frac{A_{n}(t)}{(1-t)^{n+1}}=\sum_{k=0}^{\infty}k^{n}t^{k} \end{align} $$
$$ \begin{align} \frac{A_{n}(t)}{(1-t)^{n+1}}=\sum_{k=0}^{\infty}k^{n}t^{k} \end{align} $$
for the (ordinary) Eulerian polynomials
Several years after the work of Carlitz–Roselle–Scoville and Roselle, Garsia and Gessel [Reference Garsia and Gesse11] used the theory of P-partitions to derive the formula
 $$ \begin{align} \sum_{n=0}^{\infty}\frac{A_{n}(s,t,q,r)}{(1-s)(1-qs)\cdots(1-q^{n}s)(1-t)(1-rt)\cdots(1-r^{n}t)}x^{n}=\sum_{i,j=0}^{\infty}s^{i}t^{j}\prod_{k=0}^{i}\prod_{l=0}^{j}\frac{1}{1-xq^{k}r^{l}}\quad \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty}\frac{A_{n}(s,t,q,r)}{(1-s)(1-qs)\cdots(1-q^{n}s)(1-t)(1-rt)\cdots(1-r^{n}t)}x^{n}=\sum_{i,j=0}^{\infty}s^{i}t^{j}\prod_{k=0}^{i}\prod_{l=0}^{j}\frac{1}{1-xq^{k}r^{l}}\quad \end{align} $$
for the quadrivariate polynomials
The Garsia–Gessel formula (1.4) specializes to both the Carlitz–Roselle–Scoville formula (1.1) for
![]() $(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
as well as Roselle’s formula for
$(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
as well as Roselle’s formula for
![]() $(\operatorname {\mathrm {maj}},\operatorname {\mathrm {imaj}})$
.
$(\operatorname {\mathrm {maj}},\operatorname {\mathrm {imaj}})$
.
The two-sided Eulerian polynomials have since received renewed attention due to a refined
![]() $\gamma $
-positivity conjecture of Gessel, which was later proven by Lin [Reference Lin16]. The joint statistic
$\gamma $
-positivity conjecture of Gessel, which was later proven by Lin [Reference Lin16]. The joint statistic
![]() $(\operatorname {\mathrm {des}},\operatorname {\mathrm {maj}},\operatorname {\mathrm {ides}},\operatorname {\mathrm {imaj}})$
and the sum
$(\operatorname {\mathrm {des}},\operatorname {\mathrm {maj}},\operatorname {\mathrm {ides}},\operatorname {\mathrm {imaj}})$
and the sum
![]() $\operatorname {\mathrm {des}}+\operatorname {\mathrm {ides}}$
have also been studied in the probability literature; see, for example, [Reference Brück and Röttger4, Reference Chatterjee and Diaconis6, Reference Féray7, Reference Vatutin27].
$\operatorname {\mathrm {des}}+\operatorname {\mathrm {ides}}$
have also been studied in the probability literature; see, for example, [Reference Brück and Röttger4, Reference Chatterjee and Diaconis6, Reference Féray7, Reference Vatutin27].
Throughout this paper, let us call a pair of the form
![]() $(\operatorname {\mathrm {st}},\operatorname {\mathrm {ist}})$
a two-sided permutation statistic and the distribution of this statistic over
$(\operatorname {\mathrm {st}},\operatorname {\mathrm {ist}})$
a two-sided permutation statistic and the distribution of this statistic over
![]() $\mathfrak {S}_{n}$
the two-sided distribution of
$\mathfrak {S}_{n}$
the two-sided distribution of
![]() $\operatorname {\mathrm {st}}$
. If we are taking
$\operatorname {\mathrm {st}}$
. If we are taking
![]() $\operatorname {\mathrm {st}}$
to be a pair
$\operatorname {\mathrm {st}}$
to be a pair
![]() $(\operatorname {\mathrm {st}}_{1},\operatorname {\mathrm {st}}_{2})$
such as
$(\operatorname {\mathrm {st}}_{1},\operatorname {\mathrm {st}}_{2})$
such as
![]() $(\operatorname {\mathrm {des}},\operatorname {\mathrm {maj}})$
, then we consider
$(\operatorname {\mathrm {des}},\operatorname {\mathrm {maj}})$
, then we consider
![]() $(\operatorname {\mathrm {st}}_{1},\operatorname {\mathrm {ist}}_{1},\operatorname {\mathrm {st}}_{2},\operatorname {\mathrm {ist}}_{2})$
a two-sided statistic as well.
$(\operatorname {\mathrm {st}}_{1},\operatorname {\mathrm {ist}}_{1},\operatorname {\mathrm {st}}_{2},\operatorname {\mathrm {ist}}_{2})$
a two-sided statistic as well.
1.1 Descent statistics
We use the notation
![]() $L\vDash n$
to indicate that L is a composition of n. Every permutation can be uniquely decomposed into a sequence of maximal increasing consecutive subsequences—or equivalently, maximal consecutive subsequences with no descents—which we call increasing runs. The descent composition of
$L\vDash n$
to indicate that L is a composition of n. Every permutation can be uniquely decomposed into a sequence of maximal increasing consecutive subsequences—or equivalently, maximal consecutive subsequences with no descents—which we call increasing runs. The descent composition of
![]() $\pi $
, denoted
$\pi $
, denoted
![]() $\operatorname {\mathrm {Comp}}(\pi )$
, is the composition whose parts are the lengths of the increasing runs of
$\operatorname {\mathrm {Comp}}(\pi )$
, is the composition whose parts are the lengths of the increasing runs of
![]() $\pi $
in the order that they appear. For example, the increasing runs of
$\pi $
in the order that they appear. For example, the increasing runs of
![]() $\pi =72485316$
are
$\pi =72485316$
are
![]() $7$
,
$7$
,
![]() $248$
,
$248$
,
![]() $5$
,
$5$
,
![]() $3$
, and
$3$
, and
![]() $16$
, so
$16$
, so
![]() $\operatorname {\mathrm {Comp}}(\pi )=(1,3,1,1,2)$
.
$\operatorname {\mathrm {Comp}}(\pi )=(1,3,1,1,2)$
.
A permutation statistic
![]() $\operatorname {\mathrm {st}}$
is called a descent statistic if
$\operatorname {\mathrm {st}}$
is called a descent statistic if
![]() $\operatorname {\mathrm {Comp}}(\pi )=\operatorname {\mathrm {Comp}}(\sigma )$
implies
$\operatorname {\mathrm {Comp}}(\pi )=\operatorname {\mathrm {Comp}}(\sigma )$
implies
![]() $\operatorname {\mathrm {st}}(\pi )=\operatorname {\mathrm {st}}(\sigma )$
—that is, if
$\operatorname {\mathrm {st}}(\pi )=\operatorname {\mathrm {st}}(\sigma )$
—that is, if
![]() $\operatorname {\mathrm {st}}$
depends only on the descent composition. Whenever
$\operatorname {\mathrm {st}}$
depends only on the descent composition. Whenever
![]() $\operatorname {\mathrm {st}}$
is a descent statistic, we may write
$\operatorname {\mathrm {st}}$
is a descent statistic, we may write
![]() $\operatorname {\mathrm {st}}(L)$
for the value of
$\operatorname {\mathrm {st}}(L)$
for the value of
![]() $\operatorname {\mathrm {st}}$
on any permutation with descent composition L. Both
$\operatorname {\mathrm {st}}$
on any permutation with descent composition L. Both
![]() $\operatorname {\mathrm {des}}$
and
$\operatorname {\mathrm {des}}$
and
![]() $\operatorname {\mathrm {maj}}$
are descent statistics, and in this paper, we will also consider the following descent statistics:
$\operatorname {\mathrm {maj}}$
are descent statistics, and in this paper, we will also consider the following descent statistics:
-
• The peak number
 $\operatorname {\mathrm {pk}}$
. We call i (where
$\operatorname {\mathrm {pk}}$
. We call i (where
 $2\leq i\leq n-1$
) a peak of
$2\leq i\leq n-1$
) a peak of
 $\pi \in \mathfrak {S}_{n}$
if
$\pi \in \mathfrak {S}_{n}$
if
 $\pi (i-1)<\pi (i)>\pi (i+1)$
. Then
$\pi (i-1)<\pi (i)>\pi (i+1)$
. Then
 $\operatorname {\mathrm {pk}}(\pi )$
is the number of peaks of
$\operatorname {\mathrm {pk}}(\pi )$
is the number of peaks of
 $\pi $
.
$\pi $
. -
• The left peak number
 $\operatorname {\mathrm {lpk}}$
. We call
$\operatorname {\mathrm {lpk}}$
. We call
 $i\in [n-1]$
a left peak of
$i\in [n-1]$
a left peak of
 $\pi \in \mathfrak {S}_{n}$
if either i is a peak of
$\pi \in \mathfrak {S}_{n}$
if either i is a peak of
 $\pi $
, or if
$\pi $
, or if
 $i=1$
and
$i=1$
and
 $\pi (1)>\pi (2)$
. Then
$\pi (1)>\pi (2)$
. Then
 $\operatorname {\mathrm {lpk}}(\pi )$
is the number of left peaks of
$\operatorname {\mathrm {lpk}}(\pi )$
is the number of left peaks of
 $\pi $
.
$\pi $
. -
• The number of biruns
 $\operatorname {\mathrm {br}}$
. A birun of a permutation
$\operatorname {\mathrm {br}}$
. A birun of a permutation
 $\pi $
is a maximal monotone consecutive subsequence. Then
$\pi $
is a maximal monotone consecutive subsequence. Then
 $\operatorname {\mathrm {br}}(\pi )$
is the number of biruns of
$\operatorname {\mathrm {br}}(\pi )$
is the number of biruns of
 $\pi $
.
$\pi $
. -
• The number of up-down runs
 $\operatorname {\mathrm {udr}}$
. An up-down run of
$\operatorname {\mathrm {udr}}$
. An up-down run of
 $\pi $
is either a birun of
$\pi $
is either a birun of
 $\pi $
, or
$\pi $
, or
 $\pi (1)$
if
$\pi (1)$
if
 $\pi (1)>\pi (2)$
. Then
$\pi (1)>\pi (2)$
. Then
 $\operatorname {\mathrm {udr}}(\pi )$
is the number of up-down runs of
$\operatorname {\mathrm {udr}}(\pi )$
is the number of up-down runs of
 $\pi $
.Footnote
2
$\pi $
.Footnote
2
For example, if
![]() $\pi =624731598$
, then the peaks of
$\pi =624731598$
, then the peaks of
![]() $\pi $
are
$\pi $
are
![]() $4$
and
$4$
and
![]() $8$
; the left peaks of
$8$
; the left peaks of
![]() $\pi $
are
$\pi $
are
![]() $1$
,
$1$
,
![]() $4$
and
$4$
and
![]() $8$
; the biruns of
$8$
; the biruns of
![]() $\pi $
are
$\pi $
are
![]() $62$
,
$62$
,
![]() $247$
,
$247$
,
![]() $731$
,
$731$
,
![]() $159$
and
$159$
and
![]() $98$
; and the up-down runs of
$98$
; and the up-down runs of
![]() $\pi $
are
$\pi $
are
![]() $6$
,
$6$
,
![]() $62$
,
$62$
,
![]() $247$
,
$247$
,
![]() $731$
,
$731$
,
![]() $159$
and
$159$
and
![]() $98$
. Therefore, we have
$98$
. Therefore, we have
![]() $\operatorname {\mathrm {pk}}(\pi )=2$
,
$\operatorname {\mathrm {pk}}(\pi )=2$
,
![]() $\operatorname {\mathrm {lpk}}(\pi )=3$
,
$\operatorname {\mathrm {lpk}}(\pi )=3$
,
![]() $\operatorname {\mathrm {br}}(\pi )=5$
and
$\operatorname {\mathrm {br}}(\pi )=5$
and
![]() $\operatorname {\mathrm {udr}}(\pi )=6$
. Other examples of descent statistics include the number of valleys, double ascents, double descents and alternating descents (see [Reference Zhuang29] for definitions).
$\operatorname {\mathrm {udr}}(\pi )=6$
. Other examples of descent statistics include the number of valleys, double ascents, double descents and alternating descents (see [Reference Zhuang29] for definitions).
In this paper, we give a general approach to the problem of finding the two-sided distribution of
![]() $\operatorname {\mathrm {st}}$
whenever
$\operatorname {\mathrm {st}}$
whenever
![]() $\operatorname {\mathrm {st}}$
is a descent statistic. In fact, our approach can be used to find distributions of mixed two-sided statistics: The joint distribution of
$\operatorname {\mathrm {st}}$
is a descent statistic. In fact, our approach can be used to find distributions of mixed two-sided statistics: The joint distribution of
![]() $\operatorname {\mathrm {st}}_{1}$
and
$\operatorname {\mathrm {st}}_{1}$
and
![]() $\operatorname {\mathrm {ist}}_{2}$
when
$\operatorname {\mathrm {ist}}_{2}$
when
![]() $\operatorname {\mathrm {st}}_{1}$
and
$\operatorname {\mathrm {st}}_{1}$
and
![]() $\operatorname {\mathrm {st}}_{2}$
are (possibly different) descent statistics. Our approach utilizes a theorem of Foulkes [Reference Foulkes9] at the intersection of permutation enumeration and symmetric function theory: The number of permutations
$\operatorname {\mathrm {st}}_{2}$
are (possibly different) descent statistics. Our approach utilizes a theorem of Foulkes [Reference Foulkes9] at the intersection of permutation enumeration and symmetric function theory: The number of permutations
![]() $\pi $
with prescribed descent composition L whose inverse
$\pi $
with prescribed descent composition L whose inverse
![]() $\pi ^{-1}$
has descent composition M is equal to the scalar product
$\pi ^{-1}$
has descent composition M is equal to the scalar product
![]() $\left \langle r_{L},r_{M}\right \rangle $
of two ribbon skew Schur functions (defined in Section 2.1). Thus, if f is a generating function for ribbon functions that keeps track of a descent statistic
$\left \langle r_{L},r_{M}\right \rangle $
of two ribbon skew Schur functions (defined in Section 2.1). Thus, if f is a generating function for ribbon functions that keeps track of a descent statistic
![]() $\operatorname {\mathrm {st}}_{1}$
and g is a similar generating function for a descent statistic
$\operatorname {\mathrm {st}}_{1}$
and g is a similar generating function for a descent statistic
![]() $\operatorname {\mathrm {st}}_{2}$
, then the scalar product
$\operatorname {\mathrm {st}}_{2}$
, then the scalar product
![]() $\left \langle f,g\right \rangle $
should give a generating function for
$\left \langle f,g\right \rangle $
should give a generating function for
![]() $(\operatorname {\mathrm {st}}_{1},\operatorname {\mathrm {ist}}_{2})$
.
$(\operatorname {\mathrm {st}}_{1},\operatorname {\mathrm {ist}}_{2})$
.
To illustrate this idea, let us sketch how our approach can be used to rederive the formula (1.1) of Carlitz, Roselle and Scoville for the two-sided Eulerian polynomials. We have
 $$\begin{align*}\frac{1}{1-tH(x)}=\frac{1}{1-t}+\sum_{n=1}^{\infty}\sum_{L\vDash n}\frac{t^{\operatorname{\mathrm{des}}(L)+1}}{(1-t)^{n+1}}r_{L}x^{n}, \end{align*}$$
$$\begin{align*}\frac{1}{1-tH(x)}=\frac{1}{1-t}+\sum_{n=1}^{\infty}\sum_{L\vDash n}\frac{t^{\operatorname{\mathrm{des}}(L)+1}}{(1-t)^{n+1}}r_{L}x^{n}, \end{align*}$$
where ![]() is the ordinary generating function for the complete symmetric functions
is the ordinary generating function for the complete symmetric functions
![]() $h_{n}$
. Then, upon applying Foulkes’s theorem, we get
$h_{n}$
. Then, upon applying Foulkes’s theorem, we get
 $$ \begin{align*} \left\langle \frac{1}{1-sH(x)},\frac{1}{1-tH(1)}\right\rangle & =\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\sum_{L,M\vDash n}\frac{s^{\operatorname{\mathrm{des}}(L)+1}t^{\operatorname{\mathrm{des}}(M)+1}}{(1-s)^{n+1}(1-t)^{n+1}}\left\langle r_{L},r_{M}\right\rangle x^{n}\\ & =\sum_{n=0}^{\infty}\frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}. \end{align*} $$
$$ \begin{align*} \left\langle \frac{1}{1-sH(x)},\frac{1}{1-tH(1)}\right\rangle & =\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\sum_{L,M\vDash n}\frac{s^{\operatorname{\mathrm{des}}(L)+1}t^{\operatorname{\mathrm{des}}(M)+1}}{(1-s)^{n+1}(1-t)^{n+1}}\left\langle r_{L},r_{M}\right\rangle x^{n}\\ & =\sum_{n=0}^{\infty}\frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}. \end{align*} $$
However, calculating the same scalar product but in a different way yields
 $$\begin{align*}\left\langle \frac{1}{1-sH(x)},\frac{1}{1-tH(1)}\right\rangle =\sum_{i,j=0}^{\infty}\frac{s^{i}t^{j}}{(1-x)^{ij}}, \end{align*}$$
$$\begin{align*}\left\langle \frac{1}{1-sH(x)},\frac{1}{1-tH(1)}\right\rangle =\sum_{i,j=0}^{\infty}\frac{s^{i}t^{j}}{(1-x)^{ij}}, \end{align*}$$
and equating these two expressions recovers (1.1).
In fact, a third way of calculating the same scalar product leads to a new formula expressing the two-sided Eulerian polynomials
![]() $A_{n}(s,t)$
in terms of the Eulerian polynomials
$A_{n}(s,t)$
in terms of the Eulerian polynomials
![]() $A_n(t)$
. Let us use the notations
$A_n(t)$
. Let us use the notations
![]() $\lambda \vdash n$
and
$\lambda \vdash n$
and
![]() $\left |\lambda \right |=n$
to indicate that
$\left |\lambda \right |=n$
to indicate that
![]() $\lambda $
is a partition of n, and let
$\lambda $
is a partition of n, and let
![]() $l(\lambda )$
denote the number of parts of
$l(\lambda )$
denote the number of parts of
![]() $\lambda $
. We write
$\lambda $
. We write
![]() $\lambda =(1^{m_{1}}2^{m_{2}}\cdots )$
to mean that
$\lambda =(1^{m_{1}}2^{m_{2}}\cdots )$
to mean that
![]() $\lambda $
has
$\lambda $
has
![]() $m_{1}$
parts of size
$m_{1}$
parts of size
![]() $1$
,
$1$
,
![]() $m_{2}$
parts of size 2 and so on, and define
$m_{2}$
parts of size 2 and so on, and define ![]() . Then it can be shown that
. Then it can be shown that
 $$\begin{align*}\left\langle \frac{1}{1-sH(x)},\frac{1}{1-tH(1)}\right\rangle =\sum_{\lambda}\frac{1}{z_{\lambda}}\frac{A_{l(\lambda)}(s)A_{l(\lambda)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}x^{\left|\lambda\right|}, \end{align*}$$
$$\begin{align*}\left\langle \frac{1}{1-sH(x)},\frac{1}{1-tH(1)}\right\rangle =\sum_{\lambda}\frac{1}{z_{\lambda}}\frac{A_{l(\lambda)}(s)A_{l(\lambda)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}x^{\left|\lambda\right|}, \end{align*}$$
leading to
 $$\begin{align*}A_{n}(s,t)=\sum_{\lambda\vdash n}\frac{1}{z_{\lambda}}((1-s)(1-t))^{n-l(\lambda)}A_{l(\lambda)}(s)A_{l(\lambda)}(t). \end{align*}$$
$$\begin{align*}A_{n}(s,t)=\sum_{\lambda\vdash n}\frac{1}{z_{\lambda}}((1-s)(1-t))^{n-l(\lambda)}A_{l(\lambda)}(s)A_{l(\lambda)}(t). \end{align*}$$
Collecting terms with
![]() $l(\lambda )=k$
then gives the formula
$l(\lambda )=k$
then gives the formula
 $$ \begin{align*} A_n(s,t) = \frac{1}{n!} \sum_{k=0}^n c(n,k) ((1-s)(1-t))^{n-k}A_k(s) A_k(t), \end{align*} $$
$$ \begin{align*} A_n(s,t) = \frac{1}{n!} \sum_{k=0}^n c(n,k) ((1-s)(1-t))^{n-k}A_k(s) A_k(t), \end{align*} $$
(see Theorem 3.9), where the
![]() $c(n,k)$
are the unsigned Stirling numbers of the first kind [Reference Stanley23, p. 26]. Perhaps surprisingly, many of the ‘two-sided polynomials’ that we study in this paper can be similarly expressed as a simple sum involving products of the univariate polynomials encoding the distributions of the individual statistics.
$c(n,k)$
are the unsigned Stirling numbers of the first kind [Reference Stanley23, p. 26]. Perhaps surprisingly, many of the ‘two-sided polynomials’ that we study in this paper can be similarly expressed as a simple sum involving products of the univariate polynomials encoding the distributions of the individual statistics.
Foulkes’s theorem was also used by Stanley [Reference Stanley21] in his study of alternating permutations; some of our results, notably Theorems 3.5 and 4.5, generalize results of his.
1.2 Outline
We organize this paper as follows. Section 2 is devoted to background material on symmetric functions. While we assume familiarity with basic symmetric function theory at the level of Stanley [Reference Stanley24, Chapter 7], we shall use this section to establish notation, recall some elementary facts that will be important for our work and to give an exposition of various topics and results needed to develop our approach to two-sided statistics; these include Foulkes’s theorem, plethysm and symmetric function generating functions associated with descent statistics.
Our main results are given in Sections 3–6. We begin in Section 3 by using our symmetric function approach to prove formulas for the two-sided statistic
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
, which we then specialize to formulas for
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
, which we then specialize to formulas for
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})$
,
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})$
,
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})$
and
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})$
and
![]() $(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
. We continue in Section 4 by deriving analogous formulas for
$(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
. We continue in Section 4 by deriving analogous formulas for
![]() $(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
and
$(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
and
![]() $(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
, and their specializations. Notably, our results for the two-sided distributions of
$(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
, and their specializations. Notably, our results for the two-sided distributions of
![]() $\operatorname {\mathrm {pk}}$
and of
$\operatorname {\mathrm {pk}}$
and of
![]() $\operatorname {\mathrm {lpk}}$
lead to a rederivation of Stanley’s [Reference Stanley21] generating function formula for ‘doubly alternating permutations’: alternating permutations whose inverses are alternating.
$\operatorname {\mathrm {lpk}}$
lead to a rederivation of Stanley’s [Reference Stanley21] generating function formula for ‘doubly alternating permutations’: alternating permutations whose inverses are alternating.
Section 5 considers (mixed) two-sided distributions involving the number of up-down runs, as well as a couple involving the number of biruns. In Section 6, we give a rederivation of the Garsia–Gessel formula for
![]() $(\operatorname {\mathrm {maj}},\operatorname {\mathrm {imaj}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
using our approach and give formulas for several mixed two-sided distributions involving the major index.
$(\operatorname {\mathrm {maj}},\operatorname {\mathrm {imaj}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
using our approach and give formulas for several mixed two-sided distributions involving the major index.
We conclude in Section 7 with several conjectures concerning real-rootedness and
![]() $\gamma $
-positivity of some of the polynomials appearing in our work.
$\gamma $
-positivity of some of the polynomials appearing in our work.
2 Symmetric functions background
Let
![]() $\Lambda $
denote the
$\Lambda $
denote the
![]() $\mathbb {Q}$
-algebra of symmetric functions in the variables
$\mathbb {Q}$
-algebra of symmetric functions in the variables
![]() $x_{1},x_{2},\dots $
. We recall the important bases for
$x_{1},x_{2},\dots $
. We recall the important bases for
![]() $\Lambda $
: the monomial symmetric functions
$\Lambda $
: the monomial symmetric functions
![]() $m_{\lambda }$
, the complete symmetric functions
$m_{\lambda }$
, the complete symmetric functions
![]() $h_{\lambda }$
, the elementary symmetric functions
$h_{\lambda }$
, the elementary symmetric functions
![]() $e_{\lambda }$
, the power sum symmetric functions
$e_{\lambda }$
, the power sum symmetric functions
![]() $p_{\lambda }$
and the Schur functions
$p_{\lambda }$
and the Schur functions
![]() $s_{\lambda }$
. As usual, we write
$s_{\lambda }$
. As usual, we write
![]() $h_{(n)}$
as
$h_{(n)}$
as
![]() $h_{n}$
,
$h_{n}$
,
![]() $e_{(n)}$
as
$e_{(n)}$
as
![]() $e_{n}$
and
$e_{n}$
and
![]() $p_{(n)}$
as
$p_{(n)}$
as
![]() $p_{n}$
.
$p_{n}$
.
We will also work with symmetric functions with coefficients involving additional variables such as s, t, y, z and
![]() $\alpha $
, as well as symmetric functions of unbounded degree like
$\alpha $
, as well as symmetric functions of unbounded degree like

We adopt the notation

2.1 The scalar product and Foulkes’s theorem
Let
![]() $\left \langle \cdot ,\cdot \right \rangle \colon \Lambda \times \Lambda \rightarrow \mathbb {Q}$
denote the usual scalar product on symmetric functions defined by
$\left \langle \cdot ,\cdot \right \rangle \colon \Lambda \times \Lambda \rightarrow \mathbb {Q}$
denote the usual scalar product on symmetric functions defined by
 $$\begin{align*}\left\langle m_{\lambda},h_{\mu}\right\rangle =\begin{cases} 1, & \text{if }\lambda=\mu\\ 0, & \text{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}\left\langle m_{\lambda},h_{\mu}\right\rangle =\begin{cases} 1, & \text{if }\lambda=\mu\\ 0, & \text{otherwise,} \end{cases} \end{align*}$$
for all partitions
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
and extending bilinearly, that is, by requiring that
$\mu $
and extending bilinearly, that is, by requiring that
![]() $\{m_{\lambda }\}$
and
$\{m_{\lambda }\}$
and
![]() $\{h_{\mu }\}$
be dual bases. Then we have
$\{h_{\mu }\}$
be dual bases. Then we have
 $$\begin{align*}\left\langle p_{\lambda},p_{\mu}\right\rangle =\begin{cases} z_{\lambda}, & \text{if }\lambda=\mu\\ 0, & \text{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}\left\langle p_{\lambda},p_{\mu}\right\rangle =\begin{cases} z_{\lambda}, & \text{if }\lambda=\mu\\ 0, & \text{otherwise,} \end{cases} \end{align*}$$
for all
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
[Reference Stanley23, Proposition 7.9.3]. We extend the scalar product in the obvious way to symmetric functions involving other variables as well as symmetric functions of unbounded degree. Note that the scalar product is not always defined for the latter; for example, we have
$\mu $
[Reference Stanley23, Proposition 7.9.3]. We extend the scalar product in the obvious way to symmetric functions involving other variables as well as symmetric functions of unbounded degree. Note that the scalar product is not always defined for the latter; for example, we have
![]() $\left \langle H(z),H\right \rangle =\sum _{n=0}^{\infty }z^{n}$
but
$\left \langle H(z),H\right \rangle =\sum _{n=0}^{\infty }z^{n}$
but
![]() $\left \langle H,H\right \rangle $
is undefined.
$\left \langle H,H\right \rangle $
is undefined.
Given a composition L, let
![]() $r_{L}$
denote the skew Schur function of ribbon shape L. That is, for
$r_{L}$
denote the skew Schur function of ribbon shape L. That is, for
![]() $L=(L_{1},L_{2},\dots ,L_{k})$
, we have
$L=(L_{1},L_{2},\dots ,L_{k})$
, we have
where the sum is over all
![]() $i_{1},\dots ,i_{n}$
satisfying
$i_{1},\dots ,i_{n}$
satisfying
 $$\begin{align*}\underset{L_{1}}{\underbrace{i_{1}\leq\cdots\leq i_{L_{1}}}}>\underset{L_{2}}{\underbrace{i_{L_{1}+1}\leq\cdots\leq i_{L_{1}+L_{2}}}}>\cdots>\underset{L_{k}}{\underbrace{i_{L_{1}+\cdots+L_{k-1}+1}\leq\cdots\leq i_{n}}.} \end{align*}$$
$$\begin{align*}\underset{L_{1}}{\underbrace{i_{1}\leq\cdots\leq i_{L_{1}}}}>\underset{L_{2}}{\underbrace{i_{L_{1}+1}\leq\cdots\leq i_{L_{1}+L_{2}}}}>\cdots>\underset{L_{k}}{\underbrace{i_{L_{1}+\cdots+L_{k-1}+1}\leq\cdots\leq i_{n}}.} \end{align*}$$
The next theorem, due to Foulkes [Reference Foulkes9] (see also [Reference Gessel12, Theorem 5] and [Reference Stanley24, Corollary 7.23.8]), will play a pivotal role in our approach to two-sided descent statistics.
Theorem 2.1. Let L and M be compositions. Then
![]() $\left \langle r_{L},r_{M}\right \rangle $
is the number of permutations
$\left \langle r_{L},r_{M}\right \rangle $
is the number of permutations
![]() $\pi $
with descent composition L such that
$\pi $
with descent composition L such that
![]() $\pi ^{-1}$
has descent composition M.
$\pi ^{-1}$
has descent composition M.
Foulkes’s theorem is a special case of a more general theorem of Gessel on quasisymmetric generating functions, which we briefly describe below. For a composition
![]() $L=(L_{1},L_{2},\dots ,L_{k})$
, let
$L=(L_{1},L_{2},\dots ,L_{k})$
, let ![]() , and recall that the fundamental quasisymmetric function
, and recall that the fundamental quasisymmetric function
![]() $F_{L}$
is defined by
$F_{L}$
is defined by

Moreover, given a set
![]() $\Pi $
of permutations, its quasisymmetric generating function
$\Pi $
of permutations, its quasisymmetric generating function
![]() $Q(\Pi )$
is defined by
$Q(\Pi )$
is defined by
The following is Corollary 4 of Gessel [Reference Gessel12].
Theorem 2.2. Suppose that
![]() $Q(\Pi )$
is a symmetric function. Then the number of permutations in
$Q(\Pi )$
is a symmetric function. Then the number of permutations in
![]() $\Pi $
with descent composition L is equal to
$\Pi $
with descent composition L is equal to
![]() $\left \langle r_{L},Q(\Pi )\right \rangle $
.
$\left \langle r_{L},Q(\Pi )\right \rangle $
.
Because
![]() $r_{M}$
is the quasisymmetric generating function for permutations whose inverse has descent composition M, Foulkes’s theorem follows from Theorem 2.2.
$r_{M}$
is the quasisymmetric generating function for permutations whose inverse has descent composition M, Foulkes’s theorem follows from Theorem 2.2.
Gessel and Reutenauer [Reference Gessel and Reutenauer13] showed that, for any partition
![]() $\lambda $
, the quasisymmetric generating function for permutations with cycle type
$\lambda $
, the quasisymmetric generating function for permutations with cycle type
![]() $\lambda $
is a symmetric function, and they used this fact along with Theorem 2.2 to study the joint distribution of
$\lambda $
is a symmetric function, and they used this fact along with Theorem 2.2 to study the joint distribution of
![]() $\operatorname {\mathrm {maj}}$
and
$\operatorname {\mathrm {maj}}$
and
![]() $\operatorname {\mathrm {des}}$
over sets of permutations with restricted cycle structure, including cyclic permutations, involutions and derangements. The present authors later studied the distributions of
$\operatorname {\mathrm {des}}$
over sets of permutations with restricted cycle structure, including cyclic permutations, involutions and derangements. The present authors later studied the distributions of
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {des}})$
,
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {des}})$
,
![]() $(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {des}})$
and
$(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {des}})$
and
![]() $\operatorname {\mathrm {udr}}$
over permutations with restricted cycle structure [Reference Gessel and Zhuang15]. Our current work is a continuation of this line of research but for inverse descent classes.
$\operatorname {\mathrm {udr}}$
over permutations with restricted cycle structure [Reference Gessel and Zhuang15]. Our current work is a continuation of this line of research but for inverse descent classes.
2.2 Plethysm
Let A be a
![]() $\mathbb {Q}$
-algebra of formal power series (possibly containing
$\mathbb {Q}$
-algebra of formal power series (possibly containing
![]() $\Lambda $
). Consider the operation
$\Lambda $
). Consider the operation
![]() $\Lambda \times A\rightarrow A$
, where the image of
$\Lambda \times A\rightarrow A$
, where the image of
![]() $(f,a)\in \Lambda \times A$
is denoted
$(f,a)\in \Lambda \times A$
is denoted
![]() $f[a]$
, defined by the following two properties:
$f[a]$
, defined by the following two properties:
-
1. For any
 $i\geq 1$
,
$i\geq 1$
,
 $p_{i}[a]$
is the result of replacing each variable in a with its ith power.
$p_{i}[a]$
is the result of replacing each variable in a with its ith power. -
2. For any fixed
 $a\in A$
, the map
$a\in A$
, the map
 $f\mapsto f[a]$
is a
$f\mapsto f[a]$
is a
 $\mathbb {Q}$
-algebra homomorphism from
$\mathbb {Q}$
-algebra homomorphism from
 $\Lambda $
to A.
$\Lambda $
to A.
In other words, we have
![]() $p_{i}[f(x_{1},x_{2},\dots )]=f(x_{1}^{i},x_{2}^{i},\dots )$
for any
$p_{i}[f(x_{1},x_{2},\dots )]=f(x_{1}^{i},x_{2}^{i},\dots )$
for any
![]() $f\in \Lambda $
. If f contains variables other than the
$f\in \Lambda $
. If f contains variables other than the
![]() $x_{i}$
, then they are all raised to the ith power as well. For example, if q and t are variables, then
$x_{i}$
, then they are all raised to the ith power as well. For example, if q and t are variables, then
![]() $p_{i}[q^{2}tp_{m}]=q^{2i}t^{i}p_{im}$
. The map
$p_{i}[q^{2}tp_{m}]=q^{2i}t^{i}p_{im}$
. The map
![]() $(f,a)\mapsto f[a]$
is called plethysm. As with the scalar product, we extend plethysm in the obvious way to symmetric functions of unbounded degree with coefficients involving other variables; whenever we do so, we implicitly assume that any infinite sums involved converge as formal power series so that the plethysms are defined.
$(f,a)\mapsto f[a]$
is called plethysm. As with the scalar product, we extend plethysm in the obvious way to symmetric functions of unbounded degree with coefficients involving other variables; whenever we do so, we implicitly assume that any infinite sums involved converge as formal power series so that the plethysms are defined.
We will need several technical lemmas involving plethysm in order to evaluate the scalar products needed in our work. All of these lemmas are from [Reference Gessel and Zhuang15] by the present authors (or are easy consequences of results from [Reference Gessel and Zhuang15]).
A monic term is any monomial with coefficient 1.
Lemma 2.3. Let
![]() $\mathsf {m}\in A$
be a monic term not containing any of the variables
$\mathsf {m}\in A$
be a monic term not containing any of the variables
![]() $x_{1},x_{2},\dots $
. Then the maps
$x_{1},x_{2},\dots $
. Then the maps
![]() $f\mapsto \left \langle f,H(\mathsf {m})\right \rangle $
and
$f\mapsto \left \langle f,H(\mathsf {m})\right \rangle $
and
![]() $f\mapsto \left \langle H(\mathsf {m}),f\right \rangle $
are
$f\mapsto \left \langle H(\mathsf {m}),f\right \rangle $
are
![]() $\mathbb {Q}$
-algebra homomorphisms on A.
$\mathbb {Q}$
-algebra homomorphisms on A.
Proof. By a special case of [Reference Gessel and Zhuang15, Lemma 2.5], we have
and the result follows from the fact that
![]() $f\mapsto f[\mathsf {m}]$
is a
$f\mapsto f[\mathsf {m}]$
is a
![]() $\mathbb {Q}$
-algebra homomorphism.
$\mathbb {Q}$
-algebra homomorphism.
Lemma 2.4. Let
![]() $y\in A$
be a variable and
$y\in A$
be a variable and
![]() $k\in \mathbb {Z}$
. Then the map
$k\in \mathbb {Z}$
. Then the map
![]() $f\mapsto \left \langle f,E(y)^{k}H^{k}\right \rangle $
is a
$f\mapsto \left \langle f,E(y)^{k}H^{k}\right \rangle $
is a
![]() $\mathbb {Q}$
-algebra homomorphism on A.
$\mathbb {Q}$
-algebra homomorphism on A.
Proof. Given
![]() $f\in A$
and a variable
$f\in A$
and a variable
![]() $\alpha \in A$
, it is known [Reference Gessel and Zhuang15, Lemma 3.2] that
$\alpha \in A$
, it is known [Reference Gessel and Zhuang15, Lemma 3.2] that
Then the map
![]() $f\mapsto \left \langle f,E(y)^{k}H^{k}\right \rangle $
is obtained by composing the map
$f\mapsto \left \langle f,E(y)^{k}H^{k}\right \rangle $
is obtained by composing the map
![]() $f\mapsto f[k(1-\alpha )]$
with evaluation at
$f\mapsto f[k(1-\alpha )]$
with evaluation at
![]() $\alpha =-y$
, both of which are
$\alpha =-y$
, both of which are
![]() $\mathbb {Q}$
-algebra homomorphisms.
$\mathbb {Q}$
-algebra homomorphisms.
Lemma 2.5. Let
![]() $\alpha ,\beta \in A$
be variables, and let k be an integer. Then:
$\alpha ,\beta \in A$
be variables, and let k be an integer. Then:
-
(a)
 $H(\beta )[k(1-\alpha )]=\left \langle H(\beta ),E(-\alpha )^{k}H^{k}\right \rangle =(1-{\alpha }\beta )^{k}/(1-\beta )^{k}$
.
$H(\beta )[k(1-\alpha )]=\left \langle H(\beta ),E(-\alpha )^{k}H^{k}\right \rangle =(1-{\alpha }\beta )^{k}/(1-\beta )^{k}$
. -
(b)
 $E(\beta )[k(1-\alpha )]=\left \langle E(\beta ),E(-\alpha )^{k}H^{k}\right \rangle =(1+\beta )^{k}/(1+\alpha \beta )^{k}$
.
$E(\beta )[k(1-\alpha )]=\left \langle E(\beta ),E(-\alpha )^{k}H^{k}\right \rangle =(1+\beta )^{k}/(1+\alpha \beta )^{k}$
.
Proof. Part (a) is a special case of Lemma 2.4 (d) of [Reference Gessel and Zhuang15]. Part (b) follows immediately from part (a) and the well-known identity
![]() $E(\beta )=(H(-\beta ))^{-1}$
.
$E(\beta )=(H(-\beta ))^{-1}$
.
The two lemmas below are Lemmas 3.5 and 6.6 of [Reference Gessel and Zhuang15], respectively.
Lemma 2.6. Let
![]() $f,g\in A$
, and let
$f,g\in A$
, and let
![]() $\mathsf {m}\in A$
be a monic term. Then
$\mathsf {m}\in A$
be a monic term. Then
![]() $\left \langle f[X+\mathsf {m}], g\right \rangle $
=
$\left \langle f[X+\mathsf {m}], g\right \rangle $
=
![]() $\left \langle f, H[\mathsf {m}X]g\right \rangle $
.
$\left \langle f, H[\mathsf {m}X]g\right \rangle $
.
Lemma 2.7. Let
![]() $\alpha \in A$
be a variable and
$\alpha \in A$
be a variable and
![]() $\mathsf {m}\in A$
a monic term. Then:
$\mathsf {m}\in A$
a monic term. Then:
-
(a)
 $H(\alpha )[X+\mathsf {m}]=H(\alpha )/(1-\alpha \mathsf {m})$
$H(\alpha )[X+\mathsf {m}]=H(\alpha )/(1-\alpha \mathsf {m})$
-
(b)
 $E(\alpha )[X+\mathsf {m}]=(1+\alpha \mathsf {m})E(\alpha )$
.
$E(\alpha )[X+\mathsf {m}]=(1+\alpha \mathsf {m})E(\alpha )$
.
2.3 Symmetric function generating functions for descent statistics
As mentioned in the introduction, we will need generating functions for the ribbon skew Schur functions
![]() $r_{L}$
which keep track of the descent statistics that we are studying. Such generating functions were produced in previous work by the present authors and are stated in the next lemma. Part (a) is essentially a commutative version of [Reference Gessel and Zhuang14, Lemma 17], whereas (b)–(d) are given in [Reference Gessel and Zhuang15, Lemma 2.8].
$r_{L}$
which keep track of the descent statistics that we are studying. Such generating functions were produced in previous work by the present authors and are stated in the next lemma. Part (a) is essentially a commutative version of [Reference Gessel and Zhuang14, Lemma 17], whereas (b)–(d) are given in [Reference Gessel and Zhuang15, Lemma 2.8].
Lemma 2.8. We have
 $$ \begin{align} \sum_{n=0}^{\infty}t^{n}\prod_{k=0}^{n}H(q^{k}x) & =\sum_{n=0}^{\infty}\frac{\sum_{L\vDash n}q^{\operatorname{\mathrm{maj}}(L)}t^{\operatorname{\mathrm{des}}(L)}r_{L}}{(1-t)(1-qt)\cdots(1-q^{n}t)}x^{n}, \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty}t^{n}\prod_{k=0}^{n}H(q^{k}x) & =\sum_{n=0}^{\infty}\frac{\sum_{L\vDash n}q^{\operatorname{\mathrm{maj}}(L)}t^{\operatorname{\mathrm{des}}(L)}r_{L}}{(1-t)(1-qt)\cdots(1-q^{n}t)}x^{n}, \end{align} $$
 $$ \begin{align} \frac{1}{1-tE(yx)H(x)}&=\frac{1}{1-t}+\\ &\quad\frac{1}{1+y}\sum_{n=1}^{\infty}\sum_{L\vDash n}\left(\frac{1+yt}{1-t}\right)^{n+1}\left(\frac{(1+y)^{2}t}{(y+t)(1+yt)}\right)^{\operatorname{\mathrm{pk}}(L)+1}\left(\frac{y+t}{1+yt}\right)^{\operatorname{\mathrm{des}}(L)+1}r_{L}x^{n},\nonumber \end{align} $$
$$ \begin{align} \frac{1}{1-tE(yx)H(x)}&=\frac{1}{1-t}+\\ &\quad\frac{1}{1+y}\sum_{n=1}^{\infty}\sum_{L\vDash n}\left(\frac{1+yt}{1-t}\right)^{n+1}\left(\frac{(1+y)^{2}t}{(y+t)(1+yt)}\right)^{\operatorname{\mathrm{pk}}(L)+1}\left(\frac{y+t}{1+yt}\right)^{\operatorname{\mathrm{des}}(L)+1}r_{L}x^{n},\nonumber \end{align} $$
 $$ \begin{align} \frac{H(x)}{1-tE(yx)H(x)}=\frac{1}{1-t}+ \sum_{n=1}^{\infty}\sum_{L\vDash n}\frac{(1+yt)^{n}}{(1-t)^{n+1}}\left(\frac{(1+y)^{2}t}{(y+t)(1+yt)}\right)^{\operatorname{\mathrm{lpk}}(L)}\left(\frac{y+t}{1+yt}\right)^{\operatorname{\mathrm{des}}(L)}r_{L}x^{n}, \end{align} $$
$$ \begin{align} \frac{H(x)}{1-tE(yx)H(x)}=\frac{1}{1-t}+ \sum_{n=1}^{\infty}\sum_{L\vDash n}\frac{(1+yt)^{n}}{(1-t)^{n+1}}\left(\frac{(1+y)^{2}t}{(y+t)(1+yt)}\right)^{\operatorname{\mathrm{lpk}}(L)}\left(\frac{y+t}{1+yt}\right)^{\operatorname{\mathrm{des}}(L)}r_{L}x^{n}, \end{align} $$
and
 $$ \begin{align} \frac{1+tH(x)}{1-t^{2}E(x)H(x)} & =\frac{1}{1-t}+\frac{1}{2(1-t)^{2}}\sum_{n=1}^{\infty}\sum_{L\vDash n}\frac{(1+t^{2})^{n}}{(1-t^{2})^{n-1}}\left(\frac{2t}{1+t^{2}}\right)^{\operatorname{\mathrm{udr}}(L)}r_{L}x^{n}. \end{align} $$
$$ \begin{align} \frac{1+tH(x)}{1-t^{2}E(x)H(x)} & =\frac{1}{1-t}+\frac{1}{2(1-t)^{2}}\sum_{n=1}^{\infty}\sum_{L\vDash n}\frac{(1+t^{2})^{n}}{(1-t^{2})^{n-1}}\left(\frac{2t}{1+t^{2}}\right)^{\operatorname{\mathrm{udr}}(L)}r_{L}x^{n}. \end{align} $$
Some of these generating functions have nice power sum expansions that are expressible in terms of Eulerian polynomials and type B Eulerian polynomials. The nth type B Eulerian polynomial
![]() $B_{n}(t)$
encodes the distribution of the type B descent number over the nth hyperoctahedral group (see [Reference Zhuang30, Section 2.3] for definitions) but can also be defined by the formula
$B_{n}(t)$
encodes the distribution of the type B descent number over the nth hyperoctahedral group (see [Reference Zhuang30, Section 2.3] for definitions) but can also be defined by the formula
 $$\begin{align*}\frac{B_{n}(t)}{(1-t)^{n+1}}=\sum_{k=0}^{\infty}(2k+1)^{n}t^{k} \end{align*}$$
$$\begin{align*}\frac{B_{n}(t)}{(1-t)^{n+1}}=\sum_{k=0}^{\infty}(2k+1)^{n}t^{k} \end{align*}$$
analogous to Equation (1.3). Recall that
![]() $l(\lambda )$
is the number of parts of the partition
$l(\lambda )$
is the number of parts of the partition
![]() $\lambda $
. We also define
$\lambda $
. We also define
![]() $o(\lambda )$
to be the number of odd parts of
$o(\lambda )$
to be the number of odd parts of
![]() $\lambda $
, and use the notation
$\lambda $
, and use the notation
![]() $\sum _{\lambda \text { odd}}$
for a sum over partitions in which every part is odd.
$\sum _{\lambda \text { odd}}$
for a sum over partitions in which every part is odd.
The next lemma is [Reference Gessel and Zhuang15, Lemma 2.9].
Lemma 2.9. We have
 $$ \begin{align} \frac{1}{1-tE(yx)H(x)}=\sum_{\lambda}\frac{p_{\lambda}}{z_{\lambda}}\frac{A_{l(\lambda)}(t)}{(1-t)^{l(\lambda)+1}}x^{\left|\lambda\right|}\prod_{k=1}^{l(\lambda)}(1-(-y)^{\lambda_{k}}) \end{align} $$
$$ \begin{align} \frac{1}{1-tE(yx)H(x)}=\sum_{\lambda}\frac{p_{\lambda}}{z_{\lambda}}\frac{A_{l(\lambda)}(t)}{(1-t)^{l(\lambda)+1}}x^{\left|\lambda\right|}\prod_{k=1}^{l(\lambda)}(1-(-y)^{\lambda_{k}}) \end{align} $$
where
![]() $\lambda _{1},\lambda _{2},\dots ,\lambda _{l(\lambda )}$
are the parts of
$\lambda _{1},\lambda _{2},\dots ,\lambda _{l(\lambda )}$
are the parts of
![]() $\lambda $
,
$\lambda $
,
 $$ \begin{align} \frac{H(x)}{1-tE(x)H(x)}=\sum_{\lambda}\frac{p_{\lambda}}{z_{\lambda}}\frac{B_{o(\lambda)}(t)}{(1-t)^{o(\lambda)+1}}x^{\left|\lambda\right|}, \end{align} $$
$$ \begin{align} \frac{H(x)}{1-tE(x)H(x)}=\sum_{\lambda}\frac{p_{\lambda}}{z_{\lambda}}\frac{B_{o(\lambda)}(t)}{(1-t)^{o(\lambda)+1}}x^{\left|\lambda\right|}, \end{align} $$
and
 $$ \begin{align} \frac{1+tH(x)}{1-tE(x)H(x)}=\sum_{\lambda\:\mathrm{odd}}\frac{p_{\lambda}}{z_{\lambda}}2^{l(\lambda)}\frac{A_{l(\lambda)}(t^{2})}{(1-t^{2})^{l(\lambda)+1}}x^{\left|\lambda\right|}+t\sum_{\lambda}\frac{p_{\lambda}}{z_{\lambda}}\frac{B_{o(\lambda)}(t^{2})}{(1-t^{2})^{o(\lambda)+1}}x^{\left|\lambda\right|}. \end{align} $$
$$ \begin{align} \frac{1+tH(x)}{1-tE(x)H(x)}=\sum_{\lambda\:\mathrm{odd}}\frac{p_{\lambda}}{z_{\lambda}}2^{l(\lambda)}\frac{A_{l(\lambda)}(t^{2})}{(1-t^{2})^{l(\lambda)+1}}x^{\left|\lambda\right|}+t\sum_{\lambda}\frac{p_{\lambda}}{z_{\lambda}}\frac{B_{o(\lambda)}(t^{2})}{(1-t^{2})^{o(\lambda)+1}}x^{\left|\lambda\right|}. \end{align} $$
2.4 Sums involving
 $z_\lambda $
and Stanley’s formula for doubly alternating permutations
$z_\lambda $
and Stanley’s formula for doubly alternating permutations
The remainder of this section is not strictly about symmetric functions but relates to the constants
![]() $z_\lambda $
which appear in symmetric function theory, and a connection to an enumeration formula of Stanley obtained via symmetric function techniques.
$z_\lambda $
which appear in symmetric function theory, and a connection to an enumeration formula of Stanley obtained via symmetric function techniques.
To derive some of our formulas later on, we will need to evaluate several sums like
 $$ \begin{align} \sum_{\substack{\lambda\vdash n\\unicode{x0142}(\lambda) =k}}\frac{1}{z_\lambda}. \end{align} $$
$$ \begin{align} \sum_{\substack{\lambda\vdash n\\unicode{x0142}(\lambda) =k}}\frac{1}{z_\lambda}. \end{align} $$
The key to evaluating these sums is the well-known fact that
![]() $n!/z_\lambda $
is the number of permutations in
$n!/z_\lambda $
is the number of permutations in
![]() $\mathfrak {S}_n$
of cycle type
$\mathfrak {S}_n$
of cycle type
![]() $\lambda $
; see, for example, [Reference Stanley23, Proposition 1.3.2] and [Reference Stanley24, pp. 298–299]. Thus, Equation (2.1) is equal to
$\lambda $
; see, for example, [Reference Stanley23, Proposition 1.3.2] and [Reference Stanley24, pp. 298–299]. Thus, Equation (2.1) is equal to
![]() $c(n,k)/n!$
, where as before,
$c(n,k)/n!$
, where as before,
![]() $c(n,k)$
is the unsigned Stirling number of the first kind, which counts permutations in
$c(n,k)$
is the unsigned Stirling number of the first kind, which counts permutations in
![]() $\mathfrak {S}_n$
with k cycles.
$\mathfrak {S}_n$
with k cycles.
Now, let
![]() $d(n,k)$
be the number of permutations in
$d(n,k)$
be the number of permutations in
![]() $\mathfrak {S}_n$
with k cycles, all of odd length; let
$\mathfrak {S}_n$
with k cycles, all of odd length; let
![]() $e(n,k)$
be the number of permutations in
$e(n,k)$
be the number of permutations in
![]() $\mathfrak {S}_n$
with k odd cycles (and any number of even cycles); and let
$\mathfrak {S}_n$
with k odd cycles (and any number of even cycles); and let
![]() $f(n,k,m)$
be the number of permutations in
$f(n,k,m)$
be the number of permutations in
![]() $\mathfrak {S}_n$
with k odd cycles and m cycles in total. Note that
$\mathfrak {S}_n$
with k odd cycles and m cycles in total. Note that
![]() $d(n,k)$
,
$d(n,k)$
,
![]() $e(n,k)$
and
$e(n,k)$
and
![]() $f(n,k,m)$
are 0 if
$f(n,k,m)$
are 0 if
![]() $n-k$
is odd. Then by the same reasoning as above, we have the additional sum evaluations in the next lemma.
$n-k$
is odd. Then by the same reasoning as above, we have the additional sum evaluations in the next lemma.
Lemma 2.10. We have
 $$ \begin{align} &\sum_{\substack{\lambda\vdash n\\unicode{x0142}(\lambda) =k}}\frac{1}{z_\lambda}=\frac{c(n,k)}{n!}, \end{align} $$
$$ \begin{align} &\sum_{\substack{\lambda\vdash n\\unicode{x0142}(\lambda) =k}}\frac{1}{z_\lambda}=\frac{c(n,k)}{n!}, \end{align} $$
 $$ \begin{align} &\sum_{\substack{\lambda\vdash n\\ \mathrm{odd}\\ l(\lambda)=k }} \frac{1}{z_{\lambda}}= \frac{d(n,k)}{n!}, \end{align} $$
$$ \begin{align} &\sum_{\substack{\lambda\vdash n\\ \mathrm{odd}\\ l(\lambda)=k }} \frac{1}{z_{\lambda}}= \frac{d(n,k)}{n!}, \end{align} $$
 $$ \begin{align} &\sum_{\substack{\lambda\vdash n\\ o(\lambda)=k }} \frac{1}{z_{\lambda}}=\frac{e(n,k)}{n!}, \end{align} $$
$$ \begin{align} &\sum_{\substack{\lambda\vdash n\\ o(\lambda)=k }} \frac{1}{z_{\lambda}}=\frac{e(n,k)}{n!}, \end{align} $$
and
 $$ \begin{align} &\sum_{\substack{\lambda\vdash n\\ o(\lambda)=k\\ l(\lambda)=m }} \frac{1}{z_{\lambda}}=\frac{f(n,k,m)}{n!}. \end{align} $$
$$ \begin{align} &\sum_{\substack{\lambda\vdash n\\ o(\lambda)=k\\ l(\lambda)=m }} \frac{1}{z_{\lambda}}=\frac{f(n,k,m)}{n!}. \end{align} $$
The numbers
![]() $c(n,k)$
,
$c(n,k)$
,
![]() $d(n,k)$
,
$d(n,k)$
,
![]() $e(n,k)$
and
$e(n,k)$
and
![]() $f(n,k,m)$
all have simple exponential generating functions. Let
$f(n,k,m)$
all have simple exponential generating functions. Let

Proposition 2.11. We have
 $$ \begin{align} &\sum_{n=0}^\infty \sum_{k=0}^n c(n,k) v^k \frac{u^n}{n!} = e^{-v\log(1-u)}=\frac{1}{(1-u)^v}, \end{align} $$
$$ \begin{align} &\sum_{n=0}^\infty \sum_{k=0}^n c(n,k) v^k \frac{u^n}{n!} = e^{-v\log(1-u)}=\frac{1}{(1-u)^v}, \end{align} $$
 $$ \begin{align} &\sum_{n=0}^\infty \sum_{k=0}^n d(n,k) v^k \frac{u^n}{n!} = e^{vL(u)}=\left(\frac{1+u}{1-u}\right)^{v/2}, \end{align} $$
$$ \begin{align} &\sum_{n=0}^\infty \sum_{k=0}^n d(n,k) v^k \frac{u^n}{n!} = e^{vL(u)}=\left(\frac{1+u}{1-u}\right)^{v/2}, \end{align} $$
 $$ \begin{align} &\sum_{n=0}^\infty\sum_{k=0}^n e(n,k) v^k \frac{u^n}{n!} =\frac{e^{vL(u)}}{\sqrt{1-u^2}}=\frac{(1+u)^{(v-1)/2}}{(1-u)^{(v+1)/2}}, \end{align} $$
$$ \begin{align} &\sum_{n=0}^\infty\sum_{k=0}^n e(n,k) v^k \frac{u^n}{n!} =\frac{e^{vL(u)}}{\sqrt{1-u^2}}=\frac{(1+u)^{(v-1)/2}}{(1-u)^{(v+1)/2}}, \end{align} $$
and
 $$ \begin{align} &\sum_{n=0}^\infty\sum_{k,m=0}^n f(n,k,m) v^k w^m \frac{u^n}{n!} =\frac{e^{vwL(u)}}{(1-u^2)^{w/2}} =\frac{(1+u)^{(v-1)w/2}}{(1-u)^{(v+1)w/2}}. \end{align} $$
$$ \begin{align} &\sum_{n=0}^\infty\sum_{k,m=0}^n f(n,k,m) v^k w^m \frac{u^n}{n!} =\frac{e^{vwL(u)}}{(1-u^2)^{w/2}} =\frac{(1+u)^{(v-1)w/2}}{(1-u)^{(v+1)w/2}}. \end{align} $$
Proof. We prove only (c); the proofs of the other formulas are similar (and (a) is well known). For (c) we want to count permutations in which odd cycles are weighted v and even cycles are weighted 1. So by the exponential formula for permutations [Reference Stanley24, Corollary 5.1.9], we have
 $$ \begin{align*} \sum_{n=0}^\infty \sum_{k=0}^n e(n,k) \frac{u^n}{n!} v^k &=\exp\biggl(v\sum_{m=1}^\infty \frac{u^{2m-1}}{2m-1} +\sum_{m=1}^\infty \frac{u^{2m}}{2m}\biggr)\\ &=\exp\Bigl(\frac{v}{2}\bigl(-\log(1-u)+\log(1+u)\bigr)+\frac{1}{2}\bigl(-\log(1-u) -\log(1+u)\bigr)\Bigr)\\ &=\frac{(1+u)^{(v-1)/2}}{(1-u)^{(v+1)/2}}.\\[-47pt] \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty \sum_{k=0}^n e(n,k) \frac{u^n}{n!} v^k &=\exp\biggl(v\sum_{m=1}^\infty \frac{u^{2m-1}}{2m-1} +\sum_{m=1}^\infty \frac{u^{2m}}{2m}\biggr)\\ &=\exp\Bigl(\frac{v}{2}\bigl(-\log(1-u)+\log(1+u)\bigr)+\frac{1}{2}\bigl(-\log(1-u) -\log(1+u)\bigr)\Bigr)\\ &=\frac{(1+u)^{(v-1)/2}}{(1-u)^{(v+1)/2}}.\\[-47pt] \end{align*} $$
A permutation
![]() $\pi $
is called alternating if
$\pi $
is called alternating if
![]() $\pi (1)>\pi (2)<\pi (3)>\pi (4)<\cdots $
, and it is well known that alternating permutations in
$\pi (1)>\pi (2)<\pi (3)>\pi (4)<\cdots $
, and it is well known that alternating permutations in
![]() $\mathfrak {S}_n$
are counted by the nth Euler number
$\mathfrak {S}_n$
are counted by the nth Euler number
![]() $E_{n}$
, whose exponential generating function is
$E_{n}$
, whose exponential generating function is
![]() $\sum _{n=0}^\infty E_n x^n/n! = \sec x + \tan x$
. The series
$\sum _{n=0}^\infty E_n x^n/n! = \sec x + \tan x$
. The series
![]() $L(u)$
defined above makes an appearance in Stanley’s work on doubly alternating permutations: alternating permutations whose inverses are alternating. Let
$L(u)$
defined above makes an appearance in Stanley’s work on doubly alternating permutations: alternating permutations whose inverses are alternating. Let
![]() $\tilde E_n$
denote the number of doubly alternating permutations in
$\tilde E_n$
denote the number of doubly alternating permutations in
![]() $\mathfrak {S}_n$
. Stanley showed that the ordinary generating function for doubly alternating permutations is
$\mathfrak {S}_n$
. Stanley showed that the ordinary generating function for doubly alternating permutations is
 $$ \begin{align} \sum_{n=0}^{\infty} \tilde E_n u^n = \frac{1}{\sqrt{1-u^{2}}}\sum_{r=0}^{\infty}E_{2r}^{2}\frac{L(u)^{2r}}{(2r)!}+\sum_{r=0}^{\infty}E_{2r+1}^{2}\frac{L(u)^{2r+1}}{(2r+1)!} \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty} \tilde E_n u^n = \frac{1}{\sqrt{1-u^{2}}}\sum_{r=0}^{\infty}E_{2r}^{2}\frac{L(u)^{2r}}{(2r)!}+\sum_{r=0}^{\infty}E_{2r+1}^{2}\frac{L(u)^{2r+1}}{(2r+1)!} \end{align} $$
[Reference Stanley21, Theorem 3.1]. Stanley’s proof of Equation (2.2) uses Foulkes’s theorem, but Equation (2.2) can also be recovered from our results, as shall be demonstrated at the end of Sections 3.2 and 4.3.
We note that Stanley’s formula (2.2) can be expressed in terms of the numbers
![]() $d(n,k)$
and
$d(n,k)$
and
![]() $e(n,k)$
. By Proposition 2.11, we have
$e(n,k)$
. By Proposition 2.11, we have
 $$ \begin{gather*} \frac{1}{\sqrt{1-u^2}}\frac{L(u)^{2r}}{(2r)!} = \sum_{n=0}^\infty e(n, 2r) \frac{u^n}{n!} \qquad\text{and}\qquad \frac{L(u)^{2r+1}}{(2r+1)!} = \sum_{d=0}^\infty d(n, 2r+1) \frac{u^n}{n!}. \end{gather*} $$
$$ \begin{gather*} \frac{1}{\sqrt{1-u^2}}\frac{L(u)^{2r}}{(2r)!} = \sum_{n=0}^\infty e(n, 2r) \frac{u^n}{n!} \qquad\text{and}\qquad \frac{L(u)^{2r+1}}{(2r+1)!} = \sum_{d=0}^\infty d(n, 2r+1) \frac{u^n}{n!}. \end{gather*} $$
Thus, Equation (2.2) is equivalent to the statement that
 $$ \begin{align*} \tilde E_n = \begin{cases} \displaystyle\frac{1}{n!}\sum_r e(n,2r)E_{2r}^2 = \frac{1}{n!}\sum_{k=0}^n e(n,k) E_{k}^2,& \text{ if }n\text{ is even,}\\ \displaystyle\frac{1}{n!}\sum_r d(n, 2r+1)E_{2r+1}^2 = \frac{1}{n!}\sum_{k=0}^n d(n,k) E_{k}^2,& \text{ if }n\text{ is odd.} \end{cases} \end{align*} $$
$$ \begin{align*} \tilde E_n = \begin{cases} \displaystyle\frac{1}{n!}\sum_r e(n,2r)E_{2r}^2 = \frac{1}{n!}\sum_{k=0}^n e(n,k) E_{k}^2,& \text{ if }n\text{ is even,}\\ \displaystyle\frac{1}{n!}\sum_r d(n, 2r+1)E_{2r+1}^2 = \frac{1}{n!}\sum_{k=0}^n d(n,k) E_{k}^2,& \text{ if }n\text{ is odd.} \end{cases} \end{align*} $$
3 Two-sided peak and descent statistics
We are now ready to proceed to the main body of our work. Our first task will be to derive formulas for the two-sided distribution of
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {des}})$
—that is, the joint distribution of
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {des}})$
—that is, the joint distribution of
![]() $\operatorname {\mathrm {pk}}$
,
$\operatorname {\mathrm {pk}}$
,
![]() $\operatorname {\mathrm {ipk}}$
,
$\operatorname {\mathrm {ipk}}$
,
![]() $\operatorname {\mathrm {des}}$
and
$\operatorname {\mathrm {des}}$
and
![]() $\operatorname {\mathrm {ides}}$
over
$\operatorname {\mathrm {ides}}$
over
![]() $\mathfrak {S}_{n}$
—and then we shall specialize our results to the (mixed) two-sided statistics
$\mathfrak {S}_{n}$
—and then we shall specialize our results to the (mixed) two-sided statistics
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})$
,
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})$
,
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})$
and
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})$
and
![]() $(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
.
$(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
.
3.1 Peaks, descents and their inverses
Define the polynomials
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})}(y,z,s,t)$
by
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})}(y,z,s,t)$
by
which encodes the desired two-sided distribution.
Theorem 3.1. We have
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{\left(\frac{(1+ys)(1+zt)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1+y)(1+z)}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{(1+yx)(1+zx)}{(1-yzx)(1-x)}\right)^{ij}s^{i}t^{j}\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{\left(\frac{(1+ys)(1+zt)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1+y)(1+z)}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{(1+yx)(1+zx)}{(1-yzx)(1-x)}\right)^{ij}s^{i}t^{j}\nonumber \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} &\frac{\left(\frac{(1+ys)(1+zt)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1+y)(1+z)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{\lambda\vdash n}\frac{\prod_{i=1}^{l(\lambda)}(1-(-y)^{\lambda_{i}})(1-(-z)^{\lambda_{i}})}{z_{\lambda}}\frac{A_{l(\lambda)}(s)A_{l(\lambda)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}.\nonumber \end{align} $$
$$ \begin{align} &\frac{\left(\frac{(1+ys)(1+zt)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1+y)(1+z)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{\lambda\vdash n}\frac{\prod_{i=1}^{l(\lambda)}(1-(-y)^{\lambda_{i}})(1-(-z)^{\lambda_{i}})}{z_{\lambda}}\frac{A_{l(\lambda)}(s)A_{l(\lambda)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}.\nonumber \end{align} $$
Proof. To prove this theorem, we shall compute
![]() $\left \langle (1-sE(yx)H(x))^{-1},(1-tE(z)H)^{-1}\right \rangle $
in three different ways. First, from Lemma 2.8 (b) we have
$\left \langle (1-sE(yx)H(x))^{-1},(1-tE(z)H)^{-1}\right \rangle $
in three different ways. First, from Lemma 2.8 (b) we have
 $$ \begin{align} & \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \notag \\ & \qquad\qquad\qquad\qquad=\frac{1}{(1-s)(1-t)}+\sum_{m,n=1}^{\infty}\frac{\left(\frac{1+ys}{1-s}\right)^{m+1}\left(\frac{1+zt}{1-t}\right)^{n+1}\sum_{L\vDash m,\,M\vDash n}N_{L,M}\left\langle r_{L},r_{M}\right\rangle }{(1+y)(1+z)}x^{m}, \end{align} $$
$$ \begin{align} & \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \notag \\ & \qquad\qquad\qquad\qquad=\frac{1}{(1-s)(1-t)}+\sum_{m,n=1}^{\infty}\frac{\left(\frac{1+ys}{1-s}\right)^{m+1}\left(\frac{1+zt}{1-t}\right)^{n+1}\sum_{L\vDash m,\,M\vDash n}N_{L,M}\left\langle r_{L},r_{M}\right\rangle }{(1+y)(1+z)}x^{m}, \end{align} $$
where

Upon applying Foulkes’s theorem (Theorem 2.1), Equation (3.1) simplifies to
 $$ \begin{align} & \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \nonumber \\ & \quad=\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{\left(\frac{(1+ys)(1+zt)}{(1-s)(1-t)}\right)^{n+1}\sum_{\pi\in\mathfrak{S}_{n}}N_{\operatorname{\mathrm{Comp}}(\pi),\operatorname{\mathrm{Comp}}(\pi^{-1})}}{(1+y)(1+z)}x^{n}\nonumber \\ & \quad=\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{\left(\frac{(1+ys)(1+zt)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1+y)(1+z)}x^{n}. \end{align} $$
$$ \begin{align} & \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \nonumber \\ & \quad=\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{\left(\frac{(1+ys)(1+zt)}{(1-s)(1-t)}\right)^{n+1}\sum_{\pi\in\mathfrak{S}_{n}}N_{\operatorname{\mathrm{Comp}}(\pi),\operatorname{\mathrm{Comp}}(\pi^{-1})}}{(1+y)(1+z)}x^{n}\nonumber \\ & \quad=\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{\left(\frac{(1+ys)(1+zt)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1+y)(1+z)}x^{n}. \end{align} $$
Second, we have
 $$ \begin{align} \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle & =\left\langle \sum_{i=0}^{\infty}E(yx)^{i}H(x)^{i}s^{i},\sum_{j=0}^{\infty}E(z)^{j}H^{j}t^{j}\right\rangle \nonumber \\ & =\sum_{i,j=0}^{\infty}\left\langle E(yx)^{i}H(x)^{i},E(z)^{j}H^{j}\right\rangle s^{i}t^{j}\nonumber \\ & =\sum_{i,j=0}^{\infty}\left\langle E(yx),E(z)^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E(z)^{j}H^{j}\right\rangle ^{i}s^{i}t^{j}\nonumber \\ & =\sum_{i,j=0}^{\infty}\frac{(1+yx)^{ij}}{(1-yzx)^{ij}}\frac{(1+zx)^{ij}}{(1-x)^{ij}}s^{i}t^{j}, \end{align} $$
$$ \begin{align} \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle & =\left\langle \sum_{i=0}^{\infty}E(yx)^{i}H(x)^{i}s^{i},\sum_{j=0}^{\infty}E(z)^{j}H^{j}t^{j}\right\rangle \nonumber \\ & =\sum_{i,j=0}^{\infty}\left\langle E(yx)^{i}H(x)^{i},E(z)^{j}H^{j}\right\rangle s^{i}t^{j}\nonumber \\ & =\sum_{i,j=0}^{\infty}\left\langle E(yx),E(z)^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E(z)^{j}H^{j}\right\rangle ^{i}s^{i}t^{j}\nonumber \\ & =\sum_{i,j=0}^{\infty}\frac{(1+yx)^{ij}}{(1-yzx)^{ij}}\frac{(1+zx)^{ij}}{(1-x)^{ij}}s^{i}t^{j}, \end{align} $$
where the last two steps are obtained using Lemmas 2.4 and 2.5, respectively. Finally, from Lemma 2.9 (a) we have
 $$ \begin{align} & \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \nonumber \\ & \qquad\qquad=\sum_{\lambda,\mu}\frac{\prod_{i=1}^{l(\lambda)}(1-(-y)^{\lambda_{i}})\prod_{j=1}^{l(\mu)}(1-(-z)^{\mu_{i}})}{z_{\lambda}z_{\mu}}\frac{A_{l(\lambda)}(s)A_{l(\mu)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\mu)+1}}\left\langle p_{\lambda},p_{\mu}\right\rangle x^{\left|\lambda\right|}\nonumber \\ & \qquad\qquad=\sum_{\lambda}\frac{\prod_{i=1}^{l(\lambda)}(1-(-y)^{\lambda_{i}})(1-(-z)^{\lambda_{i}})}{z_{\lambda}}\frac{A_{l(\lambda)}(s)A_{l(\lambda)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}x^{\left|\lambda\right|}. \end{align} $$
$$ \begin{align} & \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \nonumber \\ & \qquad\qquad=\sum_{\lambda,\mu}\frac{\prod_{i=1}^{l(\lambda)}(1-(-y)^{\lambda_{i}})\prod_{j=1}^{l(\mu)}(1-(-z)^{\mu_{i}})}{z_{\lambda}z_{\mu}}\frac{A_{l(\lambda)}(s)A_{l(\mu)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\mu)+1}}\left\langle p_{\lambda},p_{\mu}\right\rangle x^{\left|\lambda\right|}\nonumber \\ & \qquad\qquad=\sum_{\lambda}\frac{\prod_{i=1}^{l(\lambda)}(1-(-y)^{\lambda_{i}})(1-(-z)^{\lambda_{i}})}{z_{\lambda}}\frac{A_{l(\lambda)}(s)A_{l(\lambda)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}x^{\left|\lambda\right|}. \end{align} $$
Combining Equation (3.2) with Equation (3.3) yields part (a), whereas combining Equation (3.2) with Equation (3.4) and then extracting coefficients of
![]() $x^{n}$
yields part (b).
$x^{n}$
yields part (b).
The formulas in Theorem 3.1 and others appearing later in this paper can be ‘inverted’ upon making appropriate substitutions. For example, Theorem 3.1 (a) can be rewritten as
 $$ \begin{align*} &\frac{1}{(1-\alpha)(1-\beta)}+\frac{1}{(1+u)(1+v)}\sum_{n=1}^{\infty}\left(\frac{(1+u\alpha)(1+v\beta)}{(1-\alpha)(1-\beta)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}(y,z,s,t)x^{n}\\ &\quad=\sum_{i,j=0}^{\infty}\left(\frac{(1+ux)(1+vx)}{(1-uvx)(1-x)}\right)^{ij}\alpha^{i}\beta^{j}, \end{align*} $$
$$ \begin{align*} &\frac{1}{(1-\alpha)(1-\beta)}+\frac{1}{(1+u)(1+v)}\sum_{n=1}^{\infty}\left(\frac{(1+u\alpha)(1+v\beta)}{(1-\alpha)(1-\beta)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}(y,z,s,t)x^{n}\\ &\quad=\sum_{i,j=0}^{\infty}\left(\frac{(1+ux)(1+vx)}{(1-uvx)(1-x)}\right)^{ij}\alpha^{i}\beta^{j}, \end{align*} $$
where
 $$ \begin{align*} u&=\frac{1+s^{2}-2ys-(1-s)\sqrt{(1+s)^{2}-4ys}}{2(1-y)s}, & \alpha&=\frac{(1+s)^{2}-2ys-(1+s)\sqrt{(1+s)^{2}-4ys}}{2ys},\\ v&=\frac{1+t^{2}-2zt-(1-t)\sqrt{(1+t)^{2}-4zt}}{2(1-z)t}, \quad\text{and} & \beta&=\frac{(1+t)^{2}-2zt-(1+t)\sqrt{(1+t)^{2}-4zt}}{2zt}. \end{align*} $$
$$ \begin{align*} u&=\frac{1+s^{2}-2ys-(1-s)\sqrt{(1+s)^{2}-4ys}}{2(1-y)s}, & \alpha&=\frac{(1+s)^{2}-2ys-(1+s)\sqrt{(1+s)^{2}-4ys}}{2ys},\\ v&=\frac{1+t^{2}-2zt-(1-t)\sqrt{(1+t)^{2}-4zt}}{2(1-z)t}, \quad\text{and} & \beta&=\frac{(1+t)^{2}-2zt-(1+t)\sqrt{(1+t)^{2}-4zt}}{2zt}. \end{align*} $$
3.2 Peaks and inverse peaks
We will now consider specializations of the polynomials
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})}(y,z,s,t)$
that give the distributions of the (mixed) two-sided statistics
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})}(y,z,s,t)$
that give the distributions of the (mixed) two-sided statistics
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})$
,
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})$
,
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})$
and
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})$
and
![]() $(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
. Let us begin with the two-sided distribution of
$(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
. Let us begin with the two-sided distribution of
![]() $\operatorname {\mathrm {pk}}$
, which is encoded by
$\operatorname {\mathrm {pk}}$
, which is encoded by
Theorem 3.2. We have
 $$ \begin{align} \frac{1}{(1-s)(1-t)}+\frac{1}{4}\sum_{n=1}^{\infty}\left(\frac{(1+s)(1+t)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n} =\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}s^{i}t^{j} \end{align} $$
$$ \begin{align} \frac{1}{(1-s)(1-t)}+\frac{1}{4}\sum_{n=1}^{\infty}\left(\frac{(1+s)(1+t)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n} =\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}s^{i}t^{j} \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} \quad\left(\frac{(1+s)(1+t)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =4\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{2ij \choose k}{2ij+n-k-1 \choose n-k}s^{i}t^{j} \end{align} $$
$$ \begin{align} \quad\left(\frac{(1+s)(1+t)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =4\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{2ij \choose k}{2ij+n-k-1 \choose n-k}s^{i}t^{j} \end{align} $$
and
 $$ \begin{align} \quad\left(\frac{(1+s)(1+t)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =\frac{1}{n!}\sum_{k=0}^n 4^{k+1}d(n,k)\frac{A_{k}(s)A_{k}(t)}{(1-s)^{k+1}(1-t)^{k+1}}\quad \end{align} $$
$$ \begin{align} \quad\left(\frac{(1+s)(1+t)}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =\frac{1}{n!}\sum_{k=0}^n 4^{k+1}d(n,k)\frac{A_{k}(s)A_{k}(t)}{(1-s)^{k+1}(1-t)^{k+1}}\quad \end{align} $$
with
![]() $d(n,k)$
as defined in Section 2.4.
$d(n,k)$
as defined in Section 2.4.
Proof. Parts (a) and (c) are obtained from evaluating Theorem 3.1 (a) and (b), respectively, at
![]() $y=z=1$
, with the sum on
$y=z=1$
, with the sum on
![]() $\lambda $
in (c) evaluated by Lemma 2.10 (b). From the identities
$\lambda $
in (c) evaluated by Lemma 2.10 (b). From the identities
 $$\begin{align*}(1+x)^{k}=\sum_{n=0}^{k}{k \choose n}x^{n}\quad\text{and}\quad(1-x)^{-k}=\sum_{n=0}^{\infty}{k+n-1 \choose n}x^{n}, \end{align*}$$
$$\begin{align*}(1+x)^{k}=\sum_{n=0}^{k}{k \choose n}x^{n}\quad\text{and}\quad(1-x)^{-k}=\sum_{n=0}^{\infty}{k+n-1 \choose n}x^{n}, \end{align*}$$
we obtain
 $$ \begin{align} \left(\frac{1+x}{1-x}\right)^{2ij}=\sum_{n=0}^{\infty}\sum_{k=0}^{n}{2ij \choose k}{2ij+n-k-1 \choose n-k}x^{n}. \end{align} $$
$$ \begin{align} \left(\frac{1+x}{1-x}\right)^{2ij}=\sum_{n=0}^{\infty}\sum_{k=0}^{n}{2ij \choose k}{2ij+n-k-1 \choose n-k}x^{n}. \end{align} $$
Substituting Equation (3.5) into (a) and extracting coefficients of
![]() $x^{n}$
yields (b).
$x^{n}$
yields (b).
The first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})}(s,t)$
are displayed in Table 1. The coefficients of
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})}(s,t)$
are displayed in Table 1. The coefficients of
![]() $s^{k}t$
—equivalently, the coefficients of
$s^{k}t$
—equivalently, the coefficients of
![]() $st^{k}$
by symmetry—are characterized by the following proposition.
$st^{k}$
by symmetry—are characterized by the following proposition.
Table 1 Joint distribution of
![]() $\operatorname {\mathrm {pk}}$
and
$\operatorname {\mathrm {pk}}$
and
![]() $\operatorname {\mathrm {ipk}}$
over
$\operatorname {\mathrm {ipk}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

Proposition 3.3. For any
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $k\geq 0$
, the number of permutations
$k\geq 0$
, the number of permutations
![]() $\pi \in \mathfrak {S}_{n}$
with
$\pi \in \mathfrak {S}_{n}$
with
![]() $\operatorname {\mathrm {pk}}(\pi )=k$
and
$\operatorname {\mathrm {pk}}(\pi )=k$
and
![]() $\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
$\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
![]() ${n \choose 2k+1}$
.
${n \choose 2k+1}$
.
Proposition 3.3 was first stated as a corollary of a more general result of Troyka and Zhuang [Reference Troyka and Zhuang26], namely, that for any composition L of
![]() $n\geq 1$
, there is exactly one permutation in
$n\geq 1$
, there is exactly one permutation in
![]() $\pi \in \mathfrak {S}_{n}$
with descent composition L such that
$\pi \in \mathfrak {S}_{n}$
with descent composition L such that
![]() $\operatorname {\mathrm {ipk}}(\pi )=0$
. However, it is also possible to prove Proposition 3.3 directly from Theorem 3.2.
$\operatorname {\mathrm {ipk}}(\pi )=0$
. However, it is also possible to prove Proposition 3.3 directly from Theorem 3.2.
Next, we obtain a surprisingly simple formula expressing the two-sided peak polynomials
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})}(s,t)$
in terms of products of the ordinary peak polynomials
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})}(s,t)$
in terms of products of the ordinary peak polynomials
giving the distribution of the peak number over
![]() $\mathfrak {S}_{n}$
.
$\mathfrak {S}_{n}$
.
Theorem 3.4. For all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align*} P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s,t) &= \frac{1}{n!}\sum_{k=0}^n d(n,k) \left((1-s)(1-t)\right)^{\frac{n-k}{2}}P_{k}^{\operatorname{\mathrm{pk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t). \end{align*} $$
$$ \begin{align*} P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s,t) &= \frac{1}{n!}\sum_{k=0}^n d(n,k) \left((1-s)(1-t)\right)^{\frac{n-k}{2}}P_{k}^{\operatorname{\mathrm{pk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t). \end{align*} $$
Since
![]() $d(n,k)=0$
when
$d(n,k)=0$
when
![]() $n-k$
is odd, the above formula does not involve any square roots.
$n-k$
is odd, the above formula does not involve any square roots.
Proof. It is known [Reference Stembridge25] that
 $$ \begin{align} A_{n}(t)=\left(\frac{1+t}{2}\right)^{n+1}P_{n}^{\operatorname{\mathrm{pk}}}\left(\frac{4t}{(1+t)^{2}}\right) \end{align} $$
$$ \begin{align} A_{n}(t)=\left(\frac{1+t}{2}\right)^{n+1}P_{n}^{\operatorname{\mathrm{pk}}}\left(\frac{4t}{(1+t)^{2}}\right) \end{align} $$
for
![]() $n\geq 1$
. Combining Equation (3.6) with Theorem 3.2 (c) and then replacing the variables s and t with u and v, respectively, yields
$n\geq 1$
. Combining Equation (3.6) with Theorem 3.2 (c) and then replacing the variables s and t with u and v, respectively, yields
 $$ \begin{align*} P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}\left(\frac{4u}{(1+u)^{2}},\frac{4v}{(1+v)^{2}}\right) =\frac{1}{n!}\sum_{k=0}^n d(n,k)\left(\frac{(1-u)(1-v)}{(1+u)(1+v)}\right)^{n-k}P_{k}^{\operatorname{\mathrm{pk}}}\left(\frac{4u}{(1+u)^{2}}\right)P_{k}^{\operatorname{\mathrm{pk}}}\left(\frac{4v}{(1+v)^{2}}\right). \end{align*} $$
$$ \begin{align*} P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}\left(\frac{4u}{(1+u)^{2}},\frac{4v}{(1+v)^{2}}\right) =\frac{1}{n!}\sum_{k=0}^n d(n,k)\left(\frac{(1-u)(1-v)}{(1+u)(1+v)}\right)^{n-k}P_{k}^{\operatorname{\mathrm{pk}}}\left(\frac{4u}{(1+u)^{2}}\right)P_{k}^{\operatorname{\mathrm{pk}}}\left(\frac{4v}{(1+v)^{2}}\right). \end{align*} $$
Setting
![]() $s=4u/(1+u)^{2}$
and
$s=4u/(1+u)^{2}$
and
![]() $t=4v/(1+v)^{2}$
, we obtain
$t=4v/(1+v)^{2}$
, we obtain
 $$ \begin{align} P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s,t) =\frac{1}{n!}\sum_{k=0}^n d(n,k) \left(\frac{(1-u)(1-v)}{(1+u)(1+v)}\right)^{n-k}P_{k}^{\operatorname{\mathrm{pk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t). \end{align} $$
$$ \begin{align} P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s,t) =\frac{1}{n!}\sum_{k=0}^n d(n,k) \left(\frac{(1-u)(1-v)}{(1+u)(1+v)}\right)^{n-k}P_{k}^{\operatorname{\mathrm{pk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t). \end{align} $$
It can be verified that
![]() $u=2s^{-1}(1-\sqrt {1-s})-1$
and
$u=2s^{-1}(1-\sqrt {1-s})-1$
and
![]() $v=2t^{-1}(1-\sqrt {1-t})-1$
, which lead to
$v=2t^{-1}(1-\sqrt {1-t})-1$
, which lead to
Substituting Equation (3.8) into Equation (3.7) completes the proof.
The substitution used in the proof of Theorem 3.4 allows us to invert the formulas in Theorem 3.2 and others involving the same quadratic transformation. For example, Theorem 3.2 (b) is equivalent to
 $$ \begin{align*} \begin{aligned} \frac{P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s,t)}{(1-s)^{\frac{n+1}{2}}(1-t)^{\frac{n+1}{2}}} & =4\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{2ij \choose k}{2ij+n-k-1 \choose n-k}u^{i}v^{j}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s,t)}{(1-s)^{\frac{n+1}{2}}(1-t)^{\frac{n+1}{2}}} & =4\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{2ij \choose k}{2ij+n-k-1 \choose n-k}u^{i}v^{j}, \end{aligned} \end{align*} $$
where, as before,
![]() $u=2s^{-1}(1-\sqrt {1-s})-1$
and
$u=2s^{-1}(1-\sqrt {1-s})-1$
and
![]() $v=2t^{-1}(1-\sqrt {1-t})-1$
. In fact, we can express u and v in terms of the Catalan generating function
$v=2t^{-1}(1-\sqrt {1-t})-1$
. In fact, we can express u and v in terms of the Catalan generating function

as
![]() $u=(s/4)C(s/4)^{2}$
and
$u=(s/4)C(s/4)^{2}$
and
![]() $v=(t/4)C(t/4)^{2}$
.
$v=(t/4)C(t/4)^{2}$
.
If we multiply the formula of Theorem 3.4 by
![]() $u^n$
and sum over n using Proposition 2.11 (b), we obtain the following generating function for the two-sided peak polynomials
$u^n$
and sum over n using Proposition 2.11 (b), we obtain the following generating function for the two-sided peak polynomials
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})}(s,t)$
.
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})}(s,t)$
.
Theorem 3.5. We have
 $$ \begin{align*} \sum_{n=0}^\infty P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s,t) u^n = \sum_{k=0}^\infty \frac{1}{k!} \left(\frac{L(\sqrt{(1-s)(1-t)}u)}{\sqrt{(1-s)(1-t)}}\right)^k P_{k}^{\operatorname{\mathrm{pk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t), \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s,t) u^n = \sum_{k=0}^\infty \frac{1}{k!} \left(\frac{L(\sqrt{(1-s)(1-t)}u)}{\sqrt{(1-s)(1-t)}}\right)^k P_{k}^{\operatorname{\mathrm{pk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t), \end{align*} $$
with
![]() $L(u)$
as defined in Section 2.4.
$L(u)$
as defined in Section 2.4.
We can derive the odd part of Stanley’s generating function (2.2) for doubly alternating permutations from Theorem 3.5. While an alternating permutation
![]() $\pi $
satisfies
$\pi $
satisfies
![]() $\pi (1)>\pi (2)<\pi (3)>\pi (4)<\cdots $
, we say that
$\pi (1)>\pi (2)<\pi (3)>\pi (4)<\cdots $
, we say that
![]() $\pi $
is reverse alternating if
$\pi $
is reverse alternating if
![]() $\pi (1)<\pi (2)>\pi (3)<\pi (4)>\cdots $
. It is evident by symmetry that reverse alternating permutations are also counted by the Euler numbers
$\pi (1)<\pi (2)>\pi (3)<\pi (4)>\cdots $
. It is evident by symmetry that reverse alternating permutations are also counted by the Euler numbers
![]() $E_n$
. As shown by Stanley [Reference Stanley21], the number of doubly alternating permutations in
$E_n$
. As shown by Stanley [Reference Stanley21], the number of doubly alternating permutations in
![]() $\mathfrak {S}_n$
is equal to the number
$\mathfrak {S}_n$
is equal to the number
![]() $\tilde {E}_n$
of reverse alternating permutations in
$\tilde {E}_n$
of reverse alternating permutations in
![]() $\mathfrak {S}_n$
whose inverses are reverse alternating.
$\mathfrak {S}_n$
whose inverses are reverse alternating.
It is readily verified that a permutation
![]() $\pi $
in
$\pi $
in
![]() $\mathfrak {S}_n$
has at most
$\mathfrak {S}_n$
has at most
![]() $(n-1)/2$
peaks and has exactly
$(n-1)/2$
peaks and has exactly
![]() $(n-1)/2$
peaks if and only if n is odd and
$(n-1)/2$
peaks if and only if n is odd and
![]() $\pi $
is reverse alternating. Thus, we have
$\pi $
is reverse alternating. Thus, we have
 $$\begin{align*}\lim_{s\rightarrow0}P_{k}^{\operatorname{\mathrm{pk}}}(s^{-2})s^{k+1}=\lim_{s\rightarrow0}\sum_{\pi\in\mathfrak{S}_{k}}s^{k-2\operatorname{\mathrm{pk}}(\pi)-1}=\begin{cases} 0, & \text{if }k\text{ is even,}\\ E_{k}, & \text{if }k\text{ is odd.} \end{cases} \end{align*}$$
$$\begin{align*}\lim_{s\rightarrow0}P_{k}^{\operatorname{\mathrm{pk}}}(s^{-2})s^{k+1}=\lim_{s\rightarrow0}\sum_{\pi\in\mathfrak{S}_{k}}s^{k-2\operatorname{\mathrm{pk}}(\pi)-1}=\begin{cases} 0, & \text{if }k\text{ is even,}\\ E_{k}, & \text{if }k\text{ is odd.} \end{cases} \end{align*}$$
Similarly, we have
 $$\begin{align*}\lim_{s\rightarrow0}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s^{-2},t^{-2})s^{n+1}t^{n+1}=\begin{cases} 0, & \text{if }n\text{ is even,}\\ \tilde{E}_{n}, & \text{if }n\text{ is odd.} \end{cases} \end{align*}$$
$$\begin{align*}\lim_{s\rightarrow0}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ipk}})}(s^{-2},t^{-2})s^{n+1}t^{n+1}=\begin{cases} 0, & \text{if }n\text{ is even,}\\ \tilde{E}_{n}, & \text{if }n\text{ is odd.} \end{cases} \end{align*}$$
So, to obtain Stanley’s formula from Theorem 3.5, we first replace s with
![]() $s^{-2}$
, t with
$s^{-2}$
, t with
![]() $t^{-2}$
and u with
$t^{-2}$
and u with
![]() $stu$
; then we multiply by
$stu$
; then we multiply by
![]() $st$
and take the limit as
$st$
and take the limit as
![]() $s,t\to 0$
. The substitution takes
$s,t\to 0$
. The substitution takes
 $$\begin{align*}\left(\frac{L(\sqrt{(1-s)(1-t)}u)}{\sqrt{(1-s)(1-t)}}\right)^k P_{k}^{\operatorname{\mathrm{pk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t) \end{align*}$$
$$\begin{align*}\left(\frac{L(\sqrt{(1-s)(1-t)}u)}{\sqrt{(1-s)(1-t)}}\right)^k P_{k}^{\operatorname{\mathrm{pk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t) \end{align*}$$
to
 $$ \begin{align*} \left(\frac{L(\sqrt{(s^{2}-1)(t^{2}-1)}u)}{\sqrt{(1-s^{-2})(1-t^{-2})}}\right)^{k}P_{k}^{\operatorname{\mathrm{pk}}}(s^{-2})P_{k}^{\operatorname{\mathrm{pk}}}(t^{-2}) =\left(\frac{L(\sqrt{(s^{2}-1)(t^{2}-1)}u)}{\sqrt{(s^{2}-1)(t^{2}-1)}}\right)^{k}s^{k}P_{k}^{\operatorname{\mathrm{pk}}}(s^{-2})t^{k}P_{k}^{\operatorname{\mathrm{pk}}}(t^{-2}); \end{align*} $$
$$ \begin{align*} \left(\frac{L(\sqrt{(s^{2}-1)(t^{2}-1)}u)}{\sqrt{(1-s^{-2})(1-t^{-2})}}\right)^{k}P_{k}^{\operatorname{\mathrm{pk}}}(s^{-2})P_{k}^{\operatorname{\mathrm{pk}}}(t^{-2}) =\left(\frac{L(\sqrt{(s^{2}-1)(t^{2}-1)}u)}{\sqrt{(s^{2}-1)(t^{2}-1)}}\right)^{k}s^{k}P_{k}^{\operatorname{\mathrm{pk}}}(s^{-2})t^{k}P_{k}^{\operatorname{\mathrm{pk}}}(t^{-2}); \end{align*} $$
multiplying by
![]() $st$
and taking
$st$
and taking
![]() $s,t\to 0$
gives
$s,t\to 0$
gives
![]() $L(u)^k E_k^2$
for k odd and
$L(u)^k E_k^2$
for k odd and
![]() $0$
for k even, as desired.
$0$
for k even, as desired.
We will later get the even part of Stanley’s generating function (2.2) in a similar way from Theorem 4.4, which is the analogue of Theorem 3.5 for left peaks.
Before proceeding, we note that every formula like Theorem 3.4 has an analogous generating function like Theorem 3.5. We will only write out these generating functions for
![]() $(\operatorname {\mathrm {pk}}, \operatorname {\mathrm {ipk}})$
and
$(\operatorname {\mathrm {pk}}, \operatorname {\mathrm {ipk}})$
and
![]() $(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}})$
– which are used in our rederivation of Stanley’s formula – as well as for
$(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}})$
– which are used in our rederivation of Stanley’s formula – as well as for
![]() $(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
.
$(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
.
3.3 Peaks and inverse descents
Next, define the polynomials
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
by
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
by
We omit the proof of the next theorem as it is similar to that of Theorem 3.2, with the main difference being that we specialize at
![]() $y=1$
and
$y=1$
and
![]() $z=0$
(as opposed to
$z=0$
(as opposed to
![]() $y=z=1$
).
$y=z=1$
).
Theorem 3.6. We have
 $$ \begin{align} \qquad\frac{1}{(1-s)(1-t)}+\frac{1}{2}\sum_{n=1}^{\infty}\left(\frac{1+s}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) =\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{ij}s^{i}t^{j}\qquad \end{align} $$
$$ \begin{align} \qquad\frac{1}{(1-s)(1-t)}+\frac{1}{2}\sum_{n=1}^{\infty}\left(\frac{1+s}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) =\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{ij}s^{i}t^{j}\qquad \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} \qquad\left(\frac{1+s}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) & =2\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{ij \choose k}{ij+n-k-1 \choose n-k}s^{i}t^{j} \end{align} $$
$$ \begin{align} \qquad\left(\frac{1+s}{(1-s)(1-t)}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) & =2\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{ij \choose k}{ij+n-k-1 \choose n-k}s^{i}t^{j} \end{align} $$
and
 $$ \begin{align} \quad\, \left(\frac{1+t}{(1-s)(1-t)}\right)^{\! n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) &=\frac{1}{n!}\sum_{k=0}^n 2^{k+1} d(n,k) \frac{A_{k}(s)A_{k}(t)}{(1-s)^{k+1}(1-t)^{k+1}}. \end{align} $$
$$ \begin{align} \quad\, \left(\frac{1+t}{(1-s)(1-t)}\right)^{\! n+1}P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) &=\frac{1}{n!}\sum_{k=0}^n 2^{k+1} d(n,k) \frac{A_{k}(s)A_{k}(t)}{(1-s)^{k+1}(1-t)^{k+1}}. \end{align} $$
We display the first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
in Table 2, collecting terms with the same power of s in order to display the symmetry in their coefficients. This symmetry follows from the fact that the reverse
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
in Table 2, collecting terms with the same power of s in order to display the symmetry in their coefficients. This symmetry follows from the fact that the reverse ![]() of a permutation
of a permutation
![]() $\pi \in \mathfrak {S}_{n}$
satisfies
$\pi \in \mathfrak {S}_{n}$
satisfies
![]() $\operatorname {\mathrm {ides}}(\pi ^{r})=n-1-\operatorname {\mathrm {ides}}(\pi )$
[Reference Zhuang31, Proposition 2.6 (c)] but has the same number of peaks as
$\operatorname {\mathrm {ides}}(\pi ^{r})=n-1-\operatorname {\mathrm {ides}}(\pi )$
[Reference Zhuang31, Proposition 2.6 (c)] but has the same number of peaks as
![]() $\pi $
.
$\pi $
.
Table 2 Joint distribution of
![]() $\operatorname {\mathrm {pk}}$
and
$\operatorname {\mathrm {pk}}$
and
![]() $\operatorname {\mathrm {ides}}$
over
$\operatorname {\mathrm {ides}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

Furthermore, observe that the coefficients of
![]() $t^{k}s$
in
$t^{k}s$
in
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
are binomial coefficients; this is a consequence of the following proposition, which is Corollary 9 of [Reference Troyka and Zhuang26].
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
are binomial coefficients; this is a consequence of the following proposition, which is Corollary 9 of [Reference Troyka and Zhuang26].
Proposition 3.7. For any
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $k\geq 0$
, the number of permutations
$k\geq 0$
, the number of permutations
![]() $\pi \in \mathfrak {S}_{n}$
with
$\pi \in \mathfrak {S}_{n}$
with
![]() $\operatorname {\mathrm {des}}(\pi )=k$
and
$\operatorname {\mathrm {des}}(\pi )=k$
and
![]() $\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
$\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
![]() ${n-1 \choose k}$
.
${n-1 \choose k}$
.
In addition to being symmetric, the coefficients of
![]() $s^{k}$
in
$s^{k}$
in
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
seem to be unimodal polynomials in t, which we know holds for
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
seem to be unimodal polynomials in t, which we know holds for
![]() $k=0$
in light of Proposition 3.7. In the last section of this paper, we will state the conjecture that the polynomials
$k=0$
in light of Proposition 3.7. In the last section of this paper, we will state the conjecture that the polynomials
![]() $[s^{k}]\,P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
are in fact
$[s^{k}]\,P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
are in fact
![]() $\gamma $
-positive, a property which implies unimodality and symmetry.
$\gamma $
-positive, a property which implies unimodality and symmetry.
The next formula expresses
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
in terms of the products
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
in terms of the products
![]() $P_{k}^{\operatorname {\mathrm {pk}}}(s)A_{k}(t)$
. The proof is very similar to that of Theorem 3.4 and so it is omitted.
$P_{k}^{\operatorname {\mathrm {pk}}}(s)A_{k}(t)$
. The proof is very similar to that of Theorem 3.4 and so it is omitted.
Theorem 3.8. For all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align*} P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ides}})}(s,t) & =\frac{1}{n!}\sum_{k=0}^n d(n,k)\left((1-s)^{1/2}(1-t)\right)^{n-k}P_{k}^{\operatorname{\mathrm{pk}}}(s)A_{k}(t). \end{align*} $$
$$ \begin{align*} P_{n}^{(\operatorname{\mathrm{pk}},\operatorname{\mathrm{ides}})}(s,t) & =\frac{1}{n!}\sum_{k=0}^n d(n,k)\left((1-s)^{1/2}(1-t)\right)^{n-k}P_{k}^{\operatorname{\mathrm{pk}}}(s)A_{k}(t). \end{align*} $$
3.4 Descents and inverse descents
To conclude this section, we state the analogous results for the two-sided Eulerian polynomials
Recall that parts (a) and (b) were originally due to Carlitz, Roselle and Scoville [Reference Carlitz, Roselle and Scoville5], whereas (c) and (d) are new.
Theorem 3.9. We have
 $$ \begin{align} \qquad\sum_{n=0}^{\infty}\frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n} & =\sum_{i,j=0}^{\infty}\frac{s^{i}t^{j}}{(1-x)^{ij}} \end{align} $$
$$ \begin{align} \qquad\sum_{n=0}^{\infty}\frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n} & =\sum_{i,j=0}^{\infty}\frac{s^{i}t^{j}}{(1-x)^{ij}} \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} \qquad\frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}} & =\sum_{i,j=0}^{\infty}{ij+n-1 \choose n}s^{i}t^{j} \end{align} $$
$$ \begin{align} \qquad\frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}} & =\sum_{i,j=0}^{\infty}{ij+n-1 \choose n}s^{i}t^{j} \end{align} $$
and
 $$ \begin{align} \qquad A_{n}(s,t) =\frac{1}{n!}\sum_{k=0}^n c(n,k) \left((1-s)(1-t)\right)^{n-k}A_{k}(s)A_{k}(t). \end{align} $$
$$ \begin{align} \qquad A_{n}(s,t) =\frac{1}{n!}\sum_{k=0}^n c(n,k) \left((1-s)(1-t)\right)^{n-k}A_{k}(s)A_{k}(t). \end{align} $$
Moreover, we have
 $$ \begin{align} \qquad \sum_{n=0}^\infty A_n(s,t) u^n = \sum_{k=0}^\infty \frac{1}{k!}\left(\log\frac{1}{1-(1-s)(1-t)u}\right)^k \frac{A_k(s)A_k(t)}{(1-s)^k(1-t)^k}. \end{align} $$
$$ \begin{align} \qquad \sum_{n=0}^\infty A_n(s,t) u^n = \sum_{k=0}^\infty \frac{1}{k!}\left(\log\frac{1}{1-(1-s)(1-t)u}\right)^k \frac{A_k(s)A_k(t)}{(1-s)^k(1-t)^k}. \end{align} $$
Parts (a)–(c) are proven similarly to Theorems 3.2, 3.4 and 3.6 except that we evaluate Theorem 3.1 at
![]() $y=z=0$
. Part (c) can also be derived directly from (b):
$y=z=0$
. Part (c) can also be derived directly from (b):
 $$ \begin{align*} \frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}} &=\sum_{i,j=0}^{\infty}{ij+n-1 \choose n}s^{i}t^{j}\\ &=\sum_{i,j=0}^{\infty}\frac{1}{n!}\sum_{k=0}^n c(n,k) (ij)^k s^{i}t^{j}\\ &=\frac{1}{n!}\sum_{k=0}^n c(n,k)\sum_{i=0}^\infty i^k s^i \sum_{j=0}^\infty j^k t^j\\ &=\frac{1}{n!}\sum_{k=0}^n c(n,k)\frac{A_k(s)}{(1-t)^{k+1}}\frac{A_k(t)}{(1-t)^{k+1}}. \end{align*} $$
$$ \begin{align*} \frac{A_{n}(s,t)}{(1-s)^{n+1}(1-t)^{n+1}} &=\sum_{i,j=0}^{\infty}{ij+n-1 \choose n}s^{i}t^{j}\\ &=\sum_{i,j=0}^{\infty}\frac{1}{n!}\sum_{k=0}^n c(n,k) (ij)^k s^{i}t^{j}\\ &=\frac{1}{n!}\sum_{k=0}^n c(n,k)\sum_{i=0}^\infty i^k s^i \sum_{j=0}^\infty j^k t^j\\ &=\frac{1}{n!}\sum_{k=0}^n c(n,k)\frac{A_k(s)}{(1-t)^{k+1}}\frac{A_k(t)}{(1-t)^{k+1}}. \end{align*} $$
Part (d) is obtained from (c) using Proposition 2.11 (a).
4 Two-sided left peak statistics
4.1 Left peaks, descents and their inverses
In this section, we will examine (mixed) two-sided distributions involving the left peak number
![]() $\operatorname {\mathrm {lpk}}$
. Let us first derive a generating function formula for the polynomials
$\operatorname {\mathrm {lpk}}$
. Let us first derive a generating function formula for the polynomials
giving the joint distribution of
![]() $\operatorname {\mathrm {lpk}}$
,
$\operatorname {\mathrm {lpk}}$
,
![]() $\operatorname {\mathrm {ilpk}}$
,
$\operatorname {\mathrm {ilpk}}$
,
![]() $\operatorname {\mathrm {des}}$
and
$\operatorname {\mathrm {des}}$
and
![]() $\operatorname {\mathrm {ides}}$
over
$\operatorname {\mathrm {ides}}$
over
![]() $\mathfrak {S}_{n}$
.
$\mathfrak {S}_{n}$
.
Theorem 4.1. We have
 $$ \begin{align*} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+ys)^{n}(1+zt)^{n}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\frac{(1+yx)^{i(j+1)}(1+zx)^{(i+1)j}}{(1-yzx)^{ij}(1-x)^{(i+1)(j+1)}}s^{i}t^{j}. \end{align*} $$
$$ \begin{align*} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+ys)^{n}(1+zt)^{n}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\frac{(1+yx)^{i(j+1)}(1+zx)^{(i+1)j}}{(1-yzx)^{ij}(1-x)^{(i+1)(j+1)}}s^{i}t^{j}. \end{align*} $$
Proof. From Lemma 2.8 (c), we have
 $$ \begin{align} & \left\langle \frac{H(x)}{1-sE(yx)H(x)},\frac{H}{1-tE(z)H}\right\rangle \nonumber \\ & \qquad\qquad\qquad=\frac{1}{(1-s)(1-t)}+\sum_{m,n=1}^{\infty}\sum_{\substack{L\vDash m\\ M\vDash n } }\frac{(1+ys)^{m}(1+zt)^{n}}{(1-s)^{m+1}(1-t)^{n+1}}\acute{N}_{L,M}\left\langle r_{L},r_{M}\right\rangle x^{m}, \end{align} $$
$$ \begin{align} & \left\langle \frac{H(x)}{1-sE(yx)H(x)},\frac{H}{1-tE(z)H}\right\rangle \nonumber \\ & \qquad\qquad\qquad=\frac{1}{(1-s)(1-t)}+\sum_{m,n=1}^{\infty}\sum_{\substack{L\vDash m\\ M\vDash n } }\frac{(1+ys)^{m}(1+zt)^{n}}{(1-s)^{m+1}(1-t)^{n+1}}\acute{N}_{L,M}\left\langle r_{L},r_{M}\right\rangle x^{m}, \end{align} $$
where

By Foulkes’s theorem (Theorem 2.1), Equation (4.1) simplifies to
 $$ \begin{align} & \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \nonumber \\ & \quad=\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+ys)^{n}(1+zt)^{n}\sum_{\pi\in\mathfrak{S}_{n}}\acute{N}_{\operatorname{\mathrm{Comp}}(\pi),\operatorname{\mathrm{Comp}}(\pi^{-1})}}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}\nonumber \\ & \quad=\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+ys)^{n}(1+zt)^{n}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}. \end{align} $$
$$ \begin{align} & \left\langle \frac{1}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \nonumber \\ & \quad=\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+ys)^{n}(1+zt)^{n}\sum_{\pi\in\mathfrak{S}_{n}}\acute{N}_{\operatorname{\mathrm{Comp}}(\pi),\operatorname{\mathrm{Comp}}(\pi^{-1})}}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}\nonumber \\ & \quad=\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+ys)^{n}(1+zt)^{n}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1-s)^{n+1}(1-t)^{n+1}}x^{n}. \end{align} $$
We now compute the same scalar product in a different way. We have
 $$ \begin{align} \left\langle \frac{H(x)}{1-sE(yx)H(x)},\frac{H}{1-tE(z)H}\right\rangle &=\left\langle \sum_{i=0}^{\infty}E(yx)^{i}H(x)^{i+1}s^{i},\sum_{j=0}^{\infty}E(z)^{j}H^{j+1}t^{j}\right\rangle \nonumber \\ &=\sum_{i,j=0}^{\infty}\left\langle E(yx)^{i}H(x)^{i+1},E(z)^{j}H^{j+1}\right\rangle s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\left\langle (E(yx)^{i}H(x)^{i+1})[X+1],E(z)^{j}H^{j}\right\rangle s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\left\langle (E(yx)[X+1])^{i}(H(x)[X+1])^{i+1},E(z)^{j}H^{j}\right\rangle s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\left\langle \frac{(1+yx)^{i}}{(1-x)^{i+1}}E(yx)^{i}H(x)^{i+1},E(z)^{j}H^{j}\right\rangle s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\frac{(1+yx)^{i}}{(1-x)^{i+1}}\left\langle E(yx),E(z)^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E(z)^{j}H^{j}\right\rangle ^{i+1}s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\frac{(1+yx)^{i(j+1)}}{(1-yzx)^{ij}}\frac{(1+zx)^{(i+1)j}}{(1-x)^{(i+1)(j+1)}}s^{i}t^{j}; \end{align} $$
$$ \begin{align} \left\langle \frac{H(x)}{1-sE(yx)H(x)},\frac{H}{1-tE(z)H}\right\rangle &=\left\langle \sum_{i=0}^{\infty}E(yx)^{i}H(x)^{i+1}s^{i},\sum_{j=0}^{\infty}E(z)^{j}H^{j+1}t^{j}\right\rangle \nonumber \\ &=\sum_{i,j=0}^{\infty}\left\langle E(yx)^{i}H(x)^{i+1},E(z)^{j}H^{j+1}\right\rangle s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\left\langle (E(yx)^{i}H(x)^{i+1})[X+1],E(z)^{j}H^{j}\right\rangle s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\left\langle (E(yx)[X+1])^{i}(H(x)[X+1])^{i+1},E(z)^{j}H^{j}\right\rangle s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\left\langle \frac{(1+yx)^{i}}{(1-x)^{i+1}}E(yx)^{i}H(x)^{i+1},E(z)^{j}H^{j}\right\rangle s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\frac{(1+yx)^{i}}{(1-x)^{i+1}}\left\langle E(yx),E(z)^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E(z)^{j}H^{j}\right\rangle ^{i+1}s^{i}t^{j}\nonumber \\ &=\sum_{i,j=0}^{\infty}\frac{(1+yx)^{i(j+1)}}{(1-yzx)^{ij}}\frac{(1+zx)^{(i+1)j}}{(1-x)^{(i+1)(j+1)}}s^{i}t^{j}; \end{align} $$
here, we are using Lemma 2.6 for the third equality, and in the last three steps, we apply Lemmas 2.7, 2.4 and 2.5, respectively. Combining (4.2) and (4.3) completes the proof.
4.2 Left peaks, inverse peaks, descents and inverse descents
Next, let us consider the joint distribution of
![]() $\operatorname {\mathrm {lpk}}$
,
$\operatorname {\mathrm {lpk}}$
,
![]() $\operatorname {\mathrm {ipk}}$
,
$\operatorname {\mathrm {ipk}}$
,
![]() $\operatorname {\mathrm {des}}$
and
$\operatorname {\mathrm {des}}$
and
![]() $\operatorname {\mathrm {ides}}$
over
$\operatorname {\mathrm {ides}}$
over
![]() $\mathfrak {S}_{n}$
. Define
$\mathfrak {S}_{n}$
. Define
Theorem 4.2. We have
 $$ \begin{align*} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+ys)^{n}(1+zt)^{n+1}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1+z)(1-s)^{n+1}(1-t)^{n+1}}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+yx}{1-yzx}\right)^{ij}\left(\frac{1+zx}{1-x}\right)^{(i+1)j}s^{i}t^{j}. \end{align*} $$
$$ \begin{align*} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+ys)^{n}(1+zt)^{n+1}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(\frac{(1+y)^{2}s}{(y+s)(1+ys)},\frac{(1+z)^{2}t}{(z+t)(1+zt)},\frac{y+s}{1+ys},\frac{z+t}{1+zt}\right)}{(1+z)(1-s)^{n+1}(1-t)^{n+1}}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+yx}{1-yzx}\right)^{ij}\left(\frac{1+zx}{1-x}\right)^{(i+1)j}s^{i}t^{j}. \end{align*} $$
Proof. The two sides of the above equation are obtained from evaluating the scalar product
 $$\begin{align*}\left\langle \frac{H}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \end{align*}$$
$$\begin{align*}\left\langle \frac{H}{1-sE(yx)H(x)},\frac{1}{1-tE(z)H}\right\rangle \end{align*}$$
in two different ways; the proof is similar to that of Theorem 3.1 and so we omit the details.
4.3 Left peaks and inverse left peaks
We now consider specializations of
![]() $P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})}(y,z,s,t)$
and
$P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})}(y,z,s,t)$
and
![]() $P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})}(y,z,s,t)$
, beginning with the two-sided left peak polynomials
$P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})}(y,z,s,t)$
, beginning with the two-sided left peak polynomials
Theorem 4.3. We have
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{((1+s)(1+t))^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\frac{(1+x)^{2ij+i+j}}{(1-x)^{2ij+i+j+1}}s^{i}t^{j}\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{((1+s)(1+t))^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\frac{(1+x)^{2ij+i+j}}{(1-x)^{2ij+i+j+1}}s^{i}t^{j}\nonumber \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} \:\frac{((1+s)(1+t))^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{2ij+i+j \choose k}{2ij+i+j+n-k \choose n-k}s^{i}t^{j} \end{align} $$
$$ \begin{align} \:\frac{((1+s)(1+t))^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{2ij+i+j \choose k}{2ij+i+j+n-k \choose n-k}s^{i}t^{j} \end{align} $$
and
 $$ \begin{align} \quad\,\,\,\frac{((1+s)(1+t))^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) &=\sum_{k=0}^n e(n,k) \frac{B_{k}(s)B_{k}(t)}{(1-s)^{k+1}(1-t)^{k+1}} \end{align} $$
$$ \begin{align} \quad\,\,\,\frac{((1+s)(1+t))^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) &=\sum_{k=0}^n e(n,k) \frac{B_{k}(s)B_{k}(t)}{(1-s)^{k+1}(1-t)^{k+1}} \end{align} $$
with
![]() $e(n,k)$
as defined in Section 2.4.
$e(n,k)$
as defined in Section 2.4.
Proof. Evaluating Theorem 4.1 at
![]() $y=z=1$
yields part (a), whereas (b) follows from (a) and
$y=z=1$
yields part (a), whereas (b) follows from (a) and
 $$\begin{align*}\frac{(1+x)^{2ij+i+j}}{(1-x)^{2ij+i+j+1}}=\sum_{n=0}^{\infty}\sum_{k=0}^{n}{2ij+i+j \choose k}{2ij+i+j+n-k \choose n-k}x^{n}. \end{align*}$$
$$\begin{align*}\frac{(1+x)^{2ij+i+j}}{(1-x)^{2ij+i+j+1}}=\sum_{n=0}^{\infty}\sum_{k=0}^{n}{2ij+i+j \choose k}{2ij+i+j+n-k \choose n-k}x^{n}. \end{align*}$$
To prove (c), first observe that Lemma 2.9 (b) implies
 $$ \begin{align*} \begin{aligned} \left\langle \frac{H(x)}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle & =\sum_{\lambda,\mu}\frac{1}{z_{\lambda}z_{\mu}}\frac{B_{o(\lambda)}(s)B_{o(\mu)}(t)}{(1-s)^{o(\lambda)+1}(1-t)^{o(\mu)+1}}\left\langle p_{\lambda},p_{\mu}\right\rangle x^{\left|\lambda\right|}\\ & =\sum_{\lambda}\frac{1}{z_{\lambda}}\frac{B_{o(\lambda)}(s)B_{o(\lambda)}(t)}{(1-s)^{o(\lambda)+1}(1-t)^{o(\lambda)+1}}x^{\left|\lambda\right|}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left\langle \frac{H(x)}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle & =\sum_{\lambda,\mu}\frac{1}{z_{\lambda}z_{\mu}}\frac{B_{o(\lambda)}(s)B_{o(\mu)}(t)}{(1-s)^{o(\lambda)+1}(1-t)^{o(\mu)+1}}\left\langle p_{\lambda},p_{\mu}\right\rangle x^{\left|\lambda\right|}\\ & =\sum_{\lambda}\frac{1}{z_{\lambda}}\frac{B_{o(\lambda)}(s)B_{o(\lambda)}(t)}{(1-s)^{o(\lambda)+1}(1-t)^{o(\lambda)+1}}x^{\left|\lambda\right|}, \end{aligned} \end{align*} $$
but this same scalar product is also given by
 $$ \begin{align*} \left\langle \frac{H(x)}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle =\frac{1}{(1-s)(1-t)}\sum_{n=1}^{\infty}\frac{((1+s)(1+t))^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n}, \end{align*} $$
$$ \begin{align*} \left\langle \frac{H(x)}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle =\frac{1}{(1-s)(1-t)}\sum_{n=1}^{\infty}\frac{((1+s)(1+t))^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n}, \end{align*} $$
which is obtained from evaluating Equation (4.2) at
![]() $y=z=1$
. Equating these two expressions, extracting coefficients of
$y=z=1$
. Equating these two expressions, extracting coefficients of
![]() $x^{n}$
, and applying Lemma 2.10 (c) completes the proof.
$x^{n}$
, and applying Lemma 2.10 (c) completes the proof.
See Table 3 for the first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}})}(s,t)$
.
$P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}})}(s,t)$
.
Table 3 Joint distribution of
![]() $\operatorname {\mathrm {lpk}}$
and
$\operatorname {\mathrm {lpk}}$
and
![]() $\operatorname {\mathrm {ilpk}}$
over
$\operatorname {\mathrm {ilpk}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

Next, we express these two-sided left peak polynomials as a sum involving products of the ordinary left peak polynomials
Theorem 4.4. For all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align*} P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}(s,t) & =\frac{1}{n!}\sum_{k=0}^n e(n,k)\left((1-s)(1-t)\right)^{\frac{n-k}{2}}P_{k}^{\operatorname{\mathrm{lpk}}}(s)P_{k}^{\operatorname{\mathrm{lpk}}}(t). \end{align*} $$
$$ \begin{align*} P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}(s,t) & =\frac{1}{n!}\sum_{k=0}^n e(n,k)\left((1-s)(1-t)\right)^{\frac{n-k}{2}}P_{k}^{\operatorname{\mathrm{lpk}}}(s)P_{k}^{\operatorname{\mathrm{lpk}}}(t). \end{align*} $$
Proof. The proof follows in the same way as the proof of Theorem 3.4 except that we use the formula
 $$ \begin{align} B_{n}(t)=(1+t)^{n}P_{n}^{\operatorname{\mathrm{lpk}}}\left(\frac{4t}{(1+t)^{2}}\right) \end{align} $$
$$ \begin{align} B_{n}(t)=(1+t)^{n}P_{n}^{\operatorname{\mathrm{lpk}}}\left(\frac{4t}{(1+t)^{2}}\right) \end{align} $$
[Reference Petersen18, Proposition 4.15] in place of (3.6). The details are omitted.
From Theorem 4.4 and Proposition 2.11 (c), we can obtain a generating function for the two-sided left peak polynomials, analogous to Theorem 3.5 for the two-sided peak polynomials.
Theorem 4.5. We have
 $$ \begin{align*} \sum_{n=0}^\infty P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}(s,t) u^n = \frac{1}{\sqrt{1-(1-s)(1-t)u^2}}\sum_{k=0}^\infty \frac{1}{k!} \left(\frac{L(\sqrt{(1-s)(1-t)}u)}{\sqrt{(1-s)(1-t)}}\right)^{\! k} P_{k}^{\operatorname{\mathrm{lpk}}}(s)P_{k}^{\operatorname{\mathrm{lpk}}}(t). \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}(s,t) u^n = \frac{1}{\sqrt{1-(1-s)(1-t)u^2}}\sum_{k=0}^\infty \frac{1}{k!} \left(\frac{L(\sqrt{(1-s)(1-t)}u)}{\sqrt{(1-s)(1-t)}}\right)^{\! k} P_{k}^{\operatorname{\mathrm{lpk}}}(s)P_{k}^{\operatorname{\mathrm{lpk}}}(t). \end{align*} $$
Just as we derived from Theorem 3.5 the odd part of Stanley’s formula (2.2) for doubly alternating permutations, we can derive the even part of (2.2) from Theorem 4.5. First, we note that a permutation
![]() $\pi $
in
$\pi $
in
![]() $\mathfrak {S}_n$
has at most
$\mathfrak {S}_n$
has at most
![]() $n/2$
left peaks and has exactly
$n/2$
left peaks and has exactly
![]() $n/2$
left peaks if and only if n is even and
$n/2$
left peaks if and only if n is even and
![]() $\pi $
is alternating. Then we have
$\pi $
is alternating. Then we have
 $$\begin{align*}\lim_{s\rightarrow0}P_{k}^{\operatorname{\mathrm{lpk}}}(s^{-2})s^{k}=\lim_{s\rightarrow0}\sum_{\pi\in\mathfrak{S}_{k}}s^{k-2\operatorname{\mathrm{lpk}}(\pi)}=\begin{cases} 0, & \text{if }n\text{ is odd,}\\ E_{k}, & \text{if }n\text{ is even}, \end{cases} \end{align*}$$
$$\begin{align*}\lim_{s\rightarrow0}P_{k}^{\operatorname{\mathrm{lpk}}}(s^{-2})s^{k}=\lim_{s\rightarrow0}\sum_{\pi\in\mathfrak{S}_{k}}s^{k-2\operatorname{\mathrm{lpk}}(\pi)}=\begin{cases} 0, & \text{if }n\text{ is odd,}\\ E_{k}, & \text{if }n\text{ is even}, \end{cases} \end{align*}$$
and similarly
 $$\begin{align*}\lim_{s\rightarrow0}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}(s^{-2},t^{-2})s^{n}t^{n}=\begin{cases} 0, & \text{if }n\text{ is odd,}\\ \tilde{E}_{n}, & \text{if }n\text{ is even.} \end{cases} \end{align*}$$
$$\begin{align*}\lim_{s\rightarrow0}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ilpk}})}(s^{-2},t^{-2})s^{n}t^{n}=\begin{cases} 0, & \text{if }n\text{ is odd,}\\ \tilde{E}_{n}, & \text{if }n\text{ is even.} \end{cases} \end{align*}$$
Therefore, to obtain the even part of Stanley’s formula, we take Theorem 4.5 and replace s with
![]() $s^{-2}$
, t with
$s^{-2}$
, t with
![]() $t^{-2}$
and u with
$t^{-2}$
and u with
![]() $stu$
; then we take the limit as
$stu$
; then we take the limit as
![]() $s,t\to 0$
, similarly to the computation for the odd part.
$s,t\to 0$
, similarly to the computation for the odd part.
4.4 Left peaks and inverse peaks
We proceed to give analogous formulas for the polynomials
encoding the joint distribution of
![]() $\operatorname {\mathrm {lpk}}$
and
$\operatorname {\mathrm {lpk}}$
and
![]() $\operatorname {\mathrm {ipk}}$
over
$\operatorname {\mathrm {ipk}}$
over
![]() $\mathfrak {S}_n$
.
$\mathfrak {S}_n$
.
Theorem 4.6. We have
 $$ \begin{align} \frac{1}{(1-s)(1-t)}+\frac{1}{2}\sum_{n=1}^{\infty}\frac{(1+s)^{n}(1+t)^{n+1}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n} =\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij+j}s^{i}t^{j} \end{align} $$
$$ \begin{align} \frac{1}{(1-s)(1-t)}+\frac{1}{2}\sum_{n=1}^{\infty}\frac{(1+s)^{n}(1+t)^{n+1}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n} =\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij+j}s^{i}t^{j} \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} \frac{(1+s)^{n}(1+t)^{n+1}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =2\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{2ij+j \choose k}{2ij+j+n-k-1 \choose n-k}s^{i}t^{j} \end{align} $$
$$ \begin{align} \frac{(1+s)^{n}(1+t)^{n+1}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =2\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{2ij+j \choose k}{2ij+j+n-k-1 \choose n-k}s^{i}t^{j} \end{align} $$
and
 $$ \begin{align} \quad\frac{(1+s)^{n}(1+t)^{n+1}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =\frac{1}{n!}\sum_{k=0}^n 2^{k+1} d(n,k) \frac{B_{k}(s)A_{k}(t)}{(1-s)^{k+1}(1-t)^{k+1}}. \end{align} $$
$$ \begin{align} \quad\frac{(1+s)^{n}(1+t)^{n+1}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right) =\frac{1}{n!}\sum_{k=0}^n 2^{k+1} d(n,k) \frac{B_{k}(s)A_{k}(t)}{(1-s)^{k+1}(1-t)^{k+1}}. \end{align} $$
Proof. The proof of parts (a) and (b) is the same as that of Theorem 4.3 (a) and (b), except that we specialize Theorem 4.2 as opposed to Theorem 4.1. To prove (c), notice that from Lemma 2.9 (a)–(b) we have
 $$ \begin{align} \left\langle \frac{1}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle & =\sum_{\lambda\text{ odd}}\sum_{\mu}\frac{2^{l(\lambda)}}{z_{\lambda}z_{\mu}}\frac{A_{l(\lambda)}(s)B_{o(\mu)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{o(\mu)+1}}\left\langle p_{\lambda},p_{\mu}\right\rangle x^{\left|\mu\right|}\nonumber \\ & =\sum_{\lambda\text{ odd}}\frac{2^{l(\lambda)}}{z_{\lambda}}\frac{A_{l(\lambda)}(s)B_{l(\lambda)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}x^{\left|\lambda\right|}, \end{align} $$
$$ \begin{align} \left\langle \frac{1}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle & =\sum_{\lambda\text{ odd}}\sum_{\mu}\frac{2^{l(\lambda)}}{z_{\lambda}z_{\mu}}\frac{A_{l(\lambda)}(s)B_{o(\mu)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{o(\mu)+1}}\left\langle p_{\lambda},p_{\mu}\right\rangle x^{\left|\mu\right|}\nonumber \\ & =\sum_{\lambda\text{ odd}}\frac{2^{l(\lambda)}}{z_{\lambda}}\frac{A_{l(\lambda)}(s)B_{l(\lambda)}(t)}{(1-s)^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}x^{\left|\lambda\right|}, \end{align} $$
and the same scalar product can be shown to be equal to
 $$ \begin{align} &\left\langle \frac{1}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle =\frac{1}{(1-s)(1-t)}\nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\frac{1}{2}\sum_{n=1}^{\infty}\frac{(1+s)^{n+1}(1+t)^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n} \end{align} $$
$$ \begin{align} &\left\langle \frac{1}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle =\frac{1}{(1-s)(1-t)}\nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\frac{1}{2}\sum_{n=1}^{\infty}\frac{(1+s)^{n+1}(1+t)^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}\left(\frac{4s}{(1+s)^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n} \end{align} $$
by using Lemma 2.8 (b)–(c). Equating Equations (4.5) and (4.6), extracting coefficients of
![]() $x^{n}$
, and then applying Lemma 2.10 (b) completes the proof of (c).
$x^{n}$
, and then applying Lemma 2.10 (b) completes the proof of (c).
Table 4 displays the first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ipk}})}(s,t)$
. The following proposition, which is Corollary 11 of [Reference Troyka and Zhuang26], characterizes the coefficients of
$P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ipk}})}(s,t)$
. The following proposition, which is Corollary 11 of [Reference Troyka and Zhuang26], characterizes the coefficients of
![]() $s^{k}t$
in
$s^{k}t$
in
![]() $P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ipk}})}(s,t)$
.
$P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ipk}})}(s,t)$
.
Table 4 Joint distribution of
![]() $\operatorname {\mathrm {lpk}}$
and
$\operatorname {\mathrm {lpk}}$
and
![]() $\operatorname {\mathrm {ipk}}$
over
$\operatorname {\mathrm {ipk}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

Proposition 4.7. For any
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $k\geq 0$
, the number of permutations
$k\geq 0$
, the number of permutations
![]() $\pi \in \mathfrak {S}_{n}$
with
$\pi \in \mathfrak {S}_{n}$
with
![]() $\operatorname {\mathrm {lpk}}(\pi )=k$
and
$\operatorname {\mathrm {lpk}}(\pi )=k$
and
![]() $\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
$\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
![]() ${n \choose 2k}$
.
${n \choose 2k}$
.
The next formula expresses the polynomial
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ilpk}})}(s,t)$
as a sum involving products of the peak and left peak polynomials. The proof follows in the same way as that of Theorem 3.4, except that we begin by substituting both Equations (3.6) and (4.4) into Theorem 4.6 (c).
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ilpk}})}(s,t)$
as a sum involving products of the peak and left peak polynomials. The proof follows in the same way as that of Theorem 3.4, except that we begin by substituting both Equations (3.6) and (4.4) into Theorem 4.6 (c).
Theorem 4.8. For all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align*} P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}(s,t) & =\frac{1}{n!}\sum_{k=0}^n d(n,k) \left((1-s)(1-t)\right)^{\frac{n-k}{2}}P_{k}^{\operatorname{\mathrm{lpk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t). \end{align*} $$
$$ \begin{align*} P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ipk}})}(s,t) & =\frac{1}{n!}\sum_{k=0}^n d(n,k) \left((1-s)(1-t)\right)^{\frac{n-k}{2}}P_{k}^{\operatorname{\mathrm{lpk}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t). \end{align*} $$
4.5 Left peaks and inverse descents
Finally, define
We omit the proofs of the following theorems as they are very similar to the proofs of analogous results presented earlier.
Theorem 4.9. We have
 $$ \begin{align} \frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+s)^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right)x^{n} =\sum_{i,j=0}^{\infty}\frac{(1+x)^{i(j+1)}}{(1-x)^{(i+1)(j+1)}}s^{i}t^{j}, \end{align} $$
$$ \begin{align} \frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+s)^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right)x^{n} =\sum_{i,j=0}^{\infty}\frac{(1+x)^{i(j+1)}}{(1-x)^{(i+1)(j+1)}}s^{i}t^{j}, \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} \qquad\frac{(1+s)^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) =\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{i(j+1) \choose k}{ij+i+j+n-k \choose n-k}s^{i}t^{j}\qquad \end{align} $$
$$ \begin{align} \qquad\frac{(1+s)^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) =\sum_{i,j=0}^{\infty}\sum_{k=0}^{n}{i(j+1) \choose k}{ij+i+j+n-k \choose n-k}s^{i}t^{j}\qquad \end{align} $$
and
 $$ \begin{align} \quad\,\frac{(1+s)^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) & =\frac{1}{n!}\sum_{k,m=0}^n f(n,k,m)\frac{B_{k}(s)A_{m}(t)}{(1-s)^{k+1}(1-t)^{m+1}} \end{align} $$
$$ \begin{align} \quad\,\frac{(1+s)^{n}}{((1-s)(1-t))^{n+1}}P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ides}})}\left(\frac{4s}{(1+s)^{2}},t\right) & =\frac{1}{n!}\sum_{k,m=0}^n f(n,k,m)\frac{B_{k}(s)A_{m}(t)}{(1-s)^{k+1}(1-t)^{m+1}} \end{align} $$
with
![]() $f(n,k,m)$
as defined in Section 2.4.
$f(n,k,m)$
as defined in Section 2.4.
Theorem 4.10. For all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align*} P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ides}})}(s,t) & =\frac{1}{n!}\sum_{k,m=0}^n f(n,k,m) (1-s)^{\frac{n-k}{2}}(1-t)^{n-m}P_{k}^{\operatorname{\mathrm{lpk}}}(s)A_{m}(t). \end{align*} $$
$$ \begin{align*} P_{n}^{(\operatorname{\mathrm{lpk}},\operatorname{\mathrm{ides}})}(s,t) & =\frac{1}{n!}\sum_{k,m=0}^n f(n,k,m) (1-s)^{\frac{n-k}{2}}(1-t)^{n-m}P_{k}^{\operatorname{\mathrm{lpk}}}(s)A_{m}(t). \end{align*} $$
See Table 5 for the first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ides}})}(s,t)$
.
$P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ides}})}(s,t)$
.
Table 5 Joint distribution of
![]() $\operatorname {\mathrm {lpk}}$
and
$\operatorname {\mathrm {lpk}}$
and
![]() $\operatorname {\mathrm {ides}}$
over
$\operatorname {\mathrm {ides}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

5 Up-down runs and biruns
We will now give analogous formulas for (mixed) two-sided distributions involving the number of up-down runs, as well as a couple involving the number of biruns.
5.1 Up-down runs and inverse up-down runs
Consider the two-sided up-down run polynomials
Theorem 5.1. We have
 $$ \begin{align*} &\frac{1}{(1-s)(1-t)}+\frac{1}{4(1-s)^{2}(1-t)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}(1+t^{2})^{n}}{(1-s^{2})^{n-1}(1-t^{2})^{n-1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{iudr}})}\left(\frac{2s}{1+s^{2}},\frac{2t}{1+t^{2}}\right)x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}+t\left(\frac{1+x}{1-x}\right)^{i}+st\frac{(1+x)^{i+j}}{(1-x)^{i+j+1}}\right)s^{2i}t^{2j}. \end{align*} $$
$$ \begin{align*} &\frac{1}{(1-s)(1-t)}+\frac{1}{4(1-s)^{2}(1-t)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}(1+t^{2})^{n}}{(1-s^{2})^{n-1}(1-t^{2})^{n-1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{iudr}})}\left(\frac{2s}{1+s^{2}},\frac{2t}{1+t^{2}}\right)x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}+t\left(\frac{1+x}{1-x}\right)^{i}+st\frac{(1+x)^{i+j}}{(1-x)^{i+j+1}}\right)s^{2i}t^{2j}. \end{align*} $$
The proof of Theorem 5.1 follows the same structure as our proofs from Sections 3–4: We compute an appropriate scalar product in multiple ways and set them equal to each other. We shall provide the full proof here but will omit the proofs for all remaining results in this section due to their similarity with what has been presented earlier.
Proof. First, Lemma 2.8 (d) along with Foulkes’s theorem (Theorem 2.1) leads to
 $$ \begin{align} & \left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{1+tH}{1-t^{2}EH}\right\rangle =\frac{1}{(1-s)(1-t)}\nonumber \\ & \qquad\qquad\qquad+\frac{1}{4(1-s)^{2}(1-t)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}(1+t^{2})^{n}}{(1-s^{2})^{n-1}(1-t^{2})^{n-1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{iudr}})}\left(\frac{2s}{1+s^{2}},\frac{2t}{1+t^{2}}\right)x^{n}. \end{align} $$
$$ \begin{align} & \left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{1+tH}{1-t^{2}EH}\right\rangle =\frac{1}{(1-s)(1-t)}\nonumber \\ & \qquad\qquad\qquad+\frac{1}{4(1-s)^{2}(1-t)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}(1+t^{2})^{n}}{(1-s^{2})^{n-1}(1-t^{2})^{n-1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{iudr}})}\left(\frac{2s}{1+s^{2}},\frac{2t}{1+t^{2}}\right)x^{n}. \end{align} $$
Next, using Lemmas 2.4 and 2.5, we obtain
 $$ \begin{align} & \left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{1}{1-t^{2}EH}\right\rangle =\sum_{i,j=0}^{\infty}\left\langle (1+sH(x))E(x)^{i}H(x)^{i},E^{j}H^{j}\right\rangle s^{2i}t^{2j}\nonumber \\ & \qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\left\langle E(x)^{i}H(x)^{i},E^{j}H^{j}\right\rangle +s\left\langle E(x)^{i}H(x)^{i+1},E^{j}H^{j}\right\rangle \right)s^{2i}t^{2j}\nonumber \\& \qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\left\langle E(x),E^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E^{j}H^{j}\right\rangle ^{i}+s\left\langle E(x),E^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E^{j}H^{j}\right\rangle ^{i+1}\right)s^{2i}t^{2j}\nonumber \\ & \qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\left(\frac{1+x}{1-x}\right)^{2ij}+s\left(\frac{1+x}{1-x}\right)^{2ij+j}\right)s^{2i}t^{2j}\nonumber \\ & \qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}\right)s^{2i}t^{2j}. \end{align} $$
$$ \begin{align} & \left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{1}{1-t^{2}EH}\right\rangle =\sum_{i,j=0}^{\infty}\left\langle (1+sH(x))E(x)^{i}H(x)^{i},E^{j}H^{j}\right\rangle s^{2i}t^{2j}\nonumber \\ & \qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\left\langle E(x)^{i}H(x)^{i},E^{j}H^{j}\right\rangle +s\left\langle E(x)^{i}H(x)^{i+1},E^{j}H^{j}\right\rangle \right)s^{2i}t^{2j}\nonumber \\& \qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\left\langle E(x),E^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E^{j}H^{j}\right\rangle ^{i}+s\left\langle E(x),E^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E^{j}H^{j}\right\rangle ^{i+1}\right)s^{2i}t^{2j}\nonumber \\ & \qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\left(\frac{1+x}{1-x}\right)^{2ij}+s\left(\frac{1+x}{1-x}\right)^{2ij+j}\right)s^{2i}t^{2j}\nonumber \\ & \qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}\right)s^{2i}t^{2j}. \end{align} $$
Similarly, using Lemmas 2.4–2.7, we obtain
 $$ \begin{align} & \left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{tH}{1-t^{2}EH}\right\rangle =\sum_{i,j=0}^{\infty}\left\langle (1+sH(x))E(x)^{i}H(x)^{i},E^{j}H^{j+1}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left\langle ((1+sH(x))E(x)^{i}H(x)^{i})[X+1],E^{j}H^{j}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left\langle (E(x)^{i}H(x)^{i}+sE(x)^{i}H(x)^{i+1})[X+1],E^{j}H^{j}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left\langle (E(x)^{i}H(x)^{i}+sE(x)^{i}H(x)^{i+1})[X+1],E^{j}H^{j}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left\langle \left(\frac{1+x}{1-x}\right)^{i}E(x)^{i}H(x)^{i}+s\frac{(1+x)^{i}}{(1-x)^{i+1}}E(x)^{i}H(x)^{i+1},E^{j}H^{j}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\Bigg(\left(\frac{1+x}{1-x}\right)^{i}\left\langle E(x),E^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E^{j}H^{j}\right\rangle ^{i}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad\quad +s\frac{(1+x)^{i}}{(1-x)^{i+1}}\left\langle E(x),E^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E^{j}H^{j}\right\rangle ^{i+1}\Bigg)s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\left(\frac{1+x}{1-x}\right)^{2ij+i}+s\frac{(1+x)^{2ij+i+j}}{(1-x)^{2ij+i+j+1}}\right)s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(t\left(\frac{1+x}{1-x}\right)^{i}+st\frac{(1+x)^{i+j}}{(1-x)^{i+j+1}}\right)s^{2i}t^{2j}. \end{align} $$
$$ \begin{align} & \left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{tH}{1-t^{2}EH}\right\rangle =\sum_{i,j=0}^{\infty}\left\langle (1+sH(x))E(x)^{i}H(x)^{i},E^{j}H^{j+1}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left\langle ((1+sH(x))E(x)^{i}H(x)^{i})[X+1],E^{j}H^{j}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left\langle (E(x)^{i}H(x)^{i}+sE(x)^{i}H(x)^{i+1})[X+1],E^{j}H^{j}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left\langle (E(x)^{i}H(x)^{i}+sE(x)^{i}H(x)^{i+1})[X+1],E^{j}H^{j}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left\langle \left(\frac{1+x}{1-x}\right)^{i}E(x)^{i}H(x)^{i}+s\frac{(1+x)^{i}}{(1-x)^{i+1}}E(x)^{i}H(x)^{i+1},E^{j}H^{j}\right\rangle s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\Bigg(\left(\frac{1+x}{1-x}\right)^{i}\left\langle E(x),E^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E^{j}H^{j}\right\rangle ^{i}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad\quad +s\frac{(1+x)^{i}}{(1-x)^{i+1}}\left\langle E(x),E^{j}H^{j}\right\rangle ^{i}\left\langle H(x),E^{j}H^{j}\right\rangle ^{i+1}\Bigg)s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\left(\frac{1+x}{1-x}\right)^{2ij+i}+s\frac{(1+x)^{2ij+i+j}}{(1-x)^{2ij+i+j+1}}\right)s^{2i}t^{2j+1}\nonumber \\ & \qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(t\left(\frac{1+x}{1-x}\right)^{i}+st\frac{(1+x)^{i+j}}{(1-x)^{i+j+1}}\right)s^{2i}t^{2j}. \end{align} $$
Summing Equations (5.2) and (5.3) yields
 $$ \begin{align*} \left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{1+tH}{1-t^{2}EH}\right\rangle = \sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}+t\left(\frac{1+x}{1-x}\right)^{i}+st\frac{(1+x)^{i+j}}{(1-x)^{i+j+1}}\right)s^{2i}t^{2j}; \end{align*} $$
$$ \begin{align*} \left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{1+tH}{1-t^{2}EH}\right\rangle = \sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}+t\left(\frac{1+x}{1-x}\right)^{i}+st\frac{(1+x)^{i+j}}{(1-x)^{i+j+1}}\right)s^{2i}t^{2j}; \end{align*} $$
comparing this with Equation (5.1) completes the proof.
The first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {iudr}})}(s,t)$
are given in Table 6. We note that the permutations in
$P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {iudr}})}(s,t)$
are given in Table 6. We note that the permutations in
![]() $\mathfrak {S}_{n}$
with n up-down runs are precisely the alternating permutations in
$\mathfrak {S}_{n}$
with n up-down runs are precisely the alternating permutations in
![]() $\mathfrak {S}_{n}$
, so the coefficient of
$\mathfrak {S}_{n}$
, so the coefficient of
![]() $s^{n}t^{n}$
of
$s^{n}t^{n}$
of
![]() $P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {iudr}})}(s,t)$
is the number of doubly alternating permutations in
$P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {iudr}})}(s,t)$
is the number of doubly alternating permutations in
![]() $\mathfrak {S}_{n}$
. In fact, Stanley’s formula (2.2) for doubly alternating permutations can be derived from Theorem 5.1, although it is simpler to work with our formulas for
$\mathfrak {S}_{n}$
. In fact, Stanley’s formula (2.2) for doubly alternating permutations can be derived from Theorem 5.1, although it is simpler to work with our formulas for
![]() $(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})$
and
$(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})$
and
![]() $(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}})$
.
$(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}})$
.
Table 6 Joint distribution of
![]() $\operatorname {\mathrm {udr}}$
and
$\operatorname {\mathrm {udr}}$
and
![]() $\operatorname {\mathrm {iudr}}$
over
$\operatorname {\mathrm {iudr}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

To invert Theorem 5.1 and other formulas in this section, we will need to solve
![]() $s=2u/(1+u^{2})$
for u, and the solution is given by
$s=2u/(1+u^{2})$
for u, and the solution is given by
![]() $u=s^{-1}(1-\sqrt {1-s^{2}})=(s/2)C(s^{2}/4)$
, where
$u=s^{-1}(1-\sqrt {1-s^{2}})=(s/2)C(s^{2}/4)$
, where
![]() $C(x)$
is the Catalan number generating function. Hence, Theorem 5.1 can be written as
$C(x)$
is the Catalan number generating function. Hence, Theorem 5.1 can be written as
 $$ \begin{align*} &\frac{1}{(1-u)(1-v)}+\frac{1}{4(1-u)^{2}(1-v)^{2}}\sum_{n=1}^{\infty}\frac{(1+u^{2})^{n}(1+v^{2})^{n}}{(1-u^{2})^{n-1}(1-v^{2})^{n-1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{iudr}})}(s,t)x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+u\left(\frac{1+x}{1-x}\right)^{j}+v\left(\frac{1+x}{1-x}\right)^{i}+uv\frac{(1+x)^{i+j}}{(1-x)^{i+j+1}}\right)u^{2i}v^{2j}, \end{align*} $$
$$ \begin{align*} &\frac{1}{(1-u)(1-v)}+\frac{1}{4(1-u)^{2}(1-v)^{2}}\sum_{n=1}^{\infty}\frac{(1+u^{2})^{n}(1+v^{2})^{n}}{(1-u^{2})^{n-1}(1-v^{2})^{n-1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{iudr}})}(s,t)x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+u\left(\frac{1+x}{1-x}\right)^{j}+v\left(\frac{1+x}{1-x}\right)^{i}+uv\frac{(1+x)^{i+j}}{(1-x)^{i+j+1}}\right)u^{2i}v^{2j}, \end{align*} $$
where
![]() $u=s^{-1}(1-\sqrt {1-s^{2}})=(s/2)C(s^{2}/4)$
and
$u=s^{-1}(1-\sqrt {1-s^{2}})=(s/2)C(s^{2}/4)$
and
![]() $v=t^{-1}(1-\sqrt {1-t^{2}})=(t/2)C(t^{2}/4)$
.
$v=t^{-1}(1-\sqrt {1-t^{2}})=(t/2)C(t^{2}/4)$
.
5.2 Up-down runs, inverse peaks and inverse descents
Next, let us study the statistic
![]() $(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {ides}})$
and its specializations
$(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}},\operatorname {\mathrm {ides}})$
and its specializations
![]() $(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})$
and
$(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})$
and
![]() $(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ides}})$
. Define
$(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ides}})$
. Define

Theorem 5.2. We have
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\left(\frac{1+yt}{1-t}\right)^{n+1}\frac{P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},\frac{(1+y)^{2}t}{(y+t)(1+yt)},\frac{y+t}{1+yt}\right)}{2(1-s)^{2}(1+y)}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{(1+x)(1+yx)}{(1-yx)(1-x)}\right)^{ij}\left(1+s\left(\frac{1+yx}{1-x}\right)^{j}\right)s^{2i}t^{j}\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\left(\frac{1+yt}{1-t}\right)^{n+1}\frac{P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},\frac{(1+y)^{2}t}{(y+t)(1+yt)},\frac{y+t}{1+yt}\right)}{2(1-s)^{2}(1+y)}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{(1+x)(1+yx)}{(1-yx)(1-x)}\right)^{ij}\left(1+s\left(\frac{1+yx}{1-x}\right)^{j}\right)s^{2i}t^{j}\nonumber \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} \qquad & \frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\left(\frac{1+yt}{1-t}\right)^{n+1}\frac{P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},\frac{(1+y)^{2}t}{(y+t)(1+yt)},\frac{y+t}{1+yt}\right)}{2(1-s)^{2}(1+y)}\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{\substack{\lambda\vdash n\\ \mathrm{odd} } }\frac{2^{l(\lambda)}}{z_{\lambda}}\frac{A_{l(\lambda)}(s^{2})A_{l(\lambda)}(t)}{(1-s^{2})^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}\prod_{k=1}^{l(\lambda)}(1-(-y)^{\lambda_{k}})\nonumber\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad+s\sum_{\lambda\vdash n}\frac{1}{z_{\lambda}}\frac{B_{o(\lambda)}(s^{2})A_{l(\lambda)}(t)}{(1-s^{2})^{o(\lambda)+1}(1-t)^{l(\lambda)+1}}\prod_{k=1}^{l(\lambda)}(1-(-y)^{\lambda_{k}}).\nonumber \end{align} $$
$$ \begin{align} \qquad & \frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\left(\frac{1+yt}{1-t}\right)^{n+1}\frac{P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},\frac{(1+y)^{2}t}{(y+t)(1+yt)},\frac{y+t}{1+yt}\right)}{2(1-s)^{2}(1+y)}\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{\substack{\lambda\vdash n\\ \mathrm{odd} } }\frac{2^{l(\lambda)}}{z_{\lambda}}\frac{A_{l(\lambda)}(s^{2})A_{l(\lambda)}(t)}{(1-s^{2})^{l(\lambda)+1}(1-t)^{l(\lambda)+1}}\prod_{k=1}^{l(\lambda)}(1-(-y)^{\lambda_{k}})\nonumber\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad+s\sum_{\lambda\vdash n}\frac{1}{z_{\lambda}}\frac{B_{o(\lambda)}(s^{2})A_{l(\lambda)}(t)}{(1-s^{2})^{o(\lambda)+1}(1-t)^{l(\lambda)+1}}\prod_{k=1}^{l(\lambda)}(1-(-y)^{\lambda_{k}}).\nonumber \end{align} $$
As before, we set
![]() $y=1$
to specialize to
$y=1$
to specialize to
![]() $(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})$
, immediately arriving at parts (a) and (b) of the following theorem. Part (c) is proven similarly to Theorem 3.4, except that we also use the formula
$(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})$
, immediately arriving at parts (a) and (b) of the following theorem. Part (c) is proven similarly to Theorem 3.4, except that we also use the formula
 $$ \begin{align*} 2^{n}A_{n}(t^{2})+tB_{n}(t^{2})=\frac{(1+t)^{2}(1+t^{2})^{n}}{2}P_{n}^{\operatorname{\mathrm{udr}}}\left(\frac{2t}{1+t^{2}}\right) \end{align*} $$
$$ \begin{align*} 2^{n}A_{n}(t^{2})+tB_{n}(t^{2})=\frac{(1+t)^{2}(1+t^{2})^{n}}{2}P_{n}^{\operatorname{\mathrm{udr}}}\left(\frac{2t}{1+t^{2}}\right) \end{align*} $$
[Reference Gessel and Zhuang15, Section 6.3], where
Theorem 5.3. We have
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{4(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\left(\frac{1+t}{1-t}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n}\\ &\quad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}\right)s^{2i}t^{j}\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{4(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\left(\frac{1+t}{1-t}\right)^{n+1}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n}\\ &\quad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}\right)s^{2i}t^{j}\nonumber \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} \frac{1}{4(1-s)^{2}}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\left(\frac{1+t}{1-t}\right)^{n+1}&P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)\\ &\quad=\frac{1}{n!}\sum_{k=0}^n 2^{k}d(n,k)\frac{(2^{k}A_{k}(s^{2})+sb:{k}(s^{2}))A_{k}(t)}{(1-s^{2})^{k+1}(1-t)^{k+1}}\nonumber \end{align} $$
$$ \begin{align} \frac{1}{4(1-s)^{2}}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\left(\frac{1+t}{1-t}\right)^{n+1}&P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)\\ &\quad=\frac{1}{n!}\sum_{k=0}^n 2^{k}d(n,k)\frac{(2^{k}A_{k}(s^{2})+sb:{k}(s^{2}))A_{k}(t)}{(1-s^{2})^{k+1}(1-t)^{k+1}}\nonumber \end{align} $$
and
 $$ \begin{align} P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}})}(s,t) & =\frac{1}{n!}\sum_{k=0}^n d(n,k)\left((1-s^{2})(1-t)\right)^{\frac{n-k}{2}}P_{k}^{\operatorname{\mathrm{udr}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t). \end{align} $$
$$ \begin{align} P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ipk}})}(s,t) & =\frac{1}{n!}\sum_{k=0}^n d(n,k)\left((1-s^{2})(1-t)\right)^{\frac{n-k}{2}}P_{k}^{\operatorname{\mathrm{udr}}}(s)P_{k}^{\operatorname{\mathrm{pk}}}(t). \end{align} $$
The first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})}(s,t)$
are displayed in Table 7. The coefficients of
$P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})}(s,t)$
are displayed in Table 7. The coefficients of
![]() $s^{k}t$
in
$s^{k}t$
in
![]() $P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})}(s,t)$
are binomial coefficients, just like the coefficients of
$P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})}(s,t)$
are binomial coefficients, just like the coefficients of
![]() $st^{k}$
in
$st^{k}$
in
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
from Table 2.
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
from Table 2.
Table 7 Joint distribution of
![]() $\operatorname {\mathrm {udr}}$
and
$\operatorname {\mathrm {udr}}$
and
![]() $\operatorname {\mathrm {ipk}}$
over
$\operatorname {\mathrm {ipk}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

Proposition 5.4. For any
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $k\geq 0$
, the number of permutations
$k\geq 0$
, the number of permutations
![]() $\pi \in \mathfrak {S}_{n}$
with
$\pi \in \mathfrak {S}_{n}$
with
![]() $\operatorname {\mathrm {udr}}(\pi )=k$
and
$\operatorname {\mathrm {udr}}(\pi )=k$
and
![]() $\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
$\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
![]() ${n-1 \choose k-1}$
.
${n-1 \choose k-1}$
.
Unlike the analogous results given earlier, Proposition 5.4 was not proven in [Reference Troyka and Zhuang26], so we shall supply a proof here.
Proof. Let us define the up-down composition of a permutation
![]() $\pi $
, denoted
$\pi $
, denoted
![]() $\operatorname {\mathrm {udComp}}(\pi )$
, in the following way: If
$\operatorname {\mathrm {udComp}}(\pi )$
, in the following way: If
![]() $u_{1},u_{2},\dots ,u_{k}$
are the lengths of the up-down runs of
$u_{1},u_{2},\dots ,u_{k}$
are the lengths of the up-down runs of
![]() $\pi $
in the order that they appear, then
$\pi $
in the order that they appear, then ![]() . For example, if
. For example, if
![]() $\pi =312872569$
, then
$\pi =312872569$
, then
![]() $\operatorname {\mathrm {udComp}}(\pi )=(1,1,2,2,3)$
. Note that if
$\operatorname {\mathrm {udComp}}(\pi )=(1,1,2,2,3)$
. Note that if
![]() $\pi \in \mathfrak {S}_{n}$
, then
$\pi \in \mathfrak {S}_{n}$
, then
![]() $\operatorname {\mathrm {udComp}}(\pi )$
is a composition of n. It is not hard to verify that the descent composition determines the up-down composition and vice versa.
$\operatorname {\mathrm {udComp}}(\pi )$
is a composition of n. It is not hard to verify that the descent composition determines the up-down composition and vice versa.
According to [Reference Troyka and Zhuang26, Theorem 5], for any composition
![]() $L\vDash n$
, there exists exactly one permutation
$L\vDash n$
, there exists exactly one permutation
![]() $\pi \in \mathfrak {S}_{n}$
with descent composition L such that
$\pi \in \mathfrak {S}_{n}$
with descent composition L such that
![]() $\operatorname {\mathrm {ipk}}(\pi )=0$
. In light of this fact and Proposition 3.7, it suffices to construct a bijection between compositions
$\operatorname {\mathrm {ipk}}(\pi )=0$
. In light of this fact and Proposition 3.7, it suffices to construct a bijection between compositions
![]() $L\vDash n$
with k parts and compositions
$L\vDash n$
with k parts and compositions
![]() $K\vDash n$
satisfying
$K\vDash n$
satisfying
![]() $\operatorname {\mathrm {udr}}(K)=k$
. This bijection is obtained by mapping L to the descent composition K of any permutation with up-down composition L. For example, the composition
$\operatorname {\mathrm {udr}}(K)=k$
. This bijection is obtained by mapping L to the descent composition K of any permutation with up-down composition L. For example, the composition
![]() $L=(1,1,2,2,3)$
is mapped to
$L=(1,1,2,2,3)$
is mapped to
![]() $K=(1,3,1,4)$
, which is the descent composition of the permutation
$K=(1,3,1,4)$
, which is the descent composition of the permutation
![]() $\pi $
from above.
$\pi $
from above.
Setting
![]() $y=0$
in Theorem 5.2 yields the analogous result for
$y=0$
in Theorem 5.2 yields the analogous result for
![]() $(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ides}})$
.
$(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ides}})$
.
Theorem 5.5. We have
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{2(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}(1-t)^{n+1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},t\right)x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{ij}\left(1+\frac{s}{(1-x)^{j}}\right)s^{2i}t^{j}\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{2(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}(1-t)^{n+1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},t\right)x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{ij}\left(1+\frac{s}{(1-x)^{j}}\right)s^{2i}t^{j}\nonumber \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} &\frac{(1+s^{2})^{n}}{2(1-s)^{2}(1-s^{2})^{n-1}(1-t)^{n+1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},t\right)x^{n}\\ &\qquad\quad\qquad=\frac{1}{n!}\sum_{k=0}^n 2^k d(n,k)\frac{A_{k}(s^{2})A_{k}(t)}{(1-s^{2})^{k+1}(1-t)^{k+1}} +\frac{s}{n!}\sum_{k,m=0}^n f(n,k,m)\frac{B_{k}(s^{2})A_{m}(t)}{(1-s^{2})^{k+1}(1-t)^{m+1}}. \nonumber \end{align} $$
$$ \begin{align} &\frac{(1+s^{2})^{n}}{2(1-s)^{2}(1-s^{2})^{n-1}(1-t)^{n+1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},t\right)x^{n}\\ &\qquad\quad\qquad=\frac{1}{n!}\sum_{k=0}^n 2^k d(n,k)\frac{A_{k}(s^{2})A_{k}(t)}{(1-s^{2})^{k+1}(1-t)^{k+1}} +\frac{s}{n!}\sum_{k,m=0}^n f(n,k,m)\frac{B_{k}(s^{2})A_{m}(t)}{(1-s^{2})^{k+1}(1-t)^{m+1}}. \nonumber \end{align} $$
Table 8 contains the first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ides}})}(s,t)$
.
$P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ides}})}(s,t)$
.
Table 8 Joint distribution of
![]() $\operatorname {\mathrm {udr}}$
and
$\operatorname {\mathrm {udr}}$
and
![]() $\operatorname {\mathrm {ides}}$
over
$\operatorname {\mathrm {ides}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

5.3 Up-down runs, inverse left peaks and inverse descents
Define

Theorem 5.6. We have
 $$ \begin{align*} &\frac{1}{(1-s)(1-t)}+\frac{1}{2(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}(1+yt)^{n}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ilpk}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},\frac{(1+y)^{2}t}{(y+t)(1+yt)},\frac{y+t}{1+yt}\right)}{(1-s^{2})^{n-1}(1-t)^{n+1}}x^{n}\\[7pt] &\qquad\qquad\qquad\qquad\qquad\quad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{i(j+1)}\left(\frac{1+yx}{1-yx}\right)^{ij}\left(1+s\frac{(1+yx)^{j}}{(1-x)^{j+1}}\right)s^{2i}t^{j}. \end{align*} $$
$$ \begin{align*} &\frac{1}{(1-s)(1-t)}+\frac{1}{2(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}(1+yt)^{n}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ilpk}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},\frac{(1+y)^{2}t}{(y+t)(1+yt)},\frac{y+t}{1+yt}\right)}{(1-s^{2})^{n-1}(1-t)^{n+1}}x^{n}\\[7pt] &\qquad\qquad\qquad\qquad\qquad\quad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{i(j+1)}\left(\frac{1+yx}{1-yx}\right)^{ij}\left(1+s\frac{(1+yx)^{j}}{(1-x)^{j+1}}\right)s^{2i}t^{j}. \end{align*} $$
Setting
![]() $y=1$
in Theorem 5.6 yields part (a) of the following theorem. Part (b) is obtained by computing the scalar product
$y=1$
in Theorem 5.6 yields part (a) of the following theorem. Part (b) is obtained by computing the scalar product
 $$\begin{align*}\left\langle \frac{1+sH(x)}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle \end{align*}$$
$$\begin{align*}\left\langle \frac{1+sH(x)}{1-sE(x)H(x)},\frac{H}{1-tEH}\right\rangle \end{align*}$$
using Lemmas 2.8 (c)–(d) and 2.9 (b)–(c). Part (c) is obtained from (b) in a way similar to the proof of Theorem 4.4, making use of Equation (4.4).
Theorem 5.7. We have
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{2(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}(1+t)^{n}}{(1-s^{2})^{n-1}(1-t)^{n+1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ilpk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n}\\[7pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{i(2j+1)}\left(1+s\frac{(1+x)^{j}}{(1-x)^{j+1}}\right)s^{2i}t^{j}\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{2(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}(1+t)^{n}}{(1-s^{2})^{n-1}(1-t)^{n+1}}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ilpk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)x^{n}\\[7pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{i(2j+1)}\left(1+s\frac{(1+x)^{j}}{(1-x)^{j+1}}\right)s^{2i}t^{j}\nonumber \end{align} $$
and, for all
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
 $$ \begin{align} &\frac{(1+s^{2})^{n}(1+t)^{n}}{2(1-s)^{2}(1-s^{2})^{n-1}(1-t)^{n+1}} P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ilpk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)\\[7pt] &\qquad\qquad\quad\qquad=\frac{1}{n!}\sum_{k=0}^n 2^k d(n,k) \frac{A_{k}(s^{2})B_{k}(t)}{(1-s^{2})^{k+1}(1-t)^{k+1}} +\frac{s}{n!}\sum_{k=0}^n e(n,k) \frac{B_{k}(s^{2})B_{k}(t)}{(1-s^{2})^{k+1}(1-t)^{k+1}}\nonumber \end{align} $$
$$ \begin{align} &\frac{(1+s^{2})^{n}(1+t)^{n}}{2(1-s)^{2}(1-s^{2})^{n-1}(1-t)^{n+1}} P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ilpk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)\\[7pt] &\qquad\qquad\quad\qquad=\frac{1}{n!}\sum_{k=0}^n 2^k d(n,k) \frac{A_{k}(s^{2})B_{k}(t)}{(1-s^{2})^{k+1}(1-t)^{k+1}} +\frac{s}{n!}\sum_{k=0}^n e(n,k) \frac{B_{k}(s^{2})B_{k}(t)}{(1-s^{2})^{k+1}(1-t)^{k+1}}\nonumber \end{align} $$
and
 $$ \begin{align} &(1+s)^{2}(1+s^{2})^{n}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ilpk}})}\left(\frac{2s}{1+s^{2}},t\right)\\ & \quad\qquad =\frac{1}{n!}\sum_{k=0}^n 2^{k+1} d(n,k) \left((1-s^{2})(1-t)^{1/2}\right)^{n-k}A_{k}(s^{2})P_{k}^{\operatorname{\mathrm{lpk}}}(t)\nonumber\\ & \qquad\qquad\quad +\frac{2s}{n!}\sum_{k=0}^n e(n,k)\left((1-s^{2})(1-t)^{1/2}\right)^{n-k}B_{k}(s^{2})P_{k}^{\operatorname{\mathrm{lpk}}}(t).\nonumber \end{align} $$
$$ \begin{align} &(1+s)^{2}(1+s^{2})^{n}P_{n}^{(\operatorname{\mathrm{udr}},\operatorname{\mathrm{ilpk}})}\left(\frac{2s}{1+s^{2}},t\right)\\ & \quad\qquad =\frac{1}{n!}\sum_{k=0}^n 2^{k+1} d(n,k) \left((1-s^{2})(1-t)^{1/2}\right)^{n-k}A_{k}(s^{2})P_{k}^{\operatorname{\mathrm{lpk}}}(t)\nonumber\\ & \qquad\qquad\quad +\frac{2s}{n!}\sum_{k=0}^n e(n,k)\left((1-s^{2})(1-t)^{1/2}\right)^{n-k}B_{k}(s^{2})P_{k}^{\operatorname{\mathrm{lpk}}}(t).\nonumber \end{align} $$
See Table 9 for the first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ilpk}})}(s,t)$
.
$P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ilpk}})}(s,t)$
.
Table 9 Joint distribution of
![]() $\operatorname {\mathrm {udr}}$
and
$\operatorname {\mathrm {udr}}$
and
![]() $\operatorname {\mathrm {ilpk}}$
over
$\operatorname {\mathrm {ilpk}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

5.4 Biruns
Recall that a birun is a maximal monotone consecutive subsequence, whereas an up-down run is either a birun or an initial descent. In [Reference Gessel and Zhuang15], the authors gave the formula
 $$ \begin{align*} \frac{2+tH(x)+tE(x)}{1-t^{2}E(x)H(x)} & =\frac{2}{1-t}+\frac{2t}{(1-t)^{2}}xh_{1}+\frac{(1+t)^{3}}{2(1-t)}\sum_{n=2}^{\infty}\sum_{L\vDash n}\frac{(1+t^{2})^{n-1}}{(1-t^{2})^{n}}\left(\frac{2t}{1+t^{2}}\right)^{\operatorname{\mathrm{br}}(L)}x^{n}r_{L} \end{align*} $$
$$ \begin{align*} \frac{2+tH(x)+tE(x)}{1-t^{2}E(x)H(x)} & =\frac{2}{1-t}+\frac{2t}{(1-t)^{2}}xh_{1}+\frac{(1+t)^{3}}{2(1-t)}\sum_{n=2}^{\infty}\sum_{L\vDash n}\frac{(1+t^{2})^{n-1}}{(1-t^{2})^{n}}\left(\frac{2t}{1+t^{2}}\right)^{\operatorname{\mathrm{br}}(L)}x^{n}r_{L} \end{align*} $$
(cf. Lemma 2.8), which allows us to produce formulas for (mixed) two-sided distributions involving the number of biruns. For example, computing the scalar product
 $$ \begin{align} \left\langle \frac{2+sH(x)+sE(x)}{1-s^{2}E(x)H(x)},\frac{2+tH+tE}{1-t^{2}EH}\right\rangle \end{align} $$
$$ \begin{align} \left\langle \frac{2+sH(x)+sE(x)}{1-s^{2}E(x)H(x)},\frac{2+tH+tE}{1-t^{2}EH}\right\rangle \end{align} $$
would yield a formula for the two-sided distribution of
![]() $\operatorname {\mathrm {br}}$
, but we chose not to derive this formula as it would be complicated to write down. Looking back at the formula in Theorem 5.1 for the two-sided distribution of
$\operatorname {\mathrm {br}}$
, but we chose not to derive this formula as it would be complicated to write down. Looking back at the formula in Theorem 5.1 for the two-sided distribution of
![]() $\operatorname {\mathrm {udr}}$
, we see that the right-hand side is a summation whose summands are each a sum involving four terms, which is because the numerators in the scalar product
$\operatorname {\mathrm {udr}}$
, we see that the right-hand side is a summation whose summands are each a sum involving four terms, which is because the numerators in the scalar product
 $$\begin{align*}\left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{1+tH}{1-t^{2}EH}\right\rangle \end{align*}$$
$$\begin{align*}\left\langle \frac{1+sH(x)}{1-s^{2}E(x)H(x)},\frac{1+tH}{1-t^{2}EH}\right\rangle \end{align*}$$
that we sought to compute has two terms each. The numerators in the scalar product (5.4) contain three terms each, which will lead to nine terms in the formula for
![]() $(\operatorname {\mathrm {br}},\operatorname {\mathrm {ibr}})$
as opposed to four.
$(\operatorname {\mathrm {br}},\operatorname {\mathrm {ibr}})$
as opposed to four.
On the other hand, formulas for the polynomials
have fewer such terms, and so we present them below.
Theorem 5.8. We have
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{2stx}{(1-s)^{2}(1-t)^{2}}+\frac{(1+s)^{3}}{8(1-s)}\sum_{n=2}^{\infty}\frac{(1+s^{2})^{n-1}(1+t)^{n+1}P_{n}^{(\operatorname{\mathrm{br}},\operatorname{\mathrm{ipk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)}{(1-s^{2})^{n}(1-t)^{n+1}}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}\right)s^{2i}t^{j}\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{2stx}{(1-s)^{2}(1-t)^{2}}+\frac{(1+s)^{3}}{8(1-s)}\sum_{n=2}^{\infty}\frac{(1+s^{2})^{n-1}(1+t)^{n+1}P_{n}^{(\operatorname{\mathrm{br}},\operatorname{\mathrm{ipk}})}\left(\frac{2s}{1+s^{2}},\frac{4t}{(1+t)^{2}}\right)}{(1-s^{2})^{n}(1-t)^{n+1}}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{2ij}\left(1+s\left(\frac{1+x}{1-x}\right)^{j}\right)s^{2i}t^{j}\nonumber \end{align} $$
and
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{stx}{(1-s)^{2}(1-t)^{2}}+\frac{(1+s)^{3}}{4(1-s)}\sum_{n=2}^{\infty}\frac{(1+s^{2})^{n-1}P_{n}^{(\operatorname{\mathrm{br}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},t\right)}{(1-s^{2})^{n}(1-t)^{n+1}}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\frac{1}{2}\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{ij}\left(2+\frac{s}{(1-x)^{j}}+s(1+x)^{j}\right)s^{2i}t^{j}.\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{stx}{(1-s)^{2}(1-t)^{2}}+\frac{(1+s)^{3}}{4(1-s)}\sum_{n=2}^{\infty}\frac{(1+s^{2})^{n-1}P_{n}^{(\operatorname{\mathrm{br}},\operatorname{\mathrm{ides}})}\left(\frac{2s}{1+s^{2}},t\right)}{(1-s^{2})^{n}(1-t)^{n+1}}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\frac{1}{2}\sum_{i,j=0}^{\infty}\left(\frac{1+x}{1-x}\right)^{ij}\left(2+\frac{s}{(1-x)^{j}}+s(1+x)^{j}\right)s^{2i}t^{j}.\nonumber \end{align} $$
The first several polynomials
![]() $P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ipk}})}(s,t)$
and
$P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ipk}})}(s,t)$
and
![]() $P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ides}})}(s,t)$
are displayed in Tables 10–11. Notice that the coefficients of
$P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ides}})}(s,t)$
are displayed in Tables 10–11. Notice that the coefficients of
![]() $s^{k}t$
in
$s^{k}t$
in
![]() $P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ipk}})}(t)$
are twice the coefficients of
$P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ipk}})}(t)$
are twice the coefficients of
![]() $s^{k}t$
in
$s^{k}t$
in
![]() $P_{n-1}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})}(t)$
; we shall give a simple proof of this fact.
$P_{n-1}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})}(t)$
; we shall give a simple proof of this fact.
Table 10 Joint distribution of
![]() $\operatorname {\mathrm {br}}$
and
$\operatorname {\mathrm {br}}$
and
![]() $\operatorname {\mathrm {ipk}}$
over
$\operatorname {\mathrm {ipk}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

Table 11 Joint distribution of
![]() $\operatorname {\mathrm {br}}$
and
$\operatorname {\mathrm {br}}$
and
![]() $\operatorname {\mathrm {ides}}$
over
$\operatorname {\mathrm {ides}}$
over
![]() $\mathfrak {S}_{n}$
$\mathfrak {S}_{n}$

Proposition 5.9. For any
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $k\geq 0$
, the number of permutations in
$k\geq 0$
, the number of permutations in
![]() $\mathfrak {S}_{n}$
with
$\mathfrak {S}_{n}$
with
![]() $\operatorname {\mathrm {br}}(\pi )=k$
and
$\operatorname {\mathrm {br}}(\pi )=k$
and
![]() $\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
$\operatorname {\mathrm {ipk}}(\pi )=0$
is equal to
![]() $2{n-2 \choose k-1}$
, twice the number of permutations in
$2{n-2 \choose k-1}$
, twice the number of permutations in
![]() $\mathfrak {S}_{n-1}$
with
$\mathfrak {S}_{n-1}$
with
![]() $\operatorname {\mathrm {udr}}(\pi )=k$
and
$\operatorname {\mathrm {udr}}(\pi )=k$
and
![]() $\operatorname {\mathrm {ipk}}(\pi )=0$
.
$\operatorname {\mathrm {ipk}}(\pi )=0$
.
Proof. In light of Proposition 5.4 and its proof, it suffices to construct a one-to-two map from compositions
![]() $L\vDash n-1$
with k parts to compositions
$L\vDash n-1$
with k parts to compositions
![]() $K\vDash n$
satisfying
$K\vDash n$
satisfying
![]() $\operatorname {\mathrm {br}}(K)=k$
. We claim that such a map is given by sending
$\operatorname {\mathrm {br}}(K)=k$
. We claim that such a map is given by sending
![]() $L=(L_{1},L_{2},\dots ,L_{k})$
to the descent compositions corresponding to the up-down compositions
$L=(L_{1},L_{2},\dots ,L_{k})$
to the descent compositions corresponding to the up-down compositions
![]() $J=(L_{1}+1,L_{2},\dots ,L_{k})$
and
$J=(L_{1}+1,L_{2},\dots ,L_{k})$
and
![]() $J^{\prime }=(1,L_{1},L_{2},\dots ,L_{k})$
. It is easy to see that
$J^{\prime }=(1,L_{1},L_{2},\dots ,L_{k})$
. It is easy to see that
![]() $\operatorname {\mathrm {br}}(\pi )=k$
if and only if
$\operatorname {\mathrm {br}}(\pi )=k$
if and only if
![]() $\operatorname {\mathrm {udComp}}(\pi )$
has k parts with initial part greater than 1 or if
$\operatorname {\mathrm {udComp}}(\pi )$
has k parts with initial part greater than 1 or if
![]() $\operatorname {\mathrm {udComp}}(\pi )$
has
$\operatorname {\mathrm {udComp}}(\pi )$
has
![]() $k+1$
parts with initial part 1, so this map is well defined. For example, let
$k+1$
parts with initial part 1, so this map is well defined. For example, let
![]() $L=(4,1,1,2)$
. Then permutations with up-down compositions
$L=(4,1,1,2)$
. Then permutations with up-down compositions
![]() $J=(5,1,1,2)$
and
$J=(5,1,1,2)$
and
![]() $J^{\prime }=(1,4,1,1,2)$
have descent compositions
$J^{\prime }=(1,4,1,1,2)$
have descent compositions
![]() $K=(5,2,1,1)$
and
$K=(5,2,1,1)$
and
![]() $K^{\prime }=(1,1,1,1,2,3)$
, respectively, so our map sends L to K and
$K^{\prime }=(1,1,1,1,2,3)$
, respectively, so our map sends L to K and
![]() $K^{\prime }$
. The reverse procedure is given by first taking the up-down composition corresponding to the descent composition input and then removing the first part if it is equal to 1 and subtracting 1 from the first part otherwise.
$K^{\prime }$
. The reverse procedure is given by first taking the up-down composition corresponding to the descent composition input and then removing the first part if it is equal to 1 and subtracting 1 from the first part otherwise.
In Table 11, we first collect powers of s in displaying the
![]() $P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ides}})}(s,t)$
to showcase the symmetry present in the coefficients of
$P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ides}})}(s,t)$
to showcase the symmetry present in the coefficients of
![]() $s^{k}$
. This symmetry can be explained in the same way as for the polynomials
$s^{k}$
. This symmetry can be explained in the same way as for the polynomials
![]() $P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
: Upon taking reverses, we have that
$P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ides}})}(s,t)$
: Upon taking reverses, we have that
![]() $\operatorname {\mathrm {ides}}(\pi ^{r})=n-1-\operatorname {\mathrm {ides}}(\pi )$
but
$\operatorname {\mathrm {ides}}(\pi ^{r})=n-1-\operatorname {\mathrm {ides}}(\pi )$
but
![]() $\operatorname {\mathrm {br}}(\pi ^{r})=\operatorname {\mathrm {br}}(\pi )$
. Note that the coefficients of
$\operatorname {\mathrm {br}}(\pi ^{r})=\operatorname {\mathrm {br}}(\pi )$
. Note that the coefficients of
![]() $s^{k}$
for
$s^{k}$
for
![]() $k\geq 2$
also seem to be unimodal, but in general they are not
$k\geq 2$
also seem to be unimodal, but in general they are not
![]() $\gamma $
-positive.
$\gamma $
-positive.
6 Major index
6.1 A rederivation of the Garsia–Gessel formula
We now return full circle by showing how our approach can be used to rederive Garsia and Gessel’s formula (1.4) for the polynomials
![]() $A_{n}(s,t,q,r)=\sum _{\pi \in \mathfrak {S}_{n}}s^{\operatorname {\mathrm {des}}(\pi )}t^{\operatorname {\mathrm {ides}}(\pi )}q^{\operatorname {\mathrm {maj}}(\pi )}r^{\operatorname {\mathrm {imaj}}(\pi )}$
.
$A_{n}(s,t,q,r)=\sum _{\pi \in \mathfrak {S}_{n}}s^{\operatorname {\mathrm {des}}(\pi )}t^{\operatorname {\mathrm {ides}}(\pi )}q^{\operatorname {\mathrm {maj}}(\pi )}r^{\operatorname {\mathrm {imaj}}(\pi )}$
.
Proof of the Garsia–Gessel formula.
We seek to compute the the scalar product
 $$\begin{align*}\left\langle \sum_{i=0}^{\infty}s^{i}\prod_{k=0}^{i}H(q^{k}x),\sum_{j=0}^{\infty}t^{j}\prod_{l=0}^{j}H(r^{l})\right\rangle \end{align*}$$
$$\begin{align*}\left\langle \sum_{i=0}^{\infty}s^{i}\prod_{k=0}^{i}H(q^{k}x),\sum_{j=0}^{\infty}t^{j}\prod_{l=0}^{j}H(r^{l})\right\rangle \end{align*}$$
in two different ways. First, from Lemma 2.8 (a) we have
 $$ \begin{align} & \left\langle \sum_{i=0}^{\infty}s^{i}\prod_{k=0}^{i}H(q^{k}x),\sum_{j=0}^{\infty}t^{j}\prod_{l=0}^{j}H(r^{l})\right\rangle \nonumber \\ & \qquad\qquad\qquad\qquad=\sum_{m,n=0}^{\infty}\frac{\sum_{L\vDash m,M\vDash n}s^{\operatorname{\mathrm{des}}(L)}t^{\operatorname{\mathrm{des}}(M)}q^{\operatorname{\mathrm{maj}}(L)}r^{\operatorname{\mathrm{maj}}(M)}\left\langle r_{L},r_{M}\right\rangle }{(1-s)(1-qs)\cdots(1-q^{m}s)(1-t)(1-rt)\cdots(1-r^{n}t)}x^{m}\nonumber \\ & \qquad\qquad\qquad\qquad=\sum_{n=0}^{\infty}\frac{\sum_{\pi\in\mathfrak{S}_{n}}s^{\operatorname{\mathrm{des}}(\pi)}t^{\operatorname{\mathrm{ides}}(\pi)}q^{\operatorname{\mathrm{maj}}(\pi)}r^{\operatorname{\mathrm{imaj}}(\pi)}}{(1-s)(1-qs)\cdots(1-q^{n}s)(1-t)(1-rt)\cdots(1-r^{n}t)}x^{n}\nonumber \\ & \qquad\qquad\qquad\qquad=\sum_{n=0}^{\infty}\frac{A_{n}(s,t,q,r)}{(1-s)(1-qs)\cdots(1-q^{n}s)(1-t)(1-rt)\cdots(1-r^{n}t)}x^{n}, \end{align} $$
$$ \begin{align} & \left\langle \sum_{i=0}^{\infty}s^{i}\prod_{k=0}^{i}H(q^{k}x),\sum_{j=0}^{\infty}t^{j}\prod_{l=0}^{j}H(r^{l})\right\rangle \nonumber \\ & \qquad\qquad\qquad\qquad=\sum_{m,n=0}^{\infty}\frac{\sum_{L\vDash m,M\vDash n}s^{\operatorname{\mathrm{des}}(L)}t^{\operatorname{\mathrm{des}}(M)}q^{\operatorname{\mathrm{maj}}(L)}r^{\operatorname{\mathrm{maj}}(M)}\left\langle r_{L},r_{M}\right\rangle }{(1-s)(1-qs)\cdots(1-q^{m}s)(1-t)(1-rt)\cdots(1-r^{n}t)}x^{m}\nonumber \\ & \qquad\qquad\qquad\qquad=\sum_{n=0}^{\infty}\frac{\sum_{\pi\in\mathfrak{S}_{n}}s^{\operatorname{\mathrm{des}}(\pi)}t^{\operatorname{\mathrm{ides}}(\pi)}q^{\operatorname{\mathrm{maj}}(\pi)}r^{\operatorname{\mathrm{imaj}}(\pi)}}{(1-s)(1-qs)\cdots(1-q^{n}s)(1-t)(1-rt)\cdots(1-r^{n}t)}x^{n}\nonumber \\ & \qquad\qquad\qquad\qquad=\sum_{n=0}^{\infty}\frac{A_{n}(s,t,q,r)}{(1-s)(1-qs)\cdots(1-q^{n}s)(1-t)(1-rt)\cdots(1-r^{n}t)}x^{n}, \end{align} $$
where, as usual, we apply Foulkes’s theorem (Theorem 2.1) to calculate the scalar product
![]() $\left \langle r_{L},r_{M}\right \rangle $
. Second, observe that
$\left \langle r_{L},r_{M}\right \rangle $
. Second, observe that
 $$ \begin{align*} \left\langle \sum_{i=0}^{\infty}s^{i}\prod_{k=0}^{i}H(q^{k}x),\sum_{j=0}^{\infty}t^{j}\prod_{l=0}^{j}H(r^{l})\right\rangle & =\sum_{i,j=0}^{\infty}s^{i}t^{i}\left\langle \prod_{k=0}^{i}H(q^{k}x),\prod_{l=0}^{j}H(r^{l})\right\rangle \\ & =\sum_{i,j=0}^{\infty}s^{i}t^{i}\prod_{k=0}^{i}\prod_{l=0}^{j}\left\langle H(q^{k}x),H(r^{l})\right\rangle \end{align*} $$
$$ \begin{align*} \left\langle \sum_{i=0}^{\infty}s^{i}\prod_{k=0}^{i}H(q^{k}x),\sum_{j=0}^{\infty}t^{j}\prod_{l=0}^{j}H(r^{l})\right\rangle & =\sum_{i,j=0}^{\infty}s^{i}t^{i}\left\langle \prod_{k=0}^{i}H(q^{k}x),\prod_{l=0}^{j}H(r^{l})\right\rangle \\ & =\sum_{i,j=0}^{\infty}s^{i}t^{i}\prod_{k=0}^{i}\prod_{l=0}^{j}\left\langle H(q^{k}x),H(r^{l})\right\rangle \end{align*} $$
by Lemma 2.3. To evaluate
![]() $\left \langle H(q^{k}x),H(r^{l})\right \rangle $
, let us recall that
$\left \langle H(q^{k}x),H(r^{l})\right \rangle $
, let us recall that
![]() $h_{n}=\sum _{\lambda \vdash n}m_{\lambda }$
. Then
$h_{n}=\sum _{\lambda \vdash n}m_{\lambda }$
. Then
 $$ \begin{align*} \left\langle H(q^{k}x),H(r^{l})\right\rangle & =\left\langle \sum_{i=0}^{\infty}h_{i}q^{ki}x^{i},\sum_{j=0}^{\infty}h_{j}r^{lj}\right\rangle \\ & =\sum_{i=0}^{\infty}\sum_{j=0}^{\infty}\sum_{\lambda\vdash i}\left\langle m_{\lambda},h_{j}\right\rangle q^{ki}x^{i}r^{lj}\\ & =\sum_{j=0}^{\infty}q^{kj}x^{j}r^{lj}\\ & =\frac{1}{1-xq^{k}r^{l}}, \end{align*} $$
$$ \begin{align*} \left\langle H(q^{k}x),H(r^{l})\right\rangle & =\left\langle \sum_{i=0}^{\infty}h_{i}q^{ki}x^{i},\sum_{j=0}^{\infty}h_{j}r^{lj}\right\rangle \\ & =\sum_{i=0}^{\infty}\sum_{j=0}^{\infty}\sum_{\lambda\vdash i}\left\langle m_{\lambda},h_{j}\right\rangle q^{ki}x^{i}r^{lj}\\ & =\sum_{j=0}^{\infty}q^{kj}x^{j}r^{lj}\\ & =\frac{1}{1-xq^{k}r^{l}}, \end{align*} $$
whence
 $$ \begin{align} \left\langle \sum_{i=0}^{\infty}s^{i}\prod_{k=0}^{i}H(q^{k}x),\sum_{j=0}^{\infty}t^{j}\prod_{l=0}^{j}H(r^{l})\right\rangle =\sum_{i,j=0}^{\infty}s^{i}t^{i}\prod_{k=0}^{i}\prod_{l=0}^{j}\frac{1}{1-xq^{k}r^{l}}. \end{align} $$
$$ \begin{align} \left\langle \sum_{i=0}^{\infty}s^{i}\prod_{k=0}^{i}H(q^{k}x),\sum_{j=0}^{\infty}t^{j}\prod_{l=0}^{j}H(r^{l})\right\rangle =\sum_{i,j=0}^{\infty}s^{i}t^{i}\prod_{k=0}^{i}\prod_{l=0}^{j}\frac{1}{1-xq^{k}r^{l}}. \end{align} $$
Combining Equations (6.1) and (6.2) yields Garsia and Gessel’s formula (1.4).
6.2 Major index and other statistics
Lemma 2.8 (a) also enables us to derive formulas for mixed two-sided distributions involving the major index. Define

We leave the proofs of the following formulas to the interested reader.
Theorem 6.1. We have
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{1+y}\sum_{n=1}^{\infty}\left(\frac{1+yt}{1-t}\right)^{n+1}\frac{P_{n}^{(\operatorname{\mathrm{maj}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(q,\frac{(1+y)^{2}t}{(y+t)(1+yt)},s,\frac{y+t}{1+yt}\right)}{(1-s)(1-qs)\cdots(1-q^{n}s)}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}s^{i}t^{j}\prod_{k=0}^{i}\left(\frac{1+q^{k}yx}{1-q^{k}x}\right)^{j},\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{1+y}\sum_{n=1}^{\infty}\left(\frac{1+yt}{1-t}\right)^{n+1}\frac{P_{n}^{(\operatorname{\mathrm{maj}},\operatorname{\mathrm{ipk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(q,\frac{(1+y)^{2}t}{(y+t)(1+yt)},s,\frac{y+t}{1+yt}\right)}{(1-s)(1-qs)\cdots(1-q^{n}s)}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}s^{i}t^{j}\prod_{k=0}^{i}\left(\frac{1+q^{k}yx}{1-q^{k}x}\right)^{j},\nonumber \end{align} $$
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+t)^{n}}{(1-t)^{n+1}}\frac{P_{n}^{(\operatorname{\mathrm{maj}},\operatorname{\mathrm{ilpk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(q,\frac{(1+y)^{2}t}{(y+t)(1+yt)},s,\frac{y+t}{1+yt}\right)}{(1-s)(1-qs)\cdots(1-q^{n}s)}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}s^{i}t^{j}\prod_{k=0}^{i}\frac{(1+q^{k}yx)^{j}}{(1-q^{k}x)^{j+1}}\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\sum_{n=1}^{\infty}\frac{(1+t)^{n}}{(1-t)^{n+1}}\frac{P_{n}^{(\operatorname{\mathrm{maj}},\operatorname{\mathrm{ilpk}},\operatorname{\mathrm{des}},\operatorname{\mathrm{ides}})}\left(q,\frac{(1+y)^{2}t}{(y+t)(1+yt)},s,\frac{y+t}{1+yt}\right)}{(1-s)(1-qs)\cdots(1-q^{n}s)}x^{n}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}s^{i}t^{j}\prod_{k=0}^{i}\frac{(1+q^{k}yx)^{j}}{(1-q^{k}x)^{j+1}}\nonumber \end{align} $$
and
 $$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{2(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\frac{P_{n}^{(\operatorname{\mathrm{maj}},\operatorname{\mathrm{iudr}},\operatorname{\mathrm{des}})}\left(q,\frac{2s}{1+s^{2}},t\right)}{(1-t)(1-qt)\cdots(1-q^{n}t)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}s^{2i}t^{j}\left(1+s\prod_{k=0}^{j}\frac{1}{1-q^{k}x}\right)\prod_{k=0}^{j}\left(\frac{1+q^{k}x}{1-q^{k}x}\right)^{i}.\nonumber \end{align} $$
$$ \begin{align} &\frac{1}{(1-s)(1-t)}+\frac{1}{2(1-s)^{2}}\sum_{n=1}^{\infty}\frac{(1+s^{2})^{n}}{(1-s^{2})^{n-1}}\frac{P_{n}^{(\operatorname{\mathrm{maj}},\operatorname{\mathrm{iudr}},\operatorname{\mathrm{des}})}\left(q,\frac{2s}{1+s^{2}},t\right)}{(1-t)(1-qt)\cdots(1-q^{n}t)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{i,j=0}^{\infty}s^{2i}t^{j}\left(1+s\prod_{k=0}^{j}\frac{1}{1-q^{k}x}\right)\prod_{k=0}^{j}\left(\frac{1+q^{k}x}{1-q^{k}x}\right)^{i}.\nonumber \end{align} $$
One may obtain formulas for
![]() $(\operatorname {\mathrm {maj}},\operatorname {\mathrm {ipk}})$
,
$(\operatorname {\mathrm {maj}},\operatorname {\mathrm {ipk}})$
,
![]() $(\operatorname {\mathrm {maj}},\operatorname {\mathrm {ilpk}})$
and
$(\operatorname {\mathrm {maj}},\operatorname {\mathrm {ilpk}})$
and
![]() $(\operatorname {\mathrm {maj}},\operatorname {\mathrm {iudr}})$
by specializing Theorem 6.1 appropriately. For example, setting
$(\operatorname {\mathrm {maj}},\operatorname {\mathrm {iudr}})$
by specializing Theorem 6.1 appropriately. For example, setting
![]() $y=1$
in Theorem 6.1 (a), multiplying both sides by
$y=1$
in Theorem 6.1 (a), multiplying both sides by
![]() $1-s$
, and then taking the limit of both sides as
$1-s$
, and then taking the limit of both sides as
![]() $s\rightarrow 1$
yields
$s\rightarrow 1$
yields
 $$\begin{align*}\frac{1}{1-t}+\frac{1}{2}\sum_{n=1}^{\infty}\left(\frac{1+t}{1-t}\right)^{n+1}\frac{P_{n}^{(\operatorname{\mathrm{maj}},\operatorname{\mathrm{ipk}})}\left(q,\frac{4t}{(1+t)^{2}}\right)}{(1-q)(1-q^{2})\cdots(1-q^{n})}x^{n}=\sum_{j=0}^{\infty}t^{j}\prod_{k=0}^{\infty}\left(\frac{1+q^{k}x}{1-q^{k}x}\right)^{j}, \end{align*}$$
$$\begin{align*}\frac{1}{1-t}+\frac{1}{2}\sum_{n=1}^{\infty}\left(\frac{1+t}{1-t}\right)^{n+1}\frac{P_{n}^{(\operatorname{\mathrm{maj}},\operatorname{\mathrm{ipk}})}\left(q,\frac{4t}{(1+t)^{2}}\right)}{(1-q)(1-q^{2})\cdots(1-q^{n})}x^{n}=\sum_{j=0}^{\infty}t^{j}\prod_{k=0}^{\infty}\left(\frac{1+q^{k}x}{1-q^{k}x}\right)^{j}, \end{align*}$$
where ![]() .
.
7 Conjectures
We conclude with a discussion of some conjectures concerning some of the permutation statistic distributions studied in this paper.
7.1 Real-rootedness
A univariate polynomial is called real-rooted if it has only real roots. We conjecture that the distributions of
![]() $\operatorname {\mathrm {ipk}}$
and
$\operatorname {\mathrm {ipk}}$
and
![]() $\operatorname {\mathrm {ilpk}}$
over permutations in
$\operatorname {\mathrm {ilpk}}$
over permutations in
![]() $\mathfrak {S}_{n}$
with any fixed value of
$\mathfrak {S}_{n}$
with any fixed value of
![]() $\operatorname {\mathrm {pk}}$
,
$\operatorname {\mathrm {pk}}$
,
![]() $\operatorname {\mathrm {lpk}}$
, and
$\operatorname {\mathrm {lpk}}$
, and
![]() $\operatorname {\mathrm {udr}}$
—as well as that of
$\operatorname {\mathrm {udr}}$
—as well as that of
![]() $\operatorname {\mathrm {ipk}}$
upon fixing
$\operatorname {\mathrm {ipk}}$
upon fixing
![]() $\operatorname {\mathrm {br}}$
—are all encoded by real-rooted polynomials. This conjecture has been empirically verified for all
$\operatorname {\mathrm {br}}$
—are all encoded by real-rooted polynomials. This conjecture has been empirically verified for all
![]() $n\leq 50$
; our formulas from Sections 3–6 played a crucial role in formulating and gathering supporting evidence for this conjecture as they have allowed us to efficiently compute the polynomials in question.
$n\leq 50$
; our formulas from Sections 3–6 played a crucial role in formulating and gathering supporting evidence for this conjecture as they have allowed us to efficiently compute the polynomials in question.
Conjecture 7.1. The following polynomials are real-rooted for all
![]() $n\geq 1$
:
$n\geq 1$
:
-
(a)
 ${\displaystyle [s^{k+1}]\,P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {pk}}(\pi )=k } }}t^{\operatorname {\mathrm {ipk}}(\pi )+1}$
for
${\displaystyle [s^{k+1}]\,P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ipk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {pk}}(\pi )=k } }}t^{\operatorname {\mathrm {ipk}}(\pi )+1}$
for
 $0\leq k\leq \left \lfloor (n-1)/2\right \rfloor $
,
$0\leq k\leq \left \lfloor (n-1)/2\right \rfloor $
, -
(b)
 ${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {lpk}}(\pi )=k } }}t^{\operatorname {\mathrm {ilpk}}(\pi )}$
for
${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {lpk}},\operatorname {\mathrm {ilpk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {lpk}}(\pi )=k } }}t^{\operatorname {\mathrm {ilpk}}(\pi )}$
for
 $0\leq k\leq \left \lfloor n/2\right \rfloor $
,
$0\leq k\leq \left \lfloor n/2\right \rfloor $
, -
(c)
 ${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ilpk}})}(t,s)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {lpk}}(\pi )=k } }}t^{\operatorname {\mathrm {ipk}}(\pi )+1}$
for
${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ilpk}})}(t,s)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {lpk}}(\pi )=k } }}t^{\operatorname {\mathrm {ipk}}(\pi )+1}$
for
 $0\leq k\leq \left \lfloor n/2\right \rfloor $
,
$0\leq k\leq \left \lfloor n/2\right \rfloor $
, -
(d)
 ${\displaystyle [s^{k+1}]\,P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ilpk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {pk}}(\pi )=k } }}t^{\operatorname {\mathrm {ilpk}}(\pi )}$
for
${\displaystyle [s^{k+1}]\,P_{n}^{(\operatorname {\mathrm {pk}},\operatorname {\mathrm {ilpk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {pk}}(\pi )=k } }}t^{\operatorname {\mathrm {ilpk}}(\pi )}$
for
 $0\leq k\leq \left \lfloor (n-1)/2\right \rfloor $
,
$0\leq k\leq \left \lfloor (n-1)/2\right \rfloor $
, -
(e)
 ${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {udr}}(\pi )=k } }}t^{\operatorname {\mathrm {ipk}}(\pi )+1}$
for
${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ipk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {udr}}(\pi )=k } }}t^{\operatorname {\mathrm {ipk}}(\pi )+1}$
for
 $1\leq k\leq n$
,
$1\leq k\leq n$
, -
(f)
 ${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ilpk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {udr}}(\pi )=k } }}t^{\operatorname {\mathrm {ilpk}}(\pi )}$
for
${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {udr}},\operatorname {\mathrm {ilpk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {udr}}(\pi )=k } }}t^{\operatorname {\mathrm {ilpk}}(\pi )}$
for
 $1\leq k\leq n$
and
$1\leq k\leq n$
and -
(g)
 ${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ipk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {br}}(\pi )=k } }}t^{\operatorname {\mathrm {ipk}}(\pi )+1}$
for
${\displaystyle [s^{k}]\,P_{n}^{(\operatorname {\mathrm {br}},\operatorname {\mathrm {ipk}})}(s,t)=\sum _{\substack {\pi \in \mathfrak {S}_{n}\\ \operatorname {\mathrm {br}}(\pi )=k } }}t^{\operatorname {\mathrm {ipk}}(\pi )+1}$
for
 $1\leq k\leq n$
.
$1\leq k\leq n$
.
Conjecture 7.1 would imply that all of these polynomials are unimodal and log-concave and can be used to show that the distributions of
![]() $\operatorname {\mathrm {ipk}}$
and
$\operatorname {\mathrm {ipk}}$
and
![]() $\operatorname {\mathrm {ilpk}}$
over permutations in
$\operatorname {\mathrm {ilpk}}$
over permutations in
![]() $\mathfrak {S}_{n}$
with a fixed value k for the relevant statistics each converge to a normal distribution as
$\mathfrak {S}_{n}$
with a fixed value k for the relevant statistics each converge to a normal distribution as
![]() $n\rightarrow \infty $
.
$n\rightarrow \infty $
.
It is worth noting that the peak and left peak polynomials
are known to be real-rooted (see, e.g., [Reference Petersen18, Reference Stembridge25]), so Conjecture 7.1 would also have the consequence that both of these ‘real-rooted distributions’ can be partitioned into real-rooted distributions based on the value of another statistic.
7.2 Gamma-positivity
Real-rootedness provides a powerful method of proving unimodality results in combinatorics, but when the polynomials in question are known to be symmetric,Footnote
3
an alternate avenue to unimodality is
![]() $\gamma $
-positivity. Any symmetric polynomial
$\gamma $
-positivity. Any symmetric polynomial
![]() $f(t)\in \mathbb {R}[t]$
with center of symmetry
$f(t)\in \mathbb {R}[t]$
with center of symmetry
![]() $n/2$
can be written uniquely as a linear combination of the polynomials
$n/2$
can be written uniquely as a linear combination of the polynomials
![]() $\{t^{j}(1+t)^{n-2j}\}_{0\leq j\leq \left \lfloor n/2\right \rfloor }$
—referred to as the gamma basis—and
$\{t^{j}(1+t)^{n-2j}\}_{0\leq j\leq \left \lfloor n/2\right \rfloor }$
—referred to as the gamma basis—and
![]() $f(t)$
is called
$f(t)$
is called
![]() $\gamma $
-positive if its coefficients in the gamma basis are nonnegative. The
$\gamma $
-positive if its coefficients in the gamma basis are nonnegative. The
![]() $\gamma $
-positivity of a polynomial directly implies its unimodality, and
$\gamma $
-positivity of a polynomial directly implies its unimodality, and
![]() $\gamma $
-positivity has appeared in many contexts within combinatorics and geometry; see [Reference Athanasiadis1] for a detailed survey.
$\gamma $
-positivity has appeared in many contexts within combinatorics and geometry; see [Reference Athanasiadis1] for a detailed survey.
The prototypical example of a family of
![]() $\gamma $
-positive polynomials are the Eulerian polynomials
$\gamma $
-positive polynomials are the Eulerian polynomials
![]() $A_{n}(t)$
, as established by Foata and Schützenberger [Reference Foata and Schützenberger8], and there is also a sizable literature on the
$A_{n}(t)$
, as established by Foata and Schützenberger [Reference Foata and Schützenberger8], and there is also a sizable literature on the
![]() $\gamma $
-positivity of ‘Eulerian distributions’ (polynomials encoding the distribution of the descent number
$\gamma $
-positivity of ‘Eulerian distributions’ (polynomials encoding the distribution of the descent number
![]() $\operatorname {\mathrm {des}}$
) over various restricted subsets of
$\operatorname {\mathrm {des}}$
) over various restricted subsets of
![]() $\mathfrak {S}_{n}$
. For example, the Eulerian distribution over linear extensions of sign-graded posets [Reference Brändén2], r-stack-sortable permutations [Reference Brändén3], separable permutations [Reference Fu, Lin and Zeng10] and involutions [Reference Wang28] are all known to be
$\mathfrak {S}_{n}$
. For example, the Eulerian distribution over linear extensions of sign-graded posets [Reference Brändén2], r-stack-sortable permutations [Reference Brändén3], separable permutations [Reference Fu, Lin and Zeng10] and involutions [Reference Wang28] are all known to be
![]() $\gamma $
-positive. The two-sided Eulerian distribution
$\gamma $
-positive. The two-sided Eulerian distribution
![]() $(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
is also known to satisfy a refined
$(\operatorname {\mathrm {des}},\operatorname {\mathrm {ides}})$
is also known to satisfy a refined
![]() $\gamma $
-positivity property which was conjectured by Gessel and later proved by Lin [Reference Lin16].
$\gamma $
-positivity property which was conjectured by Gessel and later proved by Lin [Reference Lin16].
Define

to be the polynomial encoding the distribution of
![]() $\operatorname {\mathrm {ides}}$
over permutations in
$\operatorname {\mathrm {ides}}$
over permutations in
![]() $\mathfrak {S}_{n}$
with k peaks, or equivalently, the distribution of
$\mathfrak {S}_{n}$
with k peaks, or equivalently, the distribution of
![]() $\operatorname {\mathrm {des}}$
(i.e., the Eulerian distribution) over permutations in
$\operatorname {\mathrm {des}}$
(i.e., the Eulerian distribution) over permutations in
![]() $\mathfrak {S}_{n}$
whose inverses have k peaks. We conjecture that these polynomials are
$\mathfrak {S}_{n}$
whose inverses have k peaks. We conjecture that these polynomials are
![]() $\gamma $
-positive as well.
$\gamma $
-positive as well.
Conjecture 7.2. For all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $0\leq k\leq \left \lfloor (n-1)/2\right \rfloor $
, the polynomials
$0\leq k\leq \left \lfloor (n-1)/2\right \rfloor $
, the polynomials
![]() $\hat {A}_{n,k}(t)$
are
$\hat {A}_{n,k}(t)$
are
![]() $\gamma $
-positive with center of symmetry
$\gamma $
-positive with center of symmetry
![]() $(n+1)/2$
.
$(n+1)/2$
.
In fact, we shall give a stronger conjecture which refines by ‘pinnacle sets’. Given a permutation
![]() $\pi \in \mathfrak {S}_{n}$
, the pinnacle set
$\pi \in \mathfrak {S}_{n}$
, the pinnacle set
![]() $\operatorname {\mathrm {Pin}}(\pi )$
of
$\operatorname {\mathrm {Pin}}(\pi )$
of
![]() $\pi $
is defined by
$\pi $
is defined by
In other words,
![]() $\operatorname {\mathrm {Pin}}(\pi )$
contains all of the values
$\operatorname {\mathrm {Pin}}(\pi )$
contains all of the values
![]() $\pi (k)$
at which k is a peak of
$\pi (k)$
at which k is a peak of
![]() $\pi $
. Given
$\pi $
. Given
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $S\subseteq [n]$
, define the polynomial
$S\subseteq [n]$
, define the polynomial
![]() $\hat {A}_{n,S}^{\operatorname {\mathrm {ides}}}(t)$
by
$\hat {A}_{n,S}^{\operatorname {\mathrm {ides}}}(t)$
by

this gives the distribution of the inverse descent number over permutations in
![]() $\mathfrak {S}_{n}$
with a fixed pinnacle set S or, equivalently, the Eulerian distribution over permutations in
$\mathfrak {S}_{n}$
with a fixed pinnacle set S or, equivalently, the Eulerian distribution over permutations in
![]() $\mathfrak {S}_{n}$
with ‘inverse pinnacle set’ S.
$\mathfrak {S}_{n}$
with ‘inverse pinnacle set’ S.
Conjecture 7.3. For all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $S\subseteq [n]$
, the polynomials
$S\subseteq [n]$
, the polynomials
![]() $\hat {A}_{n,S}^{\operatorname {\mathrm {ides}}}(t)$
are
$\hat {A}_{n,S}^{\operatorname {\mathrm {ides}}}(t)$
are
![]() $\gamma $
-positive with center of symmetry
$\gamma $
-positive with center of symmetry
![]() $(n+1)/2$
.
$(n+1)/2$
.
Note that
 $$\begin{align*}\hat{A}_{n,k}^{\operatorname{\mathrm{ides}}}(t)=\sum_{\substack{S\subseteq[n]\\ \left|S\right|=k } }\hat{A}_{n,S}^{\operatorname{\mathrm{ides}}}(t). \end{align*}$$
$$\begin{align*}\hat{A}_{n,k}^{\operatorname{\mathrm{ides}}}(t)=\sum_{\substack{S\subseteq[n]\\ \left|S\right|=k } }\hat{A}_{n,S}^{\operatorname{\mathrm{ides}}}(t). \end{align*}$$
Because the sum of
![]() $\gamma $
-positive polynomials with the same center of symmetry is again
$\gamma $
-positive polynomials with the same center of symmetry is again
![]() $\gamma $
-positive, a positive resolution to Conjecture 7.3 would imply Conjecture 7.2. However, we do not have nearly as much empirical evidence to support Conjecture 7.3. Since we do not have a formula for the polynomials
$\gamma $
-positive, a positive resolution to Conjecture 7.3 would imply Conjecture 7.2. However, we do not have nearly as much empirical evidence to support Conjecture 7.3. Since we do not have a formula for the polynomials
![]() $\hat {A}_{n,k}^{\operatorname {\mathrm {ides}}}(t)$
, we were only able to verify Conjecture 7.3 up to
$\hat {A}_{n,k}^{\operatorname {\mathrm {ides}}}(t)$
, we were only able to verify Conjecture 7.3 up to
![]() $n=10$
, whereas Conjecture 7.2 has been verified for all
$n=10$
, whereas Conjecture 7.2 has been verified for all
![]() $n\leq 80$
with the assistance of Theorem 3.6 (a).
$n\leq 80$
with the assistance of Theorem 3.6 (a).
Acknowledgements
We thank Kyle Petersen for insightful discussions concerning the work in this paper, and in particular for his suggestion to look at refining Conjecture 7.2 by pinnacle sets. We also thank two anonymous referees for their careful reading of an earlier version of this paper and providing thoughtful comments.
Competing interests
The authors have no competing interest to declare.
Financial support
YZ was partially supported by an AMS-Simons Travel Grant and NSF grant DMS-2316181.


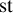
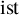
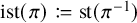 . We give a general approach, based on the theory of symmetric functions, for finding the joint distribution of
. We give a general approach, based on the theory of symmetric functions, for finding the joint distribution of