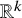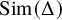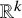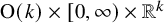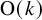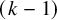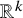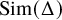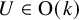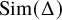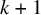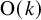1 Introduction
There is a general type of problem of finding special geometric configurations on families of manifolds. Quite often such problems seek to find some kind of polyhedron or polytope inscribed in a circle or sphere embedded in space. Our paper seeks to find constructible nondegenerate simplices inscribed in spheres smoothly embedded in ![]() $\mathbb {R}^k$. Specifically, for a given nondegenerate k-simplex
$\mathbb {R}^k$. Specifically, for a given nondegenerate k-simplex ![]() $\Delta $, we show that among all smoothly embedded
$\Delta $, we show that among all smoothly embedded ![]() $(k-1)$ spheres in
$(k-1)$ spheres in ![]() $\mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in
$\mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in ![]() $\mathbb {R}^k$, there is a dense family of spheres, such that each sphere has an inscribed simplex similar to
$\mathbb {R}^k$, there is a dense family of spheres, such that each sphere has an inscribed simplex similar to ![]() $\Delta $ corresponding to each
$\Delta $ corresponding to each ![]() $U\in \operatorname {O}(k)$. An example of an embedded 2-sphere in
$U\in \operatorname {O}(k)$. An example of an embedded 2-sphere in ![]() $\mathbb {R}^3$ with an inscribed equilateral tetrahedra is found in Figure 1. We, in fact, prove more: If we let
$\mathbb {R}^3$ with an inscribed equilateral tetrahedra is found in Figure 1. We, in fact, prove more: If we let ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ denote the configuration space of simplices in
$\operatorname {\mathrm {Sim}}(\Delta )$ denote the configuration space of simplices in ![]() $\mathbb {R}^k$ similar to a nondegenerate k-simplex
$\mathbb {R}^k$ similar to a nondegenerate k-simplex ![]() $\Delta $, then in
$\Delta $, then in ![]() $\operatorname {\mathrm {Sim}}(\Delta )$, the top homology class of the inscribed simplices similar to
$\operatorname {\mathrm {Sim}}(\Delta )$, the top homology class of the inscribed simplices similar to ![]() $\Delta $ on an embedded sphere maps to the top class in
$\Delta $ on an embedded sphere maps to the top class in ![]() $\operatorname {O}(k)$.
$\operatorname {O}(k)$.

Figure 1 On the left, we see an irregular embedding of ![]() $S^2$ in
$S^2$ in ![]() $\mathbb {R}^3$ described in spherical coordinates as a graph over the unit sphere by the function
$\mathbb {R}^3$ described in spherical coordinates as a graph over the unit sphere by the function ![]() $r(\phi ,\theta ) = 1 + \sin ^3\phi \sin 3\theta /5 - |\cos ^7\phi |$. The centre and right images show different views of a single regular tetrahedron inscribed in this surface with edge lengths close to
$r(\phi ,\theta ) = 1 + \sin ^3\phi \sin 3\theta /5 - |\cos ^7\phi |$. The centre and right images show different views of a single regular tetrahedron inscribed in this surface with edge lengths close to ![]() $1.15$. If this embedding of
$1.15$. If this embedding of ![]() $S^2$ is transverse to the submanifold of regular tetrahedra, this tetrahedron is a member of the family of inscribed regular tetrahedra predicted by Theorem 5.4. This tetrahedron was found by computer search. Its vertices have spherical
$S^2$ is transverse to the submanifold of regular tetrahedra, this tetrahedron is a member of the family of inscribed regular tetrahedra predicted by Theorem 5.4. This tetrahedron was found by computer search. Its vertices have spherical ![]() $(\phi ,\theta )$ coordinates
$(\phi ,\theta )$ coordinates ![]() $(0.224399, 0.224399), (1.5708, 3.36599), (1.5708, 2.0196), (2.91719, 0.224399)$
$(0.224399, 0.224399), (1.5708, 3.36599), (1.5708, 2.0196), (2.91719, 0.224399)$
In 1969, Gromov [Reference Gromov16] showed that every ![]() $C^1$-smooth embedding of a
$C^1$-smooth embedding of a ![]() $(k-1)$-sphere in
$(k-1)$-sphere in ![]() $\mathbb {R}^k$ contains an inscribed simplex similar to
$\mathbb {R}^k$ contains an inscribed simplex similar to ![]() $\Delta $ for each pose
$\Delta $ for each pose ![]() $U\in \operatorname {O}(k)$. Our results go further than Gromov. We show that the inscribed simplices in embedded spheres form a manifold cobordant to
$U\in \operatorname {O}(k)$. Our results go further than Gromov. We show that the inscribed simplices in embedded spheres form a manifold cobordant to ![]() $\operatorname {O}(k)$ by using configuration spaces and transversality as in [Reference Cantarella, Denne and McCleary10].
$\operatorname {O}(k)$ by using configuration spaces and transversality as in [Reference Cantarella, Denne and McCleary10].
Another closely related result is the 2009 work of Blagojević and Ziegler [Reference Blagojević and Ziegler6]. They prove that for every injective continuous map of ![]() $f\colon \! S^2 \rightarrow \mathbb {R}^3$, there are four distinct points in the image of f with the property that two opposite edges have the same length and the other four edges are also of equal length. While this result holds for injective maps, our theorem recovers an even more general result for generic smooth embeddings. In addition, Matschke [Reference Matschke31] proved that any smoothly embedded compact surface S inscribes a particular type of tetrahedron.
$f\colon \! S^2 \rightarrow \mathbb {R}^3$, there are four distinct points in the image of f with the property that two opposite edges have the same length and the other four edges are also of equal length. While this result holds for injective maps, our theorem recovers an even more general result for generic smooth embeddings. In addition, Matschke [Reference Matschke31] proved that any smoothly embedded compact surface S inscribes a particular type of tetrahedron.
All of these theorems generalise the classical results on inscribing families of triangles in planar and spatial curves. In 1978, Meyerson [Reference Meyerson34] proved that for a fixed arbitrary triangle, every simple closed curve in the plane contains the vertices of a triangle similar to the given one. He also proved that for every simple closed curve ![]() $\gamma $ in the plane, then for all, except perhaps two, points x on
$\gamma $ in the plane, then for all, except perhaps two, points x on ![]() $\gamma $, we can find points y and z in
$\gamma $, we can find points y and z in ![]() $\gamma $, such that
$\gamma $, such that ![]() $xyz$ is an equilateral triangle. In 1992, Nielsen [Reference Nielsen35] proved that for any triangle T and any simple closed curve
$xyz$ is an equilateral triangle. In 1992, Nielsen [Reference Nielsen35] proved that for any triangle T and any simple closed curve ![]() $\gamma $ in the plane, there are infinitely many triangles similar to T inscribed in
$\gamma $ in the plane, there are infinitely many triangles similar to T inscribed in ![]() $\gamma $. In fact, he proves that the set of vertices corresponding to the vertex of the smallest angle in T is dense in
$\gamma $. In fact, he proves that the set of vertices corresponding to the vertex of the smallest angle in T is dense in ![]() $\gamma $. In 2011, Matschke [Reference Matschke31] proved a more general result. He looked at n-gons whose edge lengths are in a prescribed ratio. He showed such polygons are inscribed in generic
$\gamma $. In 2011, Matschke [Reference Matschke31] proved a more general result. He looked at n-gons whose edge lengths are in a prescribed ratio. He showed such polygons are inscribed in generic ![]() $C^\infty $-smooth embeddings of
$C^\infty $-smooth embeddings of ![]() $S^1$ into a (complete) Riemannian manifold, and, moreover, there is a 1-parameter family of such polygons. He proves that there are an odd number of loops of such polygons that wind an odd number of times around the embedded
$S^1$ into a (complete) Riemannian manifold, and, moreover, there is a 1-parameter family of such polygons. He proves that there are an odd number of loops of such polygons that wind an odd number of times around the embedded ![]() $S^1$. Our main theorem and Matschke’s results are very similar for triangles inscribed in embedded curves in the plane, except that we prove (Corollary 5.6) that the degree of the map is 1. In 2021, Gupta and Rubinstein-Salzedo [Reference Gupta and Rubinstein-Salzedo18] generalised Nielsen’s result to any Jordan curve embedded in
$S^1$. Our main theorem and Matschke’s results are very similar for triangles inscribed in embedded curves in the plane, except that we prove (Corollary 5.6) that the degree of the map is 1. In 2021, Gupta and Rubinstein-Salzedo [Reference Gupta and Rubinstein-Salzedo18] generalised Nielsen’s result to any Jordan curve embedded in ![]() $\mathbb {R}^n$ for a restricted set of triangles dependent on certain geometric conditions. They then get a wider class of inscribed triangles by adding in regularity conditions. Namely, they show that if the curve is differentiable at a point, then any triangle can be inscribed at that point.
$\mathbb {R}^n$ for a restricted set of triangles dependent on certain geometric conditions. They then get a wider class of inscribed triangles by adding in regularity conditions. Namely, they show that if the curve is differentiable at a point, then any triangle can be inscribed at that point.
We pause to note that many of the inscribed triangle results were inspired by the square-peg problem: finding four points on any Jordan curve (a simple closed curve in the plane) which are the vertices of a square. This question was posed by Toeplitz in 1911 [Reference Toeplitz44], and progress on this problem has chiefly been an extension of the regularity class of simple closed curves for which the square can be found. The interested reader can find numerous articles [Reference Cantarella, Denne and McCleary9, Reference Klee and Wagon26, Reference Matschke32, Reference Pak36, Reference Tao42] summarising the problem and describing the classes of curves for which the square-peg problem has been proved. There have also been many papers [Reference Akopyan and Avvakumov1, Reference Aslam, Chen, Frick, Saloff-Coste, Setiabrata and Thomas3, Reference Greene and Lobb15, Reference Hugelmeyer22, Reference Hugelmeyer23, Reference Makeev28, Reference Matschke33, Reference Schwartz39, Reference Vrećica and Živaljević45] examining quadrilaterals and polygons inscribed in curves and, more recently, making progress towards solving the rectangular-peg problem (finding rectangles of any aspect ratio inscribed in Jordan curves).
There are yet more results about inscribed and circumscribed polyhedra in spheres. For example, Kakutani’s theorem [Reference Kakutani24] that a compact convex body in ![]() $\mathbb {R}^3$ has a circumscribed cube, that is, a cube each of whose faces touch the convex body. As Matschke [Reference Matschke32] notes, most smooth embeddings
$\mathbb {R}^3$ has a circumscribed cube, that is, a cube each of whose faces touch the convex body. As Matschke [Reference Matschke32] notes, most smooth embeddings ![]() $S^{k-1}\hookrightarrow \mathbb {R}^k$ do not inscribe a k-cube for
$S^{k-1}\hookrightarrow \mathbb {R}^k$ do not inscribe a k-cube for ![]() $k\geq 3$ (intuitively, the number of equations to fulfil is larger than the degrees of freedom). Instead, asking whether crosspolytopesFootnote 1 are inscribed in such an embedding might be a better generalisation of inscribing a square. Makeev [Reference Makeev30] proved the
$k\geq 3$ (intuitively, the number of equations to fulfil is larger than the degrees of freedom). Instead, asking whether crosspolytopesFootnote 1 are inscribed in such an embedding might be a better generalisation of inscribing a square. Makeev [Reference Makeev30] proved the ![]() $k=3$ case, and Karasev [Reference Karasev25] generalised the proof to arbitrary odd prime powers. Later, Akoypan and Karasev [Reference Akopyan and Karasev2] used a limit argument to show that a simple convex polytope admits an inscribed regular octahedron. In addition, there is the work of Kuperberg [Reference Kuperberg27] and Makeev [Reference Makeev29] on inscribed and circumscribed polyhedra in convex bodies and spheres.
$k=3$ case, and Karasev [Reference Karasev25] generalised the proof to arbitrary odd prime powers. Later, Akoypan and Karasev [Reference Akopyan and Karasev2] used a limit argument to show that a simple convex polytope admits an inscribed regular octahedron. In addition, there is the work of Kuperberg [Reference Kuperberg27] and Makeev [Reference Makeev29] on inscribed and circumscribed polyhedra in convex bodies and spheres.
The inscribed simplex problem can be framed in terms of compactified configuration spaces. We give a short overview of the basics about these spaces in Section 2. We consider the compactified configuration space ![]() $C_{k+1}[\mathbb {R}^k]$ of ordered
$C_{k+1}[\mathbb {R}^k]$ of ordered ![]() $(k+1)$-tuples of points in
$(k+1)$-tuples of points in ![]() $\mathbb {R}^k$ as a manifold-with-boundary (and corners). The existence of inscribed simplices in embedded spheres can be viewed as finding the intersection of two submanifolds of
$\mathbb {R}^k$ as a manifold-with-boundary (and corners). The existence of inscribed simplices in embedded spheres can be viewed as finding the intersection of two submanifolds of ![]() $C_{k+1}[\mathbb {R}^k]$. The first is the submanifold of
$C_{k+1}[\mathbb {R}^k]$. The first is the submanifold of ![]() $(k+1)$-tuples of points on a
$(k+1)$-tuples of points on a ![]() $C^\infty $-smooth embedding
$C^\infty $-smooth embedding ![]() $\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ of a
$\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ of a ![]() $(k-1)$-sphere in
$(k-1)$-sphere in ![]() $\mathbb {R}^k$; and the second is the submanifold of simplices in
$\mathbb {R}^k$; and the second is the submanifold of simplices in ![]() $\mathbb {R}^k$ which are similar to a given simplex
$\mathbb {R}^k$ which are similar to a given simplex ![]() $\Delta $, denoted by
$\Delta $, denoted by ![]() $\operatorname {\mathrm {Sim}}(\Delta )$.
$\operatorname {\mathrm {Sim}}(\Delta )$.
Theorems about intersections of manifolds are often proved by transversality arguments. There are many examples in the literature [Reference Guillemin and Pollack17, Reference Samelson37, Reference Thom43]. In [Reference Cantarella, Denne and McCleary10], we provide a framework for this kind of argument adapted to configuration spaces, which we will use again in this paper. Section 3 gives a description of this method, and we give a very quick overview here. We consider a smooth embedding ![]() $\gamma \colon \! S^l \hookrightarrow \mathbb {R}^k$ of
$\gamma \colon \! S^l \hookrightarrow \mathbb {R}^k$ of ![]() $S^l$ in
$S^l$ in ![]() $\mathbb {R}^k$. Then, in the compactified configuration space
$\mathbb {R}^k$. Then, in the compactified configuration space ![]() $C_n[\mathbb {R}^k]$ of n points in
$C_n[\mathbb {R}^k]$ of n points in ![]() $\mathbb {R}^k$, we consider
$\mathbb {R}^k$, we consider ![]() $C_n[\gamma (S^l)]$, the compactified configuration space of n points on
$C_n[\gamma (S^l)]$, the compactified configuration space of n points on ![]() $\gamma (S^l)$; and Z, the subspace of tuples of n points in
$\gamma (S^l)$; and Z, the subspace of tuples of n points in ![]() $\mathbb {R}^k$ that satisfy the conditions of a special configuration. Now, suppose there is a different, well-known, smooth embedding
$\mathbb {R}^k$ that satisfy the conditions of a special configuration. Now, suppose there is a different, well-known, smooth embedding ![]() $i\colon \! S^l\hookrightarrow \mathbb {R}^k$ of
$i\colon \! S^l\hookrightarrow \mathbb {R}^k$ of ![]() $S^l$ in
$S^l$ in ![]() $\mathbb {R}^k$, and assume that the configuration space
$\mathbb {R}^k$, and assume that the configuration space ![]() $C_n[i(S^l)]$ is transverse to Z in
$C_n[i(S^l)]$ is transverse to Z in ![]() $C_n[\mathbb {R}^k]$. We can use Haefliger’s theorem [Reference Haefliger19] to find a differentiable isotopy between
$C_n[\mathbb {R}^k]$. We can use Haefliger’s theorem [Reference Haefliger19] to find a differentiable isotopy between ![]() $i(S^l)$ and
$i(S^l)$ and ![]() $\gamma (S^l)$ (the differentiable isotopy may need to go through
$\gamma (S^l)$ (the differentiable isotopy may need to go through ![]() $\mathbb {R}^K$ for
$\mathbb {R}^K$ for ![]() $K\geq k$). The key idea is that we ought to be able to vary
$K\geq k$). The key idea is that we ought to be able to vary ![]() $C_n[i(S^l)]$ to
$C_n[i(S^l)]$ to ![]() $C_n[\gamma (S^l)]$ while maintaining the transversality of the intersection with Z. To do so, we need to make several assumptions about Z and
$C_n[\gamma (S^l)]$ while maintaining the transversality of the intersection with Z. To do so, we need to make several assumptions about Z and ![]() $C_n[\gamma (S^l)]$ (see Section 3) and to use technical tools like multijet transversality. In the end, we are able to deduce that there is, for all m, a
$C_n[\gamma (S^l)]$ (see Section 3) and to use technical tools like multijet transversality. In the end, we are able to deduce that there is, for all m, a ![]() $C^m$-denseFootnote 2 set of smooth embeddings
$C^m$-denseFootnote 2 set of smooth embeddings ![]() $\gamma '\colon \! S^l\hookrightarrow \mathbb {R}^k$, such that the corresponding embeddings
$\gamma '\colon \! S^l\hookrightarrow \mathbb {R}^k$, such that the corresponding embeddings ![]() $C_n[\gamma ']$ on configuration spaces are
$C_n[\gamma ']$ on configuration spaces are ![]() $C^0$-close to
$C^0$-close to ![]() $C_n[\gamma ]$, and that
$C_n[\gamma ]$, and that ![]() $C_n[\gamma '(S^l)]$ is transverse to Z. Moreover,
$C_n[\gamma '(S^l)]$ is transverse to Z. Moreover, ![]() $C_n[i(S^l)] \cap Z$ and
$C_n[i(S^l)] \cap Z$ and ![]() $C_n[\gamma '(S^l)] \cap Z$ represent the same homology class in Z. We apply this method to the inscribed simplices problem in the final two sections of the paper.
$C_n[\gamma '(S^l)] \cap Z$ represent the same homology class in Z. We apply this method to the inscribed simplices problem in the final two sections of the paper.
In Section 4, we first describe a nondegenerate simplex in terms of the distances between distinct vertices. We then use the Cayley-Menger determinant (see Theorem 4.2) to give a description of when it is possible to construct a simplex from a set of distances. Secondly, we change our perspective and view a simplex ![]() $\Delta $ in
$\Delta $ in ![]() $\mathbb {R}^k$ as an ordered
$\mathbb {R}^k$ as an ordered ![]() $(k+1)$-tuple of distinct points in the configuration space
$(k+1)$-tuple of distinct points in the configuration space ![]() $C_{k+1}(\mathbb {R}^k)$. We then define
$C_{k+1}(\mathbb {R}^k)$. We then define ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ to be the space of simplices similar to
$\operatorname {\mathrm {Sim}}(\Delta )$ to be the space of simplices similar to ![]() $\Delta $ (through a translation, rotation or nonzero scaling of
$\Delta $ (through a translation, rotation or nonzero scaling of ![]() $\mathbb {R}^k$). In Theorems 4.8 and 4.9, we prove that
$\mathbb {R}^k$). In Theorems 4.8 and 4.9, we prove that ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ is a submanifold of
$\operatorname {\mathrm {Sim}}(\Delta )$ is a submanifold of ![]() $C_{k+1}[\mathbb {R}^k]$ diffeomorphic to
$C_{k+1}[\mathbb {R}^k]$ diffeomorphic to ![]() $\operatorname {O}(k)\times [0,\infty )\times \mathbb {R}^k$.
$\operatorname {O}(k)\times [0,\infty )\times \mathbb {R}^k$.
In Section 5, we apply our method from Section 3. Given a ![]() $C^\infty $-smooth embedding
$C^\infty $-smooth embedding ![]() $\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ of
$\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$, we let
$\mathbb {R}^k$, we let ![]() $C_{k+1}[\gamma (S^{k-1})]$ be the submanifold of
$C_{k+1}[\gamma (S^{k-1})]$ be the submanifold of ![]() $C_{k+1}[\mathbb {R}^k]$ corresponding to
$C_{k+1}[\mathbb {R}^k]$ corresponding to ![]() $(k+1)$-tuples of points on the embedded sphere
$(k+1)$-tuples of points on the embedded sphere ![]() $\gamma (S^{k-1})$. In Proposition 5.1, we show that
$\gamma (S^{k-1})$. In Proposition 5.1, we show that ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ and
$\operatorname {\mathrm {Sim}}(\Delta )$ and ![]() $C_{k+1}[\gamma (S^{k-1}]$ are boundary disjoint in
$C_{k+1}[\gamma (S^{k-1}]$ are boundary disjoint in ![]() $C_{k+1}[\mathbb {R}^k]$. We then restrict our attention to the standard embedding of
$C_{k+1}[\mathbb {R}^k]$. We then restrict our attention to the standard embedding of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$, with corresponding configuration space
$\mathbb {R}^k$, with corresponding configuration space ![]() $C_{k+1}[S^{k-1}]$. In Proposition 5.2, we show that
$C_{k+1}[S^{k-1}]$. In Proposition 5.2, we show that ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ intersects
$\operatorname {\mathrm {Sim}}(\Delta )$ intersects ![]() $C_{k+1}[S^{k-1}]$ transversally and the intersection
$C_{k+1}[S^{k-1}]$ transversally and the intersection ![]() $\operatorname {\mathrm {Sim}}(\Delta )\cap C_{k+1}[S^{k-1}]$ is diffeomorphic to
$\operatorname {\mathrm {Sim}}(\Delta )\cap C_{k+1}[S^{k-1}]$ is diffeomorphic to ![]() $\operatorname {O}(k)$. Since
$\operatorname {O}(k)$. Since ![]() $\operatorname {O}(k)$ is disconnected, we restrict our attention to
$\operatorname {O}(k)$ is disconnected, we restrict our attention to ![]() $\operatorname {\mathrm {Sim}}^+(\Delta )$, which is the submanifold diffeomorphic to
$\operatorname {\mathrm {Sim}}^+(\Delta )$, which is the submanifold diffeomorphic to ![]() $\operatorname {SO}(k)\times [0,\infty ) \times \mathbb {R}^k$. We then show in Proposition 5.3 that the top class in
$\operatorname {SO}(k)\times [0,\infty ) \times \mathbb {R}^k$. We then show in Proposition 5.3 that the top class in ![]() $\operatorname {\mathrm {Sim}}^+(\Delta )$ corresponds to the top homology class of
$\operatorname {\mathrm {Sim}}^+(\Delta )$ corresponds to the top homology class of ![]() $\operatorname {SO}(k)$, which also corresponds to the top class of the intersection
$\operatorname {SO}(k)$, which also corresponds to the top class of the intersection ![]() $\operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[S^{k-1}]$. Finally in Theorem 5.4, we prove there is a dense set of smooth embeddings of
$\operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[S^{k-1}]$. Finally in Theorem 5.4, we prove there is a dense set of smooth embeddings of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$ which are isotopic to the identity through a differentiable isotopy in
$\mathbb {R}^k$ which are isotopic to the identity through a differentiable isotopy in ![]() $\mathbb {R}^k$, such that the subset of
$\mathbb {R}^k$, such that the subset of ![]() $\operatorname {\mathrm {Sim}}^+(\Delta )$ of simplices inscribed in each sphere contains a similar simplex corresponding to each
$\operatorname {\mathrm {Sim}}^+(\Delta )$ of simplices inscribed in each sphere contains a similar simplex corresponding to each ![]() $U\in \operatorname {SO}(k)$. While we chose to restrict our attention to
$U\in \operatorname {SO}(k)$. While we chose to restrict our attention to ![]() $\operatorname {\mathrm {Sim}}^+(\Delta )$, the same results hold for
$\operatorname {\mathrm {Sim}}^+(\Delta )$, the same results hold for ![]() $\operatorname {\mathrm {Sim}}^-(\Delta ):=\operatorname {\mathrm {Sim}}(\Delta )\setminus \operatorname {\mathrm {Sim}}^+(\Delta )$. In the special case of a smooth embedding of a circle in the plane, our results show that there are loops of triangles inscribed on an embedded circle
$\operatorname {\mathrm {Sim}}^-(\Delta ):=\operatorname {\mathrm {Sim}}(\Delta )\setminus \operatorname {\mathrm {Sim}}^+(\Delta )$. In the special case of a smooth embedding of a circle in the plane, our results show that there are loops of triangles inscribed on an embedded circle ![]() $C^0$-close to the given embedding (see Corollary 5.6 for a precise statement).
$C^0$-close to the given embedding (see Corollary 5.6 for a precise statement).
2 Configuration spaces
The compactified configuration space of ![]() $k+1$ points in
$k+1$ points in ![]() $\mathbb {R}^k$ is the natural setting for finding inscribed simplices in embedded spheres. In this section, we give a very brief overview of compactified configuration spaces. There are many versions of this classical material (see, e.g., [Reference Axelrod and Singer4, Reference Fulton and MacPherson13]), but we follow Sinha [Reference Sinha40], as this approach is more appropriate to our work. A discussion similar to the one found below is found in [Reference Cantarella, Denne and McCleary10].
$\mathbb {R}^k$ is the natural setting for finding inscribed simplices in embedded spheres. In this section, we give a very brief overview of compactified configuration spaces. There are many versions of this classical material (see, e.g., [Reference Axelrod and Singer4, Reference Fulton and MacPherson13]), but we follow Sinha [Reference Sinha40], as this approach is more appropriate to our work. A discussion similar to the one found below is found in [Reference Cantarella, Denne and McCleary10].
A reader familiar with configuration spaces may skip much of this section. However, we recommend paying attention to the notation we have used for the spaces. Definitions 2.2, 2.3, 2.9, Remark 2.5 and Theorem 2.7 are particularly useful.
Definition 2.1 ([Reference Sinha40]).
Given an m-dimensional smooth manifold M, let ![]() $M^{\times n}$ denote the n-fold product M with itself, and define
$M^{\times n}$ denote the n-fold product M with itself, and define ![]() $C_n(M)$ to be the subspace of points
$C_n(M)$ to be the subspace of points ![]() ${\mathbf {p}}=(p_1,\dots , p_n)\in M^{\times n}$, such that
${\mathbf {p}}=(p_1,\dots , p_n)\in M^{\times n}$, such that ![]() $p_j\neq p_k$ if
$p_j\neq p_k$ if ![]() $j\neq k$. Let
$j\neq k$. Let ![]() $\iota $ denote the inclusion map of
$\iota $ denote the inclusion map of ![]() $C_n(M)$ in
$C_n(M)$ in ![]() $M^{\times n}$.
$M^{\times n}$.
The space ![]() $C_n(M)$ is an open submanifold of
$C_n(M)$ is an open submanifold of ![]() $M^{\times n}$. We next compactify
$M^{\times n}$. We next compactify ![]() $C_n(M)$ to a closed manifold-with-boundary and corners, which we will denote
$C_n(M)$ to a closed manifold-with-boundary and corners, which we will denote ![]() $C_n[M]$, without changing its homotopy type. The resulting manifold will be homeomorphic to
$C_n[M]$, without changing its homotopy type. The resulting manifold will be homeomorphic to ![]() $M^{\times n}$ with an open neighborhood of the fat diagonal removed. Recall that the fat diagonal is the subset of
$M^{\times n}$ with an open neighborhood of the fat diagonal removed. Recall that the fat diagonal is the subset of ![]() $M^{\times n}$ of n-tuples for which (at least) two entries are equal, that is, where some collection of points comes together at a single point. The construction of
$M^{\times n}$ of n-tuples for which (at least) two entries are equal, that is, where some collection of points comes together at a single point. The construction of ![]() $C_n[M]$ preserves information about the directions and relative rates of approach of each group of collapsing points.
$C_n[M]$ preserves information about the directions and relative rates of approach of each group of collapsing points.
Definition 2.2 ([Reference Budney, Conant, Scannell and Sinha8, Reference Sinha40]).
Given an ordered pair ![]() $(i,j)$ of distinct elements from
$(i,j)$ of distinct elements from ![]() $\{1,\dots ,n\}$, let the map
$\{1,\dots ,n\}$, let the map ![]() $\pi _{ij}\colon \! C_n(\mathbb {R}^k)\rightarrow S^{k-1}$ send
$\pi _{ij}\colon \! C_n(\mathbb {R}^k)\rightarrow S^{k-1}$ send ![]() $\mathbf {p}=(\mathbf {p}_1,\dots \mathbf {p}_n)$ to
$\mathbf {p}=(\mathbf {p}_1,\dots \mathbf {p}_n)$ to  $\displaystyle \frac {\mathbf {p}_i-\mathbf {p}_j}{\left | \mathbf {p}_i-\mathbf {p}_j \right |}$, the unit vector in the direction of
$\displaystyle \frac {\mathbf {p}_i-\mathbf {p}_j}{\left | \mathbf {p}_i-\mathbf {p}_j \right |}$, the unit vector in the direction of ![]() $\mathbf {p}_i-\mathbf {p}_j$. Let
$\mathbf {p}_i-\mathbf {p}_j$. Let ![]() $[0,\infty ]$ be the one-point compactification of
$[0,\infty ]$ be the one-point compactification of ![]() $[0,\infty )$. Given an ordered triple
$[0,\infty )$. Given an ordered triple ![]() $(i,j,l)$ of distinct elements in
$(i,j,l)$ of distinct elements in ![]() $\{1,\dots ,n\}$, let
$\{1,\dots ,n\}$, let ![]() $r_{ijl} \colon \! C_n(\mathbb {R}^k)\rightarrow [0,\infty ]$ be the map which sends
$r_{ijl} \colon \! C_n(\mathbb {R}^k)\rightarrow [0,\infty ]$ be the map which sends ![]() $\mathbf {p}$ to
$\mathbf {p}$ to  $\displaystyle \frac {\left | {\mathbf {p}_i}-{\mathbf {p}_j} \right | }{\left | \mathbf {p}_i-{\mathbf {p}_l} \right | }$, the ratio of distances between
$\displaystyle \frac {\left | {\mathbf {p}_i}-{\mathbf {p}_j} \right | }{\left | \mathbf {p}_i-{\mathbf {p}_l} \right | }$, the ratio of distances between ![]() $\mathbf {p}_i$ and
$\mathbf {p}_i$ and ![]() $\mathbf {p}_j$, and
$\mathbf {p}_j$, and ![]() $\mathbf {p}_i$ and
$\mathbf {p}_i$ and ![]() $\mathbf {p}_l$.
$\mathbf {p}_l$.
We then compactify ![]() $C_n(\mathbb {R}^k)$ as follows:
$C_n(\mathbb {R}^k)$ as follows:
Definition 2.3 ([Reference Sinha40]).
1. Let
 $A_n[\mathbb {R}^k]$ be the product
$A_n[\mathbb {R}^k]$ be the product  $(\mathbb {R}^k)^{n}\times (S^{k-1})^{n(n-1)} \times [0,\infty ]^{n(n-1)(n-2)}$. Define
$(\mathbb {R}^k)^{n}\times (S^{k-1})^{n(n-1)} \times [0,\infty ]^{n(n-1)(n-2)}$. Define  $C_n[\mathbb {R}^k]$ to be the closure of the image of
$C_n[\mathbb {R}^k]$ to be the closure of the image of  $C_n(\mathbb {R}^k)$ under the map
$C_n(\mathbb {R}^k)$ under the map  $$ \begin{align*}\alpha_n= \iota \times (\pi_{ij}) \times (r_{ijl}) \colon\! C_n(\mathbb{R}^k)\rightarrow A_n[\mathbb{R}^k].\end{align*} $$
$$ \begin{align*}\alpha_n= \iota \times (\pi_{ij}) \times (r_{ijl}) \colon\! C_n(\mathbb{R}^k)\rightarrow A_n[\mathbb{R}^k].\end{align*} $$2. We assume that all manifolds M are smoothly embedded in
 $\mathbb {R}^k$, which allows us to define the restrictions of the maps
$\mathbb {R}^k$, which allows us to define the restrictions of the maps  $\pi _{ij}$ and
$\pi _{ij}$ and  $r_{ijl}$. Then
$r_{ijl}$. Then  $C_n(M)$ is smoothly embedded in
$C_n(M)$ is smoothly embedded in  $C_n(\mathbb {R}^k)$, and we define
$C_n(\mathbb {R}^k)$, and we define  $C_n[M]$ to be the closure of
$C_n[M]$ to be the closure of  $C_n(M)$ in
$C_n(M)$ in  $M^{n}\times (S^{k-1})^{n(n-1)} \times [0,\infty ]^{n(n-1)(n-2)}$. We denote the boundary of
$M^{n}\times (S^{k-1})^{n(n-1)} \times [0,\infty ]^{n(n-1)(n-2)}$. We denote the boundary of  $C_n[M]$ by
$C_n[M]$ by  $\partial C_n[M]=C_n[M]\setminus C_n(M)$.
$\partial C_n[M]=C_n[M]\setminus C_n(M)$.
We now summarise some of the important features of this construction, including the fact that ![]() $C_n[M]$ does not depend on the choice of embedding of M in
$C_n[M]$ does not depend on the choice of embedding of M in ![]() $\mathbb {R}^k$.
$\mathbb {R}^k$.
Theorem 2.4 ([Reference Budney, Conant, Scannell and Sinha8, Reference Sinha40]).
1.
 $C_n[M]$ is a manifold-with-boundary and corners with interior
$C_n[M]$ is a manifold-with-boundary and corners with interior  $C_n(M)$ having the same homotopy type as
$C_n(M)$ having the same homotopy type as  $C_n[M]$. The topological type of
$C_n[M]$. The topological type of  $C_n[M]$ is independent of the embedding of M in
$C_n[M]$ is independent of the embedding of M in  $\mathbb {R}^k$, and
$\mathbb {R}^k$, and  $C_n[M]$ is compact when M is.
$C_n[M]$ is compact when M is.2. The inclusion of
 $C_n(M)$ in
$C_n(M)$ in  $M^{\times n}$ extends to a surjective map from
$M^{\times n}$ extends to a surjective map from  $C_n[M]$ to
$C_n[M]$ to  $M^{\times n}$, which is a homeomorphism over points in
$M^{\times n}$, which is a homeomorphism over points in  $C_n(M)$.
$C_n(M)$.
Remark 2.5. When discussing points in ![]() $C_n[\mathbb {R}^k]$ or
$C_n[\mathbb {R}^k]$ or ![]() $C_n[M]$, it is easy to become confused. We pause to clarify notation.
$C_n[M]$, it is easy to become confused. We pause to clarify notation.
• A point in
 $\mathbb {R}^k$ is denoted by
$\mathbb {R}^k$ is denoted by  $\mathbf {x}=(x_1, \dots , x_k)$, where each
$\mathbf {x}=(x_1, \dots , x_k)$, where each  $x_i\in \mathbb {R}$.
$x_i\in \mathbb {R}$.• Points in
 $(\mathbb {R}^k)^{\times n}$ are also denoted by
$(\mathbb {R}^k)^{\times n}$ are also denoted by  $\mathbf {x}$, where
$\mathbf {x}$, where  $\mathbf {x} = (\mathbf {x}_1, \dots , \mathbf {x}_n)$ and each
$\mathbf {x} = (\mathbf {x}_1, \dots , \mathbf {x}_n)$ and each  $\mathbf {x}_i\in \mathbb {R}^k$ (it will be clear from context which is meant).
$\mathbf {x}_i\in \mathbb {R}^k$ (it will be clear from context which is meant).• A point in
 $C_n[\mathbb {R}^k]$ or
$C_n[\mathbb {R}^k]$ or  $C_n[M]$, is denoted
$C_n[M]$, is denoted  $\overrightarrow {\mathbf {x}} $.
$\overrightarrow {\mathbf {x}} $.
The space ![]() $C_n[M]$ may be viewed as a polytope with a combinatorial structure based on the different ways groups of points in M can come together. This structure defines a stratification of
$C_n[M]$ may be viewed as a polytope with a combinatorial structure based on the different ways groups of points in M can come together. This structure defines a stratification of ![]() $C_n[M]$ into a collection of closed faces of various dimensions whose intersections are members of the collection. Full details can be found in [Reference Budney, Conant, Scannell and Sinha8, Reference Sinha40]. The main structure we will consider is the
$C_n[M]$ into a collection of closed faces of various dimensions whose intersections are members of the collection. Full details can be found in [Reference Budney, Conant, Scannell and Sinha8, Reference Sinha40]. The main structure we will consider is the ![]() $(0,1,\dots ,k)$-face of
$(0,1,\dots ,k)$-face of ![]() $\partial C_n[M]$. This is the boundary component where all the points come together at the same time.
$\partial C_n[M]$. This is the boundary component where all the points come together at the same time.
Any pair ![]() $\mathbf {p}$,
$\mathbf {p}$, ![]() $\mathbf {q}$ of disjoint points in
$\mathbf {q}$ of disjoint points in ![]() $\mathbb {R}^k$ has a direction
$\mathbb {R}^k$ has a direction ![]() $(\mathbf {p}-\mathbf {q})/\left | \mathbf {p}-\mathbf {q} \right |$ associated to it, while every triple of disjoint points
$(\mathbf {p}-\mathbf {q})/\left | \mathbf {p}-\mathbf {q} \right |$ associated to it, while every triple of disjoint points ![]() $\mathbf {p}$,
$\mathbf {p}$, ![]() $\mathbf {q}$,
$\mathbf {q}$, ![]() $\mathbf {r}$ has a corresponding distance ratio
$\mathbf {r}$ has a corresponding distance ratio ![]() $\left | \mathbf {p}-\mathbf {q} \right |/\left | \mathbf {p}-\mathbf {r} \right |$. One way to think of the coordinates of
$\left | \mathbf {p}-\mathbf {q} \right |/\left | \mathbf {p}-\mathbf {r} \right |$. One way to think of the coordinates of ![]() $C_n[M]$ is that they extend the definition of these directions and ratios to the boundary.
$C_n[M]$ is that they extend the definition of these directions and ratios to the boundary.
Theorem 2.6 ([Reference Budney, Conant, Scannell and Sinha8, Reference Sinha40]).
Given a manifold ![]() $M \subset \mathbb {R}^k$, then in any configuration of points
$M \subset \mathbb {R}^k$, then in any configuration of points ![]() $\overrightarrow {\mathbf {p}} \in C_n[M]$, the following holds.
$\overrightarrow {\mathbf {p}} \in C_n[M]$, the following holds.
1. Each pair of points
 $\mathbf {p}_i$,
$\mathbf {p}_i$,  $\mathbf {p}_j$ has associated to it a well-defined unit vector in
$\mathbf {p}_j$ has associated to it a well-defined unit vector in  $\mathbb {R}^k$ giving the direction from
$\mathbb {R}^k$ giving the direction from  $\mathbf {p}_i$ to
$\mathbf {p}_i$ to  $\mathbf {p}_j$. If the pair of points project to the same point
$\mathbf {p}_j$. If the pair of points project to the same point  $\mathbf {p}$ of M, this vector lies in
$\mathbf {p}$ of M, this vector lies in  $T_{\mathbf {p}} M$.
$T_{\mathbf {p}} M$.2. Each triple of points
 $\mathbf {p}_i$,
$\mathbf {p}_i$,  $\mathbf {p}_j$,
$\mathbf {p}_j$,  $\mathbf {p}_k$ has associated to it a well-defined scalar in
$\mathbf {p}_k$ has associated to it a well-defined scalar in  $[0,\infty ]$ corresponding to the ratio of the distances
$[0,\infty ]$ corresponding to the ratio of the distances  $\left | \mathbf {p}_i - \mathbf {p}_j \right |$ and
$\left | \mathbf {p}_i - \mathbf {p}_j \right |$ and  $\left | \mathbf {p}_i - \mathbf {p}_k \right |$. If any pair of
$\left | \mathbf {p}_i - \mathbf {p}_k \right |$. If any pair of  $\{\mathbf {p}_i, \mathbf {p}_j,\mathbf {p}_k\}$ projects to the same point in M (or all three do), this ratio is a limiting ratio of distances.
$\{\mathbf {p}_i, \mathbf {p}_j,\mathbf {p}_k\}$ projects to the same point in M (or all three do), this ratio is a limiting ratio of distances.3. The functions
 $\pi _{ij}$ and
$\pi _{ij}$ and  $r_{ijl}$ are continuous on all of
$r_{ijl}$ are continuous on all of  $C_n[M]$ and smooth on each face of
$C_n[M]$ and smooth on each face of  $\partial C_n[M]$.
$\partial C_n[M]$.
It turns out that for connected manifolds of dimension at least ![]() $2$, the combinatorial structure of the strata of
$2$, the combinatorial structure of the strata of ![]() $C_n[M]$ depends only on the number of points. Regardless of dimension, this construction and division of
$C_n[M]$ depends only on the number of points. Regardless of dimension, this construction and division of ![]() $\partial C_n[M]$ into strata is functorial in the following sense.
$\partial C_n[M]$ into strata is functorial in the following sense.
Theorem 2.7 ([Reference Sinha40]).
Suppose M and N are embedded submanifolds of ![]() $\mathbb {R}^k$ and
$\mathbb {R}^k$ and ![]() $f\colon \! M\hookrightarrow N$ is an embedding. This induces an embedding of manifolds-with-corners called the evaluation map
$f\colon \! M\hookrightarrow N$ is an embedding. This induces an embedding of manifolds-with-corners called the evaluation map ![]() $C_n[f] \colon \! C_n[M]\hookrightarrow C_n[N]$ that respects the stratifications. This map is defined by choosing the ambient embedding of M in
$C_n[f] \colon \! C_n[M]\hookrightarrow C_n[N]$ that respects the stratifications. This map is defined by choosing the ambient embedding of M in ![]() $\mathbb {R}^k$ to be the composition of f with the ambient embedding of N.
$\mathbb {R}^k$ to be the composition of f with the ambient embedding of N.
For an embedding ![]() $f \colon M \hookrightarrow N$, the image of the induced embedding
$f \colon M \hookrightarrow N$, the image of the induced embedding ![]() $C_n[f]\colon C_n[M] \hookrightarrow C_n[N]$ will be denoted by
$C_n[f]\colon C_n[M] \hookrightarrow C_n[N]$ will be denoted by ![]() $C_n[f(M)]$.
$C_n[f(M)]$.
Corollary 2.8. Let ![]() $f\colon \!\mathbb {R}^k\rightarrow \mathbb {R}^k$ be a smooth diffeomorphism. Then the induced map of configuration spaces
$f\colon \!\mathbb {R}^k\rightarrow \mathbb {R}^k$ be a smooth diffeomorphism. Then the induced map of configuration spaces ![]() $C_n[f]\colon \! C_n[\mathbb {R}^k]\rightarrow C_n[\mathbb {R}^k]$ is also a smooth diffeomorphism (on each face of
$C_n[f]\colon \! C_n[\mathbb {R}^k]\rightarrow C_n[\mathbb {R}^k]$ is also a smooth diffeomorphism (on each face of ![]() $C_n[\mathbb {R}^k]$).
$C_n[\mathbb {R}^k]$).
Proof. This is an immediate corollary of the previous theorem.
Finally, we will need a metric on the set of evaluation maps ![]() $C_n[f] \colon \! C_n[M]\hookrightarrow C_n[N]$. The definition of compactified configuration spaces allows us to view
$C_n[f] \colon \! C_n[M]\hookrightarrow C_n[N]$. The definition of compactified configuration spaces allows us to view ![]() $C_n[N] \subset (\mathbb {R}^k)^{n} \times (S^{k-1})^{n(n-1)} \times [0,\infty ]^{n(n-1)(n-2)}$ as a metric space with the sup norm. If we define the mapping
$C_n[N] \subset (\mathbb {R}^k)^{n} \times (S^{k-1})^{n(n-1)} \times [0,\infty ]^{n(n-1)(n-2)}$ as a metric space with the sup norm. If we define the mapping ![]() ${\mathrm {pr}}_i$ to be the projection onto the ith space of the product, then this naturally leads to a metric on the set of continuous functions
${\mathrm {pr}}_i$ to be the projection onto the ith space of the product, then this naturally leads to a metric on the set of continuous functions ![]() $C^0(C_n[M], C_n[N])$.
$C^0(C_n[M], C_n[N])$.
Definition 2.9. With the above assumptions, the metric on the set ![]() $C^0(C_n[M], C_n[N])$ is given by
$C^0(C_n[M], C_n[N])$ is given by
Thus, given the embeddings ![]() $f, g\colon \! M\hookrightarrow N$, we say that the corresponding maps on configuration spaces
$f, g\colon \! M\hookrightarrow N$, we say that the corresponding maps on configuration spaces ![]() $C_n[f],C_n[g]\colon \! C_n[M]\hookrightarrow C_n[N]$ are
$C_n[f],C_n[g]\colon \! C_n[M]\hookrightarrow C_n[N]$ are ![]() $C^0$-close if for all
$C^0$-close if for all ![]() $\epsilon>0$, we have
$\epsilon>0$, we have ![]() $\|C_n[f]-C_n[g]\|_0<\epsilon $.
$\|C_n[f]-C_n[g]\|_0<\epsilon $.
3 Finding special configurations with multijet transversality
In this section, we set up a general method for tackling problems where we seek a special configuration of n points on a compact manifold M that is smoothly embedded in ![]() $\mathbb {R}^k$ (cf. [Reference Cantarella, Denne and McCleary10]). In both the square-peg problem and the inscribed simplex problem, M is a sphere (either
$\mathbb {R}^k$ (cf. [Reference Cantarella, Denne and McCleary10]). In both the square-peg problem and the inscribed simplex problem, M is a sphere (either ![]() $S^1$ or
$S^1$ or ![]() $S^{k-1}$). We thus denote the
$S^{k-1}$). We thus denote the ![]() $C^\infty $ smooth embedding by
$C^\infty $ smooth embedding by ![]() $\gamma \colon \! S^l \hookrightarrow \mathbb {R}^k$, and the corresponding compactified configuration space of n points on
$\gamma \colon \! S^l \hookrightarrow \mathbb {R}^k$, and the corresponding compactified configuration space of n points on ![]() $\gamma (S^l)$ is
$\gamma (S^l)$ is ![]() $C_{n}[\gamma (S^l)]$. We let Z denote the subspace of tuples of n points in
$C_{n}[\gamma (S^l)]$. We let Z denote the subspace of tuples of n points in ![]() $\mathbb {R}^k$ that satisfy the conditions of a special configuration. For example, in [Reference Cantarella, Denne and McCleary10], Z is the set of all square-like quadrilaterals in
$\mathbb {R}^k$ that satisfy the conditions of a special configuration. For example, in [Reference Cantarella, Denne and McCleary10], Z is the set of all square-like quadrilaterals in ![]() $\mathbb {R}^k$. In this paper, we are interested in
$\mathbb {R}^k$. In this paper, we are interested in ![]() $Z=\operatorname {\mathrm {Sim}}(\Delta )$ (see Section 4), which is the set of all
$Z=\operatorname {\mathrm {Sim}}(\Delta )$ (see Section 4), which is the set of all ![]() $(k+1)$-simplices in
$(k+1)$-simplices in ![]() $\mathbb {R}^k$ which are similar to a given nondegenerate simplex
$\mathbb {R}^k$ which are similar to a given nondegenerate simplex ![]() $\Delta $.
$\Delta $.
The central idea is as follows: suppose there is a different, well-understood, smooth embedding of ![]() $S^l$ in
$S^l$ in ![]() $\mathbb {R}^k$ (via
$\mathbb {R}^k$ (via ![]() $i\colon \! S^l\hookrightarrow \mathbb {R}^k$), and assume that the corresponding configuration space
$i\colon \! S^l\hookrightarrow \mathbb {R}^k$), and assume that the corresponding configuration space ![]() $C_n[i(S^l)]$ is transverse to Z in
$C_n[i(S^l)]$ is transverse to Z in ![]() $C_n[\mathbb {R}^k]$. Also assume that
$C_n[\mathbb {R}^k]$. Also assume that ![]() $i(S^l)$ is smoothly homotopy equivalent to
$i(S^l)$ is smoothly homotopy equivalent to ![]() $\gamma (S^l)$ in
$\gamma (S^l)$ in ![]() $\mathbb {R}^k$. Standard transversality arguments should allow us to vary
$\mathbb {R}^k$. Standard transversality arguments should allow us to vary ![]() $C_n[i(S^l)]$ to
$C_n[i(S^l)]$ to ![]() $C_n[\gamma (S^l)]$ while maintaining the transversality of the intersection with Z. There are various technical obstacles to overcome, all of which are handled in detail in [Reference Cantarella, Denne and McCleary10]. Here are the key steps.
$C_n[\gamma (S^l)]$ while maintaining the transversality of the intersection with Z. There are various technical obstacles to overcome, all of which are handled in detail in [Reference Cantarella, Denne and McCleary10]. Here are the key steps.
Step 1: It is possible that special configurations on ![]() $\gamma (S^l)$ shrink away to the boundary of
$\gamma (S^l)$ shrink away to the boundary of ![]() $C_n[\mathbb {R}^k]$ during the isotopy. To prevent this, we first prove
$C_n[\mathbb {R}^k]$ during the isotopy. To prevent this, we first prove
(a) that n-tuples of points in
 $\mathbb {R}^k$ satisfying the geometric condition, Z, are a submanifold in
$\mathbb {R}^k$ satisfying the geometric condition, Z, are a submanifold in  $C_n(\mathbb {R}^k)$, and that
$C_n(\mathbb {R}^k)$, and that  $\partial Z\subset \partial C_n[\mathbb {R}^k]$;
$\partial Z\subset \partial C_n[\mathbb {R}^k]$;(b) that
 $C_n[\gamma (S^l)]$ and Z are boundary-disjoint.
$C_n[\gamma (S^l)]$ and Z are boundary-disjoint.
For ![]() $Z=\operatorname {\mathrm {Sim}}(\Delta )$, we prove 1(a) in Theorems 4.8 and 4.9. We prove 1(b) in Proposition 5.1.
$Z=\operatorname {\mathrm {Sim}}(\Delta )$, we prove 1(a) in Theorems 4.8 and 4.9. We prove 1(b) in Proposition 5.1.
Step 2: For a standard embedding ![]() $i\colon \! S^l\hookrightarrow \mathbb {R}^k$, we need to do two things
$i\colon \! S^l\hookrightarrow \mathbb {R}^k$, we need to do two things
(a) prove that the intersection between
 $C_n[i(S^l)]$ and Z is nonempty and transverse (in other words,
$C_n[i(S^l)]$ and Z is nonempty and transverse (in other words,  $C_n[i]\pitchfork Z$).
$C_n[i]\pitchfork Z$).(b) compute the homology class of the intersection
 $C_n[i(S^l)] \cap Z$ in Z.
$C_n[i(S^l)] \cap Z$ in Z.
For our inscribed simplex problem, we use the standard embedding ![]() $\operatorname {\mathrm {id}} \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ of
$\operatorname {\mathrm {id}} \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$. We prove 2(a) in Proposition 5.2 and 2(b) in Proposition 5.3.
$\mathbb {R}^k$. We prove 2(a) in Proposition 5.2 and 2(b) in Proposition 5.3.
Step 3: Note that in order to apply our transversality arguments, we need to be able to perturb ![]() $C_n[\gamma (S^l)]$ so the intersection of Z remains transverse. However, there is no guarantee that the perturbed submanifold consists of configurations on a perturbed smooth embedding of
$C_n[\gamma (S^l)]$ so the intersection of Z remains transverse. However, there is no guarantee that the perturbed submanifold consists of configurations on a perturbed smooth embedding of ![]() $S^l$ in
$S^l$ in ![]() $\mathbb {R}^k$. We deal with this issue by applying the multijet transversality theorem [Reference Golubitsky and Guillemin14, Theorem II.4.13]. This allows us to conclude (see [Reference Cantarella, Denne and McCleary10] Theorem 17) that for any
$\mathbb {R}^k$. We deal with this issue by applying the multijet transversality theorem [Reference Golubitsky and Guillemin14, Theorem II.4.13]. This allows us to conclude (see [Reference Cantarella, Denne and McCleary10] Theorem 17) that for any ![]() $\epsilon>0$, there is a
$\epsilon>0$, there is a ![]() $C^\infty $-open neighborhood of
$C^\infty $-open neighborhood of ![]() $\gamma $ in which there is, for all m, a
$\gamma $ in which there is, for all m, a ![]() $C^m$-dense set of smooth embeddings
$C^m$-dense set of smooth embeddings ![]() $\gamma '\colon \! S^l \hookrightarrow \mathbb {R}^k$, such that
$\gamma '\colon \! S^l \hookrightarrow \mathbb {R}^k$, such that ![]() $\|C_n[\gamma '] - C_n[\gamma ]\|_0< \epsilon $, and
$\|C_n[\gamma '] - C_n[\gamma ]\|_0< \epsilon $, and ![]() $C_n[\gamma '] \pitchfork Z$, and for which
$C_n[\gamma '] \pitchfork Z$, and for which ![]() $\partial Z$ and
$\partial Z$ and ![]() $\partial C_n[\gamma '(S^l)]$ are disjoint in
$\partial C_n[\gamma '(S^l)]$ are disjoint in ![]() $\partial C_n[\mathbb {R}^k]$.
$\partial C_n[\mathbb {R}^k]$.
In order to fully appreciate Step 3, first recall that the metric on the set ![]() $C^0(C_n[S^l], C_n[\mathbb {R}^k])$ was given in Definition 2.9. Second, to understand the statement about density, we need to give the topology of the spaces we are working in. In general, for manifolds
$C^0(C_n[S^l], C_n[\mathbb {R}^k])$ was given in Definition 2.9. Second, to understand the statement about density, we need to give the topology of the spaces we are working in. In general, for manifolds ![]() $M(=S^l)$ and
$M(=S^l)$ and ![]() $N(=\mathbb {R}^k)$, the space
$N(=\mathbb {R}^k)$, the space ![]() $C^\infty (M,N)$ has the Whitney
$C^\infty (M,N)$ has the Whitney ![]() $C^\infty $-topology (see, e.g., [Reference Hirsch20]). The sets of the form
$C^\infty $-topology (see, e.g., [Reference Hirsch20]). The sets of the form
give a subbasis for the Whitney ![]() $C^t$-topology on
$C^t$-topology on ![]() $C^t(M,N)$ (where t is finite). This subbasis consists of subsets of functions
$C^t(M,N)$ (where t is finite). This subbasis consists of subsets of functions ![]() $g\colon M\to N$ that are smooth, and for coordinate charts
$g\colon M\to N$ that are smooth, and for coordinate charts ![]() $\phi \colon (U' \subset M) \to (U\subset \mathbb {R}^m)$ and
$\phi \colon (U' \subset M) \to (U\subset \mathbb {R}^m)$ and ![]() $\psi \colon (V' \subset N) \to (V\subset \mathbb {R}^k)$ and
$\psi \colon (V' \subset N) \to (V\subset \mathbb {R}^k)$ and ![]() $K \subset U$ compact with
$K \subset U$ compact with ![]() $g(\phi (K)) \subset V'$, then we have, for all
$g(\phi (K)) \subset V'$, then we have, for all ![]() $s \leq r$, and all
$s \leq r$, and all ![]() $x \in \phi (K)$,
$x \in \phi (K)$,
Here, ![]() $D^s F$ for a function
$D^s F$ for a function ![]() $F \colon (U\subset \mathbb {R}^m) \to (V \subset \mathbb {R}^k)$ is the k-tuple of the sth homogeneous parts of the Taylor series representations of the projections of F. Finally, the subspace
$F \colon (U\subset \mathbb {R}^m) \to (V \subset \mathbb {R}^k)$ is the k-tuple of the sth homogeneous parts of the Taylor series representations of the projections of F. Finally, the subspace ![]() $C^\infty (M,N)$ has the Whitney
$C^\infty (M,N)$ has the Whitney ![]() $C^\infty $-topology generated by taking the union of all subbases for all
$C^\infty $-topology generated by taking the union of all subbases for all ![]() $t\geq 0$.
$t\geq 0$.
Note that Step 3 can be applied immediately to the inscribed simplex problem.
Step 4: We need to deform standard spheres into spheres of interest and then consider what happens on the level of configuration spaces. We know precisely when such a deformation of spheres exists due to the following result of Haefliger (which we have stated in a form useful to us).
Theorem 3.1 ([Reference Haefliger19]).
Any two differentiable embeddings of ![]() $S^l$ in
$S^l$ in ![]() $\mathbb {R}^k$ are homotopic through a differentiable isotopy in
$\mathbb {R}^k$ are homotopic through a differentiable isotopy in ![]() $\mathbb {R}^K \supset \mathbb {R}^k$ when
$\mathbb {R}^K \supset \mathbb {R}^k$ when ![]() $K> 3(l+1)/2$.
$K> 3(l+1)/2$.
We use Theorem 3.1 to find a smooth map ![]() $E\colon \! S^l \times I \rightarrow \mathbb {R}^K$ with
$E\colon \! S^l \times I \rightarrow \mathbb {R}^K$ with ![]() $E(-,0)=i$ our standard embedding and
$E(-,0)=i$ our standard embedding and ![]() $E(-,1) = \gamma '$ (where K may be greater than our original k). Recalling that both
$E(-,1) = \gamma '$ (where K may be greater than our original k). Recalling that both ![]() $C_n[i]$ and
$C_n[i]$ and ![]() $C_n[\gamma ']$ are transverse to Z allows us to conclude that using functorality, we get a homotopy
$C_n[\gamma ']$ are transverse to Z allows us to conclude that using functorality, we get a homotopy ![]() $H\colon \! C_n(S^l) \times I\rightarrow C_n(\mathbb {R}^K)$ with
$H\colon \! C_n(S^l) \times I\rightarrow C_n(\mathbb {R}^K)$ with ![]() $H(-,0)=C_n[i]$ and
$H(-,0)=C_n[i]$ and ![]() $H(-,1)=C_n[\gamma ']$. In [Reference Cantarella, Denne and McCleary10], we then use the Transversality Homotopy Extension Theorem (see [Reference Guillemin and Pollack17]), to find a map
$H(-,1)=C_n[\gamma ']$. In [Reference Cantarella, Denne and McCleary10], we then use the Transversality Homotopy Extension Theorem (see [Reference Guillemin and Pollack17]), to find a map ![]() $H'$ homotopic to H and with
$H'$ homotopic to H and with ![]() $H'(-,0)=H(-,0)$,
$H'(-,0)=H(-,0)$, ![]() $H'(-,1)=H(-,1)$ and
$H'(-,1)=H(-,1)$ and ![]() $H'$ is transverse to Z. This then implies that in Z, the intersections
$H'$ is transverse to Z. This then implies that in Z, the intersections ![]() $C_n[i(S^l)] \cap Z$ and
$C_n[i(S^l)] \cap Z$ and ![]() $C_n[\gamma '(S^l)] \cap Z$ represent the same homology class. In other words, we have sketched a proof of the following:
$C_n[\gamma '(S^l)] \cap Z$ represent the same homology class. In other words, we have sketched a proof of the following:
Theorem 3.2 ([Reference Cantarella, Denne and McCleary10] Theorem 20).
Suppose there are two embeddings ![]() $\eta , i:S^l\hookrightarrow \mathbb {R}^k$ of an l-sphere in
$\eta , i:S^l\hookrightarrow \mathbb {R}^k$ of an l-sphere in ![]() $\mathbb {R}^k$. Assume that Z is a closed topological space contained in
$\mathbb {R}^k$. Assume that Z is a closed topological space contained in ![]() $C_n[\mathbb {R}^k]$, such that
$C_n[\mathbb {R}^k]$, such that ![]() $Z \cap C_n(\mathbb {R}^k)$ is a submanifold of
$Z \cap C_n(\mathbb {R}^k)$ is a submanifold of ![]() $C_n(\mathbb {R}^k)$,
$C_n(\mathbb {R}^k)$, ![]() $\partial Z\subset \partial C_n[\mathbb {R}^k]$, and
$\partial Z\subset \partial C_n[\mathbb {R}^k]$, and ![]() $\partial Z$ is disjoint from
$\partial Z$ is disjoint from ![]() $\partial C_n[i(S^l)]$. Also assume that both
$\partial C_n[i(S^l)]$. Also assume that both ![]() $C_n[i]$ and
$C_n[i]$ and ![]() $C_n[\eta ]$ are transverse to Z. Then in Z, the homology class of
$C_n[\eta ]$ are transverse to Z. Then in Z, the homology class of ![]() $C_n[i(S^l)]\cap Z$ and
$C_n[i(S^l)]\cap Z$ and ![]() $C_n[\eta (S^l)]\cap Z$ are equal.
$C_n[\eta (S^l)]\cap Z$ are equal.
In this paper, we will not be making full use of Haefliger’s Theorem in Step 4. Instead, we will restrict our attention to smooth embeddings of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$ which are differentiably isotopic to the identity through a differentiable isotopy in
$\mathbb {R}^k$ which are differentiably isotopic to the identity through a differentiable isotopy in ![]() $\mathbb {R}^k$. The conclusion of Theorem 3.2 still holds for such embeddings. Putting all of our steps together allows us to conclude the following theorem.
$\mathbb {R}^k$. The conclusion of Theorem 3.2 still holds for such embeddings. Putting all of our steps together allows us to conclude the following theorem.
Theorem 3.3 ([Reference Cantarella, Denne and McCleary10] Theorem 21).
Suppose ![]() $\gamma \colon \! S^l\hookrightarrow \mathbb {R}^k$ is a smooth embedding of
$\gamma \colon \! S^l\hookrightarrow \mathbb {R}^k$ is a smooth embedding of ![]() $S^l$ in
$S^l$ in ![]() $\mathbb {R}^k$, with a corresponding embedding of compactified configuration spaces
$\mathbb {R}^k$, with a corresponding embedding of compactified configuration spaces ![]() $C_n[\gamma ]\colon \! C_n[S^l]\hookrightarrow C_n[\mathbb {R}^k]$. Assume that Z is a closed topological space contained in
$C_n[\gamma ]\colon \! C_n[S^l]\hookrightarrow C_n[\mathbb {R}^k]$. Assume that Z is a closed topological space contained in ![]() $C_n[\mathbb {R}^k]$, such that
$C_n[\mathbb {R}^k]$, such that ![]() $Z \cap C_n(\mathbb {R}^k)$ is a submanifold of
$Z \cap C_n(\mathbb {R}^k)$ is a submanifold of ![]() $C_n(\mathbb {R}^k)$, and
$C_n(\mathbb {R}^k)$, and ![]() $\partial Z\subset \partial C_n[\mathbb {R}^k]$. Also assume that
$\partial Z\subset \partial C_n[\mathbb {R}^k]$. Also assume that ![]() $C_n[\gamma (S^l)]$ and Z are boundary-disjoint. Suppose there is a standard embedding
$C_n[\gamma (S^l)]$ and Z are boundary-disjoint. Suppose there is a standard embedding ![]() $i\colon \! S^l\hookrightarrow \mathbb {R}^k$, such that
$i\colon \! S^l\hookrightarrow \mathbb {R}^k$, such that ![]() $C_n[i]\pitchfork Z$ in
$C_n[i]\pitchfork Z$ in ![]() $C_n[\mathbb {R}^k]$.
$C_n[\mathbb {R}^k]$.
Then for all ![]() $\epsilon>0$, there is a
$\epsilon>0$, there is a ![]() $C^\infty $-open neighborhood of
$C^\infty $-open neighborhood of ![]() $\gamma $, in which there is, for all m, a
$\gamma $, in which there is, for all m, a ![]() $C^m$-dense set of smooth embeddings
$C^m$-dense set of smooth embeddings ![]() $\gamma ':S^l\hookrightarrow \mathbb {R}^k$, such that
$\gamma ':S^l\hookrightarrow \mathbb {R}^k$, such that ![]() $\| C_n[\gamma '] - C_n[\gamma ]\|_0< \epsilon $, and
$\| C_n[\gamma '] - C_n[\gamma ]\|_0< \epsilon $, and ![]() $C_n[\gamma '] \pitchfork Z$. Moreover,
$C_n[\gamma '] \pitchfork Z$. Moreover, ![]() $C_n[i(S^l)] \cap Z$ and
$C_n[i(S^l)] \cap Z$ and ![]() $C_n[\gamma '(S^l)] \cap Z$ represent the same homology class in Z.
$C_n[\gamma '(S^l)] \cap Z$ represent the same homology class in Z.
Intuitively, this theorem shows that any smooth embedding ![]() $\gamma $ of
$\gamma $ of ![]() $S^l$ in
$S^l$ in ![]() $\mathbb {R}^k$ has a neighborhood in which there is a dense set of smooth embeddings
$\mathbb {R}^k$ has a neighborhood in which there is a dense set of smooth embeddings ![]() $\gamma '$ for which
$\gamma '$ for which ![]() $C_n[\gamma '(S^l)]$ is guaranteed to have certain intersections with various submanifolds of
$C_n[\gamma '(S^l)]$ is guaranteed to have certain intersections with various submanifolds of ![]() $C_n[\mathbb {R}^k]$ defined by geometric conditions. Stated in a different way, we have the idea that a dense set of embeddings of
$C_n[\mathbb {R}^k]$ defined by geometric conditions. Stated in a different way, we have the idea that a dense set of embeddings of ![]() $S^l$ always contain certain inscribed configurations of points.
$S^l$ always contain certain inscribed configurations of points.
4 Simplices
4.1 Nondegenerate simplices
Definition 4.1. By a simplex ![]() $\Delta $ in
$\Delta $ in ![]() $\mathbb {R}^k$, we mean a set of
$\mathbb {R}^k$, we mean a set of ![]() $k+1$ distinct points
$k+1$ distinct points ![]() $\{\mathbf {p}_0, \dots , \mathbf {p}_k\}$ in
$\{\mathbf {p}_0, \dots , \mathbf {p}_k\}$ in ![]() $\mathbb {R}^k$ in general position.
$\mathbb {R}^k$ in general position.
By general position, we mean that no hyperplane in ![]() $\mathbb {R}^k$ contains more than k points of
$\mathbb {R}^k$ contains more than k points of ![]() $\Delta $. As a first consequence of this definition, we note that the volume of the simplex
$\Delta $. As a first consequence of this definition, we note that the volume of the simplex ![]() $\Delta $ is nonzero. This means that for us, a simplex is nondegenerate. In addition, to each simplex
$\Delta $ is nonzero. This means that for us, a simplex is nondegenerate. In addition, to each simplex ![]() $\Delta $, we can associate several sets:
$\Delta $, we can associate several sets:
• the nonzero distances
 $\{d_{ij}(\Delta )\} =\{\|\mathbf {p}_i-\mathbf {p}_j \|\}$, and observe that
$\{d_{ij}(\Delta )\} =\{\|\mathbf {p}_i-\mathbf {p}_j \|\}$, and observe that  $d_{ij}=d_{ji}$;
$d_{ij}=d_{ji}$;• the unit vectors
 $\{\pi _{ij} (\Delta )\} = \{\frac {\mathbf {p}_i-\mathbf {p}_j}{\|\mathbf {p}_i-\mathbf {p}_j\|}\}$;
$\{\pi _{ij} (\Delta )\} = \{\frac {\mathbf {p}_i-\mathbf {p}_j}{\|\mathbf {p}_i-\mathbf {p}_j\|}\}$;• the ratios
 $\{r_{ijl} (\Delta )\}= \{\frac {\|\mathbf {p}_i-\mathbf {p}_j\|}{\|\mathbf {p}_i-\mathbf {p}_l\|}\}= \{\frac {d_{ij}}{d_{il}}\}$.
$\{r_{ijl} (\Delta )\}= \{\frac {\|\mathbf {p}_i-\mathbf {p}_j\|}{\|\mathbf {p}_i-\mathbf {p}_l\|}\}= \{\frac {d_{ij}}{d_{il}}\}$.
Here, we assume that ![]() $i\neq j$ (and
$i\neq j$ (and ![]() $j\neq l, i\neq l$), so the set of
$j\neq l, i\neq l$), so the set of ![]() $k(k+1) / 2$ distances consists of nonzero values, and the set of ratios has values in
$k(k+1) / 2$ distances consists of nonzero values, and the set of ratios has values in ![]() $(0,\infty )$.
$(0,\infty )$.
A natural question to ask is, given a set of nonzero distances ![]() $\mathcal {D}=\{d_{ij}\}$, is there a simplex that can be constructed with those distances? The theory of distance geometry allows us to decide which sets of distances
$\mathcal {D}=\{d_{ij}\}$, is there a simplex that can be constructed with those distances? The theory of distance geometry allows us to decide which sets of distances ![]() $\mathcal {D}$ are constructible. We start be defining the Cayley-Menger determinant for
$\mathcal {D}$ are constructible. We start be defining the Cayley-Menger determinant for ![]() $\{\mathbf {p}_0,\mathbf {p}_1,\dots ,\mathbf {p}_k\}$, or equivalently for
$\{\mathbf {p}_0,\mathbf {p}_1,\dots ,\mathbf {p}_k\}$, or equivalently for ![]() $\mathcal {D}=\{d_{ij}\} =\{\|\mathbf {p}_i-\mathbf {p}_j \|\}$ (see, e.g., [Reference Blumenthal and Gillam7, Reference Sippl and Scheraga41]):
$\mathcal {D}=\{d_{ij}\} =\{\|\mathbf {p}_i-\mathbf {p}_j \|\}$ (see, e.g., [Reference Blumenthal and Gillam7, Reference Sippl and Scheraga41]):
 $$ \begin{align*} \operatorname{\mathrm{CM}}(\{\mathbf{p}_0,\mathbf{p}_1,\dots ,\mathbf{p}_k\}) = \operatorname{\mathrm{CM}}(\mathcal{D}) = \left| \begin{matrix} 0 & 1 & 1 & \dots & 1 \\ 1 & 0 & d_{01}^2 & \dots & d_{0k}^2 \\ 1 & d_{10}^2 & 0 & \dots & d_{1k}^2 \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & d_{k0}^2 & d_{k1}^2 & \dots & 0 \\ \end{matrix} \right|. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{CM}}(\{\mathbf{p}_0,\mathbf{p}_1,\dots ,\mathbf{p}_k\}) = \operatorname{\mathrm{CM}}(\mathcal{D}) = \left| \begin{matrix} 0 & 1 & 1 & \dots & 1 \\ 1 & 0 & d_{01}^2 & \dots & d_{0k}^2 \\ 1 & d_{10}^2 & 0 & \dots & d_{1k}^2 \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & d_{k0}^2 & d_{k1}^2 & \dots & 0 \\ \end{matrix} \right|. \end{align*} $$Theorem 4.2 ([Reference Berger5] Theorems 9.7.3.4 and 9.14.23).
Given a set of nonzero distances ![]() $\mathcal {D}=\{d_{ij}\}$ for
$\mathcal {D}=\{d_{ij}\}$ for ![]() $i,j = 0,1,\dots , k$, a necessary and sufficient condition for the existence of a simplex
$i,j = 0,1,\dots , k$, a necessary and sufficient condition for the existence of a simplex ![]() $\{\mathbf {p}_0,\dots , \mathbf {p}_k\}$ with
$\{\mathbf {p}_0,\dots , \mathbf {p}_k\}$ with ![]() $d_{ij}=\| \mathbf {p}_i-\mathbf {p}_j\|$ is that for every
$d_{ij}=\| \mathbf {p}_i-\mathbf {p}_j\|$ is that for every ![]() $h=2,\dots ,k$, and every h-element subset of
$h=2,\dots ,k$, and every h-element subset of ![]() $\{0,1,\dots , k\}$, the corresponding Cayley-Menger determinant be nonzero and its sign be
$\{0,1,\dots , k\}$, the corresponding Cayley-Menger determinant be nonzero and its sign be ![]() $(-1)^{h}$.
$(-1)^{h}$.
Moreover, when ![]() $\mathcal {D}=\{d_{ij}\} = \{\|\mathbf {p}_i - \mathbf {p}_j\|\}$ for
$\mathcal {D}=\{d_{ij}\} = \{\|\mathbf {p}_i - \mathbf {p}_j\|\}$ for ![]() $\mathbf {p}_0,\dots ,\mathbf {p}_{k}\in \mathbb {R}^k$, the volume V of the simplex with vertices
$\mathbf {p}_0,\dots ,\mathbf {p}_{k}\in \mathbb {R}^k$, the volume V of the simplex with vertices ![]() $\mathbf {p}_0, \dots , \mathbf {p}_{k}$ obeys
$\mathbf {p}_0, \dots , \mathbf {p}_{k}$ obeys
 $$ \begin{align*} \operatorname{\mathrm{V}}^2 = \frac{(-1)^{k+1}}{2^k(k!)^2} \operatorname{\mathrm{CM}}(\mathcal{D}). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{V}}^2 = \frac{(-1)^{k+1}}{2^k(k!)^2} \operatorname{\mathrm{CM}}(\mathcal{D}). \end{align*} $$Recall that by definition, a simplex is nondegenerate. This means that both the volume of the simplex and Cayley-Menger determinant are nonzero.
The Cayley-Menger determinant generalises standard facts in triangle geometry: for instance, for a triangle with side lengths a, b and c, we can write this determinant explicitly as
and conclude that
This is Heron’s formula for the area of the triangle. We can see the triangle inequality (a criteria for constructability of a triangle), in these formulas: Theorem 4.2 holds if and only if one of the side lengths is greater than the sum of the other two.
4.2 Simplices and configuration spaces
We will now shift our viewpoint and, with an abuse of notation, view the simplex ![]() $\Delta $ in
$\Delta $ in ![]() $\mathbb {R}^k$ as an ordered
$\mathbb {R}^k$ as an ordered ![]() $(k+1)$-tuple of points
$(k+1)$-tuple of points ![]() $\Delta =(\mathbf {p}_0, \dots , \mathbf {p}_k)$. Thus, the simplex is a point in the open configuration space
$\Delta =(\mathbf {p}_0, \dots , \mathbf {p}_k)$. Thus, the simplex is a point in the open configuration space ![]() $C_{k+1}(\mathbb {R}^k)$. We now wish to understand the set of points
$C_{k+1}(\mathbb {R}^k)$. We now wish to understand the set of points ![]() $\{(\mathbf {q}_0, \dots , \mathbf {q}_k)\}$ in
$\{(\mathbf {q}_0, \dots , \mathbf {q}_k)\}$ in ![]() $C_{k+1}(\mathbb {R}^k)$ that correspond to simplices similar to our given simplex
$C_{k+1}(\mathbb {R}^k)$ that correspond to simplices similar to our given simplex ![]() $\Delta $. By similar, we mean there is a translation, rotation and nonzero scaling of
$\Delta $. By similar, we mean there is a translation, rotation and nonzero scaling of ![]() $\mathbb {R}^k$ which maps
$\mathbb {R}^k$ which maps ![]() $(\mathbf {q}_0, \dots , \mathbf {q}_k)$ to
$(\mathbf {q}_0, \dots , \mathbf {q}_k)$ to ![]() $\Delta $.
$\Delta $.
Definition 4.3. For a given nondegenerate simplex ![]() $\Delta =(\mathbf {p}_0,\dots , \mathbf {p}_k)$, we let
$\Delta =(\mathbf {p}_0,\dots , \mathbf {p}_k)$, we let ![]() $\operatorname {\mathrm {Sim}}(\Delta )\subset C_{k+1}(\mathbb {R}^k)$ denote the space of simplices similar to
$\operatorname {\mathrm {Sim}}(\Delta )\subset C_{k+1}(\mathbb {R}^k)$ denote the space of simplices similar to ![]() $\Delta $. Then
$\Delta $. Then ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ is the set of all
$\operatorname {\mathrm {Sim}}(\Delta )$ is the set of all ![]() $\overrightarrow {\mathbf {q}} \in C_{k+1}(\mathbb {R}^k)$, such that
$\overrightarrow {\mathbf {q}} \in C_{k+1}(\mathbb {R}^k)$, such that
That is, when ![]() $\overrightarrow {\mathbf {q}} =(\mathbf {q}_0,\dots , \mathbf {q}_k)$ is extrinsically similar to
$\overrightarrow {\mathbf {q}} =(\mathbf {q}_0,\dots , \mathbf {q}_k)$ is extrinsically similar to ![]() $\Delta $, then we have
$\Delta $, then we have
Our next aim is to show that ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ is a submanifold of
$\operatorname {\mathrm {Sim}}(\Delta )$ is a submanifold of ![]() $C_{k+1}(\mathbb {R}^k)$, by proving that
$C_{k+1}(\mathbb {R}^k)$, by proving that ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ is diffeomorphic to
$\operatorname {\mathrm {Sim}}(\Delta )$ is diffeomorphic to ![]() $\operatorname {O}(k)\times (0,\infty )\times \mathbb {R}^k$. We also aim to understand how the boundary of
$\operatorname {O}(k)\times (0,\infty )\times \mathbb {R}^k$. We also aim to understand how the boundary of ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ sits inside of
$\operatorname {\mathrm {Sim}}(\Delta )$ sits inside of ![]() $C_{k+1}[\mathbb {R}^k]$. In order to do this, we will associate a matrix to
$C_{k+1}[\mathbb {R}^k]$. In order to do this, we will associate a matrix to ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ and look at the polar decomposition of that matrix. So we will need to use some results from linear algebra along the way. These are all found in Appendix A.
$\operatorname {\mathrm {Sim}}(\Delta )$ and look at the polar decomposition of that matrix. So we will need to use some results from linear algebra along the way. These are all found in Appendix A.
Definition 4.4. Given a configuration ![]() $\overrightarrow {\mathbf {q}} =(\mathbf {q}_0,\dots , \mathbf {q}_k)$ in
$\overrightarrow {\mathbf {q}} =(\mathbf {q}_0,\dots , \mathbf {q}_k)$ in ![]() $\operatorname {\mathrm {Sim}}(\Delta )$, we define the
$\operatorname {\mathrm {Sim}}(\Delta )$, we define the ![]() $k\times k$ matrix
$k\times k$ matrix ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ by
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ by
Proposition 4.5. Given a configuration ![]() $ \overrightarrow {\mathbf {q}} = \{\mathbf {q}_0, \ldots , \mathbf {q}_k\}$ in
$ \overrightarrow {\mathbf {q}} = \{\mathbf {q}_0, \ldots , \mathbf {q}_k\}$ in ![]() $\operatorname {\mathrm {Sim}}(\Delta )$, the matrix
$\operatorname {\mathrm {Sim}}(\Delta )$, the matrix ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ has rank k, and the
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ has rank k, and the ![]() $k\times k$ matrix
$k\times k$ matrix ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )^T\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ is given by
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )^T\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ is given by
where ![]() $P(\Delta )$ is a uniquely determined symmetric positive-definite matrix.
$P(\Delta )$ is a uniquely determined symmetric positive-definite matrix.
The matrix ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )^T\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ is called the Gram matrix, and it consists of the dot products of the
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )^T\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ is called the Gram matrix, and it consists of the dot products of the ![]() $\pi _{ij}(\kern1.5pt \overrightarrow {\mathbf {q}} )$, which are the cosines of the angles between the unit vectors
$\pi _{ij}(\kern1.5pt \overrightarrow {\mathbf {q}} )$, which are the cosines of the angles between the unit vectors ![]() $\pi _{ij}(\kern1.5pt \overrightarrow {\mathbf {q}} )$.
$\pi _{ij}(\kern1.5pt \overrightarrow {\mathbf {q}} )$.
Proof. Recall the law of cosines: ![]() $c^2 = a^2 + b^2 - 2ab\cos C$, where c is the length of the side of a triangle
$c^2 = a^2 + b^2 - 2ab\cos C$, where c is the length of the side of a triangle ![]() $\triangle ABC$ opposite angle C and a and b are the lengths of the sides subtending angle C. In the case
$\triangle ABC$ opposite angle C and a and b are the lengths of the sides subtending angle C. In the case ![]() $a = \| \mathbf {q}_i - \mathbf {q}_0\|$,
$a = \| \mathbf {q}_i - \mathbf {q}_0\|$, ![]() $b = \| \mathbf {q}_j - \mathbf {q}_0\|$ and
$b = \| \mathbf {q}_j - \mathbf {q}_0\|$ and ![]() $c = \| \mathbf {q}_i - \mathbf {q}_j\|$, angle C is
$c = \| \mathbf {q}_i - \mathbf {q}_j\|$, angle C is ![]() $\theta _{ij}$, and we have
$\theta _{ij}$, and we have
 $$ \begin{align*} \cos \theta_{ij} &= \dfrac{a^2 + b^2 - c^2}{2ab} = \dfrac12 \left( \dfrac{a}{b} + \dfrac{b}{a} - \dfrac{c^2}{ab} \right) \\ &= \dfrac12 (r_{0ij}(\kern1.5pt\overrightarrow{\mathbf{q}} ) + r_{0ji}(\kern1.5pt\overrightarrow{\mathbf{q}} ) - r_{ij0}(\kern1.5pt\overrightarrow{\mathbf{q}} ) r_{ji0}(\kern1.5pt\overrightarrow{\mathbf{q}} )). \end{align*} $$
$$ \begin{align*} \cos \theta_{ij} &= \dfrac{a^2 + b^2 - c^2}{2ab} = \dfrac12 \left( \dfrac{a}{b} + \dfrac{b}{a} - \dfrac{c^2}{ab} \right) \\ &= \dfrac12 (r_{0ij}(\kern1.5pt\overrightarrow{\mathbf{q}} ) + r_{0ji}(\kern1.5pt\overrightarrow{\mathbf{q}} ) - r_{ij0}(\kern1.5pt\overrightarrow{\mathbf{q}} ) r_{ji0}(\kern1.5pt\overrightarrow{\mathbf{q}} )). \end{align*} $$Because the ![]() $r_{ijl}$ are the same for all configurations in
$r_{ijl}$ are the same for all configurations in ![]() $\operatorname {\mathrm {Sim}}(\Delta )$, this matrix is the same as for
$\operatorname {\mathrm {Sim}}(\Delta )$, this matrix is the same as for ![]() $\Pi (\Delta )$ associated with
$\Pi (\Delta )$ associated with ![]() $\Delta =(\mathbf {p}_0, \dots , \mathbf {p}_k)\in C_{k+1}(\mathbb {R}^k)$. The following shows
$\Delta =(\mathbf {p}_0, \dots , \mathbf {p}_k)\in C_{k+1}(\mathbb {R}^k)$. The following shows ![]() $\Pi (\Delta )$ has rank k:
$\Pi (\Delta )$ has rank k:
 $$ \begin{align*} 0 < {\mathrm{Vol}}_k(\Delta) &= \dfrac1{k!} \det\begin{bmatrix} \mathbf{p}_1 - \mathbf{p}_0 & \dots & \mathbf{p}_k - \mathbf{p}_0\end{bmatrix}\\[3pt] &= \dfrac{\| \mathbf{p}_1 - \mathbf{p}_0\|\times \cdots \times \| \mathbf{p}_k - \mathbf{p}_0\|}{k!} \det \begin{bmatrix}\pi_{10}(\kern1.5pt\overrightarrow{\mathbf{p}} ) &\dots & \pi_{k0}(\kern1.5pt\overrightarrow{\mathbf{p}} )\end{bmatrix} \\[3pt] &= \dfrac{\| \mathbf{p}_1 - \mathbf{p}_0\|\times \cdots \times \| \mathbf{p}_k - \mathbf{p}_0\|}{k!} \det\Pi(\Delta). \end{align*} $$
$$ \begin{align*} 0 < {\mathrm{Vol}}_k(\Delta) &= \dfrac1{k!} \det\begin{bmatrix} \mathbf{p}_1 - \mathbf{p}_0 & \dots & \mathbf{p}_k - \mathbf{p}_0\end{bmatrix}\\[3pt] &= \dfrac{\| \mathbf{p}_1 - \mathbf{p}_0\|\times \cdots \times \| \mathbf{p}_k - \mathbf{p}_0\|}{k!} \det \begin{bmatrix}\pi_{10}(\kern1.5pt\overrightarrow{\mathbf{p}} ) &\dots & \pi_{k0}(\kern1.5pt\overrightarrow{\mathbf{p}} )\end{bmatrix} \\[3pt] &= \dfrac{\| \mathbf{p}_1 - \mathbf{p}_0\|\times \cdots \times \| \mathbf{p}_k - \mathbf{p}_0\|}{k!} \det\Pi(\Delta). \end{align*} $$ By construction, ![]() $\Pi (\Delta )^T\Pi (\Delta )$ is a symmetric matrix. We have just shown that
$\Pi (\Delta )^T\Pi (\Delta )$ is a symmetric matrix. We have just shown that ![]() $\Pi (\Delta )$ has full column rank. Thus, by Theorem A.3, we know
$\Pi (\Delta )$ has full column rank. Thus, by Theorem A.3, we know ![]() $\Pi (\Delta )^T\Pi (\Delta )$ is positive-definite. Since
$\Pi (\Delta )^T\Pi (\Delta )$ is positive-definite. Since ![]() $\Pi (\Delta )^T\Pi (\Delta )=\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )^T\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$, we again use Theorem A.3 to deduce
$\Pi (\Delta )^T\Pi (\Delta )=\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )^T\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$, we again use Theorem A.3 to deduce ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ also has rank k. Now, using other standard results from linear algebra (Theorem A.1 and Remark A.2), we can deduce there is a unique symmetric positive-definite matrix
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ also has rank k. Now, using other standard results from linear algebra (Theorem A.1 and Remark A.2), we can deduce there is a unique symmetric positive-definite matrix ![]() $P(\Delta )$, such that
$P(\Delta )$, such that ![]() $P(\Delta ) = (\Pi (\Delta )^T \Pi (\Delta ))^{1/2}$.
$P(\Delta ) = (\Pi (\Delta )^T \Pi (\Delta ))^{1/2}$.
We now use the polar decomposition theorem for a matrix to get a better understanding of ![]() $\operatorname {\mathrm {Sim}}(\Delta )$. Recall, from Theorem A.4, that the polar decomposition of a
$\operatorname {\mathrm {Sim}}(\Delta )$. Recall, from Theorem A.4, that the polar decomposition of a ![]() $k\times k$ real matrix A is a factorisation of the form
$k\times k$ real matrix A is a factorisation of the form ![]() $A=UP$, where U is orthogonal and P is a positive semidefinite symmetric matrix. This decomposition is unique when A is nonsingular (intuitively, if A is interpreted as a linear transformation of
$A=UP$, where U is orthogonal and P is a positive semidefinite symmetric matrix. This decomposition is unique when A is nonsingular (intuitively, if A is interpreted as a linear transformation of ![]() $\mathbb {R}^k$, then the polar decomposition separates it into a rotation or reflection U of
$\mathbb {R}^k$, then the polar decomposition separates it into a rotation or reflection U of ![]() $\mathbb {R}^k$, and a scaling of the space along a set of k orthogonal axes).
$\mathbb {R}^k$, and a scaling of the space along a set of k orthogonal axes).
Proposition 4.6. If ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, then
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, then ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} ) P(\Delta )$, where
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} ) P(\Delta )$, where ![]() $U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is a uniquely determined
$U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is a uniquely determined ![]() $k\times k$ orthogonal matrix which is a smooth function of
$k\times k$ orthogonal matrix which is a smooth function of ![]() $ \overrightarrow {\mathbf {q}} $. The
$ \overrightarrow {\mathbf {q}} $. The ![]() $k\times k$ matrix
$k\times k$ matrix ![]() $P(\Delta )$ depends only on
$P(\Delta )$ depends only on ![]() $\Delta $, and is a symmetric positive-definite matrix.
$\Delta $, and is a symmetric positive-definite matrix.
Proof. In our case, since ![]() $\operatorname {\mathrm {rank}}\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )=k$, the polar decomposition theorem (Theorem A.4) tells us that for the
$\operatorname {\mathrm {rank}}\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )=k$, the polar decomposition theorem (Theorem A.4) tells us that for the ![]() $k\times k$ matrix
$k\times k$ matrix ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$, there is a unique decomposition into
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$, there is a unique decomposition into ![]() $k\times k$ matrices:
$k\times k$ matrices: ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )P$. Here, matrix
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )P$. Here, matrix ![]() $U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is orthogonal, and
$U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is orthogonal, and ![]() $P=(\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )^T \Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ))^{1/2}$. From Proposition 4.5, we know
$P=(\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )^T \Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ))^{1/2}$. From Proposition 4.5, we know
Thus, for each ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we have the same symmetric positive-definite
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we have the same symmetric positive-definite ![]() $P(\Delta )$ matrix. The dependence of
$P(\Delta )$ matrix. The dependence of ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ on
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$ on ![]() $ \overrightarrow {\mathbf {q}} $ is clearly smooth; that
$ \overrightarrow {\mathbf {q}} $ is clearly smooth; that ![]() $U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ depends smoothly on
$U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ depends smoothly on ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$, and, hence, on
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} )$, and, hence, on ![]() $ \overrightarrow {\mathbf {q}} $, and
$ \overrightarrow {\mathbf {q}} $, and ![]() $U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is smooth, were shown in [Reference Dieci and Eirola12] (see Remark A.5).
$U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is smooth, were shown in [Reference Dieci and Eirola12] (see Remark A.5).
Let ![]() $\operatorname {O}(k)$ be the set of all orthogonal
$\operatorname {O}(k)$ be the set of all orthogonal ![]() $k\times k$ matrices. Roughly speaking, Proposition 4.6 says that for a (nondegenerate) simplex
$k\times k$ matrices. Roughly speaking, Proposition 4.6 says that for a (nondegenerate) simplex ![]() $\Delta $, we can obtain a different configuration in
$\Delta $, we can obtain a different configuration in ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ by multiplying
$\operatorname {\mathrm {Sim}}(\Delta )$ by multiplying ![]() $P(\Delta )$ on the left by a matrix in
$P(\Delta )$ on the left by a matrix in ![]() $\operatorname {O}(k)$. This leads us to define the following map.
$\operatorname {O}(k)$. This leads us to define the following map.
Definition 4.7. The pose map ![]() $ps: \operatorname {\mathrm {Sim}}(\Delta ) \rightarrow \operatorname {O}(k)$ is defined by
$ps: \operatorname {\mathrm {Sim}}(\Delta ) \rightarrow \operatorname {O}(k)$ is defined by ![]() $ps(\kern1.5pt \overrightarrow {\mathbf {q}} )=U(\kern1.5pt \overrightarrow {\mathbf {q}} )$, where
$ps(\kern1.5pt \overrightarrow {\mathbf {q}} )=U(\kern1.5pt \overrightarrow {\mathbf {q}} )$, where ![]() $U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is the unique orthogonal matrix
$U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is the unique orthogonal matrix ![]() $U(\kern1.5pt \overrightarrow {\mathbf {q}} )$, such that
$U(\kern1.5pt \overrightarrow {\mathbf {q}} )$, such that ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )P(\Delta )$ (as found in Proposition 4.6). For a simplex
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )P(\Delta )$ (as found in Proposition 4.6). For a simplex ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we call the corresponding element
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we call the corresponding element ![]() $U(\kern1.5pt \overrightarrow {\mathbf {q}} ) \in \operatorname {O}(k)$ the pose of
$U(\kern1.5pt \overrightarrow {\mathbf {q}} ) \in \operatorname {O}(k)$ the pose of ![]() $ \overrightarrow {\mathbf {q}} $.
$ \overrightarrow {\mathbf {q}} $.
We can now deduce the structure of ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ as a submanifold of
$\operatorname {\mathrm {Sim}}(\Delta )$ as a submanifold of ![]() $C_{k+1}[\mathbb {R}^k]$.
$C_{k+1}[\mathbb {R}^k]$.
Theorem 4.8. If ![]() $\Delta $ is a nondegenerate k-simplex in
$\Delta $ is a nondegenerate k-simplex in ![]() $\mathbb {R}^k$, then
$\mathbb {R}^k$, then ![]() $\operatorname {\mathrm {Sim}}(\Delta )\subset C_{k+1}(\mathbb {R}^k)$ is a submanifold diffeomorphic to
$\operatorname {\mathrm {Sim}}(\Delta )\subset C_{k+1}(\mathbb {R}^k)$ is a submanifold diffeomorphic to ![]() $\operatorname {O}(k) \times (0, \infty ) \times \mathbb {R}^k$.
$\operatorname {O}(k) \times (0, \infty ) \times \mathbb {R}^k$.
Proof. We will define the following pair of maps:
We will then prove that both maps are smooth, that the first map ![]() $i_\Delta $ is onto
$i_\Delta $ is onto ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ and the composition is the identity. This will prove that
$\operatorname {\mathrm {Sim}}(\Delta )$ and the composition is the identity. This will prove that ![]() $i_\Delta $ is a diffeomorphism onto
$i_\Delta $ is a diffeomorphism onto ![]() $\operatorname {\mathrm {Sim}}(\Delta )$.
$\operatorname {\mathrm {Sim}}(\Delta )$.
We have been given ![]() $\Delta =(\mathbf {p}_0,\ldots , \mathbf {p}_k)\in C_{k+1}(\mathbb {R}^k)$. We can then define the set of ratios
$\Delta =(\mathbf {p}_0,\ldots , \mathbf {p}_k)\in C_{k+1}(\mathbb {R}^k)$. We can then define the set of ratios ![]() $\{ r_{ijl}(\Delta )\}$, the set of unit vectors
$\{ r_{ijl}(\Delta )\}$, the set of unit vectors ![]() $\{\pi _{ij}(\Delta )\}$ and the matrix
$\{\pi _{ij}(\Delta )\}$ and the matrix ![]() $\Pi (\Delta )$. We know that
$\Pi (\Delta )$. We know that ![]() $\Pi (\Delta ) = U(\Delta )P(\Delta )$, from Proposition 4.6. Moreover, without loss of generality, we can assume that
$\Pi (\Delta ) = U(\Delta )P(\Delta )$, from Proposition 4.6. Moreover, without loss of generality, we can assume that ![]() $\Delta $ is chosen such that
$\Delta $ is chosen such that ![]() $U(\Delta )=I_k$ (the identity matrix), and so
$U(\Delta )=I_k$ (the identity matrix), and so ![]() $\Pi (\Delta ) = P(\Delta )$.
$\Pi (\Delta ) = P(\Delta )$.
Let ![]() $A=\begin {bmatrix} \mathbf {v}_1 \ \dots \ \mathbf {v}_k\end {bmatrix}\in \operatorname {O}(k)$, and define a new set of unit vectors by
$A=\begin {bmatrix} \mathbf {v}_1 \ \dots \ \mathbf {v}_k\end {bmatrix}\in \operatorname {O}(k)$, and define a new set of unit vectors by ![]() $\pi _{ij} =\begin {bmatrix} \mathbf {v}_1 \ \dots \ \mathbf {v}_k\end {bmatrix} \pi _{ij}(\Delta )$ (intuitively, the new
$\pi _{ij} =\begin {bmatrix} \mathbf {v}_1 \ \dots \ \mathbf {v}_k\end {bmatrix} \pi _{ij}(\Delta )$ (intuitively, the new ![]() $\pi _{ij}$ are
$\pi _{ij}$ are ![]() $\pi _{ij}(\Delta )$ rotated/reflected by A). If we also let
$\pi _{ij}(\Delta )$ rotated/reflected by A). If we also let ![]() $r_{ijl} = r_{ijl}(\Delta )$, then we define the map
$r_{ijl} = r_{ijl}(\Delta )$, then we define the map ![]() $i_\Delta $ by
$i_\Delta $ by
This map ![]() $i_\Delta $ is clearly smooth in A,
$i_\Delta $ is clearly smooth in A, ![]() $\lambda $ and
$\lambda $ and ![]() $\mathbf {q}_0$. Furthermore,
$\mathbf {q}_0$. Furthermore, ![]() $i_\Delta (A, \lambda , \mathbf {q}_0)$ has
$i_\Delta (A, \lambda , \mathbf {q}_0)$ has ![]() $r_{ijl}(\kern1.5pt \overrightarrow {\mathbf {q}} )=r_{ijl}(\Delta )$ by construction, and so lies in
$r_{ijl}(\kern1.5pt \overrightarrow {\mathbf {q}} )=r_{ijl}(\Delta )$ by construction, and so lies in ![]() $\operatorname {\mathrm {Sim}}(\Delta )$.
$\operatorname {\mathrm {Sim}}(\Delta )$.
We prove that ![]() $i_\Delta $ is onto
$i_\Delta $ is onto ![]() $\operatorname {\mathrm {Sim}}(\Delta )$. Given
$\operatorname {\mathrm {Sim}}(\Delta )$. Given ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we use Proposition 4.6, and our assumption that
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we use Proposition 4.6, and our assumption that ![]() $U(\Delta )=I_k$, to write
$U(\Delta )=I_k$, to write
This means that ![]() $\pi _{j0}(\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )\pi _{j0}(\Delta )$ for
$\pi _{j0}(\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )\pi _{j0}(\Delta )$ for ![]() $j=1,\dots , k$. Remembering that
$j=1,\dots , k$. Remembering that ![]() $\pi _{j0}=-\pi _{0j}$, we then deduce the other values of
$\pi _{j0}=-\pi _{0j}$, we then deduce the other values of ![]() $\pi _{j}(\kern1.5pt \overrightarrow {\mathbf {q}} )$ satisfy the same relationship:
$\pi _{j}(\kern1.5pt \overrightarrow {\mathbf {q}} )$ satisfy the same relationship:
 $$ \begin{align*} \pi_{ij}(\kern1.5pt \overrightarrow{\mathbf{q}} ) &= \dfrac{\mathbf{q}_j - \mathbf{q}_i}{\|\mathbf{q}_j - \mathbf{q}_i\|} = \dfrac{\mathbf{q}_j - \mathbf{q}_0}{\|\mathbf{q}_j - \mathbf{q}_i\|} + \dfrac{\mathbf{q}_0 - \mathbf{q}_i}{\|\mathbf{q}_j - \mathbf{q}_i\|} \\[5pt] &= \dfrac{\| \mathbf{q}_j - \mathbf{q}_0\|}{\| \mathbf{q}_j - \mathbf{q}_i\|} \dfrac{\mathbf{q}_j - \mathbf{q}_0}{\|\mathbf{q}_j - \mathbf{q}_0\|} + \dfrac{\|\mathbf{q}_0 - \mathbf{q}_i\|} {\| \mathbf{q}_j - \mathbf{q}_i\|} \dfrac{\mathbf{q}_0 - \mathbf{q}_i}{\|\mathbf{q}_0 - \mathbf{q}_i\|} \\[5pt] & = r_{j0i}(\kern1.5pt \overrightarrow{\mathbf{q}} ) \pi_{j0}(\kern1.5pt \overrightarrow{\mathbf{q}} ) + r_{i0j}(\kern1.5pt \overrightarrow{\mathbf{q}} ) \pi_{0i}(\kern1.5pt \overrightarrow{\mathbf{q}} ) \\[5pt] & = r_{j0i}(\kern1.5pt \overrightarrow{\mathbf{q}} ) U(\kern1.5pt \overrightarrow{\mathbf{q}} )\pi_{j0}(\Delta) + r_{i0j}(\kern1.5pt \overrightarrow{\mathbf{q}} ) U(\kern1.5pt \overrightarrow{\mathbf{q}} )\pi_{0i}(\Delta) = U(\kern1.5pt \overrightarrow{\mathbf{q}} )\pi_{ij}(\Delta). \end{align*} $$
$$ \begin{align*} \pi_{ij}(\kern1.5pt \overrightarrow{\mathbf{q}} ) &= \dfrac{\mathbf{q}_j - \mathbf{q}_i}{\|\mathbf{q}_j - \mathbf{q}_i\|} = \dfrac{\mathbf{q}_j - \mathbf{q}_0}{\|\mathbf{q}_j - \mathbf{q}_i\|} + \dfrac{\mathbf{q}_0 - \mathbf{q}_i}{\|\mathbf{q}_j - \mathbf{q}_i\|} \\[5pt] &= \dfrac{\| \mathbf{q}_j - \mathbf{q}_0\|}{\| \mathbf{q}_j - \mathbf{q}_i\|} \dfrac{\mathbf{q}_j - \mathbf{q}_0}{\|\mathbf{q}_j - \mathbf{q}_0\|} + \dfrac{\|\mathbf{q}_0 - \mathbf{q}_i\|} {\| \mathbf{q}_j - \mathbf{q}_i\|} \dfrac{\mathbf{q}_0 - \mathbf{q}_i}{\|\mathbf{q}_0 - \mathbf{q}_i\|} \\[5pt] & = r_{j0i}(\kern1.5pt \overrightarrow{\mathbf{q}} ) \pi_{j0}(\kern1.5pt \overrightarrow{\mathbf{q}} ) + r_{i0j}(\kern1.5pt \overrightarrow{\mathbf{q}} ) \pi_{0i}(\kern1.5pt \overrightarrow{\mathbf{q}} ) \\[5pt] & = r_{j0i}(\kern1.5pt \overrightarrow{\mathbf{q}} ) U(\kern1.5pt \overrightarrow{\mathbf{q}} )\pi_{j0}(\Delta) + r_{i0j}(\kern1.5pt \overrightarrow{\mathbf{q}} ) U(\kern1.5pt \overrightarrow{\mathbf{q}} )\pi_{0i}(\Delta) = U(\kern1.5pt \overrightarrow{\mathbf{q}} )\pi_{ij}(\Delta). \end{align*} $$Thus, for ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we have
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we have ![]() $\pi _{ij}(\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )\pi _{ij}(\Delta )$. For the map
$\pi _{ij}(\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )\pi _{ij}(\Delta )$. For the map ![]() $i_\Delta $, we let
$i_\Delta $, we let ![]() $\lambda =\|\mathbf {q}_1-\mathbf {q}_0\|$, then
$\lambda =\|\mathbf {q}_1-\mathbf {q}_0\|$, then ![]() $i_\Delta ( U(\kern1.5pt \overrightarrow {\mathbf {q}} ), \|\mathbf {q}_1-\mathbf {q}_0\|, \mathbf {q}_0) = (\mathbf {q}_0,\mathbf {q}_1,\dots , \mathbf {q}_k)= \overrightarrow {\mathbf {q}} $. To see this last equation, note that
$i_\Delta ( U(\kern1.5pt \overrightarrow {\mathbf {q}} ), \|\mathbf {q}_1-\mathbf {q}_0\|, \mathbf {q}_0) = (\mathbf {q}_0,\mathbf {q}_1,\dots , \mathbf {q}_k)= \overrightarrow {\mathbf {q}} $. To see this last equation, note that
We can now define the map ![]() $ps_\Delta \colon \! \operatorname {\mathrm {Sim}}(\Delta )\rightarrow \operatorname {O}(k)\times (0,\infty )\times \mathbb {R}^k$ using the pose map from Definition 4.7. We define
$ps_\Delta \colon \! \operatorname {\mathrm {Sim}}(\Delta )\rightarrow \operatorname {O}(k)\times (0,\infty )\times \mathbb {R}^k$ using the pose map from Definition 4.7. We define ![]() $ps_\Delta (\kern1.5pt \overrightarrow {\mathbf {q}} ) := (ps(\kern1.5pt \overrightarrow {\mathbf {q}} ),\|\mathbf {q}_1-\mathbf {q}_0\|, \mathbf {q}_0) = (U(\kern1.5pt \overrightarrow {\mathbf {q}} ),\|\mathbf {q}_1-\mathbf {q}_0\|, \mathbf {q}_0) $. From Proposition 4.6, we know
$ps_\Delta (\kern1.5pt \overrightarrow {\mathbf {q}} ) := (ps(\kern1.5pt \overrightarrow {\mathbf {q}} ),\|\mathbf {q}_1-\mathbf {q}_0\|, \mathbf {q}_0) = (U(\kern1.5pt \overrightarrow {\mathbf {q}} ),\|\mathbf {q}_1-\mathbf {q}_0\|, \mathbf {q}_0) $. From Proposition 4.6, we know ![]() $U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ depends smoothly on
$U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ depends smoothly on ![]() $ \overrightarrow {\mathbf {q}} $, and, hence,
$ \overrightarrow {\mathbf {q}} $, and, hence, ![]() $ps_\Delta $ depends smoothly on
$ps_\Delta $ depends smoothly on ![]() $ \overrightarrow {\mathbf {q}} $. A moment’s thought shows that, by construction, we have
$ \overrightarrow {\mathbf {q}} $. A moment’s thought shows that, by construction, we have ![]() $ps_\Delta \circ i_\Delta =\operatorname {\mathrm {id}}$.
$ps_\Delta \circ i_\Delta =\operatorname {\mathrm {id}}$.
This means that ![]() $i_\Delta $ (and, hence,
$i_\Delta $ (and, hence, ![]() $ps_\Delta $) is a diffeomorphism, and
$ps_\Delta $) is a diffeomorphism, and ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ is a submanifold of
$\operatorname {\mathrm {Sim}}(\Delta )$ is a submanifold of ![]() $C_{k+1}(\mathbb {R}^k)$.
$C_{k+1}(\mathbb {R}^k)$.
We note that this theorem shows that the polar decomposition is a diffeomorphism for matrices of full rank. This is analogous to the smoothness result for the polar decomposition of Dieci and Eirola [Reference Dieci and Eirola12]. This theorem is not true for rank-deficient matrices, which explains why we have restricted our attention to spheres ![]() $S^{k-1}$ isotopic to each other in
$S^{k-1}$ isotopic to each other in ![]() $\mathbb {R}^k$; Haefliger’s theorem might guarantee the existence of an isotopy of the spheres in a higher-dimensional
$\mathbb {R}^k$; Haefliger’s theorem might guarantee the existence of an isotopy of the spheres in a higher-dimensional ![]() $\mathbb {R}^K$, but
$\mathbb {R}^K$, but ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ would still consist of rank
$\operatorname {\mathrm {Sim}}(\Delta )$ would still consist of rank ![]() $k < K$ matrices and, hence, be harder to control.
$k < K$ matrices and, hence, be harder to control.
The next theorem shows ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ has a well-understood structure in the boundary
$\operatorname {\mathrm {Sim}}(\Delta )$ has a well-understood structure in the boundary ![]() $\partial C_{k+1}[\mathbb {R}^k]$.
$\partial C_{k+1}[\mathbb {R}^k]$.
Theorem 4.9. If ![]() $\Delta $ is a nondegenerate k-simplex in
$\Delta $ is a nondegenerate k-simplex in ![]() $\mathbb {R}^k$, then the boundary of
$\mathbb {R}^k$, then the boundary of ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ corresponds to configurations in the interior of the
$\operatorname {\mathrm {Sim}}(\Delta )$ corresponds to configurations in the interior of the ![]() $(0, \ldots , k)$ face of
$(0, \ldots , k)$ face of ![]() $\partial C_{k+1}[\mathbb {R}^k]$, and is diffeomorphic to
$\partial C_{k+1}[\mathbb {R}^k]$, and is diffeomorphic to ![]() $\operatorname {O}(k) \times \{0\} \times \mathbb {R}^k$.
$\operatorname {O}(k) \times \{0\} \times \mathbb {R}^k$.
Proof. By assumption, the given simplex ![]() $\Delta =(\mathbf {p}_0, \dots , \mathbf {p}_k)$ is nondegenerate, so none of the vertices of
$\Delta =(\mathbf {p}_0, \dots , \mathbf {p}_k)$ is nondegenerate, so none of the vertices of ![]() $\Delta $ coincide, and the ratios
$\Delta $ coincide, and the ratios ![]() $r_{ijl}(\Delta )$ are never 0 nor
$r_{ijl}(\Delta )$ are never 0 nor ![]() $\infty $. If we take
$\infty $. If we take ![]() $(A,\lambda ,\mathbf {p})\in \operatorname {O}(k)\times [0,\infty )\times \mathbb {R}^k$ and consider the points in
$(A,\lambda ,\mathbf {p})\in \operatorname {O}(k)\times [0,\infty )\times \mathbb {R}^k$ and consider the points in ![]() $i_\Delta (A,\lambda , \mathbf {p}_0)$, we see these points coincide if and only if
$i_\Delta (A,\lambda , \mathbf {p}_0)$, we see these points coincide if and only if ![]() $\lambda =0$, in which case, they all coincide. This means
$\lambda =0$, in which case, they all coincide. This means ![]() $i_\Delta (A,0, \mathbf {p}_0)\subset \partial C_{k+}[\mathbb {R}^k]$ and is in the
$i_\Delta (A,0, \mathbf {p}_0)\subset \partial C_{k+}[\mathbb {R}^k]$ and is in the ![]() $(0,1,\dots , k)$ face. Since the boundary of the
$(0,1,\dots , k)$ face. Since the boundary of the ![]() $(0,1,\dots , k)$ face consists of configurations with
$(0,1,\dots , k)$ face consists of configurations with ![]() $r_{ijl}(\Delta ) = 0$, or
$r_{ijl}(\Delta ) = 0$, or ![]() $r_{ijl}(\Delta ) = \infty $, it follows immediately that
$r_{ijl}(\Delta ) = \infty $, it follows immediately that ![]() $i_\Delta (A,0, \mathbf {p}_0)$ is in the interior of this face.
$i_\Delta (A,0, \mathbf {p}_0)$ is in the interior of this face.
Corollary 4.10. If ![]() $\Delta $ is a nondegenerate k-simplex in
$\Delta $ is a nondegenerate k-simplex in ![]() $\mathbb {R}^k$, then
$\mathbb {R}^k$, then ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ is a submanifold of
$\operatorname {\mathrm {Sim}}(\Delta )$ is a submanifold of ![]() $C_{k+1}[\mathbb {R}^k]$ that is diffeomorphic to
$C_{k+1}[\mathbb {R}^k]$ that is diffeomorphic to ![]() $\operatorname {O}(k) \times [0,\infty ) \times \mathbb {R}^k$.
$\operatorname {O}(k) \times [0,\infty ) \times \mathbb {R}^k$.
5 Simplices inscribed in spheres
We next move to Step 1 of the method described in Section 3. We will be looking at ![]() $C^\infty $-smooth embeddings of
$C^\infty $-smooth embeddings of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$. We will always assume that these embeddings are regular, that is, the embedding induces an injection of tangent spaces everywhere. This is particularly relevant for embeddings of
$\mathbb {R}^k$. We will always assume that these embeddings are regular, that is, the embedding induces an injection of tangent spaces everywhere. This is particularly relevant for embeddings of ![]() $S^1$ in
$S^1$ in ![]() $\mathbb {R}^2$, where we assume the tangent vector is nowhere zero (otherwise, it is possible to smoothly describe an embedded curve with corners, by allowing the tangent vector to smoothly change to zero at each corner). Now, given any such regular
$\mathbb {R}^2$, where we assume the tangent vector is nowhere zero (otherwise, it is possible to smoothly describe an embedded curve with corners, by allowing the tangent vector to smoothly change to zero at each corner). Now, given any such regular ![]() $C^\infty $-smooth embedding
$C^\infty $-smooth embedding ![]() $\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$, we can view the corresponding configuration space
$\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$, we can view the corresponding configuration space ![]() $C_{k+1}[\gamma (S^{k-1})]$ as a submanifold of
$C_{k+1}[\gamma (S^{k-1})]$ as a submanifold of ![]() $C_{k+1}[\mathbb {R}^k]$.
$C_{k+1}[\mathbb {R}^k]$.
Proposition 5.1. Given a nondegenerate simplex ![]() $\Delta \in C_{k+1}(\mathbb {R}^k)$, and a regular
$\Delta \in C_{k+1}(\mathbb {R}^k)$, and a regular ![]() $C^\infty $-smooth embedding
$C^\infty $-smooth embedding ![]() $\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ with corresponding configuration space
$\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ with corresponding configuration space ![]() $C_{k+1}[\gamma (S^{k-1})]$, then
$C_{k+1}[\gamma (S^{k-1})]$, then ![]() $\partial \operatorname {\mathrm {Sim}}(\Delta )$ and
$\partial \operatorname {\mathrm {Sim}}(\Delta )$ and ![]() $\partial C_{k+1}[\gamma (S^{k-1})]$ are disjoint in
$\partial C_{k+1}[\gamma (S^{k-1})]$ are disjoint in ![]() $\partial C_{k+1}[\mathbb {R}^k]$.
$\partial C_{k+1}[\mathbb {R}^k]$.
Proof. From Theorem 4.9, we know that ![]() $\partial \operatorname {\mathrm {Sim}}(\Delta )$ is in the
$\partial \operatorname {\mathrm {Sim}}(\Delta )$ is in the ![]() $(0,1,\dots , k)$ face of
$(0,1,\dots , k)$ face of ![]() $\partial C_{k+1}[\mathbb {R}^k]$, so we restrict our attention to that boundary face. Since
$\partial C_{k+1}[\mathbb {R}^k]$, so we restrict our attention to that boundary face. Since ![]() $\Delta $ is nondegenerate, no hyperplane in
$\Delta $ is nondegenerate, no hyperplane in ![]() $\mathbb {R}^k$ contains more than k points of
$\mathbb {R}^k$ contains more than k points of ![]() $\Delta $, and so not all of the
$\Delta $, and so not all of the ![]() $\pi _{ij}(\Delta )$ vectors are coplanar. However, for a point in
$\pi _{ij}(\Delta )$ vectors are coplanar. However, for a point in ![]() $\partial C_{k+1}[\gamma (S^{k-1})]$, all of the
$\partial C_{k+1}[\gamma (S^{k-1})]$, all of the ![]() $\pi _{ij}$ vectors must be coplanar. Hence,
$\pi _{ij}$ vectors must be coplanar. Hence, ![]() $\operatorname {\mathrm {Sim}} (\Delta )$ and
$\operatorname {\mathrm {Sim}} (\Delta )$ and ![]() $C_{k+1}[\gamma (S^{k-1})]$ are boundary disjoint.
$C_{k+1}[\gamma (S^{k-1})]$ are boundary disjoint.
We next move to Step 2. We take the standard embedding of the ![]() $(k-1)$ sphere in
$(k-1)$ sphere in ![]() $\mathbb {R}^k$, that is,
$\mathbb {R}^k$, that is, ![]() $\operatorname {\mathrm {id}} \colon \! S^{k-1} \hookrightarrow \mathbb {R}^k$, and consider the corresponding configuration spaces. In this special case, we use the notation
$\operatorname {\mathrm {id}} \colon \! S^{k-1} \hookrightarrow \mathbb {R}^k$, and consider the corresponding configuration spaces. In this special case, we use the notation ![]() $C_{k+1}[S^{k-1}] = C_{k+1}[\operatorname {\mathrm {id}}(S^{k-1})]$.
$C_{k+1}[S^{k-1}] = C_{k+1}[\operatorname {\mathrm {id}}(S^{k-1})]$.
We need to show that there is a transverse intersection between ![]() $C_{k+1}[S^{k-1}]$ and
$C_{k+1}[S^{k-1}]$ and ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ in
$\operatorname {\mathrm {Sim}}(\Delta )$ in ![]() $C_{k+1}[\mathbb {R}^k]$, in other words,
$C_{k+1}[\mathbb {R}^k]$, in other words, ![]() $C_{k+1}(\operatorname {\mathrm {id}})\pitchfork \operatorname {\mathrm {Sim}}(\Delta )$. We also need to compute the homology class of the intersection of
$C_{k+1}(\operatorname {\mathrm {id}})\pitchfork \operatorname {\mathrm {Sim}}(\Delta )$. We also need to compute the homology class of the intersection of ![]() $C_{k+1}[S^{k-1}]\cap \operatorname {\mathrm {Sim}}(\Delta )$ in
$C_{k+1}[S^{k-1}]\cap \operatorname {\mathrm {Sim}}(\Delta )$ in ![]() $\operatorname {\mathrm {Sim}}(\Delta )$.
$\operatorname {\mathrm {Sim}}(\Delta )$.
Proposition 5.2. Given the configuration space ![]() $C_{k+1}[S^{k-1}]$ corresponding to the standard embedding of
$C_{k+1}[S^{k-1}]$ corresponding to the standard embedding of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$, and given a nondegenerate simplex
$\mathbb {R}^k$, and given a nondegenerate simplex ![]() $\Delta \in C_{k+1}(\mathbb {R}^k)$, then
$\Delta \in C_{k+1}(\mathbb {R}^k)$, then ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ intersects
$\operatorname {\mathrm {Sim}}(\Delta )$ intersects ![]() $C_{k+1}[S^{k-1}]$ transversally, and the intersection
$C_{k+1}[S^{k-1}]$ transversally, and the intersection ![]() $\operatorname {\mathrm {Sim}}(\Delta )\cap C_{k+1}[S^{k-1}]$ is diffeomorphic to
$\operatorname {\mathrm {Sim}}(\Delta )\cap C_{k+1}[S^{k-1}]$ is diffeomorphic to ![]() $\operatorname {O}(k)$.
$\operatorname {O}(k)$.
Proof. Since ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ and
$\operatorname {\mathrm {Sim}}(\Delta )$ and ![]() $C_{k+1}[S^{k-1}]$ are boundary disjoint (Proposition 5.1), we just need to consider
$C_{k+1}[S^{k-1}]$ are boundary disjoint (Proposition 5.1), we just need to consider ![]() $\operatorname {\mathrm {Sim}}(\Delta ) \cap C_{k+1}(S^{k-1})$. Now, every simplex
$\operatorname {\mathrm {Sim}}(\Delta ) \cap C_{k+1}(S^{k-1})$. Now, every simplex ![]() $\Delta $ has a unique circumsphere; a
$\Delta $ has a unique circumsphere; a ![]() $(k-1)$-sphere passing through all of the
$(k-1)$-sphere passing through all of the ![]() $k+1$ vertices. The radius of the circumsphere and coordinates of the circumcentre are well known (see, for instance, Proposition 9.7.3.7 [Reference Berger5] or [Reference Coxeter11, Reference Schoenberg38]). Indeed, the circumradius R of the simplex
$k+1$ vertices. The radius of the circumsphere and coordinates of the circumcentre are well known (see, for instance, Proposition 9.7.3.7 [Reference Berger5] or [Reference Coxeter11, Reference Schoenberg38]). Indeed, the circumradius R of the simplex ![]() $\Delta $ is given by
$\Delta $ is given by
 $$ \begin{align*} R^2 = - \frac{ \left| \begin{matrix} 0 & d_{01}^2 & \cdots & d_{0k}^2 \\ d_{10}^2 & 0 & \cdots & d_{1k}^2 \\ \vdots & \vdots & & \vdots \\ d_{k0}^2 & d_{k2}^2 & \cdots & 0 \end{matrix} \right| } {2 \operatorname{\mathrm{CM}}(\{\mathbf{p}_0,\dots, \mathbf{p}_k\})}. \end{align*} $$
$$ \begin{align*} R^2 = - \frac{ \left| \begin{matrix} 0 & d_{01}^2 & \cdots & d_{0k}^2 \\ d_{10}^2 & 0 & \cdots & d_{1k}^2 \\ \vdots & \vdots & & \vdots \\ d_{k0}^2 & d_{k2}^2 & \cdots & 0 \end{matrix} \right| } {2 \operatorname{\mathrm{CM}}(\{\mathbf{p}_0,\dots, \mathbf{p}_k\})}. \end{align*} $$ Given ![]() $\Delta $, we can scale and translate it to give a new
$\Delta $, we can scale and translate it to give a new ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$ with circumradius
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$ with circumradius ![]() $R=1$, and circumcentre
$R=1$, and circumcentre ![]() $\mathbf {0}$. Thus,
$\mathbf {0}$. Thus, ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta ) \cap C_{k+1}(S^{k-1})$ and the intersection is nonempty. Intuitively, we obtain all other points of
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta ) \cap C_{k+1}(S^{k-1})$ and the intersection is nonempty. Intuitively, we obtain all other points of ![]() $\operatorname {\mathrm {Sim}}(\Delta ) \cap C_{k+1}(S^{k-1})$ by rotating/reflecting
$\operatorname {\mathrm {Sim}}(\Delta ) \cap C_{k+1}(S^{k-1})$ by rotating/reflecting ![]() $ \overrightarrow {\mathbf {q}} $ via
$ \overrightarrow {\mathbf {q}} $ via ![]() $A \overrightarrow {\mathbf {q}} $ for
$A \overrightarrow {\mathbf {q}} $ for ![]() $A\in \operatorname {O}(k)$. More formally, we define the diffeomorphism
$A\in \operatorname {O}(k)$. More formally, we define the diffeomorphism ![]() $r\colon \! \operatorname {O}(k)\rightarrow \operatorname {\mathrm {Sim}}(\Delta ) \cap C_{k+1}(S^{k-1})$ by
$r\colon \! \operatorname {O}(k)\rightarrow \operatorname {\mathrm {Sim}}(\Delta ) \cap C_{k+1}(S^{k-1})$ by ![]() $r(A) =A \overrightarrow {\mathbf {q}} = (A\mathbf {q}_0, \dots , A\mathbf {q}_k)$.
$r(A) =A \overrightarrow {\mathbf {q}} = (A\mathbf {q}_0, \dots , A\mathbf {q}_k)$.
We now want to show that ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ intersects
$\operatorname {\mathrm {Sim}}(\Delta )$ intersects ![]() $C_{k+1}[S^{k-1}]$ transversally. Specifically, we take any inscribed simplex
$C_{k+1}[S^{k-1}]$ transversally. Specifically, we take any inscribed simplex ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )\cap C_{k+1}[S^{k-1}]$, and we want to show that
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )\cap C_{k+1}[S^{k-1}]$, and we want to show that
We first note that the orthogonal complement of ![]() $T_{ \overrightarrow {\mathbf {q}} } (C_{k+1}[S^{k-1}])$ in
$T_{ \overrightarrow {\mathbf {q}} } (C_{k+1}[S^{k-1}])$ in ![]() $T_{ \overrightarrow {\mathbf {q}} }(C_{k+1}[\mathbb {R}^{k}])$ is the
$T_{ \overrightarrow {\mathbf {q}} }(C_{k+1}[\mathbb {R}^{k}])$ is the ![]() $(k+1)$-dimensional space with orthonormal basis
$(k+1)$-dimensional space with orthonormal basis ![]() $\mathcal {B} = \{(\mathbf {q}_0, 0, \dots , 0), \dots , (0,\dots ,\mathbf {q}_{k})\}$. Next, observe that
$\mathcal {B} = \{(\mathbf {q}_0, 0, \dots , 0), \dots , (0,\dots ,\mathbf {q}_{k})\}$. Next, observe that ![]() $T_{ \overrightarrow {\mathbf {q}} } (\operatorname {\mathrm {Sim}}(\Delta )) \cong T_{ \overrightarrow {\mathbf {q}} }(\operatorname {O}(k))\oplus T_{ \overrightarrow {\mathbf {q}} }[0,\infty ) \oplus T_{ \overrightarrow {\mathbf {q}} }(\mathbb {R}^k)$. The tangent space
$T_{ \overrightarrow {\mathbf {q}} } (\operatorname {\mathrm {Sim}}(\Delta )) \cong T_{ \overrightarrow {\mathbf {q}} }(\operatorname {O}(k))\oplus T_{ \overrightarrow {\mathbf {q}} }[0,\infty ) \oplus T_{ \overrightarrow {\mathbf {q}} }(\mathbb {R}^k)$. The tangent space ![]() $T_{ \overrightarrow {\mathbf {q}} }(\operatorname {\mathrm {Sim}}(\Delta ))$ thus contains the vectors
$T_{ \overrightarrow {\mathbf {q}} }(\operatorname {\mathrm {Sim}}(\Delta ))$ thus contains the vectors ![]() $(\mathbf {e}_1, \dots , \mathbf {e}_1), \dots , (\mathbf {e}_k,\dots ,\mathbf {e}_k)$ from the translational component of
$(\mathbf {e}_1, \dots , \mathbf {e}_1), \dots , (\mathbf {e}_k,\dots ,\mathbf {e}_k)$ from the translational component of ![]() $\operatorname {\mathrm {Sim}}(\Delta )$, as well as the vector
$\operatorname {\mathrm {Sim}}(\Delta )$, as well as the vector ![]() $(\mathbf {q}_0,\dots ,\mathbf {q}_{k})$ from scaling the configuration
$(\mathbf {q}_0,\dots ,\mathbf {q}_{k})$ from scaling the configuration ![]() $ \overrightarrow {\mathbf {q}} $. Writing these vectors in the basis
$ \overrightarrow {\mathbf {q}} $. Writing these vectors in the basis ![]() $\mathcal {B}$, we get the matrix:
$\mathcal {B}$, we get the matrix:
 $$ \begin{align*} M = \left( \begin{matrix} q_{0,0} & q_{1,0} & \cdots & q_{k,0} \\ q_{0,1} & q_{1,1} & \cdots & q_{k,1} \\ \vdots & \vdots & & \vdots \\ q_{0,k} & q_{1,k} & \cdots & q_{k,k} \\ 1 & 1 & \cdots & 1 \\ \end{matrix} \right). \end{align*} $$
$$ \begin{align*} M = \left( \begin{matrix} q_{0,0} & q_{1,0} & \cdots & q_{k,0} \\ q_{0,1} & q_{1,1} & \cdots & q_{k,1} \\ \vdots & \vdots & & \vdots \\ q_{0,k} & q_{1,k} & \cdots & q_{k,k} \\ 1 & 1 & \cdots & 1 \\ \end{matrix} \right). \end{align*} $$Subtracting the last column from the rest, we get
 $$ \begin{align*} M' = \left( \begin{matrix} \mathbf{q}_0 - \mathbf{q}_{k} & \mathbf{q}_1 - \mathbf{q}_{k} & \cdots & \mathbf{q}_{k-1} - \mathbf{q}_{k} & \mathbf{q}_{k} \\ 0 & 0 & \cdots & 0 & 1 \\ \end{matrix} \right). \end{align*} $$
$$ \begin{align*} M' = \left( \begin{matrix} \mathbf{q}_0 - \mathbf{q}_{k} & \mathbf{q}_1 - \mathbf{q}_{k} & \cdots & \mathbf{q}_{k-1} - \mathbf{q}_{k} & \mathbf{q}_{k} \\ 0 & 0 & \cdots & 0 & 1 \\ \end{matrix} \right). \end{align*} $$The determinant of this matrix is ![]() $\pm 1$ multiplied by the determinant of the upper-left
$\pm 1$ multiplied by the determinant of the upper-left ![]() $k \times k$ principal minor. But that determinant is positive because
$k \times k$ principal minor. But that determinant is positive because ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$ and is nondegenerate. Thus, the
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$ and is nondegenerate. Thus, the ![]() $k+1$ tangent vectors are linearly independent, and we have proven transversality.
$k+1$ tangent vectors are linearly independent, and we have proven transversality.
Before we move on to determine the homology class corresponding to inscribed simplices, we pause to remember that ![]() $\operatorname {O}(k)$ has two connected components. One component,
$\operatorname {O}(k)$ has two connected components. One component, ![]() $\operatorname {SO}(k)$, is a subgroup of
$\operatorname {SO}(k)$, is a subgroup of ![]() $\operatorname {O}(k)$, and consists of all orthogonal matrices with determinant
$\operatorname {O}(k)$, and consists of all orthogonal matrices with determinant ![]() $+1$. The other component contains all orthogonal matrices with determinant
$+1$. The other component contains all orthogonal matrices with determinant ![]() $-1$.
$-1$.
In order to sensibly discuss homology classes, we restrict our attention to the submanifold of simplices diffeomorphic to ![]() $\operatorname {SO}(k)\times [0,\infty )\times \mathbb {R}^k$, which we denote
$\operatorname {SO}(k)\times [0,\infty )\times \mathbb {R}^k$, which we denote ![]() $\operatorname {\mathrm {Sim}}^+(\Delta )$. We could equally restrict our attention to
$\operatorname {\mathrm {Sim}}^+(\Delta )$. We could equally restrict our attention to ![]() $\operatorname {\mathrm {Sim}}^-(\Delta ) := \operatorname {\mathrm {Sim}}(\Delta )\setminus \operatorname {\mathrm {Sim}}^+(\Delta )$.
$\operatorname {\mathrm {Sim}}^-(\Delta ) := \operatorname {\mathrm {Sim}}(\Delta )\setminus \operatorname {\mathrm {Sim}}^+(\Delta )$.
Proposition 5.3. Given a nondegenerate simplex ![]() $\Delta =(\mathbf {p}_0,\dots , \mathbf {p}_k)\in C_{k+1}(\mathbb {R}^k)$, and given the configuration space
$\Delta =(\mathbf {p}_0,\dots , \mathbf {p}_k)\in C_{k+1}(\mathbb {R}^k)$, and given the configuration space ![]() $C_{k+1}[S^{k-1}]$ corresponding to the standard embedding of
$C_{k+1}[S^{k-1}]$ corresponding to the standard embedding of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$, then in
$\mathbb {R}^k$, then in ![]() $\operatorname {\mathrm {Sim}}(\Delta )$
$\operatorname {\mathrm {Sim}}(\Delta )$
Moreover, the pose map is a diffeomorphism ![]() $ps\colon \! \operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[S^{k-1}] \rightarrow \operatorname {SO}(k)$ which induces an isomorphism on integral homology taking the top class of
$ps\colon \! \operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[S^{k-1}] \rightarrow \operatorname {SO}(k)$ which induces an isomorphism on integral homology taking the top class of ![]() $\operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[S^{k-1}]$ in
$\operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[S^{k-1}]$ in ![]() $\operatorname {\mathrm {Sim}}(\Delta ^+)$ to the top class of
$\operatorname {\mathrm {Sim}}(\Delta ^+)$ to the top class of ![]() $\operatorname {SO}(k)$. A similar result holds for
$\operatorname {SO}(k)$. A similar result holds for ![]() $\operatorname {\mathrm {Sim}}^-(\Delta )\cap C_{k+1}[S^{k-1}]$.
$\operatorname {\mathrm {Sim}}^-(\Delta )\cap C_{k+1}[S^{k-1}]$.
Proof. Without loss of generality, we can normalise ![]() $\Delta =(\mathbf {p}_1,\dots , \mathbf {p}_k)$ so that it lies on
$\Delta =(\mathbf {p}_1,\dots , \mathbf {p}_k)$ so that it lies on ![]() $S^{k-1}$; that is
$S^{k-1}$; that is ![]() $\Delta $ has circumcentre
$\Delta $ has circumcentre ![]() $\mathbf {0}$ and circumradius
$\mathbf {0}$ and circumradius ![]() $R=1$. We then have the following maps
$R=1$. We then have the following maps
Here, the map r is the rotation/reflections diffeomorphism previously defined in Proposition 5.2. That is, for ![]() $A\in \operatorname {O}(k)$, we define
$A\in \operatorname {O}(k)$, we define ![]() $r(A)= A\Delta =(A\mathbf {p}_0, \dots , A\mathbf {p}_k)$. The map
$r(A)= A\Delta =(A\mathbf {p}_0, \dots , A\mathbf {p}_k)$. The map ![]() $ps$ is the pose map from Definition 4.7: for
$ps$ is the pose map from Definition 4.7: for ![]() $ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we define
$ \overrightarrow {\mathbf {q}} \in \operatorname {\mathrm {Sim}}(\Delta )$, we define ![]() $ps(\kern1.5pt \overrightarrow {\mathbf {q}} )=U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ (where
$ps(\kern1.5pt \overrightarrow {\mathbf {q}} )=U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ (where ![]() $U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is the unique orthogonal matrix, such that
$U(\kern1.5pt \overrightarrow {\mathbf {q}} )$ is the unique orthogonal matrix, such that ![]() $\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )\Pi (\Delta )$). From Proposition 5.2, we know that r is a diffeomorphism, and by construction,
$\Pi (\kern1.5pt \overrightarrow {\mathbf {q}} ) = U(\kern1.5pt \overrightarrow {\mathbf {q}} )\Pi (\Delta )$). From Proposition 5.2, we know that r is a diffeomorphism, and by construction, ![]() $ps\circ r = \operatorname {\mathrm {id}}$. Hence, the pose map is also a diffeomorphism.
$ps\circ r = \operatorname {\mathrm {id}}$. Hence, the pose map is also a diffeomorphism.
From Proposition 5.2, we recall that ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ intersects
$\operatorname {\mathrm {Sim}}(\Delta )$ intersects ![]() $C_{k+1}[S^{k-1}]$ transversally, and, moreover, that the intersection is diffeomorphic to
$C_{k+1}[S^{k-1}]$ transversally, and, moreover, that the intersection is diffeomorphic to ![]() $\operatorname {O}(k)$. Now, since
$\operatorname {O}(k)$. Now, since ![]() $\operatorname {\mathrm {Sim}}(\Delta )\cong \operatorname {O}(k)\times [0,\infty )\times \mathbb {R}^k$, we have
$\operatorname {\mathrm {Sim}}(\Delta )\cong \operatorname {O}(k)\times [0,\infty )\times \mathbb {R}^k$, we have ![]() $\operatorname {\mathrm {Sim}}(\Delta )\cap C_{k+1}[S^{k-1}]$ is a deformation retract of
$\operatorname {\mathrm {Sim}}(\Delta )\cap C_{k+1}[S^{k-1}]$ is a deformation retract of ![]() $\operatorname {\mathrm {Sim}}(\Delta )$.
$\operatorname {\mathrm {Sim}}(\Delta )$.
When we put this together and take the homology of the spaces, we see
Since ![]() $ps_* \circ r_* = \operatorname {\mathrm {id}}$, we know
$ps_* \circ r_* = \operatorname {\mathrm {id}}$, we know ![]() $ps_*$ is an isomorphism. Hence,
$ps_*$ is an isomorphism. Hence,
We could also choose to restrict r and ![]() $ps$ as follows:
$ps$ as follows:
Then, repeating the previous argument gives
We now have all the pieces needed for our main theorem.
Theorem 5.4. Suppose ![]() $\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ is a
$\gamma \colon \! S^{k-1}\hookrightarrow \mathbb {R}^k$ is a ![]() $C^\infty $-smooth embedding of
$C^\infty $-smooth embedding of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in
$\mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in ![]() $\mathbb {R}^k$, with a corresponding embedding of compactified configuration spaces
$\mathbb {R}^k$, with a corresponding embedding of compactified configuration spaces ![]() $C_{k+1}[\gamma ]\colon \! C_{k+1}[S^{k-1}]\hookrightarrow C_{k+1}[\mathbb {R}^k]$. Assume that
$C_{k+1}[\gamma ]\colon \! C_{k+1}[S^{k-1}]\hookrightarrow C_{k+1}[\mathbb {R}^k]$. Assume that ![]() $\Delta \in C_{k+1}(\mathbb {R}^k)$ is a nondegenerate simplex.
$\Delta \in C_{k+1}(\mathbb {R}^k)$ is a nondegenerate simplex.
Then for all ![]() $\epsilon>0$, there is a
$\epsilon>0$, there is a ![]() $C^\infty $-open neighborhood of
$C^\infty $-open neighborhood of ![]() $\gamma $, in which there is, for all m, a
$\gamma $, in which there is, for all m, a ![]() $C^m$-dense set of smooth embeddings
$C^m$-dense set of smooth embeddings ![]() $\gamma ':S^{k-1}\hookrightarrow \mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in
$\gamma ':S^{k-1}\hookrightarrow \mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in ![]() $\mathbb {R}^k$, such that
$\mathbb {R}^k$, such that ![]() $\| C_{k+1}[\gamma '] - C_{k+1}[\gamma ]\|_0< \epsilon $, and
$\| C_{k+1}[\gamma '] - C_{k+1}[\gamma ]\|_0< \epsilon $, and ![]() $C_{k+1}[\gamma '] \pitchfork \operatorname {\mathrm {Sim}}(\Delta )$. Moreover, in
$C_{k+1}[\gamma '] \pitchfork \operatorname {\mathrm {Sim}}(\Delta )$. Moreover, in ![]() $\operatorname {\mathrm {Sim}}(\Delta ^+)$, both
$\operatorname {\mathrm {Sim}}(\Delta ^+)$, both ![]() $C_{k+1}[S^{k-1}] \cap \operatorname {\mathrm {Sim}}^+(\Delta )$ and
$C_{k+1}[S^{k-1}] \cap \operatorname {\mathrm {Sim}}^+(\Delta )$ and ![]() $C_{k+1}[\gamma '(S^{k-1})] \cap \operatorname {\mathrm {Sim}}^+(\Delta )$ represent the top homology class of
$C_{k+1}[\gamma '(S^{k-1})] \cap \operatorname {\mathrm {Sim}}^+(\Delta )$ represent the top homology class of ![]() $\operatorname {SO}(k)$. A similar result holds for
$\operatorname {SO}(k)$. A similar result holds for ![]() $\operatorname {\mathrm {Sim}}^-(\Delta )$.
$\operatorname {\mathrm {Sim}}^-(\Delta )$.
We immediately recover Gromov’s result [Reference Gromov16] (but for ![]() $C^\infty $-smooth embeddings) as a corollary.
$C^\infty $-smooth embeddings) as a corollary.
Corollary 5.5. For any nondegenerate k-simplex ![]() $\Delta $ in
$\Delta $ in ![]() $\mathbb {R}^k$, there is a dense family of smoothly embedded
$\mathbb {R}^k$, there is a dense family of smoothly embedded ![]() $(k-1)$-spheres in
$(k-1)$-spheres in ![]() $\mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in
$\mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in ![]() $\mathbb {R}^k$, such that the subset of
$\mathbb {R}^k$, such that the subset of ![]() $\operatorname {\mathrm {Sim}}(\Delta )$ of simplices inscribed in each embedded sphere contains a similar simplex corresponding to each
$\operatorname {\mathrm {Sim}}(\Delta )$ of simplices inscribed in each embedded sphere contains a similar simplex corresponding to each ![]() $U\in \operatorname {O}(k)$.
$U\in \operatorname {O}(k)$.
In fact, we have proved more than Gromov.
Corollary 5.6. For any nondegenerate k-simplex ![]() $\Delta $ in
$\Delta $ in ![]() $\mathbb {R}^k$, there is a dense family of smoothly embedded
$\mathbb {R}^k$, there is a dense family of smoothly embedded ![]() $(k-1)$-spheres in
$(k-1)$-spheres in ![]() $\mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in
$\mathbb {R}^k$ isotopic to the identity through a differentiable isotopy in ![]() $\mathbb {R}^k$, such that the subset
$\mathbb {R}^k$, such that the subset ![]() $\operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[\gamma (S^{k-1})]$ of simplices inscribed in each embedded sphere is a smooth orientable submanifold of
$\operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[\gamma (S^{k-1})]$ of simplices inscribed in each embedded sphere is a smooth orientable submanifold of ![]() $\operatorname {\mathrm {Sim}}^+(\Delta )$. Furthermore, the pose map
$\operatorname {\mathrm {Sim}}^+(\Delta )$. Furthermore, the pose map ![]() $ps\colon \! \operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[\gamma (S^{k-1})]\rightarrow \operatorname {SO}(k)$ is onto and is a degree 1 map.
$ps\colon \! \operatorname {\mathrm {Sim}}^+(\Delta )\cap C_{k+1}[\gamma (S^{k-1})]\rightarrow \operatorname {SO}(k)$ is onto and is a degree 1 map.
In particular, the set of triangles similar to a given triangle ![]() $\triangle ABC$ inscribed in a generic smooth plane curve is a collection of loops
$\triangle ABC$ inscribed in a generic smooth plane curve is a collection of loops ![]() $L_1,\dots , L_n$. Furthermore, the sum of the degrees of the pose maps
$L_1,\dots , L_n$. Furthermore, the sum of the degrees of the pose maps ![]() $ps_1,\dots , ps_n$ is one.
$ps_1,\dots , ps_n$ is one.
Proof. The first statement follows from Theorem 3.2. That the pose map is onto follows from Corollary 5.5. For the standard embedding of ![]() $S^{k-1}$ in
$S^{k-1}$ in ![]() $\mathbb {R}^k$, the pose map is a diffeomorphism, and, hence, of degree 1. Proposition 5.3 and homotopy invariance show the pose map is always of degree 1 for our embeddings.
$\mathbb {R}^k$, the pose map is a diffeomorphism, and, hence, of degree 1. Proposition 5.3 and homotopy invariance show the pose map is always of degree 1 for our embeddings.
When ![]() $k=2$, we know
$k=2$, we know ![]() $\operatorname {SO}(2)\cong S^1$. Hence, the set of inscribed triangles similar to
$\operatorname {SO}(2)\cong S^1$. Hence, the set of inscribed triangles similar to ![]() $\Delta $ is a collection of loops.
$\Delta $ is a collection of loops.
In [Reference Matschke31], Matschke proves that for generic ![]() $C^\infty $-smooth embeddings of the circle in the plane, there are an odd number of loops of inscribed triangles similar to
$C^\infty $-smooth embeddings of the circle in the plane, there are an odd number of loops of inscribed triangles similar to ![]() $\Delta $ that wind an odd number of times around the embedded circle. Figure 2 shows such a loop of inscribed equilateral triangles in an irregular embedding of a circle in the plane. We recover Matschke’s result in Corollary 5.6, and strengthen it with the fact that the degree of the map is 1.
$\Delta $ that wind an odd number of times around the embedded circle. Figure 2 shows such a loop of inscribed equilateral triangles in an irregular embedding of a circle in the plane. We recover Matschke’s result in Corollary 5.6, and strengthen it with the fact that the degree of the map is 1.

Figure 2 In this irregular embedding of a circle in the plane, we see a series of inscribed equilateral triangles. By following the highlighted vertex around the curve, we see there is a loop of such inscribed triangles.
We end by, again, noting that Meyerson [Reference Meyerson34] and Nielsen [Reference Nielsen35] have results about inscribed triangles that are for Jordan curves (just assuming continuity of the embedding). By adding both a generic and smoothness assumption on our embeddings, we are able to provide more information about the structure of the set of inscribed triangles.
Appendix A Results from linear algebra
We will let ![]() $M_n$ denote the set of all
$M_n$ denote the set of all ![]() $n\times n$ matrices, and let
$n\times n$ matrices, and let ![]() $M_{n,m}$ denote the set of all
$M_{n,m}$ denote the set of all ![]() $n\times m$ matrices. Recall that a symmetric matrix is a square matrix that is equal to its transpose:
$n\times m$ matrices. Recall that a symmetric matrix is a square matrix that is equal to its transpose: ![]() $A=A^T$. That is,
$A=A^T$. That is, ![]() $A=[a_{ij}]$ is symmetric if and only if
$A=[a_{ij}]$ is symmetric if and only if ![]() $a_{ij}=a_{ji}$. Also recall that
$a_{ij}=a_{ji}$. Also recall that
• an
 $n\times n$ symmetric real matrix M is positive-definite if
$n\times n$ symmetric real matrix M is positive-definite if  $\mathbf {x}^*M\mathbf {x}>0$ for all
$\mathbf {x}^*M\mathbf {x}>0$ for all  $\mathbf {x} \in \mathbb {R}^n\setminus \{\mathbf {0}\}$.
$\mathbf {x} \in \mathbb {R}^n\setminus \{\mathbf {0}\}$.• an
 $n\times n$ symmetric real matrix M is positive semidefinite or nonnegative-definite if
$n\times n$ symmetric real matrix M is positive semidefinite or nonnegative-definite if  $\mathbf {x}^*M\mathbf {x} \geq 0$ for all
$\mathbf {x}^*M\mathbf {x} \geq 0$ for all  $\mathbf {x} \in \mathbb {R}^n$.
$\mathbf {x} \in \mathbb {R}^n$.• similar definitions hold for negative-definite and negative-semidefinite.
We now review some theorems about symmetric matrices.
Theorem A.1 (see [Reference Horn and Johnson21] Theorem 7.2.6).
Let A be an ![]() $n\times n$ symmetric and positive semidefinite matrix, let
$n\times n$ symmetric and positive semidefinite matrix, let ![]() $r=\operatorname {\mathrm {rank}}(A)$ and let
$r=\operatorname {\mathrm {rank}}(A)$ and let ![]() $k=\{2, 3, \dots \}$. Then there is a unique symmetric positive semidefinite matrix B, such that
$k=\{2, 3, \dots \}$. Then there is a unique symmetric positive semidefinite matrix B, such that ![]() $B^k=A$.
$B^k=A$.
Remark A.2. While this theorem only guarantees a unique positive semidefinite square root for a semidefinite matrix A, an examination of the proof in [Reference Horn and Johnson21] shows that more has been proven. The proof shows there is a unique positive definite square root for a positive definite matrix A.
Theorem A.3 (see [Reference Horn and Johnson21] Theorem 7.2.7).
Let A be an ![]() $n\times n$ symmetric matrix. If
$n\times n$ symmetric matrix. If ![]() $A=B^TB$, with B an
$A=B^TB$, with B an ![]() $m\times n$ matrix, then A is positive definite if and only if B has full column rank.
$m\times n$ matrix, then A is positive definite if and only if B has full column rank.
The polar decomposition of a matrix is incredibly useful. Below, we give the version that best applies to our work.
Theorem A.4 (see [Reference Horn and Johnson21] Theorem 7.3.1 Polar decomposition).
Let A be an ![]() $n\times n$ real matrix. Then
$n\times n$ real matrix. Then ![]() $A=PU=UQ$, in which
$A=PU=UQ$, in which ![]() $P,Q\in M_n$ are positive semidefinite and
$P,Q\in M_n$ are positive semidefinite and ![]() $U\in M_n$ is orthogonal. The factors
$U\in M_n$ is orthogonal. The factors ![]() $P=(AA^T)^{1/2}$ and
$P=(AA^T)^{1/2}$ and ![]() $Q=(A^TA)^{1/2}$ are uniquely determined; P is a polynomial in
$Q=(A^TA)^{1/2}$ are uniquely determined; P is a polynomial in ![]() $AA^T$, and Q is a polynomial in
$AA^T$, and Q is a polynomial in ![]() $A^TA$. The factor U is uniquely determined if A is nonsingular.
$A^TA$. The factor U is uniquely determined if A is nonsingular.
Remark A.5 (see [Reference Dieci and Eirola12] Section 2.3 (c)).
Suppose A is an ![]() $m\times n$ matrix with full rank and
$m\times n$ matrix with full rank and ![]() $A(t)$ depends
$A(t)$ depends ![]() $C^k$-smoothly on t. Then we can write
$C^k$-smoothly on t. Then we can write ![]() $A(t)=O(t)P(t)$, where O is orthonormal, P is symmetric positive definite and O and P are as smooth as A.
$A(t)=O(t)P(t)$, where O is orthonormal, P is symmetric positive definite and O and P are as smooth as A.
Acknowledgments
We would like to thank all the people who have discussed these problems with us over the years, especially Jordan Ellenberg, Benjamin Matschke and Gunter Ziegler. This research was supported by a grant from the Simons Collaboration Grant #524120 (Cantarella). All authors contributed equally to the research and writing.
Conflict of Interest
The authors have no conflict of interest to declare.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Supplementary material
None.