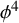Quadratic Klein-Gordon equations with a potential in one dimension

Abstract

This paper proposes a fairly general new point of view on the question of asymptotic stability of (topological) solitons. Our approach is based on the use of the distorted Fourier transform at the nonlinear level; it does not rely only on Strichartz or virial estimates and is therefore able to treat low-power nonlinearities (hence also nonlocalised solitons) and capture the global (in space and time) behaviour of solutions.

More specifically, we consider quadratic nonlinear Klein-Gordon equations with a regular and decaying potential in one space dimension. Additional assumptions are made so that the distorted Fourier transform of the solution vanishes at zero frequency. Assuming also that the associated Schrödinger operator has no negative eigenvalues, we obtain global-in-time bounds, including sharp pointwise decay and modified asymptotics, for small solutions.

These results have some direct applications to the asymptotic stability of (topological) solitons, as well as several other potential applications to a variety of related problems. For instance, we obtain full asymptotic stability of kinks with respect to odd perturbations for the double sine-Gordon problem (in an appropriate range of the deformation parameter). For the $\phi ^4$ problem, we obtain asymptotic stability for small odd solutions, provided the nonlinearity is projected on the continuous spectrum. Our results also go beyond these examples since our framework allows for the presence of a fully coherent phenomenon (a space-time resonance) at the level of quadratic interactions, which creates a degeneracy in distorted Fourier space. We devise a suitable framework that incorporates this and use multilinear harmonic analysis in the distorted setting to control all nonlinear interactions.

1 Introduction

This work concerns the global-in-time behaviour of small solutions of one-dimensional quadratic Klein-Gordon equations with an external potential. The class of equations that we treat in this paper appears when studying the asymptotic stability of special solutions of nonlinear dispersive and hyperbolic equations, such as solitons, travelling waves and kinks.

1.1 The model and motivation

1.1.1 The equation

We consider the equation

(KG) $$ \begin{align} \partial_t^2 u + (- \partial_x^2 + V(x) + m^2) u = a(x) u^2 \end{align} $$

where the unknown $u = u(t,x) \in {\mathbb R}$ , the space and time variables $(t,x) \in {\mathbb R}\times {\mathbb R}$ , $m>0$ is the mass parameter, V is a real-valued, decaying and smooth external potential, and a is a sufficiently smooth function with $a(x) - \ell _{\pm \infty }$ decaying quickly as $x\rightarrow \pm \infty $ , $\ell _{\pm \infty } \in {\mathbb R}$ . The addition of cubic and higher-order terms (with constant or nonconstant coefficients) does not bring any further complication, so we omit it for the sake of explanation.¹

Equation (KG) derives from the Hamiltonian

(1.1) $$ \begin{align} \mathscr{H}(u) = \frac{1}{2}\int_{{\mathbb R}} \left[ (\partial_t u)^2 + (\partial_x u)^2 + m^2 u^2 + Vu^2 \right] \, dx + \frac{1}{3}\int_{{\mathbb R}} a(x) u^3 \, dx. \end{align} $$

By rescaling, we can set $m=1$ without loss of generality; we will do so in the rest of the paper. We will be interested in the Cauchy problem with small initial data $(u(0,x),u_t(0,x)) = (u_0(x),u_1(x))$ in suitable weighted Sobolev spaces. In short, under some spectral assumptions on V, our main result, Theorem 1.1, gives the existence of global small solutions with sharp pointwise time-decay and long-range asymptotics.

We will consider a broad class of external potentials in equation (KG), both generic and exceptional, with some additional assumptions in the latter case. In all cases, we assume that there is no discrete spectrum. The class of nongeneric potentials that we consider arises in applications such as, for example, pure power nonlinear Klein-Gordon and the $\phi ^4$ model; see Section 1.4.

1.1.2 Motivation

Nonlinear equations with external potentials arise from the perturbation of full nonlinear problems around special solutions, such as solitons. The quadratic problem in equation (KG) is inspired by the long-standing open question of the full asymptotic stability of the kink solution $K=\mathrm {tanh}(x/\sqrt {2})$ for the $\phi ^4$ model $\phi _{tt}-\phi _{xx} = \phi - \phi ^3$ (see Section 1.4.1 and [45]). It is also closely related to similar questions about solitons of nonlinear Klein-Gordon, kinks of other relativistic Ginzburg-Landau theories and generalised sine-Gordon theories in $1+1$ dimensions.

One-dimensional kinks are the simplest example of topological solitons: that is, non-spatially localised special solutions, as opposed to the more standard solitons that are localised in space. While the mathematical theory on the stability (or instability) of solitons is very well-developed in many models, this is not the case for topological solitons. There are in fact major difficulties in dealing with these objects even in the most basic one-dimensional case. As we will explain below, our paper aims to address some of these difficulties by treating the deceptively simple-looking quadratic model in equation (KG) under fairly general assumptions. Note that models with quadratic nonlinearities, such as equation (KG), also arise in the linearisation of quadratic equations (e.g., water waves, Euler-Poisson, Zakharov, etc.) around (localised) soliton solutions.

Furthermore, the study of asymptotic stability (or instability) of solitons - as opposed to orbital or local asymptotic stability - is motivated by problems in the theory of quasilinear equations, where this is often the only relevant type of stability that one can hope to achieve, since the equations are usually not even locally well-posed in the energy space.

Before describing our result in more detail, let us briefly mention some important aspects of our paper:

• • We can treat a large class of equations provided that the property $\widetilde {u}(0,t)=0$ holds; here $\widetilde {u}$ denotes the distorted Fourier transform of u. Under this sole assumption, we need to allow for a loss of regularity in Fourier space of our solutions. This loss of regularity was previously observed in some $2$ d (unperturbed: that is, with no potential) models [14, 15]; in the $1$ d case under consideration, it is caused by a coherent phenomenon - that is, a full (space-time) nonlinear resonance - that appears because of the potential. See Section 2.3 for more on this.

• • Loss of regularity in Fourier space is expected to be a crucial phenomenon in dimension one. First, it should occur generically due to resonant nonlinear interactions within the continuous spectrum. Also, singularities can arise through the coupling of internal modes of oscillations (discrete spectrum) and the continuous spectrum through the ‘Fermi golden rule’ [67, 69]; furthermore, they can appear due to zero energy resonances of the linear(ised) operator.²

• • Our global stability and decay result for equation (KG) has direct applications to the stability of stationary states of nonlinear evolution problems, under additional symmetry assumptions, when restricting the nonlinear interactions to the continuous spectrum; see Section 1.4. We also obtain full asymptotic stability for certain families of kinks of the double sine-Gordon equation (a generalised sine-Gordon theory); see Section 1.4.3.

• • We believe that our treatment of equation (KG) helps clarify the interconnected roles of the zero-energy resonances, symmetries of the equation and low-frequency behaviour (or improved local decay) in the study of global space-time asymptotics; see, for example, the discussion in Section 1.4.2.

• • More generally, we believe that the approach laid out in this paper enables a precise analysis of the nonlinear interactions of perturbed waves that are localised, yielding optimal results as far as decay is concerned, for instance. In this respect, it goes beyond classical methods that rely on dispersive or Strichartz estimates or virial-type identities.

1.2 Previous results

1.2.1 Methods for solitons and topological solitons

The literature on soliton stability is extensive, and a complete overview is beyond the scope of this paper, and our abilities. We refer readers to the excellent surveys [71, 68, 64] and the book [9] and references therein.

One immediately noticeable difference between solitons, which are spatially localised, and topological solitons, which are not, is in the linearised equations. In fact, since topological solitons do not decay to zero, lower-order nonlinear terms are typically powers of the small perturbation times a nondecaying coefficient; see equation (1.18) as an example. This lack of localisation prevents the efficient use of improved local decay type estimates, which are often a key tool when dealing with (standard) solitons.

In general, the treatment of low-power nonlinearities (in low dimensions) for equations with potentials is a well-known problem. Linear dispersive tools (e.g., $L^p-L^q$ estimates for the linear group, Strichartz estimates, improved local decay, etc.) and energy estimates are typically not enough to treat these equations. Similar issues arise when $V=0$ , but in this case, one can resort to well-established methods, such as normal forms, vectorfields, the space-time resonance method and multilinear harmonic analysis tools.

In the perturbed case $V\neq 0$ , all these methods are not directly applicable: the (large) potential decorrelates linear frequencies, ruling out standard normal form analysis and multilinear Fourier analysis, and at the same time destroys the invariance properties of the equation, ruling out vectorfields. To address these fundamental issues, we initiated a systematic approach based on the distorted Fourier transform in our work with F. Rousset [24] on the basic³ $1$ d cubic NLS model with a generic potential. In this paper, we advance our theory by treating the much more complex case of equation (KG).

Let us now review some of the existing literature, starting with results on flat/unperturbed $1$ d Klein-Gordon equations and then turning to recent advances in the treatment of perturbed equations.

1.2.2 Klein-Gordon in the flat ( $V=0$ ) case in dimension one

In this case, Delort [11] obtained small data (modified) scattering for quasilinear quadratic nonlinearities. Similar results were obtained in the semilinear cubic and quadratic case, respectively, in [52] and [30]. In the last few years, some works have been dedicated to inhomogeneous models of the form

(1.2) $$ \begin{align} u_{tt} - u_{xx} + u = a(x) u^2 + b(x) u^3. \end{align} $$

Lindblad-Soffer [53] and Sterbenz [70] treated the case of constant a; see also [54] for a recent proof when $a=0$ . Lindblad-Soffer-Luhrman [55] also recently treated equation (1.2) under the assumption that a decays to zero at infinity and either $\widehat {a}(\pm \sqrt {3}) = 0$ , or $\widehat {a}(\pm \sqrt {3}) \neq 0$ but $b=0$ . In Section 2.3, we will discuss the key role of the frequencies $\xi = \pm \sqrt {3}$ for the evolution of solutions of equation (KG). As one of the byproducts of our main result, we also obtain globally decaying solutions with modified asymptotics for equation (1.2) in the case of odd initial data and a general odd a and even b; see Remark (9) after Theorem 1.1.

1.2.3 Equations with potentials in dimension one

In the analysis of nonlinear equations with potentials, the first step is to understand the dispersive properties of the perturbed linear operator. There is a vast literature on dispersive properties, such as decay estimates and Strichartz estimates; for brevity we just refer to the classical works [38, 25] and [64] and references therein. The literature on linear scattering theory for Schrödinger operators is also substantial; limiting ourselves to the $1$ d case, we refer to Deift-Trubowitz [10], Weder [75] and the books [73, 77, 49].

As discussed above, linear tools are generally not sufficient to deal with low-power nonlinearities, which are the ones of interest for the stability of topological solitons. Recently, a few works have been dedicated to this situation in the one-dimensional case; see the works on cubic NLS [12, 60, 24, 7, 59], and [16, 17] on wave equations.

Concerning kink solutions, Kowalczyk, Martel and Muñoz [45] proved asymptotic stability locally in the energy space for odd perturbations of the kink of the $\phi ^4$ equation (1.17); the more classical orbital stability was proven in [31, 26]. See also the related result on KG/wave models [46, 47], the proof of local asymptotic stability for a large class of $1$ d scalar field equations by Kowalczyk, Martel, Muñoz and Van Den Bosch [48] and the paper of Jendrej-Kowalczyk-Lawrie [37] on kink-antikink interactions. Full asymptotic stability for kinks of relativistic GL equations (1.24) was proven by Komech-Kopylova [41, 42] when $p \geq 13$ . In a very recent paper, Delort and Masmoudi [13] proved long time stability for the kink of the $\phi ^4$ model, reaching times of order $\epsilon ^{-4}$ for data of size $\epsilon $ ; their analysis is based on a semi-classical approach using conjugation by the wave operators. Concerning this last problem, as a consequence of our general results on equation (KG), we can obtain a global stability result (in the odd class) provided the nonlinearity is projected onto the continuous spectrum. This latter is, of course, an important restriction, and we do not claim any new results in the case of a full coupling to the internal mode. However, we are hopeful that our techniques will be relevant in this case, too; see Section 1.4.1 for more on the $\phi ^4$ problem.

Finally, for results on the related problem of asymptotic stability of solitary waves for NLS, we refer to the classical works [1, 2] and Krieger-Schlag [44] and references therein. For supercritical NLKG, see Krieger-Nakanishi-Schlag [43].

1.2.4 Higher dimensions

Equations with potentials and questions about the stability of (nontopological) solitons in higher dimensions have also been extensively studied. Without going too much into details, we refer the reader to the classical results [67, 74, 69, 72, 27] and the surveys [68, 64, 65] and references therein. Finally, let us mention some $3$ d works that are close in spirit to ours: [20] laid out some basic multilinear harmonic analysis tools and treated the nonlinear Schrödinger equation in the case of a nonresonant $\overline {u}^2$ nonlinearity, while [50, 51], respectively [62], considered the case of a small, respectively large, potentials and a $u^2$ nonlinearity.

1.3 Main result

Let us now state our main result. In short, for sufficiently small and localised data (as in equation (1.3)), and assuming that the distorted Fourier transform of the solution vanishes at the zero frequency, we can construct global solutions for quadratic Klein-Gordon equations that decay at the optimal (i.e., linear) rate (see equation (1.4)); moreover, we obtain full asymptotics with modified scattering via a logarithmic phase corrections (see equation (1.13) below).

The statement of our main theorem requires some technical definitions, for which we give precise references to later parts of the paper.

Theorem 1.1. Let

$$ \begin{align*}H := -\partial_x^2 + V \end{align*} $$

denote the Schrödinger operator, and assume it has no bound states. Let $V=V(x)$ and $a=a(x)$ be smooth and such that $V(x)$ and $a(x) - \ell _{\pm \infty }$ and their derivatives decay super-polynomially⁴ as $x \rightarrow \pm \infty $ .

Consider either one of the following two equations:

• • Either

  (KG) $$ \begin{align} \partial_t^2 u + (H + 1) u = a(x) u^2 \end{align} $$
  under one of the following three assumptions (see Sections 3 and 3.1.3 for definitions):

  1. (A) V is generic, or

  2. (B) V is exceptional and even, the zero energy resonance is even, and $a(x)$ is odd, or

  3. (C) V is exceptional and even, the zero energy resonance is odd, and $a(x)$ is even.

• • Or

  (KG2) $$ \begin{align} \partial_t^2 u + (H + 1) u = \sqrt{H} (a(x) u^2) \end{align} $$
  under one of the following two assumptions:

  1. (D) V is generic, or

  2. (E) V is exceptional, and the distorted Fourier transform associated to H (defined in Section 3.2) of the data $(u,\partial _tu)(0,x)$ is vanishing at frequency zero.⁵

Consider data at the initial time

$$ \begin{align*}(u,\partial_t u)(t=0) = (u_0,u_1) \end{align*} $$

with

(1.3) $$ \begin{align} {\big\| (\sqrt{H+1}u_0, u_1) \big\|}_{H^4} + {\big\| \langle x \rangle (\sqrt{H+1}u_0, u_1) \big\|}_{H^1} = {\varepsilon}_0. \end{align} $$

Then the following holds:

• • (Global existence) There exists $\overline {{\varepsilon }}>0$ such that for all ${\varepsilon }_0\leq \overline {{\varepsilon }}$ , equation (KG) with initial data $(u,\partial _tu)(t=0) = (u_0,u_1)$ admits a unique global solution $u\in C({\mathbb R},H^5({\mathbb R}))$ .

• • (Pointwise decay) For all $t\in {\mathbb R}$

  (1.4) $$ \begin{align} {\big\| \big(\sqrt{H+1}u, \partial_tu \big)(t) \big\|}_{L^{\infty}_x} \lesssim {\varepsilon}_0 (1+|t|)^{-1/2}. \end{align} $$

• • (Global bounds in $L^2$ spaces) The solution satisfies the global-in-time bounds

  (1.5) $$ \begin{align} {\big\| u(t) \big\|}_{H^5} + {\big\| \partial_t u(t) \big\|}_{H^4} \lesssim {\varepsilon}_0 \langle t \rangle^{p_0}, \end{align} $$
  for some small $p_0>0$ . Moreover, if we define the profile
  (1.6) $$ \begin{align} g = e^{it\sqrt{H+1}}\big(\partial_t - i\sqrt{H+1}) u \end{align} $$
  we have
  (1.7) $$ \begin{align} {\big\| \langle \xi \rangle \partial_{\xi} \widetilde{g}(t) \big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_0 \langle t \rangle^{1/2+\delta}, \end{align} $$
  for some small $\delta>0$ , where $\widetilde {g}$ denotes the distorted Fourier transform of g (as defined in equation (3.21); see also Proposition 3.6).

• • (Asymptotic behaviour) There exists a quadratic transformation B (satisfying bilinear Hölder type bounds) such that, as $|t| \rightarrow \infty $ , the ‘renormalised’ profile $f:= g-B(g,g)$ scatters to a time-independent profile up to a logarithmic phase correction. See Remark 6 for more details.

Here are a few remarks about the statement and our main assumptions.

Remark 1.2 (Vanishing at the zero frequency)

Hypotheses (A), (B), (C) for equation (KG) and hypothesis (D) and (E) for equation (KG2) are ways of ensuring that $\widetilde {f}(0)=0$ , where $\widetilde {f}$ is the distorted Fourier transform of f associated to the operator H; see Section 3 for the definitions and equation (2) below for the vanishing property. The zero frequency for the distorted Fourier transform is linked to a resonant phenomenon, hence the necessity for the cancellation $\widetilde {f}(0)=0$ for our proof to apply; see the discussion in Section 2.3.

Remark 1.3. In the course of our proof, we will work (most of the time) just with the assumption that $\widetilde {f}(0)=0$ , so as to be able to treat all cases in a unified way. In particular, we will carry out all our main estimates for equation (KG), but everything can be easily adapted to equation (KG2). In some instances, we will need to distinguish between the different cases, such as (A) vs. (B), and will specify when this is so (see, for example, the proof of Lemma 5.8).

Remark 1.4. Theorem 1.1 remains true if the operator H is allowed to have bound states, but the data and the nonlinearities in equations (KG) and (KG2) are projected on the continuous spectrum of the operator.

Remark 1.5. Note that the parity assumptions in (B), respectively (C), imply that the solutions are odd, respectively even. However, in the case of equation (KG2), no parity assumptions are needed.

Moreover, Theorem 1.1 remains valid if one includes cubic and higher-order terms in equation (KG), provided this is done by keeping the proper parity. For example, in both cases (B) and (C), one can add a term $b(x)u^3$ to equation (KG) with an even and sufficiently regular (but not necessarily decaying) b. Similarly, one can add any cubic or higher-order terms to equation (KG2) inside the parentheses on the right-hand side.

Let us now make some remarks about our results and some of their implications. More specific applications are discussed in Section 1.4.1.

1. 1. Assumptions on the potential: generic and exceptional.

   The assumption that V is generic is the following:

   (1.8) $$ \begin{align} \int_{\mathbb R} V(x) \, m(x) \, dx \neq 0, \end{align} $$
   where m is the unique solution of $(-\partial _{x}^2 + V)m = 0$ with $\lim _{x\rightarrow \infty }m(x) = 1$ . One can see that equation (1.8) is equivalent to the condition that the transmission coefficient T (see equation (3.13) for the definition) satisfies $T(0) = 0$ . This is also equivalent to the fact that the $0$ energy level is not a resonance: that is, there does not exist a bounded solution in the kernel of H; See Lemma 3.3. A nongeneric potential is called ‘exceptional’.

2. 2. The zero frequency and symmetries.

   For generic V, one has that $\widetilde {f}$ is continuous everywhere for $f \in L^1$ , and $\widetilde {f}(0) = 0$ . See the remarks after Proposition 3.6. In the case of exceptional potentials, one does not have continuity of $\widetilde {f}$ at $0$ in general. Continuity holds if $T(0)=1$ or, equivalently, $a:=m(-\infty )=1$ , since

   (1.9) $$ \begin{align} \widetilde{f}(0+) = \frac{2a}{1+a^2} \frac{1}{\sqrt{2\pi}} \int m(x) f(x) \,dx \qquad \mbox{and} \qquad \widetilde{f}(0-) = \frac{1}{a}\widetilde{f}(0+), \end{align} $$
   where m is the zero energy resonance; see equation (3.23). In the context of our nonlinear problem in equation (KG), we are interested in the low-frequency behaviour of the solution and, in particular, the vanishing of $\widetilde {u}(t,\xi )$ at $\xi =0$ . While for generic potentials, we are guaranteed that indeed $\widetilde {u}(t,0) = 0$ for all times t, in the case of exceptional V, we need to impose some additional (symmetry) conditions for this to hold, as in (B), (C) or (E) of Theorem 1.1.

   Since in case (B), respectively (C), we have odd, respectively even, solutions (see Remark 1.5), equation (1.9) shows that when the zero energy resonance $m(x)$ is even, respectively odd, we indeed have $\widetilde {u}(t,0)=0$ .

   The structure of the equation might also guarantee the desired vanishing condition, which is what we exploit for equation (KG2). Indeed, in case (E), the initial data is assumed to be such that $(\widetilde {u},\widetilde {u_t})(t=0,\xi =0) = 0$ , and this condition is preserved by the flow of equation (KG2), since applying the distorted Fourier transform and evaluating at $\xi =0$ gives $\widetilde {u_{tt}}(t,0) + u(t,0) = 0$ .

3. 3. Improved local decay.

   An important aspect in the study of nonlinear problems with potentials is local decay. Roughly speaking, the potential, which is localised around the origin, typically reflects low-energy particles away from it, leading to an improved local decay estimate of the form

   (1.10) $$ \begin{align} {\big\| \langle x \rangle^{-\sigma_1} P_c e^{it\sqrt{H+1}}f \big\|}_{L^{\infty}} \lesssim |t|^{-a} {\| \langle x \rangle^{\sigma_2} f \|}_{L^1} \end{align} $$
   for some $\sigma _1,\sigma _2> 0$ , and a rate of decay a larger than $1/2$ , which is the optimal one for general linear waves. $P_c$ in equation (1.10) denotes the projection to the continuous spectrum of H. While we do not directly make use of estimates like equation (1.10), we do rely on the dual improved behaviour for small frequencies.

   For generic potentials, it can be shown that equation (1.10) holds with $a=3/2$ and $\sigma _2 = 1$ [44, 64] (the value of $\sigma _1$ is unimportant for this discussion); such an estimate is essentially equivalent to (and scales like)

   (1.11) $$ \begin{align} {\big\| \langle x \rangle^{-\sigma_1} P_c e^{it\sqrt{H+1}}f \big\|}_{L^{\infty}} \lesssim |t|^{-1} {\| \langle x \rangle f \|}_{L^2}. \end{align} $$
   To see the difference with the exceptional case, it suffices to consider the flat case $V=0$ . From a stationary phase expansion, one sees that linear solutions satisfy, as $t \to \infty $ ,
   (1.12) $$ \begin{align} e^{it \langle \partial_x \rangle} f \approx \frac{e^{i \frac{\pi}{4}}}{\sqrt{2t}} \langle \xi_0 \rangle^{3/2} e^{i t \langle \xi_0 \rangle + i x \xi_0} \widehat{f} \left( \xi_0 \right), \qquad \frac{\xi_0}{\langle \xi_0 \rangle} := - \frac{x}{t}, \end{align} $$
   where $\widehat {f}$ is the regular Fourier transform. Thus, there is no improvement to the local decay rate unless $\widehat {f}(0)=0$ . However, in general, the next term in the expansion is only of the order of $|t|^{-3/4}{\| \langle x \rangle f\|}_{L^2}$ . The difference between this and the faster $|t|^{-1}$ decay in equation (1.11) turns out to be a major issue when dealing with equation (KG) under our very general assumptions.

   Local decay is also stronger for exceptional potentials if, in addition to $\widetilde {f}(0) = 0$ , further cancellations occur due to symmetries. This suggests the possibility of simplifications to parts of our arguments if one of the assumptions (A), (B) or (C) in Theorem 1.1 holds. In particular, one may be able to adopt a less refined functional framework than the one we use here (see Section 2.5).

4. 4. The functional framework and degenerate norms.

   To deal with an example such as equation (KG2) where only $\widetilde {f}(0) = 0$ can be assumed, we need to pay particular attention to a phenomenon of loss of regularity in frequency space. As we explain in Section 2.3, when the distorted frequency $\xi $ approaches $\pm \sqrt {3}$ , the $L^2$ weighted norm of the (renormalised) profile f becomes singular. We then need to use a norm that captures this degenerate behaviour; see equation (2.30).

   It is important to point out that while some of the complications may be avoided by making less general assumptions, we expect that degenerate norms like the one we use in this paper will play a key role when internal modes (positive eigenvalues of $H+1$ ) are present, as well as when considering general (nonsymmetric) solutions.

5. 5. Violating the zero frequency condition

   The above discussion emphasised the technical reasons leading to the requirement that the solution of equation (KG) vanishes at zero frequency. The works [55, 56] address a setup where the coefficient $a(x)$ is localised but the solution does not have to vanish at zero in (distorted) Fourier space. In these papers, it is shown that the decay in time slows by a logarithmic factor compared to the linear case; see also the discussion at the end of Section 2.3. Since the linear decay rate was already critical at the level of the cubic interaction, this additional logarithm is expected to make the nonlinear analysis of the full problem (including cubic terms or a nondecaying a) extremely delicate.

6. 6. Modified asymptotics.

   In the last point of Theorem 1.1, we state that a renormalised profile $f=g-B(g,g)$ undergoes modified scattering. Let us postpone for the moment the exact definition of f and just think of $B(g,g) \approx g^2$ . For the profile f, we prove the following asymptotic formula: there exists an asymptotic profile $W^{\infty } = (W^{\infty }_+, W^{\infty }_-) \in \big (\langle \xi \rangle ^{-3/2}L^{\infty }_{\xi }\big )^2$ such that, for $\xi>0$ ,

   (1.13) $$ \begin{align} \begin{aligned} & \big(\widetilde{f}(t,\xi),\widetilde{f}(t,-\xi)\big) \\ &\quad = S^{-1}(\xi) \exp\Big( -\frac{5i}{12} \mathrm{diag}\big( \ell_{+\infty}^2\big| W^{\infty}_+(\xi) \big|^2, \ell_{-\infty}^2\big| W^{\infty}_-(\xi) \big|^2 \big) \log t \Big) W^{\infty}(\xi) + O\big({\varepsilon}_0^2 \langle t \rangle^{-\delta_0}\big) \end{aligned} \end{align} $$
   as $t \rightarrow \infty $ , for some $\delta _0>0$ ; here $S(\xi )$ is the scattering matrix associated to the potential V defined in equation (3.12). As $t \rightarrow -\infty $ , using the time-reversal symmetry, one obtains a similar (in fact, simpler) formula that resembles the flat case. While this correction to scattering is most naturally viewed in distorted Fourier space, it translates to physical space by standard arguments. Note that because of the potential V, this logarithmic phase correction depends on the scattering matrix S (at least in one time direction) and ‘mixes’ positive and negative frequencies. We refer the reader to Proposition 10.1 and the comments after it for more details.

   The phenomenon of modified scattering by a logarithmic phase correction is one of the fundamental types of nonlinear phenomena that one may observe for scattering critical (long-range) equations. We refer the reader to the papers on NLS [29, 53, 39, 32] and on KG [11, 30, 55] where this type of modified scattering is proved using various approaches for equations without potentials. For equation with potentials, see the already cited [12, 60, 24, 7].

7. 7. Assumptions on the data.

   The assumptions in equation (1.3) are quite standard for these types of problems. Finiteness of the weighted norm guarantees $|t|^{-1/2}$ pointwise decay for linear solutions. Propagating a suitable weighted bound for all times will be one of the main goals of our proof. For the profile g, we can only propagate the weak bound in equation (1.7), while we will be able to control a stronger weighted norm of f.

   A certain amount of Sobolev regularity is helpful in many parts of the proof when we deal with high frequencies. However, although equation (KG) is a semilinear problem, it seems to us that it is not straightforward to propagate any desired amount of Sobolev regularity, unlike in many other similar problems. This is essentially because the nonlinearity contains quadratic terms that cannot be eliminated by normal forms, and (localised) decay is at best $|t|^{-3/4}$ in the absence of symmetries.

8. 8. Global bounds and bootstrap spaces.

   Most of our analysis is performed in the distorted Fourier space. The main task is to prove a priori estimates in suitably constructed spaces for a renormalised profile obtained after a partial normal form transformation. This is the profile⁶ $f:=g-B(g,g)$ alluded to in the main Theorem. We refer the reader to Section 5, and in particular to Section 5.7, for the definition of f.

   The profile f is measured in three norms: a Sobolev norm (like g), a weighted-type norm that incorporates the degeneration close to the bad frequencies $\pm \sqrt {3}$ , and the sup-norm of its distorted Fourier transform. We refer to Section 2.5 for details about the functional framework and to the beginning of Section 7 for the main bootstrap propositions on f and g.

9. 9. The flat case.

   For the sake of explanation, it is interesting to consider equation (KG) in the simplified case $V=0$

   (1.14) $$ \begin{align} \partial_t^2 u + (- \partial_x^2 + 1) u = a(x) u^2, \end{align} $$
   where $a(x)$ is odd and fast approaching $\pm \ell $ as $x\rightarrow \pm \infty $ . Cubic terms of the form $u^3$ and $b(x)u^3$ (with b even) can be included in the model. For equation (1.14), our result gives globally decaying solutions for odd initial data. However, as discussed in Remark (3) above, this specific case of odd symmetry is simpler due to faster local decay. A related, and more difficult, toy model that we can include in our treatment is (see equation (KG2))
   (1.15) $$ \begin{align} \partial_t^2 u + (- \partial_x^2 + 1) u = \partial_x( a(x) u^2 ) \end{align} $$
   with zero average initial data. Note that symmetries are not needed here, and other variants are possible provided the zero average condition is preserved.

   As mentioned after equation (1.2), the flat case in equation (1.14) with nonsymmetric localised data, and decaying coefficient $a(x)$ , was treated in [54], where a logarithmic slowdown of the decay rate was also shown to occur. Cubic terms are also included in the results of [54], provided $\widehat {a}(\pm \sqrt {3})=0$ . The general case of equation (1.14) without symmetries and with nondecaying $a(x)$ is still open.

1.4 Applications

In this subsection, we discuss the relevance of our results to questions on the asymptotic stability of stationary solutions for several important physical problems. We will be considering one-dimensional scalar field theories

$$ \begin{align*}\partial_t^2 \phi - \partial_x^2 \phi + U'(\phi) = 0 \end{align*} $$

deriving from the Hamiltonian

(1.16) $$ \begin{align} \mathscr{H} = \frac{1}{2} \int \left( \phi_t^2 + \phi_x^2 \right) \, dx + \int U(\phi) \,dx. \end{align} $$

Choosing the potential U with a double-well (Ginzburg-Landau) structure, special solutions connecting stable states at $\pm \infty $ , known as kinks, emerge. The question of their stability, or asymptotic behaviour, depends very delicately on the potential U and leads to a wealth of interesting mathematical problems. Our analysis sheds light on this question for various models, some of which we review below.

1.4.1 The $\phi ^4$ model

This fundamental model corresponds to the choice

$$ \begin{align*}U(\phi) = U_0(\phi) = \frac{1}{4}(1-\phi^2)^2, \end{align*} $$

leading to the equation

(1.17) $$ \begin{align} \partial_{t}^2 \phi - \partial_x^2 \phi = \phi - \phi^3, \end{align} $$

which admits the kink solution $K_0(x) = \tanh (x/\sqrt {2})$ . Setting $\phi = K_0+v$ , where v is a small (localised) perturbation, we see that

(1.18) $$ \begin{align} (\partial_t^2 + H_0 + 2)v = - 3K_0 v^2 - v^3, \qquad H_0 := -\partial_x^2 + V_0, \qquad V_0(x) := - 3 \mathrm{sech}^2(x/\sqrt 2). \end{align} $$

It is known (see [8, 9, 54]) that the spectrum of the Schrödinger operator $H_0$ has the following structure: the $-2$ eigenvalue corresponding to the translation symmetry, an even zero energy resonance (a bounded solution of $H\psi = 0$ ) and the eigenvalue $\lambda _1=-1/2$ corresponding to an odd exponentially decaying eigenfunction $\psi _{-1/2}$ . The latter is the so-called internal mode. For the sake of explanation, let us restrict our attention to the subspace of odd functions.⁷ By projecting onto the discrete and continuous modes, one can decompose $v = c_0(t) \psi _{-1/2} + P_c \, u(t,x)$ , where $P_c$ is the projection onto the continuous spectrum of $H_0$ , and obtain the equation $(\partial _t^2 + H_0 + 2)u = P_c(-3K_0 v^2 - v^3)$ for the radiation component. One is then naturally led to analysing the ‘continuous subsystem’

(1.19) $$ \begin{align} \begin{aligned} (\partial_t^2 + H_0 + 2)u & = P_c \left( -3K_0 u^2 - u^3 \right). \end{aligned} \end{align} $$

Since $V_0$ and its zero energy resonance are even, our results apply to show global bounds and decay for equation (1.19) with odd data.

Thus, we are able to settle at least part of the kink stability problem; the remaining difficulty, in the odd case, is to prove that the coupling of the internal mode to the continuous spectrum causes the energy of the internal mode to be dispersed through the phenomenon of ‘radiation damping’ [69, 13]. This is a serious obstacle since the presence of the internal mode leads to the formation of a singularity in distorted Fourier space, at the frequency given by the Fermi golden rule. However, notice that a very similar phenomenon is dealt with in the present paper, with the formation of a singularity at the distorted frequencies $\pm \sqrt {3}$ .

For general data, one has to deal with the resonance at zero frequency, which should at least lead to a logarithmic slowdown of the decay, as observed in [55, 56]. Since the decay rate is already critical for the cubic nonlinearity, this makes this question extremely delicate.

1.4.2 The sine-Gordon equation

Choosing $U(\phi ) = U_{SG}(\phi ) = 1 - \cos \phi $ in equation (1.16) gives the sine-Gordon equation

(1.20) $$ \begin{align} \partial_{t}^2 \phi - \partial_x^2 \phi + \sin\phi = 0, \end{align} $$

which is integrable and admits the kink solution $K_{\mathrm {SG}}(x) = 4 \arctan (e^x)$ [9, Chapter 2]. Setting $\phi = K_{\mathrm {SG}}+v$ , the perturbation v solves

(1.21) $$ \begin{align} \partial_t^2 v + (H_{\mathrm{SG}} + 1)v = (\sin K_{\mathrm{SG}}) v^2 + O(v^3), \qquad H_{\mathrm{SG}} = -\partial_x^2 - 2 \operatorname{sech}^2(x). \end{align} $$

$H_{\mathrm {SG}}$ has no internal mode (only the eigenvalue $\lambda = -1$ associated with the translation invariance), and it is exceptional, but with an odd zero energy resonance; thus, the distorted Fourier transform of an odd function does not vanish at zero energy. Therefore, despite its similarities with the $\phi ^4$ model, equation (1.20) does not a priori fall into the class of equations that we can treat with our approach.

The asymptotic stability of the kink could, however, be proved by means of inverse scattering by Chen, Liu and Lu [6], since the sine-Gordon equation is completely integrable. After the first version of the present paper appeared online, another proof of the asymptotic stability of the kink was published by Lührmann and Schlag [57]; their beautiful and (relatively) short paper avoids the use of inverse scattering or the distorted Fourier transform. They rely on two key observations: on the one hand, the linearised operator around the kink can be factorised in a very convenient way; and on the other hand, the nonlinear coupling of the resonance to the continuous spectrum is cancelled by the specific form of the equation. In hindsight, we believe that the latter observation would allow us to treat the sine-Gordon problem within the framework developed in the present paper.

1.4.3 The double sine-Gordon equation

More interestingly, our results apply to the perturbation of equation (1.20) given by the double sine-Gordon model

(1.22) $$ \begin{align} \partial_t^2 \phi - \partial_x^2 \phi + U^{\prime}_{DSG}(\phi) = 0, \qquad U_{DSG}(\phi) = \frac{1}{1+|4\eta|} \big[ \eta(1-\cos \phi) + 1 + \cos\big(\tfrac{\phi}{2}\big) \big], \end{align} $$

where $\eta \in {\mathbb R}$ . This model is not integrable for $\eta \neq 0$ ; see also [9] and Campbell-Peyrard-Sodano [4] and references therein for a description of the various physical contexts where equation (1.22) has been classically used. For $\eta < 0$ , we obtain asymptotic stability results for kinks of equation (1.22). More precisely, there are two ranges of the parameter $\eta $ with corresponding families of kinks that we can consider:

1. 1. For $-1/4 < \eta < 0$ , equation (1.22) has (up to symmetries) a single odd kink connecting the minima of the potential $\pm 2\pi $ ; let us call this kink $K_1$ .

2. 2. For $\eta <-1/4$ , equation (1.22) has an odd kink connecting the minima of the potential $\pm \phi _0$ with $\cos (\phi _0/2) = 1/4\eta $ ; let us denote this kink by $K_2$ . There is also another kink in this range of $\eta $ that we do not consider since we cannot apply our results to it.

We have the following asymptotic stability of the $K_1$ and $K_2$ kink solutions for odd perturbations:

Corollary 1.6. Consider equation (1.22) with $\eta \in (-1/4,0)$ , respectively $\eta < -1/4$ , with an initial condition of the form $(\phi ,\phi _t)(0,x)= (K_1(x),0) + (u_{1,0}(x),u_{1,1}(x))$ , respectively $(\phi ,\phi _t)(0,x)= (K_2(x),0) + (u_{2,0}(x),u_{2,1}(x))$ . Assume that $(u_{i,0},u_{i,1})$ , $i=1,2$ are odd and satisfy the same smallness condition in equation (1.3). Then the associated global solution $\phi $ can be written as

$$ \begin{align*} \phi(t,x) = K_i(x) + u_i(t,x), \end{align*} $$

where $u_i$ decays globally on ${\mathbb R}$ as in equation (1.4), satisfies the bounds in equation (1.5) and has the asymptotic behaviour described in equation (1.13).⁸

Proof. We let $\phi = K_i + v$ , with $i=1,2$ and denote $U_1 := U_{DSG}$ when $-1/4 < \eta < 0$ , and $U_2 := U_{DSG}$ when $\eta < -1/4$ . Then from equation (1.22), we get

(1.23) $$ \begin{align} \begin{aligned} & (\partial_t^2 + H_i + m_i^2)v = - U_i'(K_i+v) + U_i'(K_i) + U_i''(K_i) v \\ & H_i = -\partial_x^2 + V_i, \qquad V_i(x) = U_i''(K_i)-m_i^2, \qquad m_i^2 := \lim_{x\rightarrow \pm \infty} U_i''(K_i)> 0. \end{aligned} \end{align} $$

More precisely, $m_1^2 = (1-4\eta )^{-1}(\eta +1/4)$ and $m_2^2 = 1/(16\eta ) - \eta $ .

It can be shown that $H_i$ is generic and has no eigenvalues, except the translation mode; see Appendix A for a short proof relying on the arguments of [48, Section 5.6]. In particular, the assumptions of Theorem 1.1 hold for odd solutions of equation (1.23). The conclusions of Theorem 1.1 applied to v then imply the statement of this corollary.

For the double sine-Gordon model in equation (1.22) in the same range of $\eta $ above (and also for several other scalar field models with the same spectral properties), Kowalczyk-Martel-Muñoz-Van Den Bosch [48] proved local asymptotic stability in the energy space. Compared to this latter result, Corollary 1.6 gives asymptotic stability on the full real line, and modified scattering, provided the data is (mildly) localised and odd.

1.4.4 General relativistic Ginzburg-Landau theories

Our approach and results apply similarly to general relativistic Ginzburg-Landau theories, where the potential in equation (1.16) is taken to be of double-well type, with the following expansion at the minima $\pm a$ :

(1.24) $$ \begin{align} U(\phi) = U_{\mathrm{GL}}(\phi) = \frac{1}{2}(|\phi|-a)^2 + O\big((|\phi|-a)^{p+1}\big), \qquad p \geq 2. \end{align} $$

The corresponding equations $\phi _{tt} - \phi _{xx} + U_{GL}'(\phi ) = 0$ admit kink solutions $K_{\mathrm {GL}}$ exponentially converging to $\pm a$ at $\pm \infty $ ; see [41, 42, 37]. The dynamics for the perturbation v (up to a standard modulation if necessary) become

(1.25) $$ \begin{align} \begin{aligned} & (\partial_t^2 + H_{\mathrm{GL}} + 1)v = -U_{GL}'''(K_{\mathrm{GL}}) v^2 + \frac{1}{2} U_{GL}^{(4)}(K_{\mathrm{GL}}) v^3 + O(v^4), \\ & H_{\mathrm{GL}} = -\partial_x^2 + V_{\mathrm{GL}}, \qquad V_{\mathrm{GL}}(x) = U_{\mathrm{GL}}''(K)-1. \end{aligned} \end{align} $$

In analogy with the discussion on the $\phi ^4$ model, our analysis can be applied directly to the ‘continuous subsystem’ (the analogue of equation (1.19)) that takes the form

(1.26) $$ \begin{align} (\partial_t^2 + H_{GL} + 1)u = P_c \big( -U_{GL}'''(K_{GL}) u^2 + \frac{1}{2} U_{GL}^{(4)}(K_{GL}) u^3 + O(u^4) \big). \end{align} $$

If one assumes that the minima of the well are sufficiently flat – or, in other words, that p is sufficiently big – the coefficients $U_{\mathrm {GL}}^{(k)}(K_{GL})$ , $3\leq k\leq p+1$ , become exponentially decaying, and this simplifies the nonlinear analysis considerably. Komech-Kopylova fully analysed the radiation-damping phenomenon associated to the internal mode and obtained asymptotic stability in [41] for $p \geq 14$ . While Komech-Kopylova required a large p, the methods introduced in the present paper certainly allow the treatment of smaller values of p (e.g., one should be able to comfortably reach $p=5$ : that is, a nonlocalised quintic nonlinearity).

1.4.5 The nonlinear Klein-Gordon equation

This final example involves localised solitons. The potential

$$ \begin{align*}U(\phi) = U_{p}(\phi) = \frac{1}{2} \phi^2 - \frac{1}{p+1} \phi^{p+1} \end{align*} $$

gives the $1+1$ focusing nonlinear Klein-Gordon equations

(1.27) $$ \begin{align} \partial_{t}^2 \phi - \partial_x^2 \phi + \phi = \phi^p \end{align} $$

for $p=2,3,4,\dots $ . These admit the soliton solution

(1.28) $$ \begin{align} Q(x) = Q_p(x):= (\alpha+1)^{\frac{1}{2\alpha}} \mathrm{sech}^{1/\alpha}(\alpha x), \qquad \alpha := \tfrac{1}{2}(p -1). \end{align} $$

By assuming even symmetry, we may neglect the soliton manifold obtained under Lorentz transformations. The equation for the perturbation v ( $\phi =Q+v$ ) is

(1.29) $$ \begin{align} \begin{aligned} & (\partial_t^2 + H_{p} + 1)v = \frac{1}{2}p(p-1) Q^{p-2} v^2 + \cdots + v^p. \\ & H_{p} := -\partial_x^2 + V_{p}, \qquad V_{p}(x) := -pQ^{p-1}. \end{aligned} \end{align} $$

It is known that $H_{p}$ has a negative eigenvalue at $-\alpha (\alpha +2)-1$ , which makes the soliton unstable. However, besides this and the $-1$ eigenvalue associated to the translation invariance, $H_{p}$ has no other negative eigenvalues when $p>3$ [5, 47]. Note that when $p=3$ , $H_3$ coincides (up to a rescaling) with $H_0$ (see equation (1.18)); since the resonance is even, our results do not apply to the corresponding continuous subsystem.

When $p=2$ instead, the linearised operator $H_2$ has an odd resonance. Therefore, asymptotic stability holds for small even solutions of the continuous subsystem

(1.30) $$ \begin{align} (\partial_t^2 + H_2 + 1)u = P_c\, u^2. \end{align} $$

A natural question for equation (1.27) is the construction of stable manifolds for solutions suitably close to the soliton, and the asymptotic stability of the subclass of global solutions. For $p>5$ this was done by Krieger-Nakanishi-Schlag [43]. More recently, [47] proved a conditional asymptotic stability result locally in the energy space for global solutions. For $p\leq 5$ , the problem of full asymptotic stability appears to be still open. A serious obstacle to the construction of a stable manifold is to prove a robust small data scattering theory for low-power nonlinearities. While this cannot be done using Strichartz-type estimates, which only exploit the decay of the solution, it becomes amenable to our techniques, which take advantage of the full resonant structure. In particular, the cases $p=2,4$ and $5$ can be directly approached with our methods. Note that even for $p=4$ (or $5$ ), despite the quadratic and cubic terms in the nonlinearity being localised, one would still need to exploit oscillations in frequency space to deal with the weak decaying quartic (or quintic) nonlinearity.

2 Ideas of the proof

The starting ingredient in our approach is the Fourier transform adapted to the Schrödinger operator $-\partial _{xx} + V$ , the so-called distorted Fourier transform (or Weyl-Kodaira-Titchmarsh theory). The basic idea is to try to extend Fourier analytical techniques used to study small solutions of nonlinear equations without potentials and develop new tools in the perturbed setting.

In the setting of the distorted Fourier transform, we begin by filtering the solution by the linear (perturbed) group and view the (nonlinear) Duhamel’s formula as an oscillatory integral in frequency and time. In the unperturbed case $V=0$ , this point of view was proposed in the works [21, 19, 22] with the so-called ‘space-time resonance’ method; see also [28]. In the past 10 years, this proved to be a very useful approach to studying the long-time behaviour of weakly nonlinear dispersive equations in the Euclidean/unperturbed setting. As already mentioned in Section 1.2, the presence of a potential introduces some fundamental differences, which lead to a number of new phenomena and difficulties.

2.1 Setup: dFT and the quadratic spectral distribution

We refer to Section 3 for a more detailed presentation of the distorted Fourier transform (dFT) and admit for the moment the existence of generalised eigenfunctions $\psi = \psi (x,\xi )$ such that

(2.1) $$ \begin{align} \forall \quad \xi \in {\mathbb R}, \qquad (- \partial_x^2 + V ) \psi(x,\xi) = \xi^2 \psi(x,\xi), \end{align} $$

and the familiar formulas relating the Fourier transform and its inverse in dimension $d=1$ hold if one replaces (up to a constant) $e^{i\xi x}$ by $\psi (x,\xi )$ :

(2.2) $$ \begin{align} \widetilde{f}(\xi) = \int_{\mathbb R} \overline{\psi(x,\xi)} f(x)\,dx \qquad \mbox{and} \qquad f(x) = \int_{\mathbb R} {\psi(x,\xi)} \widetilde{f}(\xi) \,d\xi. \end{align} $$

Let us consider a solution of the equation

$$ \begin{align*} \partial_t^2 u + (- \partial_x^2 + V(x) + 1) u = a(x)u^2, \qquad (u,u_t)(t=0) = (u_0,u_1). \end{align*} $$

Defining the profile g by

(2.3) $$ \begin{align} \begin{aligned} & g(t,x):=e^{it\sqrt{H+ 1}}\big(\partial_t -i \sqrt{ H + 1 } \big)u, \qquad \widetilde{g}(t,\xi) = e^{it\langle \xi \rangle}\big(\partial_t - i\langle \xi \rangle \big) \widetilde{u}, \end{aligned} \end{align} $$

and denoting $\widetilde {g}_+=\widetilde {g}$ , $\widetilde {g}_-= \overline {\widetilde {g}}$ , one sees that $\widetilde {g}$ satisfies an equation of the form

(2.4) $$ \begin{align} \partial_t \widetilde{g}(t,\xi) & = - \sum_{\iota_1,\iota_2\in\{+,-\}} \iota_1\iota_2 \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \widetilde{g}_{\iota_1}(t,\eta) \widetilde{g}_{\iota_2}(t,\sigma) \, \frac{\mu_{\iota_1\iota_2}(\xi,\eta,\sigma)}{4\langle \eta \rangle \langle \sigma \rangle} \, d\eta \, d\sigma, \end{align} $$

where the oscillatory phase is given by

(2.5) $$ \begin{align} \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma) = \langle \xi \rangle - \iota_1 \langle \eta \rangle - \iota_2 \langle \sigma \rangle, \end{align} $$

and

(2.6) $$ \begin{align} \mu_{\iota_1\iota_2}(\xi,\eta,\sigma) := \int a(x) \overline{\psi(x,\xi)} \psi_{\iota_2}(x,\eta) \psi_{\iota_1}(x,\sigma) \, dx \end{align} $$

is what we refer to as the (quadratic) ‘nonlinear spectral distribution’ (NSD).

For the sake of exposition we will drop the signs $(\iota _1,\iota _2)$ from $\widetilde {g}$ and $\mu $ since they do not play any major role. We will instead keep the relevant signs in equation (2.5) and the analogous expressions for cubic interactions. We also drop the factor $\langle \eta \rangle \langle \sigma \rangle $ in equation (2.4). With this simplifications, integrating equation (2.4) over time gives

(2.7) $$ \begin{align} \widetilde{g}(t,\xi) = \widetilde{g_0}(\xi) -i \sum_{\iota_1,\iota_2 \in \{+,-\}} \int_0^t \iint e^{is \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \widetilde{g}(s,\eta) \widetilde{g}(s,\sigma) \mu(\xi,\eta,\sigma) \,d\eta\, d\sigma\,ds. \end{align} $$

The first task is to analyse $\mu $ in equation (2.6), and we immediately see an essential difference from the flat case $V=0$ : in the absence of a potential, the generalised eigenfunctions $\psi (x,\xi )$ should be replaced by $e^{i\xi x}$ , in which case $\mu (\xi ,\eta ,{\sigma }) = \delta (\xi -\eta -{\sigma })$ – in particular, the sum of the frequencies of the two inputs: that is, $\eta $ and ${\sigma }$ , gives the output frequency $\xi $ . This can be thought of as a ‘conservation of momentum’ or ‘correlation’ between the frequencies. But if $V\neq 0$ , the structure of $\mu $ becomes more involved, and there is no a priori relation between the frequencies. This can be seen as a ‘decorrelation’ or ‘uncertainty’ due to the presence of the potential.

For the sake of this presentation, we can essentially think that

(2.8) $$ \begin{align} \begin{aligned} \mu(\xi,\eta,\sigma) & = \sum_{\mu,\nu \in\{+,-\}} \Big[ A_{\mu,\nu}(\xi,\eta,\sigma) \delta(\xi + \mu \eta + \nu {\sigma}) \\ &\quad +\, B_{\mu,\nu}(\xi,\eta,\sigma) \, \mathrm{p.v.} \frac{1}{\xi + \mu \eta + \nu {\sigma}} \Big] + C(\xi,\eta,\sigma), \end{aligned} \end{align} $$

where $A_{\mu ,\nu }$ , $B_{\mu ,\nu }$ and C are smooth functions and ‘ $\mathrm {p.v.}$ ’ stands for principal value.

The $\delta $ component of $\mu $ gives a contribution to equation (2.7) that is essentially the same as in the flat case, only algebraically more complicated due to the different signs combinations and the coefficients (which are related to the transmission and reflection coefficients of the potential). One could expect to treat these terms as in the classical flat case, that is, using a normal form transformation to eliminate the quadratic term in favour of cubic ones [66, 11, 30].

The $\mathrm {p.v.}$ term in equation (2.8) seriously impacts the nature of the problem at hand. When the variable $\xi + \mu \eta + \nu {\sigma }$ that determines the singularity is very small, one could think that the corresponding interactions are not so different from those allowed by the $\delta $ distribution, possibly only logarithmically worse. When instead $\xi + \mu \eta + \nu {\sigma }$ is not too small, we have in essence a smooth kernel. While this might seem like a favourable situation, it is in fact a major complication. The decorrelation between the input and output frequencies prevents the application of a normal form transformation (quadratic terms cannot be eliminated); even more, it creates a genuinely nonlinear phenomenon of loss of regularity (in Fourier space) at specific bad frequencies. We explain this in more detail in the following paragraphs.

2.2 Oscillations and resonances: Singular vs. regular terms

Let us consider the quadratic interactions in equation (2.7) and, according to equation (2.8), write them as

(2.9) $$ \begin{align} \int_0^t \iint e^{is \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \widetilde{g}(s,\eta) \widetilde{g}(s,\sigma) \, \mathfrak{m}(\xi,\eta,\sigma) \,d\eta\, d\sigma \, ds, \end{align} $$

where $\mathfrak {m}(\xi ,\eta ,\sigma )$ can be a distribution (i.e., a $\delta $ or a $\mathrm {p.v.}$ ) or a smooth function. The properties of equation (2.9) are dictated by the oscillations of the exponential factor and the structure of the singularities of $\mathfrak {m}$ . More precisely,

• • If $\mathfrak {m}=\delta (\xi - \mu \eta - \nu \sigma )$ or $\mathfrak {m} = \mathrm {p.v.} \frac {1}{\xi - \mu \eta - \nu \sigma }$ , resonant oscillations can be characterised as the stationary points of the phase $s \Phi _{\iota _1 \iota _2}$ , restricted to the singular hypersurface $\{ \xi - \mu \eta - \nu \sigma = 0 \}$ . Up to changing coordinates, we can reduce to the phase

  (2.10) $$ \begin{align} \Phi^S_{\iota_1 \iota_2}(\xi,\eta) = \langle \xi \rangle - \iota_1 \langle \eta \rangle - \iota_2 \langle \xi-\eta \rangle \end{align} $$
  (where we added the superscript S to emphasise that we consider a singular $\mathfrak {m}$ ), for which stationary points satisfy
  (2.11) $$ \begin{align} \Phi^S_{\iota_1 \iota_2}(\xi,\eta) = \partial_{\eta} \Phi^S_{\iota_1 \iota_2}(\xi,\eta) = 0. \end{align} $$
  These are the classical resonances.

• • If $\mathfrak {m}$ is smooth, we need to look at the unrestricted stationary points of the phase $s \Phi ^R_{\iota _1 \iota _2} = s(\langle \xi \rangle -\iota _1\langle \eta \rangle -\iota _2\langle \sigma \rangle )$ (where we added the superscript R to emphasise that we consider a regular $\mathfrak {m}$ ): that is,

  (2.12) $$ \begin{align} \Phi^R_{\iota_1 \iota_2}(\xi,\eta,\sigma) = \partial_{\eta} \Phi^R_{\iota_1 \iota_2}(\xi,\eta,\sigma) = \partial_{\sigma} \Phi_{\iota_1 \iota_2}^R(\xi,\eta,\sigma) = 0. \end{align} $$

This simple and natural distinction has important implications on the behaviour of equation (2.9), hence on the solution of the nonlinear equation, which we now discuss.

2.3 Regular quadratic terms and bad frequencies

Let us first look at the case when $\mathfrak {m}$ is smooth. The regular quadratic phase $\Phi ^R_{\iota _1 \iota _2}(\xi ,\eta ,\sigma ) = \langle \xi \rangle - \iota _1 \langle \eta \rangle - \iota _2 \langle \sigma \rangle $ leads to rather harmless interactions if $(\iota _1\iota _2) \neq (++)$ since in this case, there are no solutions to equation (2.12). For the $(\iota _1\iota _2)=(++)$ interaction, we have that

(2.13) $$ \begin{align} \Phi^R_{++}= \partial_{\eta} \Phi^R_{++} = \partial_{\sigma} \Phi^R_{++} = 0 \quad \Longleftrightarrow \quad (\xi,\eta,{\sigma})=(\pm\sqrt{3},0,0). \end{align} $$

This is a full resonance or coherent interaction and it is the source of many of the difficulties. Notice that this sort of interaction is generic in dimension $1$ in the presence of a potential, since in equation (2.12) there are $3$ variables and as many equations to solve. Obviously, a similar phenomenon would occur already in the case $V=0$ and a nonlinear term of the form $a(x)u^2$ .

Recall that the classical theory of quadratic/cubic one-dimensional dispersive problems revolves around trying to control weighted-type norms of the form $\|x g\|_{L^2}$ . The natural candidate in our context is then $\| \partial _{\xi } \widetilde {g}\|_{L^2_{\xi }}$ . In some cases, such as equation (KG), or the more standard examples of flat cubic NLS and cubic KG equations, one knows that a uniform-in-time bound cannot be achieved due to long-range effects already present in the corresponding flat problem. As the next best thing, one can try to establish

(2.14) $$ \begin{align} \| \partial_{\xi} \widetilde{g}\|_{L^2_{\xi}} \lesssim \langle t \rangle^{\alpha} \end{align} $$

for some small $\alpha>0$ .

Let us now explain how equation (2.14) is incompatible with the nonlinear resonance equation (2.13). Since our assumptions will always guarantee $\widetilde {g}(0) = 0$ , equation (2.14) implies

(2.15) $$ \begin{align} |\widetilde{g}(\xi)| \lesssim \langle t \rangle^{\alpha} |\xi|^{1/2}. \end{align} $$

Consider then the main $(++)$ contribution to the right-hand side of equation (2.9), namely

(2.16) $$ \begin{align} \mathcal{Q}^R_{++}(t,\xi) := \int_0^t \iint e^{is \Phi_{++}(\xi,\eta,\sigma)} \widetilde{g}(s,\eta) \widetilde{g}(s,\sigma) \mathfrak{q}(\xi,\eta,\sigma) \,d\eta\, d\sigma\,ds, \end{align} $$

where $\mathfrak {q}$ is a smooth symbol. Up to lower-order terms,

(2.17) $$ \begin{align} \partial_{\xi} \mathcal{Q}^R_{++}(t,\xi) \approx \int_0^t \iint s \frac{\xi}{\langle \xi \rangle} e^{is \Phi_{++}(\xi,\eta,\sigma)} \mathfrak{q}(\xi,\eta,\sigma) \widetilde{g}(s,\eta) \widetilde{g}(s,\sigma) \, d\eta\,d\sigma. \end{align} $$

Observe that $|s \Phi _{++} | \ll 1$ if $|\xi - \sqrt {3}| + |\eta |^2 + |\sigma |^2 \ll \langle s \rangle ^{-1}$ and that in this region there are no oscillations that can help. Thus, when $\mathfrak {q}(\pm \sqrt {3},0,0) \neq 0$ , we are led to the following heuristic lower bound: for $||\xi | - \sqrt {3}| \approx r$ ,

(2.18) $$ \begin{align} \big| \partial_{\xi} \mathcal{Q}^R_{++}(t,\xi) \big| \gtrsim \int_1^{\mathrm{min}(\frac{1}{r},t)} s \cdot \langle s \rangle^{2\alpha} \int_{|\eta|^2 + |\sigma|^2 \leq s^{-1}} |\eta|^{1/2} |\sigma|^{1/2} \,d\eta\,d\sigma \,ds \approx \mathrm{min}\Big(\frac{1}{r},t\Big)^{\frac{1}{2} + 2\alpha}. \end{align} $$

This implies that, if $\langle t \rangle ^{-1} \leq r \ll \langle t \rangle ^{-1/2}$ ,

(2.19) $$ \begin{align} {\big\| \partial_{\xi} \mathcal{Q}^R_{++} \big\|}_{L^2(|\xi-\sqrt{3}| \approx r)} \gtrsim r^{-2\alpha} \gg \langle t \rangle^{\alpha}, \end{align} $$

which is inconsistent with the bootstrap hypothesis in equation (2.14). We then need to modify the bootstrap norm to a version of $\| \partial _{\xi } \widetilde {f} \|_{L^2}$ that is localised dyadically around $\pm \sqrt {3}$ and degenerates as $|\xi | \rightarrow \sqrt {3}$ . The analysis needed to propagate such a degenerate norm turns out to be quite delicate. A phenomenon similar to the one described above was previously observed in [14, 15] in the two-dimensional (unperturbed) setting.

Note that in the heuristics in equation (2.19), one would get better bounds, consistent with equation (2.15), when $\mathfrak {q}(\pm \sqrt {3},0,0) = 0$ . For the model in equation (KG2), one has $\mathfrak {q}(\pm \sqrt {3},0,0) \neq 0$ when V is nongeneric (case (E)) and $\widetilde {a}(\pm \sqrt {3}) \neq 0$ . A true degeneracy in frequency space will then occur for these models. For equation (KG), under the assumptions (A) or (B) or (C), it is instead possible to show that $\mathfrak {q}(\xi ,0,0) = 0$ ; this is connected to the discussion at the end of Remark (3) and the possibility of simplifying the functional framework in this case.

Remark 2.1. The argument above also shows that, if $\widetilde {g}(0) \neq 0$ , then

$$ \begin{align*} \mathcal{Q}^R_{++}(t,\xi) \approx \int_0^t e^{is (\langle \xi \rangle-2)} \mathfrak{q}(\xi,0,0) \big( \widetilde{g}(s,0) \big)^2 \frac{ds}{s+1} + \cdots \end{align*} $$

so that $\mathcal {Q}^R_{++}(t,\pm \sqrt {3})$ is logarithmically diverging if $\mathfrak {q}(\pm \sqrt {3},0,0) \neq 0$ . This suggests that $\widetilde {g}$ is not uniformly bounded, which in turn implies that the solution cannot decay pointwise at the linear rate; see equation (1.12). In the case of equation (1.14) with localised $a(x)$ such that $\widehat {a}(\pm \sqrt {3}) \neq 0$ (and no cubic terms), this has been rigorously proved in [55], where the authors construct global solutions that decay in $L^{\infty }_x$ at the optimal rate of $\log t /t$ . This result was then extended in [56] to the case of any nongeneric potential with the corresponding condition $\widetilde {a}(\pm \sqrt {3}) = 0 $ .

Also note that $\widetilde {g}(0)\neq 0$ will give an asymptotic of the form $\partial _{\xi } \mathcal {Q}^R_{++}(t,\xi ) \approx |\langle \xi \rangle -2|^{-1}$ . When localised at the scale $||\xi |-\sqrt {3}| \approx 2^{\ell }$ , this gives an $L^2$ norm of size $2^{-\ell /2}$ . The functional framework that we will adopt does not quite allow for such a singularity, as this would correspond to choosing the parameter $\beta =1/2$ in the definition of the norm in equation (2.30) (this is the norm in which we will measure the derivative of our [renormalised] profile in frequency space). However, we can allow essentially any slightly less singular behaviour; this seems to suggest that a zero-energy resonance may be treated by our methods at least for long times.

2.4 Singular quadratic and cubic terms

Let us now consider the quadratic interactions in equation (2.7) that correspond to the first two terms in equation (2.8). Disregarding the irrelevant signs $\mu ,\nu $ and the coefficients $A,B$ , let us denote them by

(2.20) $$ \begin{align} \mathcal{Q}^M_{\iota_1\iota_2}(t,\xi) := \int_0^t \iint e^{is \Phi^S_{\iota_1\iota_2}(\xi,\eta,\sigma)} \widetilde{g}(s,\eta) \widetilde{g}(s,\sigma) M(\xi-\eta-\sigma) \,d\eta\, d\sigma\,ds, \quad M \in \{ \delta,\mathrm{p.v.}\}. \end{align} $$

The $\delta $ case

The case of the $\delta $ distribution corresponds to the Euclidean ( $V=0$ ) quadratic Klein-Gordon, which is not resonant (in any dimension), in the sense that for any $\xi ,\eta \in {\mathbb R}$ and $\iota _1,\iota _2\in \{+,-\}$ , equation (2.10) never vanishes, and more precisely

(2.21) $$ \begin{align} \big| \langle \xi \rangle -\iota_1 \langle \eta \rangle -\iota_2 \langle \xi -\eta \rangle \big| \gtrsim \mathrm{min}(\langle \xi \rangle, \langle \eta \rangle,\langle\xi-\eta\rangle)^{-1}.\end{align} $$

This implies that the quadratic interactions $\mathcal {Q}^{\delta }_{\iota _1\iota _2}(t,\xi )$ can be eliminated by a normal form transformation. This was first shown in the seminal work of Shatah [66] in $3$ d and crucially used in the $1$ d case in [11] and [30].

Applying a normal form transformation to equation (2.20) gives quadratic boundary terms that we disregard for simplicity and cubic terms when $\partial _t$ hits the profile $\widetilde {g}$ . From equations (2.7)–(2.8), we see that these cubic terms can be of several types depending on the various combinations of convolutions between $\delta ,\mathrm {p.v.}$ and smooth functions. Without going into the details of these (we refer the reader to Section 5), we concentrate on the simplest interaction: that is, the ‘flat’ one

(2.22) $$ \begin{align} \begin{aligned} \mathcal{C}^{S}_{\iota_1 \iota_2 \iota_3} (t,\xi) & = \iint e^{it \Phi^S_{\iota_1 \iota_2 \iota_3}(\xi,\eta,\zeta)} \mathfrak{c}^S_{\iota_1 \iota_2 \iota_3}(\xi,\eta,\zeta) \, \widetilde{g}_{\iota_1}(t,\xi-\eta) \widetilde{g}_{\iota_2}(t,\xi-\eta-\zeta) \widetilde{g}_{\iota_3}(t,\xi-\zeta) \, d\eta \, d\zeta \end{aligned} \end{align} $$

with a smooth symbol $\mathfrak {c}^S_{\iota _1 \iota _2 \iota _3}$ and phase functions

$$ \begin{align*}\Phi^S_{\iota_1 \iota_2 \iota_3} (\xi,\eta,\zeta) = \langle \xi \rangle - \iota_1 \langle \xi - \eta \rangle - \iota_2 \langle \xi - \eta -\zeta \rangle -\iota_3 \langle \xi - \zeta \rangle. \end{align*} $$

We observe that if $\{\iota _1,\iota _2,\iota _3\} \neq \{+,+,-\}$ , the equations $\partial _{\eta } \Phi ^S_{\iota _1 \iota _2 \iota _3} = \partial _{\zeta } \Phi ^S_{\iota _1 \iota _2 \iota _3} = \Phi ^S_{\iota _1 \iota _2 \iota _3} = 0$ have no solutions, and therefore the case $\{\iota _1,\iota _2,\iota _3\} = \{+,+,-\}$ is the main one. If we look at the $(+-+)$ phase for simplicity, we see that, for every fixed $\xi $ ,

$$ \begin{align*}\Phi^S_{+-+} = \partial_{\eta} \Phi^S_{+-+} = \partial_{\zeta} \Phi^S_{+-+} = 0 \quad \Longleftrightarrow \quad \eta = \zeta = 0. \end{align*} $$

This resonance is responsible for the logarithmic phase correction appearing in equation (1.13). We refer the reader to [39, 32, 24] where a similar phenomenon has been dealt with. We should point out, however, that in our case, the asymptotic behaviour in equation (1.13) is slightly harder to capture because of the degenerate weighted norm and the algebraic complications due to the treatment of potentials with general transmission and reflection coefficients.

The $\mathrm {p.v.}$ case

The main observation that allows us to treat the terms $\mathcal {Q}^{\mathrm {p.v.}}_{\iota _1\iota _2}$ is the following: when $|\xi -\eta -{\sigma }|$ is much smaller than the right-hand side of equation (2.21), these terms are similar to $\mathcal {Q}^S_{\iota _1\iota _2}$ . When instead $|\xi -\eta -{\sigma }|$ is away from zero, the symbol in equation (2.20) is actually smooth, which gives a term like the regular $\mathcal {Q}^R_{\iota _1\iota _2}$ discussed before.

2.5 The functional framework

To measure the evolution of our solutions, we need to take into account various aspects including pointwise decay, spatial localisation (which we measure through regularity on the distorted Fourier side), the coherent space-time resonance phenomenon in equation (2.13) (which dictates the choice of our $L^2$ -based norm) and long-range asymptotics. We describe our functional setting below after introducing the necessary notation.

2.5.1 Notation

To introduce our functional framework, we first define the Littlewood-Paley frequency decomposition.

Frequency decomposition. We fix a smooth even cutoff function $\varphi : {\mathbb R} \to [0,1]$ supported in $[-8/5,8/5]$ and equal to $1$ on $[-5/4,5/4]$ . Note that the choice of the number $8/5$ for the support of $\varphi $ is fairly arbitrary, and other choices are possible; however, this number is chosen to be less than $\sqrt {3}$ so that when we define the cutoffs $\chi _{\ell }$ centred around $\pm \sqrt {3}$ in equation (2.27), we can start the indexing at $0$ .

For $k \in {\mathbb Z}$ , we define $\varphi _k(x) := \varphi (2^{-k}x) - \varphi (2^{-k+1}x)$ , so that the family $(\varphi _k)_{k \in {\mathbb Z}}$ forms a partition of unity,

$$ \begin{align*} \sum_{k\in{\mathbb Z}}\varphi_k(\xi)=1, \quad \xi \neq 0. \end{align*} $$

We let

(2.23) $$ \begin{align} \varphi_{I}(x) := \sum_{k \in I \cap {\mathbb Z}}\varphi_k, \quad \text{for any} \quad I \subset {\mathbb R}, \quad \varphi_{\leq a}(x) := \varphi_{(-\infty,a]}(x), \quad \varphi_{> a}(x) = \varphi_{(a,\infty)}(x), \end{align} $$

with similar definitions for $\varphi _{< a},\varphi _{\geq a}$ . We will also denote $\varphi _{\sim k}$ a generic smooth cutoff function that is supported around $|\xi | \approx 2^k$ , for example $\varphi _{[k-2,k+2]}$ or $\varphi ^{\prime }_k$ .

We denote by $P_k$ , $k\in {\mathbb Z}$ , the Littlewood-Paley projections adapted to the regular Fourier transform:

$$ \begin{align*} \widehat{P_k f}(\xi) = \varphi_k(\xi) \widehat{f}(\xi), \quad \widehat{P_{\leq k} f}(\xi) = \varphi_{\leq k}(\xi) \widehat{f}(\xi), \quad \textrm{ and so on.} \end{align*} $$

We will avoid using, as a recurrent notation, the distorted analogue of these projections.

We also define the cutoff functions

(2.24) $$ \begin{align} \varphi_k^{(k_0)}(\xi) = \left\{ \begin{array}{ll} \varphi_k(\xi) \quad & \mbox{if} \quad k> \lfloor k_0 \rfloor, \\ \varphi_{\leq \lfloor k_0 \rfloor }(\xi) \quad & \mbox{if} \quad k= \lfloor k_0 \rfloor, \end{array} \right. \end{align} $$

and

(2.25) $$ \begin{align} \varphi_k^{[k_0,k_1]}(\xi) = \left\{ \begin{array}{ll} \varphi_k(\xi) \quad & \mbox{if} \quad k \in (\lfloor k_0 \rfloor, \lfloor k_1 \rfloor) \cap {\mathbb Z}, \\ \varphi_{\leq \lfloor k_0 \rfloor}(\xi) \quad & \mbox{if} \quad k= \lfloor k_0 \rfloor, \\ \varphi_{\geq \lfloor k_1 \rfloor}(\xi) \quad & \mbox{if} \quad k= \lfloor k_1 \rfloor. \end{array} \right. \end{align} $$

We are adopting the standard notation $\lfloor x \rfloor $ to denote the largest integer smaller than x. Note that the indexes $k_0$ and $k_1$ in equations (2.24)–(2.25) do not need to be integers. We also adopt the convention that if $k_0=k_1$ , then $\varphi _k^{[k_0,k_1]}=1$ .

We will denote by T a positive time, and always work on an interval $[0,T]$ for our bootstrap estimates; see, for example, Proposition 7.1. To decompose the time integrals such as equation (2.7) for any $t \in [0,T]$ (this is first done in equation (8.12) and then systematically throughout Sections 8–11), we will use a suitable decomposition of the indicator function $\mathbf {1}_{[0,t]}$ by fixing functions $\tau _0,\tau _1,\cdots , \tau _{L+1}: {\mathbb R} \to [0,1]$ , for an integer L with $|L-\log _2 (t+2)| < 2$ , with the properties that

(2.26) $$ \begin{align} \begin{aligned} & \sum_{n=0}^{L+1}\tau_n(s) = \mathbf{1}_{[0,t]}(s), \qquad \,\mbox{supp}\, (\tau_0) \subset [0,2], \quad \,\mbox{supp}\, (\tau_{L+1}) \subset \big[{\tfrac{1}{4}}t,t\big], \\ & \mbox{and} \quad \,\mbox{supp}\,(\tau_n) \subseteq [2^{n-1},2^{n+1}], \quad |\tau_n'({s})|\lesssim 2^{-n}, \quad \mbox{for} \quad n= 1,\dots, L. \end{aligned} \end{align} $$

In all our arguments, we also will often restrict to $n\geq 1$ , as the contribution for $n=0$ is always trivial to handle.

In light of the coherent phenomenon explained in Section 2.3, we also need cutoff functions

(2.27) $$ \begin{align} \chi_{\ell,\sqrt 3}(z) = \varphi_{\ell}(|z|-\sqrt{3}), \quad \ell \in {\mathbb Z} \cap (-\infty,0], \end{align} $$

which localise around $\pm \sqrt {3}$ at a scale $\approx 2^{\ell }$ . In analogy with equations (2.23) and (2.24), we also define

(2.28) $$ \begin{align} \chi_{\ast,\sqrt 3}(z) = \varphi_\ast(|z|-\sqrt{3}), \qquad \chi_{\ell,\sqrt 3}^{\ast}(z) = \varphi_{\ell}^{\ast}(|z|-\sqrt{3}).\end{align} $$

More notation.

For any $k \in {\mathbb Z}$ , let $k^+ := \mathrm {max}(k,0)$ and $k^- := \mathrm {min}(k,0)$ .

We denote as $\mathbf {1}_A$ the characteristic function of a set $A\subset {\mathbb R}$ and let $\mathbf {1}_\pm $ be the characteristic function of $\{\pm x> 0\}$ .

We use $a\lesssim b$ when $a \leq Cb$ for some absolute constant $C>0$ independent on a and b. $a \approx b$ means that $a\lesssim b$ and $b\lesssim a$ . When a and b are expressions depending on variables or parameters, the inequalities are assumed to hold uniformly over these.

Given $c\in {\mathbb R}$ , we will use the notation $c+$ to denote a number d larger than c but that can be chosen arbitrarily close to it. Similarly, we will use $c-$ for a number smaller than c that can be chosen arbitrarily close to it; see, for example, equation (6.9). We will sometimes use this convention also with $c=\infty $ to denote an arbitrarily large number (see, for example, equation (6.27)).

We will denote by $\mathrm {min}(x_1,x_2,\dots )$ , respectively $\mathrm {max}(x_1,x_2,\dots )$ , the minimum, respectively maximum, over the set $\{x_1,x_2,\dots \}$ . We will also denote by $\mathrm {min}_2(x_1,x_2,\dots )$ , respectively $\mathrm {max}_2(x_1,x_2,\dots )$ , the second smallest, respectively second largest, element in the set $\{x_1,x_2,\dots \}$ . We are also using $\mathrm {med}(x_1,x_2,x_3)$ for $\mathrm {max}_2(x_1,x_2,x_3)$ ; see, for example, equation (5.60) or equation (8.76).

We denote by

(2.29) $$ \begin{align} \widehat{f}=\widehat{{\mathcal{F}}}(f):= \frac{1}{\sqrt{2\pi}} \int_{\mathbb R} e^{-ix\xi} f(x) \, dx \end{align} $$

the standard Fourier transform of f.

We use the standard notation for Lebesgue $L^p$ spaces and for Sobolev spaces $W^{k,p}$ and $H^k=W^{k,2}$ .

2.5.2 Norms

For $T>0$ , we let $W_T$ be the space given by the norm

(2.30) $$ \begin{align} {\| h \|}_{W_T} := \sup_{n \geq 0} \sup_{\ell \in \mathbb{Z} \cap [\lfloor -\gamma n\rfloor,0]} {\big\| \chi_{\ell,\sqrt{3}}^{[-\gamma n,0]}(\,\cdot\,) \, \tau_n(t) \, h(t,\cdot) \mathbf{1}_{0 \leq t \leq T} \big\|}_{L^{\infty}_t L^2_{\xi}} 2^{\beta \ell} 2^{-\alpha n}, \end{align} $$

where⁹ $\tau _n$ here denotes a partition of unity as in equation (2.26) with T in place of t, and where the parameters $0 < \alpha , \beta , \gamma < \frac {1}{2}$ satisfy

(2.31) $$ \begin{align} \gamma \beta' < \alpha < \frac{\beta'}{2}, \quad \beta' \ll 1, \qquad \beta' := \frac{1}{2} - \beta, \quad \gamma' := \frac 1 2 - \gamma. \end{align} $$

$\beta '$ is a fixed constant that needs to be chosen small enough to satisfy various inequalities that we will impose in the course of the proof. Note that we automatically have $\gamma <1/2$ and that one possible way to impose all of the conditions in equation (2.31) is to choose $\alpha $ sufficiently small and

$$ \begin{align*}\beta' = 2\alpha + 2\alpha^2, \quad \gamma' = 2\alpha + \alpha^2.\end{align*} $$

Let us briefly explain the choice of the norm and parameters:

• • The norm in equation (2.30) will be used to measure our solution on the Fourier side. More precisely, we will show that ${\|\langle \xi \rangle \partial _{\xi } \widetilde {f}\|}_{W_T} \lesssim {\varepsilon }_0$ , where $\widetilde {f}$ is a renormalised version of the profile $\widetilde {g}$ in equation (1.6). As already pointed out, measuring $\partial _{\xi }$ on the Fourier side is akin to measuring a weighted norm in real space.

• • The quantity $2^{\ell }$ measures the distance from $\pm \sqrt {3}$ starting at smallest scale $2^{-{\gamma } n}$ , where $2^n \approx |t|$ and the norm is penalised by the factor $2^{\beta \ell }$ . The additional penalization of $2^{-\alpha n}$ is added globally to take into account long-range effects that are present at every frequency.

• • To make sure that localisation and derivation in the $W_T$ norm commute (under the hypothesis that $\widetilde {f}$ is uniformly bounded), one needs $\beta ' \gamma \leq \alpha $ .

• • In order to deduce from a bound on the $W_T$ norm (together with a bound on the $\widetilde {{\mathcal {F}}}^{-1}\langle \xi \rangle ^{-3/2}L^{\infty }$ ) the necessary linear decay estimate at the optimal rate of $\langle t \rangle ^{-1/2}$ , we need $\alpha + \beta \gamma < 1/4$ ; see Proposition 3.11. Since

  $$ \begin{align*}\alpha + \beta \gamma = \alpha + 1/4 - \beta{\gamma}' - \beta'/2,\end{align*} $$
  it suffices to impose $\beta ' \geq 2\alpha $ .

2.6 The main bootstrap and proof of Theorem 1.1

For $T>0$ , consider a local solution $u\in C([0,T],H^5({\mathbb R})) \cap C^1([0,T],H^4({\mathbb R}))$ of equation (KG) constructed by standard methods. Our proof is based on showing an a priori estimate for the following norm:

(2.32) $$ \begin{align} {\| u \|}_{X_T} = \sup_{t\in[0,T]} \Big[ \langle t \rangle^{-p_0} {\big\| (\sqrt{H+1}\,u,u_t)(t) \big\|}_{H^4} + \langle t \rangle^{1/2} {\| (\partial_t,\partial_x)u(t) \|}_{L^{\infty}} \Big], \qquad 0<p_0<\alpha. \end{align} $$

Under the initial smallness condition in equation (1.3), we will assume the a priori bound

(2.33) $$ \begin{align} {\|u \|}_{X_T} \leq {\varepsilon}_1, \end{align} $$

and show that this implies

(2.34) $$ \begin{align} {\| u \|}_{X_T} \leq C{\varepsilon}_{0} + C{\varepsilon}_{1}^2, \end{align} $$

for some absolute constant $C>0$ . Picking ${\varepsilon }_0$ sufficiently small and using a standard bootstrap argument with ${\varepsilon }_1 = 2 C {\varepsilon }_0$ , equation (2.34) gives global existence of solutions that are small in the space $X_\infty $ . Also, using time reversibility, we obtain solutions for all times.

The structure of the paper and the proof of Theorem 1.1, with details on how the main bootstrap equation (2.34) will be proved, are described below.

2.7 Structure of the paper and the proof of Theorem 1.1

In this subsection, we discuss the organization of the paper, describe the overall structure of the proof, and give more details about the various estimates needed to show equation (2.34), under the a priori assumption in equation (2.33).

• • Section 3 contains an exposition of the elements of the scattering theory for Schrödinger operators $H:=-\partial _x^2 + V$ on ${\mathbb R}$ , which we will need.

  After introducing the Jost functions $f_\pm $ (see equation (3.1)) and the transmission and reflection coefficients T and $R_\pm $ (see equations (3.7) and (3.13)), we define the distorted Fourier transform (dFT) as in equation (2.2) (see equation (3.21)), with the ‘distorted’ (or generalised) exponentials (or eigenfunctions) $\psi (x,\xi )$ given by equation (3.19).

  Some basic properties of the dFT are discussed in Section 3.2.1. Then the $\psi (x,\xi )$ are analysed in detail in Section 3.3 and decomposed into a singular and a regular part. The singular part behaves at spatial infinity like linear combinations of (standard) complex exponentials, while the regular part is fast decaying. This decomposition is also at the heart of the decomposition of the nonlinear spectral distribution $\mu $ defined in equation (2.6).

  In Section 3.4, we prove the first nontrivial result involving the dFT: that is, the estimate for the linear flow $e^{it\sqrt {H+1}} = e^{it\langle \widetilde {D}\rangle }$ (see the notation for Fourier multipliers in Section 3.2.2) given in equation (3.32), which involves the degenerate norm $W_T$ . This estimate shows that sharp $L^{\infty }_x$ decay (i.e., at the rate of $t^{-1/2}$ ) for the evolution $e^{it\sqrt {H+1}} h(t)$ of a (time-dependent) profile h on an interval $[0,T]$ , follows from controlling the norms

  (2.35) $$ \begin{align} \sup_{t \in [0,T]} {\big\| \langle \xi \rangle^{3/2} \widetilde{h}(t) \big\|}_{L^{\infty}_{\xi}} \leq C, \qquad {\| \langle \xi \rangle \partial_{\xi} \widetilde{h} \|}_{W_T} \leq C, \qquad \sup_{t \in[0,T]} \big( \langle t \rangle^{-p_0} {\| \langle \xi \rangle^4 \widetilde{h} \|}_{L^2} \big) \leq C, \end{align} $$
  where $W_T$ is the norm defined in equation (2.30), with the restriction on the parameters in equation (2.31), $p_0$ sufficiently small, and C an absolute constant independent of T. As it turns out, we cannot control the norms in equation (2.35) for the profile associated to the solution u and infer the bound for the $L^{\infty }_x$ norm in equation (2.32) from this. Instead, we need to take a longer route and estimate norms as in equation (2.35) for a renormalised profile, which is defined in Section 5; see equation (5.53).

• • Before moving on to the analysis of the nonlinear time evolution, we study more precisely the nonlinear spectral measure in Section 4.

  The main Proposition 4.1 describes the precise structure of the NSD $\mu $ (see equation (2.6)); for lighter notation, we omit the indexes $\iota _1,\iota _2$ here. The main goal is to decompose $\mu $ into a ‘singular’ and a ‘regular’ part.

  The singular part, denoted $\mu ^S$ , is a linear combination of $\delta $ and $\mathrm {p.v.}$ distributions, as anticipated in equation (2.8); the precise definition is given by equations (4.2)–(4.3), with formulas for the coefficients given in equations (4.4)–(4.5). Notice that these coefficients may not be smooth at $\xi =0$ (e.g., in the generic case). As is apparent, handling formulas involving these coefficients requires quite a lot of somewhat tedious bookkeeping; however, this is necessary for two main reasons: first, we need the exact expressions to calculate the final asymptotics for the solution of equation (KG); and second, we will need to check some smoothness properties for the multipliers of the trilinear terms that will appear after a normal form transformation and involve these coefficients.

  The regular part of the NSD, denoted $\mu ^R$ , is defined in equation (4.6) with equation (4.7), and it is essentially a smooth function of the three frequencies $(\xi ,\eta ,{\sigma })$ up to possible jump singularities on the axes. The mapping properties of the associated bilinear operator are established in Section 4.2, with equation (4.29) showing that it essentially behaves like multiplication by a localised function.

• • In Section 5, we begin the analysis of the time evolution by defining the profile associated to u as

  (2.36) $$ \begin{align} g := e^{it\sqrt{H+1}} (\partial_t - i\sqrt{H+1})u; \end{align} $$
  see equations (5.5) and (5.2). From the main equation (KG), we write the nonlinear evolution for $\widetilde {g}$ as in equations (5.7)–(5.8) (which is the same as the formula in equation (2.4)).

  Using the decomposition of $\mu = \mu ^S + \mu ^R$ , we would like to decompose accordingly the quadratic terms in the formula for $\partial _t\widetilde {g}$ into singular terms and regular terms. However, as briefly mentioned in equation (2.4), because of the presence of the $\mathrm {p.v.}$ term coming from $\mu ^S$ , we cannot do this decomposition directly. We instead need a further distinction within the terms containing the $\mathrm {p.v.}$ into ‘truly’ singular terms, where the $\mathrm {p.v.}$ is restricted close to its singularity, and more regular ones that are supported away from the singularity. This is the role of the cutoff $\varphi ^{\ast }$ defined in equation (5.12) and appearing in equation (5.11). The singular terms are then defined according to equations (5.10)–(5.11). The precise choice of $\varphi ^{\ast }$ is made so that, on its support, we can derive lower bounds for the oscillating phases $\Phi $ in equation (5.8).

  The main motivation for the splitting

  $$ \begin{align*}\partial_t\widetilde{g} = \mathcal{Q}^S + \mathcal{Q}^R,\end{align*} $$
  as done in Section 5.2, is that the singular quadratic terms resemble the quadratic terms that one would get for a flat ( $V=0$ ) quadratic KG equation. In particular, the oscillating phases are lower bounded on the support of $\mathcal {Q}^S$ , as established in Lemma 5.2; then we can apply a normal form transformation to recast these terms into cubic ones.

  The algebra for the normal form step is carried out in Section 5.4. Starting from the simple identity in equation (5.27), we naturally define the bilinear normal form transformation ¹⁰ T in equation (5.29), which arises from the boundary terms in the time-integration by parts. More precisely (but still omitting the various sums over the signs such as $\iota _1$ and $\iota _2$ ) we have

  (2.37) $$ \begin{align} \int_0^t\mathcal{Q}^S \,ds = \widetilde{{\mathcal{F}}}{T}(g,g)(t) - \widetilde{{\mathcal{F}}}{T}(g,g)(0) + \int_0^t B_1(s) + B_2(s) \, ds \end{align} $$
  where the bulk terms $B_1$ and $B_2$ are the expressions defined in equations (5.34) and (5.35) and are cubic in g. The only quadratic terms left are then the $\mathcal {Q}^R$ terms that include the contribution from $\mu ^R$ , and the $\mathrm {p.v.}$ part restricted outside the support of $\varphi ^{\ast }$ .

  In Section 5.5, respectively, Section 5.6, we analyse the leading order symbol $\mathfrak {b}^1$ , respectively, the lower-order symbol $\mathfrak {b}^2$ , of the bulk term $B_1$ , respectively, $B_2$ above. These are somewhat complicated expressions since they involve the symbol equation (5.11) and its variant without the cutoff $\varphi ^{\ast }$ and therefore combinations of the (nonsmooth) coefficients in equation (4.4). The leading order symbol is made by the convolution of $\delta $ and $\mathrm {p.v.}$ -type distributions; see equations (5.36)–(5.38). For the later nonlinear analysis, we need to make sure that this symbol is nice enough so that the associated trilinear operators satisfy Hölder type bounds. An important technical point then is the verification of the smoothness with respect to variable in which the convolution is performed; this is done in Section 5.5.1. In Section 5.5.2, we then calculate precisely the top order (singular $\delta $ and $\mathrm {p.v.}$ -type) contribution from $\mathfrak {b}^1$ : that is, the symbol $\mathfrak {c}^S$ in equation (5.46); the associated trilinear operator will be denoted by $\mathcal {C}^S$ . Other contributions from $\mathfrak {b}^1$ and the symbol $\mathfrak {b}^2$ are analysed in Section 5.6; the associated trilinear operator will be denoted by $\mathcal {C}^R$ . The mapping properties of these trilinear operators are analysed in Section 6.

  In the last Section 5.7, we finally arrive at the definition in equation (5.53) of the renormalised profile

  (2.38) $$ \begin{align} f = g - T(g,g). \end{align} $$
  We see that f satisfies an equation where the only quadratic terms are regular ones, and the cubic terms are those analysed in the previous subsections. Equation (5.55) for $\widetilde {f}$ is the starting point for the nonlinear analysis, and we record it here for ease of reference in a slightly simplified form (omitting the easier regular cubic terms; see equations (5.59)–(5.60))
  (2.39) $$ \begin{align} \partial_t \widetilde{f} = \mathcal{Q}^R(g,g) + \mathcal{C}^{S}(g,g,g); \end{align} $$
  see the definitions in equations (5.56)–(5.57).

  The heart of the proof of the bootstrap equation (2.34) is another bootstrap argument for the renormalised profile f involving the norms in equation (2.35) and is based on (a renormalisation of) equation (2.39). See the description of the contents of Section 7 below.

• • Section 6 contains bilinear and trilinear estimates for the various operators appearing in our problem. Here we need to analyse different types of pseudo-product operators, from the standard bilinear ones (equation (6.1)) to trilinear ones involving a $\mathrm {p.v.}$ (equation (6.5)). Bounds for general bilinear and trilinear operators of the types that appear in our proof are established in Lemmas 6.5 and 6.7, and basic criteria to check the assumptions in these lemmas are also given.

  In Section 6.3, we analyse in detail the normal form operator T and establish, in Lemma 6.10, that it satisfies Hölder-type bounds with a gain of regularity on the inputs.

  The other main results in this Section are Lemma 6.11, which gives improved Hölder-type inequalities for the smooth bilinear operator $\mathcal {Q}^R$ , and Lemma 6.13, which gives sharp Hölder-type bounds with some gain of regularity for the singular cubic terms $\mathcal {C}^S$ .

• • In Section 7, we set up the proof of the main bootstrap bound in equation (2.34). As mentioned above, these estimates will mostly involve the renormalised profile f, but we first need to relate the desired bounds for g (and u, as stated in equations (1.4)–(1.5)) to the necessary bounds on f. Here is how we proceed.

  With ${\varepsilon }_0$ as in equation (1.3), we let ${\varepsilon }_2 \gg {\varepsilon }_1 \gg {\varepsilon }_0$ . Proposition 7.1 gives an a priori bootstrap on g for the norms

  (2.40) $$ \begin{align} \sup_{t\in[0,T]} \Big[ \langle t \rangle^{-p_0} {\big\| \langle \xi \rangle^{4} \widetilde{g}(t) \big\|}_{L^{2}} + \langle t \rangle^{1/2} {\| e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D)\mathcal{W}^* g(t) \|}_{L^{\infty}} \Big], \end{align} $$
  where $\mathcal {W}^{\ast }$ is the adjoint of the wave operator defined in equation (3.24); we assume that equation (2.40) is bounded by $2{\varepsilon }_2$ and claim that it can bounded by ${\varepsilon }_2$ . Proposition 7.2 instead gives the main bootstrap for the following norms of f
  (2.41) $$ \begin{align} \sup_{t\in[0,T]} \Big[ \langle t \rangle^{-p_0} {\big\| \langle \xi \rangle^{4} \widetilde{f}(t) \big\|}_{L^{2}} + {\| \langle \xi \rangle \partial_{\xi} \widetilde{f} \|}_{W_t} + {\| \langle \xi \rangle^{3/2} \widetilde{f}(t) \|}_{L^{\infty}} \Big]; \end{align} $$
  assuming that equation (2.41) is bounded by $2{\varepsilon }_1$ , we claim that it can be bounded by ${\varepsilon }_1$ . Note that we are assuming much stronger information on f than on g.

  Section 7.1 is dedicated to showing how the a priori bound on equation (2.41) by $2{\varepsilon }_1$ can be used to close the claimed bootstrap for the norms in equation (2.40). This is not too hard to do using the relation $g = f + T(g,g)$ (see equation (2.38)), the bilinear bounds on the T operator established in Section 6.3 and the linear estimate in equation (3.32).

  Note that once we have proven a bound for equation (2.40) by ${\varepsilon }_2 = C{\varepsilon }_0$ , we can immediately deduce the Sobolev bound in equation (1.5) from equation (2.36) and the boundedness of wave operators (Theorem 3.10). The decay bound in equation (1.4) does not follow directly from the $L^{\infty }$ bound in equation (2.40) (because wave operators may be unbounded on $L^{\infty }$ ), and it is proved separately in equation (7.9). The weighted bound in equation (1.7) is proved in Lemma 7.6. Since equations (1.4)–(1.7) follow from the bound on equation (2.40), the proof of the main theorem has been reduced to proving the bootstrap Proposition 7.2. As part of the arguments needed to prove these bootstrap estimates on f, we will also establish its asymptotic behaviour; see equation (1.13) (and Section 10).

  The rest of Section 7 prepares for later analysis and the proof of Proposition 7.2. Section 7.2 contains some preliminary bounds on f that follow from the a priori bound on the norms in equation (2.41) (Lemma 7.5). Then, in Section 7.3, using equation (2.38), we rewrite the equation for f (see equation (2.39)) as

  (2.42) $$ \begin{align} \widetilde{f}(t) - \widetilde{f}(0) = \int_0^t \mathcal{Q}^R(f,f) \,ds + \int_0^t \mathcal{C}^{S}(f,f,f) \,ds + \cdots + \mathcal{R}(t), \end{align} $$
  where the ‘ $\dots $ ’ denotes other cubic and quartic terms in f and $\mathcal {R}$ s denote terms that have a higher degree of homogeneity in f and g and can be treated as remainders. We actually use expansions at different orders depending on which norm we are trying to estimate.

  To close the bootstrap for f, we then need to estimate the terms on the right-hand side of equation (2.42). Lemmas 7.8 and 7.9 give, among other things, suitable bounds on the remainders $\mathcal {R}$ , in all the norms in equation (2.41).

  In Section 7.4, for the convenience of the reader, we summarise the bounds obtained thus far and list all the bounds that are left to prove.

• • Sections 8 and 9 constitute the heart of the paper and the more technical part of the analysis. The goal of these two sections is to carry out the main parts of the estimates for the weighted $L^2$ norm in equation (2.30) of the regular quadratic terms, $\mathcal {Q}^R(f,f)$ , and of the singular cubic terms, $\mathcal {C}^S(f,f,f)$ .The desired weighted bound for $\mathcal {Q}^R(f,f)$ is equation (8.1) in Proposition 8.1. Section 8 is then entirely dedicated to proving this key bound when the interactions are restricted to the main resonant ones: that is, $(\eta ,\sigma ) = (0,0) \longrightarrow \xi = \pm \sqrt {3}$ (see the notation used in equations (8.8) and (8.2)).

  Sections 8.1–8.3 give some preliminary bounds and reductions. We first take care of frequencies $\xi $ that are very close to $\pm \sqrt {3}$ and reduce the desired bound to showing equation (8.35) with equation (8.36) for the localised operator¹¹ $I(t,\xi )$ defined in equation (8.32); these reductions are summarised in Lemma 8.4.

  Note that the estimate in equation (8.32) involves localisation in the size of the input variables $|\eta |$ and $|{\sigma }|$ , in the distance $||\xi |-\sqrt {3}|$ , in the size of the oscillating phase $|\Phi |$ , and in the integrated time s, at dyadic scales with respective parameters $k_1,k_2,\ell ,p$ and m. These localisations allow us to distinguish various cases and to exploit the oscillations efficiently in either frequency space or time depending on the relative size of the quantities involved. The estimates are split into four main regions, as described in equation (8.48), and treating each of these regions occupies one of the Sections 8.4–8.7.

  We remark that a useful quantity is the one defined in equation (8.17), which incorporates some improved decay properties of the solution (for small frequencies).

• • In Section 9, we estimate the weighted $L^2$ norm for the singular cubic terms $\mathcal {C}^S(f,f,f)$ of the form in equation (2.22) (see equation (5.57) with equation (5.46) for the precise definition), focusing on the case of the main resonant interactions $\pm (\sqrt {3},\sqrt {3},\sqrt {3}) \rightarrow \pm \sqrt {3}$ . In particular, we achieve the main step in the proof of Proposition 9.1, which deals with the interactions of the type $(+-+)$ , where the signs correspond to the signs of the oscillating factors in the cubic phases in equation (5.57).

  Section 9.2 treats the terms that involve a $\delta $ factor, while Section 9.3 treats those with a $\mathrm {p.v.}$ (recall the form of the cubic symbols in equation (5.46)). Once again, we need to distinguish various cases depending on the distance of the input and output variables from the bad frequency $\sqrt {3}$ , relative to time and the size of their differences (see, for example, the dyadic localisations in equation (9.16)).

• • With Sections 8 and 9, we have taken care of estimating the weighted norm for the leading-order terms on the right-hand side of equation (2.42) in the case of the main resonant interactions. All of the other nonresonant interactions are estimated in Section 11.

  Section 10 contains the main part of the proof for the control of the Fourier- $L^{\infty }$ norm in equation (2.41): that is, the proof of Proposition 10.1, which gives asymptotics for the singular cubic terms $\mathcal {C}^S$ (see equation (10.2), where the Hamiltonian function is given in equation (10.27)). From this, we can then derive an asymptotic ODE for $\widetilde {f}$ and thus the asymptotic behaviour of the solution as in equation (10.4) (see equation (1.13)).

  Section 10.1 provides first a formal computation for the asymptotics, based on the stationary phase lemma. Section 10.2 utilises these computations to give the exact structure of the long-range asymptotics and the form of the Hamiltonian H appearing in the statement of Proposition 10.1). Rigorous bounds are then proved in equation (10.3).

• • Section 11 contains the estimates needed to control all the contributions from the nonlinear terms on the right-hand side of equation (2.42) that have not been dealt with in Sections 7–10, since they are lower-order compared to the main ones. We refer the reader to the first paragraph of Section 11 for a list of the estimates that are carried out there and the details on how they complete the proofs of the main propositions stated in the previous sections.

  The estimates of Section 11 complete the bootstrap on the norm in equation (2.41).

• • Finally, Appendix A contains a verification of the spectral assumptions needed to apply our results to the double sine-Gordon model in equation (1.22) and obtain Corollary 1.6.

3 Spectral theory and distorted Fourier transform in $1$ d

We develop in this section the spectral and scattering theory of

$$ \begin{align*}H = - \partial_x^2 + V, \end{align*} $$

assuming that $V \in \mathcal {S}$ and that H only has a continuous spectrum. We state the results that are needed for the nonlinear problem that interests us here and sketch the important proofs.

This theory is due to Weyl, Kodaira and Titchmarsh (who also considered more general Sturm-Liouville problems). Complete expositions can be found in [18] and [77]; we mention in particular Yafaev [73, Chapter 5], where the operator H is considered and direct proofs are given.

3.1 Linear scattering theory

3.1.1 Jost solutions

Define $f_{+}(x,\xi )$ and $f_-(x,\xi )$ by the requirements that

(3.1) $$ \begin{align} (- \partial_x^2 + V) f_{\pm} = \xi^2 f_{\pm}, \quad \mbox{for all}\ x,\xi\in{\mathbb R}, \quad \mbox{and} \quad \left\{ \begin{array}{ll} \lim_{x\rightarrow \infty} |f_{+}(x,\xi) - e^{ix\xi}| = 0, \\ \lim_{x\rightarrow -\infty} |f_{-}(x,\xi) - e^{- ix\xi}| = 0. \end{array} \right. \end{align} $$

Define further

(3.2) $$ \begin{align} m_{+}(x,\xi) = e^{-i\xi x} f_{+}(x,\xi) \quad \mbox{and} \quad m_{-}(x,\xi) = e^{i\xi x} f_{-}(x,\xi), \end{align} $$

so that $m_{\pm }$ is a solution of

(3.3) $$ \begin{align} \partial_x^2 m_{\pm} \pm 2i\xi \partial_x m_{\pm} = Vm_{\pm}, \qquad m_\pm(x,\xi) \to 1 \;\mbox{as}\ x \to \pm \infty. \end{align} $$

The functions $m_\pm $ satisfy symbol type bounds for $\pm x>0$ , as stated in the following lemma.

Lemma 3.1. For all nonnegative integers $\alpha , \beta , N$ ,

(3.4) $$ \begin{align} & \big| \partial_x^{\alpha} \partial_{\xi}^{\beta} (m_{\pm}(x,\xi) - 1) \big| \lesssim \langle x \rangle^{-N} \langle \xi \rangle^{-1-\beta}, \quad \pm x \geq -1, \end{align} $$

(3.5) $$ \begin{align} & \big| \partial_x^{\alpha} \partial_{\xi}^{\beta} (m_{\pm}(x,\xi) - 1) \big| \lesssim \langle x \rangle^{1+\beta}\langle \xi \rangle^{-1-\beta}, \quad \pm x \leq 1.\quad \end{align} $$

The estimates in equations (3.4)–(3.5) can be obtained from the integral form of equation (3.3)

(3.6) $$ \begin{align} & m_+(x,\xi) = 1 + \int_x^{\infty} D_{\xi}(y-x) V(y) m_+(y,\xi) \,dy, \nonumber\\ & m_-(x,\xi) = 1 + \int_{-\infty}^x D_{\xi}(x-y) V(y) m_-(y,\xi) \,dy, \end{align} $$

where

$$ \begin{align*}D_{\xi}(z) = \frac{e^{2i\xi z} - 1}{2i\xi}. \end{align*} $$

Since the proof is fairly standard, we skip the details and refer the reader to [12, Appendix A].

3.1.2 Transmission and reflection coefficients

A classical reference for the formulas that we recall here is [10] (see also [76], [73], for example). Denote as $T(\xi )$ and $R_{\pm }(\xi )$ , respectively, the transmission and reflection coefficients associated to the potential V. These coefficients are such that

(3.7) $$ \begin{align} &f_+ (x,\xi) = \frac{1}{T_+(\xi)} f_-(x,-\xi) + \frac{R_-(\xi)}{T_+(\xi)} f_-(x,\xi), \nonumber\\ &f_- (x,\xi) = \frac{1}{T_-(\xi)} f_+(x,-\xi) + \frac{R_+(\xi)}{T_-(\xi)} f_+(x,\xi), \end{align} $$

or, equivalently,

$$ \begin{align*} &f_+ (x,\xi) \sim \frac{1}{T_+(\xi)} e^{i\xi x} + \frac{R_-(\xi)}{T_+(\xi)} e^{-i\xi x} \quad \mbox{as}\ x \to - \infty, \\ &f_- (x,\xi) \sim \frac{1}{T_-(\xi)} e^{-i\xi x} + \frac{R_+(\xi)}{T_-(\xi)} e^{i\xi x} \quad \mbox{as}\ x \to \infty. \end{align*} $$

In the equalities above, $T_+$ and $T_-$ do a priori differ; however, since the Wronskian

(3.8) $$ \begin{align} W(\xi) := W(f_+(\xi),f_-(\xi)), \qquad W(f,g) = f'g - fg' \end{align} $$

is independent of the point x, where it is computed for solutions of equation (3.1), one sees (taking $x\rightarrow \pm \infty )$ that $T_+ = T_- = T$ and

(3.9) $$ \begin{align} W(\xi) = \frac{2i\xi}{T(\xi)}. \end{align} $$

Since $\overline {f_{\pm }(x,\xi )} = f_{\pm }(x,-\xi )$ , we obtain furthermore that

(3.10) $$ \begin{align} \overline{T(\xi)} = T(-\xi) \qquad \mbox{and} \qquad \overline{R_{\pm}(\xi)} = R_{\pm}(-\xi). \end{align} $$

Finally, computing $W(f_{+}(\xi ),f_-(\xi ))$ , $W(f_{+}(\xi ),f_+(-\xi ))$ , $W(f_{-}(\xi ),f_-(-\xi ))$ at $x = \pm \infty $ gives

(3.11) $$ \begin{align} & |R_{\pm}(\xi)|^2 + |T(\xi)|^2 = 1, \qquad \mbox{and} \qquad T(\xi)\overline{R_-(\xi)} + R_+(\xi)\overline{T(\xi)} = 0. \end{align} $$

As a consequence, the scattering matrix associated to the potential V is unitary:

(3.12) $$ \begin{align} S(\xi) := \left( \begin{array}{cc} T(\xi) & R_+(\xi) \\ R_-(\xi) & T(\xi) \end{array} \right), \qquad S^{-1}(\xi) := \left( \begin{array}{cc} \overline{T(\xi)} & \overline{R_-(\xi)} \\ \overline{R_+(\xi)} & \overline{T(\xi)} \end{array} \right). \end{align} $$

Starting from the integral formula in equation (3.6) giving $m_{\pm }$ , letting $x \to \mp \infty $ and relating it to the definition of T and $R_{\pm }$ gives

(3.13) $$ \begin{align} \begin{aligned} &T(\xi) = \frac{2i\xi}{2i\xi - \int V(x) m_{\pm} (x,\xi)\,dx},\\[6pt] & R_{\pm}(\xi) = \frac{\int e^{\mp 2i\xi x} V(x) m_{\mp}(x,\xi)\,dx}{2i\xi - \int V(x) m_{\pm} (x,\xi)\,dx}. \end{aligned} \end{align} $$

These formulas are only valid for $\xi \neq 0$ a priori. But a moment of reflection shows that T and $R_{\pm }$ can be extended to be smooth functions on the whole real line. Combining these formulas with Lemma 3.1 gives the following lemma.

Lemma 3.2. Let T and $R_\pm $ be defined as in equation (3.13). Then under our assumptions on V, for any $\beta $ and N, we have

(3.14) $$ \begin{align} |\partial_{\xi}^{\beta} [T(\xi) - 1]| \lesssim \langle \xi \rangle^{-1-\beta}, \qquad |\partial_{\xi}^{\beta} R_{\pm}(\xi) | \lesssim \langle \xi \rangle^{-N}.\end{align} $$

3.1.3 Generic and exceptional potentials

We call the potential V

• • generic if $\displaystyle \int V(x) m_{\pm } (x,0)\,dx \neq 0$

• • exceptional if $\displaystyle \int V(x) m_{\pm } (x,0)\,dx = 0$

• • very exceptional if $\displaystyle \int V(x) m_{\pm } (x,0)\,dx = \int x V(x) m_{\pm } (x,0)\,dx = 0$

Lemma 3.3. The following four assertions are equivalent:

1. (i) V is generic.

2. (ii) $\displaystyle T(0) = 0, R_{\pm }(0) = -1$ .

3. (iii) $W(0) \neq 0$ .

4. (iv) The potential V does not have a resonance at $\xi =0$ ; in other words, there does not exist a bounded nontrivial solution in the kernel of $-\partial _x^2 + V$ .

Checking the equivalence of these assertions is easy based on the formulas in equation (3.13).

Proposition 3.4 (Low-energy scattering)

If V is generic, there exists $\alpha \in i \mathbb {R}$ such that

(3.15) $$ \begin{align} T(\xi) = \alpha \xi + O(\xi^2). \end{align} $$

If V is exceptional, let

$$ \begin{align*}a := f_+(-\infty,0) \in \mathbb{R} \setminus \{ 0 \}. \end{align*} $$

Then

(3.16) $$ \begin{align} T(0) = \frac{2a}{1+a^2}, \qquad R_+(0) = \frac{1 - a^2}{1+ a^2}, \qquad \mbox{and} \qquad R_-(0) = \frac{a^2-1}{1+ a^2}. \end{align} $$

Proof. In the generic case, observe that

$$ \begin{align*}T(\xi) = \frac{2i}{-\int V(x) m_{\pm}(x,0)\,dx} \xi + O(\xi^2), \end{align*} $$

hence the desired result since $m_{\pm }(\cdot ,0)$ is real-valued.

We now turn to the exceptional case. Denoting

$$ \begin{align*}b = \int V(x) \partial_{\xi} m_{\pm}(x,0) \,dx, \quad \mbox{and} \quad c_{\pm} = \int V(x) x m_{\pm}(x,0)\,dx, \end{align*} $$

$T(0)$ and $R_{\pm }(0)$ can, thanks to equation (3.13), be expressed as

(3.17) $$ \begin{align} T(0) = \frac{2i}{2i-b}, \qquad R_{\pm}(0) = \frac{b \mp 2ic_{\mp}}{2i-b}. \end{align} $$

It remains to determine the values of b and $c_{\pm }$ . In order to determine $c_{+}$ , recall the integral equation (3.6) satisfied by $m_+$ , and let $\xi \to 0$ and $x \to -\infty $ in that formula. Taking advantage of the condition $\int V(y) m_+(y,0)\,dy=0$ , we observe that

(3.18) $$ \begin{align} a = m_+(-\infty,0) = 1 + \int_{-\infty}^{\infty} y V(y) m_+(y,0)\,dy = 1 + c_+. \end{align} $$

Similarly, we find $\frac {1}{a} = 1 - c_-$ .

Turning to b, we first claim that it is purely imaginary. Indeed, differentiating equation (3.3), setting $\xi = 0$ and taking the real part, we obtain that

$$ \begin{align*}\mathfrak{Re} \left[ (\partial_x^2 - V) \partial_{\xi} m_+(x,0) \right] = 0. \end{align*} $$

Since $\partial _{\xi } m_+(x,0) \to 0$ as $x \to \infty $ , we deduce that $\mathfrak {Re} \partial _{\xi } m_+ = 0$ . Using this fact and plugging the formulas in equation (3.17) into the identity $|T(0)|^2 + |R_{-}(0)|^2 = 1$ , we find

$$ \begin{align*}b = \left(2 - a - \frac{1}{a}\right)i. \end{align*} $$

The formulas giving b and c in terms of a now lead to the desired formulas for $T(0)$ and $R(0)$ .

Remark 3.5. From equation (3.18), we see that in the very exceptional case (see the definition before Lemma 3.3), we have $a=1$ , and therefore $T(0) = 1$ and $R_\pm (0) = 0$ . Also, notice that $a=1$ in the exceptional case when the zero-energy resonance is even. When instead it is odd, we have $a=-1$ , and therefore $T(0)=-1$ and $R_\pm (0)=0$ .

3.1.4 Resolvent and spectral projection

If $\mathfrak {Im} \lambda \neq 0$ , the resolvent of H is defined by $R_V(\lambda ) = (H - \lambda ^{-1})^{-1}$ .

Assuming first that $\mathfrak {Re}(\lambda )>0$ and $\mathfrak {Im} \lambda> 0$ , we let $\xi + i \eta = \sqrt {\lambda }$ , with $\xi ,\eta>0$ . Then $f_{\pm }(\xi + i \eta )$ can be defined through natural extensions of the above definition, and the resolvent $R_V(\lambda )$ is given by the kernel

$$ \begin{align*}R_V(\lambda)(x,y) = -\frac{1}{W(\xi + i \eta)} [f_+(\mathrm{max}(x,y),\xi+i\eta) f_-(\mathrm{min}(x,y),\xi+i\eta)]. \end{align*} $$

Letting $\mathfrak {Im} \lambda \to 0$ (and still with the convention that $\xi>0$ ),

$$ \begin{align*}R_V(\xi^2 + i0) = - \frac{1}{W(\xi)} f_+(\mathrm{max}(x,y),\xi) f_-(\mathrm{min}(x,y),\xi). \end{align*} $$

Similarly,

$$ \begin{align*}R_V(\xi^2 - i0) = - \frac{1}{W(-\xi)} f_+(\mathrm{max}(x,y),-\xi) f_-(\mathrm{min}(x,y),-\xi). \end{align*} $$

By Stone’s formula, the spectral measure associated to H is, for $\lambda>0$ ,

$$ \begin{align*}E(d\lambda) = \frac{1}{2\pi i} [R_V(\lambda + i 0) - R_V(\lambda - i0)] d\lambda. \end{align*} $$

The formulas above for $R_V(\lambda \pm i 0)$ lead to

$$ \begin{align*}E(d\lambda)(x,y) = \frac{1}{4\pi} \frac{|T(\sqrt \lambda)|^2}{\sqrt \lambda} [f_-(x,\sqrt \lambda) \overline{f_-(y,\sqrt \lambda)} + f_+(x,\sqrt \lambda) \overline{f_+(y,\sqrt \lambda)}] d\lambda. \end{align*} $$

3.2 Distorted Fourier transform

3.2.1 Definition and first properties

We adopt the following normalisation for the (flat) Fourier transform on the line

$$ \begin{align*}\widehat{\mathcal{F}} \phi (\xi) = \widehat{\phi}(\xi) = \frac{1}{\sqrt{2\pi}} \int e^{-i\xi x} \phi(x) \, dx. \end{align*} $$

As is well-known,

$$ \begin{align*}\widehat{\mathcal{F}}^{-1} \phi = \frac{1}{\sqrt{2\pi}} \int e^{i\xi x} \phi(\xi) \, d\xi= \widehat{\mathcal{F}}^* \phi, \end{align*} $$

and $\mathcal {F}$ is an isometry on $L^2(\mathbb {R})$ .

We now define the wave functions associated to H:

(3.19) $$ \begin{align} \psi(x,\xi) := \frac{1}{\sqrt{2\pi}} \left\{ \begin{array}{ll} T(\xi) f_+(x,\xi) & \mbox{for}\ \xi \geq 0 \\ \\ T(-\xi) f_-(x,-\xi) & \mbox{for}\ \xi < 0. \end{array} \right. \end{align} $$

Once again, this definition a priori only makes sense for $\xi \neq 0$ , but it can be extended by continuity to $\xi =0$ . It follows from the estimates on T and $f_{\pm }$ that for any $\alpha $ , $\beta $ and $\xi \neq 0$ ,

(3.20) $$ \begin{align} |\partial_x^{\alpha} \partial_{\xi}^{\beta} \psi (x,\xi)| \lesssim \langle x \rangle^{\beta} \langle \xi \rangle^{\alpha}. \end{align} $$

The distorted Fourier transform is then defined by

(3.21) $$ \begin{align} \widetilde{\mathcal{F}} \phi(\xi) = \widetilde {\phi}(\xi) = \int_{\mathbb{R}} \overline{\psi(x,\xi)} \phi(x)\,dx. \end{align} $$

Proposition 3.6 (Mapping properties of the distorted Fourier transform)

With $\widetilde {{\mathcal {F}}}$ defined in equation (3.21),

1. (i) $\widetilde {\mathcal {F}}$ is a unitary operator from $L^2$ onto $L^2$ . In particular, its inverse is

   $$ \begin{align*}\widetilde{\mathcal{F}}^{-1} \phi(x) = {\widetilde{\mathcal{F}}}^{\ast} \phi(x) = \int_{\mathbb R} \psi(x,\xi) \phi(\xi)\,d\xi. \end{align*} $$

2. (ii) $\widetilde {\mathcal {F}}$ maps $L^1(\mathbb {R})$ to functions in $L^{\infty }(\mathbb {R})$ that are continuous at every point except $0$ and converge to $0$ at $\pm \infty $ .

3. (iii) $\widetilde {\mathcal {F}}$ maps the Sobolev space $H^s(\mathbb {R})$ onto the weighted space $L^2(\langle \xi \rangle ^{2s} \,d\xi )$ .

4. (iv) If $\widetilde {f}$ is continuous at zero, then for any integer $s \geq 0$ ,

   $$ \begin{align*} \|\langle \xi \rangle^s \partial_{\xi} \widetilde{f} \|_{L^2} \lesssim \| f \|_{H^s} + \| \langle x \rangle f \|_{H^s}. \end{align*} $$

Proof. As in other parts of this section, we follow Yafaev [73, Chap. 5].

$(i)$ To see that $\mathcal {F}$ is an isometry, we use the Stone formula derived in the previous subsection to write, for any functions $g,h \in L^2$ (recall that E is the spectral measure associated to H),

$$ \begin{align*} \langle g, h \rangle & = \int E (d\lambda) g \, \overline{h} \\ & = \frac{1}{4\pi} \iiint \frac{|T(\sqrt{\lambda})|^2}{\sqrt \lambda} \left[ f_-(x, \sqrt{\lambda}) \overline{f_-(y,\sqrt \lambda)} + f_+(x,\sqrt \lambda) \overline{f_+(y,\sqrt \lambda)} \right] g(y) \overline{h(x)} \,dy \,dx \,d\lambda. \end{align*} $$

Changing the integration variable to $\xi = \sqrt {\lambda }$ , this is

$$ \begin{align*} \frac{1}{2\pi} \int_{\xi \in {\mathbb R}_+} \int_{{\mathbb R}_x} \int_{{\mathbb R}_y} |T(\xi)|^2 \left[ f_-(x,\xi) \overline{f_-(y,\xi)} + f_+(x,\xi) \overline{f_+(y,\xi)} \right] g(y) \overline{h(x)} \,dy \,dx \, d\xi = \langle \widetilde{g} \,,\, \widetilde{h} \rangle. \end{align*} $$

To see that the range of $\widetilde {\mathcal {F}}$ is $L^2$ , we argue by contradiction. If this was not the case, there would exist $g \in L^2$ not zero such that, for any $f \in \mathcal {C}^{\infty }_0$ and any $0<R_0<R_1$ ,

$$ \begin{align*}\langle g \,,\,\widetilde{\mathcal{F}} E([R_0^2,R_1^2]) f \rangle = 0.\end{align*} $$

Using the spectral theorem representation and the intertwining identity $\widetilde {{\mathcal {F}}} H = k^2 \widetilde {{\mathcal {F}}}$ , we deduce that

$$ \begin{align*}\widetilde{\mathcal{F}} \left[ E([R_0^2,R_1^2]) f \right] (\xi) = \big( \mathbf{1}_{[-R_1,-R_0]}(\xi) + \mathbf{1}_{[R_0,R_1]}(\xi) \big) \widetilde{f}(\xi). \end{align*} $$

Therefore, for any $f \in \mathcal {C}^{\infty }_0$ ,

$$ \begin{align*} 0 = \langle g \,,\,\widetilde{\mathcal{F}} E([R_0^2,R_1^2]) f \rangle = \int_{R_0}^{R_1} \int \big[ \psi(x,\xi) g(\xi) + \psi(x,-\xi) g(-\xi) \big] \overline{f(x)} \,dx \,d\xi. \end{align*} $$

This implies that

$$ \begin{align*}\int_{R_0}^{R_1} \big[ \psi(x,\xi)g(\xi) + \psi(x,-\xi) g(-\xi) \big] \,d\xi = 0. \end{align*} $$

Since $R_0,R_1$ are arbitrary, we deduce $ \psi (x,\xi )g(\xi ) + \psi (x,-\xi ) g(-\xi ) = 0, $ a.e. $\xi $ . Since $x \mapsto \psi (x,\xi )$ and $x \mapsto \psi (x,-\xi )$ are independent functions (nonvanishing Wronskian), this implies $g = 0$ .

$(ii)$ is a consequence of equation (3.20) and the Riemann-Lebesgue lemma.

$(iii)$ is a consequence of Theorem 3.10 below.

$(iv)$ Focusing on $x>0$ (through a smooth cutoff function $\chi _+$ ) and $\xi>0$ , the distorted Fourier transform can be written as a pseudodifferential operator

$$ \begin{align*}\widetilde{\mathcal{F}} \left[ \chi_+ f \right] (\xi) = \int a(x,\xi) e^{-ix\xi} f(x)\,dx \end{align*} $$

with symbol

$$ \begin{align*}a(x,\xi) = \frac{1}{\sqrt{2\pi}} \overline{T(\xi) m_+(x,\xi)}. \end{align*} $$

Taking a derivative in $\xi $ ,

$$ \begin{align*}\partial_{\xi} \widetilde{\mathcal{F}} \left[ \chi_+ f \right] (\xi) = \int \partial_{\xi} a(x,\xi) e^{-ix\xi} f(x)\,dx + \int a(x,\xi) e^{-ix\xi} (-ix) f(x)\,dx. \end{align*} $$

From the bounds in equations (3.4) and (3.14), along with a classical theorem on the boundedness of pseudo-differential operators, the statement $(iv)$ follows for $s = 0$ . If $s\in \mathbb {N}$ , it suffices to multiply the above by $\langle \xi \rangle ^s$ and integrate by parts in x in the integrals. We only discussed the case of positive frequencies, but the case of negative frequencies is identical. It remains to check that no singularity arises at $\xi =0$ when applying $\xi>0$ , which is ensured by the assumption that $\widetilde {f}$ is continuous.

Lemma 3.7. If the potential V is even, then the distorted Fourier transform preserves evenness and oddness.

Proof. Observe that when V is even, we have the relation $f_+(x,\xi ) = f_-(-x,\xi )$ between the generalised eigenfunctions in equation (3.1), by uniqueness of solutions for the ODE. From this and the definition in equation (3.19), we see that $\psi (x,\xi )=\psi (-x,-\xi )$ . The preservation of parity for the distorted Fourier transform then follows directly from the definition in equation (3.21).

As appears in Proposition 3.6, one of the main differences between the mapping properties of $\widehat {\mathcal {F}}$ and $\widetilde {\mathcal {F}}$ has to do with zero frequency. Since the zero frequency furthermore plays a key role in the nonlinear analysis developed in the present paper, we investigate this question a bit more.

• • If V is generic, then $\psi (x,0) = 0$ and $\widetilde {f}(0) = 0$ if $f \in L^1$ . Furthermore, assuming better integrability properties at $\infty $ ,

  (3.22) $$ \begin{align} \begin{aligned} & \mbox{if}\ \xi> 0, \qquad \widetilde{f}(\xi) = - \frac{\alpha\xi}{\sqrt{2\pi}} \int f(x) f_+(x,0)\,dx +O(\xi^2) \\ & \mbox{if}\ \xi < 0, \qquad \widetilde{f}(\xi) = \frac{\alpha\xi}{\sqrt{2\pi}} \int f(x) f_-(x,0)\,dx+O(\xi^2), \end{aligned} \end{align} $$
  where $\alpha $ was defined in equation (3.15). Thus, $\widetilde {f}$ is typically continuous but not continuously differentiable at zero.

• • If V is exceptional, then

  $$\begin{align*}\sqrt{2\pi} \, \psi(x,0+) = \frac{2a}{1+a^2} f_+(x,0), \qquad \mbox{and} \qquad \sqrt{2\pi} \, \psi(x,0-) = \frac{1}{a} \psi(x,0+), \end{align*}$$
  where a was defined in Proposition 3.4. Therefore, if $f \in L^1$ ,
  (3.23) $$ \begin{align} \begin{aligned} \widetilde{f}(0+) = \frac{2a}{1+a^2} \frac{1}{\sqrt{2\pi}} \int f(x) f_+(x,0) \,dx \qquad \mbox{and} \qquad \widetilde{f}(0-) = \frac{1}{a} \widetilde{f}(0+). \end{aligned} \end{align} $$
  As a consequence, $\widetilde {f}$ is continuous if $a=1$ but might not be otherwise.

3.2.2 Fourier multipliers

Given m a function on the real line, the flat and distorted Fourier multipliers are defined by

$$ \begin{align*} & m(D) = \widehat{\mathcal F}^{-1} m(\xi) \widehat{\mathcal F} \\ & m(\widetilde D) = \widetilde{\mathcal F}^{-1} m(\xi) \widetilde{\mathcal F}. \end{align*} $$

Denoting $H_0$ and H for the flat and perturbed Schrödinger operators

$$ \begin{align*}H_0 = - \partial_x^2, \qquad H = - \partial_x^2 + V, \end{align*} $$

these operators are diagonalised by $\widehat {\mathcal {F}}$ and $\widetilde {\mathcal {F}}$ , giving the functional calculus

$$ \begin{align*} & f(H_0) = \widehat{\mathcal{F}}^{-1} f(\xi^2)\widehat{\mathcal{F}}\\ & f(H) = \widetilde{\mathcal{F}}^{-1} f(\xi^2) \widetilde{\mathcal{F}}. \end{align*} $$

In particular,

$$ \begin{align*}e^{it \sqrt{1 + H_0}} = e^{it \langle D \rangle} \qquad \mbox{and} \qquad e^{it \sqrt{1 + H}} = e^{it \langle \widetilde D \rangle}. \end{align*} $$

Lemma 3.8. Assume that f is real-valued and that m is even and real-valued. Then $m(\widetilde {D}) f$ is real-valued.

Proof. This follows from the simple observation that f is real-valued if and only if

$$ \begin{align*}\left\{ \begin{array}{ll} T(\xi) \widetilde{f}(\xi) = - T(-\xi) R_+(\xi) \overline{\widetilde{f}(\xi)} + \overline{\widetilde{f}(-\xi)} &\mbox{for}\ \xi>0 \\[4pt] T(-\xi) \widetilde{f}(\xi) = - T(\xi) R_-(-\xi) \overline{\widetilde{f}(\xi)} + \overline{\widetilde{f}(-\xi)} & \mbox{for}\ \xi<0. \end{array} \right. \end{align*} $$

3.2.3 The wave operator

The wave operator $\mathcal {W}$ is given by

$$ \begin{align*}\mathcal{W} = \operatorname{s-lim}_{t\to \infty} e^{itH} e^{-itH_0}. \end{align*} $$

Proposition 3.9. The wave operator is unitary on $L^2$ and given by

$$ \begin{align*}\mathcal{W} = \widetilde{\mathcal{F}}^{-1} \widehat{\mathcal{F}}. \end{align*} $$

As a consequence,

(3.24) $$ \begin{align} \mathcal{W}^{-1} = \mathcal{W}^* = \widehat{\mathcal{F}}^{-1} \widetilde{\mathcal{F}}, \end{align} $$

and the wave operator intertwines H and $H_0$ :

$$ \begin{align*}f(H) = \mathcal{W} f(H_0) \mathcal{W}^*. \end{align*} $$

Proof. In order to prove the desired formula for the wave operator, it suffices to check that, for any $f \in L^2$ ,

$$ \begin{align*}\left\| e^{itH} e^{-itH_0} f - \widetilde{\mathcal{F}}^{-1} \widehat{\mathcal{F}} f \right\|_2 \rightarrow 0. \end{align*} $$

By the functional calculus, this is equivalent to

$$ \begin{align*}\left\| \widehat{\mathcal{F}}^{-1} e^{it \xi^2} f - \widetilde{\mathcal{F}}^{-1} e^{it \xi^2} f \right\|_2 \rightarrow 0. \end{align*} $$

By unitarity, it suffices to check the above for a dense subset of f, and thus we might assume $f \in \mathcal {C}^{\infty }_0$ . By symmetry between positive and negative frequencies, we can furthermore assume that $\operatorname {Supp} f \subset (0,\infty )$ . Therefore, matters reduce to proving that

$$ \begin{align*}\left\| \int_0^{\infty} e^{i(x\xi + t\xi^2)} (1- T(\xi) m_+(x,\xi)) f(\xi)\,d\xi \right\|_{L^2_x} \rightarrow 0. \end{align*} $$

To see that the above is true, we split the function whose $L^2$ norm we want to estimate into

$$ \begin{align*} & \int_0^{\infty} e^{i(x\xi + t\xi^2)} \mathbf{1}_+(x) (1-T(\xi) m_+(x,\xi)) f(\xi)\,d\xi - \int_0^{\infty} e^{i(-x\xi + t\xi^2)} \mathbf{1}_-(x) R_-(\xi) m_-(x,\xi) f(\xi)\,d\xi \\ & \qquad + \int_0^{\infty} e^{i(x\xi + t\xi^2)} \mathbf{1}_-(x) (1- m_-(x,\xi)) f(\xi)\,d\xi \\ & = I + II + III. \end{align*} $$

The terms I and $II$ have nonstationary phases, from which it follows that they converge to zero as $t \to \infty $ . As for $III$ , it goes to zero pointwise by the stationary phase lemma and is uniformly (in t) bounded by a decaying function of x, as follows from the estimates on $m_-$ ; therefore, it goes to zero in $L^2$ by the dominated convergence theorem.

Finally, the following theorem gives the boundedness of the wave operators on Sobolev spaces.

Theorem 3.10 (Weder [75])

$\mathcal {W}$ and $\mathcal {W}^*$ extend to bounded operators on $W^{k,p}({\mathbb R})$ for any k and $1 < p < \infty $ . Furthermore, in the exceptional case, if $f_+(-\infty ,0) = 1$ , this remains true if $p=1$ or $\infty $ .

3.2.4 What if discrete spectrum is present?

The above discussion relied on the assumption that

$$ \begin{align*}L^2_{ac} = P_{ac} L^2 = L^2, \end{align*} $$

where we denoted $P_{ac}$ the projector on the absolutely continuous spectrum of H. Since we are assuming $V \in \mathcal {S}$ , we can exclude singularly continuous spectrum as well as embedded discrete spectrum, but there might be a finite number of negative eigenvalues $\lambda _N < \dots < \lambda _1 < 0$ with corresponding eigenfunctions $\phi _1,\dots ,\phi _N$ ; see [10]. Then all the statements made above require small adaptations. Indeed, $\widetilde {\mathcal {F}}$ is zero on $\phi _j$ for all j and unitary from $L^2_{ac}$ to $L^2$ . Thus,

$$ \begin{align*} \widetilde{{\mathcal{F}}} \widetilde{{\mathcal{F}}}^{-1} = \operatorname{Id}_{L^2} \qquad \mbox{and} \qquad \widetilde{{\mathcal{F}}}^{-1} \widetilde{{\mathcal{F}}} = P_{ac}. \end{align*} $$

3.3 Decomposition of $\psi (x,\xi )$

Let $\rho $ be an even, smooth, nonnegative function equal to $0$ outside of $B(0,2)$ and such that $\int \rho = 1$ . Define $\chi _{\pm }$ by

(3.25) $$ \begin{align} \chi_+(x) = H * \rho = \int_{-\infty}^{x} \rho(y)\,dy , \quad \mbox{and} \quad \chi_+(x) + \chi_-(x) = 1, \end{align} $$

where H is the Heaviside function, $H=\mathbf {1}_{+}$ . Notice that

$$ \begin{align*}\chi_+(x) = \chi_-(-x). \end{align*} $$

With $\chi _\pm $ as above, and using the definition of $\psi $ in equation (3.19) and $f_\pm $ and $m_\pm $ in equations (3.1)–(3.2), as well as the identity in equation (3.7), we can write

(3.26) $$ \begin{align} \begin{aligned} \mbox{for} \quad \xi>0 \qquad \sqrt{2\pi}\psi(x,\xi) & = \chi_+(x)T(\xi)m_+(x,\xi)e^{ix\xi} \\ &\quad + \chi_-(x) \big[ m_-(x,-\xi)e^{i\xi x} + R_-(\xi) m_-(x,\xi)e^{-i\xi x} \big], \end{aligned} \end{align} $$

and

(3.27) $$ \begin{align} \begin{aligned} \mbox{for} \quad \xi<0 \qquad \sqrt{2\pi}\psi(x,\xi) & = \chi_-(x)T(-\xi)m_-(x,-\xi)e^{ix\xi} \\ &\quad + \chi_+(x) \big[m_+(x,\xi) e^{i\xi x} + R_+(-\xi)m_+(x,-\xi) e^{-i\xi x} \big]. \end{aligned} \end{align} $$

We then decompose

(3.28) $$ \begin{align} \sqrt{2\pi}\psi(x,\xi) = \psi^S(x,\xi) + \psi^R(x,\xi) , \end{align} $$

where, on the one hand, the singular part (nondecaying in x) is

(3.29) $$ \begin{align} \begin{aligned} \mbox{for} \quad \xi>0 \qquad \psi^S(x,\xi) & := \chi_+(x) T(\xi) e^{i\xi x } + \chi_-(x) (e^{i\xi x} + R_-(\xi) e^{-i\xi x}), \\ \mbox{for} \quad \xi<0 \qquad \psi^S(x,\xi) & := \chi_-(x) T(-\xi) e^{i\xi x} + \chi_+(x) (e^{i\xi x} + R_+(-\xi) e^{-i\xi x}), \end{aligned} \end{align} $$

and the regular part is

(3.30) $$ \begin{align} \begin{aligned} \mbox{for} \quad \xi>0 \qquad \psi^R(x,\xi) & := \chi_+(x) T(\xi) (m_+(x,\xi)-1) e^{i\xi x} \\ &\quad + \chi_-(x) \big[ (m_-(x,-\xi) - 1)e^{i\xi x} + R_-(\xi)(m_-(x,\xi) - 1) e^{-ix\xi} \big], \\ \mbox{for} \quad \xi<0 \qquad \psi^R(x,\xi) & := \chi_-(x) T(-\xi) (m_-(x,-\xi)-1) e^{i\xi x} \\ &\quad + \chi_+(x) \big[ (m_+(x,\xi) - 1)e^{i\xi x} + R_+(-\xi)(m_+(x,-\xi) - 1) e^{-ix\xi} \big]. \end{aligned} \end{align} $$

3.4 Linear estimates

Recall that $\langle D \rangle = \sqrt { -\partial _x^2 + 1 }$ and $\langle \widetilde {D} \rangle = \sqrt { -\partial _x^2 + V + 1} = \widetilde {{\mathcal {F}}}^{-1} \langle \xi \rangle \widetilde {{\mathcal {F}}}$ .

Proposition 3.11 (Dispersive estimates)

Recall the definition in equation (2.30) with equation (2.31). The following statements hold true:

1. (i) For any $0\leq |t| \leq T$ , and for $I = [0,\infty )$ or $(-\infty ,0]$ ,

   (3.31) $$ \begin{align} \begin{aligned} {\| e^{\pm it\langle D \rangle} \mathbf{1}_I (D) f \|}_{L^{\infty}_x} \lesssim \frac{1}{\langle t \rangle^{1/2}} \, {\big\| \langle \xi \rangle^{3/2} \widehat{f} \big\|}_{L^{\infty}_{\xi}} + \frac{1}{\langle t \rangle^{3/4 - \alpha - \beta \gamma}} {\big\| \langle \xi \rangle \partial_{\xi} \widehat{f} \big\|}_{W_T} + \frac{1}{\langle t \rangle^{7/12}} {\| \langle \xi \rangle^4 \widehat{f} \|}_{L^2}. \end{aligned} \end{align} $$

2. (ii) If V satisfies the a priori assumptions of Theorem 1.1, then for any $0\leq |t| \leq T$ ,

   (3.32) $$ \begin{align} \begin{aligned} {\big\| e^{\pm it \langle \widetilde{D} \rangle} f \big\|}_{L^{\infty}_x} \lesssim \frac{1}{\langle t \rangle^{1/2}} \, {\big\| \langle \xi \rangle^{3/2} \widetilde{f} \big\|}_{L^{\infty}_{\xi}} + \frac{1}{\langle t \rangle^{3/4 - \alpha - \beta{\gamma}}} {\big\| \langle \xi \rangle \partial_{\xi} \widetilde{f} \big\|}_{W_T} + \frac{1}{\langle t \rangle^{7/12}} {\| \langle \xi \rangle^4 \widetilde{f} \|}_{L^2}. \end{aligned} \end{align} $$

A more precise asymptotic formula with an explicit leading order term can be read off the proof of Proposition 3.11; in particular, up to a faster-decaying remainder of the same form of those appearing in equation (3.32), we have

(3.33) $$ \begin{align} e^{it\langle \widetilde D \rangle} f \approx \frac{e^{i \frac{\pi}{4}}}{\sqrt{2t}} \langle \xi_0 \rangle^{3/2} e^{i t \langle \xi_0 \rangle + i x \xi_0} \widetilde{f} \left( \xi_0 \right) \qquad \mbox{as}\ t \to \infty, \quad \frac{\xi_0}{\langle \xi_0 \rangle} = - \frac{x}{t}. \end{align} $$

Remark 3.12. Note that, in view of equation (2.31), we have $\alpha + \beta \gamma < 1/4$ . Therefore, uniform-in-time control of the profile in $\widetilde {{\mathcal {F}}}^{-1}\langle \xi \rangle ^{-3/2} L^{\infty }$ and $W_t$ , and in $H^4$ with small time growth gives the sharp $|t|^{-1/2}$ decay for linear solutions through equation (3.32).

Furthermore, let $\mathbf {a}$ be any of the coefficients defined in equation (4.5). In view of equation (3.31) and the regularity of $T(\xi )$ and $R(\xi )$ in equation (3.14), we have

(3.34) $$ \begin{align} \begin{aligned} {\big\| e^{\pm it \langle D \rangle} \widehat{{\mathcal{F}}}^{-1} \big(\mathbf{a}(\xi) \widetilde{f} \, \big) \big\|}_{L^{\infty}_x} & \lesssim \frac{1}{\langle t \rangle^{1/2}} {\| \langle \xi \rangle^{3/2} \widetilde{f} \|}_{L^{\infty}_{\xi}} + \frac{1}{\langle t \rangle^{3/4-\alpha -\beta\gamma}} \big( {\| \langle \xi \rangle \partial_{\xi} \widetilde{f} \|}_{W_t} + {\| \widetilde{f} \|}_{L^2} \big) \\ &\quad + \frac{1}{\langle t \rangle^{7/12}} {\| \langle \xi \rangle^4 \widetilde{f} \|}_{L^2}. \end{aligned} \end{align} $$

Remark 3.13. Besides the pointwise decay estimates of Proposition 3.11 above, we will also use the following variant: for $k \geq 5$ ,

(3.35) $$ \begin{align} {\| e^{\pm it\langle D \rangle} \varphi_k(D) f \|}_{L^{\infty}} \lesssim \frac{1}{t^{1/2}} 2^{3k/2} {\big\| \varphi_k\widehat{f} \big\|}_{L^2}^{1/2} \big( {\big\| \varphi_k\partial_{\xi}\widehat{f} \big\|}_{L^2} + {\big\| \varphi_k\widehat{f} \big\|}_{L^2} \big)^{1/2}, \end{align} $$

which follows from the standard $L^1\rightarrow L^{\infty }$ decay and the interpolation inequality

$$ \begin{align*} {\big\| \varphi_k(D) f \big\|}_{L^1} \lesssim {\big\| \varphi_k(D) f \big\|}_{L^2}^{1/2} {\big\| x \, \varphi_k(D) f \big\|}_{L^2}^{1/2}. \end{align*} $$

Notice that equation (3.35) also implies (see equation (3.24))

(3.36) $$ \begin{align} {\| e^{\pm it\langle D \rangle} \mathcal{W}^* \varphi_k(\widetilde{D}) f \|}_{L^{\infty}} \lesssim \frac{1}{|t|^{1/2}} 2^{3k/2} {\big\| \varphi_k\widetilde{f} \big\|}_{L^2}^{1/2} \big( {\big\| \varphi_k\partial_{\xi}\widetilde{f} \big\|}_{L^2} + {\big\| \varphi_k\widetilde{f} \big\|}_{L^2} \big)^{1/2}. \end{align} $$

To prove Proposition 3.11, we use the following stationary phase lemma:

Lemma 3.14. Consider for $X \in \mathbb {R}$ , $t \geq 0$ , $x\in {\mathbb R}$ the integrals

$$ \begin{align*} I_{\mu, \nu}(t,X,x) = \int_{{\mathbb R}_{\mu}} e^{it ( \nu \langle \xi \rangle - \xi X)} a(x,\xi) g(\xi)\, d\xi, \qquad \mu,\nu \in \{+,-\}, \end{align*} $$

and assume that

(3.37) $$ \begin{align} \sup_{x \in {\mathbb R}, \, \xi \in {\mathbb R}_\mu}\left(|a(x,\xi)| + \langle \xi \rangle |\partial_{\xi}a(x,\xi)| \right)\lesssim 1. \end{align} $$

Then we have the estimate

(3.38) $$ \begin{align} \begin{aligned} \big| I_{\mu, \nu}(t,X,x) \big| \lesssim \frac{1}{\langle t \rangle^{1/2}} {\| \langle \xi \rangle^{3/2} g(\xi) \|}_{L^{\infty}} + \frac{1}{\langle t \rangle^{3/4 - \alpha - \beta\gamma}} {\| \langle \xi \rangle \partial_{\xi} g \|}_{W_T} + \frac{1}{\langle t \rangle^{7/12}} {\| \langle \xi \rangle^4 g \|}_{L^2}. \end{aligned} \end{align} $$

We postpone the proof of the lemma and give first the proof of Proposition 3.11.

Proof of Proposition 3.11

In order to prove equation (3.31), we write

$$ \begin{align*} e^{\pm i t \langle D \rangle} \mathbf{1}_I (D) f = \frac{1}{\sqrt{2\pi}} \int_{I} e^{i t(\pm \langle \xi \rangle - \xi X)} \widehat{f}(\xi)\, d\xi, \quad X := - x/t \end{align*} $$

and use Lemma 3.14 on $I={\mathbb R}_{+}$ or ${\mathbb R}_{-}$ and $a\equiv 1$ .

To prove equation (3.32), we use the distorted Fourier inversion (see equation (3.6)) to write

$$ \begin{align*} e^{\pm i t \langle \widetilde{D} \rangle} f = \int_{{\mathbb R}_+} e^{\pm i t \langle \xi \rangle} \psi(x,\xi) \widetilde{f}(\xi)\, d\xi + \int_{{\mathbb R}_-} e^{\pm i t \langle \xi \rangle} \psi (x,\xi) \widetilde{f}(\xi)\, d\xi. \end{align*} $$

Let us estimate the first integral, the other one being similar. Using equation (3.26), we can write

$$ \begin{align*} \sqrt{2\pi} \int_{{\mathbb R}_{+}} e^{\pm i t \langle \xi \rangle} \psi(x,\xi) f(\xi)\, d\xi & = \chi_+(x) \int_{{\mathbb R}_+} e^{ i t(\pm \langle \xi \rangle - \xi X)} T(\xi) m_{+}(x,\xi) f(\xi)\, d\xi \\ &\quad + \chi_-(x) \int_{{\mathbb R}_+} e^{i t(\pm \langle \xi \rangle - \xi X)} m_{-}(x,-\xi) f(\xi)\, d\xi \\ &\quad + \chi_-(x) \int_{{\mathbb R}_+} e^{ i t(\pm \langle \xi \rangle + \xi X)} R_{-}(\xi) m_{-}(x,\xi) f(\xi)\, d\xi. \end{align*} $$

Then the desired estimate follows by using Lemma 3.14 with $a(x,\xi )= T(\xi ) m_{+}(x,\xi )$ , $m_{-}(x,-\xi )$ and $R_-(\xi )m_{-}(x,\xi )$ , where the assumption in equation (3.37) holds thanks to Lemmas 3.1 and 3.2.

Proof of Lemma 3.14

It suffices to consider only the case $\mu =+$ , $\nu =+$ and $t \geq 1$ , $X \geq 0$ ; all other cases are similar or easier. We let

(3.39) $$ \begin{align} I_{++} = \sum_{k\in{\mathbb Z}} I_k , \qquad I_k(t,X) := \int_{{\mathbb R}_+} e^{it ( \langle \xi \rangle - \xi X)} a(x,\xi) g(\xi) \varphi_k(\xi) \, d\xi. \end{align} $$

First, notice that since

(3.40) $$ \begin{align} \big| I_k(t,x) \big| \lesssim \int_{{\mathbb R}_+} | g(\xi) | \varphi_k(\xi) \, d\xi \lesssim \mathrm{min} \big( 2^k {\| g \|}_{L^{\infty}}, 2^{-7k/2} {\| \langle \xi \rangle^4 g \|}_{L^2} \big), \end{align} $$

we see that $|I_{++}|$ enjoys the desired bound if $2^k \gtrsim t^{1/6}$ , or $2^k \lesssim t^{-1/2}$ . From now on, we assume

(3.41) $$ \begin{align} C t^{-1/2} \leq 2^k \leq (1/C) t^{1/6} \end{align} $$

for a suitably large absolute constant $C>0$ .

Let us denote

(3.42) $$ \begin{align} \begin{aligned} & \phi_{X}(\xi) := \langle \xi \rangle - \xi X, \quad \\ & \phi_X'(\xi) = \frac{\xi}{\langle \xi \rangle} - X, \quad \phi_{X}''(\xi) = \frac{1}{\langle \xi \rangle^3}, \qquad \xi_{0} := X/\sqrt{1-X^2}, \end{aligned} \end{align} $$

and note that the phase $\phi _X$ has no stationary points if $X \geq 1$ , and a unique, nondegenerate, stationary point at $\xi _0$ for any $X \in [0, 1)$ . Consider $n \in {\mathbb Z}_+$ such that $t \in [2^{n-1},2^n]$ , and let $q_0 \in {\mathbb Z}$ be the smallest integer such that $2^{q_0} \geq 2^{(3/2)k^+} 2^{-n/2} \approx \langle \xi \rangle ^{3/2} t^{-1/2}$ . Note that $2^{q_0} \ll \mathrm {min}(2^k,1)$ if C in equation (3.41) is large enough.

In what follows, we may assume that $|\xi _0|\approx 2^k$ , for otherwise there is no stationary point on the support of equation (3.39), $|\phi _X'(\xi )| \gtrsim 2^k 2^{-3k^+}$ , and the proof of the statement is easier. In other words, for fixed $\xi _0$ , we may assume that there is a finite number of indexes k for which $I_k$ does not vanish.

Using the notation in equation (2.25), we decompose

(3.43) $$ \begin{align} I_k = \sum_{q \in [q_0,\infty) \cap {\mathbb Z}} I_{k,q}, \qquad I_{k,q}(t,X) := \int_{{\mathbb R}_+} e^{it ( \langle \xi \rangle - \xi X)} a(x,\xi) \, \varphi_q^{(q_0)}(\xi-\xi_0) \, \varphi_k(\xi) \, g(\xi)\, d\xi. \end{align} $$

Bounding the contribution to the sum over k of the term with $q = q_0$ is immediate. Let us then consider $q> q_0$ and note that on the support of the integral in equation (3.43), we have

(3.44) $$ \begin{align} |\phi_X'(\xi)| \approx |\xi-\xi_0| |\phi_X''| \approx 2^{q} 2^{-3k^+} \gtrsim 2^{-n/2} 2^{-(3/2)k^+}. \end{align} $$

Integrating by parts using $(it \phi _{X}')^{-1} \partial _{\xi } e^{it \phi _X} = e^{it \phi _X}$ , we obtain

(3.45) $$ \begin{align} \begin{aligned} & I_{k,q} = \frac{1}{it} \big[ J_{k,q}^{(1)} + J_{k,q}^{(2)} + J_{k,q}^{(3)} + J_{k,q}^{(4)} \big] , \\ & J_{k,q}^{(1)}(t,X) = \int_{{\mathbb R}_+} e^{it ( \langle \xi \rangle - \xi X)} \frac{\phi_X''}{(\phi_X')^2} a(x,\xi) \, \varphi_q(\xi-\xi_0) \, \varphi_k(\xi) \, g(\xi) \, d\xi, \\ & J_{k,q}^{(2)}(t,X) = -\int_{{\mathbb R}_+} e^{it ( \langle \xi \rangle - \xi X)} \frac{1}{\phi_X'} \, \partial_{\xi} a(x,\xi) \, \varphi_q(\xi-\xi_0) \, \varphi_k(\xi) \, g(\xi) \, d\xi, \\ & J_{k,q}^{(3)}(t,X) = - \int_{{\mathbb R}_+} e^{it ( \langle \xi \rangle - \xi X)} \frac{1}{\phi_X'} a(x,\xi) \, \partial_{\xi} \big[ \varphi_q(\xi-\xi_0) \, \varphi_k(\xi) \big] \, g(\xi) \, d\xi, \\ & J_{k,q}^{(4)}(t,X) = - \int_{{\mathbb R}_+} e^{it ( \langle \xi \rangle - \xi X)} \frac{1}{\phi_X'} a(x,\xi) \, \varphi_q(\xi-\xi_0) \, \varphi_k(\xi) \, \partial_{\xi} g(\xi) \, d\xi. \end{aligned} \end{align} $$

Using equations (3.42) and (3.44) and changing the index of summation $q \mapsto p+(3/2)k^+$ , we have

(3.46) $$ \begin{align} \begin{aligned} \Big| \sum_{q\geq q_0, k} J_{k,q}^{(1)}(t,X) \Big|& \lesssim \sum_{p \geq -n/2, k} \int_{{\mathbb R}_+} \frac{\langle \xi \rangle^3}{(\xi-\xi_0)^2} \, \varphi_{\sim p}\big( (\xi-\xi_0)2^{-(3/2)k^+} \big) \, \varphi_k(\xi) \, |g(\xi)| \, d\xi \\ & \lesssim t^{1/2} {\| \langle \xi \rangle^{3/2} g \|}_{L^{\infty}}. \end{aligned} \end{align} $$

For the second term, using $|\partial _{\xi } a|\leq 1$ , we can estimate

(3.47) $$ \begin{align} \begin{aligned} \Big| \sum_{q\geq q_0, k} J_{k,q}^{(2)}(t,X) \Big| &\lesssim \sum_{p \geq -n/2, k} \int_{{\mathbb R}_+} \frac{\langle \xi \rangle^3}{|\xi-\xi_0|} \, \varphi_{\sim p}\big( (\xi-\xi_0) 2^{-(3/2)k^+} \big) \, \varphi_k(\xi) \, |g(\xi)| \, d\xi \\ & \lesssim t^{1/2} {\| g \|}_{L^{\infty}}. \end{aligned} \end{align} $$

The third term in equation (3.45) is similar to the first one:

(3.48) $$ \begin{align} \begin{aligned} \Big| \sum_{q\geq q_0, k} J_{k,q}^{(3)}(t,X) \Big| \lesssim t^{1/2} {\| \langle \xi \rangle^{3/2} g \|}_{L^{\infty}}. \end{aligned} \end{align} $$

The upper bounds in equations (3.46)–(3.48), after being multiplied by $t^{-1}$ , are bounded by the first term on the right-hand side of equation (3.38).

For the last integral in equation (3.45), we want to distinguish cases depending on the location of $\xi $ relative to the frequency $\sqrt {3}$ . We insert cutoffs $\varphi _{\ell }^{(\ell _0)}(\xi -\sqrt {3})$ , for $\ell _0 := -\gamma n$ , and bound

(3.49) $$ \begin{align} \begin{aligned} & t^{-1} \big| J_{k,q}^{(4)} \big| \lesssim t^{-1} \big[ K_{\leq \ell_0} + \sum_{\ell_0 < \ell \leq 0} K_{\ell} + K_{>0} \big] \\ & K_{\ast}(t,X) = \int_{{\mathbb R}_+} \frac{1}{|\phi_X'|} |a(x,\xi)| \, \varphi_q(\xi-\xi_0) \, \varphi_k(\xi) \, \varphi_{\ast}\big(\xi-\sqrt{3}\big) \, |\partial_{\xi} g(\xi)| \, d\xi. \end{aligned} \end{align} $$

The first term can be estimated as follows:

$$ \begin{align*} t^{-1} \sum_{q> q_0} \big| K_{\leq \ell_0}(t,X) \big| & \lesssim t^{-1} \sum_{q>q_0} 2^{-q} \cdot 2^{\mathrm{min}(q,-{\gamma} n)/2} \cdot {\big\| \varphi_{\leq -{\gamma} n} \big(\xi-\sqrt{3}\big)\partial_{\xi} g \big\|}_{L^2} \\ & \lesssim t^{-1} \sum_{q>q_0} 2^{-q/2} 2^{({\beta} {\gamma} +\alpha) n} {\| \chi_{\leq 0,\sqrt{3}} \, \partial_{\xi} g \|}_{W_T} \\ & \lesssim t^{-1} 2^{-q_0/2} t^{{\beta}{\gamma} +\alpha} {\| \chi_{\leq 0,\sqrt{3}} \, \partial_{\xi} g \|}_{W_T}, \end{align*} $$

consistently with equation (3.38), since we must have $|k|\leq 5$ and $2^{q_0} \approx t^{-1/2}$ . The last term in equation (3.49) can be estimated similarly:

(3.50) $$ \begin{align} \begin{aligned} t^{-1} \sum_{q>q_0} \big| K_{>0}(t,X) \big| & \lesssim t^{-1} \sum_{q>q_0} 2^{3k^+-q} \cdot 2^{\mathrm{min}(q,k)/2} \cdot {\big\| \varphi_k \varphi_{>0} \big(\xi-\sqrt{3}\big) \partial_{\xi} g \big\|}_{L^2} \\ & \lesssim t^{-3/4} 2^{(5/4)k^+} \cdot t^{\alpha} {\| \chi_{> 0,\sqrt{3}} \langle \xi \rangle \partial_{\xi} g \|}_{W_T}. \end{aligned} \end{align} $$

Upon summing over $2^k \leq t^{1/6}$ the right-hand side of equation (3.50), we obtain a contribution bounded by the second term on the right-hand side of equation (3.38), since $-3/4 + (5/4) (1/6) + \alpha < -3/4 + \alpha + \beta \gamma $ with our choice of parameters in equation (2.31) (provided, for example, that $\beta ',\gamma ' < 1/24$ ).

Finally, we estimate

$$ \begin{align*} t^{-1} \big| K_{\ell}(t,X) \big| & \lesssim t^{-1} 2^{-q} \cdot 2^{\mathrm{min}(q,\ell)/2} \cdot {\big\| \varphi_{\ell}\big(\xi-\sqrt{3}\big)\partial_{\xi} g \big\|}_{L^2} \\ & \lesssim t^{-1} 2^{-q/2} \cdot 2^{-{\beta} \ell} 2^{\alpha n} {\| \chi_{\leq 0,\sqrt{3}} \, \partial_{\xi} g \|}_{W_T}, \end{align*} $$

and, using again that $|k|\leq 5$ for $\ell \leq 0$ , we see that this contributions can be summed over $q>q_0$ with $2^{q_0} \gtrsim t^{-1/2}$ , and $\ell> \ell _0$ with $2^{\ell _0} \gtrsim t^{-{\gamma }}$ , and be bounded by the second term on the right-hand side of equation (3.38).

4 The quadratic spectral distribution

In this section, we study the distribution in equation (2.6).

4.1 The structure of the quadratic spectral distribution

Recall that we denote, for a function f,

$$ \begin{align*}f_+(x) = f(x) \quad \mbox{and} \quad f_-(x) = \overline{f(x)}. \end{align*} $$

Proposition 4.1. Under the assumptions on $V=V(x)$ and $a=a(x)$ in Theorem 1.1, there exists a tempered distribution $\mu _{\iota _1 \iota _2} \in \mathcal {S}'({\mathbb R}^3)$ for $\iota _1,\iota _2 \in \{+,-\}$ such that, if $f,g \in \mathcal {S}$ ,

$$ \begin{align*}\widetilde{\mathcal{F}} \left[ a(x) f_{\iota_1} g_{\iota_2} \right] (\xi) = \iint \widetilde{f}_{\iota_1} (\eta) \widetilde{g}_{\iota_2}(\sigma) \mu_{\iota_1 \iota_2} (\xi,\eta,\sigma) \,d\eta \,d\sigma. \end{align*} $$

The distribution $\mu _{\iota _1 \iota _2}$ can be decomposed into

(4.1) $$ \begin{align} \begin{aligned} 2\pi \mu_{\iota_1 \iota_2} (\xi,\eta,\sigma) = \mu_{\iota_1 \iota_2}^S(\xi,\eta,\sigma) + \mu_{\iota_1 \iota_2}^R(\xi,\eta,\sigma), \end{aligned} \end{align} $$

where the following hold:

• • The ‘ $\mathrm {singular}$ ’ part of the distribution can be written as

  (4.2) $$ \begin{align} \mu_{\iota_1 \iota_2}^S(\xi,\eta,\sigma) = \mu_{\iota_1 \iota_2} ^{S,-}(\xi,\eta,\sigma) + \mu_{\iota_1 \iota_2} ^{S,+}(\xi,\eta,\sigma), \end{align} $$
  with $\epsilon \in \{+,-\}$ ,
  (4.3) $$ \begin{align} \begin{aligned} \mu_{\iota_1 \iota_2}^{S,\epsilon} (\xi,\eta,\sigma) & := \ell_{\epsilon\infty} \sum_{\lambda,\mu,\nu \in \{+,-\}} a_{\substack{- \iota_1 \iota_2 \\ \lambda \mu \nu}}^{\epsilon} (\xi,\eta, \sigma) \, \Big[\sqrt{\frac \pi 2} \delta(p) + \epsilon \mathrm{p.v.} \frac{\widehat \phi(p)}{ip} \Big], \\ p &:= \lambda \xi - \iota_1 \mu \eta - \iota_2 \nu \sigma, \end{aligned} \end{align} $$
  where $\phi $ is a smooth, even, real-valued, compactly supported function with integral one; the coefficients are given by
  (4.4) $$ \begin{align} a_{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda \mu \nu}}^{\epsilon}(\xi,\eta,\sigma) = \mathbf{a}_{\lambda,\iota_0}^{\epsilon}(\xi) \mathbf{a}_{\mu,\iota_1}^{\epsilon}(\eta) \mathbf{a}_{\nu,\iota_2}^{\epsilon}(\sigma) \qquad \mbox{with} \qquad \mathbf{a}_{\mu,\iota}^{\epsilon} = \big( \mathbf{a}_{\mu}^{\epsilon} \big)_{\iota} \end{align} $$
  and
  (4.5) $$ \begin{align} \left\{ \begin{array}{l} \mathbf{a}^-_+(\xi) = \mathbf{1}_+(\xi) + \mathbf{1}_-(\xi) T(-\xi) \\ \mathbf{a}^-_-(\xi) = \mathbf{1}_+(\xi) R_-(\xi) \end{array} \right. \qquad \left\{ \begin{array}{l} \mathbf{a}^+_+(\xi) = T(\xi) \mathbf{1}_+(\xi) + \mathbf{1}_-(\xi) \\ \mathbf{a}^+_-(\xi) = \mathbf{1}_-(\xi) R_+(-\xi). \end{array} \right. \end{align} $$

• • The ‘ $\mathrm {regular}$ ’ part of the distribution $\mu ^R_{\iota _1\iota _2}$ can be written as a linear combination of the form

  (4.6) $$ \begin{align} \mu_{\iota_1 \iota_2}^R(\xi,\eta,\sigma) = \sum_{\epsilon_1,\epsilon_2,\epsilon_3 \in \{+,-\}} \mathbf{1}_{\epsilon_1}(\xi)\mathbf{1}_{\epsilon_2}(\eta)\mathbf{1}_{\epsilon_3}({\sigma}) \mathfrak{r}_{\epsilon_1\epsilon_2\epsilon_3}(\xi,\eta,\sigma), \end{align} $$
  where the symbols $\mathfrak {r}_{\epsilon _1\epsilon _2\epsilon _3}: {\mathbb R}^3 \rightarrow {\mathbb C}$ are smooth and satisfy, for any nonnegative integer N and $a,b,c$ ,
  (4.7) $$ \begin{align} \begin{aligned} \big|\partial_{\xi}^a \partial_{\eta}^b \partial_{\sigma}^c \mathfrak{r}_{\epsilon_1\epsilon_2\epsilon_3}(\xi,\eta,{\sigma}) \big| \lesssim \langle \inf_{\mu,\nu} |\xi - \mu \eta - \nu \sigma| \rangle^{-N}. \end{aligned} \end{align} $$

Proof. We proceed in a few steps.

The Fourier transform of $(\chi _{\pm })^3$ . By the choice in equation (3.25) of $\chi _{-}$ , $ \partial _{x} (\chi _-)^3$ is a $\mathcal {C}^{\infty }_{c}$ function, which we can write as $ \partial _{x} (\chi _-)^3= \phi ^o - \phi ^e$ , where $\phi ^o$ and $\phi ^e$ are, respectively, odd and even and $\mathcal {C}^{\infty }_{c}$ . Furthermore, since $\phi ^o$ is odd, we can write $\phi ^o = \partial _{x} \psi $ , where $\psi \in \mathcal {C}^{\infty }_{c}$ and $\psi $ is even. We have thus obtained that

$$ \begin{align*} (\chi_-)^3= \psi + \int_{x}^{+ \infty} \phi^e (y)\, dy = \psi + \phi^e \ast \mathbf{1}_-, \qquad \int_{\mathbb R}\phi^e (y)\,dy =1, \end{align*} $$

where we denoted by $\mathbf {1}_\pm $ the characteristic function of $\{\pm x> 0\}$ . Taking the Fourier transform and using the classical formulas

(4.8) $$ \begin{align} \widehat{f \ast g} = \sqrt{2\pi} \widehat{f} \cdot \widehat{g}, \qquad \widehat{1} = \sqrt{2\pi} \delta_0, \qquad \widehat{ \mbox{sign} x} = \mathrm{p.v.} \sqrt{\frac{2}{\pi}}\frac{1}{i\xi}, \end{align} $$

we see that $\widehat {\mathbf {1}_-} = \sqrt {\dfrac {\pi }{2}} \delta - \dfrac {1}{\sqrt {2\pi }} \mathrm {p.v.}\dfrac {1}{i\xi }$ , and therefore, since $\widehat {\phi ^e}(0) = \dfrac {1}{\sqrt {2\pi }}$ ,

$$ \begin{align*} \widehat{(\chi_-)^3} - \widehat{\psi} = \widehat{\mathcal{F}} \big(\phi^e \ast \mathbf{1}_- \big) = \sqrt{2\pi} \widehat{\mathbf{1}_-}(\xi) \widehat{\phi^e}(\xi) = \sqrt{\frac{\pi}{2}} \delta(\xi) - \mathrm{p.v.}\frac{\widehat{\phi^e}(\xi)}{i\xi}. \end{align*} $$

Since $\chi _+(-x) = \chi _-(x)$ , this implies a corresponding formula for $\chi _+$ . To summarise, setting $\phi = \phi ^e$ ,

(4.9) $$ \begin{align} \widehat{(\chi_{\pm})^3}(\xi) = \sqrt{\frac{\pi}{2}} \delta(\xi) \pm \mathrm{p.v.} {\widehat{\phi}(\xi)\over i\xi} + \widehat{\psi}(\xi). \end{align} $$

The regularization step. Consider for simplicity the case $\iota _1 = \iota _2 = +$ . If $f,g,h \in \mathcal {S}$ , denoting w a cutoff function,

(4.10) $$ \begin{align} \nonumber \langle \widetilde{a(x)fg}(\xi) ,\widetilde{h}(\xi) \rangle & = \iint \overline{\psi(x,\xi)} a(x) \int \widetilde{f}(\eta) \psi(x,\eta)\,d\eta \int \widetilde{g}(\sigma) \psi(x,\sigma)\,d\sigma \,dx \, \overline{\widetilde{h}(\xi)} \,d\xi \\ \nonumber & = \lim_{R \to \infty} \iint a(x) w(x/R) \overline{\psi(x,\xi)} \int \widetilde{f}(\eta) \psi(x,\eta)\,d\eta \int \widetilde{g}(\sigma) \psi(x,\sigma)\,d\sigma \,dx \, \overline{\widetilde{h}(\xi)} \,d\xi \\ \nonumber & = \lim_{R \to \infty} \iiint \widetilde{f}(\eta) \widetilde{g}(\sigma) \overline{\widetilde{h}(\xi)} \Big( \int a(x) w(x/R) \overline{\psi(x,\xi)} \psi(x,\eta) \psi(x,\sigma) \,dx \Big) \,d\eta \,d\sigma \,d\xi \\ & = \iiint \widetilde{f}(\eta) \widetilde{g}(\sigma) \overline{\widetilde{h}(\xi)} \mu_{++} (\xi,\eta,\sigma) \,d\eta \,d\sigma \,d\xi, \end{align} $$

where $\mu _{++}$ is defined as the limit in the sense of (tempered) distributions

(4.11) $$ \begin{align} \mu_{++} (\xi,\eta,\sigma) = \lim_{R \to \infty} \int a(x) w(x/R) \overline{\psi(x,\xi)} \psi(x,\eta) \psi(x,\sigma) \,dx. \end{align} $$

Note that while the limit in equation (4.11) can be easily seen to exist in the sense of (tempered) distribution, the limit leading to equation (4.10) needs to be understood in a different topology. In fact, although $\mu _{++}$ is a tempered distribution, $\widetilde {f}$ is not a Schwartz function, even if f is a Schwartz function: $\widetilde {f}$ might not be smooth, or may even be discontinuous, at zero; see equations (3.22) and (3.23). Nevertheless, one can still make sense rigorously of the limit and the pairing in equation (4.10) for $f,g,h \in \mathcal {S}$ . It actually suffices to consider $\widetilde {f},\widetilde {g},\widetilde {h} \in L^1\cap L^{\infty }$ , for example.

First, let us see that $\mu _{++}$ can be integrated against $\widetilde {f}(\eta ) \widetilde {g}(\sigma ) \overline {\widetilde {h}(\xi )}$ provided that $\widetilde {f}$ , $\widetilde {g}$ and $\widetilde {h}$ are in $L^1 \cap L^2$ (which is the case if $f,g,h \in \mathcal {S}$ ). Indeed, we will see that, up to more regular terms, $\mu _{++}$ is a linear combination of $\delta (p)$ and $\mathrm {p.v.} \frac {1}{p}$ distributions, where p is as in equation (4.3), with piecewise smooth coefficients in the variables $\xi ,\eta $ and ${\sigma }$ . The coefficients do not matter, so it suffices to look at the cases $\mu _{++} = \delta (\xi - \eta - \sigma )$ or $\mathrm {p.v.} \frac {1}{\xi - \eta - \sigma }$ (since the signs $\lambda , \mu , \nu $ in the definition of p also are not relevant). Then in the case of the $\delta $ distribution, we have

$$ \begin{align*}\iiint \delta(\xi - \eta - \sigma) \widetilde{f}(\eta) \widetilde{g}(\sigma) \overline{\widetilde{h}(\xi)} d\eta \, d\sigma \,d\xi = \iint \widetilde{f}(\eta) \widetilde{g}(\sigma) \overline{\widetilde{h}(\eta + \sigma)} d\eta \, d\sigma, \end{align*} $$

which is well defined by the Cauchy-Schwarz inequality if $\widetilde {f}, \widetilde {g}, \widetilde {h} \in L^1 \cap L^2$ . In the case of the $\mathrm {p.v.} \frac {1}{p}$ distribution, denoting by H the (standard) Hilbert transform, we have

$$ \begin{align*}\iiint \mathrm{p.v.} \frac{1}{\xi - \eta - \sigma} \widetilde{f}(\eta) \widetilde{g}(\sigma) \overline{\widetilde{h}(\xi)} d\eta \, d\sigma \,d\xi = \iint \widetilde{f}(\eta) \widetilde{g}(\sigma) \overline{[H \widetilde{h}](\eta + \sigma)} d\eta \, d\sigma, \end{align*} $$

which is well defined by the boundedness of the Hilbert transform on $L^2$ , and the Cauchy-Schwarz inequality.

Second, to justify the limit in equation (4.10), let us split

$$ \begin{align*}\widetilde{f} = \widetilde{f} (1 - \chi(\cdot / \epsilon) ) + \widetilde{f} \chi(\cdot / \epsilon) = \widetilde{f_{1,\epsilon}} + \widetilde{f_{2,\epsilon}}, \end{align*} $$

where $\chi $ is a smooth cutoff function equal to $1$ in a neighbourhood of $0$ , and similarly for g and h. We can then write

(4.12) $$ \begin{align} \langle \widetilde{{\mathcal{F}}}\big( a(x)w(x/R) fg\big)(\xi), \widetilde{h}(\xi) \rangle & = \langle \widetilde{{\mathcal{F}}}\big( a(x)w(x/R) f_{1,\epsilon} g_{1,\epsilon}\big)(\xi),\widetilde{h}_{1,\epsilon}(\xi) \rangle \qquad\qquad\quad \end{align} $$

(4.13) $$ \begin{align} &\phantom{\qquad\langle \widetilde{{\mathcal{F}}}\big( a(x)w(x/R) fg\big)(\xi), \widetilde{h}(\xi) \rangle} + \langle \widetilde{{\mathcal{F}}}\big(a(x)w(x/R)f_{2,\epsilon} g_{1,\epsilon}\big)(\xi),\widetilde{h}_{1,\epsilon}(\xi) \rangle + \{ \mbox{similar terms}\}. \end{align} $$

Here, the ‘similar terms’ contain at least one factor with an index $2$ , namely $g_{2,\epsilon }$ or $h_{2,\epsilon }$ . We claim that the terms in equation (4.13) are $O(\epsilon )$ remainder terms uniformly in R. If this is the case, then

$$ \begin{align*}\langle \widetilde{{\mathcal{F}}}\big( a(x)w(x/R)fg\big)(\xi), \widetilde{h}(\xi) \rangle = \langle \widetilde{{\mathcal{F}}} \big(a(x) w(x/R) f_{1,\epsilon} g_{1,\epsilon} \big)(\xi), \widetilde{h_{1,\epsilon}}(\xi) \rangle + O(\epsilon). \end{align*} $$

For the main term on the right-hand side above, the limit as in equation (4.10) is justified, since the functions involved are Schwartz. Therefore, one can let $R \to \infty $ first, then let $\epsilon \to 0$ , and obtain the desired formula.

To show that the remainder terms in equation (4.13) are $O(\epsilon )$ , we use the properties of the distorted Fourier transform:

$$ \begin{align*} \Big| \langle \widetilde{{\mathcal{F}}} \big( a(x)w(x/R)f_{2,\epsilon} g_{1,\epsilon} \big) (\xi), \widetilde{h_{1,\epsilon}}(\xi) \rangle \Big| & = \Big| \langle a(x) w(x/R) f_{2,\epsilon} g_{1,\epsilon}, h_{1,\epsilon} \rangle \Big| \\ &\lesssim {\| f_{2,\epsilon} \|}_{L^{\infty}} {\| g_{1,\epsilon} \|}_{L^2} \| h_{1,\epsilon} \|_{L^2} \lesssim {\| \widetilde{f_{2,\epsilon}} \|}_{L^1} {\| g_{1,\epsilon} \|}_{L^2} {\| h_{1,\epsilon} \|}_{L^2} \\ &\lesssim \epsilon {\| \widetilde{f} \|}_{L^{\infty}} {\| g \|}_{L^2} {\| h \|}_{L^2} \lesssim \epsilon. \end{align*} $$

In the following, we simply denote

$$ \begin{align*}\mu_{\iota_1 \iota_2} (\xi,\eta,\sigma) = \int a(x) \overline{\psi(x,\xi)} \psi_{\iota_1}(x,\eta) \psi_{\iota_2}(x,\sigma) \, dx. \end{align*} $$

Decomposition of the quadratic spectral distribution. We can write $\mu _{\iota _1\iota _2}$ as a sum of terms of the form

(4.14) $$ \begin{align} \frac{1}{(2\pi)^{3/2}} \int a(x) \overline{\psi^A(x,\xi)}\psi_{\iota_1}^B(x,\eta) \psi_{\iota_2}^C(x,\sigma) \, dx, \qquad A,B,C \in \{S,R\}, \end{align} $$

where we are using our main decomposition of $\psi $ in equation (3.28).

The singular part $\mu _S$ . The main singular component comes from part of the contribution to equation (4.14) with $A,B,C = S$ . The decomposition equation (3.29) can be written under the form

(4.15) $$ \begin{align} \begin{aligned} \psi^S(x,\xi)& = \chi_+(x) \sum_{\lambda \in \{+,-\} } \mathbf{a}_{\lambda}^+(\xi) e^{i \lambda \xi x} + \chi_-(x) \sum_{\lambda \in \{+,-\} } \mathbf{a}_{\lambda}^-(\xi) e^{i \lambda \xi x} \\ & =: \chi_+(x) \psi^{S,+}(x,\xi) + \chi_-(x) \psi^{S,-}(x,\xi), \end{aligned} \end{align} $$

where

(4.16) $$ \begin{align} \mathbf{a}_{\lambda}^-(\xi) = \left\{ \begin{array}{llll} 1 & \mbox{if} \qquad \lambda = + & & \mbox{and} \qquad \xi> 0, \\ R_-(\xi) & \mbox{if} \qquad \lambda = - & & \mbox{and} \qquad \xi > 0, \\ T(-\xi) & \mbox{if} \qquad \lambda= + & & \mbox{and} \qquad \xi < 0, \\ 0 & \mbox{if} \qquad \lambda = - & & \mbox{and} \qquad \xi < 0, \end{array} \right. \end{align} $$

and

(4.17) $$ \begin{align} \mathbf{a}_{\lambda}^+(\xi) = \left\{ \begin{array}{llll} T(\xi) & \mbox{if} \qquad \lambda = + & & \mbox{and} \qquad \xi> 0, \\ 0 & \mbox{if} \qquad \lambda = - & & \mbox{and} \qquad \xi > 0, \\ 1 & \mbox{if} \qquad \lambda= + & & \mbox{and} \qquad \xi < 0, \\ R_+(-\xi) & \mbox{if} \qquad \lambda = - & & \mbox{and} \qquad \xi < 0, \end{array} \right. \end{align} $$

or, equivalently,

(4.18) $$ \begin{align} \begin{aligned} & \mathbf{a}^-_+(\xi) = \mathbf{1}_+(\xi) + \mathbf{1}_-(\xi) T(-\xi) \\ & \mathbf{a}^-_-(\xi) = \mathbf{1}_+(\xi) R_-(\xi) \\ & \mathbf{a}^+_+(\xi) = T(\xi) \mathbf{1}_+(\xi) + \mathbf{1}_-(\xi) \\ & \mathbf{a}^+_-(\xi) = \mathbf{1}_-(\xi) R_+(-\xi). \end{aligned} \end{align} $$

Consider the terms in equation (4.14) with $A,B,C = S$ and such that in each decomposition of $\psi ^S$ there are only contributions containing $\chi _+$ (that is, $\psi ^{S,+}$ ) or $\chi _-$ (that is, $\psi ^{S,-}$ ). We can write this as

(4.19) $$ \begin{align} \begin{aligned} & \frac{1}{\sqrt{2\pi}} \int_{\mathbb R} a(x) \chi_\pm^3(x) \overline{\psi^{S,\pm}(x,\xi)} \psi^{S,\pm}_{\iota_1}(x,\eta) \psi^{S,\pm}_{\iota_2}(x,{\sigma}) \,dx \\ &\quad = \frac{1}{\sqrt{2\pi}} \sum_{\lambda,\mu,\nu \in \{\pm \}} \int_{\mathbb R} a(x) \chi_\pm^3(x) \, {a}^{\pm}_{\substack{- \iota_1 \iota_2 \\ \lambda \mu \nu}}(\xi,\eta,\sigma) \, \overline{e^{\lambda i\xi x}} e^{\iota_1 \mu i\eta x}e^{\iota_2 \nu i \sigma x} \, dx, \\ &\quad = \sum_{\lambda,\mu,\nu \in \{\pm\}} \widehat{{\mathcal{F}}}\big(a(x)(\chi_{\pm})^3\big)(\lambda \xi - \iota_1 \mu \eta - \iota_2 \nu \sigma) \, a^{\pm}_{\substack{- \iota_1 \iota_2 \\ \lambda \mu \nu}}(\xi,\eta,\sigma). \end{aligned} \end{align} $$

We then write $a(x)(\chi _{\pm })^3 = \ell _{\pm \infty }(\chi _{\pm })^3 + (a(x)-\ell _{\pm \infty })(\chi _{\pm })^3$ , where this last function is Schwartz. Using the formula in equation (4.9) for $\widehat {(\chi _{\pm })^3}$ , we see that the first terms in the right-hand side of equation (4.9), namely $\frac {\sqrt {\pi }}{2} \delta \pm \mathrm {p.v.} \frac {\widehat {\phi }}{i\xi }$ , make up the singular part of the distribution $\mu ^{S,\pm }$ in equation (4.3). The contribution corresponding to the last term, $\widehat {\psi }(\xi )$ , together with the one from $\widehat {{\mathcal {F}}} \big (a(x)-\ell _{\pm \infty }\big )$ , can be absorbed into the regular part of the distribution $\mu ^R$ ; see equation (4.27).

The regular part $\mu _R$ . The regular part $\mu _R$ contains all other contributions. These are of two main types: terms of the form in equation (4.14) when one of the indexes $A,B,C$ is R, or contributions where both $\chi _+$ and $\chi _-$ appear; see equation (4.15). More precisely, we can write

(4.20) $$ \begin{align} \mu_{\iota_1 \iota_2}^R(\xi,\eta,\sigma) = \mu_{\iota_1 \iota_2}^{R1}(\xi,\eta,\sigma) + \mu_{\iota_1 \iota_2}^{R2}(\xi,\eta,\sigma), \end{align} $$

where, if we let $X_R = \{ (A_1,A_2,A_3) \, : \, \exists \, j=1,2,3 \,\, \mbox { s.t.} \, A_j = R\}$ ,

(4.21) $$ \begin{align} \mu_{\iota_1 \iota_2}^{R1}(\xi,\eta,\sigma) & := \sum_{(A,B,C) \in X_R} \int a(x) \, \overline{\psi^A(x,\xi)}\psi^B_{\iota_1}(x,\eta) \psi^C_{\iota_2}(x,\sigma) \, dx \end{align} $$

and

(4.22) $$ \begin{align} \begin{aligned} \mu_{\iota_1 \iota_2}^{R2}(\xi,\eta,\sigma) := \sum_{A,B,C = S} \int a(x) \, \overline{\psi^A(x,\xi)} \psi^B_{\iota_1}(x,\eta) \psi^C_{\iota_2}(x,\sigma) \, dx - \mu^S_{\iota_1\iota_2} (\xi,\eta,\sigma). \end{aligned} \end{align} $$

In the remainder of the proof, we verify the properties in equations (4.6)–(4.7) for equations (4.21)–(4.22).

To understand equation (4.21), we start by looking at the case $A=R$ and $B,C=S$ . We restrict our analysis to $\xi>0$ (see equation (3.30)); $\xi <0$ can be treated in the same way. According to equation (3.30), this gives the terms

(4.23) $$ \begin{align} \begin{aligned} & \int a(x) \overline{\chi_+(x) T(\xi) (m_+(x,\xi)-1) e^{i\xi x} } \psi^S(x,\eta) \psi^S(x,\sigma) \, dx \\ &\quad + \int a(x) \overline{\chi_-(x) \big[ (m_-(x,-\xi) - 1)e^{i\xi x} + R_-(\xi)(m_-(x,\xi) - 1) e^{-ix\xi} \big]} \psi^S(x,\eta) \psi^S(x,\sigma) \, dx. \end{aligned} \end{align} $$

Let us look at the first term above and only at the contributions to $\psi ^S$ coming from $\psi ^{S,+}$ (see equation (4.15)): that is,

(4.24) $$ \begin{align} R_{\mu\nu}(\xi,\eta,{\sigma}) & := \overline{T(\xi)} \mathbf{a}_\mu^+(\eta) \mathbf{a}_\nu^+(\sigma) \int a(x) \chi_+^3(x) (\overline{m_+(x,\xi)}-1) \, e^{-i\xi x} e^{i\mu \eta x} e^{i\nu{\sigma} x} \, dx. \end{align} $$

Notice that the coefficients in front of the integral are products of indicator functions and smooth functions, consistent with equations (4.6)–(4.7). Dropping the irrelevant signs $\mu ,\nu $ , it then suffices to treat

(4.25) $$ \begin{align} R(\xi,\eta,{\sigma}) & := \int a(x) \chi^3_+(x) (\overline{m_+(x,\xi)}-1) \, e^{-i x\xi} \, e^{ix(\eta+{\sigma})} \, dx. \end{align} $$

We use the fast decay and smoothness of $m_+-1$ from Lemma 3.1 to integrate by parts. More precisely, for any M, we write

$$ \begin{align*} \big| R(\xi,\eta,{\sigma}) \big| & = \Big| \frac{1}{[i(\xi-\eta-{\sigma})]^M} \int e^{-i x\xi} \, e^{ix(\eta+{\sigma})} \partial_x^M \big[ a(x) \chi_+^3(x) \overline{(m_+(x,\xi)-1)} \big] \, dx \Big| \\ & \lesssim \frac{1}{|\xi-\eta-{\sigma}|^M} \sum_{0 \leq \alpha \leq M} \int_{x\geq -1} \big| \partial_x^{\alpha} (m_+(x,\xi)-1) \big|\, dx \lesssim \frac{1}{|\xi-\eta-{\sigma}|^M}, \end{align*} $$

having used equation (3.4) for the last inequality.

We have therefore bounded the expression in equation (4.24) by the right-hand side of equation (4.7) for $a=b=c=0$ .

To estimate the derivatives, notice that applying multiple $\eta $ - and ${\sigma }$ -derivatives is harmless since these result in additional powers of x, but $m_+-1$ decays as fast as desired. Similarly, again from equation (3.4), we see that $\partial _{\xi }$ derivatives can also be handled easily since $\partial _{\xi }^{\alpha } m$ decays fast as well. Notice that the second line in equation (4.23) can be treated exactly like the first one, using the properties of $m_-$ from equation (3.4). All the other terms in equation (4.21) can be treated the same way.

Let us look at the remaining piece in equation (4.22). We can write, according to the notation in equation (4.15) and the definition in equation (4.19),

(4.26) $$ \begin{align} \begin{aligned} \mu_{\iota_1 \iota_2}^{R2}(\xi,\eta,\sigma) = \sum \int a(x) \, \chi_{\epsilon_1}(x)\chi_{\epsilon_2}(x)\chi_{\epsilon_3}(x) \overline{\psi^{S,\epsilon_1}(x,\xi)} \psi^{S,\epsilon_2}(x,\eta) \psi^{S,\epsilon_3}(x,\sigma) \, dx, \qquad \end{aligned} \end{align} $$

where the sum is over $(\epsilon _1,\epsilon _2,\epsilon _3) \neq (+,+,+), (-,-,-)$ . In particular, this means that $a \, \chi _{\epsilon _1}\chi _{\epsilon _2}\chi _{\epsilon _3}$ is a smooth compactly supported function, which we denote by $\chi $ (omitting the dependence on the signs, which is not relevant here), and equation (4.26) is a linear combination of terms of the form

(4.27) $$ \begin{align} \begin{aligned} \int \chi(x) \overline{\mathbf{a}_\lambda^{\epsilon_1}(\xi) e^{i\lambda \xi x}} \mathbf{a}_\mu^{\epsilon_2}(\eta) e^{i\mu \eta x} \mathbf{a}_\nu^{\epsilon_3}({\sigma}) e^{i\nu {\sigma} x} \, dx = \widehat{\chi}(\lambda\xi -\mu\eta-\nu{\sigma}) \overline{\mathbf{a}_\lambda^{\epsilon_1}(\xi)}\mathbf{a}_\mu^{\epsilon_2}(\eta)\mathbf{a}_\nu^{\epsilon_3}({\sigma}). \end{aligned} \end{align} $$

The desired conclusion in equations (4.6)–(4.7) follows from the properties of the coefficients $\mathbf {a}_{\epsilon }^{\lambda }$ and the fact that $\widehat \chi $ is Schwartz.

4.2 Mapping properties for the regular part of the quadratic spectral distribution

The product operation $(f,g) \mapsto fg$ obviously satisfies Hölder’s inequality; but it is natural to ask about the mapping properties of the bilinear operators associated to the distributions $\mu ^S$ and $\mu ^R$

$$ \begin{align*}(f,g) \mapsto \widetilde{\mathcal{F}}^{-1} \int \mu^{S,R}(\xi,\eta,\sigma) \widetilde{f}(\eta) \widetilde{f}(\sigma) \,d\eta\,d\sigma. \end{align*} $$

The singular part $\mu ^S$ can be thought of as the leading order term; and indeed, it does satisfy Hölder’s inequality, and this is optimal. The regular part is lower-order in that it gains integrability ‘at $\infty $ ’, but it does not gain regularity. Thus, it can essentially be thought of as an operator of the type $(f,g) \mapsto F f g$ , where F is bounded and rapidly decaying. The following lemma gives a rigorous statement along these lines.

Lemma 4.2 Bilinear estimate for $\mu ^R$

Under the same assumptions and with the same notations as in Proposition 4.1, consider the measure $\mu ^R = \mu ^R_{\iota _1\iota _2}$ and the corresponding bilinear operator

(4.28) $$ \begin{align} M_R[a,b] := \widetilde{\mathcal{F}}^{-1} \iint \mu^R(\xi,\eta,{\sigma}) \widetilde{a}(\eta) \widetilde{b}({\sigma}) d\eta\,d{\sigma}. \end{align} $$

Then for all

$$ \begin{align*} p_1,p_2\in[2,\infty), \qquad \frac{1}{p_1}+\frac{1}{p_2} \leq \frac{1}{2} \end{align*} $$

it holds that

(4.29) $$ \begin{align} \begin{aligned} {\big\| M_R[a,b] \big\|}_{L^2} \lesssim {\| a \|}_{L^{p_1}} {\| b \|}_{L^{p_2}}. \end{aligned} \end{align} $$

Moreover, for $p_1,p_2$ as above and $p_3,p_4$ another pair satisfying the same assumptions, we have, for any integer $l\geq 0$ ,

(4.30) $$ \begin{align} \begin{aligned} {\big\| \langle \partial_x \rangle^l M_R[a,b] \big\|}_{L^2} \lesssim {\| \langle \partial_x \rangle^l a \|}_{L^{p_1}} {\| b \|}_{L^{p_2}} + {\| a \|}_{L^{p_3}} {\| \langle \partial_x \rangle^l b \|}_{L^{p_4}}. \end{aligned} \end{align} $$

Proof of Lemma 4.2

The starting point is the splitting of $\mu ^R$ in equations (4.20)–(4.22). We will omit the irrelevant signs $\iota _1\iota _2$ in what follows and just denote $\mu ^{R1,2}=\mu _{\iota _1 \iota _2}^{R1,2}$ . Also notice that in the definition of $M_R$ , we can replace all the distorted Fourier transforms by flat Fourier transforms, in view of the boundedness of the (adjoint) wave operator $\mathcal {W}^* := \widehat {{\mathcal {F}}}^{-1} \widetilde {{\mathcal {F}}}$ on $L^p$ , $p\in [2,\infty )$ ; see Proposition 3.9 and Theorem 3.10.

Proof of equation (4.29). From equation (4.21), we see that $\mu ^{R1}$ is a linear combination of terms of the form

(4.31) $$ \begin{align} \int \overline{\psi^A(x,\xi)}\psi^B(x,\eta) \psi^C(x,\sigma) \, dx, \end{align} $$

where at least one of the apexes $A,B$ or C is equal to R; recall the definition of $\psi ^S$ and $\psi ^R$ in equations (3.29) and (3.30). It suffices to look at the two cases $A=R$ or $B=R$ .

Let us first look at the case $A=R$ and further restrict our attention to $\xi>0$ and the contribution from $\chi _+$ ; all the other contributions can be handled the same way. We are then looking at the distribution

(4.32) $$ \begin{align} \mu_1(\xi,\eta,{\sigma}) := \int \overline{\chi_+(x) T(\xi) (m_+(x,\xi)-1) e^{i\xi x}} \psi^B(x,\eta) \psi^C(x,\sigma) \, dx, \qquad B,C = S \mbox{ or } R. \end{align} $$

The bilinear operator associated to it is

(4.33) $$ \begin{align} \begin{aligned} M_1[a,b] &= \widehat{{\mathcal{F}}}^{-1}_{\xi\mapsto x} \iint \mu_1(\xi,\eta,{\sigma}) \widehat{a}(\eta) \widehat{b}({\sigma}) d\eta\,d{\sigma} \\ & = \widehat{{\mathcal{F}}}^{-1}_{\xi\mapsto x}\! \int \! \chi_+(y) \overline{T(\xi) (m_+(y,\xi)-1)} e^{-i\xi y} \Big( \int_{\mathbb R} \widehat{a}(\eta) \psi^B(y,\eta) d\eta \Big) \Big( \int_{\mathbb R} \widehat{b}({\sigma}) \psi^C(y,\sigma) \, d{\sigma} \Big) \, dy. \end{aligned} \end{align} $$

If we define

(4.34) $$ \begin{align} u^A(x) := \int_{\mathbb R} \widehat{u}(\xi) \psi^A(x,\xi)\,d\xi, \qquad A=S,R, \end{align} $$

and the symbol $m(y,\xi ):= \langle y \rangle \chi _+(y) \overline {T(\xi ) (m_+(y,\xi )-1)}$ , we see that

$$ \begin{align*} {\| M_1[a,b] \|}_{L^2} & \lesssim {\Big\|\int_{\mathbb R} m(y,\xi) e^{-i\xi y} \cdot \langle y \rangle^{-1} \cdot a^B(y) \cdot b^C(y) \, dy \Big\|}_{L^2_{\xi}}. \end{align*} $$

In view of Lemmas 3.1 and 3.2, we see that $m=m(y,\xi )$ satisfies standard pseudo-differential symbol estimates and deduce that the associated operator is bounded $L^2\mapsto L^2$ . It follows that

(4.35) $$ \begin{align} \begin{aligned} {\| M_1[a,b] \|}_{L^2} & \lesssim {\| \langle y \rangle^{-1} \cdot a^B \cdot b^C \|}_{L^2_y} \lesssim {\| a^B \|}_{L^{p_1}} {\| b^C \|}_{L^{p_2}}. \end{aligned} \end{align} $$

The estimate in equation (4.35) gives us the right-hand side of equation (4.29), provided we show that $u \mapsto u^S , u^R$ as defined in equation (4.34) are bounded on $L^p$ , $p\in [2,\infty )$ . Since $u^S + u^R = u$ , it suffices to show ${\| u^S \|}_{L^p} \lesssim {\| u \|}_{L^p}$ . From the definition of $\psi ^S$ in equations (3.29) and (4.15)–(4.18), we see that this reduces to proving

(4.36) $$ \begin{align} {\Big\| \int_{\mathbb R} e^{i\lambda x\xi} \mathbf{a}_{\lambda}^{\pm}(\xi) \widehat{u}(\xi) \,d\xi \Big\|}_{L^p} \lesssim {\|u\|}_{L^p}. \end{align} $$

In view of the boundedness of the Hilbert transform, it is enough to obtain the same bound where the coefficients $\mathbf {a}_{\lambda }^{\pm }$ are replaced just by $T(\pm \xi )$ or $R_{\pm }(\mp \xi )$ . The desired bound then follows since $T(\pm \xi )-1$ and $R_{\pm }(\mp \xi )$ are $H^1$ functions (see equation (3.14)) so that their Fourier transforms are in $L^1$ .

Consider next the case $B=R$ . Again, without loss of generality, we may restrict our attention to $\eta>0$ and the contribution from $\chi _+$ : that is, we look at the measure

(4.37) $$ \begin{align} \mu_1'(\xi,\eta,{\sigma}) := \int \chi_+(x) \psi^S(x,\xi) \overline{T(\eta) (m_+(x,\eta)-1) e^{i\eta x}} \psi^C(x,\sigma) \, dx, \qquad C = S \mbox{ or } R. \end{align} $$

Letting the associated operator be

(4.38) $$ \begin{align} \begin{aligned} M_1'[a,b] &:= \widehat{{\mathcal{F}}}^{-1}_{\xi\mapsto x} \iint \mu_1'(\xi,\eta,{\sigma}) \widehat{a}(\eta) \widehat{b}({\sigma}) \,d\eta\,d{\sigma} \\ & = \widehat{{\mathcal{F}}}^{-1}_{\xi\mapsto x} \int \chi_+(y) \psi^S(y,\xi) \Big( \int_{\mathbb R} \widehat{a}(\eta) \overline{T(\eta) (m_+(y,\eta)-1) e^{i\eta y}} \, d\eta \Big) \Big( \int_{\mathbb R} \widehat{b}({\sigma}) \psi^C(y,\sigma) \, d{\sigma} \Big) \, dy, \end{aligned} \end{align} $$

we see that

$$ \begin{align*} {\| M_1'[a,b] \|}_{L^2} & \lesssim {\Big\| \langle y \rangle \int_{\mathbb R} \overline{T(\eta) (m_+(y,\eta)-1) e^{i\eta y}} \, \widehat{a}(\eta) \, d\eta \Big\|}_{L^{p_1}} {\| b^C \|}_{L^{p_2}} \end{align*} $$

having used that $\psi ^S$ defines a bounded PDO on $L^2$ , as we showed above. The desired conclusion in equation (4.29) then follows since $\langle x \rangle T(\eta ) (m_+(x,\eta )-1)$ is the symbol of a bounded PDO on $L^p$ , for $p\in (2,\infty )$ in view of Lemmas 3.1, 3.2 and standard results on PDOs; see, for example, [3].

We now analyse the $\mu ^{R,2}$ component from equation (4.22) by looking at the more explicit expression for it in equation (4.27). From this, we see that it suffices to look at bilinear operators of the form

(4.39) $$ \begin{align} M_2[a,b] := \widehat{{\mathcal{F}}}^{-1}_{\xi\mapsto x} \iint_{{\mathbb R}\times{\mathbb R}} \widehat{\chi}(\lambda\xi -\mu\eta-\nu{\sigma}) \overline{\mathbf{a}_\lambda^{\epsilon_1}(\xi)}\mathbf{a}_\mu^{\epsilon_2}(\eta)\mathbf{a}_\nu^{\epsilon_3}({\sigma}) \widehat{a}(\eta) \widehat{b}({\sigma}) \,d\eta\,d{\sigma}, \end{align} $$

where $\chi $ is Schwartz. By boundedness of the Fourier multipliers $\mathbf {a}^{\epsilon }_{\lambda }$ ,

$$ \begin{align*} {\| M_2[a,b] \|}_{L^2} & \lesssim {\big\| \chi \cdot \widehat{{\mathcal{F}}}^{-1}\big( \mathbf{a}_\mu^{\epsilon_2} \widehat{a}\big) \widehat{{\mathcal{F}}}^{-1}\big( \mathbf{a}_\nu^{\epsilon_3}\widehat{b} \big) \big\|}_{L^2} \\ & \lesssim {\big\| \widehat{{\mathcal{F}}}^{-1}\big( \mathbf{a}_\mu^{\epsilon_2} \widehat{a}\big) \big\|}_{L^{p_1}} {\big\| \widehat{{\mathcal{F}}}^{-1}\big( \mathbf{a}_\nu^{\epsilon_3}\widehat{b} \big) \big\|}_{L^{p_2}} \lesssim {\| a \|}_{L^{p_1}} {\| b \|}_{L^{p_2}}. \end{align*} $$

Proof of equation (4.30). We proceed similarly to the proof of equation (4.29) and reduce to estimating derivatives of the bilinear operators $M_1, M_1^{\prime }$ and $M_2$ , respectively, defined in equation (4.33), equation (4.38) and (4.39);

Applying derivatives to $M_1$ gives

(4.40) $$ \begin{align} \begin{aligned} \partial_x^l M_1[a,b] & = \widehat{{\mathcal{F}}}^{-1}_{\xi\mapsto x} \int_{\mathbb R} \chi_+(y) \overline{T(\xi) (m_+(y,\xi)-1)} \, (i\xi)^l e^{-i\xi y} a^A(y) \, b^B(y) \, dy. \end{aligned} \end{align} $$

Integrating by parts in y and distributing derivatives on $a^A$ , $b^B$ and $m_+-1$ gives a linear combination of terms of the form

(4.41) $$ \begin{align} \begin{aligned} M_{l_1,l_2}[a,b] := \widehat{{\mathcal{F}}}^{-1}_{\xi\mapsto x} \int_{\mathbb R} \overline{T(\xi)} \, \partial_y^{l_1} \big( \chi_+(y) (\overline{m_+(y,\xi)-1} ) \big) \, e^{-i\xi y} \cdot \partial_y^{l_2} \big(a^A(y) \, b^B(y) \big) \, dy \end{aligned} \end{align} $$

with $l_1+l_2=l$ . From Lemmas 3.1, 3.2, we see that $m_{l_1}(x,\xi ) := \overline {T(\xi )} \, \partial _x^{l_1} \big ( \chi _+(x) (\overline {m_+(x,\xi )-1} ) \big )$ gives rise to a standard PDO bounded on $L^2$ . Therefore, to bound in equation (4.41) by the right-hand side of equation (4.30), it suffices to use product Sobolev inequalities and ${\| \partial _x^l u^S \|}_{L^p} \lesssim {\| \langle \partial _x \rangle ^l u \|}_{L^p}$ , $p\in [2,\infty )$ , which follows from the inequality in equation (4.36) with $\partial _x^lu$ instead of u.

A similar argument can be used for $M_1^{\prime }$ : from equation (4.38), we see that x-derivatives become powers of $\xi $ , which in turn can be transformed to y-derivatives since $\psi ^S(y,\xi )$ is a linear combination of exponentials $e^{\pm i y\xi }$ by harmless $\xi $ -dependent coefficients; integrating by parts in y and using the boundedness on $L^p$ of the PDO with symbol $\langle x \rangle m_{l_1}(x,\xi ) $ gives the desired bound.

The argument for $M_2$ is straightforward, using that $T-1$ is a bounded multiplier and $\chi $ is Schwartz:

$$ \begin{align*} {\| \langle \partial_x \rangle^l M_2[a,b] \|}_{L^2} \lesssim {\Big\| \langle \partial_x \rangle^l \Big[ \chi \cdot \widehat{{\mathcal{F}}}^{-1}\big( a_\mu^{\epsilon_2} \widehat{a}\big) \widehat{{\mathcal{F}}}^{-1}\big( a_\nu^{\epsilon_3}\widehat{b} \big) \Big] \Big\|}_{L^2} \lesssim {\Big\| \langle \partial_x \rangle^l \Big[ \widehat{{\mathcal{F}}}^{-1}\big( a_\mu^{\epsilon_2} \widehat{a}\big) \widehat{{\mathcal{F}}}^{-1}\big( a_\nu^{\epsilon_3}\widehat{b} \big) \Big] \Big\|}_{L^q} \end{align*} $$

with $1/q=1/p_1+1/p_2$ , and we can use standard Gagliardo-Nirenberg-Sobolev inequalities and equation (4.36) to obtain equation (4.30).

5 The main nonlinear decomposition

In this section, we first write Duhamel’s formula in distorted Fourier space and decompose the nonlinear terms according to the results in Section 4 and their nonlinear resonance properties. In particular, in Section 5.2, we give our main splitting of the quadratic terms into ‘singular’ and ‘regular’. In Section 5.3, we prove lower bounds for the oscillating phases that appear in the singular quadratic terms and use this in Section 5.4 to apply normal form transformations. We then analyse the various resulting cubic terms in Sections 5.5 and 5.6. Here, there is a substantial algebraic component because we are treating general transmission and reflection coefficients, and we need to keep track of exact expressions to calculate asymptotics later; moreover, the coefficients in equation (4.5) may have jump discontinuities that we need to take care of after the normal form transformations; finally, we also need to study convolutions of $\delta $ distributions and (cutoff) $\mathrm {p.v.}$ -type distributions and prove various symbol type estimates on the expressions obtained after the normal forms. In the final Section 5.7, we introduce the renormalised profile f on which we will perform all main estimates moving forward; we then recapitulate all the formulas and properties obtained so far and prove regularity in $\xi $ for the symbols of the relevant operators.

5.1 Duhamel’s formula

Let $u = u(t,x)$ be a solution of the quadratic Klein-Gordon equation

(KG) $$ \begin{align} \begin{aligned} & \partial_{t}^2 u +( - \partial_x^2 +V + 1) u = a(x)u^2, \qquad (u,u_t)(t=0) = (u_0,u_1), \end{aligned} \end{align} $$

with the assumptions of Theorem 1.1. In the distorted Fourier space, equation (KG) is

(5.1) $$ \begin{align} & \partial_{t}^2 \widetilde{u} + (\xi^2 + 1) \widetilde{u} = \widetilde{\mathcal{F}}(a(x)u^2), \qquad (\widetilde{u},\widetilde{u_t})(t=0) = (\widetilde{u_0},\widetilde{u_1}). \end{align} $$

To write Duhamel’s formula in the distorted Fourier space, we define (recall $H = - \partial _x^2 + V$ )

(5.2) $$ \begin{align} & v(t,x) := \big(\partial_{t} -i \sqrt{ H + 1 } \big)u, \qquad \widetilde{v}(t,\xi) := \big(\partial_{t} - i \langle \xi \rangle \big) \widetilde{u}. \end{align} $$

Notice that, by Lemma 3.8, $\sqrt {H + 1} u$ is real-valued since u is; therefore,

(5.3) $$ \begin{align} & u = \frac{v-\overline{v}}{-2i\sqrt{H + 1}} \end{align} $$

and

(5.4) $$ \begin{align} & \big(\partial_{t} +i \sqrt{H + 1}\big)v = a(x)u^2, \qquad \big(\partial_{t} + i \langle \xi \rangle \big)\widetilde{v} = \widetilde{\mathcal{F}}(a(x)u^2). \end{align} $$

By defining the profile

(5.5) $$ \begin{align} & g(t,x) := \Big(e^{it\sqrt{H+ 1}}v(t,\cdot) \Big)(x), \qquad \widetilde{g}(t,\xi) = e^{it\langle \xi \rangle} \widetilde{v}(t,\xi), \end{align} $$

we have

(5.6) $$ \begin{align} & \partial_t \widetilde{g}(t,\xi) = e^{it\langle \xi \rangle} \widetilde{\mathcal{F}}(a(x)u^2). \end{align} $$

Using the definition of the distorted Fourier transform equation (3.21), in view of equations (5.3) and (5.5), this becomes

(5.7) $$ \begin{align} \partial_t \widetilde{g}(t,\xi) & = \sum_{\iota_1,\iota_2 \in \{+,-\}} \iota_1 \iota_2 e^{it \langle \xi \rangle} \iint \left( \int a(x) \overline{\psi(x,\xi)} \psi_{\iota_1}(x,\eta) \psi_{\iota_2}(x,\sigma) \, dx \right) \nonumber \\ &\quad \times \frac{e^{-\iota_1 i t \langle \eta \rangle}}{2i\langle \eta \rangle}\widetilde{g}_{\iota_1}(t,\eta) \frac{e^{-\iota_2 i t \langle \sigma \rangle}}{2i\langle \sigma \rangle}\widetilde{g}_{\iota_2}(t,\sigma) \, d\eta\, d\sigma \\ \nonumber & = - \sum_{\iota_1,\iota_2 \{+,-\}} \iota_1\iota_2 \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \widetilde{g}_{\iota_1}(t,\eta) \widetilde{g}_{\iota_2}(t,\sigma) \, \frac{1}{4\langle \eta \rangle \langle \sigma \rangle} \mu_{\iota_1\iota_2}(\xi,\eta,\sigma) \, d\eta \, d\sigma, \end{align} $$

where the quadratic spectral distribution $\mu _{\iota _1 \iota _2}$ is defined in Proposition 4.1,

(5.8) $$ \begin{align} & \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma) := \langle \xi \rangle - \iota_1 \langle \eta \rangle - \iota_2 \langle \sigma \rangle, \end{align} $$

and we have denoted

$$ \begin{align*} \widetilde{g}_{+} = \widetilde{g}, \qquad \widetilde{g}_{-} = \overline{\widetilde{g}}. \end{align*} $$

5.2 Decomposition of the quadratic nonlinearity

Starting from equations (5.7)–(5.8) and using the decomposition of the distribution $\mu $ in Proposition 4.1, we can decompose the nonlinearity accordingly. More precisely, we write

(5.9) $$ \begin{align} \partial_t \widetilde{g} & = \mathcal{Q}^S + \mathcal{Q}^R = \sum_{\iota_1,\iota_2 \in \{+,-\}} \mathcal{Q}^{S}_{\iota_1\iota_2} + \mathcal{Q}_{\iota_1\iota_2}^R, \end{align} $$

where $ \mathcal {Q}^{S}_{\iota _1\iota _2}$ and $\mathcal {Q}_{\iota _1\iota _2}^R$ are defined below.

Notation convention. When summing over different combinations of signs, such as in the formula in equation (5.9), we will often just indicate the indexes or apexes with the understanding that they can be either $+$ or $-$ . Also, we will have expressions that depend on several signs, such as the ones appearing in equation (5.11). In such cases, we will only separate the various indexes or apexes with commas when there is a risk of confusion; see, for example, equation (5.32) versus equation (5.10).

The singular quadratic interaction $\mathcal {Q}^S_{\iota _1\iota _2}$ . We define $\mathcal {Q}^S_{\iota _1\iota _2}$ to be the contribution coming from the singular part of $\mu $ (see equations (4.1)–(4.2)) with an additional cutoff in frequency that localises the principal value part to a suitable neighbourhood of the singularity

(5.10) $$ \begin{align} \begin{aligned} & \mathcal{Q}_{\iota_1\iota_2}^{S} (t,\xi) := -\iota_1\iota_2 \sum_{\substack{\lambda,\mu,\nu \in \{+,-\}\\ \epsilon \in \{+,-\}}} \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \widetilde{g}_{\iota_1}(t,\eta) \widetilde{g}_{\iota_2}(t, \sigma) Z^{\epsilon} _{\substack{- \iota_1 \iota_2 \\ \lambda \mu \nu}}(\xi,\eta,\sigma)\, d\eta \,d\sigma, \end{aligned} \end{align} $$

with

(5.11) $$ \begin{align} \begin{aligned} Z^{\epsilon} _{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda \mu \nu}}(\xi,\eta,\sigma) & := \ell_{\epsilon \infty} \frac{a^{\epsilon}_{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda\mu\nu}} (\xi, \eta,\sigma)}{8\pi\langle \eta \rangle \langle \sigma \rangle} \left[ \sqrt{\frac{\pi}{2}} \delta(p) + \epsilon \varphi^{\ast}(p,\eta,\sigma) \, \mathrm{p.v.} \frac{\widehat{\phi}(p)}{ip} \right], \end{aligned} \end{align} $$

where

(5.12) $$ \begin{align} \varphi^{\ast}(p,\eta,\sigma) := \varphi_{\leq -D_0}\big(p R(\eta,\sigma)\big), \qquad p = - \iota_0 \lambda \xi - \iota_1 \mu \eta - \iota_2 \nu \sigma, \end{align} $$

for $D_0$ a suitably large absolute constant, and

(5.13) $$ \begin{align} R(\eta,\sigma) = \frac{\langle \eta \rangle \langle \sigma \rangle}{\langle \eta \rangle + \langle \sigma \rangle}. \end{align} $$

The last expression may be thought of as a regularization of $\mathrm {min}(\langle \eta \rangle ,\langle \sigma \rangle )$ , and satisfies

(5.14) $$ \begin{align} | \partial_{\eta}^a \partial_{\sigma}^b R(\eta,\sigma)| \lesssim \mathrm{min}(\langle \eta \rangle ,\langle \sigma \rangle) \langle \eta \rangle^{-a} \langle \sigma \rangle^{-b}. \end{align} $$

The regular quadratic interaction $\mathcal {Q}_{\iota _1\iota _2}^R$ . The term $\mathcal {Q}_{\iota _1\iota _2}^R$ gathers the contributions coming from the smooth distribution $\mu ^R$ (see equations (4.1) and (4.6)-s(4.7)) and the smooth part from the $\mathrm {p.v.}$ that is not included in equation (5.11). We can write it as

(5.15) $$ \begin{align} \begin{aligned} & \mathcal{Q}_{\iota_1\iota_2}^R(t,\xi) := -\iota_1\iota_2 \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \, \mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,\sigma) \, \widetilde{g}_{\iota_1}(t,\eta) \widetilde{g}_{\iota_2}(t,\sigma) \, d\eta \, d\sigma, \end{aligned} \end{align} $$

where $\Phi _{\iota _1\iota _2}$ is the phase in equation (5.8) and the symbol is

(5.16) $$ \begin{align} \begin{aligned} & \mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,\sigma) = \mathfrak{q}_{\iota_1\iota_2}^+(\xi,\eta,\sigma) + \mathfrak{q}_{\iota_1\iota_2}^-(\xi,\eta,\sigma) + \frac{1}{8\pi \langle \eta \rangle\langle \sigma \rangle}\mu^R_{\iota_1\iota_2}(\xi,\eta,\sigma), \\ & \mathfrak{q}^{\epsilon}_{\iota_1\iota_2}(\xi,\eta,\sigma) = \frac{\epsilon}{8\pi\langle \eta \rangle\langle \sigma \rangle} \sum_{\lambda, \mu, \nu} a^{\epsilon}_{\substack{- \iota_1 \iota_2 \\ \lambda\mu\nu}} (\xi,\eta,\sigma) \big(1 - \varphi^{\ast}(p,\eta,\sigma) \big) \frac{\widehat{\phi}(p)}{i p}, \end{aligned} \end{align} $$

with $\mu ^R_{\iota _1\iota _2}$ satisfying the properties in equations (4.6)–(4.7) (also recall that $p = \lambda \xi - \iota _1 \mu \eta - \iota _2 \nu \sigma $ ). Here is a remark that will help us simplify the notation:

Remark 5.1 (A more convenient rewriting of $\mathcal {Q}_{\iota _1\iota _2}^R$ )

For $\iota ,\kappa = \pm 1$ , let

(5.17) $$ \begin{align} \widetilde{g}^{\kappa}_{\iota}(\xi) := \widetilde{g}_\iota (\xi) \mathbf{1}_{\kappa}(\xi), \end{align} $$

and notice that for all $\iota ,\kappa $ , $\widetilde {g}_\iota ^{\kappa }$ enjoys the same bootstrap assumptions as $\widetilde {g}$ ; see equation (7.7). Then inspecting the definition of equation (5.15) and its symbol in equation (5.16), and recalling the definitions of the coefficients in equations (4.4)–(4.5) and the property of $\mu ^R_{\iota _1\iota _2}$ in equations (4.6)–(4.7), we see that we can peel off all indicator functions and write

(5.18) $$ \begin{align} \begin{aligned} \mathcal{Q}^R_{\iota_1 \iota_2} & = \displaystyle \sum_{\kappa_0, \kappa_1, \kappa_2} \mathcal{Q}^R_{\substack{\iota_1 \iota_2 \\ \kappa_0 \kappa_1 \kappa_2}}, \\ \mathcal{Q}^R_{\substack{\iota_1 \iota_2 \\ \kappa_0 \kappa_1 \kappa_2}} & := -\iota_1\iota_2 \mathbf{1}_{\kappa_0}(\xi) \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \, \mathfrak{q}_{\substack{\iota_1 \iota_2 \\ \kappa_0\kappa_1 \kappa_2}} (\xi,\eta,\sigma) \, \widetilde{g}_{\iota_1}^{\kappa_1} (t,\eta) \widetilde{g}_{\iota_2}^{\kappa_2}(t,\sigma) \, d\eta \, d{\sigma}, \end{aligned} \end{align} $$

where the symbols $\mathfrak {q}_{\substack {\iota _1 \iota _2 \\ \kappa _0\kappa _1 \kappa _2}}$ are smooth. In what follows, we will often omit the signs $\kappa _0,\kappa _1,\kappa _2$ in our notation (for the operators and the symbols), as these play no essential role. We will instead keep the $\iota _1,\iota _2$ signs since they do play a role: the case $\iota _1,\iota _2=+$ is the main resonant one, while the other cases are relatively easier to treat. Also notice that the indicator function in the output variable $\xi $ will not be a problem upon differentiation (which will happen when estimating weighted $L^2$ -norms; see equation (2.35)), as shown in Lemma 5.9.

5.3 Estimates on the phases

As a preparation for the normal form transformation to come, we need very precise estimates on the phase. The complication here arises since the quadratic modulus of resonance, although positive for all interactions, degenerates at $\infty $ in certain directions.

Lemma 5.2 (Lower bound for the phases)

For any $\eta ,\sigma \in {\mathbb R}$ ,

(5.19) $$ \begin{align} \langle \eta + \sigma \rangle - \langle \eta \rangle - \langle \sigma \rangle \approx \left\{ \begin{array}{ll} - \mathrm{min}( \langle \eta \rangle , \langle \sigma \rangle) & \mbox{if}\ \eta \sigma < 0 \\ \displaystyle - \frac{1}{\mathrm{min}( \langle \eta \rangle , \langle \sigma \rangle)} & \mbox{if}\ \eta \sigma> 0 \,. \end{array} \right. \end{align} $$

As a consequence, for any choice of $\iota _1,\iota _2 \in \{+,-\}$ and any $\eta ,\sigma \in {\mathbb R}$ ,

(5.20) $$ \begin{align} \left| \frac{1}{\Phi_{\iota_1 \iota_2}(\eta + \sigma,\eta,\sigma)} \right| \lesssim \mathrm{min}(\langle \eta + \sigma \rangle, \langle \eta \rangle, \langle \sigma \rangle). \end{align} $$

Furthermore, if $p:= \xi - \iota _1\eta - \iota _2{\sigma }$ is such that

$$ \begin{align*} |p| \leq \frac{2^{-D_0+2}}{ R(\eta, \sigma)}, \end{align*} $$

with $D_0$ sufficiently large, then

(5.21) $$ \begin{align} \left| \frac{1}{\Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \right| \lesssim \mathrm{min}( \langle \eta \rangle, \langle \sigma \rangle). \end{align} $$

Proof. In order to prove equation (5.19), we focus on the case where $\eta $ and $\sigma $ have equal signs since the other case is trivial. The expression under study can be written

$$ \begin{align*}\langle \eta + \sigma \rangle - \langle \eta \rangle - \langle \sigma \rangle = \frac{-1 + 2\eta \sigma - 2 \langle \eta \rangle \langle \sigma \rangle }{\langle \eta + \sigma \rangle + \langle \eta \rangle + \langle \sigma \rangle}. \end{align*} $$

If $\eta $ and $\sigma $ are $O(1)$ , the result is obvious, so we focus on the case where $\eta + \sigma \gg 1$ . On the one hand, the denominator above is $\sim \mathrm {max}(\langle \eta \rangle , \langle \sigma \rangle )$ . On the other hand, if $\eta \approx \sigma $ , the numerator above can be expanded as

$$ \begin{align*} -1 + 2\eta \sigma - 2 \langle \eta \rangle \langle \sigma \rangle & = -1 + 2 \eta \sigma \left(- \frac{1}{2\eta^2} - \frac{1}{2 \sigma^2} + O\left(\frac{1}{ \eta^4} \right) \right) \approx -1. \end{align*} $$

If $\eta \gg \sigma $ , the numerator can be written

$$ \begin{align*} -1 + 2\eta \sigma - 2 \langle \eta \rangle \langle \sigma \rangle & = -1 + 2 \eta \left(\sigma - \langle \sigma \rangle - \frac{\langle \sigma \rangle}{2 \eta^2} + O \left( \frac{\langle \sigma \rangle}{\eta^4} \right)\right) \approx - \frac{\eta}{\langle \sigma \rangle}, \end{align*} $$

where the above line follows from $\sigma - \langle \sigma \rangle \approx - \frac {1}{\langle \sigma \rangle }$ and $\frac {\langle \sigma \rangle }{\eta ^2} \ll \frac {1}{\langle \sigma \rangle }$ . Equation (5.19) follows from the above relations.

In order to prove equation (5.20), we observe that the case $\iota _1,\iota _2 = +$ was just treated, while the case $--$ is trivial. There remains the case $+-$ , which easily reduces to $++$ .

Finally, in order to prove equation (5.21), only the cases $++$ and $+-$ require attention. We focus on the former, the argument for the latter being an immediate adaptation. It follows from the estimate in equation (5.19) that only the case $\eta ,\sigma> 0$ requires attention. Then

(5.22) $$ \begin{align} \begin{aligned} \big| \Phi_{++}(\xi,\eta,{\sigma}) \big| & = | \langle \xi \rangle - \langle \eta \rangle - \langle \xi - \eta \rangle + (\langle \xi - \eta \rangle - \langle \sigma \rangle)| \\ & \geq | \langle \xi \rangle - \langle \eta \rangle - \langle \xi - \eta \rangle | - \frac{| \xi - \eta|^2 - |{\sigma}|^2}{\langle \xi - \eta \rangle + \langle \sigma \rangle} \\ & \geq \frac{C}{R(\eta,\sigma)} - |p| \cdot \frac{| \xi - \eta + {\sigma}|}{\langle \xi - \eta \rangle + \langle \sigma \rangle}. \end{aligned} \end{align} $$

By choosing the absolute constant $D_0$ large enough, it follows that

(5.23) $$ \begin{align} \big| \Phi_{++}(\xi,\eta,\sigma) \big| \gtrsim \frac{1}{R(\eta,\sigma)} \approx\frac{1}{\mathrm{min}( \langle \eta \rangle, \langle \sigma \rangle)}. \end{align} $$

Lemma 5.3 (Derivatives of the phases)

Assume that $|p| \leq 2^{-D_0+2} R(\eta ,\sigma )^{-1}$ (note that here p is regarded as an independent variable), and let $a,b,c$ be arbitrary nonnegative integers. Then:

1. (i) For any $\eta , \sigma>0$ ,

   (5.24) $$ \begin{align} \left| \partial_{\eta}^a \partial_{\sigma}^b \partial_p^c \frac{1}{\langle p+\eta+{\sigma} \rangle - \langle \eta \rangle - \langle \sigma \rangle} \right| \lesssim \frac{R(\eta,\sigma)^{1+c}}{\langle \eta \rangle^a \langle \sigma \rangle^b}. \end{align} $$

2. (ii) For any $\eta , \sigma>0$ ,

   (5.25) $$ \begin{align} \left| \partial_{\eta}^a \partial_{\sigma}^b \partial_p^c \frac{1}{\langle p+\eta+{\sigma} \rangle + \langle \eta \rangle - \langle \sigma \rangle} \right| \lesssim \frac{1}{\langle \eta \rangle^a \langle \sigma \rangle^b}. \end{align} $$

3. (iii) For any $\iota _1,\iota _2 \in \{+,-\}$ ,

   (5.26) $$ \begin{align} \left| \partial_{\eta}^a \partial_{\sigma}^b \partial_p^c \frac{1}{\Phi_{\iota_1 \iota_2}(p+\eta+{\sigma},\eta,\sigma)} \right| \lesssim \mathrm{min}(\langle p+\eta+{\sigma} \rangle, \langle \eta \rangle, \langle \sigma \rangle)^{1+c}. \end{align} $$

Proof. Let us denote $\xi =p+\eta +{\sigma }$ . The proof of the first assertion relies on the lower bound $|\Phi _{++}(\xi ,\eta ,\sigma )| \gtrsim R(\eta ,\sigma )^{-1}$ and on the bounds on derivatives

$$ \begin{align*} & \left| \partial_{\eta}^a \Phi_{++}(\xi,\eta,\sigma) \right| \lesssim \langle \eta \rangle^{-a-1} \\ & \left| \partial_{\sigma}^a \Phi_{++}(\xi,\eta,\sigma) \right| \lesssim \langle \sigma \rangle^{-a-1} \\ & \left| \partial_p \Phi_{++}(\xi,\eta,\sigma) \right| \lesssim 1 \\ & \left| \partial_p^a \partial_{\eta}^b \partial_{\sigma}^c \Phi_{++}(\xi,\eta,\sigma) \right| \lesssim \langle \eta + \sigma \rangle^{-a-b-c-1} \qquad \mbox{if at most one of}\ a,b,c\ \mbox{vanishes, or}\ a \geq 2. \end{align*} $$

Similarly, the proof of the second assertion relies on the lower bound $|\Phi _{-+}(\xi ,\eta ,\sigma )| \gtrsim \langle \eta \rangle $ and on the bounds on derivatives

$$ \begin{align*} & \left| \partial_{\eta}^a \Phi_{-+}(\xi,\eta,\sigma) \right| \lesssim 1 \qquad \mbox{if}\ a=1, \quad \mbox{and} \quad \langle \eta \rangle^{-a-1} \quad \mbox{if}\ a\geq 2 \\ & \left| \partial_{\sigma}^a \Phi_{-+}(\xi,\eta,\sigma) \right| \lesssim \langle \sigma \rangle^{-a-1} \\ & \left| \partial_p \Phi_{-+}(\xi,\eta,\sigma) \right| \lesssim 1 \\ & \left| \partial_p^a \partial_{\eta}^b \partial_{\sigma}^c \Phi_{-+}(\xi,\eta,\sigma) \right| \lesssim \langle \eta + \sigma \rangle^{-a-b-c-1} \qquad \mbox{if at most one of}\ a,b,c\ \mbox{vanishes, or}\ a \geq 2. \end{align*} $$

In order to prove the third assertion, we must distinguish several cases. First, the case $(\iota _1,\iota _2) = (-,-)$ is trivial. Second, if $(\iota _1,\iota _2) = (+,+)$ and $\eta , \sigma $ have the same sign, then it suffices to use equation (5.24), while if they have opposite signs, the inequality is trivial. Finally, if $(\iota _1,\iota _2) = (-,+)$ , the only difficult case is that for which $\eta \sigma <0$ and $|\sigma |> |\eta |$ . In that case, $\Phi _{-+}$ enjoys the lower bound

$$ \begin{align*}|\Phi_{-+} (\xi,\eta,\sigma) | \sim \mathrm{min}( \langle \xi \rangle,\langle \eta \rangle)^{-1} \sim \mathrm{min}( \langle \xi \rangle,\langle \eta \rangle,\langle \sigma \rangle)^{-1}, \end{align*} $$

while its derivatives can be bounded as follows:

$$ \begin{align*} & \left| \partial_{\eta}^a \Phi_{-+}(\xi,\eta,\sigma) \right| \lesssim \mathrm{min}(\langle \eta \rangle, \langle \eta + \sigma \rangle )^{-a-1} \\ & \left| \partial_{\sigma}^a \Phi_{-+}(\xi,\eta,\sigma) \right| \lesssim \langle \eta + \sigma \rangle^{-a-1} \\ & \left| \partial_p \Phi_{-+}(\xi,\eta,\sigma) \right| \lesssim 1 \\ & \left| \partial_p^a \partial_{\eta}^b \partial_{\sigma}^c \Phi_{-+}(\xi,\eta,\sigma) \right| \lesssim \langle \eta + \sigma \rangle^{-a-b-c-1} \qquad \mbox{if at most one of}\ a,b,c\ \mbox{vanishes, or}\ a \geq 2. \end{align*} $$

Combining these estimates gives the desired bound equation (5.26).

5.4 Performing the normal form transformation

We will now perform a normal form transformation on $\mathcal {Q}^{S}$ . It is not possible to do so globally on $\mathcal {Q}^R$ , which is ultimately one of the main difficulties in the nonlinear analysis. The lower bounds in Lemma 5.2 allow us to integrate by parts using the identity

(5.27) $$ \begin{align} \frac{1}{i \Phi_{\iota_1\iota_2}} \partial_s e^{is \Phi_{\iota_1\iota_2}} = e^{is \Phi_{\iota_1 \iota_2}}. \end{align} $$

By symmetry, it will suffice to consider the case when the time derivative hits the second function. This gives

(5.28) $$ \begin{align} \sum_{\substack{\iota_1,\iota_2 }} \int_0^t \mathcal{Q}_{\iota_1\iota_2}^{S} (s,\xi) \, ds = \{ \mbox{boundary terms} \} + \{ \mbox{integrated terms} \}. \end{align} $$

The boundary terms are given by the following expression:

(5.29) $$ \begin{align} \begin{aligned} & \{ \mbox{boundary terms} \} = \sum_{\substack{\iota_1,\iota_2 }} {\widetilde{\mathcal{F}}} T_{\iota_1\iota_2}(g,g)(t) - {\widetilde{\mathcal{F}}} T_{\iota_1\iota_2}(g,g)(0) \\ & {\widetilde{\mathcal{F}}} \big(T_{\iota_1\iota_2}(g,g)\big)(t,\xi) := - \iota_1\iota_2 \sum_{\substack{\lambda, \mu, \nu \\ \epsilon} } \iint e^{it \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \widetilde{g}_{\iota_1}(t,\eta) \widetilde{g}_{\iota_2}(t, \sigma) \frac{Z^{\epsilon} _{\substack{- \iota_1 \iota_2 \\ \lambda \mu \nu}}(\xi,\eta,\sigma)}{i \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)}\, d\eta\, d\sigma. \\ \end{aligned} \end{align} $$

The integrated terms read

(5.30) $$ \begin{align} \begin{aligned} & \{ \mbox{integrated terms} \} = \\ & \qquad \qquad \sum_{\substack{\iota_1, \iota_2 \\ \epsilon}} 2 \iota_1\iota_2 \int_0^t \sum_{\lambda, \mu, \nu} \iint e^{it \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \widetilde{g}_{\iota_1}(s,\eta) \partial_s \widetilde{g}_{\iota_2}(s,{\sigma}) \frac{Z^{\epsilon}_{\substack{- \iota_1 \iota_2 \\ \lambda \mu \nu}}(\xi,\eta,\sigma)}{i \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)}\, d\eta\, d\sigma\,ds. \end{aligned} \end{align} $$

We now plug in $\partial _s \widetilde {g} = \sum _{\iota _1,\iota _2} \mathcal {Q}^{S \sharp }_{\iota _1\iota _2} + \mathcal {Q}^{R \sharp }_{\iota _1\iota _2}$ , where $\mathcal {Q}^{R\sharp ,S\sharp }_{\iota _1\iota _2}$ are defined exactly as $\mathcal {Q}^{R,S}_{\iota _1\iota _2}$ (see equations (5.10) and (5.15)), with the exception that $\varphi ^*$ is replaced by $1$ ; similarly for $Z^{\sharp \,\epsilon }_{\substack { \iota _0,\iota _1 , \iota _2 \\ \lambda \mu \nu }}$ versus $Z^{\epsilon }_{\substack { \iota _0,\iota _1 , \iota _2 \\ \lambda \mu \nu }}$ , and $\mathfrak {q}^{\sharp }$ versus $\mathfrak {q}$ below. In particular (see equation (5.16)), $\mathfrak {q}^{\sharp }(\xi ,\eta ,\sigma ) = (8\pi \langle \eta \rangle \langle \sigma \rangle )^{-1}\mu ^R_{\iota _1\iota _2}(\xi ,\eta ,\sigma )$ .

An important observation is that, since $\widehat {\phi }$ is even and real-valued,

$$ \begin{align*}\left( Z^{\epsilon'}_{\substack{\iota_0',\iota_1',\iota_2' \\ \\\lambda',\mu',\nu'}}(\sigma,\eta',\sigma') \right)_{\iota_2} = Z^{\epsilon'}_{\substack{\iota_2 \iota_0',\iota_2 \iota_1',\iota_2 \iota_2' \\ \\\lambda',\mu',\nu'}}(\sigma,\eta',\sigma'). \end{align*} $$

This gives

(5.31) $$ \begin{align} & \{ \mbox{integrated terms} \} = \int_0^t \big( B_1(s) + B_2(s) \big) \, ds, \end{align} $$

where

(5.32) $$ \begin{align} \begin{aligned} B_1(s) & = -2 \sum_{\substack{\epsilon, \epsilon' \\ \lambda, \mu, \nu \\ \lambda', \mu', \nu' \\ \iota_1, \iota_2, \iota_1', \iota_2'}} \iota_1\iota_2 \iota_1' \iota_2' \iiiint e^{is \Phi_{\iota_1, \iota_2 \iota_1',\iota_2 \iota_2'}(\xi,\eta,\eta',\sigma')} Z^{\sharp \,\epsilon'} _{\substack{- \iota_2,\iota_2 \iota_1', \iota_2 \iota_2' \\ \lambda' \mu' \nu'}}({\sigma}, \eta',\sigma') \frac{Z^{\epsilon} _{\substack{- \iota_1 \iota_2 \\ \lambda \mu \nu}}(\xi,\eta,\sigma)}{i \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \\ & \quad\times \widetilde{g}_{\iota_1}(s,\eta) \widetilde{g}_{\iota_2 \iota_1'}(s,\eta') \widetilde{g}_{\iota_2 \iota_2'}(s,\sigma') \, d\eta\, d\eta' \, d{\sigma}\, d\sigma', \end{aligned} \end{align} $$

and

(5.33) $$ \begin{align} \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',{\sigma}') := \langle \xi \rangle - \kappa_1 \langle \eta \rangle - \kappa_2 \langle \eta' \rangle - \kappa_3 \langle {\sigma}' \rangle. \end{align} $$

Upon setting $\kappa _1 := \iota _1$ , $\kappa _2 := \iota _2 \iota _1'$ , $\kappa _3 := \iota _2 \iota _2'$ , this becomes

(5.34) $$ \begin{align} B_1(s) = \sum_{\kappa_1 \kappa_2 \kappa_3} \iiint e^{is \Phi_{\kappa_1 \kappa_2 \kappa_3 }(\xi,\eta,\eta',\sigma')} \mathfrak{b}^1_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',\sigma') \widetilde{g}_{\kappa_1}(s,\eta) \widetilde{g}_{\kappa_2} (s,\eta') \widetilde{g}_{\kappa_3}(s,\sigma') \, d\eta\, d\eta' \, d\sigma', \end{align} $$

with the natural definition of the symbol $\mathfrak {b}^1_{\kappa _1 \kappa _2 \kappa _3}$ obtained by carrying out the $d{\sigma }$ integration in equation (5.32).

Similarly,

(5.35) $$ \begin{align} \begin{aligned} B_2(s) & = - 2 \sum_{\substack{\epsilon \\ \lambda \mu \nu \\ \iota_1,\iota_2, \iota_1', \iota_2'}} \iota_1\iota_2 \iota^{\prime}_1\iota^{\prime}_2 \iiiint e^{is \Phi_{\iota_1, \iota_2 \iota_1',\iota_2 \iota_2'}(\xi,\eta,\eta',\sigma')} \mathfrak{q}^{\sharp}_{\iota_1'\iota_2'}({\sigma},\eta',{\sigma}') \frac{Z^{\epsilon} _{\substack{-,\iota_1 ,\iota_2 \\ \lambda, \mu ,\nu}}(\xi,\eta,\sigma)}{i \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \\ & \qquad \times \widetilde{g}_{\iota_1}(s,\eta) \widetilde{g}_{\iota_2 \iota_1'}(s,\eta') \widetilde{g}_{\iota_2 \iota_2'}(s,\sigma') \, d\eta\, d\eta' \, d{\sigma}\, d\sigma' \\ & = \sum_{\kappa_1 \kappa_2 \kappa_3} \iiint e^{is \Phi_{\kappa_1 \kappa_2 \kappa_3 }(\xi,\eta,\eta',\sigma')} \mathfrak{b}^2_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',\sigma') \widetilde{g}_{\kappa_1}(s,\eta) \widetilde{g}_{\kappa_2} (s,\eta') \widetilde{g}_{\kappa_3}(s,\sigma') \, d\eta\, d\eta' \, d\sigma', \end{aligned} \end{align} $$

with the natural definition of the symbol $\mathfrak {b}^2_{\kappa _1 \kappa _2 \kappa _3}$ .

It remains to obtain a good description of the symbols $ \mathfrak {b}^1_{\kappa _1 \kappa _2 \kappa _3}$ and $ \mathfrak {b}^2_{\kappa _1 \kappa _2 \kappa _3}$ obtained when carrying out the integration over $\sigma $ in the expressions above. We do this in the following two subsections. Section 5.5 deals with the top-order symbol $\mathfrak {b}^1$ whose description requires us to study, and obtain precise formulas for, the convolutions of $\delta $ and $\mathrm {p.v.} 1/\xi $ distributions that are cut off as in equation (5.11). Section 5.6 deals with the symbol $\mathfrak {b}^2$ , which is lower-order since $\mathfrak {q}^{\sharp }$ is smooth.

5.5 Top-order symbols

5.5.1 Regularity in $\sigma $

The first question we need to address is that of the possible lack of regularity of the coefficients in the top-order symbols, which could arise from the lack of regularity of the coefficient $\mathbf {a}^{\epsilon }_{{\lambda }}$ defined in equation (4.5) (for instance, in the case of a generic potential, these are discontinuous at the origin).

First, we observe that the coefficients of the type $\mathbf {a}^{\epsilon }_{{\lambda }}(x)$ with $x=\xi ,\eta ,\eta '$ or $\sigma '$ , which appear in equations (5.32)–(5.35), are not harmful. For the input variables $\eta ,\eta '$ and ${\sigma }'$ , this follows from the fact that the corresponding input functions, $\widetilde {g}$ , vanish at zero; in particular, the nonsmooth coefficients can be handled as in Remark 5.1 by pairing the indicator functions with the input profiles; see also Lemma 5.8, which guarantees that the renormalised profile $\widetilde {f}$ (see equation (5.53)), which will be put in place of $\widetilde {g}$ , vanishes at 0. For the output variable $\xi $ , we can also disregard the jump singularities of $\mathbf {a}^{\epsilon }_{{\lambda }}(\xi )$ thanks to the following: first, Lemma 5.10 and Remark 5.11(iii) allow us to differentiate once in $\xi $ as needed to estimate the weighted $L^2$ -norms; second, we will always estimate the $L^p$ -norms of the operators with $1<p<\infty $ , where $\mathbf {1}_\pm (\xi )$ is a bounded symbol.

Therefore, we do not need to worry about the coefficients $\mathbf {a}^{\epsilon }_{{\lambda }}(x)$ , with $x=\xi ,\eta ,\eta '$ or $\sigma '$ , and can just assume they are smooth disregarding the $\mathbf {1}_\pm (x)$ factors that they contain. However, coefficients $\mathbf {a}^{\epsilon }_{{\lambda }}(\sigma )$ , which enter the definition of $\mathfrak {b}^1$ through integration over $\sigma $ (see equations (5.32)–(5.34)), might be harmful. We now check that a cancellation occurs upon a proper symmetrisation of the symbol.

The symbol $\mathfrak {b}^1_{\kappa _1 \kappa _2 \kappa _3}$ can be written

(5.36) $$ \begin{align} \mathfrak{b}^1_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',\sigma') & = -2 \kappa_1 \kappa_2 \kappa_3 \sum_{\iota_2} \iota_2 \sum_{\substack{\lambda, \mu, \mu', \nu'\\ \epsilon, \epsilon'}} \int M(\xi,\eta,{\sigma},\eta',{\sigma}')\,d\sigma, \end{align} $$

(5.37) $$ \begin{align} M (\xi,\eta,{\sigma},\eta',{\sigma}') & := \frac{1}{i \Phi_{\kappa_1 \iota_2}(\xi,\eta,\sigma)} \sum_{\nu, \lambda'} Z^{\sharp \epsilon'} _{\substack{- \iota_2,\kappa_2, \kappa_3 \\ \lambda' ,\mu' ,\nu'}}({\sigma},\eta',\sigma') \, Z^{\epsilon}_{\substack{-, \kappa_1, \iota_2 \\ \lambda, \mu, \nu}}(\xi,\eta,\sigma), \end{align} $$

where we have omitted the dependence on the signs for easier notation. We can write this out as

(5.38) $$ \begin{align} \begin{aligned} M (\xi,\eta,{\sigma},\eta',{\sigma}') & := \sum_{\nu, \lambda'} \frac{1}{64 \pi^2 \langle \eta \rangle \langle \sigma \rangle\langle \eta' \rangle \langle \sigma' \rangle} \frac{1}{i \Phi_{\kappa_1 \iota_2}(\xi,\eta,\sigma)} \, a^{\epsilon}_{\substack{- ,\kappa_1, \iota_2 \\ \lambda,\mu,\nu}} (\xi, \eta,\sigma) \, a^{\epsilon'}_{\substack{- \iota_2,\kappa_2, \kappa_3 \\ \lambda', \mu' ,\nu'}} ({\sigma},\eta',\sigma') \\ &\quad \times \ell_{\epsilon \infty} \ell_{\epsilon' \infty} \left[ \sqrt{\frac{\pi}{2}} \delta(p) + \epsilon \, \varphi^{\ast}(p,\eta,\sigma) \, \frac{\widehat{\phi}(p)}{ip} \right] \left[ \sqrt{\frac{\pi}{2}} \delta(p') + \epsilon' \mathrm{p.v.} \frac{\widehat{\phi}(p')}{ip'} \right], \end{aligned} \end{align} $$

where $p := \lambda \xi - \kappa _1 \mu \eta - \iota _2 \nu \sigma $ as in equation (5.12), and we denoted

$$ \begin{align*}p' := \iota_2\lambda' {\sigma} - \kappa_2 \mu' \eta' - \kappa_3 \nu' \sigma',\end{align*} $$

and dropped the $\mathrm {p.v.}$ symbols for brevity.

The main observation is that exchanging ${\sigma } \mapsto -{\sigma }$ and $(\nu ,\lambda ')\mapsto (-\nu ,-\lambda ')$ simultaneously leaves $\Phi _{\iota _1 \iota _2}$ , p and $p'$ invariant, and therefore in particular does not change the distributions in square brackets in equation (5.38); therefore, the coefficients appearing in the first line of equation (5.38) can be symmetrised and we may instead write

(5.39) $$ \begin{align} \begin{aligned} & \frac{1}{2} \left[ a^{\epsilon'} _{\substack{-\iota_2, \kappa_2, \kappa_3 \\ \lambda' \mu' \nu'}}({\sigma},\eta',\sigma') \cdot a^{\epsilon}_{\substack{-, \kappa_1, \iota_2 \\ \lambda, \mu, \nu}}(\xi,\eta,\sigma) + a^{\epsilon'} _{\substack{- \iota_2,\kappa_2 , \kappa_3 \\ -\lambda', \mu', \nu'}}(-{\sigma},\eta',\sigma') \cdot a^{\epsilon}_{\substack{-, \kappa_1, \iota_2 \\ \lambda, \mu, -\nu}}(\xi,\eta,-\sigma) \right]. \end{aligned} \end{align} $$

Recalling equation (4.4), the terms in the sum above can be written more explicitly as

(5.40) $$ \begin{align} \begin{aligned} & = \frac{1}{2} \left[ \mathbf{a}_{\lambda',-\iota_2}^{\epsilon'}({\sigma}) \mathbf{a}_{\mu',\kappa_2}^{\epsilon'}(\eta') \mathbf{a}_{\nu', \kappa_3}^{\epsilon'}({\sigma}') \cdot \mathbf{a}_{\lambda,-}^{\epsilon}(\xi) \mathbf{a}_{\mu,\kappa_1}^{\epsilon}(\eta) \mathbf{a}_{\nu,\iota_2}^{\epsilon}(\sigma) \right. \\ & \quad\left. +\, \mathbf{a}_{-\lambda',-\iota_2}^{\epsilon'}(-{\sigma}) \mathbf{a}_{\mu',\kappa_2}^{\epsilon'}(\eta') \mathbf{a}_{\nu',\kappa_3}^{\epsilon'}({\sigma}') \cdot \mathbf{a}_{\lambda,-}^{\epsilon}(\xi) \mathbf{a}_{\mu,\iota_1}^{\epsilon}(\eta) \mathbf{a}_{-\nu,\iota_2}^{\epsilon}(-\sigma) \right] \\ & = \underbrace{\frac{1}{2} \Big[ \mathbf{a}_{\lambda',-\iota_2}^{\epsilon'}({\sigma}) \mathbf{a}_{\nu,\iota_2}^{\epsilon}(\sigma) + \mathbf{a}_{-\lambda',-\iota_2}^{\epsilon'}(-{\sigma}) \mathbf{a}_{-\nu,\iota_2}^{\epsilon}(-\sigma) \Big]}_{ := \Big(\displaystyle A^{\epsilon, \epsilon'}_{\nu,\lambda'}(\sigma) \Big)_{\iota_2}} \, \cdot \, \underbrace{\mathbf{a}_{\lambda,-}^{\epsilon}(\xi) \mathbf{a}_{\mu,\kappa_1}^{\epsilon}(\eta) \mathbf{a}_{\mu',\kappa_2}^{\epsilon'}(\eta') \mathbf{a}_{\nu',\kappa_3}^{\epsilon'}({\sigma}')}_{\displaystyle := a^{\epsilon,\epsilon'}_{\substack{\lambda,\mu,\mu',\nu' \\ -,\kappa_1,\kappa_2,\kappa_3}}}. \end{aligned} \end{align} $$

Using the formulas for the coefficients $\bf {a}^{\epsilon }_\lambda $ in equation (4.5) and the relations in equations (3.10)–(3.11) for the transmission and reflection coefficients, we have

$$ \begin{align*} 2 A^{+,+}_{+,+}(\sigma) & = \overline{\mathbf{a}_+^+({\sigma})} \mathbf{a}_{+}^+(\sigma) + \overline{\mathbf{a}_{-}^{+}(-{\sigma})} \mathbf{a}_{-}^+(-\sigma) \\ & = \big( |T(\sigma)|^2 \mathbf{1}_+(\sigma) + \mathbf{1}_-(\sigma) \big) + \mathbf{1}_+(\sigma) |R_+(\sigma)|^2 \equiv 1, \end{align*} $$

and

$$ \begin{align*} 2 A^{+,+}_{+,-}(\sigma) & = \overline{\mathbf{a}_-^+({\sigma})} \mathbf{a}_{+}^+(\sigma) + \overline{\mathbf{a}_{+}^{+}(-{\sigma})} \mathbf{a}_{-}^+(-\sigma) \\ & = \overline{R_+(-\sigma)} \mathbf{1}_-(\sigma) + R_+(\sigma) \mathbf{1}_+(\sigma) \equiv R_+(\sigma). \end{align*} $$

We can similarly calculate the other expression and arrive at the following formulas:

(5.41) $$ \begin{align} \begin{aligned} & A^{+,+}_{+,+}(\sigma) = A^{+,+}_{-,-}(-\sigma) = \frac{1}{2}, \qquad A^{+,+}_{+,-}(\sigma) = A^{+,+}_{-,+}(-\sigma) = \frac{1}{2}R_+(\sigma), \\ & A^{-,-}_{+,+}(\sigma) = A^{-,-}_{-,-}(-\sigma) = \frac{1}{2}, \qquad A^{-,-}_{+,-}(\sigma) = A^{-,-}_{-,+}(-\sigma) = \frac{1}{2}R_-(-\sigma), \\ & A^{+,-}_{+,+}(\sigma) = A^{+,-}_{-,-}(-\sigma) = \frac{1}{2} T(\sigma), \qquad A^{+,-}_{+,-}(\sigma) = A^{+,-}_{-,+}(-\sigma) = 0, \\ & A^{-,+}_{+,+}(\sigma) = A^{-,+}_{-,-}(-\sigma) = \frac{1}{2} T(-\sigma), \qquad A^{-,+}_{+,-}(\sigma) = A^{-,+}_{-,+}(-\sigma) = 0. \end{aligned} \end{align} $$

In particular, we see that this coefficient is smooth. The exact values above will be relevant when computing the nonlinear scattering correction in Section 10.2.

5.5.2 Integrating over $\sigma $

There remains to integrate equation (5.38) over $\sigma $ . Observe that the integrand is singular when the variable p or $p'$ hits zero. They can be written

(5.42) $$ \begin{align} \left\{ \begin{array}{l} p = \iota_2 \nu( \Sigma_0 - \sigma) \\ p' = \iota_2 \lambda'(\sigma -\Sigma_1) \end{array} \right. \qquad \mbox{with} \qquad \left\{ \begin{array}{l} \Sigma_0 = \iota_2 \nu (\lambda \xi - \iota_1 \mu \eta) \\ \Sigma_1 = \lambda' \iota_2(\kappa_2\mu' \eta' + \kappa_3 \nu' \sigma'). \end{array} \right. \end{align} $$

Furthermore, let

(5.43) $$ \begin{align} p_* := \iota_2 \nu p + \iota_2 \lambda' p' = \Sigma_0 - \Sigma_1. \end{align} $$

Depending on whether Z and $Z^{\sharp }$ contribute $\delta $ or $\frac {1}{x}$ , M can be split into

$$ \begin{align*}M = \sum_{\nu, \lambda'} \big(M^{\delta,\delta} + M^{\delta,\frac{1}{x}} + M^{\frac{1}{x},\delta} + M^{\frac{1}{x},\frac{1}{x}}\big) \end{align*} $$

with

(5.44) $$ \begin{align} \begin{aligned} & M^{\delta,\delta} (\xi,\eta,{\sigma},\eta',{\sigma}') :=\mathcal{M}(\xi,\eta,{\sigma},\eta',{\sigma}') \frac{\pi}{2} \delta(p) \delta(p'), \\ & M^{\delta,\frac{1}{x}}(\xi,\eta,{\sigma},\eta',{\sigma}') := \mathcal{M}(\xi,\eta,{\sigma},\eta',{\sigma}') \sqrt{\frac{\pi}{2}} \delta(p) \epsilon' \frac{\widehat{\phi}(p')}{ip'}, \\ & M^{\frac{1}{x},\delta}(\xi,\eta,{\sigma},\eta',{\sigma}') := \mathcal{M}(\xi,\eta,{\sigma},\eta',{\sigma}') \epsilon \, \varphi^{\ast}(p,\eta,\sigma) \, \frac{\widehat{\phi}(p)}{ip} \sqrt{\frac{\pi}{2}} \delta(p'), \\ & M^{\frac{1}{x},\frac{1}{x}}(\xi,\eta,{\sigma},\eta',{\sigma}') := \mathcal{M}(\xi,\eta,{\sigma},\eta',{\sigma}') \epsilon \epsilon' \, \varphi^{\ast}(p,\eta,\sigma) \, \frac{\widehat{\phi}(p)}{ip} \frac{\widehat{\phi}(p')}{ip'}, \end{aligned} \end{align} $$

where

(5.45) $$ \begin{align} \mathcal{M}(\xi,\eta,{\sigma},\eta',{\sigma}') := \frac{\ell_{\epsilon\infty}\ell_{\epsilon'\infty}}{64 \pi^2 \langle \eta \rangle \langle \sigma \rangle \langle \eta' \rangle \langle \sigma' \rangle} \frac{1}{i \Phi_{\kappa_1 \iota_2}(\xi,\eta,\sigma)} \Big(A^{\epsilon,\epsilon'}_{\nu,{\lambda}'}(\sigma)\Big)_{\iota_2} a^{\epsilon,\epsilon'}_{\substack{\lambda,\mu,\mu',\nu' \\ -,\kappa_1,\kappa_2,\kappa_3}}(\xi,\eta,\eta',\sigma'). \end{align} $$

When integrating over $\sigma $ , we rely on the identities

$$ \begin{align*}\delta * \delta = \delta , \qquad \delta * \frac{1}{x} = \frac{1}{x} \qquad \frac{1}{x} * \frac{1}{x} = - \pi^2 \delta, \end{align*} $$

(see equation (4.8)), which imply that, for a smooth function F,

$$ \begin{align*} & \int \delta(p) \delta(p') F(\sigma) \,d\sigma = F(\Sigma_0) \delta(p_*) \\ & \int \delta(p) \frac{\widehat{\phi}(p')}{p'}F(\sigma)\,d\sigma = \iota_2 \lambda' F(\Sigma_0) \frac{\widehat{\phi}(p_*)}{p_*} \\ & \int \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \delta(p')F(\sigma) \,d\sigma = \iota_2 \nu F(\Sigma_0) \frac{\widehat{\phi}(p_*)}{p_*} + \{\mbox{error}\} \\ & \int \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p}\frac{\widehat{\phi}(p')}{p'}F(\sigma)\,d\sigma = -\frac{\pi}{2} \nu \lambda' F(\Sigma_0) \delta(p_*) + \{\mbox{error}\}. \end{align*} $$

The error terms will be dealt with in the following subsection in Lemmas 5.5 and 5.7. For the moment, we record the top-order contribution to $\mathfrak {b}^1$ , namely

(5.46) $$ \begin{align} & \mathfrak{c}^S_{\kappa_1,\kappa_2,\kappa_3}(\xi,\eta,\eta',\sigma') \nonumber\\ & \quad = -2 \kappa_1 \kappa_2 \kappa_3 \sum_{\substack{\epsilon,\epsilon',\iota_2 \nonumber\\ \lambda,\mu,\nu,\lambda',\mu',\nu'}} \frac{1}{64 \pi^2 \langle \eta \rangle \langle \Sigma_0 \rangle \langle \eta' \rangle \langle \sigma' \rangle } \frac{\big( A^{\epsilon,\epsilon'}_{\nu,\lambda'}(\Sigma_0) \big)_{\iota_2}}{i \Phi_{\kappa_1 \iota_2} (\xi,\eta,\Sigma_0)} a^{\epsilon,\epsilon'}_{\substack{\lambda,\mu,\mu',\nu' \\ -,\kappa_1,\kappa_2,\kappa_3}}(\xi,\eta,\eta',\sigma') \nonumber\\ & \qquad \times \ell_{\epsilon \infty} \ell_{\epsilon' \infty} \left[\iota_2 \frac{\pi}{2}({1+ \epsilon \epsilon' \nu \lambda'} ) \delta(p_*) + \sqrt{ \frac{\pi}{2}} (\epsilon' \lambda'+ \epsilon \nu) \frac{\widehat{\phi}(p_*)}{i p_*} \right] \\ & \quad = \mathfrak{c}^{S,1}_{\kappa_1,\kappa_2,\kappa_3}(\xi,\eta,\eta',\sigma') + \mathfrak{c}^{S,2}_{\kappa_1,\kappa_2,\kappa_3}(\xi,\eta,\eta',\sigma'), \nonumber\end{align} $$

where $\mathfrak {c}^{S,1}$ gathers all terms containing $\delta $ functions, while $\mathfrak {c}^{S,2}$ gathers all terms containing terms of the type $\widehat {\phi }(p_*)/p_*$ .

The multilinear operator with symbol $\mathfrak {c}^S_{\kappa _1,\kappa _2,\kappa _3}$ will be denoted $\mathcal {C}^S_{\kappa _1,\kappa _2,\kappa _3}$ . The decomposition of $\mathfrak {c}^S_{\kappa _1,\kappa _2,\kappa _3}$ into $\mathfrak {c}^{S,1}_{\kappa _1,\kappa _2,\kappa _3} + \mathfrak {c}^{S,2}_{\kappa _1,\kappa _2,\kappa _3}$ gives a further decomposition of $\mathcal {C}^S_{\kappa _1,\kappa _2,\kappa _3}$ :

(5.47) $$ \begin{align} \mathcal{C}^S_{\kappa_1,\kappa_2,\kappa_3} = \mathcal{C}^{S,1}_{\kappa_1,\kappa_2,\kappa_3} + \mathcal{C}^{S,2}_{\kappa_1,\kappa_2,\kappa_3}. \end{align} $$

5.6 Lower-order symbols

5.6.1 The symbol $ \mathfrak {b}^2$

Dropping unnecessary subscripts and superscripts, the symbol $\mathfrak {b}^2$ in equation (5.35) can be written as a sum of terms of the type

$$ \begin{align*}\mathbf{a}(\xi) \mathbf{a}(\eta) C(\xi,\eta,\eta',\sigma') \end{align*} $$

with

$$ \begin{align*} &C(\xi,\eta,\eta',\sigma') \\ &\quad = \frac{1}{\langle \eta \rangle \langle \sigma' \rangle \langle \eta' \rangle} \int \frac{1}{\langle \sigma \rangle} \mu^R(\sigma,\eta',\sigma') \mathbf{a}(\sigma) \left[ \sqrt{\frac{\pi}{2}} \delta(p) \pm \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \right] \frac{1}{\Phi(\xi,\eta,\sigma)} \,d\sigma. \end{align*} $$

In what follows, we adopt the convention that the measure $\mu _R$ appearing above is smooth in the variables $\eta '$ and ${\sigma }'$ ; in other words, we are disregarding indicator functions in these two variables, which, as explained at the beginning of Section 5.5, can be done without loss of generality.

Lemma 5.4. The symbol C can be split into

$$ \begin{align*} C(\xi,\eta,\eta',\sigma') = \mathbf{a}(\Sigma_0) C_1(\xi,\eta,\eta',\sigma') + C_2(\xi,\eta,\eta',\sigma'), \end{align*} $$

where $\Sigma _0$ is defined as in equation (5.42), and with

(5.48) $$ \begin{align} & |\partial_{\xi}^a \partial_{\eta}^b \partial_{\eta'}^c \partial_{\sigma'}^d C_1(\xi,\eta,\eta',\sigma')| \lesssim \frac{1}{\langle \eta \rangle \langle \sigma' \rangle \langle \eta' \rangle} \langle \inf_{\mu,\nu}| \Sigma_0 + \mu \eta' + \nu \sigma' | \rangle^{-N}, \qquad\qquad\qquad\quad \end{align} $$

(5.49) $$ \begin{align} & |\partial_{\xi}^a \partial_{\Sigma_0}^b \partial_{\eta'}^c \partial_{\sigma'}^d C_2(\xi,\eta,\eta',\sigma') | \lesssim \frac{1}{\langle \eta \rangle \langle \sigma' \rangle \langle \eta' \rangle} \langle \inf_{\mu,\nu} | \Sigma_0 + \mu \eta' + \nu \sigma'| \rangle^{-N} \left\{ \begin{array}{ll} | \log |\Sigma_0| | & \mbox{if}\ a+b=0 \\ |\Sigma_0|^{-a-b} & \mbox{if}\ a+b\geq 1. \end{array} \right. \end{align} $$

Note that in equation (5.48), we regard $\Sigma _0$ as a dependent variable (since the main singular dependence on $\Sigma _0$ can be factorised), while in equation (5.49), we regard it as an independent one.

Proof. The term $C_1$ is given by the contribution of the $\delta $ term to the symbol C:

$$ \begin{align*} C_1(\xi,\eta,\eta',\sigma') = \frac{1}{\langle \eta \rangle \langle \sigma' \rangle \langle \eta' \rangle \langle \Sigma_0 \rangle} \mu^R(\Sigma_0,\eta',\sigma')\frac{1}{\Phi(\xi,\eta,\Sigma_0)}. \end{align*} $$

It satisfies the desired estimates by equations (5.26) and (4.6)–(4.7). As for the contribution of the principal value term, it can be written as the sum of $C_2'$ and $C_2''$ defined as follows:

$$ \begin{align*} C_2'(\xi,\eta,\eta',\sigma') &= \frac{1}{\langle \eta \rangle \langle \sigma' \rangle \langle \eta' \rangle} \Lambda(\xi,\eta,0) \int \mathbf{a}(\sigma)\mu^R(\sigma,\eta',\sigma') \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \,dp \\ C_2''(\xi,\eta,\eta',\sigma') &= \frac{1}{\langle \eta \rangle \langle \sigma' \rangle \langle \eta' \rangle} \int \mathbf{a}(\sigma)\mu^R(\sigma,\eta',\sigma') [\Lambda(\xi,\eta,-\iota_2 \nu p) \\ &\quad - \Lambda(\xi,\eta,0)] \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \,dp; \end{align*} $$

here we changed the integration variable to p, so that $\sigma $ is now considered a function of p: $\sigma = \Sigma _0 - \iota _2 \nu p$ , and denoted

(5.50) $$ \begin{align} \Lambda(\xi,\eta,q) := \frac{1}{\Phi(\xi,\eta,\Sigma_0 + q) \langle \Sigma_0 + q \rangle}, \end{align} $$

which, by equation (5.26), and provided $|q| \ll \frac {1}{R(\eta ,\Sigma _0)}$ , satisfies

(5.51) $$ \begin{align} \left| \partial_{\xi}^a \partial_{\eta}^b \partial_{q}^c \Lambda(\xi,\eta,q) \right| \lesssim R(\eta,\Sigma_0)^c. \end{align} $$

This bound, together with the estimates on $\mu ^R$ in equations (4.6)–(4.7), and the possible singularity of $\mathbf {a}$ at the origin, lead to the estimate in equation (5.49) on $C_2'$ . In order to bound $C_2''$ , observe that

(5.52) $$ \begin{align} f(\xi,\eta,p) = \varphi^*(p,\eta,\sigma) \left[\Lambda(\xi,\eta,-\iota_2 \nu p) - \Lambda(\xi,\eta,0) \right] \frac{\widehat{\phi}(p)}{p} \end{align} $$

satisfies, by equation (5.26),

$$ \begin{align*}\operatorname{Supp} f \subset \{ |p| \lesssim R(\eta,\Sigma_0)^{-1} \} \qquad \mbox{and} \qquad \left|\partial_{\xi}^a \partial_{\eta}^b \partial_p^c f(\xi,\eta,p) \right| \lesssim R(\eta,\Sigma_0)^{1+c}. \end{align*} $$

In other words, we can think of $f(p,\eta ,\sigma )$ as a normalised cutoff function (in p) at scale $R(\eta ,\Sigma _0)^{-1}$ , such as $R(\eta ,\Sigma _0) \chi (R(\eta ,\Sigma _0) p)$ . Coming back to $C_2''$ , it can be written

$$ \begin{align*}C_2''(\xi,\eta,\eta',\sigma') = \frac{1}{\langle \eta \rangle \langle \sigma' \rangle \langle \eta' \rangle} \int \mathbf{a}(\sigma)\mu^R(\sigma,\eta',\sigma') f(\xi,\eta,p)\,dp, \end{align*} $$

from which the desired estimate in equation (5.49) follows.

5.6.2 The remainder from integrating $M^{\frac {1}{x},\delta }$

Dropping irrelevant indexes and constants, the integral in ${\sigma }$ of $M^{\frac {1}{x},\delta }$ can be written as

$$ \begin{align*}\frac{\mathbf{a}(\xi) \mathbf{a}(\eta) \mathbf{a}(\eta') \mathbf{a}(\sigma')}{\langle \eta \rangle \langle \sigma' \rangle \langle \eta' \rangle} \int \frac{A(\sigma)}{\Phi(\xi,\eta,\sigma) \langle \sigma \rangle} \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \delta(p') \,d\sigma. \end{align*} $$

The following lemma extracts the leading order contribution and bounds the remainder term.

Lemma 5.5. Recalling the definitions of p, $p'$ , $\Sigma _0$ , $\Sigma _1$ in equation (5.42) as well as $p_*$ in equation (5.43), we have the following decomposition

$$ \begin{align*} & \int \frac{A(\sigma)}{\Phi(\xi,\eta,\sigma) \langle \sigma \rangle} \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \delta(p') \,d\sigma = - \iota_2 \nu \frac{A( \Sigma_0)}{\Phi(\xi,\eta,\Sigma_0) \langle \Sigma_0 \rangle}\frac{\widehat{\phi}(p_*)}{p_*} + C(\xi,\eta,\eta',p_*), \end{align*} $$

where, for any $a,b,c,d \in \mathbb {N}_0$ ,

$$ \begin{align*} |\partial_{\xi}^a \partial_{\eta}^b \partial_{\eta'}^c \partial_{p_*}^d C(\xi,\eta,\eta',p_*)| \lesssim \frac{1}{(|p_\ast| + \frac{1}{R(\eta,\Sigma_0)})^{1+d}}. \end{align*} $$

Remark 5.6. In the above lemma, we chose to parametrise C as a function of $p_*,\xi ,\eta $ and $\eta '$ . Of course, other choices are also possible; the main point is that derivatives across level sets of $p_*$ are more singular (larger) than along them.

Proof of Lemma 5.5

First, note that, due to the fast decay of $\widehat {\phi }$ , we can assume $|p_*| = |\Sigma _0 - \Sigma _1| \lesssim 1$ , hence $R(\eta ,\Sigma _0) \approx R(\eta ,\Sigma _1)$ . By definition of $\Sigma _0$ and $\Sigma _1$ in equation (5.42), and recalling the formula for $\Lambda $ in equation (5.50),

$$ \begin{align*}\int \frac{A(\sigma)}{\Phi(\xi,\eta,\sigma) \langle \sigma \rangle} \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \delta(p') \,d\sigma = \iota_2 \nu \varphi^*(p_*,\eta,\Sigma_1) A(\Sigma_1) \Lambda(\xi,\eta,\Sigma_1 - \Sigma_0) \frac{\widehat{\phi}(p_*)}{p_*}. \end{align*} $$

We can now decompose

$$ \begin{align*} &\iota_2 \nu \varphi^*(p_*,\eta,\Sigma_1)A(\Sigma_1) \Lambda(\xi,\eta,\Sigma_1 - \Sigma_0) \frac{\widehat{\phi}(p_*)}{p_*} \\ &\quad = \iota_2 \nu A(\Sigma_0) \Lambda(\xi,\eta,0) \frac{\widehat{\phi}(p_*)}{p_*} + \iota_2 \nu A(\Sigma_0) \Lambda(\xi,\eta,0) [\varphi^*(p_*,\eta,\Sigma_1) - 1] \frac{\widehat{\phi}(p_*)}{p_*} \\ & \qquad + \iota_2 \nu \varphi^*(p_*,\eta,\Sigma_1) [A(\Sigma_1) \Lambda(\xi,\eta,\Sigma_1 - \Sigma_0) - A(\Sigma_0) \Lambda(\xi,\eta,0)] \frac{\widehat{\phi}(p_*)}{p_*} \\ &\quad = I + II + III. \end{align*} $$

The term I is the desired leading order term. As for $II$ and $III$ , they make up the error term $C(\xi ,\eta ,\eta ',\sigma ')$ , and it follows from equation (5.51) that they satisfy the desired estimates.

5.6.3 The remainder from integrating $M^{\frac {1}{x},\frac {1}{x}}$

Dropping irrelevant indexes, $\int M^{\frac {1}{x},\frac {1}{x}} \,d\sigma $ can be written as

$$ \begin{align*}\frac{\mathbf{a}(\xi) \mathbf{a}(\eta) \mathbf{a}(\eta') \mathbf{a}(\sigma')}{\langle \eta \rangle \langle \sigma' \rangle \langle \eta' \rangle}\int \frac{A(\sigma)}{\Phi(\xi,\eta,\sigma) \langle \sigma \rangle} \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma. \end{align*} $$

The following lemma extracts the leading order contribution and bounds the remainder term.

Lemma 5.7. Recalling the definitions of p, $p'$ , $\Sigma _0$ , $\Sigma _1$ in equation (5.42) as well as $p_*$ in equation (5.43), we have the following decomposition

$$ \begin{align*} & \int \frac{A(\sigma)}{\Phi(\xi,\eta,\sigma) \langle \sigma \rangle} \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma = - \nu \lambda' \frac{\pi}{2}\frac{A( \Sigma_0)}{\Phi(\xi,\eta,\Sigma_0) \langle \Sigma_0 \rangle}\delta(p_\ast) + C(\xi,\eta,\eta',p_*), \end{align*} $$

where, for any $a,b,c,d \in \mathbb {N}_0$ ,

$$ \begin{align*} |\partial_{\xi}^a \partial_{\eta}^b \partial_{\eta'}^c \partial_{p_*}^d C(\xi,\eta,\eta',p_*)| \lesssim \frac{1}{(|p_\ast| + \frac{1}{R(\eta,\Sigma_0)})^{1+d}}. \end{align*} $$

Proof. It will be convenient to adopt lighter notations by setting

$$ \begin{align*} \alpha = - \iota_2 \nu, \qquad \alpha' = \iota_2 \lambda', \end{align*} $$

so that

$$ \begin{align*} p = \alpha (\sigma - \Sigma_0) \qquad \mbox{and} \qquad p' = \alpha' (\sigma - \Sigma_1). \end{align*} $$

The integral can be decomposed as follows:

$$ \begin{align*} & \int A(\sigma) \Lambda(\xi,\eta,\sigma-\Sigma_0) \varphi^*(p,\eta,\sigma) \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma \\ & \quad =A(\Sigma_0)\Lambda(\xi,\eta,0) \int \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma + A(\Sigma_0) \Lambda(\xi,\eta,0) \int [ \varphi^*(p,\eta,\sigma) - 1] \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma \\ & \qquad +\, \int \varphi^*(p,\eta,\sigma) \left[A(\sigma) \Lambda(\xi,\eta,p) - A(\Sigma_0) \Lambda(\xi,\eta,0) \right] \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma \\ & \quad = I + II + III. \end{align*} $$

Using that $\frac {\widehat {\phi }(\sigma )}{\sigma } = \frac {i}{2} \widehat {\mathcal {F}} [\phi * \operatorname {sign}]$ , $\widehat {f} * \widehat {g} = \sqrt {2\pi } \widehat {fg}$ and $\widehat {1} = \sqrt {2\pi } \delta $ , we get that

$$ \begin{align*} \int \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma & = \int \frac{\widehat{\phi}(\alpha( \sigma - \Sigma_0 + \Sigma_1)}{\alpha( \sigma - \Sigma_0 + \Sigma_1)} \frac{\widehat{\phi}(\alpha' \sigma)}{\alpha' \sigma} \,d\sigma = - \alpha \alpha' \left[ \frac{\widehat{\phi}(\sigma)}{\sigma} * \frac{\widehat{\phi}(\sigma)}{\sigma} \right](\Sigma_0 - \Sigma_1) \\ & = \alpha \alpha' \frac{\sqrt{2\pi}}{4} \widehat{\mathcal{F}}[(\phi * \operatorname{sign})^2](\Sigma_0 - \Sigma_1) =\frac{\sqrt{2\pi}}{4} \alpha \alpha' \widehat{\mathcal{F}}[1 + \widehat{\mathcal{F}}^{-1} G_0]( \Sigma_0 - \Sigma_1) \\ & = \frac{\pi}{2}\alpha \alpha' \delta(\Sigma_0 - \Sigma_1) + \frac{\sqrt{2\pi}}{4} \alpha \alpha' G_0 (\Sigma_0 - \Sigma_1), \end{align*} $$

where $G_0$ is a Schwartz function. Therefore, modifying the definition of $G_0$ to take the constant factor into account,

$$ \begin{align*}I = \frac{\pi}{2} \alpha \alpha'A(\Sigma_0) \Lambda(\xi,\eta,0) \delta(\Sigma_0 - \Sigma_1) + A(\Sigma_0) \Lambda(\xi,\eta,0) G_0( \Sigma_0 - \Sigma_1). \end{align*} $$

Turning to $II$ , it can be written

$$ \begin{align*} II & = A(\Sigma_0) \Lambda(\xi,\eta,0) \int [ \varphi^*(p,\eta,\sigma) - 1] \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma \\ & = - A(\Sigma_0)\Lambda(\xi,\eta,0) \int \varphi_{>-D_0}(R(\eta,\Sigma_0) p) \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma \\ & \quad - \Lambda(\xi,\eta,0) \int [ \varphi_{>-D_0}(R(\eta,\sigma) p) -\varphi_{>-D_0}(R(\eta,\Sigma_0) p)] \frac{\widehat{\phi}(p)}{p} \frac{\widehat{\phi}(p')}{p'} \,d\sigma \\ & = II' + II''. \end{align*} $$

The term $II''$ is an error term that enjoys better bounds than $II'$ , so we only focus on the latter, which can be written as

$$ \begin{align*}II' = -A(\Sigma_0)\Lambda(\xi,\eta,0) \frac{\sqrt{2\pi}i}{2} \alpha \alpha' \widehat{\mathcal{F}} \big[ (\widehat{F_{R(\eta,\Sigma_0)}}*\operatorname{sign})(\phi * \operatorname{sign})\big](p_*), \end{align*} $$

where $F_R = \varphi _{>-D_0}(R \cdot ) \widehat {\phi }$ . Essentially, $F_R$ can be written as $\sum _{\frac {2^{-D_0}}{R(\eta ,\Sigma _0)} < 2^j < 1} \varphi _j$ , and therefore we need to bound

$$ \begin{align*}\left| \sum_{\frac{2^{-D_0}}{R(\eta,\Sigma_0)} < 2^j < 1} \widehat{\mathcal{F}} [ (\widehat{\varphi_j} * \mbox{sign} ) (\phi * \mbox{sign} ) (p_*)] \right|. \end{align*} $$

Since the average of $\widehat {\varphi _j}$ is zero, the convolution $\widehat {\varphi _j} * \operatorname {sign}$ can be written $\chi (2^j \cdot )$ for a Schwartz function $\chi $ . Then $(\widehat {\varphi _j} * \operatorname {sign}) (\phi * \operatorname {sign})$ enjoys the same bounds as $\chi (2^j \cdot )$ , and therefore, the above can be bounded by

$$ \begin{align*}\sum_{\frac{2^{-D_0}}{R(\eta,\Sigma_0)} < 2^j < 1} 2^{-j} \widehat{\chi}(2^{-j} p_*) \lesssim \frac{1}{\frac{1}{R(\eta,\Sigma_0)} + |p_*|}, \end{align*} $$

with natural bounds on the derivatives.

We are left with $III$ , which can be written (up to the factor A, which does not affect the estimates) as

$$ \begin{align*}\int f(p,\eta,\sigma) \frac{\widehat{\phi}(p')}{p'} \,dp, \end{align*} $$

where $f(p,\eta ,\sigma )$ was introduced in equation (5.52) (notice that we changed the integration variable to p, so that $p'$ and $\sigma $ are now thought of as functions of p). As we saw earlier, the function $f(\xi ,\eta ,p)$ can be thought of as normalised smooth function in p on a scale $R(\eta ,\Sigma _0)^{-1}$ , such as $R(\eta ,\Sigma _0) \chi (R(\eta ,\Sigma _0) p)$ , with $\chi \in \mathcal {C}_0^{\infty }$ . The desired result follows.

5.7 Final decomposition and renormalised profile

Let us summarise here our findings from the previous subsections regarding the decomposition of the nonlinearity.

We define the renormalised profile f by

(5.53) $$ \begin{align} f := g - T(g,g), \qquad T(g,g) := \sum_{\iota_1,\iota_2} T_{\iota_1 \iota_2}^+(g,g) + T_{\iota_1 \iota_2}^-(g,g), \end{align} $$

where, according to equation (5.29), we have

(5.54) $$ \begin{align} \begin{aligned} \widetilde{\mathcal{F}} T_{\iota_1 \iota_2}^{\pm}(g,g)(t) & = \iint e^{it \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \widetilde{g}(t,\eta) \widetilde{g}(t,\sigma) \mathfrak{m}_{\iota_1 \iota_2}^{\pm}(\xi,\eta,\sigma)\,d\eta \,d\sigma \\ \mathfrak{m}_{\iota_1 \iota_2}^{\pm}(\xi,\eta,{\sigma}) & := -\iota_1\iota_2 \sum_{{\lambda},\mu,\nu} \frac{Z^{\pm}_{\substack{- \iota_1 \iota_2 \\ \lambda \mu \nu}}(\xi,\eta,\sigma)}{i \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)}, \end{aligned} \end{align} $$

where the symbol Z is defined in equation (5.11). We then see that f satisfies

(5.55) $$ \begin{align} \partial_t \widetilde{f} = \mathcal{Q}^R(g,g) + \mathcal{C}^{S}(g,g,g) + \mathcal{C}^R(g,g,g), \end{align} $$

where:

• • The regular quadratic term is given by

  (5.56) $$ \begin{align} \begin{aligned} & \mathcal{Q}^R(a,b) = \sum_{\iota_1, \iota_2} \mathcal{Q}_{\iota_1\iota_2}^R(a,b) \\ & \mathcal{Q}_{\iota_1\iota_2}^R[a,b](t,\xi) = \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \, \mathfrak{q}(\xi,\eta,\sigma) \, \widetilde{a}_{\iota_1}(t,\eta) \widetilde{b}_{\iota_2}(t,\sigma) \, d\eta \, d\sigma \\ & \Phi_{\iota_1 \iota_2}(\xi,\eta,{\sigma}) := \langle \xi \rangle - \iota_1 \langle \eta \rangle - \iota_2 \langle \sigma \rangle, \end{aligned} \end{align} $$
  with equations (5.15)–(5.18).

  Notation convention for the parentheses. Note that in equation (5.56) above, we have used both square and round parentheses for the arguments of $\mathcal {Q}^R$ . When only a pair of arguments appear, we will mostly use round brackets when the arguments are either time and frequency $(t,\xi )$ or a pair of functions (such as $(a,b)$ above, or $(g,g)$ in equation (5.55)). In cases where we write both the input functions and the independent variables, we will often highlight the distinction between them by using square parentheses for the input functions, as done in the second line of equation (5.56) above, equation (6.20), equation (8.8), and so on. We will adopt a similar notation for other similar multilinear expressions (see, for example, equations (8.28) and (8.32)).

  Also, when the arguments of the bilinear form $\mathcal {Q}^R$ are given by other multilinear expressions, we will use square parentheses (throughout the given formula) to provide a clearer distinction; see, for example, equation (7.36). We will adopt a similar notation for the trilinear terms in equations (5.57) and (5.59).

• • The singular cubic term is given by

  (5.57) $$ \begin{align} \begin{aligned} & \mathcal{C}^{S}(a,b,c) = \sum_{\kappa_1 \kappa_2 \kappa_3} \mathcal{C}^{S}_{\kappa_1 \kappa_2 \kappa_3}(a,b,c) \\ & \mathcal{C}^{S}_{\kappa_1 \kappa_2 \kappa_3}[a,b,c](t,\xi) = \iiint e^{it \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\sigma,\theta)} \mathfrak{c}^S_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\sigma,\theta) \, \widetilde{a}_{{\kappa}_1}(t,\eta) \widetilde{b}_{{\kappa}_2}(t,\sigma) \widetilde{c}_{{\kappa}_3}(t,\theta) \, d\eta \, d\sigma \,d\theta, \\ & \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',{\sigma}') := \langle \xi \rangle - \kappa_1 \langle \eta \rangle - \kappa_2 \langle\sigma \rangle - \kappa_3 \langle \theta \rangle, \end{aligned} \end{align} $$
  with the exact formula for the symbol $\mathfrak {c}^S$ appearing in equation (5.46). The operator $\mathcal {C}^{S}_{\kappa _1 \kappa _2 \kappa _3}$ can be further decomposed into
  (5.58) $$ \begin{align} \mathcal{C}^{S}_{\kappa_1 \kappa_2 \kappa_3} = \mathcal{C}^{S,1}_{\kappa_1 \kappa_2 \kappa_3} + \mathcal{C}^{S,2}_{\kappa_1 \kappa_2 \kappa_3} \end{align} $$
  (see equation (5.47)).

• • The regular cubic term is given by

  (5.59) $$ \begin{align} \begin{aligned} & \mathcal{C}^{R}(a,b,c) = \sum_{\kappa_1 \kappa_2 \kappa_3} \mathcal{C}^{R}_{\kappa_1 \kappa_2 \kappa_3}(a,b,c) \\ & \mathcal{C}^{R}_{\kappa_1 \kappa_2 \kappa_3}[a,b,c](t,\xi) = \iiint e^{it \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\sigma,\theta)} \mathfrak{c}^R_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\sigma,\theta) \, \widetilde{a}_{\iota_1}(t,\eta) \widetilde{b}_{\iota_2}(t,\sigma) \widetilde{c}_{\iota_3}(t,\theta) \, d\eta \, d\sigma \,d\theta, \end{aligned} \end{align} $$
  where, in view of the estimates for the symbols appearing in Lemmas 5.4, 5.5 and 5.7, we have that $\mathfrak {c}^R$ enjoys bounds of the form
  (5.60) $$ \begin{align} \big| \partial_{\xi}^a \partial_{\eta}^b \partial_{\sigma}^c \partial_{\theta}^d \mathfrak{c}^R_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\sigma,\theta) \big| \lesssim \frac{1}{\langle \eta \rangle \langle \sigma \rangle \langle\theta\rangle} \frac{\mathrm{med}(|\eta|,|{\sigma}|,|\theta|)^{1+a+b+c+d}}{\langle\xi-\eta-{\sigma}-\theta\rangle^{N}}, \end{align} $$
  up to possible logarithmic losses like those appearing in equation (5.49); recall also the notation for $\mathrm {med}$ from the end of Section 2.5.1. We are again adopting the convention explained at the beginning of Section 5.5 of disregarding singularities at $0$ in the variables of the inputs of equation (5.59).

  We then note that the terms in equation (5.59) are essentially a cubic version of the regular quadratic terms $\mathcal {Q}^R$ in equation (5.56). A good way to think of them is that they are essentially of the form $T[\widetilde {{\mathcal {F}}}^{-1}\mathcal {Q}^{R\sharp }(g,g),g]$ . Therefore, estimating equation (5.59) is much easier than estimating equation (5.56) or other cubic terms that appear in our arguments, such as those in Section 9; see also Propositions 11.5 and 11.6, where terms similar to equation (5.59) are treated. Therefore, in all that follows, we will skip the estimate for the $\mathcal {C}^R$ terms from equation (5.55).

The next Lemma shows that the renormalised profile satisfies the key assumption about vanishing at the zero frequency like the original profile g.

Lemma 5.8. The renormalised profile equation (5.53) satisfies $\widetilde {f}(0)=0$ . Moreover, when V is exceptional and even, f has the same parity of g (even/odd in the case of odd/even resonance).

Proof. In the generic case, $\widetilde {f}(0)=0$ is automatically satisfied; see Proposition 3.6.¹² Moreover, in the case where $\widetilde {u}(0)=0$ because of the structure of the equations as for (KG2), the claimed property for $\widetilde {f}$ is easy to verify because the quadratic symbols under consideration will vanish at $\xi =0$ .

We now verify the statement in the exceptional case by distinguishing between the case of odd versus even solutions. Note that an odd, respectively even, solution u corresponds to an odd, respectively even, profile $\widetilde {g}$ in distorted Fourier space; see equations (5.2)–(5.5) and Lemma 3.7.

In the case of odd solutions, our assumptions dictate that the zero energy resonance is even – that is, $T(0)=1$ – and the the coefficient $a(x)$ is odd; hence $\ell _{+\infty } = -\ell _{-\infty }$ . In the case of even solutions instead, we have that the zero energy resonance is odd – that is, $T(0)=-1$ – and the the coefficient $a(x)$ is even; hence $\ell _{+\infty } = \ell _{-\infty }$ .

In both exceptional cases, since V is even, we have $m_+(-x,\xi )=m_-(x,\xi )$ and $R_+(\xi ) = R_-(\xi )$ ; see equation (3.13). In particular, the coefficients defined in equation (4.5) satisfy the symmetry

(5.61) $$ \begin{align} \mathbf{a}^{\epsilon}_{\lambda}(\xi) = \mathbf{a}^{-\epsilon}_{\lambda}(-\xi), \quad {\lambda},\epsilon \in \{+,-\}, \end{align} $$

and $R_\pm (0)=0$ .

Next, we inspect the formulas in equation (5.54) with equation (5.11). Since $\widetilde {g}(0)=0$ , it suffices to prove that, for fixed $\iota _1,\iota _2$ , we have that $\widetilde {{\mathcal {F}}} \big (T^+_{\iota _1\iota _2}(g,g) + T^-_{\iota _1\iota _2}(g,g) \big )$ vanishes at $\xi =0$ . The contribution to $T^{\epsilon }_{\iota _1\iota _2}(g,g)$ at fixed $\lambda ,\mu ,\nu $ when $\xi \rightarrow 0$ is

$$ \begin{align*} \lim_{\xi\rightarrow 0} \big( I_\epsilon(\xi) + I_{-\epsilon}(\xi) \big), \end{align*} $$

where

(5.62) $$ \begin{align} \begin{aligned} I_\epsilon(\xi) & := -\iota_1\iota_2 \iint e^{it \Phi_{\iota_1\iota_2}(0,\eta,\sigma)} \widetilde{g}_{\iota_1}(t,\eta) \widetilde{g}_{\iota_2}(t, \sigma) \, \frac{a^{\epsilon}_{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda\mu\nu}}(\xi,\eta,\sigma) }{8\pi i \langle \eta \rangle \langle \sigma \rangle \Phi_{\iota_1 \iota_2}(0,\eta,\sigma)} \, \\ &\quad \times \ell_{\epsilon \infty} \, \left[ \sqrt{\frac{\pi}{2}} \delta(p_0) + \epsilon \varphi^{\ast}(p_0,\eta,\sigma) \, \mathrm{p.v.} \frac{\widehat{\phi}(p_0)}{ip_0} \right] \, d\eta \,d\sigma, \qquad p_0=\iota_1\mu\eta-\iota_2\nu\sigma. \end{aligned} \end{align} $$

Note that the coefficient $\mathbf {a}^{\epsilon }_{\lambda }(\xi )$ may be discontinuous at $0$ , and this is why we kept the dependence on $\xi $ for the coefficient ‘a’ in equation (5.62) and the limit in $\xi $ .

Next, we change variables $(\eta ,\sigma ) \mapsto (-\eta ,-\sigma )$ in the expression in equation (5.62); note that $p_0\mapsto -p_0$ , and recall that $\phi $ is even. In the case of odd $\widetilde {g}$ , using equation (5.61) and $\lim _{\xi \rightarrow 0}\mathbf {a}^{\epsilon }_+(\xi ) = 1$ , $\lim _{\xi \rightarrow 0} \mathbf {a}^{\epsilon }_-(\xi ) = 0$ (here the coefficients are continuous; see (equation (4.5))), we see that

$$ \begin{align*} a^{\epsilon}_{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda\mu\nu}}(0,-\eta,-\sigma) = a^{-\epsilon}_{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda\mu\nu}}(0,\eta,\sigma). \end{align*} $$

Since $\ell _{+\infty }=-\ell _{-\infty }$ , it follows that $I_\epsilon (0) = - I_{-\epsilon }(0)$ , hence the desired conclusion.

In the case of even $\widetilde {g}$ , we have instead $\lim _{\xi \rightarrow 0}(\mathbf {a}^{\epsilon }_+(\xi ) + \mathbf {a}^{-\epsilon }_+(\xi ))=0$ and $\lim _{\xi \rightarrow 0} \mathbf {a}^{\epsilon }_-(\xi )=0$ , which give

$$ \begin{align*} \lim_{\xi\rightarrow 0} \big(a^{\epsilon}_{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda\mu\nu}}(\xi,-\eta,-\sigma) + a^{-\epsilon}_{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda\mu\nu}}(\xi,\eta,\sigma)\big)=0. \end{align*} $$

Then, changing $(\eta ,\sigma ) \mapsto (-\eta ,-\sigma )$ and taking the $\xi \rightarrow 0$ in equation (5.62), using that $\ell _{+\infty }=\ell _{-\infty }$ here, we see that $\lim _{\xi \rightarrow 0}(I_\epsilon (\xi ) + I_{-\epsilon }(\xi )) = 0$ .

To show that f has the same parity of g, we can use similar arguments. Let us just look at the case when g is even (which corresponds to an odd resonance), as the odd case is analogous. It suffices to show that for even $\widetilde {g}$ , we have that $\widetilde {T}(g,g)$ is even. Looking again at the definition of T in equation (5.54) and of Z in equations (5.11) and (4.4), we see that

$$ \begin{align*} Z^{\epsilon} _{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda \mu \nu}}(-\xi,-\eta,-\sigma) & = \ell_{\epsilon \infty} \frac{a^{-\epsilon}_{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda\mu\nu}} (\xi,\eta,\sigma)}{8\pi\langle \eta \rangle \langle \sigma \rangle} \left[ \sqrt{\frac{\pi}{2}} \delta(p) + \epsilon \varphi^{\ast}(p,\eta,\sigma) \, \mathrm{p.v.} \frac{\widehat{\phi}(p)}{-ip} \right] = Z^{-\epsilon} _{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda \mu \nu}}(\xi,\eta,\sigma) \end{align*} $$

having used equation (5.61) and $\ell _{+\infty } = \ell _{-\infty }$ . It then follows that $\widetilde {{\mathcal {F}}} T_{\iota _1 \iota _2}^+(g,g)(-\xi ) = \widetilde {{\mathcal {F}}} T_{\iota _1 \iota _2}^-(g,g)(\xi )$ and therefore (see equation (5.53)) $\widetilde {T}(g,g)(\xi )$ is even.

The next lemmas give regularity properties for the symbols of the bilinear operators $\mathcal {Q}^R$ (Lemma 5.9) and T and $\mathcal {C}^S$ (Lemma 5.10). These are based on the results from Sections 3 and 4, but we chose to place them here (although they were refereed to, and used, before) since parts of the proofs are similar to the proof of Lemma 5.8 above.

Lemma 5.9. Let $\mathcal {Q}^R = \mathcal {Q}_{\iota _1\iota _2}^R$ be the bilinear operator defined in equation (5.15), with symbol $\mathfrak {q}=\mathfrak {q}_{\iota _1,\iota _2}$ as in equation (5.16), where $\mu ^R = \mu ^R_{\iota _1\iota _2}$ is given by equations (4.6)–(4.7). Then under the assumptions of Theorem 1.1, we have that

(5.63) $$ \begin{align} \begin{aligned} \partial_{\xi} \mathcal{Q}_{\iota_1\iota_2}^R = it \frac{\xi}{\langle \xi \rangle} \mathcal{Q}_{\iota_1\iota_2}^R -\iota_1\iota_2 \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \mathfrak{q}^{\prime}_{\iota_1\iota_2}(\xi,\eta,\sigma) \, \widetilde{g}_{\iota_1}(t,\eta) \widetilde{g}_{\iota_2}(t,\sigma) \, d\eta \, d\sigma, \end{aligned} \end{align} $$

where

(5.64) $$ \begin{align} & \mathfrak{q}^{\prime}_{\iota_1\iota_2} := \mathfrak{q}_1 + \mathfrak{q}_2 + \mathfrak{q}_3, \nonumber\\ & \mathfrak{q}_1(\xi,\eta,\sigma) := \frac{1}{8\pi\langle \eta \rangle\langle \sigma \rangle}\sum_{\epsilon_1,\epsilon_2,\epsilon_3 \in \{+,-\}} \mathbf{1}_{\epsilon_1}(\xi)\mathbf{1}_{\epsilon_2}(\eta)\mathbf{1}_{\epsilon_3}({\sigma}) \partial_{\xi} \mathfrak{r}_{\epsilon_1\epsilon_2\epsilon_3}(\xi,\eta,\sigma),\qquad\quad \end{align} $$

(5.65) $$ \begin{align} & \mathfrak{q}_2(\xi,\eta,\sigma) := \frac{1}{8\pi\langle \eta \rangle\langle \sigma \rangle} \sum_{\epsilon,\lambda,\mu,\nu} \epsilon \, \overline{\mathbf{b}_\lambda^{\epsilon}(\xi)} \mathbf{a}_{\mu,\iota_1}^{\epsilon}( \eta) \mathbf{a}_{\nu,\iota_2}^{\epsilon}(\sigma) \Big[ \big(1 - \varphi^{\ast}(p,\eta,\sigma) \big) \frac{\widehat{\phi}(p)}{i p} \Big], \end{align} $$

(5.66) $$ \begin{align} & \mathfrak{q}_3(\xi,\eta,\sigma) := \frac{1}{8\pi\langle \eta \rangle\langle \sigma \rangle} \sum_{\lambda, \mu, \nu, \epsilon} \epsilon a^{\epsilon}_{\substack{- \iota_1 \iota_2 \\ \lambda\mu\nu}} (\xi,\eta,\sigma) \, \partial_{\xi} \Big[ \big(1 - \varphi^{\ast}(p,\eta,\sigma) \big) \frac{\widehat{\phi}(p)}{i p} \Big], \qquad\quad \end{align} $$

where $\mathbf {b}_\lambda ^{\epsilon }(\xi )$ is the function defined for $\xi \neq 0$ by $\mathbf {b}_\lambda ^{\epsilon }(\xi ) = \partial _{\xi } \mathbf {a}_\lambda ^{\epsilon }(\xi )$ (see equation (4.5)).

Proof. For notational convenience, let us define the operator (we will often drop the time variable, which is a fixed parameter here, and omit the $\iota _1\iota _2$ signs since they do not play any role)

(5.67) $$ \begin{align} \begin{aligned} T_{\mathfrak{m}}[F](\xi) & := \iint \mathfrak{m}_{\iota_1\iota_2}(\xi,\eta,\sigma) \, F(\xi,\eta,\sigma) \, d\eta \, d\sigma, \end{aligned} \end{align} $$

so that

(5.68) $$ \begin{align} \begin{aligned} \partial_{\xi} \mathcal{Q}_{\iota_1\iota_2}^R(t,\xi) = it \frac{\xi}{\langle \xi \rangle} \mathcal{Q}_{\iota_1\iota_2}^R(t,\xi)[g,g] + T_{\partial_{\xi} \mathfrak{q}_{\iota_1\iota_2}}[G](\xi). \end{aligned} \end{align} $$

For the second term on the right-hand side of equation (5.68), we have, recalling the definition of $\mathfrak {q}$ from equation (5.16),

$$ \begin{align*} T_{\partial_{\xi} \mathfrak{q}} [G] = T_{\mathfrak{m}_1}[G] + T_{\mathfrak{m}_2}[G] + T_{\mathfrak{q}_3}[G], \end{align*} $$

where

(5.69) $$ \begin{align} \mathfrak{m}_1(\xi,\eta,\sigma) & := \frac{1}{8\pi\langle \eta \rangle\langle \sigma \rangle} \partial_{\xi} \mu^R(\xi,\eta,\sigma),\qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad\quad \ \end{align} $$

(5.70) $$ \begin{align} \mathfrak{m}_2(\xi,\eta,\sigma) & := \frac{1}{8\pi\langle \eta \rangle\langle \sigma \rangle} \sum_{\epsilon,\lambda,\mu,\nu} \epsilon \, \partial_{\xi} \overline{\mathbf{a}_\lambda^{\epsilon}(\xi)} \mathbf{a}_{\mu,\iota_1}^{\epsilon}( \eta) \mathbf{a}_{\nu,\iota_2}^{\epsilon}(\sigma) \Big[ \big(1 - \varphi^{\ast}(p,\eta,\sigma) \big) \frac{\widehat{\phi}(p)}{i p} \Big], \end{align} $$

with $p = \lambda \xi - \iota _1 \mu \eta - \iota _2 \nu \sigma $ , and $\mathfrak {q}_3$ the symbol in equation (5.66). To prove the lemma, it then suffices to show that

(5.71) $$ \begin{align} T_{\mathfrak{m}_1}[G] = T_{\mathfrak{q}_1}[G], \end{align} $$

(5.72) $$ \begin{align} T_{\mathfrak{m}_2}[G] = T_{\mathfrak{q}_2}[G]. \end{align} $$

Proof of equation (5.71). We look back at the definition of $\mu ^R$ in equations (4.6)–(4.7) and see that equation (5.71) amounts to showing that the $\delta $ contribution that arises from $\partial _{\xi } \mu ^R$ vanishes. Recall the description of $\mu ^R = \mu ^{R1} + \mu ^{R2}$ in equations (4.20)–(4.22). Note that all the integrals under consideration are absolutely convergent because of the fast decay of $\psi ^R$ . We first look at $\mu ^{R1}$ and distinguish between the generic and exceptional cases.

In the generic case, since $T(0)=0$ and $R_{\pm }(0) = -1$ (see Lemma 3.3), we have $\partial _{\xi } \psi ^A(x,\xi =0) = 0$ , with $A=S$ or R, which suffices.

In the exceptional cases, let us write $\psi (x,\xi ) = \mathbf {1}_{+}(\xi )\psi ^{>}(x,\xi ) + \mathbf {1}_{-}(\xi )\psi ^{<}(x,\xi )$ , where $\psi ^{>}$ is given in equation (3.26) and $\psi ^{<}$ in equation (3.27), and similarly let $\psi ^A(x,\xi ) = \mathbf {1}_{+}(\xi )\psi ^{A,>}(x,\xi ) + \mathbf {1}_{-}(\xi )\psi ^{A,<}(x,\xi )$ , with $A=S,R$ , according to the formulas in equations (3.29) and (3.30). Differentiating equation (4.21), we get the singular contribution

(5.73) $$ \begin{align} \mathfrak{m}_{R1,\delta}(\xi,\eta,\sigma) := \delta(\xi) \sum_{(A,B,C) \in X_R} \int a(x) \, \big[ \overline{\psi^{A,>}(x,\xi)} - \overline{\psi^{A,<}(x,\xi)} \big]\psi^B_{\iota_1}(x,\eta) \psi^C_{\iota_2}(x,\sigma) \, dx. \end{align} $$

In the case $a:=f_+(-\infty ,0)=1$ , we have $T(0)=1$ and $R_\pm (0)=0$ (see Lemma 3.16), which shows, looking at the formulas in equations (3.26)–(3.30), that equation (5.73) vanishes.

When instead $a=-1$ , we have $T(0)=-1$ and $R_\pm (0)=0$ , and we need to look at the bilinear operator associated to equation (5.73): that is, $T_{\mathfrak {m}_{R1,\delta }}[G]$ with G as in equation (5.68). Changing variables $(\eta ,\sigma ) \rightarrow (-\eta ,-\sigma )$ leaves G unchanged in view of Lemma 3.7. At the same time, using that $a(x)$ is even and $\psi ^{A,>}(x,\xi ) = \psi ^{A,<}(-x,-\xi )$ (since $R_+=R_-$ , and $m_+(x,\xi ) = m_-(-x,\xi )$ ), changing $x\rightarrow -x$ in equation (5.73) shows that

$$ \begin{align*} \mathfrak{m}_{R1,\delta}(\xi,-\eta,-\sigma) &= \delta(\xi)\sum_{(A,B,C) \in X_R} \int a(x) \, \big[ \overline{\psi^{A,>}(-x,0)} - \overline{\psi^{A,<}(-x,0)} \big] \psi^B_{\iota_1}(x,\eta) \psi^C_{\iota_2}(x,\sigma) \, dx \\ &= - \mathfrak{m}_{R1,\delta}(\xi,\eta,\sigma). \end{align*} $$

This gives $T_{\mathfrak {m}_{1,\delta }}[G]=0$ , as desired.

For $\mu ^{R2}$ , we start from the formula in equation (4.26); upon applying $\partial _{\xi }$ , we need to look at the symbol containing a $\delta (\xi )$ contribution: that is,

(5.74) $$ \begin{align} \mathfrak{m}_{R2,\delta}(\xi,\eta,\sigma) = \sum_{\epsilon_1,\epsilon_2,\epsilon_3, \lambda,\mu,\nu} \widehat{\chi_{\epsilon_1\epsilon_2\epsilon_3}}(\lambda\xi -\mu\eta-\nu{\sigma}) \big[ \partial_{\xi} \overline{\mathbf{a}_\lambda^{\epsilon_1}(\xi)} - \mathbf{b}_\lambda^{\epsilon_1}(\xi) \big]\mathbf{a}_\mu^{\epsilon_2}(\eta)\mathbf{a}_\nu^{\epsilon_3}({\sigma}), \end{align} $$

where, recall, the sum is over triples of signs $(\epsilon _1,\epsilon _2,\epsilon _3) \neq (+,+,+), (-,-,-)$ , and we have $\chi _{\epsilon _1\epsilon _2\epsilon _3}(x) = a(x)\chi _{\epsilon _1}\chi _{\epsilon _2}\chi _{\epsilon _3}(x)$ . To show that this symbol gives a vanishing contribution, we first recall the definition of the $\mathbf {a}_\lambda ^{\epsilon }$ coefficients from equation (4.5) and see that in the generic case, we have $\partial _{\xi } \mathbf {a}_\lambda ^{\epsilon }(\xi ) = \mathbf {b}_\lambda ^{\epsilon }(\xi ) - \epsilon \lambda \delta (\xi ).$ Then the right-hand side of equation (5.74) is

$$ \begin{align*} -\delta(\xi) \sum_{\epsilon_1,\epsilon_2,\epsilon_3, \lambda,\mu,\nu} \widehat{\chi_{\epsilon_1\epsilon_2\epsilon_3}}(-\mu\eta-\nu{\sigma}) \epsilon_1\lambda\, \mathbf{a}_\mu^{\epsilon_2}(\eta)\mathbf{a}_\nu^{\epsilon_3}({\sigma}), \end{align*} $$

which vanishes upon summing over $\lambda = +$ and $-$ .

In the exceptional cases, using Lemma 3.4, we have

(5.75) $$ \begin{align} \partial_{\xi} \mathbf{a}_\lambda^{\epsilon}(\xi) = \mathbf{b}_\lambda^{\epsilon}(\xi) - \epsilon \delta(\xi) \cdot \left\{ \begin{array}{ll} 1 - \dfrac{2a}{1+a^2} & \mbox{if}\ \lambda = +\,, \\ \dfrac{a^2-1}{1+a^2} & \mbox{if}\ \lambda = -\,. \end{array} \right. \end{align} $$

Note that we can then use the formula in equation (5.75) in all cases, with the convention that $a=0$ in the generic case. When $a=1$ , the vanishing of equation (5.74) is obvious since the coefficients of the $\delta $ in equation (5.75) vanish. In the case $a=-1$ , instead, only the $\lambda =+$ term remains in equation (5.75), and we look at the bilinear operator associated to equation (5.74): that is, $T_{\mathfrak {m}_{R2,\delta }}[G]$ with G as in equation (5.68). More precisely, we can see that changing signs to $(\eta ,\sigma )$ in $T_{\mathfrak {m}_{R2,\delta }}[G]$ leaves G invariant, while

$$ \begin{align*} \mathfrak{m}_{R2,\delta}(\xi,-\eta,-\sigma) & = \delta(\xi) \sum_{\epsilon_1,\epsilon_2,\epsilon_3,\mu,\nu} \widehat{\chi_{\epsilon_1\epsilon_2\epsilon_3}}(\mu\eta+\nu{\sigma}) (-2\epsilon_1) \mathbf{a}_\mu^{\epsilon_2}(-\eta)\mathbf{a}_\nu^{\epsilon_3}(-{\sigma}) \\ & = \delta(\xi) \sum_{\epsilon_1,\epsilon_2,\epsilon_3,\mu,\nu} \widehat{\chi_{\epsilon_1\epsilon_2\epsilon_3}}(-\mu\eta-\nu{\sigma}) (2\epsilon_1) \mathbf{a}_\mu^{\epsilon_2}(\eta)\mathbf{a}_\nu^{\epsilon_3}({\sigma}) = - \mathfrak{m}_{R2,\delta}(\xi,\eta,\sigma), \end{align*} $$

having used equation (5.61) and changed the signs of the $\epsilon $ ’s to get the second identity, also using that $ \chi _{\epsilon _1\epsilon _2\epsilon _3}(-x) = \chi _{-(\epsilon _1\epsilon _2\epsilon _3)}(x)$ , since $\chi _+(-x)=\chi _-(x)$ and $a(x)$ is even.

Proof of equation (5.72). We can use arguments similar to those used above for equation (5.71). As before, it suffices to show that the contribution to equation (5.70) that contains the $\delta $ factor from equation (5.75) vanishes. In the generic case (using equation (5.75) with $a=0$ ) this contribution is

(5.76) $$ \begin{align} \mathfrak{m}_{2,\delta}(\xi,\eta,\sigma) & := \frac{1}{8\pi\langle \eta \rangle\langle \sigma \rangle} \sum_{\epsilon,\lambda,\mu,\nu} \epsilon \, \big[- \epsilon \lambda \delta(\xi) \big] \mathbf{a}_{\mu,\iota_1}^{\epsilon}(\eta) \mathbf{a}_{\nu,\iota_2}^{\epsilon}(\sigma) \Big[ \big(1 - \varphi^{\ast}(p_0,\eta,\sigma) \big) \frac{\widehat{\phi}(p_0)}{i p_0} \Big], \end{align} $$

with $p_0 := - \iota _1 \mu \eta - \iota _2 \nu \sigma $ , and vanishes upon summing over $\lambda = +,-$ . For $a=1$ the vanishing is obvious since the coefficient of the $\delta $ in equation (5.75) vanish. To see the cancellation in the case $a=-1$ , similarly to what was done in the previous paragraph, we look at the bilinear operator with symbol

$$ \begin{align*} \mathfrak{m}_{2,\delta}(\xi,\eta,\sigma) & := \frac{1}{8\pi\langle \eta \rangle\langle \sigma \rangle} \sum_{\epsilon,\mu,\nu} \big[ -2 \delta(\xi) \big] \mathbf{a}_{\mu,\iota_1}^{\epsilon}( \eta) \mathbf{a}_{\nu,\iota_2}^{\epsilon}(\sigma) \Big[ \big(1 - \varphi^{\ast}(p_0,\eta,\sigma) \big) \frac{\widehat{\phi}(p_0)}{i p_0} \Big]. \end{align*} $$

Notice that the $\epsilon $ factor from equation (5.75) and the one present initially in equation (5.70) canceled out. Using equation (5.61) and the fact that $\widehat {\phi }$ is even, recalling the definition of $\varphi ^{\ast }$ (see equation (5.12)) and then changing the sign of $\epsilon $ in the sum, we have

$$ \begin{align*} \mathfrak{m}_{2,\delta} (\xi,-\eta,-\sigma) & = \frac{1}{8\pi\langle \eta \rangle\langle \sigma \rangle} \sum_{\epsilon,\mu,\nu} \big[ -2 \delta(\xi) \big] \mathbf{a}_{\mu,\iota_1}^{-\epsilon}(\eta) \mathbf{a}_{\nu,\iota_2}^{-\epsilon}(\sigma) \Big[ \big(1 - \varphi^{\ast}(p_0,\eta,\sigma) \big) \frac{\widehat{\phi}(p_0)}{-i p_0} \Big] \\ & = - \mathfrak{m}_{2,\delta} (\xi,\eta,\sigma), \end{align*} $$

which completes the proof.

Lemma 5.10. Let $T=T_{\iota _1\iota _2}$ be the bilinear operator defined in equation (5.29) with the definitions in equations (5.11) and (5.8). Then under the assumptions of Theorem 1.1, we have that

(5.77) $$ \begin{align} \begin{aligned} \partial_{\xi} \widetilde{{\mathcal{F}}} T_{\iota_1\iota_2} = it \frac{\xi}{\langle \xi \rangle} T_{\iota_1\iota_2} -\iota_1\iota_2 \iint e^{it \Phi_{\iota_1\iota_2}} \mathfrak{t}^{\prime}_{\iota_1\iota_2}(\xi,\eta,\sigma) \, \widetilde{g}_{\iota_1}(t,\eta) \widetilde{g}_{\iota_2}(t,\sigma) \, d\eta \, d\sigma \end{aligned} \end{align} $$

with

(5.78) $$ \begin{align} & \mathfrak{t}^{\prime}_{\iota_1\iota_2} := \mathfrak{t}_1 + \mathfrak{t}_2, \nonumber\\ & \mathfrak{t}_1(\xi,\eta,\sigma):= \sum_{\epsilon,\lambda,\mu,\nu} \frac{ \ell_{\epsilon \infty} }{8i\pi\langle \eta \rangle \langle \sigma \rangle} \frac{\overline{\mathbf{b}_\lambda^{\epsilon}(\xi)} \mathbf{a}_{\mu,\iota_1}^{\epsilon}(\eta) \mathbf{a}_{\nu,\iota_2}^{\epsilon}(\sigma)}{ \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \left( \sqrt{\frac{\pi}{2}} \delta(p) + \epsilon \varphi^{\ast}(p,\eta,\sigma) \, \mathrm{p.v.} \frac{\widehat{\phi}(p)}{ip} \right), \end{align} $$

(5.79) $$ \begin{align} & \mathfrak{t}_2(\xi,\eta,\sigma):= \sum_{\epsilon,\lambda,\mu,\nu} \ell_{\epsilon \infty} \frac{a^{\epsilon}_{\substack{- \iota_1 \iota_2 \\ \lambda\mu\nu}}(\xi,\eta,\sigma)}{8 i\pi\langle \eta \rangle \langle \sigma \rangle} \partial_{\xi} \left[ \frac{1}{\Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \left( \sqrt{\frac{\pi}{2}} \delta(p) + \epsilon \varphi^{\ast}(p,\eta,\sigma) \, \mathrm{p.v.} \frac{\widehat{\phi}(p)}{ip} \right) \right], \end{align} $$

where $\mathbf {b}_\lambda ^{\epsilon }(\xi )$ is the function defined for $\xi \neq 0$ by $\mathbf {b}_\lambda ^{\epsilon }(\xi ) = \partial _{\xi } \mathbf {a}_\lambda ^{\epsilon }(\xi )$ (see equation (4.5)).

Proof. The proof follows along the same lines of the proof of Lemma 5.9 above; compare equations (5.65)–(5.66) with equations (5.78)–(5.79). Starting from the definition of the coefficient equation (5.11), we see that the only thing to prove is that the $\delta (\xi )$ contribution that arises when differentiating the $\mathbf {a}_\lambda ^{\epsilon }(\xi )$ factor in the numerator vanishes. This can be shown exactly as in the proof of equation (5.72); see the formulas for the symbols in equations (5.70) and (5.65). In particular, if we let $\mathfrak {t}_{1,\delta }$ denote the $\delta (\xi )$ contribution, that is, a symbol as in equation (5.78) with $\mathbf {b}_\lambda ^{\epsilon }$ replaced by $\partial _{\xi } \mathbf {a}_\lambda ^{\epsilon } - \mathbf {b}_\lambda ^{\epsilon }$ , and look at the exceptional case with odd resonance, we can use $\ell _{+\infty }=-\ell _{-\infty }$ and equation (5.61) to see that $\mathfrak {t}_{1,\delta }(\xi ,-\eta ,-\sigma ) = -\mathfrak {t}_{1,\delta }(\xi ,\eta ,\sigma )$ . We can then conclude as before.

Remark 5.11. Here are some remarks that we will often use in what follows:

1. (i) Lemmas 5.9 and 5.10 show that the derivatives of the symbols of the bilinear operators $\mathcal {Q}^R$ and T are smooth up to up to (possible) singularities along the axis $\xi ,\eta $ or $\sigma =0$ . These latter can then be handled as in Remark 5.1.

2. (ii) Note that the statements of Lemmas 5.9 and 5.10 remain valid when the operators are applied to any other two inputs in the generic case. In the exceptional cases, they remain valid for inputs with the same parity of g (even/odd in the case of odd/even resonance), such as $(g,f)$ or $(g, T(g,g))$ ; see Lemma 5.8. In the rest of our analysis, it will always be the case that the parity of the inputs is the proper one.

3. (iii) Also notice that formulas similar to equations (5.77)–(5.79) hold for the cubic bulk equations (5.34) and (5.35), as can be seen from equation (5.30) and the fact that $\partial _s g$ has the same parity of g.

6 Multilinear estimates

In this section, we first examine general multilinear estimates that will be useful in particular in Section 9 and then establish multilinear estimates for all the operators appearing in Section 5.7.

6.1 Bilinear operators

General bilinear operators can be written as

$$ \begin{align*}B_{\mathfrak{a}}(f,g)(x) = \widehat{\mathcal{F}}^{-1}_{\xi \to x} \iint {\mathfrak{a}}(\xi,\eta,\zeta) \widehat{f}(\eta) \widehat{g}(\zeta) \,d\eta\,d\zeta. \end{align*} $$

As far as the present paper is concerned, we are mostly interested in two classes of bilinear operators: those whose symbol $\mathfrak {a}$ contains a singular factor $\delta (\xi -\eta -\zeta )$ , and those whose symbol contains a singular factor $\mathrm {p.v.} \frac {\widehat {\phi }(\xi -\eta -\zeta )}{\xi -\eta -\zeta }$ ; for simplicity, we will drop the $\mathrm {p.v.}$ sign in what follows. We parametrise these operators as

(6.1) $$ \begin{align} \begin{aligned} C_{\mathfrak{a}}(f,g)(x) & := \widehat{\mathcal{F}}^{-1}_{\xi \to x} \int \mathfrak{a}(\eta,\xi-\eta) \widehat{f}(\eta) \widehat{g}(\xi-\eta) \,d\eta \\ & = \frac{1}{\sqrt{2\pi}} \iint \mathfrak{a}(\eta,\zeta) \widehat{f}(\eta) \widehat{g}(\zeta) e^{ix(\eta + \zeta)} \,d\eta \,d\zeta \end{aligned} \end{align} $$

and

(6.2) $$ \begin{align} \begin{aligned} D_{\mathfrak{b}}(f,g)(x) & := \widehat{\mathcal{F}}^{-1}_{\xi \to x} \iint \mathfrak{b}(\eta,\zeta,\xi-\eta-\zeta) \widehat{f}(\eta) \widehat{g}(\zeta) \frac{\widehat{\phi}(\xi - \eta - \zeta)}{\xi - \eta - \zeta} \,d\eta \,d\zeta \\ & = \frac{1}{\sqrt{2\pi}} \iiint \mathfrak{b}(\eta,\zeta,\theta) \widehat{f}(\eta) \widehat{g}(\zeta) e^{ix(\eta + \zeta+\theta)} \frac{\widehat{\phi}(\theta)}{\theta} \,d\eta \,d\zeta \, d\theta. \end{aligned} \end{align} $$

Notice that $C_{\mathfrak {a}}$ operators fall into the category of pseudo-products. As for $D_{\mathfrak {b}}$ operators, they are translation invariant to leading order since their symbol is smooth outside of the set $\{ \theta = 0\}$ .

A short computation shows that one can express these in physical space as

(6.3) $$ \begin{align} \begin{aligned} & C_{\mathfrak{a}}(f,g)(x) = \frac{1}{\sqrt{2\pi}} \iint \widehat{\mathfrak{a}}(y-x,z-x) f(y) g(z)\,dy\,dz, \\ & D_{\mathfrak{b}}(f,g)(x) = \frac{1}{\sqrt{2\pi}} \iint K(x,y,z) f(y) g(z)\,dy\,dz, \\ & \qquad \mbox{with} \quad K(x,y,z) := \int \widehat{\mathfrak{b}}(y-x,z-x,w-x) Z(w) \,dw, \quad Z := \widehat{\mathcal{F}}^{-1} \frac{\widehat{\phi}(\theta)}{\theta}. \end{aligned} \end{align} $$

For $D_{\mathfrak {b}}$ , this can be seen as follows (we omit the computation for $C_{\mathfrak {a}}$ , which is more elementary):

$$ \begin{align*} D_{\mathfrak{b}}(f,g)(x) & = \frac{1}{\sqrt{2\pi}} \iiint \mathfrak{b}(\eta,\zeta,\theta) \widehat{f}(\eta) \widehat{g}(\zeta) e^{ix(\eta + \zeta+\theta)} \frac{\widehat{\phi}(\theta)}{\theta} \,d\eta \,d\zeta \, d\theta \\ & = \frac{1}{(2\pi)^{2}} \int \dots \int \mathfrak{b}(\eta,\zeta,\theta) f(y) g(z) Z(w) e^{i\eta(x-y)} e^{i\zeta(x-z)} e^{i\theta(x-w)} \,d\theta \, d\eta \, d\zeta \,dy\,dz\,dw \\ & = \frac{1}{\sqrt{2\pi}} \iiint \widehat{\mathfrak{b}}(y-x,z-x,w-x) Z(w) f(y) g(z)\,dw\,dy\,dz. \end{align*} $$

Lemma 6.1 (Boundedness for the $C_{\mathfrak {a}}$ operators)

If $1\leq p,q,r \leq \infty $ satisfy $\frac {1}{p} + \frac {1}{q} = \frac {1}{r} $ ,

$$ \begin{align*}\left\| C_{\mathfrak{a}} \right\|_{L^p \times L^q \to L^{r}} \lesssim \big\| \, \widehat{{\mathfrak{a}}} \, \big\|_{L^1}. \end{align*} $$

This is a standard result; see, for example, [33, Lemma 5.2].

Remark 6.2 (Bounds on symbols)

Given a symbol $\mathfrak {a}$ , we will often bound its Fourier transform in $L^1$ using the following criterion: if $\mathfrak {a}$ is supported on $(\eta ,\zeta ) \in [t_1-r_1,t_1+r_1] \times [t_2-r_2,t_2 + r_2 ]$ with

$$ \begin{align*}\left| \partial_{\eta}^{k_1} \partial_{\zeta}^{k_2} \mathfrak{a} \right| \lesssim r_1^{-k_1} r_2^{-k_2}, \end{align*} $$

then

$$ \begin{align*}\left| \widehat {\mathfrak{a}}(x,y) \right| \lesssim \frac{r_1}{(1 + r_1 x)^N} \frac{r_2}{(1 + r_2 y)^N} , \end{align*} $$

so that in particular $\| \widehat {\mathfrak {a}} \|_{L^1} \lesssim 1$ . Indeed, the assumption on $\mathfrak {a}$ implies that

$$ \begin{align*}\left| \partial_{\eta}^{k_1} \partial_{\zeta}^{k_2} \mathfrak{a} (\eta,\zeta)\right| \lesssim r_1^{-k_1} r_2^{-k_2} \chi\left( \frac{\eta - t_1}{r_1} \right) \chi\left( \frac{\zeta - t_2}{r_2} \right), \end{align*} $$

where $\chi $ is a cutoff function. Taking the Fourier transform and using that it maps $L^1$ to $L^{\infty }$ gives

$$ \begin{align*}\left| x^{k_1} y^{k_2} \widehat {\mathfrak{a}}(x,y) \right| \lesssim r_1^{-k_1} r_2^{-k_2} r_1 r_2, \end{align*} $$

which is the desired result.

The criterion mentioned above can be combined with a change of coordinates since, if L is a nondegenerate linear transformation, then

$$ \begin{align*}\| \widehat{ \mathfrak{a} \circ L } \|_{L^1} = \| \widehat{ \mathfrak{a} } \|_{L^1}. \end{align*} $$

Lemma 6.3 (Boundedness for the $D_{\mathfrak {b}}$ operators)

Assume that there exists $F \in L^1$ such that

$$ \begin{align*}\left| \int \widehat {\mathfrak{b}}(x,y,z) \,dz \right| \leq F(x,y). \end{align*} $$

Then if $1\leq p,q,r\leq \infty $ satisfy $\frac {1}{p} + \frac {1}{q} = \frac {1}{r} $ ,

$$ \begin{align*}\| D_{\mathfrak{b}} \|_{L^p \times L^q \to L^r} \lesssim \| F \|_{L^1}. \end{align*} $$

Proof. Using the physical space representation in equation (6.3), the proof reduces to that of Lemma 6.1 after noticing that $Z \in L^{\infty }$ .

Remark 6.4. In order for the condition of Lemma 6.3 to be satisfied, it suffices that $\mathfrak {b}$ be supported on $(\eta ,\zeta ,\theta ) \in [t_1-r_1,t_1+r_1] \times [t_2-r_2,t_2 + r_2 ] \times [t_3-r_3,t_3 + r_3 ]$ with

$$ \begin{align*}\left| \partial_{\eta}^{k_1} \partial_{\zeta}^{k_2} \partial_{\theta}^{k_3} \mathfrak{b} \right| \lesssim r_1^{-k_1} r_2^{-k_2} r_3^{-k_3}. \end{align*} $$

Indeed, this implies that

$$ \begin{align*}\left| \widehat {\mathfrak{b}}(x,y,z) \right| \lesssim \frac{r_1}{(1 + r_1 x)^N} \frac{r_2}{(1 + r_2 y)^N} \frac{r_1}{(1 + r_3 z)^N}. \end{align*} $$

This observation can be combined with a change of coordinates: it actually suffices that, for a nondegenerate linear transformation L,

$$ \begin{align*}\left| \partial_{\eta}^{k_1} \partial_{\zeta}^{k_2} \partial_{\theta}^{k_3} \mathfrak{b}(L(\eta,\zeta),\theta) \right| \lesssim r_1^{-k_1} r_2^{-k_2} r_3^{-k_3}. \end{align*} $$

6.2 Trilinear operators

General trilinear operators can be written as

(6.4) $$ \begin{align} T_{\mathfrak{m}}(f,g,h)(x) = \widehat{\mathcal{F}}^{-1}_{\xi \to x} \iint {\mathfrak{m}}(\xi,\eta,\zeta,\theta) \widehat{f}(\eta) \widehat{g}(\zeta) \widehat{h}(\theta) \,d\eta\,d\zeta \,d\theta. \end{align} $$

Two classes of trilinear operators of particular relevance in the present paper are given by

(6.5) $$ \begin{align} \begin{aligned} & U_{\mathfrak{m}}(f,g,h)(x) = \widehat{\mathcal{F}}^{-1}_{\xi \to x} \iint {\mathfrak{m}}(\xi,\eta,\zeta) \widehat{f}(\xi-\eta) \widehat{g}(\xi-\eta-\zeta) \widehat{h}(\xi-\zeta) \,d\eta\,d\zeta, \\ & V_{\mathfrak{n}}(f,g,h)(x) = \widehat{\mathcal{F}}^{-1}_{\xi \to x} \iiint {\mathfrak{n}}(\xi,\eta,\zeta,\theta) \widehat{f}(\xi-\eta) \widehat{g}(\xi-\eta-\zeta-\theta) \widehat{h}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \,d\theta. \end{aligned} \end{align} $$

Of course, other parametrisations of $U_{\mathfrak {m}}$ and $V_{\mathfrak {n}}$ would be possible; but the parametrisation above will be particularly relevant since it is the one adopted in Section 9.

In physical space, these are given by

(6.6) $$ \begin{align} \begin{aligned} & U_{\mathfrak{m}}(f,g,h)(w) = \frac{1}{\sqrt{2\pi}} \int \widehat {\mathfrak{m}}(-w+x+y+z,-x-y,-y-z) f(x) g(y) h(z)\,dx\,dy\,dz, \\ & V_{\mathfrak{n}}(f,g,h)(w) = \iiint K(w,x,y,z) f(x) g(y) h(z) \,dx \,dy \, dz, \\ & \quad \mbox{with} \quad K(w,x,y,z) := \frac{1}{\sqrt{2\pi}} \int \widehat{\mathfrak{n}}(-w+x+y+z,-x-y,-y-z,y'-y) Z(y')\,dy', \end{aligned} \end{align} $$

with Z as in equation (6.3).

We have the following standard trilinear analogue of Lemma 6.1.

Lemma 6.5 (boundedness for the $U_{\mathfrak {m}}$ operators)

If $1\leq p,q,r,s \leq \infty $ satisfy $\frac {1}{p} + \frac {1}{q} + \frac {1}{r} = \frac {1}{s} $ ,

$$ \begin{align*}{\left\| U_{\mathfrak{m}} \right\|}_{L^p \times L^q \times L^r \to L^{s}} \lesssim \| \widehat{{\mathfrak{m}}} \|_{L^1}. \end{align*} $$

Remark 6.6. Given a symbol $\mathfrak {m}$ , to check in practice that its Fourier transform is in $L^1$ , we will use the following principles:

• • If $\mathfrak {m}$ is supported on $(\xi ,\eta ,\zeta ) \in [t_1-r_1,t_1+r_1] \times [t_2-r_2,t_2 + r_2 ] \times [t_3 - r_3 , t_3 + r_3]$ with

  $$ \begin{align*}\left| \partial_{\xi}^{k_1} \partial_{\eta}^{k_2} \partial_{\zeta}^{k_3} \mathfrak{m} \right| \lesssim r_1^{-k_1} r_2^{-k_2} r_3^{-k_3}, \end{align*} $$
  then
  $$ \begin{align*}\left| \widehat {\mathfrak{m}}(x,y,z) \right| \lesssim \frac{r_1}{(1 + r_1 x)^N} \frac{r_2}{(1 + r_2 x)^N} \frac{r_3}{(1 + r_3 x)^N}, \end{align*} $$
  so that in particular $\| \widehat {\mathfrak {m}} \|_{L^1} \lesssim 1$ .

• • By the algebra property of the space $\mathcal {F} L^1$ (Wiener algebra), there holds

  $$ \begin{align*}\left\| \mathcal{F} (\mathfrak{m} \mathfrak{n}) \right\|_{L^1} \lesssim \| \widehat {\mathfrak{m}} \|_{L^1} \| \widehat {\mathfrak{n}} \|_{L^1}. \end{align*} $$

• • The previous point can be generalised to the case where $\mathfrak {n}$ is $L^1$ in a single direction and constant in the others. For instance, for any $a,b,c$ such that $|a| + |b| + |c| \sim 1$ ,

  $$ \begin{align*}\left\| \widehat{\mathcal{F}} [ \mathfrak{m}(\xi,\eta,\zeta) \varphi_{j}(a\xi + b\eta + c\zeta) ] \right\|_{L^1} \lesssim \| \widehat {\mathfrak{m}} \|_{L^1}. \end{align*} $$
  This remains true if $\varphi _j$ is replaced by $\varphi _{<j}$ or $\varphi _{>j}$ . Indeed, for any linear transformation L of $\mathbb {R}^3$ of determinant one, $\| \widehat {\mathfrak {m}} \|_{L^1} = \| \widehat {\mathfrak {m} \circ L} \|_{L^1}$ . Therefore, it suffices to examine the case $a=1$ and $b=c=0$ , which immediately reduces to the fact that $L^1$ is an algebra for convolution.

Lemma 6.7 (Boundedness for the $V_{\mathfrak {n}}$ operators)

Assume that there exists $F \in L^1$ such that

$$ \begin{align*}\left| \int \widehat{\mathfrak{n}}(x,y,z,t) \,dt \right| \leq F(x,y,z). \end{align*} $$

Then if $1\leq p,q,r,s \leq \infty $ satisfy $\frac {1}{p} + \frac {1}{q} + \frac {1}{r} = \frac {1}{s} $ ,

$$ \begin{align*}\| V_{\mathfrak{n}} \|_{L^p \times L^q \times L^r \to L^{s}} \lesssim \| F \|_{L^1}. \end{align*} $$

Proof. Since $Z \in L^{\infty }$ , the proof reduces to that of Lemma 6.5.

Remark 6.8. Given a symbol $\mathfrak {n}$ , to check in practice that it satisfies the condition of Lemma 6.7, we will mostly rely on the following principles:

• • It suffices that

  (6.7) $$ \begin{align} | \widehat{\mathfrak{n}}(x,y,z,t) | \lesssim F(x,y,z) G(t-L(x,y,z)), \end{align} $$
  where L is a linear function, and $F,G$ are rapidly decaying functions with $L^1$ norm equal to $1$ .

• • If the condition in equation (6.7) holds for $\mathfrak {n}(\xi ,\eta ,\zeta ,\theta )$ , it also does for $\mathfrak {n}(\xi ,\eta ,\zeta ,\theta ) \varphi _{j}(a\xi + b\eta + c\zeta + d \theta )$ (for a nondegenerate choice of $a,b,c,d$ ). The same holds if $\varphi _j$ is replaced by $\varphi _{<j}$ or $\varphi _{>j}$ .

• • Finally, if $\mathfrak {n}$ is supported on $(\xi ,\eta ,\zeta ,\theta ) \in [-r_1,r_1] \times [-r_2,r_2 ] \times [r_3 \times r_3] \times [-r_4,r_4]$ with

  $$ \begin{align*}\left| \partial_{\xi}^{k_1} \partial_{\eta}^{k_2} \partial_{\zeta}^{k_3} \partial_{\theta}^{k_4} \mathfrak{n} \right| \lesssim r_1^{-k_1} r_2^{-k_2} r_3^{-k_3} r_4^{-k_4}, \end{align*} $$
  then the condition equation (6.7) is satisfied.

6.3 The normal form operator T

Recall the definition of $T^{\pm }_{\iota _1 \iota _2}$ in equation (5.54). Before bounding the full operator, we focus on an operator ( $B_{\mathfrak {m}_{\iota _1 \iota _2}}^{\pm }$ below), which shares the same symbol as $T^{\pm }_{\iota _1 \iota _2}$ , but where the phase $e^{it\Phi _{\iota _1 \iota _2}}$ is replaced by $1$ , and the distorted Fourier transform by the flat Fourier transform.

Lemma 6.9. Let $\mathfrak {m}_{\iota _1 \iota _2}^{\pm }(\xi ,\eta ,\zeta )$ be the symbol defined in equation (5.54). Then for any $\iota _1,\iota _2 \in \{+,-\}$ , the bilinear operator

(6.8) $$ \begin{align} B_{\mathfrak{m}_{\iota_1 \iota_2}^{\pm}}: \quad (f,g) \mapsto \widehat{\mathcal{F}}^{-1} \iint \widehat{f}(\eta) \widehat{g}(\zeta) \mathfrak{m}_{\iota_1 \iota_2}^{\pm}(\xi,\eta,\zeta) \,d\eta \,d\zeta \end{align} $$

is bounded from $L^p \times L^q$ to $L^r$ , where $\frac {1}{p} + \frac {1}{q} = \frac {1}{r}$ , and $1 < p,q,r < \infty $ , and almost gains a derivative:

(6.9) $$ \begin{align} \begin{aligned} {\| B_{\mathfrak{m}_{\iota_1 \iota_2}^{\pm}}(f,g) \|}_{L^r} \lesssim \mathrm{min}\big( {\| \langle \partial_x \rangle^{-1+}f \|}_{L^p} {\| g \big\|}_{L^q}, {\| f \|}_{L^p} {\| \langle \partial_x \rangle^{-1+} g \|}_{L^q} \big). \end{aligned} \end{align} $$

Here we are using the notation ‘ $-1+$ ’ from the end of Section 2.5.1 to denote any number that is strictly larger than $-1$ .

Proof. First observe that the Fourier multipliers $\mathbf {a}^{\epsilon }_{{\lambda }}(D)$ , $\epsilon ,{\lambda } \in \{+,-\}$ are bounded on $L^p$ , $1< p < \infty $ , by equation (3.14) and Mikhlin’s multiplier theorem. Three different phase functions have to be considered. The case $(\iota _1,\iota _2)=(-,-)$ is clearly the simplest and will not be examined any further. This leaves us with the cases $(+,+)$ and $(+,-)$ : in other words, it suffices to treat the operators $C_{\mathfrak {p}_1}$ , $C_{\mathfrak {p}_2}$ , $D_{\mathfrak {q}_1}$ and $D_{\mathfrak {q}_2}$ (these notations being defined in equations (6.1) and (6.2)) with

(6.10) $$ \begin{align} \begin{aligned} & \mathfrak{p}^1(\eta,\zeta) = \frac{1}{\langle \eta \rangle \langle \zeta \rangle} \frac{1}{\langle \eta + \zeta \rangle - \langle \eta \rangle - \langle \zeta \rangle}, \\ & \mathfrak{p}^2(\eta,\zeta) = \frac{1}{\langle \eta \rangle \langle \zeta \rangle} \frac{1}{\langle \eta + \zeta \rangle + \langle \eta \rangle - \langle \zeta \rangle}, \end{aligned} \end{align} $$

and

(6.11) $$ \begin{align} \begin{aligned} & \mathfrak{q}^1(\eta,\zeta,\theta) = \frac{1}{\langle \eta \rangle \langle \zeta \rangle} \frac{1}{\langle \eta + \zeta + \theta \rangle - \langle \eta \rangle - \langle \zeta \rangle} \varphi_{<-D_0} (R(\eta,\zeta) \theta), \\ & \mathfrak{q}^2(\eta,\zeta,\theta) = \frac{1}{\langle \eta \rangle \langle \zeta \rangle} \frac{1}{\langle \eta + \zeta + \theta \rangle + \langle \eta \rangle - \langle \zeta \rangle} \varphi_{<-D_0} (R(\eta,\zeta) \theta). \end{aligned} \end{align} $$

We observe that bounds for the symbols $\frac {1}{\langle \eta + \zeta \rangle - \langle \eta \rangle - \langle \zeta \rangle }$ and $\frac {1}{\langle \eta + \zeta \rangle + \langle \eta \rangle - \langle \zeta \rangle }$ , on the one hand, and $ \frac {1}{\langle \eta + \zeta + \theta \rangle - \langle \eta \rangle - \langle \zeta \rangle }$ and $ \frac {1}{\langle \eta + \zeta + \theta \rangle + \langle \eta \rangle - \langle \zeta \rangle }$ , on the other hand, can be deduced one from the other by duality. They are not quite equivalent due to the factors $\frac {1}{\langle \eta \rangle \langle \zeta \rangle }$ and $ \varphi _{<-D_0} (R(\eta ,\zeta ) \theta )$ , but the required changes in the proofs are superficial, and we shall only focus on $\mathfrak {p}_1$ and $\mathfrak {q}_1$ .

With the definition of $\chi _\epsilon $ in equation (3.25) and the definition in equation (2.24), we localise the symbols by setting

$$ \begin{align*} & \mathfrak{p}^1_{\substack{j,k \\ \epsilon_1,\epsilon_2}}(\eta,\zeta) = \mathfrak{p}^1(\eta,\zeta) \chi_{\epsilon_1} (\eta) \varphi_j^{(0)}(\eta) \chi_{\epsilon_2} (\zeta) \varphi_k^{(0)}(\zeta), \end{align*} $$

with a similar definition for $\mathfrak {q}^1_{\substack {j,k \\ \epsilon _1,\epsilon _2}}$ .

Case 1: $\epsilon _1=\epsilon _2$ . It follows from equation (5.24) that

(6.12) $$ \begin{align} & | \partial_{\eta}^a \partial_{\zeta}^b \mathfrak{p}^1_{\substack{j,k \\ \epsilon_1,\epsilon_2}} (\eta,\zeta) | \lesssim 2^{-\mathrm{max}(j,k)} 2^{-aj} 2^{-bk}\qquad\qquad \end{align} $$

(6.13) $$ \begin{align} & | \partial_{\eta}^a \partial_{\zeta}^b \partial_{\theta}^c \mathfrak{q}^1_{\substack{j,k \\ \epsilon_1,\epsilon_2}} (\eta,\zeta,\theta) | \lesssim 2^{-\mathrm{max}(j,k)} 2^{c \, \mathrm{min}(j,k)} 2^{-aj} 2^{-bk}. \end{align} $$

By remarks 6.2 and 6.4 and Lemmas 6.1 and 6.3,

$$ \begin{align*}\Big\| C_{\mathfrak{p}^1_{\substack{j,k \\ \epsilon_1,\epsilon_2}}} \Big\|_{L^p \times L^q \to L^r} + \Big\| D_{\mathfrak{q}^1_{\substack{j,k \\ \epsilon_1,\epsilon_2}}} \Big\|_{L^p \times L^q \to L^r} \lesssim 2^{-\mathrm{max}(j,k)} \end{align*} $$

and therefore, for $\delta> 0$ ,

$$ \begin{align*}\Big\| C_{\langle \eta \rangle^{1-\delta} \mathfrak{p}^1_{\substack{j,k \\ \epsilon_1,\epsilon_2}}} \Big\|_{L^p \times L^q \to L^r} + \left\| D_{\langle \eta \rangle^{1-\delta} \mathfrak{q}^1_{ \substack{j,k \\ \epsilon_1,\epsilon_2}}} \right\|_{L^p \times L^q \to L^r} \lesssim 2^{- \delta \mathrm{max}(j,k)}. \end{align*} $$

Summing over $k,j \geq 0$ gives the desired result.

Case 2: $\epsilon _1\neq \epsilon _2$ . Adding a localisation in $\eta + \zeta $ , let

$$ \begin{align*} & \mathfrak{p}^1_{\substack{j,k,\ell \\ \epsilon_1,\epsilon_2,\epsilon_3}}(\eta,\zeta) = \mathfrak{p}^1(\eta,\zeta) \chi_{\epsilon_1} (\eta) \varphi_j^{(0)}(\eta) \chi_{\epsilon_2} (\zeta) \varphi_k^{(0)}(\zeta) \chi_{\epsilon_3} (\eta + \zeta) \varphi_{\ell}^{(0)}(\eta + \zeta), \\ & \mathfrak{q}^1_{\substack{j,k,\ell \\ \epsilon_1,\epsilon_2,\epsilon_3}}(\eta,\zeta,\theta) = \mathfrak{q}^1(\eta,\zeta,\theta) \chi_{\epsilon_1} (\eta) \varphi_j^{(0)}(\eta) \chi_{\epsilon_2} (\zeta) \varphi_k^{(0)}(\zeta) \chi_{\epsilon_3} (\eta + \zeta) \varphi_{\ell}^{(0)}(\eta + \zeta). \end{align*} $$

Without loss of generality, we can assume that $\eta>0$ , $\zeta <0$ , and $|\eta |> |\zeta |$ . Changing variables to $\alpha = \eta + \zeta $ and $\beta = - \zeta $ , the above symbols become

$$ \begin{align*} & \mathfrak{P}^1_{\substack{j,k,\ell \\ \epsilon_1,\epsilon_2,\epsilon_3}}(\alpha,\beta) = \mathfrak{p}^1(\alpha+\beta,-\beta) \chi_{+} (\alpha + \beta) \varphi_j^{(0)}(\alpha + \beta) \chi_{+} (\beta) \varphi_k^{(0)}(\beta) \chi_{+} (\alpha) \varphi_{\ell}^{(0)}(\alpha), \\ & \mathfrak{Q}^1_{\substack{j,k,\ell \\ \epsilon_1,\epsilon_2,\epsilon_3}}(\alpha,\beta,\theta) = \mathfrak{q}^1(\alpha+\beta,-\beta,\theta) \chi_{+} (\alpha + \beta) \varphi_j^{(0)}(\alpha + \beta) \chi_{+} (\beta) \varphi_k^{(0)}(\beta) \chi_{+} (\alpha) \varphi_{\ell}^{(0)}(\alpha), \end{align*} $$

where $j \geq \mathrm {max}(k,\ell ) +C$ . By equations (5.24) and (5.25),

$$ \begin{align*} & \Big| \partial_\alpha^a \partial_\beta^b \mathfrak{P}^1_{\substack{j,k,\ell \\ \epsilon_1,\epsilon_2,\epsilon_3}}(\alpha,\beta) \Big| \lesssim 2^{-j-k} 2^{-a \ell} 2^{-b k}, \\ & \Big| \partial_\alpha^a \partial_\beta^b \partial_{\theta}^c \, \mathfrak{Q}^1_{\substack{j,k,\ell}}(\alpha,\beta,\theta) \Big| \lesssim 2^{-j-k} 2^{-a \ell} 2^{-b k} 2^{ck}. \end{align*} $$

The desired estimate follows through Remarks 6.2 and 6.4 (in particular the paragraphs on change of coordinates) and Lemmas 6.1 and 6.3.

In the previous lemma we derived bounds for the bilinear operator $B_{\mathfrak {m}_{\iota _1 \iota _2}^{\pm }}$ . In order to deduce bounds for $T_{\iota _1 \iota _2}^{\pm }$ itself, we need to substitute the distorted Fourier transform to the flat Fourier transform (this is achieved through the wave operator $\mathcal {W}$ ; see equation (3.24)) and take into account the phase $e^{i\Phi _{\iota _1 \iota _2}}$ .

Lemma 6.10 (Estimates for T)

Consider the operators $T^{\pm }_{\iota _1\iota _2}$ defined in equations (5.53)–(5.54). For all $p,p_1,p_2 \in (1,\infty )$ with $\frac {1}{p_1}+\frac {1}{p_2} = \frac {1}{p}$ , we have

(6.14) $$ \begin{align} \begin{aligned} {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* T^{\pm}_{\iota_1\iota_2}(f_1,f_2)(t) \big\|}_{L^p} \lesssim \mathrm{min}\Big( & {\big\| \langle \partial_x \rangle^{-1+}e^{-\iota_1it\langle \partial_x \rangle} \mathcal{W}^* f_1 \big\|}_{L^{p_1}} {\big\| e^{-\iota_2it\langle \partial_x \rangle} \mathcal{W}^*f_2 \big\|}_{L^{p_2}}, \\ & {\big\| e^{-\iota_1it\langle \partial_x \rangle} \mathcal{W}^* f_1 \big\|}_{L^{p_1}} {\big\| \langle \partial_x \rangle^{-1+}e^{-\iota_2it\langle \partial_x \rangle} \mathcal{W}^*f_2 \big\|}_{L^{p_2}}\Big). \end{aligned} \end{align} $$

Furthermore, for any $k \geq 0$

(6.15) $$ \begin{align} \begin{aligned} {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* T^{\pm}_{\iota_1 \iota_2} (f_1,f_2)(t) \big\|}_{W^{k,p}} & \lesssim {\| \langle \partial_x \rangle^{k-1+} e^{-\iota_1it\langle \partial_x \rangle} \mathcal{W}^* f_1 \|}_{L^{p_1}} {\big\| e^{-\iota_2it\langle \partial_x \rangle} \mathcal{W}^*f_2 \big\|}_{L^{p_2}} \\ & \quad + {\big\| e^{-\iota_1it\langle \partial_x \rangle}\mathcal{W}^*f_1 \big\|}_{L^{p_3}} {\| \langle \partial_x \rangle^{k-1+} e^{-\iota_2it\langle \partial_x \rangle} \mathcal{W}^* f_2 \|}_{L^{p_4}}, \end{aligned} \end{align} $$

with $(p_3,p_4)$ satisfying the same constraints as $(p_1,p_2)$ above.

Finally, if $p\in (1,\infty )$ and f is a function that satisfies the (second and third) assumptions in equation (7.10), then, for all $t\in [0,T]$

(6.16) $$ \begin{align} \begin{aligned} {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* T^{\pm}_{\iota_1\iota_2} \big( f, f_2 \big)(t) \big\|}_{L^p} & \lesssim \frac{{\varepsilon}_1}{\sqrt{t}} \cdot {\big\| \langle \partial_x \rangle^{-1+}e^{-\iota_2it\langle \partial_x \rangle} \mathcal{W}^*f_2 \big\|}_{L^p}. \end{aligned} \end{align} $$

Proof. We can write

(6.17) $$ \begin{align} \begin{aligned} e^{-it\langle \partial_x \rangle} \mathcal{W}^* T_{\iota_1 \iota_2}^{\pm}(f_1,f_2)(t) & = \widehat{\mathcal{F}}^{-1} e^{-it\langle \xi \rangle} \widetilde{\mathcal{F}} T^{\pm}_{\iota_1 \iota_2}(f_1,f_2)(t) \\ & = \widehat{\mathcal{F}}^{-1}\iint e^{-it\iota_1\langle \eta \rangle} \widetilde{f_1}(t,\eta) \, e^{-it\iota_2\langle \sigma \rangle} \widetilde{f_2}(t,\sigma) \mathfrak{m}_{\iota_1\iota_2}^{\pm}(\xi,\eta,\sigma)\,d\eta \,d\sigma \\ & = B_{\mathfrak{m}_{\iota_1\iota_2}^{\pm}} \big( e^{-it\iota_1\langle \partial_x \rangle} \mathcal{W}^*{f_1}(t), e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*{f_2}(t) \big), \end{aligned} \end{align} $$

see the notation of Lemma 6.9. Applying the conclusion of Lemma 6.9 immediately gives equation (6.14).

To prove equation (6.15), we first write

$$ \begin{align*} {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* T^{\pm}_{\iota_1 \iota_2}(f_1,f_2)(t) \|}_{W^{k,p}} & \lesssim {\big\| B_{\langle \xi \rangle^k \mathfrak{m}_{\iota_1\iota_2}} \big( e^{-it\iota_1\langle \partial_x \rangle} \langle D \rangle^k \mathcal{W}^*{f_1}(t), e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*{f_2}(t) \big) \big\|}_{L^p} \end{align*} $$

(we are dropping the irrelevant $\pm $ apex). Without loss of generality, we may assume that $|\eta | \geq |{\sigma }|$ and $|\xi | \geq 1$ on the support of equation (6.17). We then want to estimate the $L^p$ norm of

(6.18) $$ \begin{align} \begin{aligned} &\widehat{\mathcal{F}}^{-1}\iint e^{-it\iota_1\langle \eta \rangle} \langle \eta \rangle^k \widetilde{f_1}(t,\eta) \, e^{-it\iota_1\langle \sigma \rangle} \widetilde{f_2}(t,\sigma) \big[ \langle \xi \rangle^k \langle \eta \rangle^{-k} \mathfrak{m}_{\iota_1\iota_2}(\xi,\eta,\sigma) \big]\,d\eta \,d\sigma \\ &\quad = B_{\mathfrak{m}^{\prime}_{\iota_1\iota_2}} \big( e^{-it\iota_1\langle \partial_x \rangle} \mathcal{W}^*{f_1}(t), e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*{f_2}(t) \big) \end{aligned} \end{align} $$

with the obvious definition of $\mathfrak {m}_{\iota _1\iota _2}'$ . Note that from the definition in equation (5.54) with equation (5.11), $\mathfrak {m}_{\iota _1\iota _2}'$ can be written, up to irrelevant constants, as $\mathfrak {m}_{\iota _1\iota _2}' = \mathfrak {a}_{\iota _1\iota _2} + \mathfrak {b}_{\iota _1\iota _2}$ , with

(6.19) $$ \begin{align} \begin{aligned} \mathfrak{a}_{\iota_1\iota_2} & := \frac{\langle \xi \rangle^k}{\langle \eta \rangle^k} \sum_{{\lambda},\mu,\nu} a^{\pm}_{\substack{-\iota_1 \iota_2 \\ \lambda\mu\nu}}(\xi, \eta,\sigma) \frac{1}{\Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})\langle \eta \rangle \langle \sigma \rangle} \, \delta(p), \\ \mathfrak{b}_{\iota_1\iota_2} & := \frac{\langle \xi \rangle^k}{\langle \eta \rangle^k} \sum_{{\lambda},\mu,\nu} a^{\pm}_{\substack{-\iota_1 \iota_2 \\ \lambda\mu\nu}}(\xi,\eta, \sigma) \frac{\varphi^{\ast}(p,\eta,\sigma)}{\Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})\langle \eta \rangle\langle \sigma \rangle} \,\mathrm{p.v.} \frac{\widehat{\phi}(p)}{ip}, \qquad p := \lambda \xi - \mu \eta - \nu \sigma. \end{aligned} \end{align} $$

On the support of $\mathfrak {a}_{\iota _1\iota _2}$ we automatically must have $\langle \xi \rangle \lesssim \mathrm {max}(\langle \eta \rangle ,\langle \sigma \rangle ) = \langle \eta \rangle $ , so that $\mathfrak {a}_{\iota _1\iota _2}$ is a regular bounded symbol with the same properties as $\mathfrak {m}_{\iota _1\iota _2}^{\pm }$ ; from the result of Lemma 6.9, we deduce

$$ \begin{align*} \begin{aligned} & {\| B_{\mathfrak{a}_{\iota_1\iota_2}} \big( e^{-it\iota_1\langle \partial_x \rangle} \langle \partial_x \rangle^k \mathcal{W}^*{f_1}(t), e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*{f_2}(t) \big) \|}_{L^p} \\ &\quad \lesssim {\| \langle \partial_x \rangle^{k-1+} e^{-it\iota_1\langle \partial_x \rangle} \mathcal{W}^*{f_1}(t) \|}_{L^{p_1}} {\| e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*{f_2}(t) \|}_{L^{p_2}}, \end{aligned} \end{align*} $$

consistently with the right-hand side of equation (6.15).

On the support of the $\mathrm {p.v.}$ component $\mathfrak {b}_{\iota _1\iota _2}$ , we might not have that $\langle \xi \rangle \lesssim \langle \eta \rangle $ . However, if $\langle \xi \rangle \gg \langle \eta \rangle $ , then $|p| \gtrsim |\xi |$ (in particular the $\mathrm {p.v.}$ is not singular), and one can absorb the factor of $\langle \xi \rangle ^k$ . More precisely, we can write (dispensing of the $\iota _1\iota _2$ indexes)

$$ \begin{align*} \mathfrak{b} = \mathfrak{b}_{1} + \mathfrak{b}_{2}, \qquad \mathfrak{b}_{1}:=\varphi_{\leq 10}(|\xi|/|\eta|) \mathfrak{b} \end{align*} $$

and observe that $\mathfrak {b}_{1}$ has the same properties as (the $\mathrm {p.v.}$ part of) $\mathfrak {m}$ so that Lemma 6.9 applies and

$$ \begin{align*} &{\big\| B_{\mathfrak{b}_1} \big( e^{-it\iota_1\langle \partial_x \rangle} \langle \partial_x \rangle^k \mathcal{W}^*{f_1}(t), e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*{f_2}(t) \big) \big\|}_{L^p} \\ &\quad \lesssim {\| \langle \partial_x \rangle^{k-1+} e^{-it\iota_1\langle \partial_x \rangle} \mathcal{W}^* f_1 \|}_{L^{p_1}} {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*f_2 \big\|}_{L^{p_2}}. \end{align*} $$

The contribution from the remaining piece $\mathfrak {b}_2$ can be written as

$$ \begin{align*} B_{\mathfrak{b}_{2}} \big( e^{-it\iota_1\langle \partial_x \rangle} \langle \partial_x \rangle^k \mathcal{W}^*{f_1}(t), e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*{f_2}(t) \big) = B_{\mathfrak{b}'} \big( e^{-it\iota_1\langle \partial_x \rangle} \mathcal{W}^*{f_1}(t), e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*{f_2}(t) \big) \end{align*} $$

where

$$ \begin{align*} \mathfrak{b}' & := \sum_{{\lambda},\mu,\nu} a^{\pm}_{\substack{-\iota_1 \iota_2 \\ \lambda\mu\nu}}(\xi,\eta, \sigma) \frac{\varphi^{\ast}(\xi,\eta,p)}{\Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})\langle \eta \rangle\langle \sigma \rangle} \cdot \frac{\widehat{\phi}(p)}{ip} \cdot \langle \xi \rangle^k \varphi_{>10}(|\xi|/|\eta|) \varphi_{\geq 0}(|p|/|\xi|). \end{align*} $$

Since $|p| \gtrsim |\xi |$ and $\widehat {\phi }$ is a Schwartz function, the symbol $\mathfrak {b}'$ has the same properties as $\mathfrak {m}$ ; using an $L^{p_1}\times L^{p_2}$ estimate from Lemma 6.9 gives

$$ \begin{align*} {\big\| B_{\mathfrak{b}'} \big( e^{-it\iota_1\langle \partial_x \rangle} \mathcal{W}^*{f_1}(t), e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*{f_2}(t) \big) \big\|}_{L^p} \lesssim {\| e^{-it\iota_1\langle \partial_x \rangle} \mathcal{W}^* f_1 \|}_{L^{p_1}} {\big\| e^{-it\iota_2\langle \partial_x \rangle} \mathcal{W}^*f_2 \big\|}_{L^{p_2}}, \end{align*} $$

which is better than the desired conclusion.

Finally, to prove equation (6.16), we use the linear dispersive estimate in equation (3.34) to take care of the $\mathbf {a}^{\epsilon }_{\lambda }$ multipliers, instead of the Mikhlin multiplier theorem.

6.4 The smooth bilinear operator $\mathcal {Q}^R$

Lemma 6.11 (Estimates for $\mathcal {Q}^R$ )

Let $\mathcal {Q}^R$ be the bilinear term defined in equations (5.56) and (5.15)–(5.16). Then for any

$$ \begin{align*} p_1,p_2\in[2,\infty), \qquad \frac{1}{p_1}+\frac{1}{p_2} < \frac{1}{2}, \end{align*} $$

one has the improved Hölder-type inequality

(6.20) $$ \begin{align} \begin{aligned} {\big\| \mathcal{Q}^R_{\iota_1\iota_2}[f_1,f_2](t,\xi) \big\|}_{L^2} \lesssim \mathrm{min}\big( & {\| \langle \partial_x \rangle^{-1+} e^{-i\iota_1t\langle \partial_x \rangle} \mathcal{W}^*f_1 \|}_{L^{p_1}} {\| e^{-i\iota_2t\langle \partial_x \rangle} \mathcal{W}^*f_2 \|}_{L^{p_2}}, \\ & {\| e^{-i\iota_1t\langle \partial_x \rangle} \mathcal{W}^*f_1 \|}_{L^{p_1}} {\| \langle \partial_x \rangle^{-1+} e^{-i\iota_2t\langle \partial_x \rangle} \mathcal{W}^*f_2 \|}_{L^{p_2}} \big). \end{aligned} \end{align} $$

Moreover, for $k \geq 0$ ,

(6.21) $$ \begin{align} \begin{aligned} {\big\| \langle \xi \rangle^k \mathcal{Q}^R_{\iota_1\iota_2}[f_1,f_2](t,\xi) \big\|}_{L^2} & \lesssim {\| \langle \partial_x \rangle^{k-1+} e^{-i\iota_1t\langle \partial_x \rangle} \mathcal{W}^*f_1 \|}_{L^{p_1}} {\| e^{-i\iota_2t\langle \partial_x \rangle} \mathcal{W}^*f_2 \|}_{L^{p_2}} \\ & \quad + \, {\| e^{-i\iota_1t\langle \partial_x \rangle} \mathcal{W}^*f_1 \|}_{L^{p_3}} {\| \langle \partial_x \rangle^{k-1+} e^{-i\iota_2t\langle \partial_x \rangle} \mathcal{W}^*f_2 \|}_{L^{p_4}} \end{aligned} \end{align} $$

for $(p_3,p_4)$ satisfying the same constraints as $(p_1,p_2)$ above.

Proof. Recall the structure of the symbol of $\mathcal {Q}^R$ from equations (5.15)–(5.16) and (4.6)–(4.7). For the piece coming from $\mu ^R_{\iota _1\iota _2}$ , estimates stronger than the desired equations (6.20)–(6.21) follow directly from Lemma 4.2. We then only need to look at operators of the form

(6.22) $$ \begin{align} \begin{aligned} \mathcal{Q}[a,b](\xi) &= \iint \mathfrak{q}(\xi,\eta,\sigma) \, \widehat{a}(\eta) \widehat{b}(\sigma) \, d\eta \, d\sigma \\ \mathfrak{q}(\xi,\eta,\sigma) &= \frac{a^{\pm}_{\substack{\iota_0 \iota_1 \iota_2 \\ \lambda\mu\nu}}(\xi,\eta,\sigma)}{\langle \eta \rangle \langle \sigma \rangle } \big(1 - \varphi^{\ast}(p,\eta,{\sigma}) \big) \frac{\widehat{\phi}(p)}{p}, \quad p=\lambda \xi - \iota_1 \mu \eta - \iota_2 \nu \sigma, \end{aligned} \end{align} $$

and prove that

(6.23) $$ \begin{align} \begin{aligned} {\big\| \widehat{{\mathcal{F}}}^{-1} \big( \mathcal{Q}[a,b](\xi) \big) \big\|}_{L^p} \lesssim {\| \langle \partial_x \rangle^{-1+} a \|}_{L^{p_1}} {\| b \|}_{L^{p_2}}, \end{aligned} \end{align} $$

since by symmetry between the arguments a and b it follows that the right-hand side above can be replaced by $\mathrm {min}\big ( {\| \langle \partial _x \rangle ^{-1+} a \|}_{L^{p_1}} {\| b \|}_{L^{p_2}}, {\| a \|}_{L^{p_1}} {\| \langle \partial _x \rangle ^{-1+} b \|}_{L^{p_2}} \big )$ and that

(6.24) $$ \begin{align} \begin{aligned} {\big\| \langle \xi \rangle^l \mathcal{Q} [a,b](\xi) \big\|}_{L^2} \lesssim \, & \, {\| \langle \partial_x \rangle^{l-1+} a \|}_{L^{p_1}} {\| b \|}_{L^{p_2}} + {\| a \|}_{L^{p_3}} {\| \langle \partial_x \rangle^{l-1+} b \|}_{L^{p_4}}. \end{aligned} \end{align} $$

Proof of equation (6.23). As usual, the first step is to observe that the multipliers $a^{\pm }_{\substack {\iota _0 \iota _1 \iota _2 \\ \lambda \mu \nu }}(\xi ,\eta ,\sigma )$ can be discarded. Also, we may assume without loss of generality that $p=\xi -\eta -\sigma $ . Next, we insert Littlewood-Paley cutoffs in each of the variables $\eta ,{\sigma }$ and p and consider the localised operator $\mathcal {Q}_{\underline {k}}[a,b](\xi )$ , with the same form as $\mathcal {Q}$ in equation (6.22) but a localised symbol

(6.25) $$ \begin{align} \begin{aligned} \mathfrak{q}_{\underline{k}}(\xi,\eta,{\sigma}) & = \frac{\mathfrak{m}_{\underline{k}} (\xi,\eta,{\sigma})}{\langle \eta \rangle \langle \sigma \rangle} \frac{\widehat{\phi}(p)}{p} \\ \mathfrak{m}_{\underline{k}} (\xi,\eta,{\sigma}) &= \varphi_{k_1}(\eta)\varphi_{k_2}({\sigma})\varphi_{k_3}(p) ( 1 - \varphi^*(p,\eta,{\sigma})). \end{aligned} \end{align} $$

We then make the following restrictions on the indexes

$$ \begin{align*}k_1 \geq k_2 \geq 0 , \qquad \mbox{and} \qquad 0 \geq k_3 \geq -k_2^+ - D. \end{align*} $$

These can be explained as follows: $k_1 \geq k_2$ is the harder case, since it implies that the derivative gain in equation (6.23) will be on the larger input frequency; $k_2 \geq 0$ amounts to restricting to the case of frequencies $\gtrsim 1$ , which is also the hardest case; $k_3 \leq 0$ is a consequence of $\phi $ being Schwartz: values of $|p| \gg 1$ are exponentially damped, and we will not worry about them here; and finally, $k_3 \geq -k_2^+ - D$ follows from the definition of $\varphi ^{\ast }$ .

The idea then is to regard $\mathcal {Q}_{\underline {k}}(a,b)$ as a trilinear operator acting on a, b and $\psi = \mathcal {F}^{-1} (\widehat {\phi }/p)$ , and note that the symbol $\mathfrak {n}_{\underline {k}} (\eta ,{\sigma },p) := \mathfrak {m}_{\underline {k}}(\xi ,\eta ,{\sigma })$ satisfies

$$ \begin{align*}\left| \partial_{\eta}^a \partial_{\sigma}^b \partial_p^c \mathfrak{m}_{\underline{k}} (\eta,\sigma,p) \right| \lesssim 2^{-ak_1 - b k_2 - ck_3}. \end{align*} $$

Up to a change of coordinates, Lemma 6.5 and Remark 6.6 apply, leading to the estimate, for any $1 < q,p_1,p_2 < \infty $ such that $\frac {1}{q} + \frac {1}{p_1} + \frac {1}{p_2} = \frac {1}{p}$ ,

$$ \begin{align*} {\big\| \mathcal{Q}_{\underline{k}} (a,b) \big\|}_{L^p} & \lesssim {\| P_{k_3} \psi \|}_{L^q} {\| P_{k_1} \langle \partial_x \rangle^{-1} a \|}_{L^{p_1}} {\| P_{k_2} \langle \partial_x \rangle^{-1} b \|}_{L^{p_2}} \\ & \lesssim 2^{-\frac{k_3}{q}- k_2} 2^{-(0+)k_1} {\| \langle \partial_x \rangle^{-1+} P_{k_1} a \|}_{L^{p_1}} {\| P_{k_2} b \|}_{L^{p_2}}. \end{align*} $$

It remains to observe that, provided $1 < q < \infty $ ,

$$ \begin{align*}\sum_{\substack {0 \geq k_3 \geq -k_2^+ \\ k_1 \geq k_2 \geq 0}} 2^{-\frac{k_3}{q} - k_2} 2^{-(0+)k_1} < \infty. \end{align*} $$

Proof of equation (6.24). One can proceed as above, modifying the definition of $\mathfrak {m}_{\underline {k}}$ to

$$ \begin{align*}\mathfrak{m}_{\underline{k}} (\xi,\eta,\sigma) = \varphi_{k_1}(\eta)\varphi_{k_2}({\sigma})\varphi_{k_3}(p)( 1 - \varphi^*(\xi,\eta,\sigma)) \frac{\langle \xi \rangle^k}{\langle \eta \rangle^k + \langle \sigma \rangle^k}. \end{align*} $$

and observing that if $|\xi | \geq 3\mathrm {max}(|\eta |,|\sigma |)$ , then $|p| \gtrsim |\xi |$ , and any power of $\langle \xi \rangle $ can absorbed by $\widehat {\phi }(p)$ .

From the proof of Lemma 6.11 above, we can also deduce the following property, which will be useful in Section 7.3.

Claim 6.12. We have the following schematic identity for the operator $\mathcal {Q}^R$ in equation (5.56):

(6.26) $$ \begin{align} \langle \xi \rangle \partial_{\xi} \mathcal{Q}^R[f_1,f_2] \approx t \cdot \langle \xi \rangle \mathcal{Q}^R[f_1,f_2] + \langle \xi \rangle \mathcal{Q}^R\big[\widetilde{{\mathcal{F}}}^{-1}(\partial_{\xi} \widetilde{f_1}),f_2\big]. \end{align} $$

In particular, equations (6.26) and (6.20) imply the following Hölder-type estimate for $\langle \xi \rangle \partial _{\xi } \mathcal {Q}^R$ , up to lower-order terms that can be discarded:

(6.27) $$ \begin{align} \begin{aligned} {\| \langle \xi \rangle \partial_{\xi} \mathcal{Q}^R(f_1,f_2) \|}_{L^2} & \lesssim \langle t \rangle {\big\| e^{-it\langle \partial_x \rangle} \langle \partial_x \rangle^{0+} \mathcal{W}^* f_1 \big\|}_{L^{\infty-}} {\big\| e^{-it\langle \partial_x \rangle} \langle \partial_x \rangle^{0+} \mathcal{W}^*f_2 \big\|}_{L^{\infty-}} \\ &\quad + {\big\| \langle \xi \rangle^{0+} \partial_{\xi} \widetilde{f_1} \big\|}_{L^2} {\big\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^*f_2 \big\|}_{L^{\infty-}}. \end{aligned} \end{align} $$

Here, we are using $\infty -$ to denote any arbitrarily large number (see the notation at the end of Section 2.5.1). Note that this last bound is technically a little worse than what one could get: that is, a bound with only one term at a time carrying a $\langle \xi \rangle ^{0+}$ factor in the last product.

An analogous claim holds for the operator T; see Remark 7.7. For the case of T, the proof is contained in the proof of Lemma 7.6; we refer the reader to that for more details on the type of argument that leads to equation (6.26) and provide a more succinct argument below.

Proof of Claim 6.12

To see the validity of equation (6.26), we look at the expression in equations (5.15)–(5.16). Applying $\langle \xi \rangle \partial _{\xi }$ gives two contributions: one where $\langle \xi \rangle \partial _{\xi }$ hits the exponential phase and one where it hits the symbol $\mathfrak {q}$ . The first contribution is $t \xi \cdot \mathcal {Q}^R[f_1,f_2]$ , which appears on the right-hand side of equation (6.26).

When $\partial _{\xi }$ hits the symbol, we get a few more contributions. First, we observe that $\partial _{\xi } \mu _0^R$ behaves exactly like $\mu _0^R$ , so this is a lower-order term that we can disregard; see Proposition 4.1 and Lemma 4.2. When $\partial _{\xi }$ hits $\mathfrak {q}$ , we get similar lower-order terms, with the exception of the contributions coming from $\partial _{\xi }$ hitting $\mathrm {p.v.} 1/p$ or $\varphi ^{\ast }$ . Under the assumption that $|\eta |\gtrsim |{\sigma }|$ , in view of the definition of p, we convert $\partial _{\xi }$ to $\partial _{\eta }$ and integrate by parts in $\eta $ . When $\partial _{\eta }$ hits the profile $\widetilde {f_1}(\eta )$ , we get the second term on the right-hand side of equation (6.26). When $\partial _{\eta }$ hits the oscillating phase, we get a term like the first one in equation (6.26). The other terms where $\partial _{\eta }$ hits the remaining part of the symbol only contribute lower-order terms that satisfy stronger estimates than the terms in equation (6.26).

6.5 The singular cubic terms $\mathcal {C}^S$

The next Lemma is a Hölder-type estimate for the singular cubic terms.

Lemma 6.13 (Estimates for ‘cubic singular’ symbols)

With the definition in equations (5.57)–(5.58), consider $\mathcal {C}^{S} = \mathcal {C}^{Sr}_{\iota _1 \iota _2 \iota _3}$ , for $r=1$ or $2$ , and any combination of signs $\iota $ . Then for all $p,p_1,p_2,p_3 \in (1,\infty )$ with $\frac {1}{p_1} + \frac {1}{p_2} + \frac {1}{p_3} = \frac {1}{p}$ ,

(6.28) $$ \begin{align} \begin{aligned} & {\|e^{-it\langle \partial_x \rangle}\widehat{{\mathcal{F}}}^{-1}\mathcal{C}^{S}(a,b,c)\|}_{L^p} \\ & \qquad \lesssim {\| \langle \partial_x \rangle^{-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* a \|}_{L^{p_1}} {\| \langle \partial_x \rangle^{-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* b \|}_{L^{p_2}} {\| \langle \partial_x \rangle^{-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* c \|}_{L^{p_3}}. \end{aligned} \end{align} $$

Furthermore, if $k \geq 0$ , and with $(p_4,p_5,p_6)$ and $(p_7,p_8,p_9)$ satisfying the same conditions as $(p_1,p_2,p_3)$ ,

(6.29) $$ \begin{align} \begin{aligned} & {\|e^{-it\langle \partial_x \rangle}\widehat{{\mathcal{F}}}^{-1}\mathcal{C}^{S}(a,b,c)\|}_{W^{k,p}} \\ & \quad \lesssim {\| \langle \partial_x \rangle^{k-1+ } e^{-it\langle \partial_x \rangle} \mathcal{W}^* a \|}_{L^{p_1}} {\| \langle \partial_x \rangle^{-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* b \|}_{L^{p_2}} {\| \langle \partial_x \rangle^{-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* c \|}_{L^{p_3}} \\ & \qquad + {\| \langle \partial_x \rangle^{-1+ } e^{-it\langle \partial_x \rangle} \mathcal{W}^* a \|}_{L^{p_4}} {\| \langle \partial_x \rangle^{k-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* b \|}_{L^{p_5}} {\| \langle \partial_x \rangle^{-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* c \|}_{L^{p_6}} \\ & \qquad + {\| \langle \partial_x \rangle^{-1+ } e^{-it\langle \partial_x \rangle} \mathcal{W}^* a \|}_{L^{p_7}} {\| \langle \partial_x \rangle^{-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* b \|}_{L^{p_8}} {\| \langle \partial_x \rangle^{k-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* c \|}_{L^{p_9}}. \end{aligned} \end{align} $$

Finally, if $p_1 = \infty $ , and f is a function that satisfies the (second and third) assumptions in equation (7.10), then for all $t\in [0,T]$ and $ \frac {1}{p_2} + \frac {1}{p_3} = \frac {1}{p}$ , we have

(6.30) $$ \begin{align} & {\|e^{-it\langle \partial_x \rangle}\widehat{{\mathcal{F}}}^{-1}\mathcal{C}^{S}(f ,b,c)\|}_{L^p} \lesssim \frac{{\varepsilon}_1}{\sqrt{t}} {\| \langle \partial_x \rangle^{-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* b \|}_{L^{p_2}} {\| \langle \partial_x \rangle^{-1+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* c \|}_{L^{p_3}}, \end{align} $$

with a similar statement if $p_1 = p_2 = \infty $ .

Proof. Starting from the formulas in equation (5.46) giving $\mathfrak {c}^{S1}$ and $\mathfrak {c}^{S2}$ , we first discard the factors

$$ \begin{align*}a^{\epsilon,\epsilon'}_{\substack{\lambda,\mu,\mu',\nu' \\ -,\kappa_1,\kappa_2,\kappa_3}}(\xi,\eta,\eta',\sigma'),\end{align*} $$

which is possible thanks to the Mikhlin multiplier theorem. Omitting these factors and irrelevant constants and indexes, it suffices to deal with $T_{\mathfrak {e}^1}$ and $T_{\mathfrak {e}^2}$ (recall the definition in equation (6.4)), where

$$ \begin{align*} & \mathfrak{e}^1(\xi,\eta,\zeta,\theta) = \frac{A(\xi \pm \eta)}{\Phi_{\iota_1\iota_2}(\xi,\eta,\xi\pm \eta)} \frac{1}{\langle \eta \rangle \langle \xi \pm \eta\rangle \langle \zeta \rangle \langle \theta \rangle} \delta(\xi \pm \eta \pm \zeta \pm \theta), \\ & \mathfrak{e}^2(\xi,\eta,\zeta,\theta) = \frac{A(\xi \pm \eta)}{\Phi_{\iota_1\iota_2}(\xi,\eta,\xi\pm \eta)} \frac{1}{\langle \eta \rangle \langle \xi \pm \eta\rangle \langle \zeta \rangle \langle \theta \rangle} \frac{\widehat{\phi}(\xi \pm \eta \pm \zeta \pm \theta)}{\xi \pm \eta \pm \zeta \pm \theta}. \end{align*} $$

For the sake of concreteness, we make a choice of signs (which one it is exactly does not matter):

$$ \begin{align*} & \mathfrak{e}^1(\xi,\eta,\zeta,\theta) = \frac{A(\xi + \eta)}{\Phi_{\iota_1\iota_2}(\xi,\eta,\xi + \eta)} \frac{1}{\langle \eta \rangle \langle \xi + \eta\rangle \langle \zeta \rangle \langle \theta \rangle} \delta(\xi - \eta + \zeta - \theta), \\ & \mathfrak{e}^2(\xi,\eta,\zeta,\theta) = \frac{A(\xi + \eta)}{\Phi_{\iota_1\iota_2}(\xi,\eta,\xi + \eta)} \frac{1}{\langle \eta \rangle \langle \xi + \eta\rangle \langle \zeta \rangle \langle \theta \rangle} \frac{\widehat{\phi}(\xi - \eta + \zeta - \theta)}{\xi - \eta + \zeta - \theta}. \end{align*} $$

With the convention for U and V operators (see equation (6.5)), this corresponds, respectively, to the symbols

$$ \begin{align*} & \mathfrak{f}^1(\xi,\eta,\zeta)= \frac{A(2\xi-\eta)}{\Phi_{\iota_1\iota_2}(\xi,\xi-\eta,2\xi-\eta)} \frac{1}{\langle \xi-\eta \rangle \langle 2\xi-\eta\rangle \langle \xi-\eta -\zeta \rangle \langle \xi-\zeta \rangle} \\ & \mathfrak{f}^2(\xi,\eta,\zeta,\theta)= \frac{A(2\xi-\eta)}{\Phi_{\iota_1\iota_2}(\xi,\xi-\eta,2\xi-\eta)} \frac{1}{\langle \xi - \eta \rangle \langle 2 \xi - \eta\rangle \langle \xi-\eta-\zeta-\theta \rangle \langle \xi-\zeta \rangle}. \end{align*} $$

We will now only focus on $\mathfrak {f}^1$ , since $\mathfrak {f}^2$ can be treated nearly identically. Different signs $\iota _1,\iota _2$ cannot be treated identically; for the sake of brevity, we will only treat the most delicate case, namely $(\iota _1,\iota _2) = (+,+)$ . Changing coordinates to $\alpha = -\xi +\eta $ , $\beta = 2\xi - \eta $ , $\gamma = \xi -\zeta $ , and localising dyadically, this becomes

$$ \begin{align*}\mathfrak{g}^1(\alpha,\beta,\gamma)_{\underline{k}} = \underbrace{\frac{A(\beta)}{\Phi_{\iota_1\iota_2}(\alpha + \beta,\alpha,\beta)} \frac{1}{\langle \alpha \rangle \langle \beta \rangle \langle \gamma \rangle} \varphi_{k_1}^{(0)}(\alpha)\varphi_{k_2}^{(0)}(\beta)\varphi_{k_3}^{(0)}(\gamma)}_{ \displaystyle := \mathfrak{h}^{1,1}_{\underline{k}}(\alpha,\beta,\gamma)} \underbrace{ \frac{1}{\langle \gamma -2\alpha - \beta\rangle}\varphi_{k_4}^{(0)}(\gamma-2\alpha-\beta) }_{ \displaystyle := \mathfrak{h}^{1,2}_{k_4}(\gamma -2\alpha - \beta)}. \end{align*} $$

Finally, we need to distinguish cases depending on the signs of $\alpha $ and $\beta $ ; once again, we only consider the worst case, namely $\alpha , \beta>0$ . By equation (6.12), there holds, for all $a,b,c$ ,

$$ \begin{align*}\left| \partial_\alpha^a \partial_\beta^b \partial_\gamma^c \mathfrak{h}^{1,1}(\alpha,\beta,\gamma) \right| \lesssim 2^{-(1+a) k_1 - b k_2 - (1+c) k_3}, \end{align*} $$

therefore $\| \widehat {\mathfrak {h}^{1,1}_{\underline {k}}} \|_{L^1} \lesssim 2^{- k_1 - k_3}$ . Since $\| \widehat {\mathfrak {h}^{1,2}_{\underline {k_4}}} \|_{L^1} \lesssim 2^{-k_4^+}$ , we obtain that $\| \widehat {\mathfrak {h}^{1}_{\underline {k}}} \|_{L^1} \lesssim 2^{- k_1 - k_3-k_4}$ . Applying Lemma 6.5 and summing over dyadic blocks gives the desired result in equation (6.28). Equation (6.29) follows in the same way. Finally, using the linear dispersive estimate in equation (3.34) instead of Mikhlin’s multiplier theorem, we obtain the endpoint estimate in equation (6.30).

Remark 6.14 (Derivatives of the cubic symbols)

In the estimates of Sections 10 and 11, we will perform various integration by parts arguments in frequency space and will therefore end up differentiating the cubic symbols appearing in Lemma 6.13 above. The estimates satisfied by the trilinear operators associated with these differentiated symbols might vary from case to case, depending on the variables that are differentiated; the localisations imposed in each specific case will determine how these estimates need to be modified by additional factors. In any case, in all our arguments, the terms obtained when differentiating the symbols $\mathfrak {c}^{S1}$ and $\mathfrak {c}^{S2}$ will always give lower-order contributions.

7 Bootstrap and basic a priori bounds

In this section, we first give the details of our bootstrap strategy as presented in Sections 2.6 and 2.7; see equations (2.40)–(2.41). In particular, we close the bootstrap for the profile g, assuming the bootstrap for the renormalised profile f. In Section 7.2, we give some preliminary bounds on f that will be useful in later sections. In Section 7.3, we expand the nonlinear expressions in terms of f and establish several bounds that do not require the analysis of oscillations. Section 7.4 recalls the main equation for $\widetilde {f}$ and lists all the estimates that are left to be proven in the remainder of the paper.

7.1 Bootstrap strategy

Recall from equation (1.3) that we are considering initial data such that

(7.1) $$ \begin{align} {\| (\langle \partial_x \rangle u_0,u_1) \|}_{H^4} + {\| \langle x \rangle (\langle \partial_x \rangle u_0,u_1) \|}_{H^1} \leq {\varepsilon}_0. \end{align} $$

From the definition of v and g in equations (5.2) and (5.5), we see that $g_0 = u_1 - i \sqrt {H+1}u_0$ . Therefore, Proposition 3.6 and Theorem 3.10 imply that

(7.2) $$ \begin{align} {\| \langle \xi \rangle^{4} \widetilde{g_0} \|}_{L^2} + {\| \langle \xi \rangle\partial_{\xi} \widetilde{g_0} \|}_{L^2} \lesssim {\varepsilon}_0. \end{align} $$

From this and the interpolation inequality $|\varphi _k(\xi ) \widetilde {h}(\xi )|^2 \lesssim {\| \varphi _k \widetilde {h} \|}_{L^2} {\| \partial _{\xi } \varphi _k \widetilde {h} \|}_{L^2}$ , we see that

(7.3) $$ \begin{align} {\| \langle \xi \rangle^{3/2} \widetilde{g_0} \|}_{L^{\infty}} \lesssim {\varepsilon}_0. \end{align} $$

According to the definition in equations (5.53)–(5.54) for the renormalised profile, we have

$$ \begin{align*} f(t=0) =: f_0 = g_0 - T(g_0,g_0)(t=0), \end{align*} $$

so that using equation (6.15) and estimating as in the proof of Lemma 7.6 below (see in particular equation (7.29)), we have

(7.4) $$ \begin{align} {\| \langle \xi \rangle^{4} \widetilde{f_0} \|}_{L^2} + {\| \langle \xi \rangle\partial_{\xi} \widetilde{f_0} \|}_{L^2} \lesssim {\varepsilon}_0. \end{align} $$

Again, by interpolation, we obtain

(7.5) $$ \begin{align} {\| \langle \xi \rangle^{3/2} \widetilde{f_0} \|}_{L^{\infty}} \lesssim {\varepsilon}_0. \end{align} $$

In what follows, we consider ${\varepsilon }_1,{\varepsilon }_2$ satisfying

(7.6) $$ \begin{align} {\varepsilon}_0 \ll {\varepsilon}_1 \ll {\varepsilon}_2, \qquad {\varepsilon}_2 \leq \overline{{\varepsilon}_0} \end{align} $$

with $\overline {{\varepsilon }_0}$ sufficiently small. The main bootstrap estimate for g is given by the following:

Proposition 7.1. Assume that, for all $t\in [0,T]$ ,

(7.7) $$ \begin{align} \langle t \rangle^{-p_0} {\big\| \langle \xi \rangle^{4} \widetilde{g}(t) \big\|}_{L^{2}} + \langle t \rangle^{1/2} {\| e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D)\mathcal{W}^* g(t) \|}_{L^{\infty}} \leq 2{\varepsilon}_2. \end{align} $$

Then for all $t\in [0,T]$ ,

(7.8) $$ \begin{align} \langle t \rangle^{-p_0} {\big\| \langle \xi \rangle^{4} \widetilde{g}(t)\big\|}_{L^{2}} + \langle t \rangle^{1/2} {\| e^{- it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D)\mathcal{W}^* g(t) \|}_{L^{\infty}} \leq {\varepsilon}_2. \end{align} $$

Moreover, we also have

(7.9) $$ \begin{align} {\| e^{-it\langle \widetilde D \rangle}g(t) \|}_{L^{\infty}} \lesssim {\varepsilon}_2 \langle t \rangle^{-1/2}. \end{align} $$

Proposition 7.1 above implies global-in-time bounds on g and $v= e^{it\langle \widetilde {D} \rangle }g(t)$ , hence on the solution u of equation (KG) (see equation (5.3)); in particular, together with equation (7.28), it gives the the bounds in equations (1.4) and (1.5) and (1.7) stated in Theorem 1.1. However, since we cannot bootstrap directly bounds on norms of g, we reduce the proof of Proposition 7.1 to bootstrap estimates on the renormalised profile $f := g -T(g,g)$ ; see equations (5.53)–(5.54). This is our main bootstrap proposition for f:

Proposition 7.2. Assume that for all $t\in [0,T]$ , we have

(7.10) $$ \begin{align} \langle t \rangle^{-p_0} {\big\| \langle \xi \rangle^{4} \widetilde{f}(t) \big\|}_{L^{2}} + {\| \langle \xi \rangle\partial_{\xi} \widetilde{f} \|}_{W_t} + {\| \langle \xi \rangle^{3/2} \widetilde{f}(t) \|}_{L^{\infty}} \leq 2{\varepsilon}_1 \end{align} $$

and that the bounds in equation (7.7) on g hold with ${\varepsilon }_2={\varepsilon }_1^{2/3}$ . Then for all $t \in [0,T]$ ,

(7.11) $$ \begin{align} \langle t \rangle^{-p_0} {\big\| \langle \xi \rangle^{4} \widetilde{f}(t) \big\|}_{L^{2}} + {\| \langle \xi \rangle \partial_{\xi} \widetilde{f} \|}_{W_t} + {\| \langle \xi \rangle^{3/2} \widetilde{f}(t) \|}_{L^{\infty}} \leq {\varepsilon}_1. \end{align} $$

The proof of Proposition 7.2 will occupy the rest of the paper, Sections 8–11. For now, we show how Proposition 7.2 implies Proposition 7.1 by using the estimates on the operator T from Lemma 6.10. First let us make the following remarks:

Remark 7.3. Note that the a priori assumptions in equation (7.10) and the linear dispersive estimates in equations (3.32) and (3.31) imply

(7.12) $$ \begin{align} {\big\| e^{-it\langle \widetilde{D} \rangle}f(t) \big\|}_{L^{\infty}} + {\big\| e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D)\mathcal{W}^*f(t) \big\|}_{L^{\infty}} \lesssim {\varepsilon}_1\langle t \rangle^{-1/2}. \end{align} $$

Also note that, in view of the conservation of the energy equation (1.1), we have that, for all times,

(7.13) $$ \begin{align} {\| g(t) \|}_{L^2} + {\| f(t) \|}_{L^2} \leq {\varepsilon}_1. \end{align} $$

The bound for g follows from its definition, and the bound for f can be deduced from $f=g-T(g,g)$ , the bilinear bound for T in equation (6.14) and the a priori assumptions in equation (7.7).

Remark 7.4. For $\iota ,\kappa \in \{+,-\}$ ,

(7.14) $$ \begin{align} \widetilde{f}^{\kappa}_{\iota}(\xi) := \widetilde{f}_\iota (\xi) \mathbf{1}_{\kappa}(\xi), \end{align} $$

enjoys the same bootstrap assumptions as $\widetilde {f}$ , since $\widetilde {f}(0) = 0$ ; see Lemma 5.8.

Proof of Proposition 7.1 assuming Proposition 7.2

Recall from equation (5.53) that $g = f + T(g,g)$ . From this, using the bounds on the Sobolev-type norms

$$ \begin{align*} \langle t \rangle^{-p_0} {\big\| \langle \xi \rangle^{4} \widetilde{f}(t) \big\|}_{L^{2}} \leq {\varepsilon}_1, \qquad \langle t \rangle^{-p_0} {\big\| \langle \xi \rangle^{4} \widetilde{g}(t) \big\|}_{L^{2}} \leq 2 {\varepsilon}_2, \end{align*} $$

the bilinear bound in equation (6.15), and the decay estimate from equation (7.7), we get

$$ \begin{align*} {\big\| \langle \xi \rangle^{4} \widetilde{g}(t) \big\|}_{L^{2}} & \leq {\big\| \langle \xi \rangle^{4} \widetilde{f}(t) \big\|}_{L^{2}} + {\big\| \langle \xi \rangle^{4} \widetilde{\mathcal{F}}T(g,g)(t) \big\|}_{L^{2}} \leq {\varepsilon}_1\langle t \rangle^{p_0} + {\big\| \mathcal{W}^*T(g,g)(t) \big\|}_{H^{4}} \\ & \leq {\varepsilon}_1\langle t \rangle^{p_0} + C {\big\| \mathcal{W}^*g(t) \big\|}_{H^{4}} {\| e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D) \mathcal{W}^*g(t) \|}_{L^{\infty}} \\ & \leq {\varepsilon}_1\langle t \rangle^{p_0} + C{\varepsilon}_2 \langle t \rangle^{p_0} \cdot {\varepsilon}_2 \langle t \rangle^{-1/2} \\ & \leq {\varepsilon}_1\langle t \rangle^{p_0} + C{\varepsilon}_2^2. \end{align*} $$

This gives the first bound in equation (7.8).

To estimate the $L^{\infty }_x$ -norm in equation (7.8) we use successively the estimate in equation (7.12), Sobolev’s embedding and equation (6.15) to get

$$ \begin{align*} \begin{aligned} {\| e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D) \mathcal{W}^*g \|}_{L^{\infty}} & \leq C{\varepsilon}_1\langle t \rangle^{-1/2} + C {\| e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D) \mathcal{W}^* T(g,g) \|}_{L^{\infty}} \\ & \leq C{\varepsilon}_1\langle t \rangle^{-1/2} + C {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* T(g,g)\|}_{W^{0+,\infty-}} \\ & \leq C{\varepsilon}_1\langle t \rangle^{-1/2} + C {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* g \|}_{L^{\infty-}}^2 \\ & \leq C\langle t \rangle^{-1/2} ({\varepsilon}_1 + {\varepsilon}_2^2) \\ & \leq \langle t \rangle^{-1/2} {\varepsilon}_2 \end{aligned} \end{align*} $$

as desired. We have used here the notation $\infty -$ to denote an arbitrarily large (but finite) number (which may be different from line to line) consistently with the notation introduced in Section 2.5.1.

Finally, we show equation (7.9). Note that this does not follow at once from equation (7.8) since $\mathcal {W}^*$ is not necessarily bounded on $L^{\infty }$ . Observe that, by interpolation of equations (7.12) and (7.13), we have

(7.15) $$ \begin{align} {\| e^{-it\langle \widetilde D \rangle}f \|}_{L^q} + {\| e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(\partial_x)\mathcal{W}^*f \|}_{L^q} \leq C{\varepsilon}_1 \langle t \rangle^{-1/2(1-2/q)}. \end{align} $$

Therefore, for finite q, we have

$$ \begin{align*} \begin{aligned} {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \|}_{L^q} & \leq C{\varepsilon}_1\langle t \rangle^{-1/2(1-2/q)} + {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* T(g,g) \|}_{L^q} \\ & \leq C{\varepsilon}_1\langle t \rangle^{-1/2(1-2/q)} + C {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* g \|}_{L^{2q}}^2 \\ & \leq C\langle t \rangle^{-1/2(1-2/q)} ({\varepsilon}_1 + {\varepsilon}_2^2) \\ & \leq \langle t \rangle^{-1/2(1-2/q)} {\varepsilon}_2. \end{aligned} \end{align*} $$

Using Gagliardo-Nirenberg interpolation, with the Sobolev-type norm bound in equation (7.7), we obtain, provided q is large enough,

(7.16) $$ \begin{align} {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \|}_{W^{1,q}} \lesssim \langle t \rangle^{-1/3} {\varepsilon}_2. \end{align} $$

Then we can estimate, using equation (7.12) and Sobolev’s embedding,

(7.17) $$ \begin{align} \begin{aligned} \langle t \rangle^{1/2}{\| e^{-it\langle \widetilde D \rangle} g \|}_{L^{\infty}} & \leq C{\varepsilon}_1 + \langle t \rangle^{1/2} \cdot C {\| e^{-it\langle \widetilde{D} \rangle} T(g,g) \|}_{L^{\infty}} \\ & \leq C{\varepsilon}_1 + \langle t \rangle^{1/2} \cdot C {\| e^{-it\langle \widetilde{D} \rangle} T(g,g) \|}_{W^{1,\infty-}}. \end{aligned} \end{align} $$

Using equation (6.15), we have

$$ \begin{align*} {\| e^{-it\langle \widetilde{D} \rangle} T(g,g) \|}_{W^{1,\infty-}} & \lesssim {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*T(g,g) \|}_{L^{\infty-}} + {\| \langle \partial_x \rangle e^{-it\langle \partial_x \rangle} \mathcal{W}^*T(g,g) \|}_{L^{\infty-}} \\ & \lesssim {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* g \|}_{W^{1,\infty-}}^2 \lesssim {\varepsilon}_2^2 \langle t \rangle^{-2/3}. \end{align*} $$

Plugging this into equation (7.17) gives equation (7.9) provided ${\varepsilon }_2$ is sufficiently small.

7.2 Preliminary bounds

Recall that our main aim from now on is to prove Proposition 7.2. Therefore, we will work under the a priori assumptions in equation (7.10) on f, as well as the a priori assumptions in equation (7.7) on g. We collect below several bounds on f that are immediate consequences of the a priori assumptions.

Lemma 7.5. Under the a priori assumptions in equation (7.10), for all $t\in [0,T]$ , the following hold true:

1. (i) (Basic bounds for f) We have

   (7.18) $$ \begin{align} & {\| \widetilde{f}(t) \|}_{L^2} + {\| \langle \xi \rangle^{3/2} \widetilde{f}(t) \|}_{L^{\infty}} \lesssim {\varepsilon}_1,\qquad\qquad\qquad\qquad \end{align} $$
   (7.19) $$ \begin{align} & {\| \langle \xi \rangle \partial_{\xi} \widetilde{f}(t) \|}_{L^2} \lesssim {\varepsilon}_1 \langle t \rangle^{\alpha + \beta \gamma},\qquad\qquad\qquad\qquad\qquad \end{align} $$
   (7.20) $$ \begin{align} & {\| \chi_{\ell,\sqrt{3}} \partial_{\xi} \widetilde{f}(t) \|}_{L^1} \lesssim {\varepsilon}_1 2^{\beta' \ell} \langle t \rangle^{\alpha}, \qquad \langle t \rangle^{-\gamma} \leq 2^{\ell} \leq 1. \end{align} $$

2. (ii) (Improved low-frequency bounds) For all $k\leq -5$ ,

   (7.21) $$ \begin{align} & {\| \varphi_{\leq k + 2}\partial_{\xi} \widetilde{f} \|}_{L^2} \leq {\varepsilon}_1 \langle t \rangle^{\alpha}, \end{align} $$
   (7.22) $$ \begin{align} &{\| \varphi_k \widetilde{f}(t) \|}_{L^{\infty}_{\xi}} \lesssim {\varepsilon}_1 2^{k/2} \langle t \rangle^{\alpha}, \end{align} $$
   (7.23) $$ \begin{align} & {\| \varphi_k \widetilde{f}(t) \|}_{L^1_{\xi}} \lesssim {\varepsilon}_1 2^{3k/2} \langle t \rangle^{\alpha}, \end{align} $$
   and for all $k\in {\mathbb Z}$ ,
   (7.24) $$ \begin{align} {\big\| \partial_{\xi} (\varphi_k \widetilde{f})(t) \big\|}_{L^1_{\xi}} & \lesssim {\varepsilon}_1 \mathrm{min}(2^{k/2}, 1) \langle t \rangle^{\alpha}. \end{align} $$

3. (iii) (Linear dispersive estimates) For all $t\in {\mathbb R}$ , we have

   (7.25) $$ \begin{align} {\big\| e^{-it \langle \widetilde{D} \rangle} f(t) \big\|}_{L^{\infty}} + {\big\| e^{-it \langle \partial_x \rangle} \mathbf{1}_{\pm}(\partial_x) \mathcal{W}^*f(t) \big\|}_{L^{\infty}} & \lesssim {\varepsilon}_1 \langle t \rangle^{-1/2}. \end{align} $$

Proof. Proof of (i): The first norm in equation (7.18) is bounded in view of the conservation of the Hamiltonian (see equation (7.13)), while the second is part of the a priori assumptions in equation (7.10). Equation (7.19) follows from equation (7.10) and the definition of $W_t$ in equation (2.30) by summation over $\ell $ with $c\langle t \rangle ^{-\gamma } \leq 2^{\ell } \leq 1$ . For equation (7.20), we apply the Cauchy-Schwarz inequality and the a priori bound on the $W_t$ norm to estimate

$$\begin{align*}\| \chi_{\ell,\sqrt{3}} \partial_{\xi} \widetilde{f} \|_{L^1} \lesssim 2^{\ell/2} \| \chi_{\ell,\sqrt{3}} \partial_{\xi} \widetilde{f} \|_{L^2} \lesssim {\varepsilon}_1 2^{\ell/2} 2^{-\beta \ell} \langle t \rangle^{\alpha} = {\varepsilon}_1 2^{\beta'\ell} \langle t \rangle^{\alpha}. \end{align*}$$

Proof of (ii): Equation (7.21) follows from the definition of the norm in equation (2.30). Since $\widetilde {f}(0)=0$ , we have, for $k\leq -5$ ,

(7.26) $$ \begin{align} | \varphi_{k}(\xi)\widetilde{f}(\xi) | & = \varphi_{k}(\xi) \Big| \int_0^{\xi} \partial_y \widetilde{f}(y)\,dy \Big| \leq \varphi_{k}(\xi) |\xi|^{1/2} {\| \varphi_{\leq k+2} \partial_y \widetilde{f} \|}_{L^2_y} \lesssim 2^{k/2} {\varepsilon}_1 \langle t \rangle^{\alpha}, \end{align} $$

and

(7.27) $$ \begin{align} {\| \varphi_k\widetilde{f} \|}_{L^1} & \lesssim 2^k {\| \varphi_k \widetilde{f} \|}_{L^{\infty}} \lesssim {\varepsilon}_1 2^{3k/2} \langle t \rangle^{\alpha}. \end{align} $$

The estimate in equation (7.24) follows from the a priori if assumption on the weighted norm in equation (7.10) and from equations (7.22)–(7.23) above as long as $||\xi |-\sqrt {3}| \geq 1$ , and it follows from equation (7.20) when $||\xi |-\sqrt {3}| \leq 1$ (which implies $|k|\leq 5$ ).

Proof of (iii). These estimates follow directly from the linear dispersive estimate in equations (3.31) and (3.32) and the a priori bounds in equation (7.10).

We now prove a weak bound on the basic weighted norm of g. This and the a priori bounds in equation (7.7) will help us to estimate various remainders that come from expanding the nonlinear expressions in g; see the right-hand side of equation (5.55), in terms of the renormalised profile f; see Section 7.3.

Lemma 7.6. Under the a priori assumptions in equations (7.10) and (7.7), for all $t\in [0,T]$ ,

(7.28) $$ \begin{align} {\| \langle \xi \rangle \partial_{\xi} \widetilde{g} \|}_{L^2_{\xi}} \leq C{\varepsilon}_1 \langle t \rangle^{1/2+p_0/2}. \end{align} $$

Proof. We obtain equation (7.28) through a bootstrap argument. More precisely, assuming that for some C large enough, equation (7.28) holds, it suffices to show the same inequality with $C/2$ instead of C. In view of the formula $g=f+T(g,g)$ in equations (5.53)–(5.54), the bootstrap assumptions on f (in particular the bound in equation (7.19), with C above chosen much larger than the implicit constant there), it is enough to prove that

(7.29) $$ \begin{align} {\| \langle \xi \rangle \partial_{\xi} \widetilde{T}(g,g) \|}_{L^2_{\xi}} & \lesssim {\varepsilon}_2^2 \langle t \rangle^{1/2+p_0/2} \end{align} $$

under the assumptions in equations (7.28) and (7.7) (recall ${\varepsilon }_2 = {\varepsilon }_1^{2/3}$ ).

From the explicit formula in equation (5.54), we see that

(7.30) $$ \begin{align} \begin{aligned} \langle \xi \rangle \partial_{\xi} \widetilde{\mathcal{F}} T^{\pm}_{\iota_1 \iota_2}(g,g) & = T_1(g,g) + T_2(g,g), \\ T_1(f_1,f_2) & := it \xi \, \widetilde{\mathcal{F}} T^{\pm}_{\iota_1 \iota_2}(f_1,f_2), \\ T_2(f_1,f_2) & := \iint e^{it \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \widetilde{f_1}(t,\eta) \widetilde{f_2}(t,\sigma) \,\langle \xi \rangle \partial_{\xi} \mathfrak{m}_{\iota_1 \iota_2}^{\pm}(\xi,\eta,\sigma)\,d\eta \,d\sigma. \end{aligned} \end{align} $$

We need to analyse the formula for $\mathfrak {m}^{\pm }_{\iota _1\iota _2}$ from equations (5.54), (5.11) and (4.4). We can restrict our attention to the more complicated contribution involving the $\mathrm {p.v.}$ , since the $\delta $ part is easier to estimate. This main contribution is (we are dropping all the irrelevant signs, such as $\lambda ,\mu ,\nu $ , and numerical constants from our notation)

(7.31) $$ \begin{align} \begin{aligned} & \mathfrak{m}_{\mathrm{p.v.}} := \frac{1}{\Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \cdot \frac{a(\xi, \eta,\sigma)}{\langle \eta \rangle \langle \sigma \rangle} \varphi^{\ast}(p,\eta,\sigma) \, \mathrm{p.v.} \frac{\widehat{\phi}(p)}{ip}, \qquad \\ & \varphi^{\ast}(\xi,\eta,p) = \varphi_{\leq -D_0}\big(p R(\eta,\sigma)) \qquad p := \lambda \xi - \iota_1 \mu \eta - \iota_2 \nu \sigma. \end{aligned} \end{align} $$

For $T_1$ , we can use equation (6.15), the $L^{\infty }$ decay in equation (7.7) and the interpolation of equation (7.13) and the Sobolev bound in equation (7.7) to obtain

$$ \begin{align*} {\| T_1[g,g](t) \|}_{L^2} & \lesssim \langle t \rangle {\| \langle \partial_x \rangle \mathcal{W}^* T[g,g](t) \|}_{L^2} \lesssim \langle t \rangle {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* g \big\|}_{L^{\infty}} {\| \langle \partial_x \rangle^{0+}g\|}_{L^2} \\ & \lesssim \langle t \rangle \cdot {\varepsilon}_2 \langle t \rangle^{-1/2} \cdot {\varepsilon}_2 \langle t \rangle^{0+} \lesssim {\varepsilon}_2^2 \langle t \rangle^{1/2+}. \end{align*} $$

To handle $T_2$ , we need to look more closely at the formulas in equation (5.54) and equation (5.11) for $\mathfrak {m}^{\pm }_{\iota _1\iota _2}$ .We apply $\partial _{\xi }$ and write the result as

(7.32) $$ \begin{align} \begin{aligned} & \langle \xi \rangle \partial_{\xi} \mathfrak{m}_{\mathrm{p.v.}} := \mathfrak{a} + \mathfrak{b}, \\ & \mathfrak{a} := \langle \xi \rangle \partial_{\xi} \Big[ \frac{1}{\Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \cdot \frac{a(\xi, \eta,\sigma)}{\langle \eta \rangle \langle \sigma \rangle} \varphi^{\ast}(p,\eta,\sigma)\Big] \, \mathrm{p.v.} \frac{\widehat{\phi}(p)}{ip} \\ & \mathfrak{b} := \langle \xi \rangle \frac{1}{\Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \cdot \frac{a(\xi,\eta,\sigma)}{\langle \eta \rangle \langle \sigma \rangle} \varphi^{\ast}(p,\eta,\sigma)\, \partial_{\xi} \, \mathrm{p.v.} \frac{\widehat{\phi}(p)}{ip}, \end{aligned} \end{align} $$

and, according to this, we define $T_{\mathfrak {a}}$ and $T_{\mathfrak {b}}$ similarly to $T_2$ in equation (7.30).

By the estimate in equation (5.26), we deduce that $\mathfrak {a}$ is a symbol that behaves like (the $\mathrm {p.v.}$ contribution to) $\mathfrak {m}^{\pm }_{\iota _1\iota _2}$ times an extra factor of $\langle \xi \rangle \cdot R(\eta ,\sigma )$ . In practice, the factor of R loses one derivative on the input with smaller frequency. Using the Hölder bound from Lemma 6.10, estimating in $L^{\infty }$ the input with higher frequency and in $L^2$ the one with lower frequency, we obtain

$$ \begin{align*} {\| T_{\mathfrak{a}}[g,g](t) \|}_{L^2} & \lesssim {\big\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* g \big\|}_{L^{\infty}} {\| \langle \partial_x \rangle \mathcal{W}^* g \|}_{L^2} \lesssim {\varepsilon}_2^2 \langle t \rangle^{-1/2+p_0/2}, \end{align*} $$

having used interpolation of the Sobolev a priori bound in equations (7.7) and (7.13) on both norms in the last inequality.

We now estimate the contribution involving $\mathfrak {b}$ , assuming without loss of generality that $|\eta | \geq |{\sigma }|$ . The idea is to use that $p = \lambda \xi - \iota _1 \mu \eta - \iota _2 \nu \sigma $ to convert $\partial _{\xi }$ into $\partial _{\eta }$ and integrate by parts in $\eta $ ; this gives three types of terms: (1) a term where $\partial _{\eta }$ hits the profile $\widetilde {f}(\eta )$ , (2) a term where $\partial _{\eta }$ hits $e^{it\Phi _{\iota _1\iota _2}}$ and (3) a term where its hits the rest of the symbol. This last term is essentially the same as $\mathfrak {a}$ in equation (7.32) (with $\partial _{\eta }$ replacing $\partial _{\xi }$ there) and can be handled identically, so we skip it. The contribution from (2) is of the same form as that of $T_1$ in equation (7.30), with $(\eta /\langle \eta \rangle )\widetilde {f_1}$ instead of $\widetilde {f_1}$ , and therefore satisfies the same bound. The remaining term is

(7.33) $$ \begin{align} \iint e^{it \Phi_{\iota_1 \iota_2}(\xi,\eta,\sigma)} \partial_{\eta} \widetilde{g}(t,\eta) \widetilde{g}(t,\sigma) \, \langle \xi \rangle \mathfrak{m}_{\mathrm{p.v.}}(\xi,\eta,\sigma)\,d\eta \,d\sigma. \end{align} $$

This term is of the form $\langle \xi \rangle \widetilde {T}\big (\widetilde {{\mathcal {F}}}^{-1} \partial _{\eta } \widetilde {g},g\big )$ , where the symbol is given by the $\mathrm {p.v.}$ part of the full symbol $\mathfrak {m}^{\pm }_{\iota _1\iota _2}$ . An application of Lemma 6.10 with the bounds in equations (7.28) and (7.7) gives the following upper bound:

$$ \begin{align*} {\| equation\ (7.33) \|}_{L^2} &\lesssim {\big\| \widehat{{\mathcal{F}}}^{-1} \langle \xi \rangle^{0+} \partial_{\xi} \widetilde{g} \big\|}_{L^2} {\big\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* g \big\|}_{L^{\infty}} \\ & \lesssim {\varepsilon}_2 \langle t \rangle^{1/2+p_0/2} \cdot {\varepsilon}_2 \langle t \rangle^{-1/2+} \lesssim {\varepsilon}_2^2 \langle t \rangle^{p_0/2+}. \end{align*} $$

This concludes the estimate in equation (7.29).

Remark 7.7. The argument in the proof of Lemma 7.6 shows that we have the following schematic identity for the operator $\widetilde {T}$ in equation (5.54):

(7.34) $$ \begin{align} \langle \xi \rangle \partial_{\xi} \widetilde{T}(f_1,f_2) \approx t \cdot \langle \xi \rangle \widetilde{T}(f_1,f_2) + \langle \xi \rangle \widetilde{T}\big(\widetilde{{\mathcal{F}}}^{-1}\partial_{\xi} \widetilde{f_1},f_2\big). \end{align} $$

This is the analogue of equation (6.26) for $\mathcal {Q}^R$ . In particular, equation (7.34) implies, via Lemma 6.10, that

(7.35) $$ \begin{align} \begin{aligned} & {\| e^{-it\langle \partial_x \rangle} \widehat{{\mathcal{F}}}^{-1} \langle \xi \rangle \partial_{\xi} \widetilde{T}(f_1,f_2) \|}_{L^2+L^{\infty-}} \\ &\quad \lesssim \langle t \rangle {\| e^{-it\langle \partial_x \rangle} \widehat{{\mathcal{F}}}^{-1} \langle \xi \rangle \widetilde{T}(f_1,f_2) \|}_{L^{\infty-}} + {\| e^{-it\langle \partial_x \rangle} \widehat{{\mathcal{F}}}^{-1} \langle \xi \rangle \widetilde{T}\big(\widetilde{{\mathcal{F}}}^{-1}\partial_{\xi} \widetilde{f_1},f_2\big) \|}_{L^2} \\ &\quad\lesssim \langle t \rangle {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* T(f_1,f_2) \|}_{W^{1,\infty-}} + {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* T\big(\widetilde{{\mathcal{F}}}^{-1}\partial_{\xi} \widetilde{f_1},f_2\big) \|}_{H^1} \\ &\quad \lesssim \langle t \rangle {\big\| e^{-it\langle \partial_x \rangle} \langle \partial_x \rangle^{0+} \mathcal{W}^* f_1 \big\|}_{L^{\infty-}} {\big\| e^{-it\langle \partial_x \rangle} \langle \partial_x \rangle^{0+}\mathcal{W}^*f_2 \big\|}_{L^{\infty-}} \\ & \qquad + {\big\| \langle \xi \rangle^{0+} \partial_{\xi} \widetilde{f_1} \big\|}_{L^2} {\big\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^*f_2 \big\|}_{L^{\infty-}}. \end{aligned} \end{align} $$

7.3 Expansions of the nonlinear terms

Our starting point to prove Proposition 7.2 is equation (5.55). To obtain the desired bounds, we first need to convert the nonlinear terms on the right-hand side of equation (5.55) into multilinear expressions that depend only on f, plus remainders that depend on both f and g but have a higher degree of homogeneity (they are at least quartic terms) and, therefore, are easier to bound. This is done by expanding $g=f + T(g,g)$ ; see equations (5.53)–(5.54). Thanks to the expansions below, we will obtain leading order quadratic and cubic (and some quartic) terms that only depend on the renormalised f. For these leading orders, we can use the stronger bootstrap assumptions in equation (7.10), but the analysis is still quite involved and will occupy Sections 8–11. The higher-order remainder terms involving both f and g are taken care of in Lemmas 7.8 and 7.9 below.

Recall the bracket notation introduced after equation (5.56). The following Lemma gives an expansion for the regular quadratic terms.

Lemma 7.8 (Expansion of $\mathcal {Q}^R$ )

Consider $\mathcal {Q}^R$ as defined in equation (5.56) and T as in equations (5.53)–(5.54). Under the a priori assumptions in equations (7.7) and (7.10), we can write

(7.36) $$ \begin{align} \begin{aligned} \mathcal{Q}^R[g,g] & = \mathcal{Q}^R[f,f] + \mathcal{R}_1(f,g) \\ & = \mathcal{Q}^R[f,f] + \mathcal{Q}^R[f,T(f,f)] + \mathcal{Q}^R[T(f,f),f] + \mathcal{R}_2(f,g) \end{aligned} \end{align} $$

with

(7.37) $$ \begin{align} \begin{aligned} \langle t \rangle^{-p_0}{\| \langle \xi \rangle^4 \mathcal{R}_1(f,g)(t) \|}_{L^2} + \langle t \rangle^{-\alpha}{\| \langle \xi \rangle \partial_{\xi} \mathcal{R}_2(f,g)(t) \|}_{L^2}& \lesssim {\varepsilon}_2^2 \langle t \rangle^{-1}. \end{aligned} \end{align} $$

Proof. For any bilinear form A, using $g = f + T(g,g)$ , we have $A(g,g)- A(f,f) = A(f,T(g,g)) + A(T(g,g),g)$ . Thus, we see that the remainders in equation (7.36) are given by

(7.38) $$ \begin{align} \begin{aligned} \mathcal{R}_1(f,g) & = \mathcal{Q}^R[f,T(g,g)] + \mathcal{Q}^R[T(g,g),g], \end{aligned} \end{align} $$

and

(7.39) $$ \begin{align} \begin{aligned} \mathcal{R}_2(f,g) & = \mathcal{Q}^R[f,T(g,g)-T(f,f)] + \mathcal{Q}^R[T(g,g)-T(f,f),f] + \mathcal{Q}^R[T(g,g),g-f] \\ & = \mathcal{Q}^R[f,T(f,T(g,g))] + \mathcal{Q}^R[f,T(T(g,g),g)] \\ & \quad + \mathcal{Q}^R[T(f,T(g,g)),f] + \mathcal{Q}^R[T(T(g,g),g),f] + \mathcal{Q}^R[T(g,g),T(g,g)]. \end{aligned} \end{align} $$

Let us first show how to obtain the Sobolev type bound in equation (7.37). Since f enjoys better estimates than g, it suffices to bound

(7.40) $$ \begin{align} {\| \langle \xi \rangle^4 \mathcal{Q}^R[T(g,g),g] \|}_{L^2} \lesssim {\varepsilon}_2^2 \langle t \rangle^{p_0-1}. \end{align} $$

From equation (6.21), we get

(7.41) $$ \begin{align} {\big\| \langle \xi \rangle^4 \mathcal{Q}^R[a,b](t) \big\|}_{L^2} \lesssim {\| \langle \xi \rangle^{3+} \widetilde{a} \|}_{L^2} {\| e^{-i t\langle \partial_x \rangle} \mathcal{W}^*b \|}_{L^{\infty-}} + {\| e^{-i t\langle \partial_x \rangle} \mathcal{W}^*a \|}_{L^{\infty-}} {\| \langle \xi \rangle^{3+} \widetilde{b} \|}_{L^2}. \end{align} $$

Interpolating between equations (7.7) and (7.13), and using the bilinear bounds in equations (6.14) and (6.15), we have

$$ \begin{align*} & {\| \langle \xi \rangle^4 \mathcal{Q}^R[T(g,g),g] \|}_{L^2} \\ &\qquad \lesssim {\| \langle \xi \rangle^{3+} \widetilde{g} \|}_{L^2} {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*T(g,g) \|}_{L^{\infty-}} + {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* g \|}_{L^{\infty-}} {\| \langle \xi \rangle^{3+} \widetilde{T}(g,g) \|}_{L^2} \\ & \qquad\lesssim {\varepsilon}_2 \langle t \rangle^{(3/4+)p_0} {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \|}_{L^{\infty-}}^2 + {\varepsilon}_2 \langle t \rangle^{-1/2+} \cdot {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \|}_{L^{\infty-}} {\| \langle \xi \rangle^3 \widetilde{g} \|}_{L^2} \\ &\qquad \lesssim {\varepsilon}_2^3 \langle t \rangle^{(3/4+)p_0} \cdot \langle t \rangle^{-1+}, \end{align*} $$

which is bounded by ${\varepsilon }_2^3 \langle t \rangle ^{p_0-1}$ .

We now show how to obtain the weighted bound in equation (7.37) for each of the terms on the right-hand side of equation (7.39). We will use the identity in equation (6.26), which we restate here for ease of reference,

(7.42) $$ \begin{align} \langle \xi \rangle \partial_{\xi} \mathcal{Q}^R[f_1,f_2] \approx t \cdot \langle \xi \rangle \mathcal{Q}^R[f_1,f_2] + \langle \xi \rangle \mathcal{Q}^R[\widetilde{{\mathcal{F}}}^{-1}\partial_{\xi} \widetilde{f_1},f_2], \end{align} $$

and the bilinear estimate in equation (6.21). The idea is that applying $\langle \xi \rangle \partial _{\xi }$ to the quartic expressions in equation (7.39) will cost at most a factor of t as we see from equation (7.42). Then estimating all the inputs in $L^{\infty -}$ will give a decaying factor of ${\varepsilon }_2\langle t \rangle ^{-1/2+}$ for each of them, for a total gain of ${\varepsilon }_2^4\langle t \rangle ^{-2+}$ , and this will suffice to obtain equation (7.37).

Let us look more in detail at the term $\mathcal {Q}^R[T(g,g),T(g,g)]$ , the other terms being similar or better since they contain at least one f. According to equation (7.42), we need to estimate

(7.43) $$ \begin{align} t {\| \mathcal{Q}^R[ \widetilde{{\mathcal{F}}}^{-1}\langle \xi \rangle \widetilde{T}(g,g),T(g,g)] \|}_{L^2}, \qquad \mbox{and} \qquad {\| \langle \xi \rangle \mathcal{Q}^R[ \widetilde{{\mathcal{F}}}^{-1}\partial_{\xi} \widetilde{T}(g,g),T(g,g)] \|}_{L^2}.\end{align} $$

For the first term, we use equation (6.21) followed by equation (6.14):

$$ \begin{align*} & t {\| \langle \xi \rangle \mathcal{Q}^R[ T(g,g),T(g,g)](t) \|}_{L^2} \\ & \qquad\lesssim \langle t \rangle {\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^*T(g,g) \|}_{L^{\infty-}} {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*T(g,g) \|}_{L^{\infty-}} \\ & \qquad \lesssim \langle t \rangle {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \|}_{L^{\infty-}}^4 \lesssim {\varepsilon}_2^4 \langle t \rangle^{-1+}. \end{align*} $$

For the second term in equation (7.43), we first estimate the first input: using equation (7.35), the a priori bounds and equation (7.28), give us

(7.44) $$ \begin{align} \begin{aligned} & {\big\| \langle \partial_x \rangle e^{-it\langle \partial_x \rangle} \mathcal{W}^* (\widetilde{{\mathcal{F}}}^{-1} \partial_{\xi} \widetilde{T}(g,g))\big\|}_{L^2 + L^{\infty-}} \\ &\quad \lesssim \langle t \rangle {\big\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle}\mathcal{W}^* g \big\|}_{L^{\infty-}} {\big\| \langle \partial_x \rangle^{0+}e^{-it\langle \partial_x \rangle} \mathcal{W}^* g \big\|}_{L^{\infty-}} \\ &\quad\quad + {\big\| \langle \xi \rangle^{0+} \partial_{\xi} \widetilde{g} \big\|}_{L^2} {\big\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D) \mathcal{W}^* g \big\|}_{L^{\infty}} \\ &\quad \lesssim \langle t \rangle \cdot {\varepsilon}_2 \langle t \rangle^{-1/2+} \cdot {\varepsilon}_2 \langle t \rangle^{-1/2+} + {\varepsilon}_2 \langle t \rangle^{1/2+p_0/2} \cdot {\varepsilon}_2 \langle t \rangle^{-1/2} \lesssim {\varepsilon}_2^2 \langle t \rangle^{p_0/2}. \end{aligned} \end{align} $$

Then, using equation (6.21) with $p_2=p_4 = \infty -$ and $p_1=p_3=2+$ or $\infty -$ , and equation (6.15), we have

$$ \begin{align*} & {\| \langle \xi \rangle \mathcal{Q}^R[ \widetilde{{\mathcal{F}}}^{-1}\partial_{\xi} \widetilde{T}(g,g),T(g,g)](t) \|}_{L^2} \\ &\quad \lesssim {\big\| \langle \partial_x \rangle e^{-it\langle \partial_x \rangle} \mathcal{W}^* (\widetilde{{\mathcal{F}}}^{-1} \partial_{\xi} \widetilde{T}(g,g))\big\|}_{L^2 + L^{\infty-}} \cdot {\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^*T(g,g) \|}_{L^{\infty-}} \\ & \quad\lesssim {\varepsilon}_2^2 \langle t \rangle^{p_0/2} \cdot {\varepsilon}_2^2 \langle t \rangle^{-1+}, \end{align*} $$

which is sufficient since $p_0<\alpha $ .

The remaining terms in equation (7.39) can be treated similarly, using the estimates of Lemmas 6.10 and 6.11 see also the expressions for $\langle \xi \rangle \partial _{\xi }\mathcal {Q}^R$ and $\langle \xi \rangle \partial _{\xi }\widetilde {T}$ in equations (6.26)–(6.27) and (7.34)–(7.35) and the weighted bound in equation (7.28) for $\langle \xi \rangle \partial _{\xi } \widetilde {g}$ .

Here is a similar expansion for the cubic terms.

Lemma 7.9 (Expansion of $\mathcal {C}^{S}$ )

Consider $\mathcal {C}^S$ defined in equation (5.57). Under the a priori assumptions in equations (7.7) and (7.10), we have

(7.45) $$ \begin{align} \mathcal{C}^{S}[g,g,g] & = \mathcal{C}^{S}[f,f,f] + \mathcal{C}^{S}[T(f,f),f,f] + \mathcal{C}^{S}[f,T(f,f),f] + \mathcal{C}^{S}[f,f,T(f,f)] + \mathcal{R}_3(f,g) \end{align} $$

with

(7.46) $$ \begin{align} {\| \langle \xi \rangle \partial_{\xi} \mathcal{R}_3(f,g)(t) \|}_{L^2} & \lesssim {\varepsilon}_2^3 \langle t \rangle^{-1+\alpha}. \end{align} $$

Moreover,

(7.47) $$ \begin{align} {\| \langle \xi \rangle^4 \mathcal{C}^{S}(g,g,g) \|}_{L^2} \lesssim {\varepsilon}_2^3 \langle t \rangle^{-1+p_0}. \end{align} $$

Proof. We have

(7.48) $$ \begin{align} \begin{aligned} \mathcal{R}_3(f,g) & = \mathcal{C}^{S}[T(g,g),g,g] - \mathcal{C}^{S}[T(f,f),f,f] + \mathcal{C}^{S}[f,T(g,g),g] - \mathcal{C}^{S}[f,T(f,f),f] \\ &\quad + \mathcal{C}^{S}[f,f,T(g,g)] - \mathcal{C}^{S}[f,f,T(f,f)]. \end{aligned} \end{align} $$

Let us analyse the first two terms, the others being similar, and write the difference as a sum of $5$ -linear terms:

(7.49) $$ \begin{align} \begin{aligned} \mathcal{C}^{S}[T(g,g),g,g] - \mathcal{C}^{S}[T(f,f),f,f] & = \mathcal{C}^{S}[T(T(g,g),g),g,g] + \mathcal{C}^{S}[T(f,T(g,g)),g,g] \\ & \quad + \mathcal{C}^{S}[T(f,f),T(g,g),g] + \mathcal{C}^{S}[T(f,f),f,T(g,g)]. \end{aligned} \end{align} $$

The terms on the right-hand side of equation (7.49) are all $5$ -linear convolution terms with bounded and sufficiently regular symbols, where each entry, f or g, satisfies a linear decay estimate at the rate of $\langle t \rangle ^{-1/2}$ (see equations (7.7) and (7.12)) and an $L^2$ -weighted bound (see equations (7.28) and (7.19)). It suffices to look at the first term on the right-hand side of equation (7.49) – the other terms are better since they contain a factor of f, which satisfies stronger assumptions – and show that

(7.50) $$ \begin{align} {\| \langle \xi \rangle\partial_{\xi} \mathcal{C}^{S}[T(T(g,g),g),g,g] \|}_{L^2} \lesssim {\varepsilon}_1^3 \langle t \rangle^{-1}. \end{align} $$

Inspecting the formula for $\mathcal {C}^{S}$ , we see that applying $\partial _{\xi }$ gives three types of terms: (1) a term where $\partial _{\xi }$ hits the exponential, which will cost a factor of t; (2) terms where $\partial _{\xi }$ hits the symbol; and (3) terms where $\partial _{\xi }$ hits $\delta $ or $\mathrm {p.v.}$ In the terms (3), we can convert $\partial _{\xi }$ into $\partial _{\eta }$ , integrate by parts in $\eta $ and obtain terms like (1) and (2) above, plus terms where the derivatives hit one of the three inputs; see the similar argument detailed in the proof of Lemma 7.6.

The terms (2) are lower-order, so we skip them. The main contribution comes from the terms of the type (1). In the case of equation (7.50), this gives a term whose $L^2$ norm can be bounded using the trilinear estimate of Lemma 6.13 and the bilinear bounds for T in Lemma 6.10 as follows:

$$ \begin{align*} & \langle t \rangle {\| \langle \xi \rangle \mathcal{C}^{S}[T(T(g,g),g),g,g] \|}_{L^2} \\ & \qquad \lesssim \langle t \rangle {\| \langle \partial_x \rangle^{0+} \mathcal{W}^*T(T(g,g),g) \|}_{L^2} {\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \|}_{L^{\infty}}^2 \\ & \qquad \lesssim \langle t \rangle {\| \mathcal{W}^*T(g,g) \|}_{L^2} {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \|}_{L^{\infty}} \cdot {\varepsilon}_2^2 \langle t \rangle^{-1+} \\ & \qquad \lesssim \langle t \rangle {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \|}_{L^{\infty}}^2 {\| g \|}_{L^2} \cdot {\varepsilon}_2^2 \langle t \rangle^{-1+} \lesssim {\varepsilon}_2^5 \langle t \rangle^{-1+} \end{align*} $$

having also used the a priori assumptions on g in equations (7.7) and (7.13).

Terms of the type (3) above are of the form

(7.51) $$ \begin{align} {\| \langle \xi \rangle \mathcal{C}^{S}[\widetilde{{\mathcal{F}}}^{-1} \partial_{\xi} \widetilde{T}(T(g,g),g),g,g] \|}_{L^2} \qquad \mbox{and} \qquad {\| \langle \xi \rangle \mathcal{C}^{S}[T(T(g,g),g),\widetilde{{\mathcal{F}}}^{-1}(\partial_{\xi} g),g] \|}_{L^2}. \end{align} $$

The second one is estimated directly using the weak weighted bound in equation (7.28) for ${\|\partial _{\xi } \widetilde {g}\|}_{L^2}$ , and estimating the other $4$ terms in $L^{\infty }$ via Lemma 6.13 followed by Lemma 6.10: this gives a bound of ${\varepsilon }_2^5 \langle t \rangle ^{-3/2+}$ . The first term in equation (7.51) can be handled similarly to the proof of Lemma 7.8 above. In particular, iterating the identity in equation (7.34) gives

(7.52) $$ \begin{align} {\| \langle \xi \rangle \partial_{\xi} \widetilde{T}(T(g,g),g) \|}_{L^2} \lesssim {\varepsilon}_2^3 \langle t \rangle^{p_0/2}. \end{align} $$

Then up to faster-decaying terms, we can use Lemma 6.13 to bound the $L^2$ -norm of the first term in equation (7.51) by

$$ \begin{align*} & C {\| \langle \xi \rangle^{0+} \partial_{\xi} \widetilde{T}(T(g,g),g) \|}_{L^2} {\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \|}_{L^{\infty}}^2 \lesssim {\varepsilon}_2^3 \cdot {\varepsilon}_2^2 \langle t \rangle^{-1+p_0/2+}, \end{align*} $$

which suffices for equation (7.46).

The last estimate in equation (7.47) follows from a direct application of Lemma 6.13 and the a priori bounds in equation (7.7).

Since we will need to look at iterations of Duhamel’s formula, it is also useful to establish some bounds for $\partial _t f$ .

Lemma 7.10 (Estimates for $\partial _t f$ )

Let f be the renormalised profile defined in equations (5.54)–(5.53). Following the notation in equations (5.55)–(5.57), we can write, under the a priori assumptions in equations (7.7) and (7.10),

(7.53) $$ \begin{align} \partial_t \widetilde{f} = \mathcal{C}^{S}(f,f,f) + \mathcal{R}(f,g), \end{align} $$

where

(7.54) $$ \begin{align} {\| \mathcal{R}(t) \|}_{L^2_{\xi}} \lesssim {\varepsilon}_2^3 \langle t \rangle^{-3/2 + 2\alpha}. \end{align} $$

In particular, we have

(7.55) $$ \begin{align} {\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* \partial_t f \|}_{L^2+L^{\infty-}} \lesssim {\varepsilon}_2^3 \langle t \rangle^{-3/2 + 2\alpha} \end{align} $$

and

(7.56) $$ \begin{align} {\| \partial_t f \|}_{L^2} \lesssim {\varepsilon}_1^2 \langle t \rangle^{-1}. \end{align} $$

Proof. From equation (5.55), we can write

(7.57) $$ \begin{align} \begin{aligned} \partial_t \widetilde{f} & = \mathcal{Q}^R(g,g) + \mathcal{C}^{S}(g,g,g) + \mathcal{C}^R(g,g,g) = \mathcal{C}^{S}(f,f,f) + \mathcal{R}(f,g) \end{aligned} \end{align} $$

with (recall the notation introduced after equation (5.56))

(7.58) $$ \begin{align} \begin{aligned} \mathcal{R}(f,g) & := \mathcal{Q}^R[f,f] + \mathcal{Q}^R[f,T(g,g)] + \mathcal{Q}^R[T(g,g),g]+ \mathcal{C}^R(g,g,g) \\ & \quad + \mathcal{C}^{S}[T(g,g),g,g] + \mathcal{C}^{S}[f,T(g,g),g] + \mathcal{C}^{S}[f,f,T(g,g)]. \end{aligned} \end{align} $$

We estimate each of the terms above, with the exception of $\mathcal {Q}^R[f,f]$ . The treatment of this term is postponed to Section 11.3, where the desired bound is given in equation (11.45) (and proven using an argument from Section 8).

Recall the multilinear estimates of Lemmas 6.10, 6.11 and 6.13. For the second term on the right-hand side of equation (7.58), we use equation (6.20) followed by equation (6.14) and the a priori decay estimate in equation (7.25) to obtain

$$ \begin{align*} {\| \mathcal{Q}^R[f,T(g,g)] \|}_{L^2} & \lesssim {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*f \big\|}_{L^{\infty-}} {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*T(g,g) \big\|}_{L^{\infty-}} \\ & \lesssim {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*f \big\|}_{L^{\infty-}} \cdot {\big\| e^{-it\langle \partial_x \rangle}\mathcal{W}^*g \big\|}_{L^{\infty-}}^2 \\ & \lesssim {\varepsilon}_1 \langle t \rangle^{-1/2} ({\varepsilon}_2 \langle t \rangle^{-1/2+})^2, \end{align*} $$

which suffices for equation (7.54). The third term on the right-hand side of equation (7.58) can be estimated identically. For the fifth term, we have

$$ \begin{align*} {\| \mathcal{C}^S[T(g,g),g,g] \|}_{L^2} & \lesssim {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^* T(g,g) \big\|}_{L^2} {\big\| e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D) \mathcal{W}^*g \big\|}_{L^{\infty}}^2 \\ & \lesssim {\big\| e^{-it\langle \partial_x \rangle} \mathcal{W}^*g \big\|}_{L^2} {\big\| e^{-it\langle \partial_x \rangle} \mathbf{1}_{\pm}(D)\mathcal{W}^*g \big\|}_{L^{\infty}}^3 \lesssim {\varepsilon}_2^4 \langle t \rangle^{-3/2}. \end{align*} $$

The remaining two terms involving $\mathcal {C}^S$ can be estimated in the same way.

7.4 Summary and remaining estimates

Recall equation (5.55) for the evolution of $\widetilde {f}$ . According to Lemmas 7.8 and 7.9, the right-hand side of equation (5.55) can be expressed in terms of $\widetilde {f}$ itself, up to remainders of sufficiently high homogeneity (in f and g), depending on the norms that one wants to bound.

For further reference, we recall here (see equations (7.36) and (7.45)) that we can write

(7.59) $$ \begin{align} \begin{aligned} \partial_t \widetilde{f} & = \mathcal{Q}^R[f,f] + \mathcal{C}^{S}[g,g,g] + \mathcal{R}_1(f,g) \\ & = \mathcal{Q}^R[f,f] + \mathcal{Q}^R[f,T(f,f)] + \mathcal{Q}^R[T(f,f),f] + \mathcal{C}^{S}[f,f,f] \\ & \quad + \mathcal{C}^{S}[T(f,f),f,f] + \mathcal{C}^{S}[f,T(f,f),f] + \mathcal{C}^{S}[f,f,T(f,f)] + \mathcal{R}_2(f,g) + \mathcal{R}_3(f,g). \end{aligned} \end{align} $$

Notice that, compared to equation (5.55), here we are discarding the $\mathcal {C}^R$ terms, according to the discussion in Section 5.7. The remainder terms $\mathcal {R}_1$ , respectively $\mathcal {R}_2$ and $\mathcal {R}_3$ , decay sufficiently fast in the Sobolev-type, respectively, weighted norm, that they can be bounded by simply integrating in time the estimates in equation (7.37), respectively equations (7.37) and (7.46).

We now list the terms that we still need to handle in order to conclude the proof of the main bootstrap Proposition 7.2.

Sobolev estimate. In view of equations (7.59) and (7.47), only $\mathcal {Q}^R(f,f)$ remains to be bounded in the Sobolev type norm; we do this in Section 11.2.

Weighted estimate. So far, we have only taken care of higher-order remainder terms, which did not require any refined multilinear analysis. The estimate for the main terms, which are much more delicate, are distributed as follows:

• • $\mathcal {Q}^R(f,f)$ is treated in Section 8 for the main interacting frequencies and in Section 11.1 for the rest of the interactions.

• • The terms $\mathcal {Q}^R[f,T(f,f)]$ and $\mathcal {Q}^R[T(f,f),f]$ are estimated in Section 11.3.

• • For $\mathcal {C}^{S}(f,f,f)$ , see Section 9 for the main interactions and Section 11.4 for the other interactions.

• • The terms $\mathcal {C}^{S}[T(f,f),f,f]$ , $\mathcal {C}^{S}[f,T(f,f),f]$ and $\mathcal {C}^{S}[f,f,T(f,f)]$ are estimated in Section 11.3.

Distorted Fourier $L^{\infty }$ -norm. We deal with the last piece of the bootstrap norm in equation (7.10) as follows:

• • Section 10 contains the main part of the argument: we analyse the cubic terms of the form $\mathcal {C}^S(f,f,f)$ and derive an asymptotic expression for them as $t\rightarrow \infty $ . We first do this with formal stationary phase arguments in Section 10.1. The expressions obtained will lead to an ODE for $\partial _t\widetilde {f}$ , which we show is Hamiltonian at leading order, and preserves $|\widetilde {f}(k)|^2 + |\widetilde {f}(-k)|^2$ ; see Section 10.2. From this, we derive a long-range scattering correction and estimates for the leading order terms in the $L^{\infty }_{\xi }$ -type norm. Then, in Section 10.3, we show how to rigorously justify the above asymptotics and complete the control over the $L^{\infty }_{\xi }$ norm of the ‘singular’ cubic terms.

• • The results in Section 11.3 give us integrable-in-time decay for the $L^{\infty }_{\xi }$ -norm of $\mathcal {Q}^R(f,f)$ and of all the other cubic and quartic order terms on the right-hand side of equation (7.59).

8 Weighted estimates part I: the main ‘regular’ interaction

The weighted estimates for the ‘regular’ interactions are one of the most technical parts of the paper due to the presence of a fully coherent interaction at output frequencies $\pm \sqrt {3}$ . Our main goal is to show the following:

Proposition 8.1. Consider the u solution of equation (KG) such that the a priori assumptions in equation (7.10) on the renormalised profile f hold. The ‘regular’ quadratic term $\mathcal {Q}^R=\mathcal {Q}^R(f,f)$ (see equation (5.15)) satisfies

(8.1) $$ \begin{align} {\left\| \langle \xi \rangle \partial_{\xi} \int_{0}^t \mathcal{Q}^R[f,f](s,\xi) \,ds \right\|}_{W_T} \lesssim {\varepsilon}_1^2. \end{align} $$

After setting up the framework for the proof of equation (8.1), in the rest of this section we will focus on the main interactions within $\mathcal {Q}^R$ , which, using the notation from equation (5.15), are those involving frequencies

(8.2) $$ \begin{align} |\eta| + |\sigma| + |\langle \xi \rangle - 2| \ll 1. \end{align} $$

We will leave the rest of the interactions, for example those with $|\eta |\approx 1$ or $|\xi | \not \approx \sqrt {3}$ , for later; see Section 11.1.

For ease of reference, we recall the definition of the norm we are estimating (see equations (2.26)–(2.30)):

(8.3) $$ \begin{align} {\| g \|}_{W_T} := \sup_{n \geq 0 } \sup_{\ell \in \mathbb{Z} \cap [\lfloor -\gamma n \rfloor,0]} {\| \chi_{\ell,\sqrt{3}}^{[-\gamma n,0]}(\,\cdot\,) \, \tau_n(t) \mathbf{1}_{[0,T]}(t) \, g(t,\cdot) \|}_{L^{\infty}_t L^2_{\xi}} 2^{\beta \ell} 2^{-\alpha n}, \end{align} $$

where our parameters satisfy $0 < \alpha , \beta ,\gamma < 1/2 $ with

(8.4) $$ \begin{align} \gamma \beta' < \alpha < \frac{1}{2}\beta', \qquad \gamma' := \frac{1}{2} -\gamma < \beta' := \frac{1}{2} - \beta \ll 1. \end{align} $$

We also recall the a priori assumptions in equation (7.10) that we will use throughout the proof:

(8.5) $$ \begin{align} \sup_{t \in [0,T]} \left[ {\| \langle \xi \rangle^{3/2} \widetilde{f}(t) \|}_{L^{\infty}} + \langle t \rangle^{-p_0} {\| \langle \xi \rangle^4 \widetilde{f} \|}_{L^2} \right] + {\| \langle \xi \rangle \partial_{\xi} \widetilde{f} \|}_{W_T} \leq 2 {\varepsilon}_1. \end{align} $$

8.1 Setup and reductions

In view of the definitions, we aim to show that for any integer $n = 0,1,\dots , [\log _2(T+2)]+1$ and $\ell \in {\mathbb Z}$ , we have, for $t \approx 2^n$ ,

(8.6) $$ \begin{align} 2^{-\alpha n} 2^{\beta \ell} {\Big\| \chi_{\ell,\sqrt{3}}^{[-\gamma n,0]}(\xi) \, \partial_{\xi} \int_{0}^t \mathcal{Q}^R(f,f)(s) \,ds \Big\|}_{L^2} \lesssim {\varepsilon}_{1}^2. \end{align} $$

Recall from equation (5.15) and Remarks 5.1 and 7.4 that we can effectively work with

(8.7) $$ \begin{align} \mathcal{Q}^R(t,\xi) = \sum_{\substack{\iota_1,\iota_2 \in \{+,-\} \\ \kappa_0,\kappa_1, \kappa_2 \in \{+,-\}}} \mathcal{Q}^{R}_{\substack{\iota_1 \iota_2 \\ \kappa_0 \kappa_1 \kappa_2}}(t,\xi), \end{align} $$

where

(8.8) $$ \begin{align} \begin{aligned} & \mathcal{Q}^{R}_{\substack{\iota_1 \iota_2 \\ \kappa_0 \kappa_1 \kappa_2}}[f,f](t,\xi) = -\iota_1\iota_2 \mathbf{1}_{\kappa_0}(\xi) \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})} \, \mathfrak{q}_{\substack{\iota_1 \iota_2 \\ \kappa_0 \kappa_1 \kappa_2}}(\xi,\eta,{\sigma}) \, \widetilde{f}_{\iota_1}^{\kappa_1}(t,\eta) \widetilde{f}_{\iota_2}^{\kappa_2}(t,{\sigma}) \, d\eta \, d{\sigma}, \\ & \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma}) := \langle \xi \rangle - \iota_1 \langle \eta \rangle - \iota_2 \langle \sigma \rangle, \end{aligned} \end{align} $$

and the symbols satisfy for any $a,b,c$

(8.9) $$ \begin{align} | \varphi_{k_1}(\eta) \varphi_{k_2}({\sigma}) \partial_{\xi}^a \partial_{\eta}^b \partial_{\sigma}^c \, \mathfrak{q}_{\substack{\iota_1 \iota_2 \\ \kappa_0 \kappa_1 \kappa_2}}(\xi,\eta,{\sigma})| \lesssim 2^{-\mathrm{max}(k_1,k_2)} 2^{(a+b+c)\mathrm{min}(k_1,k_2)}. \end{align} $$

Notation convention for the indexes. For notational simplicity, we will drop the superscripts $\kappa _j$ , which play no role. We will also drop the subscripts $\iota _1,\iota _2$ from the profiles $\widetilde {f}$ , since $\widetilde {f}_\iota ^{\kappa }$ enjoys the same bootstrap bounds as $\widetilde {f}$ . We do keep the signs $\iota _1,\iota _2$ for the phases $\Phi _{\iota _1,\iota _2}$ as these do play a role in the estimates. Also, recall that we are adopting the notation introduced after equation (5.56).

When applying $\partial _{\xi }$ to $\mathcal {Q}_{\iota _1\iota _2}^R$ , we can, by Lemma 5.9, omit the prefactor $\mathbf {1}_{\kappa _0}(\xi )$ ; furthermore, we only need to estimate the terms where $\partial _{\xi }$ hits the phase as the terms where $\partial _{\xi }$ hits the symbols $\mathfrak {q}$ are much easier to treat. In other words, we can consider that

$$ \begin{align*}\langle \xi \rangle \partial_{\xi} \mathcal{Q}_{\iota_1\iota_2}^R(t,\xi) \approx \mathcal{I}_{\iota_1\iota_2}^R(t,\xi),\end{align*} $$

where

(8.10) $$ \begin{align} \begin{aligned} & \mathcal{I}_{\iota_1\iota_2}^R(t,\xi) := t \xi \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})} \, \mathfrak{q}(\xi,\eta,{\sigma}) \, \widetilde{f}(t,\eta) \widetilde{f}(t,{\sigma}) \, d\eta \, d{\sigma}, \end{aligned} \end{align} $$

and restrict all our attention to these terms.

In view of equation (8.6) and the definitions in equations (2.26)–(2.28), it will suffice to show that for $n=0,1,\dots , [\log _2(T+2)]+1$ and $t\approx 2^n$ ( $t \in [0,T]$ ), we have

(8.11) $$ \begin{align} {\Big\| \varphi_{\leq -\gamma n}(|\xi|-\sqrt{3}) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s,\cdot)\,ds \Big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_{1}^2 \, 2^{\alpha n} 2^{\beta \gamma n} \end{align} $$

and that for all $n=1,\dots , [\log _2(T+2)]+1$ , any $\ell \in {\mathbb Z} \cap (-\gamma n,0)$ , and for any $m =0,1,\dots $ , we have, for all $t\approx 2^n$ ,

(8.12) $$ \begin{align} {\Big\| \chi_{\ell ,\sqrt{3}}(\xi) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s,\cdot)\, \tau_m(s) \,ds \Big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_{1}^2 \, 2^{\alpha m} 2^{-\beta \ell}, \end{align} $$

where the functions $\tau _0,\tau _1,\dots $ in equation (8.12) are a partition of the interval $[0,t]$ , with properties as in equation (2.26).

We begin with a reduction of the main bounds in equations (8.11)–(8.12) to estimates for each fixed m.

Lemma 8.2. To prove equations (8.10)–(8.12), it suffices to show the following three inequalities:

1. (1) For all $m=0,1,\dots $

   (8.13a) $$ \begin{align} \begin{aligned} {\Big\| \varphi_{\leq \ell_0}(|\xi|-\sqrt{3}) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s) \, \tau_m(s) \,ds \Big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{\alpha m} 2^{\beta \gamma m}, \qquad \ell_0 := -\frac{1}{2}m - 3\beta'm; \end{aligned} \end{align} $$

2. (2) For all $m=1,2,\dots $ , and $\ell \in (\ell _0, -\gamma m] \cap {\mathbb Z}$

   (8.13b) $$ \begin{align} \begin{aligned} {\Big\| \varphi_{\ell}(|\xi|-\sqrt{3}) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s)\, \tau_m(s) \,ds \Big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{\alpha m} 2^{-\beta\ell} \cdot 2^{-2\beta'm}; \end{aligned} \end{align} $$

3. (3) For all $m=1,2,\dots $ , and $\ell \in (-\gamma m,0] \cap {\mathbb Z}$

   (8.13c) $$ \begin{align} {\Big\| \varphi_{\ell}(|\xi|-\sqrt{3}) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s)\, \tau_m(s) \,ds \Big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{\alpha m} 2^{-\beta\ell}. \end{align} $$

Proof. Let us first show how equations (8.13a)–(8.13b) imply equation (8.11). For all $n=0,1,\dots $ , we estimate

(8.14) $$ \begin{align} & {\Big\| \varphi_{\leq -\gamma n}(|\xi|-\sqrt{3}) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s)\,ds \Big\|}_{L^2_{\xi}} \leq \sum_{0\leq m \leq n} {\Big\| \varphi_{\leq -\gamma m}(|\xi|-\sqrt{3}) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s)\, \tau_m(s) \,ds \Big\|}_{L^2_{\xi}} \nonumber \\ & \quad \leq \sum_{0\leq m \leq n} {\Big\| \varphi_{\leq \ell_0}(|\xi|-\sqrt{3}) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s)\, \tau_m(s) \,ds \Big\|}_{L^2_{\xi}} \end{align} $$

(8.15) $$ \begin{align} & \phantom{\hspace{-7.6pc}} + \sum_{0\leq m \leq n} \sum_{\ell_0 < \ell \leq -\gamma m} {\Big\| \varphi_{\ell}(|\xi|-\sqrt{3}) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s)\, \tau_m(s) \,ds \Big\|}_{L^2_{\xi}}. \end{align} $$

The inequality in equation (8.13a) takes care directly of equation (8.14) giving a bound of ${\varepsilon }_{1}^2 \, 2^{\alpha n} 2^{\beta \gamma n}$ as desired. For equation (8.15), we use equation (8.13b) to obtain

$$ \begin{align*} equation\ (8.15) \lesssim {\varepsilon}_1^2 \sum_{0\leq m \leq n} \, 2^{\alpha m} 2^{-\beta\ell_0} \cdot 2^{-2\beta'm} = {\varepsilon}_1^2 \, 2^{\alpha n} 2^{\beta(1/2 + 3\beta')n} \cdot 2^{-2\beta'n} \lesssim {\varepsilon}_{1}^2 \, 2^{\alpha n} 2^{\beta \gamma n}, \end{align*} $$

where the last inequality follows from $\beta (1/2 + 3\beta ')-2\beta ' = \beta /2 + \beta '(3\beta -2) \leq \beta /2 - \beta \gamma ' = \beta \gamma $ ; see equation (8.4).

Next, observe that the inequalities in equations (8.13b) and (8.13c) directly imply equation (8.12) when $\ell \in (\ell _0,0] \cap {\mathbb Z}$ . When $-\gamma n < \ell \leq \ell _0$ , equation (8.13a) gives

$$ \begin{align*} {\Big\| \varphi_{\ell}(|\xi|-\sqrt{3}) \, \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s)\, \tau_m(s) \,ds \Big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_{1}^2 \, 2^{\alpha m} 2^{\beta \gamma m} \lesssim {\varepsilon}_{1}^2 \, 2^{\alpha m} 2^{-\beta \ell}, \end{align*} $$

since $\gamma < 1/2 < \frac {1}{2} + 3 \beta '$ .

8.2 Proof of equation (8.13a)

For any function c, $m=0,1,\dots $ and $k\leq 0$ , we define

(8.16) $$ \begin{align} X_{k,m}(c) := \mathrm{min}\Big( {\| \varphi_k \widetilde{c} \|}_{L^1}, 2^{-m-k} \big({\| \partial_{\xi}(\varphi_k\widetilde{c}) \|}_{L^1} + 2^{-k}{\| \varphi_{[k-5,k+5]} \widetilde{c} \|}_{L^1}\big) \Big). \end{align} $$

A more general variant of this quantity will appear in equation (11.11) when we will also include the treatment of input frequencies $\gtrsim 1$ . Note that in view of the a priori assumptions in equation (8.5) and the consequent bounds in equations (7.23)–(7.24), for the profile f, we have, for $k<0$ ,

(8.17) $$ \begin{align} \begin{aligned} & X_{k,m} := X_{k,m}\big( f(t)\tau_m(t) \big) \lesssim {\varepsilon}_1 \mathrm{min}\big(2^{3k/2}, 2^{-m - k/2}\big) 2^{\alpha m}, \\ & \sum_{k<0} X_{k,m} \lesssim {\varepsilon}_1 2^{-3m/4} 2^{\alpha m}. \end{aligned} \end{align} $$

We have the following lemma.

Lemma 8.3. Let $\mathcal {I}^R_{\iota _1\iota _2}$ be the term defined in equation (8.10). Then, under the a priori assumptions in equation (8.5), we have

(8.18) $$ \begin{align} {\big\| \mathcal{I}^R_{\iota_1\iota_2}(s,\cdot) \big\|}_{L^{\infty}_{\xi}} \lesssim {\varepsilon}_1^2 2^{-m/2 + 2\alpha m}, \qquad s \approx 2^m. \end{align} $$

Proof. The signs $(\iota _1\iota _2)$ are not relevant for this bound, so we drop them from our notation and denote $\mathcal {I}_{\iota _1\iota _2}^R$ simply as $\mathcal {I}$ . We look at the expression in equation (8.10) and decompose dyadically the frequencies $\eta $ and $\sigma $ , estimating

(8.19) $$ \begin{align} \begin{aligned} & \sup_{s\approx 2^m}| \mathcal{I}(s,\xi) | \lesssim 2^m \sum_{k_1,k_2} \sup_{s\approx 2^m} |I^{k_1,k_2}(s,\xi)|, \\ & I^{k_1,k_2}(s,\xi) := I^{k_1,k_2}[f,f](s,\xi), \\ & I^{k_1,k_2}[a,b](s,\xi) := \iint e^{is \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})} \, \mathfrak{q}(\xi,\eta,{\sigma}) \, \varphi_{k_1}(\eta) \varphi_{k_2}(\sigma)\,\widetilde{a}(t,\eta) \widetilde{b}(t,{\sigma}) \, d\eta \, d{\sigma}. \end{aligned} \end{align} $$

Note that we are adopting the same notation used for $\mathcal {Q}^R$ (see below equation (5.56)) for the above bilinear terms. We claim that for any two functions $a,b$ , we have

(8.20) $$ \begin{align} |I^{k_1,k_2}[a,b](s,\xi)| \lesssim X_{k_1,m}(a) \cdot X_{k_2,m}(b), \qquad s\approx 2^{m}. \end{align} $$

Then equations (8.19), (8.20) and (8.17) give the desired conclusion in equation (8.18).

Let us prove equation (8.20). A first estimate is obtained by using $|\mathfrak {q}|\lesssim 1$ :

(8.21) $$ \begin{align} \begin{aligned} | I^{k_1,k_2}[a,b](s,\xi)| & \lesssim {\| \varphi_{k_1}\widetilde{a} \|}_{L^1} {\| \varphi_{k_2}\widetilde{b} \|}_{L^1}. \end{aligned} \end{align} $$

For our second estimate, we integrate by parts in $\eta $ to obtain

(8.22) $$ \begin{align} \nonumber & |I^{k_1,k_2}[a,b](s,\xi)| \\ & \qquad \lesssim \frac{1}{s} \Big| \iint e^{is \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})} \, \partial_{\eta} \Big[ \frac{\langle \eta \rangle}{\eta} \mathfrak{q}(\xi,\eta,{\sigma}) \, \varphi_{k_1}(\eta) \,\widetilde{a}(s,\eta) \Big] \varphi_{k_2}(\sigma) \widetilde{b}(s,{\sigma}) \, d\eta \, d{\sigma} \Big|. \end{align} $$

We then have a few different contributions depending on the term upon which $\partial _{\eta }$ falls. The term when $ \partial _{\eta }$ hits $\varphi _{k_1} \widetilde {a}$ is bounded by

(8.23) $$ \begin{align} \begin{aligned} C 2^{-m} 2^{-k_1} {\| \partial_{\eta}( \varphi_{k_1} \widetilde{a}(s)) \|}_{L^1} {\| \varphi_{k_2}\, \widetilde{b}(s) \|}_{L^1}, \end{aligned} \end{align} $$

and the term when $\partial _{\eta }$ hits the factor $1/\eta $ is upper bounded by

(8.24) $$ \begin{align} \begin{aligned} C 2^{-m} 2^{-2k_1} {\|\varphi_{k_1}\widetilde{a}(s) \|}_{L^1} {\| \varphi_{k_2}\, \widetilde{b}(s) \|}_{L^1}. \end{aligned} \end{align} $$

The term where $\partial _{\eta }$ hits $\mathfrak {q}$ is a lower-order term since $|\partial _{\eta } \mathfrak {q}|\lesssim 1$ , so we can disregard it.

Finally, for our last estimate, we can integrate by parts in equation (8.22) also in the ${\sigma }$ variable. Arguing as above, we obtain

(8.25) $$ \begin{align} \begin{aligned} | I^{k_1,k_2}[a,b](s,\xi)| & \lesssim X_{k_1,m}(a) \\ & \times \big( 2^{-m} 2^{-k_2} {\| \partial_{\eta}( \varphi_{k_2} \widetilde{b}(s)) \|}_{L^1} + 2^{-m} 2^{-2k_2} {\| \varphi_{k_2} \widetilde{b}(s)) \|}_{L^1} \big). \end{aligned} \end{align} $$

Putting together equations (8.21), (8.24) and (8.25) gives equation (8.20) and completes the proof.

As an immediate application of Lemma 8.3, we complete the proof of equation (8.13a). Using Hölder’s and equation (8.18), recalling that $\ell _0 := -m/2 - 3\beta 'm$ , we have

$$ \begin{align*} 2^{-\alpha m} 2^{-\beta\gamma m} {\Big\| \varphi_{\leq \ell_0}(|\xi|-\sqrt{3}) \,\int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R\,\tau_m(s) ds \Big\|}_{L^2} & \lesssim 2^{-\alpha m} 2^{-\beta\gamma m} 2^{\ell_0/2} \cdot 2^m \sup_{s\approx2^m} {\big\| \mathcal{I}_{\iota_1\iota_2}^R(s)\big\|}_{L^{\infty}} \\ & \lesssim 2^{-\beta\gamma m} \cdot 2^{-m/4 - (3/2)\beta'm} \cdot {\varepsilon}_1^2 2^{m/2} 2^{\alpha m} \lesssim {\varepsilon}_1^2, \end{align*} $$

since, by equation (8.4),

$$\begin{align*}-\beta \gamma + 1/4 -(3/2)\beta' + \alpha = \beta'/2+\gamma'/2 - \beta'\gamma' -(3/2)\beta' + \alpha \leq -\beta' /2+ \alpha \leq 0.\end{align*}$$

In view of the above estimate and Lemma 8.2, to show the desired bounds in equations (8.11)–(8.12), it remains to prove equations (8.13b)–(8.13c).

8.3 Proof of equations (8.13b)–(8.13c): preliminary decompositions

We proceed with the proofs of equations (8.13b) and (8.13c) by looking at various subcases depending on the sizes of the modulation and frequencies relative to time. For the remainder of the section, we assume furthermore that

(8.26) $$ \begin{align} \ell \leq -7\beta' m. \end{align} $$

We will deal with $\ell> -7\beta ' m$ in Section 11.1.

For notational convenience, we slightly redefine the time-cutoff function appearing in the expression in equation (8.10) for $\mathcal {I}_{\iota _1\iota _2}^R(t)$ to be $2^{-m} t \tau _m(t)$ (but still denote it with the same letter $\tau _m$ ) so that we can estimate

(8.27) $$ \begin{align} & \Big| \chi_{\ell,\sqrt{3}} \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s)\,\tau_m(s) \, ds \Big| \lesssim 2^m \sum_{p\geq p_0, \, k_1,k_2} \Big| \chi_{\ell,\sqrt{3}} \int_{0}^t I^{p,k_1,k_2}[f,f](s,\xi)\,\tau_m(s) \, ds \Big|, \end{align} $$

where, for any two functions $a,b$ , we denote

(8.28) $$ \begin{align} \begin{aligned} I^{p,k_1,k_2}_{\iota_1\iota_2}[a,b](t,\xi) & := \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})} \, \varphi_p^{(p_0)}\big(\Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})\big) \, \mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,{\sigma}) \, \\ & \qquad \times \varphi_{k_1}(\eta) \widetilde{a}_{\iota_1}(\eta) \, \varphi_{k_2}(\sigma) \widetilde{b}_{\iota_2}({\sigma}) \, d\eta \, d{\sigma}, \qquad p_0 := -m + {\delta} m, \\ \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma}) & := \langle \xi \rangle - \iota_1 \langle \eta \rangle - \iota_2 \langle \sigma \rangle, \end{aligned} \end{align} $$

for some fixed $\delta \in (0,10^{-3})$ . Note that we have inserted a localisation $\varphi _p^{(p_0)}(\Phi _{\iota _1\iota _2})$ in the size of the phase; see the notation in equations (2.23)–(2.24). Also note that the parameter $p_0$ here is not the same as the one appearing in the a priori estimates, such as in equation (7.10); however, this should not cause any confusion here since the one in equation (8.28) is the only $p_0$ that will appear in this section.

To better focus on the main interactions, for the remainder of this section, we will assume in addition that

(8.29) $$ \begin{align} k_1,k_2 \leq -10 \end{align} $$

(see equation (8.2)), and we will deal with the complementary case in Section 11.1. Note that equations (8.29) and (8.26) imply that $p\leq 10$ . Without loss of generality, we can also assume that

$$ \begin{align*}k_1 \geq k_2.\end{align*} $$

The a priori bound in equation (7.23) gives

(8.30) $$ \begin{align} \begin{aligned} \Big| \chi_{\ell,\sqrt{3}} \int_{0}^t \mathcal{I}_{\iota_1\iota_2}^R(s)\,\tau_m(s) \, ds \Big| & \lesssim 2^{2m} \sum_{p,k_1,k_2} \sup_{s\approx 2^m} {\| \varphi_{k_1}\widetilde{f}(s) \|}_{L^1} {\| \varphi_{k_2}\widetilde{f}(s) \|}_{L^1} \\ & \lesssim 2^{2m} \sum_{p,k_1,k_2} 2^{3k_1/2} 2^{\alpha m} {\varepsilon}_1 \cdot 2^{3k_2/2} 2^{\alpha m} {\varepsilon}_1. \end{aligned} \end{align} $$

Since there are at most $O(m)$ indexes p (because $p_0\leq p \leq 10$ ), if we take the sum in equation (8.30) over $k_2 < -2m$ or $k_1 < -2m/3$ , we obtain an upper bound of $C {\varepsilon }_1^2 2^{2\alpha m} m$ , which, also in view of equations (8.26) and $\alpha <\beta '/2$ , gives equations (8.13b)–(8.13c). We can then assume $k_2 \geq -2m$ and $k_1 \geq -2m/3$ .

At this point we also restrict our estimates to the case

(8.31) $$ \begin{align} (\iota_1\iota_2)=(++) \end{align} $$

in equation (8.28) and will deal with the other relatively simpler cases in Section 11.1. We drop the signs from the expression in equation (8.28) by denoting

(8.32) $$ \begin{align} \begin{aligned} I^{p,k_1,k_2}(t,\xi) & := I^{p,k_1,k_2}_{++}[f,f](t,\xi) \\ & := \iint e^{it \Phi(\xi,\eta,{\sigma})} \, \varphi_p^{(p_0)}\big(\Phi(\xi,\eta,{\sigma})\big) \, \mathfrak{q}(\xi,\eta,{\sigma}) \varphi_{k_1}(\eta)\widetilde{f}(t,\eta) \, \varphi_{k_2}(\sigma) \widetilde{f}(t,{\sigma}) \, d\eta \, d{\sigma}, \\ \Phi(\xi,\eta,{\sigma}) &:= \langle \xi \rangle - \langle \eta \rangle - \langle \sigma \rangle. \end{aligned} \end{align} $$

Note that, since $|\eta |,|\sigma | \leq 1/100$ , we have

(8.33) $$ \begin{align} & \Phi(\xi,\eta,{\sigma}) = \frac{\sqrt 3}{2} (|\xi| - \sqrt 3) - \frac{1}{2} \eta^2 - \frac{1}{2} \sigma^2 + O( (|\xi|-\sqrt 3)^2 + \eta^4 + \sigma^4). \end{align} $$

Moreover, on the support of the integrals in equation (8.32), we have, when $p> p_0$ ,

$$ \begin{align*} |\Phi(\xi,\eta,{\sigma})| \approx 2^p, \qquad |\eta| \approx 2^{k_1}, \qquad |\xi^2-3| \approx 2^{\ell}. \end{align*} $$

Then in particular,

(8.34) $$ \begin{align} \left\{ \begin{array}{ll} 2^p \approx 2^{\ell} & \mbox{if}\ 2^{\ell} \gg 2^{2k_1}, \\ 2^p \approx 2^{2k_1} & \mbox{if}\ 2^{\ell} \ll 2^{2k_1}, \\ 2^p \lesssim 2^{\ell} & \mbox{if}\ 2^{\ell} \approx 2^{2k_1}. \end{array} \right. \end{align} $$

In the case $p=p_0$ , we have $|\Phi | \lesssim 2^{-m+\delta m} \ll 2^{\ell }$ since $\ell> \ell _0 = -m/2 - 3\beta ' m$ (see equation (8.13a)).

Summarizing the reductions above, we have the following lemma:

Lemma 8.4. Let $I^{p,k_1,k_2}$ be as in equation (8.32). To prove equations (8.13b)–(8.13c) for $(\iota _1\iota _2) = (++)$ , it will suffice to show that for all $m=1,2,\dots $

(8.35) $$ \begin{align} \begin{aligned} 2^m \left\| \chi_{\ell,\sqrt{3}}(\cdot) \int_{0}^t I^{p,k_1,k_2}(\cdot,s) \, \tau_m(s)\, ds \right\|_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{-\beta\ell} 2^{-2\beta'm} \end{aligned} \end{align} $$

for all

(8.36) $$ \begin{align} \begin{aligned} & -(1/2+3\beta') m =: \ell_0 < \ell \leq -7\beta' m, \\ & -m+\delta m =: p_0\leq p \leq 0, \\ & -2m \leq k_2 \leq k_1 \leq -10, \qquad k_1\geq -2m/3. \end{aligned} \end{align} $$

Note that the quantity on the right-hand side of equation (8.35), with no $2^{\alpha m}$ factor, also takes into consideration the summation over $k_1,k_2$ and p, which is made of at most $O(m^3)$ terms. In several cases we will not need to use cancellations coming from the time integration and will prove the following stronger version of the bound in equations (8.35)–(8.36):

(8.37) $$ \begin{align} 2^m {\big\| \chi_{\ell,\sqrt{3}}(\xi) I^{p,k_1,k_2}(s,\xi) \big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{-m} 2^{-\beta \ell} \cdot 2^{-2\beta'm}, \qquad \forall \, s \approx 2^m. \end{align} $$

Let us now prove a general lemma that improves on Lemma 8.3 and will help deal with several basic cases.

Lemma 8.5. With the definition in equation (8.28) (but omitting the signs $\iota _1,\iota _2$ for lighter notation) and equation (8.16), we have, for all $s \approx 2^m$ ,

(8.38) $$ \begin{align} \big| \chi_{\ell,\sqrt{3}} \, I^{p,k_1,k_2}[f,f](s,\xi) \big| \lesssim X_{k_1,m}(f) \cdot X_{k_2,m}(f), \end{align} $$

and, in particular,

(8.39) $$ \begin{align} {\big\| \chi_{\ell,\sqrt{3}} \, I^{p,k_1,k_2}[f,f](s) \big\|}_{L^2} \lesssim 2^{\ell/2} \cdot X_{k_1,m}(f) \cdot X_{k_2,m}(f). \end{align} $$

Furthermore,

(8.40) $$ \begin{align} {\big\| \chi_{\ell,\sqrt{3}} \, I^{p,k_1,k_2}[f,f](s) \big\|}_{L^2} \lesssim 2^{p-k_1/2} \cdot 2^{-m-k_1} \left[ {\| \partial_{\xi} [\varphi_{k_1} \widetilde{f} ] \|}_{L^2} + 2^{-k_1} \| \varphi_{[k_1 - 5,k_1 + 5]} \widetilde{f} \|_{L^2} \right] X_{k_2,m}(f). \end{align} $$

As the proof below will show, the estimates of Lemma 8.5 hold for general expressions as in equation (8.28) with any combination of signs $(\iota _1,\iota _2)$ and not only for the expression in equation (8.32). In particular, we can use this result in Section 11.1 for the proof of equation (11.5).

Proof of Lemma 8.5

The bound in equation (8.38) follows similarly to the bound in equation (8.20), the only difference being the presence of the cutoff $\varphi _p^{(p_0)}(\Phi )$ in the definition of $I^{p,k_1,k_2}$ (see equation (8.28)) versus that of $ I^{k_1,k_2}$ (see equation (8.19)). However, this is easily dealt with by observing that, for $|\eta |\approx 2^{k_1}$ ,

$$ \begin{align*} \Big| \frac{1}{s \partial_{\eta}\Phi} \partial_{\eta} \varphi_p^{(p_0)}(\Phi) \Big| = \Big| \frac{1}{s \partial_{\eta}\Phi} { \varphi_p^{(p_0)}}' (\Phi) \partial_{\eta} \Phi \Big| \lesssim 2^{-m-p} \leq 2^{-m-p_0} = 2^{-\delta m}, \end{align*} $$

so that hitting this additional cutoff gives lower-order contributions, and one can iterate the integration by parts in $\eta $ again.

Remark 8.6. We will apply the above argument several times in what follows and treat as lower-order remainders all those terms where derivatives in $\eta $ and ${\sigma }$ fall on an expression of the form $\chi (2^{-p}\Phi (\xi ,\eta ,{\sigma }))$ for some smooth $\chi $ .

Equation (8.39) follows directly from Cauchy-Schwarz in $\xi $ . Let us now prove equation (8.40). Notice that we may assume $p \leq 2k_1-10$ , for otherwise equation (8.39) already gives the desired inequality. Indeed, if $p> 2k_1-10$ , then we must have $2^{\ell } \lesssim 2^p$ and $2^{\ell /2} \lesssim 2^{p - k_1}$ so that using

$$ \begin{align*} X_{k_1,m} \lesssim 2^{-m-k_1/2} \left[ {\| \partial_{\xi} [\varphi_{k_1} \widetilde{f} ] \|}_{L^2} + 2^{-k_1} \| \varphi_{[k_1 - 5,k_1 + 5]} \widetilde{f} \|_{L^2} \right] \end{align*} $$

recalls equations (8.16)–(8.17) and we get equation (8.40) from equation (8.39).

We look at the integral in equation (8.28) and begin with an integration by parts in $\eta $ obtaining a main contribution of

(8.41) $$ \begin{align} \frac{1}{s} \iint e^{is \Phi(\xi,\eta,{\sigma})} \, \varphi_p^{(p_0)}\big(\Phi(\xi,\eta,{\sigma})\big) \frac{\langle \eta \rangle}{\eta} \, \mathfrak{q}(\xi,\eta,{\sigma}) \, \partial_{\eta}\big[ \varphi_{k_1}(\eta) \widetilde{f}(s,\eta) \big] \, \varphi_{k_2}(\sigma) \widetilde{f}(s,{\sigma}) \, d\eta \, d{\sigma}. \end{align} $$

A lower-order contribution comes from $\partial _{\eta } $ hitting the symbol $\mathfrak {q}$ . We can bound in equation (8.41) by

(8.42) $$ \begin{align} \begin{aligned} & C 2^{-m} 2^{-k_1} \int \,K(\xi,\eta) \, \big| \partial_{\eta} [\varphi_{k_1}(\eta) \widetilde{f}(s,\eta)] \big| \, d\eta, \\ & K(\xi,\eta) := \varphi_{[k_1-2,k_1+2]}(\eta) \int \varphi_p^{(p_0)} \big(\Phi(\xi,\eta,{\sigma})\big) \varphi_{k_2}(\sigma) |\widetilde{f}(s,{\sigma})| \, d{\sigma}. \end{aligned} \end{align} $$

We have

$$ \begin{align*} \begin{aligned} \int K(\xi,\eta) \, d\eta \lesssim \int \Big( \int_{E_{k_1,p}} \,d\eta \Big) \varphi_{k_2}(\sigma) |\widetilde{f}(s,{\sigma})| \, d{\sigma}, \end{aligned} \end{align*} $$

where

(8.43) $$ \begin{align} E_{k_1,p} := \{ \eta \in {\mathbb R} \,:\, |\eta| \approx 2^{k_1}, \, |-\langle \xi \rangle + \langle \eta \rangle + \langle \sigma \rangle| \approx 2^p\}. \end{align} $$

Notice that for fixed $\xi $ and ${\sigma }$ , the set $E_{k_1,p}$ is contained in at most two intervals of length $\approx 2^{p - k_1}$ . We can then estimate

(8.44) $$ \begin{align} & \sup_{\xi} \int K(\xi,\eta) \, d\eta \lesssim 2^{p-k_1} \| \varphi_{k_2} \widetilde{f} \|_{L^1}. \end{align} $$

Similarly, we also have

(8.45) $$ \begin{align} & \sup_{\eta} \int K(\xi,\eta) \, d\xi \lesssim 2^p \| \varphi_{k_2} \widetilde{f} \|_{L^1}. \end{align} $$

The first bound needed for equation (8.40) then follows from the definition in equation (8.16), equation (8.42), equations (8.44)–(8.45) and Schur’s test:

$$ \begin{align*} {\big\| \chi_{\ell,\sqrt{3}} \, I^{p,k_1,k_2}(s) \big\|}_{L^2} & \lesssim 2^{-m-k_1} {\Big\| \int \,K(\xi,\eta) \, \big| \partial_{\eta} [\varphi_{k_1}(\eta) \widetilde{f}(s,\eta)] \big| \, d\eta \Big\|}_{L^2} \\ & \lesssim 2^{-m-k_1} \cdot 2^{p-k_1/2} \cdot {\| \partial_{\eta} [\varphi_{k_1} \widetilde{f}] \|}_{L^2} {\| \varphi_{k_2} \widetilde{f} \|}_{L^1}. \end{align*} $$

To complete the proof of equation (8.40), we integrate by parts also in $\sigma $ in equation (8.41) and then use Schur’s test as above.

Before proceeding, let us note that, as a corollary of Lemma 8.5, we may assume the two following inequalities on our parameters:

(8.46) $$ \begin{align} \begin{aligned} \left(\frac{1}{2}+\beta \right) \ell + \mathrm{min}(-m - k_1/2, 3k_1/2) + \mathrm{min}(-m - k_2/2, 3k_2/2) \geq -2m -(2\alpha+2\beta')m \end{aligned} \end{align} $$

and

(8.47) $$ \begin{align} \begin{aligned} \beta \ell + p-3k_1/2 + \mathrm{min}(-m - k_2/2, 3k_2/2) \geq -m -(2\alpha+2\beta')m. \end{aligned} \end{align} $$

Indeed, if equation (8.46) does not hold, the bound in equation (8.37) follows using equation (8.39). Similarly, if equation (8.47) does not hold, then we can use equation (8.40) to obtain equation (8.37).

We now proceed with the proof of equations (8.35)–(8.36), or the stronger equation (8.37) when possible. We will analyse the following regions separately:

(8.48) $$ \begin{align} \begin{aligned} & \mbox{Region 1 (Section 8.4):} \qquad p \leq -m/2-3\beta'm -10, \\ \\ & \mbox{Region 2 (Section 8.5):} \qquad -m/2-3\beta'm - 10 \leq p \leq -m/3-10\beta'm, \,\quad \ell \geq p+10, \\ \\ & \mbox{Region 3 (Section 8.6):} \qquad -m/2-3\beta'm -10\leq p, \qquad \ell \leq p+10, \\ \\ & \mbox{Region 4 (Section 8.7):} \qquad p \geq -m/3-10\beta'm, \qquad \ell \geq p+10. \end{aligned} \end{align} $$

8.4 Case $p \leq -m/2 - 3\beta ' m-10$

In this region there is almost no oscillation in time s, and we prove equation (8.37). Since we are working under the assumptions $-m/2 - 3\beta ' m \leq \ell \leq -10$ , we have

(8.49) $$ \begin{align} |\ell - 2k_1 | \leq 5. \end{align} $$

Applying equation (8.39) and (8.40), we see that to obtain a bound consistent with equation (8.37), it suffices to show that

$$ \begin{align*} \mathrm{min} \big( 2^{\ell/2} 2^{-k_1/2}, \, 2^{p-3k_1/2} \big) \cdot 2^{(-3/4 + 2\alpha)m} \lesssim 2^{-m} 2^{-\beta\ell} 2^{-2\beta'm}.\end{align*} $$

In view of equation (8.49), it then suffices that

(8.50) $$ \begin{align} \mbox{either} \qquad 2^{3k_1/2} \lesssim 2^{-m/4} 2^{-2\alpha m} 2^{-3\beta'm} \qquad \mbox{or} \qquad 2^{p -k_1/2} \lesssim 2^{-m/4} 2^{-2\alpha m} 2^{-3\beta'm}. \end{align} $$

The verification of equation (8.50) follows from $p \leq -m/2$ .

8.5 Case $-m/2-3\beta ' m -10 \leq p \leq -m/3-10\beta 'm $ , and $\ell \geq p+10$

In this case, we also have $|\ell -2k_1|\leq 10$ . Relying again on equation (8.40), for equation (8.35) it suffices to prove that

(8.51) $$ \begin{align} 2^{p-3k_1/2} 2^{2\alpha m} 2^{-3m/4} \lesssim 2^{-m} 2^{-\beta\ell} 2^{-2\beta' m}. \end{align} $$

We then consider two possibilities:

• - If we use that $p \leq 2k_1 +20$ and $|\ell -2k_1|\leq 10$ , equation (8.51) is implied by

  (8.52) $$ \begin{align} 2^{3k_1/2} \lesssim 2^{-(1/4+2\alpha+3\beta')m}. \end{align} $$

• - If we use that $p \leq - \frac {m}{3} - 10\beta ' m$ and $|\ell -2k_1|\leq 10$ , equation (8.51) is implied by

  (8.53) $$ \begin{align} 2^{-k_1/2} \lesssim 2^{m(1/12- 2\alpha + 7\beta')}. \end{align} $$

Then we observe that equation (8.52) is satisfied if $k_1 \leq - \frac {m}{6} - \frac {2}{3}[2\alpha + 3\beta ']m$ , while equation (8.53) is satisfied if $k_1 \geq - \frac {m}{6} + (4\alpha - 14\beta ')m$ ; finally, we notice that these latter two inequalities cover all possible values of $k_1$ since $\alpha < \beta '/2$ .

8.6 Case $p \geq -m/2 - 3\beta 'm-10$ , and $\ell \leq p+10$

This case is more delicate than the previous ones. Moreover, many of the arguments that we will perform here will also be relevant in the last case in Section 8.7. In order to obtain a bound consistent with equation (8.35) for this case, it suffices to show

(8.54) $$ \begin{align} 2^{\ell/2} \, {\Big\| \chi_{\ell,\sqrt{3}}(\xi) \int_{0}^t I^{p,k_1,k_2}(s,\xi) \, \tau_m(s)\, ds \Big\|}_{L^2} \lesssim {\varepsilon}_1^2 \, 2^{-m} 2^{-3\beta'm}, \end{align} $$

for all

(8.55) $$ \begin{align} \begin{aligned} & -m/2 - 2\beta'm -10\leq p, \quad -(1/2+3\beta')m \leq \ell \leq p + 10, \quad k_2 \leq k_1 \leq -10, \quad k_1 \geq -2m/3. \end{aligned} \end{align} $$

Step 1: Integration by parts in time

The first step is to resort to integration by parts in s, using that $|\Phi | \approx 2^p \gtrsim 2^{\ell }$ . Let us denote

(8.56) $$ \begin{align}\begin{aligned} \underline{I}^{p,k_1,k_2}[g,h](s,\xi) := \iint e^{is \Phi} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}(\xi,\eta,{\sigma}) \, \varphi_{k_1}(\eta)\widetilde{g}(\eta) \, \varphi_{k_2}(\sigma) \widetilde{h}({\sigma}) \, d\eta \, d{\sigma}, \end{aligned} \end{align} $$

where we have dropped some of the dependence on the time s and on the frequencies for ease of notation. Note that we are writing $\underline {I}^{p,k_1,k_2}$ for a bilinear term similar to $I^{p,k_1,k_2}$ , but there the symbol has an additional division by $\Phi $ .

Integrating by parts in s,

(8.57) $$ \begin{align} \Big| & \chi_{\ell,\sqrt{3}}(\xi)\int_{0}^t I^{p,k_1,k_2}(s,\xi) \, \tau_m(s)\, ds \Big| \lesssim | J(t,\xi) | + | K(t,\xi) | + | L(t,\xi) |, \end{align} $$

where

(8.58) $$ \begin{align} \begin{aligned} J(t,\xi) &:= \chi_{\ell,\sqrt{3}}(\xi) \underline{I}^{p,k_1,k_2}[f,f](t,\xi) - \chi_{\ell,\sqrt{3}}(\xi) \underline{I}^{p,k_1,k_2}[f,f](0,\xi) \\ &\quad - \, \chi_{\ell,\sqrt{3}}(\xi) \int_{0}^t \underline{I}^{p,k_1,k_2}[f,f](s,\xi) \, \tfrac{d}{ds} \tau_m(s) \, ds, \end{aligned} \end{align} $$

(8.59) $$ \begin{align} K(t,\xi) &:= \chi_{\ell,\sqrt{3}}(\xi) \int_{0}^t \underline{I}^{p,k_1,k_2}[\partial_sf,f](s,\xi) \, \tau_m(s) \, ds, \qquad\qquad\quad \end{align} $$

(8.60) $$ \begin{align} L(t,\xi) &:= \chi_{\ell,\sqrt{3}}(\xi) \int_{0}^t \underline{I}^{p,k_1,k_2}[f,\partial_sf](s,\xi) \, \tau_m(s) \, ds.\qquad\qquad\quad \end{align} $$

For equation (8.54), it then suffices to prove

(8.61) $$ \begin{align} 2^{\ell/2} \, {\big\| A(t,\cdot) \big\|}_{L^2} \lesssim {\varepsilon}_1^2 2^{-m} 2^{-3\beta'm}, \qquad A = J,K,L, \end{align} $$

or the stronger

(8.62) $$ \begin{align} 2^{\ell} \, \big| A(t,\xi) \big| \lesssim {\varepsilon}_1^2 2^{-m} 2^{-3\beta'm}, \qquad A = J,K,L. \end{align} $$

In the proof, we will look at K and L in various scenarios (while J is easier and directly estimated) depending on the size of $\ell $ , p, $k_1$ and so on…We will also split them into various pieces along the argument. In most cases, we will show that the contributions we obtain are bounded as in equation (8.62), while we will bound the $L^2$ norms as in equation (8.61) only in Section 8.7.

In view of equation (8.38) in Lemma 8.5 and Remark 8.6, we see that the operator defined in equation (8.56) satisfies the estimates

(8.63) $$ \begin{align} |\underline{I}^{p,k_1,k_2}[f,f](s,\xi)| \lesssim 2^{-p} \cdot X_{k_1,m} \cdot X_{k_2,m}, \qquad s\approx 2^m. \end{align} $$

Estimate of equation (8.58)

J is a boundary term and is easy to deal with. It suffices to show

(8.64) $$ \begin{align} 2^{\ell} \, \big| \chi_{\ell,\sqrt{3}}(\xi) \, \underline{I}^{p,k_1,k_2}[f,f](s,\xi) \big| \lesssim {\varepsilon}_1^2 2^{-m} 2^{-3\beta'm} \end{align} $$

for all $s\approx 2^m$ . From equation (8.63), we obtain the bound

(8.65) $$ \begin{align} 2^{\ell} \, \big| \underline{I}^{p,k_1,k_2}[f,f](s,\xi) \big| \lesssim 2^{\ell} \cdot 2^{-p} \cdot X_{k_1,m} \cdot X_{k_2,m} \lesssim {\varepsilon}_1^2 2^{(-3/2 + 2\alpha)m}, \end{align} $$

which is more than sufficient.

Estimate of equation (8.59)

For the other terms in equation (8.57), we need to expand $\partial _s \widetilde {f}$ and analyse the resulting quartic terms in more detail. We use the identity in equation (7.53) from Lemma 7.10 and write

(8.66) $$ \begin{align} K + L & = \sum_{\iota_1\iota_2\iota_3} K^{S1}_{\iota_1\iota_2\iota_3} + K^{S2}_{\iota_1\iota_2\iota_3} + L^{S1}_{\iota_1\iota_2\iota_3} + L^{S2}_{\iota_1\iota_2\iota_3} + D^R, \qquad\qquad\qquad\qquad\quad \end{align} $$

(8.67) $$ \begin{align} K^{S1,2}_{\iota_1\iota_2\iota_3}(t,\xi) & := \chi_{\ell,\sqrt{3}}(\xi)\int_{0}^t \underline{I}^{p,k_1,k_2} \big[ \widetilde{{\mathcal{F}}}^{-1}\mathcal{C}^{S1,2}_{\iota_1\iota_2\iota_3}(f,f,f),f\big](s,\xi) \, \tau_m(s) \, ds, \qquad\qquad\qquad \end{align} $$

(8.68) $$ \begin{align} L^{S1,2}_{\iota_1\iota_2\iota_3}(t,\xi) & := \chi_{\ell,\sqrt{3}}(\xi)\int_{0}^t \underline{I}^{p,k_1,k_2} \big[f,\widetilde{{\mathcal{F}}}^{-1}\mathcal{C}_{\iota_1\iota_2\iota_3}^{S1,2}(f,f,f) \big](s,\xi) \, \tau_m(s) \, ds, \qquad\qquad\qquad \end{align} $$

(8.69) $$ \begin{align} D^R(t,\xi) & := \chi_{\ell,\sqrt{3}}(\xi) \int_{0}^t \Big( \underline{I}^{p,k_1,k_2}\big[\widetilde{{\mathcal{F}}}^{-1}\mathcal{R},f\big[(s,\xi) + \underline{I}^{p,k_1,k_2} \big[f,\widetilde{{\mathcal{F}}}^{-1}\mathcal{R} \big] (s,\xi)\Big) \, \tau_m(s) \, ds. \end{align} $$

Notice that since we assume $k_2\leq k_1$ , the expressions in equations (8.67) and (8.68) are not symmetric. We proceed to estimate in equations (8.67)–(8.69).

Step 2.1: Estimate of $K^{S1}$ in equation (8.67)

In the formulas in equations (5.46) and (5.47) for $\mathcal {C}^{S1}$ , observe that the signs $\lambda ,\nu ,\dots $ do not play any relevant role, so we can omit them and write $K^{S1}_{\iota _1\iota _2\iota _3}$ as a term of the form

(8.70) $$ \begin{align}\begin{aligned} K^{S1}_{\iota_1\iota_2\iota_3} &= \int_{0}^t \iiiint e^{is \Psi_{\iota_1\iota_2\iota_3}(\xi,\rho,\zeta,\eta,{\sigma}) } \, \frac{\varphi_p\big(\Phi(\xi,\eta,{\sigma})\big)}{\Phi(\xi,\eta,{\sigma})} \, \mathfrak{q}(\xi,\eta,{\sigma},\rho,\zeta) \, \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma) \\ &\quad \times\, \widetilde{f_{\iota_1}}(\rho) \widetilde{f_{\iota_2}}(\zeta) \widetilde{f_{\iota_3}}(\eta-\rho-\zeta) \widetilde{f}({\sigma}) \, d\eta \, d\zeta \, d\rho \, d{\sigma} \, \tau_m(s)ds, \end{aligned} \end{align} $$

where

(8.71) $$ \begin{align} \Psi_{\iota_1\iota_2\iota_3}(\xi,\rho,\zeta,\eta,{\sigma}) := \langle \xi \rangle - \iota_1\langle\rho\rangle - \iota_2\langle\zeta\rangle - \iota_3\langle\eta-\rho-\zeta\rangle - \langle \sigma \rangle, \qquad \iota_1,\iota_2,\iota_3 \in\{+,-\}, \end{align} $$

and we slightly abuse notation by still denoting $\mathfrak {q}$ for the quartic symbol above, obtained by ‘composing’ the quadratic and cubic one.

We will sometimes denote the oscillating phase equation (8.71) just by $\Psi $ and omit the dependence on the signs $\iota _i$ of the profiles f, since these play no important role.

Remark 8.7. Note that $\Psi $ involves four input frequencies $(\rho ,\zeta ,\eta -\rho -\zeta ,{\sigma })$ : the first three are ‘correlated’, while ${\sigma }$ is ‘uncorrelated’. In the following arguments, we will always keep in mind this distinction and perform different estimates for the ‘correlated’ frequencies and the ‘uncorrelated’ ones.

We further decompose the integral over the frequencies in equation (8.70) according to the sizes of $\rho ,\zeta $ and $\eta -\rho -\zeta $ by defining

(8.72) $$ \begin{align} \begin{aligned} & \underline{I}^{p,\underline{k}}(s,\xi) := \iiiint e^{is \Psi} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q} \, \varphi_{\underline{k}}(\eta,\sigma,\rho,\zeta) \, \widetilde{f}(\rho)\widetilde{f}(\zeta) \widetilde{f}(\eta-\rho-\zeta) \, \widetilde{f}({\sigma}) \, d\eta \, d\zeta \, d\rho \, d{\sigma}, \\ & \varphi_{\underline{k}}(\eta,\sigma,\rho,\zeta) = \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma)\varphi_{k_3}(\rho)\varphi_{k_4}(\zeta)\varphi_{k_5}(\eta-\rho-\zeta). \end{aligned} \end{align} $$

Recall that we are aiming to obtain the bound in equation (8.62). Without loss of generality, we may assume that, on the support of equation (8.72), we have

(8.73) $$ \begin{align} k_5 \leq k_4\leq k_3; \end{align} $$

for the moment, we also assume that $k_3 \leq -5$ ; see Remark 8.8 below for more on this.

We first dispose of all interactions with $k_5 \leq -3m$ . In this case, we can estimate all profiles $\widetilde {f}$ in $L^{\infty }$ and gain $2^{-3m}$ from integration (recall also the notation for ‘ $\mathrm {med}$ ’ in Section 2.5.1):

(8.74) $$ \begin{align} \begin{aligned} & 2^{\ell} \big| \chi_{\ell,\sqrt{3}}(\xi)\underline{I}^{p,\underline{k}}(s,\xi) \big| \\ &\quad \lesssim 2^{\ell} \, {\| \widetilde{f} \|}_{L^{\infty}}^4 \iiiint \frac{\varphi_p(\Phi)}{|\Phi|} \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma)\varphi_{k_3}(\rho)\varphi_{k_4}(\zeta)\varphi_{k_5}(\eta-\rho-\zeta) \, d\eta d\sigma d\rho d\zeta \\ & \quad\lesssim 2^{\ell} \cdot {\varepsilon}_1^4 \cdot 2^{-p} \cdot 2^{k_2} 2^{\mathrm{min}(k_1,k_3,k_4)} 2^{\mathrm{med}(k_1,k_3,k_4)} 2^{k_5} \\ &\quad \lesssim {\varepsilon}_1^4 2^{-3m}, \end{aligned} \end{align} $$

which is more than enough.

After treating these very small frequencies, we are left with $O(m^3)$ choices for $k_3,k_4$ and $k_5$ in equation (8.72), and it suffices to show the slightly stronger bound

(8.75) $$ \begin{align} 2^{\ell} \big| \chi_{\ell,\sqrt{3}}(\xi)\underline{I}^{p,\underline{k}}(s,\xi) \big| \lesssim {\varepsilon}_1^2 2^{-2m} 2^{-5\beta'm}, \end{align} $$

for all $s \approx 2^m$ and for each $5$ -tuple of frequencies $(k_1,k_2,k_3,k_4,k_5)$ with

(8.76) $$ \begin{align} |\mathrm{max}(k_1,k_3) - \mathrm{med}(k_1,k_3,k_4)|\leq 5, \quad k_5 \leq k_4\leq k_3 \leq -5. \end{align} $$

The first restriction above comes from the fact that $\eta = \rho + \zeta + (\eta -\rho -\zeta )$ , which forces $\mathrm {max}(|\eta |,|\rho |,|\zeta |,|\eta -\rho -\zeta |) \approx \mathrm {max}_2(|\eta |,|\rho |,|\zeta |,|\eta -\rho -\zeta |)$ (recall the notation for ‘ $\mathrm {max}_2$ ’ given toward the end of Section 2.5.1), so that, in view of equation (8.73) (i.e., $|\rho |\gtrsim |\zeta | \gtrsim |\eta -\rho -\zeta |$ ), we must have $\mathrm {max}(|\eta |,|\rho |) \approx \mathrm {med}(|\eta |,|\rho |,|\zeta |)$ .

Remark 8.8. Concerning the restrictions in equation (8.76), note that we can assume equation (8.73) without loss of generality but that we are imposing the additional restriction $k_3 \leq -5$ . In particular, this means we are not considering here the cases when the sizes of ‘new input frequencies’ $(\rho ,\zeta ,\eta -\rho -\zeta )$ are (a) close to the bad frequency $\sqrt {3}$ or (b) going to infinity. Both of these cases are actually easier to treat than the case of small frequencies that we will concentrate on.

We will deal with the scenarios (a) and (b) at the level of the (more complicated) quadratic and cubic interactions in Section 11; see in particular Section 11.1, the discussion at the end of Section 11.1.2 about high frequencies and the estimates in Section 11.1.3, where we deal with the bad frequencies by relying on equation (11.15) to bound the quantity $X_{k,m}(f)$ .

Finally, recall that, under the assumed frequencies localisation, the symbol $\mathfrak {q}$ in equation (8.72) is smooth, with $O(1)$ bounds on derivatives; see equations (8.9) and (5.57) with equations (5.46)–(5.47).

Before proceeding with the proof of equation (8.75), we discuss how to treat the oscillations in the ‘uncorrelated’ variable $\sigma $ .

Treatment of the uncorrelated variable $\sigma $ and a first basic bound

Examining the definitions in equations (8.70)–(8.72), we see that the only oscillation involving the variable $\sigma $ is $e^{is\langle \sigma \rangle }$ . To exploit these oscillations, we integrate by parts in ${\sigma }$ when $k_2 \geq -m/2$ using equation (7.24), and otherwise estimate the profile $\varphi _{k_2}\widetilde {f}$ in $L^1_{\sigma }$ using equation (7.23).

More precisely, we first estimate

(8.77) $$ \begin{align} \begin{aligned} 2^{\ell} \big| \underline{I}^{p,\underline{k}}(s,\xi) \big| & \lesssim 2^{\ell} \cdot 2^{-p} \cdot {\|\varphi_{k_3} \widetilde{f}\|}_{L^{\infty}} {\|\varphi_{k_4} \widetilde{f}\|}_{L^{\infty}} {\|\varphi_{k_5} \widetilde{f}\|}_{L^{\infty}} \\ &\quad \times\, \iiint \Big( \int |\varphi_{k_2} \widetilde{f}(\sigma)| \,d\sigma \Big) \, \varphi_{k_1}(\eta) \varphi_{k_3}(\rho)\varphi_{k_4}(\zeta)\varphi_{k_5}(\eta-\rho-\zeta) \, d\eta d\rho d\zeta \\ & \lesssim {\|\varphi_{k_3} \widetilde{f}\|}_{L^{\infty}} {\|\varphi_{k_4} \widetilde{f}\|}_{L^{\infty}} {\|\varphi_{k_5} \widetilde{f}\|}_{L^{\infty}} \\ &\quad \times\, 2^{k_5} 2^{\mathrm{min}(k_1,k_3,k_4)} 2^{\mathrm{med}(k_1,k_3,k_4)} \cdot {\|\varphi_{k_2} \widetilde{f}\|}_{L^1}. \end{aligned} \end{align} $$

Using equations (7.22)–(7.23), and in view of $k_5\leq k_4 \leq k_3$ (see equation (8.76)), we obtain

(8.78) $$ \begin{align}2^{\ell} \big| \underline{I}^{p,\underline{k}}(s,\xi) \big| \lesssim {\varepsilon}_1^3 2^{3\alpha m} \cdot 2^{k_5+k_4 + \mathrm{min}(k_1,k_3)} \cdot 2^{(1/2)(k_3+k_4+k_5)} \cdot \| \varphi_{k_2} \widetilde{f} \|_{L^1}. \end{align} $$

When $k_2 \geq -m/2$ , we integrate by parts in $\sigma $ and write

(8.79) $$ \begin{align} \begin{aligned} \underline{I}^{p,\underline{k}} & = K_1 + K_2, \\ K_1 & = \iiiint e^{is \Psi} \partial_{\sigma} \mathfrak{k}(\xi,\eta,\sigma,\rho,\zeta) \, \widetilde{f}(\rho)\widetilde{f}(\zeta) \widetilde{f}(\eta-\rho-\zeta) \, \, \varphi_{\sim k_2}({\sigma})\widetilde{f}({\sigma})\, d\eta \, d\rho \, d\zeta \, d{\sigma}, \\ K_2 & = \iiiint e^{is \Psi} \mathfrak{k}(\xi,\eta,{\sigma},\rho,\zeta) \, \widetilde{f}(\rho)\widetilde{f}(\zeta) \widetilde{f}(\eta-\rho-\zeta) \, \partial_{\sigma} \big(\varphi_{\sim k_2}({\sigma})\widetilde{f}({\sigma}) \big)\, d\eta \, d\rho \, d\zeta \, d{\sigma}, \end{aligned} \end{align} $$

where we denoted $\varphi _{\sim k_2}({\sigma })=\varphi _{k_2}({\sigma }) 2^{k_2} \langle \sigma \rangle /{\sigma }$ a cutoff function with the same properties as $\varphi _{k_2}$ ( $k_2 \leq 0)$ , and defined the symbol

(8.80) $$ \begin{align} \begin{aligned} & \mathfrak{k}(\xi,\eta,{\sigma},\rho,\zeta) := 2^{-k_2} s^{-1} \,\frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}(\xi,\eta,{\sigma},\rho,\zeta) \,\varphi_{k_1}(\eta)\varphi_{k_3}(\rho)\varphi_{k_4}(\zeta)\varphi_{k_5}(\eta-\rho-\zeta), \\ & |\mathfrak{k}(\xi,\eta,{\sigma},\rho,\zeta)| \lesssim 2^{-m-p-k_2} \end{aligned} \end{align} $$

for $s\approx 2^m$ . We then claim that $K_2$ is the main contribution in equation (8.79), while $K_1$ gives a term of the same form of $\underline {I}^{p,\underline {k}}$ but with a better symbol that we can treat as a lower-order term and disregard. To see this, notice that

$$ \begin{align*} |\partial_{\sigma} \mathfrak{k}| & = s^{-1} 2^{-k_2} \Big|\partial_{\sigma} \Big[ \frac{\varphi_p\big(\Phi\big)}{\Phi} \,\mathfrak{q} \Big] \varphi_{k_1}(\eta)\varphi_{k_3}(\rho)\varphi_{k_4}(\zeta) \varphi_{k_5}(\eta-\rho-\zeta)\Big| \\ & \lesssim 2^{-m} 2^{-k_2} \big[ 2^{-2p + k_2} + 2^{-p} \big] \lesssim 2^{-m/2 + 3\beta' m} \cdot 2^{-p}, \end{align*} $$

having used $p \geq -m/2 - 3\beta ' m - 10$ and $k_2 \geq -m/2$ . In particular, we see that this bound is better than $O(2^{-p})$ , which is the trivial bound for the symbol of equation (8.72) used in equation (8.77).

For the term $K_2$ in equation (8.79), we can use equations (8.80) and (7.22)–(7.24) to obtain

(8.81) $$ \begin{align} 2^{\ell} \big| K_2(s,\xi) \big| & \lesssim 2^{\ell} \cdot 2^{-p-m-k_2} \cdot {\|\varphi_{k_3} \widetilde{f}\|}_{L^{\infty}} {\|\varphi_{k_4}\widetilde{f}\|}_{L^{\infty}} {\|\varphi_{k_5}\widetilde{f}\|}_{L^{\infty}} 2^{k_5+k_4 + \mathrm{min}(k_1,k_3)} \cdot {\|\partial_{\sigma} (\varphi_{\sim k_2} \widetilde{f}) \|}_{L^1} \nonumber \\ & \lesssim {\varepsilon}_1^3 2^{3\alpha m} \cdot 2^{k_5+k_4 + \mathrm{min}(k_1,k_3)} \cdot 2^{(1/2)(k_3+k_4+k_5)} \cdot 2^{-m-k_2} \| \partial_{\sigma}(\varphi_{\sim k_2} \widetilde{f} ) \|_{L^1}. \end{align} $$

Putting together equations (8.78) and (8.81), we obtain the following bound:

(8.82) $$ \begin{align} 2^{\ell} \big| \underline{I}^{p,\underline{k}}(s,\xi) \big|\lesssim {\varepsilon}_1^3 \cdot 2^{3\alpha m} \cdot 2^{k_5+k_4 + \mathrm{min}(k_1,k_3)} \cdot 2^{(1/2)(k_3+k_4+k_5)} \cdot X_{k_2,m}. \end{align} $$

With equation (8.82) in hand, we now proceed with the proof of equation (8.75), subdividing it into two main cases. In what follows, we fix $\delta \in (0,\alpha )$ .

Case 1: $k_1 + k_4 \leq -m + \delta m$ . This case corresponds to a scenario where integration by parts in the new ‘correlated variables’ – that is, in the directions $\partial _{\eta } + \partial _{\rho }$ and $\partial _{\eta } + \partial _{\zeta }$ – is forbidden; see also equation (8.84). In this case, the inequality in equation (8.82) suffices to get the desired bound by the right-hand side of equation (8.75). Indeed, using $X_{k_2,m} \lesssim {\varepsilon }_1 2^{-3m/4+\alpha m}$ , equation (8.82) implies

(8.83) $$ \begin{align}2^{\ell} \big| \underline{I}^{p,\underline{k}}(s,\xi) \big| \lesssim {\varepsilon}_1^3 2^{(-3/4+4\alpha) m} \cdot 2^{k_1+3k_4}; \end{align} $$

recall equation (8.76). Since we are assuming $k_1+k_4 \leq -m+\delta m$ , we must also have $k_4 \leq -m/3+\delta m$ as a consequence of the lower bound on $k_1$ in equation (8.55). Then $k_1+ 3k_4 \leq -3m/2$ , and equation (8.83) suffices for equation (8.75).

Case 2: $k_1 + k_4 \geq -m+\delta m$ . In this case, we can integrate by parts in both the $\partial _{\eta }+\partial _\rho $ and $\partial _{\eta }+\partial _{\zeta }$ directions, using that

(8.84) $$ \begin{align}\begin{array}{ll} (\partial_{\eta} + \partial_\rho) \Psi_{\iota_1\iota_2} = -\iota_1 \dfrac{\rho}{\langle \rho \rangle}, \qquad & |(\partial_{\eta} + \partial_\rho) \Psi_{\iota_1\iota_2}| \approx 2^{k_3}, \\ (\partial_{\eta} + \partial_{\zeta}) \Psi_{\iota_1\iota_2} = -\iota_2\dfrac{\zeta}{\langle \zeta \rangle}, \qquad & |(\partial_{\eta} + \partial_{\zeta}) \Psi_{\iota_1\iota_2}|\approx 2^{k_4}. \end{array} \end{align} $$

To properly implement this strategy, we first need to pay attention to the cases when $k_4$ is small.

Subcase 2.1: $k_4 \leq -m/2+\delta m$ . In this case, $k_5\leq k_4 \leq -m/2+\delta m$ , and we can estimate directly using equation (8.82):

$$ \begin{align*} \begin{aligned} 2^{\ell} \big| \underline{I}^{p,\underline{k}}(s,\xi) \big| & \lesssim {\varepsilon}_1^4 2^{(-3/4+4\alpha) m} \cdot 2^{k_4+k_5} \cdot 2^{(1/2)(k_4+k_5)} \lesssim {\varepsilon}_1^4 2^{(-3/4+4\alpha+3\delta) m} 2^{-3m/2}, \end{aligned} \end{align*} $$

which is sufficient for equation (8.75).

Subcase 2.2: $k_4 \geq -m/2 + \delta m$ . In this case, we have $k_3,k_4 \geq -m/2+\delta m$ , and (see equation (8.84)), we can integrate by parts in both $\partial _{\eta }+\partial _\rho $ and $\partial _{\eta }+\partial _{\zeta }$ , also using that $k_1 +k_4 \geq -m+\delta m$ . Performing these integrations by parts, we see that

(8.85) $$ \begin{align} \begin{aligned} \big| \underline{I}^{p,\underline{k}}(s,\xi) \big| & \lesssim 2^{-2m} \sup_{s\approx 2^m} \Big| \iiiint e^{is \Psi} \, (\partial_{\eta} + \partial_{\zeta}) \Big[ \frac{1}{(\partial_{\eta}+\partial_{\zeta}) \Psi} (\partial_{\eta} + \partial_\rho) \Big( \frac{1}{(\partial_{\eta} + \partial_\rho) \Psi} \\ &\quad \times\, \frac{\varphi_p\big(\Phi\big)}{\Phi} \mathfrak{q} \varphi_{\underline{k}} \widetilde{f}(\rho) \widetilde{f}(\zeta) \widetilde{f}(\eta-\rho-\zeta)\Big) \Big] \, d\eta \, d\rho \, d\zeta\, \widetilde{f}({\sigma}) \, d{\sigma} \Big|. \end{aligned} \end{align} $$

The expression in equation (8.85) gives many different contributions, depending on which terms are hit by the derivatives $\partial _{\eta } +\partial _\rho $ and $\partial _{\eta } +\partial _{\zeta }$ . By distributing these derivatives, we see that

(8.86) $$ \begin{align} \begin{aligned} \big| \underline{I}^{p,\underline{k}}(s,\xi) \big| & \lesssim 2^{-2m} \sup_{s\approx 2^m} \big[ A(s,\xi) + B(s,\xi) + C(s,\xi) + D(s,\xi) \big], \end{aligned} \end{align} $$

where

(8.87) $$ \begin{align} \begin{aligned} A & := \Big| \iiiint e^{is \Psi} \mathfrak{a}(\xi,\eta,{\sigma},\rho,\zeta) \widetilde{f}(\rho) \widetilde{f}(\zeta) \widetilde{f}(\eta-\rho-\zeta) \, d\eta \, d\rho \, d\zeta\, \widetilde{f}({\sigma}) d{\sigma} \Big| \qquad\qquad\quad\\ \mathfrak{a} &:= (\partial_{\eta} + \partial_{\zeta}) \Big[ \frac{1}{(\partial_{\eta}+\partial_{\zeta}) \Psi} (\partial_{\eta} + \partial_\rho) \Big( \frac{1}{(\partial_{\eta} + \partial_\rho) \Psi} \frac{\varphi_p\big(\Phi\big)}{\Phi} \mathfrak{q} \varphi_{\underline{k}} \Big) \Big] , \end{aligned} \end{align} $$

(8.88) $$ \begin{align} \begin{aligned} B & := \Big| \iiiint e^{is \Psi} \mathfrak{b}(\xi,\eta,{\sigma},\rho,\zeta) \big[ \partial_\rho \widetilde{f}(\rho) \big] \widetilde{f}(\zeta) \, \widetilde{f}(\eta-\rho-\zeta) \, d\eta \, d\rho \, d\zeta\, \widetilde{f}({\sigma}) d{\sigma} \Big| \qquad\\ \mathfrak{b} &:= (\partial_{\eta} + \partial_{\zeta}) \Big[ \frac{1}{(\partial_{\eta}+\partial_{\zeta}) \Psi} \frac{1}{(\partial_{\eta} + \partial_\rho) \Psi} \frac{\varphi_p\big(\Phi\big)}{\Phi} \mathfrak{q} \varphi_{\underline{k}} \Big] , \end{aligned} \end{align} $$

(8.89) $$ \begin{align} \begin{aligned} C & := \Big| \iiiint e^{is \Psi} \mathfrak{c}(\xi,\eta,{\sigma},\rho,\zeta) \, \big[\partial_\rho \widetilde{f}(\rho) \big] \, \big[ \partial_{\zeta} \widetilde{f}(\zeta) \big] \, \widetilde{f}(\eta-\rho-\zeta) \, d\eta \, d\rho \, d\zeta\, \widetilde{f}({\sigma}) d{\sigma} \Big| \\ \mathfrak{c} &:= \frac{1}{(\partial_{\eta}+\partial_{\zeta}) \Psi} \frac{1}{(\partial_{\eta} + \partial_\rho) \Psi} \frac{\varphi_p\big(\Phi\big)}{\Phi} \mathfrak{q} \varphi_{\underline{k}}, \end{aligned} \end{align} $$

(8.90) $$ \begin{align} \begin{aligned} D & := \Big| \iiiint e^{is \Psi} \mathfrak{d}(\xi,\eta,{\sigma},\rho,\zeta) \widetilde{f}(\rho) \big[ \partial_{\zeta} \widetilde{f}(\zeta) \big] \, \widetilde{f}(\eta-\rho-\zeta) \, d\eta \, d\rho \, d\zeta\, \widetilde{f}({\sigma}) d{\sigma} \Big| \qquad\\ \mathfrak{d} & := \frac{1}{(\partial_{\eta}+\partial_{\zeta}) \Psi} (\partial_{\eta} + \partial_\rho) \Big[ \frac{1}{(\partial_{\eta} + \partial_\rho) \Psi} \frac{\varphi_p\big(\Phi\big)}{\Phi} \mathfrak{q} \varphi_{\underline{k}} \Big]. \end{aligned} \end{align} $$

To obtain the desired bound in equation (8.75), it suffices to show

(8.91) $$ \begin{align} 2^{\ell} \sup_{s\approx 2^m} \big( |A(s,\xi)| + |B(s,\xi)| + |C(s,\xi)| + |D(s,\xi)| \big) \lesssim {\varepsilon}_1^4 2^{-5\beta'm}. \end{align} $$

To estimate equation (8.87), we first observe that, in view of equation (8.84), the symbol satisfies

(8.92) $$ \begin{align} \begin{aligned} |\mathfrak{a}| & \lesssim 2^{-k_3-k_4-p} \cdot \mathrm{max}\big( 2^{-k_3}, 2^{-p+k_1}, 2^{-k_1} \big) \cdot \mathrm{max}\big( 2^{-k_4}, 2^{-p+k_1}, 2^{-k_1} \big) \\ & \lesssim 2^{-k_3-k_4-p} \cdot \mathrm{max}\big( 2^{-k_3}, 2^{-k_1} \big) \cdot \mathrm{max}\big( 2^{-k_4}, 2^{-k_1}\big) \end{aligned} \end{align} $$

having used that $ 2k_1 \leq p + 20$ . If we iterate the above integration by parts procedure and only keep the terms where the derivatives never hit the $\widetilde {f}$ , the gain at each step is

$$ \begin{align*}2^{-2m} 2^{-k_3-k_4} \mathrm{max}(2^{-k_3},2^{-k_1}) \mathrm{max}(2^{-k_4},2^{-k_1}) \lesssim 2^{-2\delta m}, \end{align*} $$

since $k_4 \geq - \frac {m}{2} + \delta m$ and $k_1 + k_4 \geq -m + \delta m$ . Thus, one obtains an arbitrarily large gain in powers of $2^m$ , leading to the desired estimates. There remain the terms where one of the $\widetilde {f}$ is hit, but they are all better behaved than B and C, to which we now turn.

To estimate equation (8.88), we first bound, similarly to equation (8.92),

(8.93) $$ \begin{align} |\mathfrak{b}| \lesssim 2^{-k_3-k_4-p} \cdot 2^{-\mathrm{min}(k_4,k_1)}. \end{align} $$

Using this, integration by parts in the ‘decorrelated’ variable ${\sigma }$ , and the a priori bounds placing $\partial _\rho \widetilde {f} \in L^2$ and the other two profiles in $L^{\infty }_{\xi }$ , we get

$$ \begin{align*} 2^{\ell} |B| & \lesssim {\varepsilon}_1^3 2^{3\alpha m} \cdot 2^{-k_3-k_4} \cdot 2^{-\mathrm{min}(k_4,k_1)} \cdot 2^{\mathrm{min}(k_5,k_1) + \mathrm{med}(k_1,k_4,k_5)} \cdot 2^{(1/2)(k_3+k_4+k_5)} \cdot X_{k_2,m} \\ & \lesssim {\varepsilon}_1^4 2^{-3m/4 + 4\alpha m}. \end{align*} $$

Finally, equation (8.89) can be dealt with in a similar way by using $|\mathfrak {c}| \lesssim 2^{-k_3-k_4-p}$ , the usual argument for the ‘decorrelated’ variable giving a factor of $X_{k_2,m}$ , estimating in $L^2$ the two differentiated profiles, and using the a priori bounds in equation (8.5):

$$ \begin{align*} 2^{\ell} |C| \lesssim {\varepsilon}_1^3 2^{3\alpha m} \cdot 2^{-k_3-k_4} \cdot 2^{\mathrm{min}(k_5,k_1)} \cdot 2^{(1/2)(k_3+k_4+k_5)} \cdot X_{k_2,m} \lesssim {\varepsilon}_1^4 2^{-3m/4 + 4\alpha m}. \end{align*} $$

Finally, we have equation (8.90), which is similar to equation (8.88), with one profile differentiated and the other derivative hitting the symbol. The symbol satisfies $|\mathfrak {d}| \lesssim 2^{-k_3-k_4-p} \cdot 2^{-\mathrm {min}(k_3,k_1)}$ , and we can estimate

$$ \begin{align*} 2^{\ell} |D| & \lesssim {\varepsilon}_1^3 2^{3\alpha m} \cdot 2^{-k_3-k_4} \cdot 2^{-\mathrm{min}(k_3,k_1)} \cdot 2^{\mathrm{min}(k_5,k_1) + \mathrm{med}(k_1,k_3,k_5)} \cdot 2^{(1/2)(k_3+k_4+k_5)} \cdot X_{k_2,m} \\ & \lesssim {\varepsilon}_1^4 2^{-3m/4 + 4\alpha m}. \end{align*} $$

The bound in equation (8.91) is proven, and equation (8.75) follows, thereby completing the estimate for the term $K^{S1}$ in equation (8.67).

Step 2.2: Estimate of $K^{S2}$ in equation (8.67)

Recall the definition of $\mathcal {C}^{S2}$ from equations (5.46) and (5.47). We can see that $K^{S2}_{\iota _1\iota _2\iota _3}$ has the form

(8.94) $$ \begin{align}\begin{aligned} K^{S2}_{\iota_1\iota_2\iota_3} = \int_{0}^t \tau_m(s) \iiiint e^{is \Gamma_{\iota_1\iota_2\iota_3}} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}_2(\xi,\eta,{\sigma},\rho,\zeta,\omega) \, \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma) \\ \widetilde{f_{\iota_1}}(\rho) \widetilde{f_{\iota_2}}(\zeta) \widetilde{f_{\iota_3}}(\eta-\rho-\zeta-\omega) \widetilde{f}({\sigma}) \, d\eta \, d\rho \, d\zeta \,d{\sigma} \, \mathrm{p.v.} \frac{\widehat{\phi}(\omega)}{\omega}d\omega \, ds, \end{aligned} \end{align} $$

with

(8.95) $$ \begin{align} \Gamma_{\iota_1\iota_2\iota_3}(\xi,\rho,\eta,\omega,{\sigma}) := \langle \xi \rangle - \iota_1\langle\rho\rangle - \iota_2\langle\zeta\rangle - \iota_3\langle\eta-\zeta-\rho-\omega\rangle - \langle \sigma \rangle, \quad \iota_1,\iota_2,\iota_3 \in \{+,-\}. \end{align} $$

As before, we may assume that the symbol $\mathfrak {q}_2$ is sufficiently regular with bounded derivatives. For lighter notation, we will often omit the $\iota _i$ indexes and some of the arguments when doing so causes no confusion. Recall that we aim to prove (see equations (8.62) and (8.66))

(8.96) $$ \begin{align} 2^{\ell} \big| \chi_{\ell,\sqrt{3}}(\xi) \, K^{S2}(t,\xi) \big| \lesssim {\varepsilon}_1^2 2^{-m} 2^{-3\beta'm}. \end{align} $$

We start by splitting

(8.97) $$ \begin{align} K^{S2}(t,\xi) = \int_{0}^t \big[ A_1(s,\xi) + A_2(s,\xi) \big] \, \tau_m(s) ds, \end{align} $$

where

(8.98) $$ \begin{align} & A_1(s,\xi) = \int F(s,\xi,\omega) \, \mathrm{p.v.} \frac{\widehat{\phi}(\omega) \varphi_{\leq -5m}(\omega)}{\omega} d\omega, \quad A_2(s,\xi) = \int F(s,\xi,\omega) \, \frac{\widehat{\phi}(\omega) \varphi_{> -5m}(\omega)}{\omega} d\omega, \end{align} $$

with

(8.99) $$ \begin{align} \begin{aligned} F(s,\xi,\omega) := \iiiint e^{is \Gamma} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}_2\, \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma) \widetilde{f}(\rho) \widetilde{f}(\zeta) \widetilde{f}(\eta-\rho-\zeta-\omega) \widetilde{f}({\sigma}) \, d\eta\, d\rho \,d\zeta \, d{\sigma}. \end{aligned} \end{align} $$

Estimate of $A_1$

In this case, $\omega $ is very small, and we need to use the principal value. We estimate, for $s\approx 2^m$ ,

(8.100) $$ \begin{align} \begin{aligned} |A_1(s,\xi)| & \lesssim \int \Big| F(s,\xi,\omega) - F(s,\xi,0) \Big| \frac{\varphi_{\leq -5m}(\omega)}{|\omega|} \, d\omega \, \\ & \lesssim 2^{-5m} \cdot \sup_{s\approx 2^m} \sup_{|\omega|\lesssim 2^{-5m}} \big|\partial_\omega F(s,\xi,\omega)\big|. \end{aligned} \end{align} $$

Inspecting the formula in equation (8.99), we see that $\partial _\omega F$ has three contributions corresponding to the derivative hitting the phase ${\Gamma }$ , the symbol $\mathfrak {q}_2$ or the profile $\widetilde {f}(\eta -\rho -\zeta -\omega )$ . The main term is the first one so that, up to lower-order (faster-decaying) terms, we have

$$ \begin{align*} \begin{aligned} \partial_\omega F(s,\xi,\omega) & \approx \iiint is ( \partial_\omega \Gamma)\, e^{is \Gamma} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}_2 \, \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma) \\ & \quad \times \, \widetilde{f}(\rho) \widetilde{f}(\zeta) \widetilde{f}(\eta-\rho-\zeta-\omega) \widetilde{f}({\sigma}) \, d\eta \, d\rho \,d\zeta \, d{\sigma}, \end{aligned} \end{align*} $$

from which we deduce that, for $s\approx 2^m$ ,

(8.101) $$ \begin{align} \begin{aligned} |\partial_\omega F(s,\xi,\omega)| \lesssim 2^m \cdot 2^{-p} {\varepsilon}_1^3. \end{aligned} \end{align} $$

From this and equation (8.100), we obtain the desired bound in equation (8.96) for $A_1$ .

Estimate of $A_2$

We decompose the support of the integral according to the size of the input frequencies $\rho $ , $\zeta $ , $\eta -\rho -\zeta -\omega $ and $\omega $ by defining

(8.102) $$ \begin{align} \begin{aligned} & A_{\underline{k},q}(t,\xi) := \int F_{\underline{k}}(s,\xi,\omega) \, \frac{\varphi_{q}(\omega)}{\omega} d\omega, \end{aligned} \end{align} $$

where

(8.103) $$ \begin{align} \begin{aligned} & F_{\underline{k}}(s,\xi,\omega) := \iiiint e^{is \Gamma} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}_2 \, \varphi_{\underline{k}}(\eta,\sigma,\rho,\zeta,\omega)\, \widetilde{f}(\rho) \widetilde{f}(\zeta) \widetilde{f}(\eta-\rho-\zeta-\omega) \widetilde{f}({\sigma}) \, d\eta \, d\rho \, d\zeta \,d{\sigma}, \\ & \varphi_{\underline{k}}(\eta,\sigma,\rho,\zeta,\omega) := \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma)\varphi_{k_3}(\rho)\varphi_{k_4}(\zeta)\varphi_{k_5}(\eta-\rho-\zeta-\omega). \end{aligned} \end{align} $$

Since we can easily dispose of the cases with $\mathrm {min}(k_1,\dots ,k_5) \leq -5m$ (see, for example, the estimate in equation (8.74)) or $\mathrm {max}(k_1,\dots ,k_5) \geq m$ (using the Sobolev-type bound in equation (7.10)), we are only left with $O(m^5)$ terms like $A_{\underline {k},q}$ . We can then reduce the proof of equation (8.96) to showing the slightly stronger bound

(8.104) $$ \begin{align} 2^{\ell} \big| \chi_{\ell,\sqrt{3}}(\xi)A_{\underline{k},q}(t,\xi) \big| \lesssim {\varepsilon}_1^2 2^{-2m} 2^{-4\beta' m}, \end{align} $$

for each fixed set of frequencies with

$$\begin{align*}|\mathrm{med}(k_1,k_3,k_4) - \mathrm{max}(k_1,k_3) |\leq 5, \qquad k_5 \leq k_4 \leq k_3\leq -5, \qquad -5m \leq q \leq -D_0,\end{align*}$$

where $D_0$ is a sufficiently large absolute constant, with the main constraints in equation (8.55) holding as well. See Remark 8.8 for a justification of the second restriction above, and notice that the case $q \geq -D_0$ is much easier to deal with since the $\mathrm {p.v.}$ is not singular.

Notice that on the support of equation (8.103), we have (see equation (8.95))

(8.105) $$ \begin{align} \big|(\partial_{\eta} + \partial_\rho) \Gamma \big| = \big|\frac{\rho}{\langle \rho \rangle}\big| \approx 2^{k_3}, \qquad |(\partial_{\eta} + \partial_{\zeta}) \Gamma| = \big|\frac{\zeta}{\langle \zeta \rangle}\big| \approx 2^{k_4}. \end{align} $$

This is identical to equation (8.84) in the case of the terms $K^{S1}_{\iota _1\iota _2}$ in equation (8.70) treated before. We can then proceed in the same way as we did in Step 2.1 above and estimate equation (8.103) for each fixed $\omega $ (note that the terms in equation (8.72) are basically the same, up to the smooth $\mathfrak {q}$ and $\mathfrak {q}_2$ symbols, as the expression in equation (8.103) evaluated at $\omega =0$ ). This procedure will give a bound by the right-hand side of equation (8.75) for $F_{\underline {k}}(s,\xi ,\omega )$ , and integrating over $\omega $ in equation (8.102), one arrives at equation (8.104).

Step 3: Estimate of $L^{S1,2}$ in equation (8.68)

As already pointed out after the formulas in equation (8.66), the terms $L^{S1,2}$ are not exactly the same as the terms $K^{S1,2}$ , since $k_1$ and $k_2$ do not play the same role, and we can deduce a little less information on the smaller frequency $|{\sigma }| \approx 2^{k_2}$ from information on $|\eta | \approx 2^{k_1}$ . Nevertheless, we can apply the same arguments as in Step 2.1 and Step 2.2 above. In particular, all the proofs based on integration by parts (see Case 2 starting on page 104) apply verbatim, just by exchanging $k_1$ and $k_2$ . The only exception is the argument in Case 1 on page 104 where the constraint $k_1 \geq -2m/3$ from equation (8.55) was used. Since such a lower bound might not hold for $k_2$ , we need some modification of the argument, which we give below.

First, analogously to equation (8.70), we use the formulas in equation (5.57) and write $L^{S1}$ as a term of the form

(8.106) $$ \begin{align}\begin{aligned} L^{S1}_{\iota_1\iota_2\iota_3} &= \int_{0}^t \iiiint e^{is \Psi^{\prime}_{\iota_1\iota_2\iota_3}} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}' \, \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma) \\ & \quad\times \widetilde{f}(\eta) \widetilde{f}(\rho) \widetilde{f}(\zeta) \widetilde{f}({\sigma}-\rho-\zeta) \, d\eta \, d{\sigma} \, d\zeta \, d\rho \, \tau_m(s) ds, \\ \Psi^{\prime}_{\iota_1\iota_2\iota_3} &:= \langle \xi \rangle - \langle \eta \rangle - \iota_1\langle \rho \rangle - \iota_2\langle\zeta\rangle - \iota_2\langle{\sigma}-\rho-\zeta\rangle, \qquad \iota_1,\iota_2,\iota_3 \in \{+,-\}, \end{aligned} \end{align} $$

where, abusing notation, we still denote by $\mathfrak {q}$ the quartic symbol. Introducing frequency cutoffs for the new correlated variables, we can reduce matters to estimating

(8.107) $$ \begin{align} \begin{aligned} & (\underline{I}^{p,\underline{k}})'(s,\xi) := \iiiint e^{is \Psi^{\prime}_{\iota_1\iota_2}} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}' \, \varphi_{\underline{k}}'(\eta,\sigma,\rho,\zeta) \, \widetilde{f}(\eta) \widetilde{f}(\rho) \widetilde{f}(\zeta) \widetilde{f}({\sigma}-\rho-\zeta) \, d\eta \, d{\sigma} \, d\zeta \, d\rho, \\ & \varphi_{\underline{k}}'(\eta,\sigma,\rho,\zeta) := \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma) \varphi_{k_3}(\rho)\varphi_{k_4}(\zeta)\varphi_{k_5}(\sigma-\rho-\zeta), \end{aligned} \end{align} $$

as follows: for all $s\approx 2^m$

(8.108) $$ \begin{align} & 2^{\ell} \big|\chi_{\ell,\sqrt{3}} (\underline{I}^{p,\underline{k}})'(s,\xi) \big| \lesssim {\varepsilon}_1^3 2^{-2m} 2^{-5\beta'm}, \end{align} $$

(8.109) $$ \begin{align} & |\mathrm{max}(k_2,k_3) - \mathrm{med}(k_2,k_3,k_4)|\leq 5, \qquad k_5 \leq k_4 \leq k_3 \leq -5, \end{align} $$

under the constraints in equation (8.55). Compare with equations (8.75)–(8.76).

Applying the same exact reasoning as in pages 103–104, we can obtain the analogue of equation (8.82) for this term: that is,

(8.110) $$ \begin{align} 2^{\ell} \big| (\underline{I}^{p,\underline{k}})'(s,\xi) \big| \lesssim {\varepsilon}_1^3 \cdot 2^{3\alpha m} \cdot 2^{k_5+k_4 + \mathrm{min}(k_2,k_3)} \cdot 2^{(1/2)(k_3+k_4+k_5)} \cdot X_{k_1,m}. \end{align} $$

As in Step 2.1 above, we distinguish two main scenarios: in the first (Case 1 below), integration by parts in the new correlated variables $\partial _{{\sigma }+\zeta }$ and $\partial _{{\sigma }+\rho }$ is forbidden and we need an argument based on equation (8.110); in the second, integration by parts is possible, and we can proceed as in Case 2 of Step 2.1.

Case 1: $k_2 + k_4 \leq -m + \delta m$ . Equation (8.110) with equation (8.17) yields

$$ \begin{align*} 2^{\ell} \big| (\underline{I}^{p,\underline{k}})'(s,\xi) \big| \lesssim {\varepsilon}_1^4 2^{(-3/4+4\alpha) m} \cdot 2^{k_2+3k_4}. \end{align*} $$

Since we are assuming $k_2+k_4 \leq -m +\delta m$ , the above bound suffices to obtain equation (8.108) if $k_4 \leq -m/7$ , since in this case

$$ \begin{align*} 2^{(-3/4+4\alpha) m} \cdot 2^{k_2+3k_4} \lesssim 2^{(-3/4+5\alpha)m} \cdot 2^{2k_4} \lesssim 2^{(-57/28+5\alpha)m}. \end{align*} $$

Notice that we indeed must have $k_4 \leq -m/7$ , for otherwise we would have $k_2 \leq -6m/7 +\delta m$ , which implies

$$\begin{align*}-3m/4 + 3k_2/2 \leq -57m/28 + 3 \delta m / 2, \end{align*}$$

contradicting the constraint in equation (8.46) for $\delta ,\alpha ,\beta '$ small enough.

Case 2: $k_2 + k_4 \geq -m + \delta m$ . This case can be treated by integration by parts as in Case 2 on page 104, so we skip the details.

Finally, notice that $L^{S2}_{\iota _1\iota _2\iota _3}$ can be treated similarly to $L^{S1}_{\iota _1\iota _2\iota _3}$ , in the same way that $K^{S2}_{\iota _1\iota _2\iota _3}$ was treated similarly to $K^{S1}_{\iota _1\iota _2\iota _3}$ , after taking care of the $\mathrm {p.v.}$ as in equations (8.97)–(8.101); we omit the details.

Step 4: Estimate of $D^R$ in equation (8.69)

These terms are relatively easy to estimate under the current assumption $\ell \leq p+10$ , relying on the estimate in equation (7.54) for the remainder term $\mathcal {R}$ . From equation (8.69), we see that

(8.111) $$ \begin{align} 2^{\ell} |D^R(t,\xi)| & \lesssim 2^{\ell} \cdot 2^m \sup_{s\approx 2^m} \Big( \big| \underline{I}^{p,k_1,k_2}\big[\widetilde{{\mathcal{F}}}^{-1}\mathcal{R}, f\big](s,\xi) \big| + \big| \underline{I}^{p,k_1,k_2}\big[f, \widetilde{{\mathcal{F}}}^{-1}\mathcal{R} \big](s,\xi) \big| \Big), \end{align} $$

where $\underline {I}^{p,k_1,k_2}$ is the bilinear operator defined in equation (8.56). Let us look at the first of the two terms on the right-hand side of equation (8.111); the other one can be treated identically. Using the integration by parts argument on the profile f (whose frequency is uncorrelated to that of $\mathcal {R}$ ), we can see that

$$ \begin{align*} 2^{\ell} \big| \underline{I}^{p,k_1,k_2}\big[\mathcal{R},f\big](s,\xi) \big| & \lesssim 2^{\ell} \cdot 2^{-p} \cdot 2^{k_1/2}{\| \mathcal{R}(s) \|}_{L^2} \cdot X_{k_2,m} \\ & \lesssim {\varepsilon}_1^4 2^{-3m/2 + 2\alpha m} \cdot 2^{-3m/4 + \alpha m} \end{align*} $$

consistently with equations (8.62) and (8.66). This completes the proof of the bound in equations (8.54)–(8.55).

8.7 Case $p \geq -m/3 - 10\beta 'm$ and $p\leq \ell -10$

First notice that we must have

(8.112) $$ \begin{align} |\ell-2k_1|\leq 10, \qquad k_1 \geq p/2 + 10 \geq -m/6 - 5\beta'm + 10.\end{align} $$

The analysis in this case is similar to the one in Section 8.6, but we have decided to separate it for better clarity and to better highlight the difficulties of the case treated in Section 8.6. Since $\Phi $ has a strong lower bound, our starting point is again the integration by parts in s giving the terms in equations (8.57)–(8.60), and we aim to prove the bound in equation (8.61) (or equation (8.62)).

Estimating as in equation (8.65) suffices to deal with the boundary term J,

$$ \begin{align*} 2^{\ell} \, \big| \underline{I}^{p,k_1,k_2}(f,f)(s,\xi) \big| & \lesssim 2^{\ell} \cdot 2^{-p} \cdot X_{k_1,m} \cdot X_{k_2,m} \\ & \lesssim {\varepsilon}_1^2 2^{-p} 2^{(-3/2 + 2\alpha)m} \lesssim {\varepsilon}_1^2 2^{-m} 2^{-3\beta'm}, \end{align*} $$

since $p \geq -m/3-10\beta ' m$ , and $2\alpha <\beta '$ sufficiently small.

Next, we write out the terms K and L in equations (8.59)–(8.60) as in equations (8.66)–(8.69) and aim to show (as usual we dispense with the $\iota $ s)

(8.113) $$ \begin{align} 2^{\ell}\big(|K^{S1}| + |K^{S2}| + |L^{S1}| + |L^{S2}|) + 2^{\ell/2}{\| D^R \|}_{L^2} \lesssim {\varepsilon}_1^3 2^{-m} 2^{-3\beta'm}, \end{align} $$

which will imply the main conclusion in equation (8.35).

The terms $K^{S2}$ and $L^{S2}$ can be treated in the same way that we will treat the terms $K^{S1}$ and $L^{S1}$ below, in analogy to how the terms $K^{S2}$ and $L^{S2}$ were treated in Step 2.2 on page 106 in the previous case $\ell \leq p+10$ . Recalling the definitions of $K^{S1}$ and $D^R$ in equations (8.67) and (8.69), we may then reduce the bound in equation (8.113) to showing the following:

(8.114) $$ \begin{align} 2^{\ell} \sup_{s\approx2^m}|\underline{I}^{p,k_1,k_2}[\widetilde{{\mathcal{F}}}^{-1}\mathcal{C}^{S1},f](s,\xi) | & \lesssim {\varepsilon}_1^3 2^{-2m} 2^{-3\beta'm}, \end{align} $$

(8.115) $$ \begin{align} 2^{\ell} \sup_{s\approx2^m}|\underline{I}^{p,k_1,k_2}[f, \widetilde{{\mathcal{F}}}^{-1}\mathcal{C}^{S1}](s,\xi) | & \lesssim {\varepsilon}_1^3 2^{-2m} 2^{-3\beta'm}, \end{align} $$

and

(8.116) $$ \begin{align} 2^{\ell/2} & \sup_{s\approx2^m} {\big\|\underline{I}^{p,k_1,k_2}[\widetilde{{\mathcal{F}}}^{-1}\mathcal{R},f](s,\xi) \big\|}_{L^2} \lesssim {\varepsilon}_1^3 2^{-2m} 2^{-3\beta'm}, \end{align} $$

(8.117) $$ \begin{align} 2^{\ell} & \sup_{s\approx2^m} \big|\underline{I}^{p,k_1,k_2}[f, \widetilde{{\mathcal{F}}}^{-1}\mathcal{R}](s,\xi) \big| \lesssim {\varepsilon}_1^3 2^{-2m} 2^{-3\beta'm}. \end{align} $$

8.7.1 Proof of equation (8.114)

We proceed in a way similar to Step 2.1 on page 102. Many of the initial computations are the same, so we will not repeat them. The way that some terms are eventually estimated differs, and we will detail this.

We write out the term $\mathcal {C}^{S1}$ (with the usual notation simplifications) and further localise the expression by considering

(8.118) $$ \begin{align} \begin{aligned} & \underline{I}^{p,\underline{k}}(s,\xi) := \iiiint e^{is \Psi_{\iota_1\iota_2\iota_3}} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q} \, \varphi_{\underline{k}}(\eta,\sigma,\rho,\zeta) \, \widetilde{f}(\rho)\widetilde{f}(\zeta) \widetilde{f}(\eta-\rho-\zeta) \, \widetilde{f}({\sigma}) \, d\eta\, d\zeta\, d\rho \, d{\sigma}, \\ & \varphi_{\underline{k}}(\eta,\sigma,\rho,\zeta) := \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma)\varphi_{k_3}(\rho)\varphi_{k_4}(\zeta)\varphi_{k_5}(\eta-\rho-\zeta), \\ & \Psi_{\iota_1\iota_2\iota_3}(\xi,\rho,\zeta,\eta,{\sigma}) := \langle \xi \rangle - \iota_1\langle\rho\rangle - \iota_2\langle\zeta\rangle - \iota_3\langle\eta-\rho-\zeta\rangle - \langle \sigma \rangle, \qquad \iota_1,\iota_2,\iota_3 = \pm, \\ & |\mathrm{max}(k_1,k_3) - \mathrm{med}(k_1,k_3,k_4)|\leq 5, \qquad -3m \leq k_5 \leq k_4\leq k_3\leq -5; \end{aligned} \end{align} $$

compare with equations (8.71)–(8.72), and notice that we are using the same notation $\underline {I}^{p,\underline {k}}$ although the terms are slightly different. Our aim then is to obtain for this term a slightly stronger bound than equation (8.114), with an extra factor of $2^{-\beta 'm}$ .

The estimates in equations (8.78) and (8.81) apply here verbatim and lead to the inequality in equation (8.82), the only difference being the $2^{\ell - p}$ factor that was dropped there and must be kept here. This gives

(8.119) $$ \begin{align} \begin{aligned} 2^{\ell} \big| \underline{I}^{p,\underline{k}} \big| \lesssim {\varepsilon}_1^4 \cdot 2^{3\alpha m} \cdot 2^{\ell} \cdot 2^{-p} \cdot 2^{k_5+k_4 + \mathrm{min}(k_1,k_3)} \cdot 2^{(1/2)(k_3+k_4+k_5)} \cdot X_{k_2,m}. \end{aligned} \end{align} $$

We fix $\delta \in (0,\alpha )$ and look at three different cases.

Case 1: $k_1 + k_4 \leq -m + \delta m$ . The inequality in equation (8.119) and $\ell \leq 2k_1 +10$ imply

(8.120) $$ \begin{align} 2^{\ell} \big| \underline{I}^{p,\underline{k}} \big| \lesssim {\varepsilon}_1^4 \cdot 2^{-p} \cdot 2^{(-3/4+4\alpha) m} \cdot 2^{3(k_1+k_4)} \lesssim {\varepsilon}_1^4 2^{-p} 2^{-7m/2}, \end{align} $$

which is easily bounded by the right-hand side of equation (8.114).

Case 2: $k_4 \leq -m/2 + \delta m$ . We can integrate by parts in the formula in equation (8.118) in the direction $\partial _{\eta }+\partial _\rho $ , using $|(\partial _{\eta }+\partial _\rho )\Psi | = | \rho /\langle \rho \rangle | \approx 2^{k_3}$ . Up to faster-decaying remainders, this gives a term of the form

(8.121) $$ \begin{align} \begin{aligned} I_1 & := \iiiint e^{is \Psi} \mathfrak{i}_1(\xi,\eta,{\sigma},\rho,\zeta) \big[ \partial_\rho \widetilde{f}(\rho) \big] \widetilde{f}(\zeta) \, \widetilde{f}(\eta-\rho-\zeta) \, d\eta \, d\rho \, d\zeta\, \widetilde{f}({\sigma}) d{\sigma}, \\ \mathfrak{i}_1 & := \frac{1}{s (\partial_{\eta} + \partial_\rho) \Psi} \frac{\varphi_p\big(\Phi\big)}{\Phi} \mathfrak{q} \varphi_{\underline{k}}. \end{aligned} \end{align} $$

Estimating $|\mathfrak {i}_1| \lesssim 2^{-m-k_3-p}$ , applying the usual argument to treat the uncorrelated variable ${\sigma }$ , and using the a priori bounds in equation (8.5), we obtain

$$ \begin{align*} 2^{\ell} \big| I_1 \big| & \lesssim {\varepsilon}_1^4 \cdot 2^{\ell} \cdot 2^{-m-p-k_3} \cdot 2^{(-3/4+\alpha) m} \cdot 2^{k_3/2} 2^{\alpha m} \cdot 2^{(3/2)(k_4+k_5)} 2^{2\alpha m} \\ & \lesssim {\varepsilon}_1^4 2^{4\alpha m} \cdot 2^{-7m/4} \cdot 2^{3k_4/2} \cdot 2^{-p}; \end{align*} $$

using $k_4 \leq -m/2+\delta m$ and $p\geq -m/3-10\beta 'm$ , we can comfortably bound this by the right-hand side of equation (8.114) as desired.

Case 3: $k_4 \geq -m/2+\delta m$ and $k_1+k_4 \geq -m +\delta m$ . In this case, we can integrate by parts in both $\partial _{\eta } + \partial _\rho $ and $\partial _{\eta } + \partial _{\zeta }$ using equation (8.84). This case corresponds to Subcase 2.2 on page 104, and the integration by parts produces the terms in equations (8.87)–(8.90). As before, the main contribution is the one where the derivatives hit the profiles: that is,

(8.122) $$ \begin{align}\begin{aligned} I_2 & := \Big| \iiiint e^{is \Psi} \mathfrak{i}_2(\xi,\eta,{\sigma},\rho,\zeta) \, \big[\partial_\rho \widetilde{f}(\rho) \big] \, \big[ \partial_{\zeta} \widetilde{f}(\zeta) \big] \, \widetilde{f}(\eta-\rho-\zeta) \, d\eta \, d\rho \, d\zeta\, \widetilde{f}({\sigma}) d{\sigma} \Big| \\ \mathfrak{i}_2 & := \frac{1}{s(\partial_{\eta}+\partial_{\zeta}) \Psi} \frac{1}{s(\partial_{\eta} + \partial_\rho) \Psi} \frac{\varphi_p\big(\Phi\big)}{\Phi} \mathfrak{q} \varphi_{\underline{k}}, \qquad |\mathfrak{i}_2| \lesssim 2^{-2m-k_3-k_4 - p}; \end{aligned} \end{align} $$

see equation (8.89). The usual integration by parts argument in ${\sigma }$ , and the a priori bounds, give

$$ \begin{align*} 2^{\ell} \big| I_2 \big| & \lesssim {\varepsilon}_1^4 \cdot 2^{\ell} \cdot 2^{-2m-p-k_3-k_4} \cdot 2^{(-3/4+\alpha) m} \cdot 2^{k_3/2} 2^{\alpha m} \cdot 2^{k_4/2} 2^{\alpha m} \cdot 2^{k_5} \\ & \lesssim {\varepsilon}_1^4 2^{3\alpha m} \cdot 2^{-11m/4} \cdot 2^{-p}, \end{align*} $$

which is enough. This concludes the proof of equation (8.114).

8.7.2 Proof of equation (8.115)

The proof of this estimate is not too dissimilar from the previous one, but we need to pay some more attention to a few additional frequency configurations. Again, the issue is that the expressions $\underline {I}^{p,k_1,k_2}[\widetilde {{\mathcal {F}}}^{-1}\mathcal {C}^{S1},f](s,\xi )$ and $\underline {I}^{p,k_1,k_2}[f,\widetilde {{\mathcal {F}}}^{-1}\mathcal {C}^{S1}](s,\xi )$ are not symmetric and we have fewer restrictions on $k_2$ than on $k_1$ ; see equation (8.112). We detail below all the terms that need different treatment than before and only sketch the estimates for the others ones.

Writing out $\mathcal {C}^{S1}$ , we further localise the expression and consider

(8.123) $$ \begin{align} \begin{aligned} & (\underline{I}^{p,\underline{k}})' := \iiiint e^{is \Psi_{\iota_1\iota_2\iota_3}'} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}' \, \varphi_{\underline{k}}'(\eta,\sigma,\rho,\zeta) \, \widetilde{f}(\rho)\widetilde{f}(\zeta) \widetilde{f}(\sigma-\rho-\zeta) \, \widetilde{f}(\eta) \, d{\sigma} \, d\zeta \, d\rho \, d\eta, \\ & \varphi_{\underline{k}}'(\eta,\sigma,\rho,\zeta) := \varphi_{k_1}(\eta)\varphi_{k_2}(\sigma)\varphi_{k_3}(\rho)\varphi_{k_4}(\zeta)\varphi_{k_5}({\sigma}-\rho-\zeta), \\ & \Psi_{\iota_1\iota_2\iota_3}'(\xi,\rho,\zeta,\eta,{\sigma}) := \langle \xi \rangle - \iota_1\langle\rho\rangle - \iota_2\langle\zeta\rangle - \iota_3\langle{\sigma}-\rho-\zeta\rangle - \langle \eta \rangle, \qquad \iota_1,\iota_2,\iota_3 = \pm, \\ & |\mathrm{max}(k_2,k_3) - \mathrm{med}(k_2,k_3,k_4)|\leq 5, \qquad -3m \leq k_5 \leq k_4 \leq k_3 \leq -5; \end{aligned} \end{align} $$

compare with equations (8.107) and (8.109). For equation (8.115), it suffices to show

$$\begin{align*}2^{\ell} \sup_{s\approx 2^m} |(\underline{I}^{p,\underline{k}})'| \lesssim 2^{-2m} 2^{-4\beta'm}. \end{align*}$$

Recall the inequality in equation (8.110) proved earlier; it applies here with an additional $2^{\ell - p}$ factor that was discarded there

(8.124) $$ \begin{align} \begin{aligned} 2^{\ell} \big| (\underline{I}^{p,\underline{k}})' \big| \lesssim {\varepsilon}_1^3 \cdot 2^{3\alpha m} \cdot 2^{\ell} \cdot X_{k_1,m} \cdot 2^{-p} \cdot 2^{k_5+k_4 + \mathrm{min}(k_2,k_3)} \cdot 2^{(1/2)(k_3+k_4+k_5)}. \end{aligned} \end{align} $$

Note that, using $\ell \leq 2k_1 + 10$ , we have $2^{\ell } \cdot X_{k_1,m} \leq 2^{-m+\alpha m}$ . Then the inequality in equation (8.124), and $k_5\leq k_4$ , give

(8.125) $$ \begin{align} 2^{\ell} \big| (\underline{I}^{p,\underline{k}})' \big| & \lesssim {\varepsilon}_1^4 \cdot 2^{4\alpha m} \cdot 2^{-m} \cdot 2^{-p} \cdot 2^{\mathrm{min}(k_2,k_3) + 3k_4}. \end{align} $$

As in the proof of equation (8.114), we fix $\delta \in (0,\alpha )$ and look at three cases.

Case 1: $k_2 + k_4 \leq -m + \delta m$ . In this case, equation (8.125) gives

(8.126) $$ \begin{align} \begin{aligned} 2^{\ell} \big| (\underline{I}^{p,\underline{k}})' \big| & \lesssim {\varepsilon}_1^4 \cdot 2^{4\alpha m} \cdot 2^{-m} \cdot 2^{-p} \cdot 2^{k_2 + 3k_4} \\ & \lesssim {\varepsilon}_1^4 \cdot 2^{5\alpha m} \cdot 2^{-2m} \cdot 2^{-p} \cdot 2^{2k_4}. \end{aligned} \end{align} $$

Since $p \geq -m/3 - 10\beta 'm$ , we see that equation (8.126) would suffice if, for example, $2k_4 \leq -4m/9 + 2\delta m$ . To see that this condition is satisfied, assume by contradiction that instead, $k_4 \geq -2m/9 + \delta m$ . Then we must have $k_2 \leq -7m/9$ , which implies $(1/2+\beta )\ell -m-k_1/2 + 3k_2/2 \leq -2m - m/6$ , violating the constraint on the parameters in equation (8.46).

Case 2: $k_4 \leq -m/2 +\delta m$ . Again using equation (8.125), we see that $2^{\ell } \big | (\underline {I}^{p,\underline {k}})' \big | \lesssim {\varepsilon }_1^4 \cdot 2^{7\alpha m} \cdot 2^{-5m/2} \cdot 2^{-p}$ , which suffices.

Case 3: $k_2 +k_4 \geq -m+\delta m$ and $k_4 \geq -m/2 +\delta m$ . In this case, which is analogous to Subcase 2 on page 104 and Case 3 on page 111 above, we have $k_2 +k_4 \geq -m+\delta m$ (and thus $k_2+k_3 \geq -m+\delta m$ as well) and have the possibility of integrating by parts in $\partial _{\sigma }+\partial _{\zeta }$ and $\partial _{\sigma } + \partial _\rho $ . Once again, the main term is the one where derivatives hit the profiles, all the other contributions being of lower order. We then want to estimate

(8.127) $$ \begin{align} \begin{aligned} H & := \Big| \iiiint e^{is \Psi'} \mathfrak{h}(\xi,\eta,{\sigma},\rho,\zeta) \, \big[\partial_\rho \widetilde{f}(\rho) \big] \, \big[ \partial_{\zeta} \widetilde{f}(\zeta) \big] \, \widetilde{f}({\sigma}-\rho-\zeta) \, d{\sigma} \, d\rho \, d\zeta\, \widetilde{f}(\eta) d\eta \Big|, \\ \mathfrak{h} & := \frac{1}{s(\partial_{\eta}+\partial_{\zeta}) \Psi} \frac{1}{s(\partial_{\eta} + \partial_\rho) \Psi} \frac{\varphi_p\big(\Phi\big)}{\Phi} \mathfrak{q}' \varphi_{\underline{k}}', \qquad |\mathfrak{h}| \lesssim 2^{-2m-k_3-k_4-p}; \end{aligned} \end{align} $$

see the analogous term in equation (8.122). Applying the usual treatment to the uncorrelated variable $\eta $ together with $2^{\ell } X_{k_1,m} \leq 2^{-m+\alpha m}$ , and using the a priori bounds in equation (8.5), we obtain

$$ \begin{align*} 2^{\ell} \big| H \big| & \lesssim {\varepsilon}_1^3 \cdot 2^{-2m-p-k_3-k_4} \cdot 2^{\ell} X_{k_1,m} \cdot 2^{k_3/2} 2^{\alpha m} \cdot 2^{k_4/2} 2^{\alpha m} \cdot 2^{k_5} \\ & \lesssim {\varepsilon}_1^4 2^{3\alpha m} \cdot 2^{-3m} \cdot 2^{-p}, \end{align*} $$

which is more than enough. This concludes the proof of equation (8.115).

8.7.3 Proof of equations (8.116) and (8.117)

To estimate these terms, we rely on the fast decay of $\mathcal {R}$ from equation (7.54). Arguing as in the proof of Lemma 8.5 (without integrating by parts in $\eta $ in equation (8.41)), we can see that the following variant of equation (8.40) holds:

(8.128) $$ \begin{align} {\|\underline{I}^{p,k_1,k_2}[\widetilde{{\mathcal{F}}}^{-1}\mathcal{R},f](s,\xi)\|}_{L^2} & \lesssim 2^{-k_1/2} \cdot {\|\mathcal{R}(s)\|}_{L^2} \cdot X_{k_2,m}. \end{align} $$

Using equation (7.54), $2^{\ell /2} \lesssim 2^{k_1}$ and equation (8.128), we see that for $s\approx 2^m$

$$ \begin{align*} 2^{\ell/2} {\|\underline{I}^{p,k_1,k_2}[\widetilde{{\mathcal{F}}}^{-1}\mathcal{R},f](s,\xi)\|}_{L^2} & \lesssim 2^{\ell/2} \cdot 2^{-k_1/2} \cdot {\|\mathcal{R}(s)\|}_{L^2} \cdot X_{k_2,m} \\ & \lesssim {\varepsilon}_1^3 2^{-3m/2 + 2\alpha m} \cdot 2^{-3m/4 + \alpha m}, \end{align*} $$

which implies equation (8.116).

For equation (8.117), we use another simple variant of equation (8.38) in Lemma 8.5 to estimate

$$ \begin{align*} 2^{\ell} \big|\underline{I}^{p,k_1,k_2}[f,\widetilde{{\mathcal{F}}}^{-1}\mathcal{R}](s,\xi) \big| & \lesssim 2^{\ell} \cdot 2^{-p} \cdot X_{k_1,m} \cdot {\| \varphi_{k_2} \,\mathcal{R}(s)\|}_{L^1} \\ & \lesssim {\varepsilon}_1^3 \cdot 2^{-p} \cdot 2^{-m} \cdot 2^{k_2/2} 2^{-3m/2 + 2\alpha m}. \end{align*} $$

This is enough since $p \geq -m/3 - 10\beta 'm$ .

We have concluded the proof of equation (8.113) and obtained the bound in equation (8.35) in Lemma 8.4. This gives the proof of the main bound in equation (8.1) for the main interactions with equation (8.2).

9 Weighted estimates part II: the main ‘singular’ interaction

9.1 Setup

The aim of this section is to prove the weighted bound on the norm in equation (2.30) of the singular cubic terms $\mathcal {C}^{S1}_{+-+}(f,f,f)$ and $\mathcal {C}^{S2}_{+-+}(f,f,f)$ defined in equations (5.57)–(5.58), with a restriction to interacting frequencies close to $\sqrt {3}$ . Interactions of other frequencies and other singular cubic contributions (namely $\mathcal {C}^{S1,2}_{\iota _1 \iota _2 \iota _3}$ , with $\{\iota _1,\iota _2,\iota _3\} \neq \{+,+,-\}$ ) will be dealt with in Section 11, together with the higher-order terms coming from $\mathcal {C}^{S1,2}_{+-+}(g,g,g) - \mathcal {C}^{S1,2}_{+-+}(f,f,f)$ (see equation (7.59)). In particular, this section contains the first and main step in the proof of the following:

Proposition 9.1. Let $W_T$ be the space defined by the norm in equation (2.30), and consider u, solution of equation (KG) such that the a priori assumptions in equation (7.10) hold for the renormalised profile f. Then

$$ \begin{align*}\left\| \int_0^t \mathcal{C}^{S1}_{+-+}(f,f,f) \,ds \right\|_{W_T} + \left\| \int_0^t \mathcal{C}^{S2}_{+-+}(f,f,f) \,ds\right\|_{W_T} \lesssim {\varepsilon}_1^3. \end{align*} $$

The proof of Proposition 9.1 will be completed in Section 11.4.

The terms $\mathcal {C}^{S1}_{+-+}$ and $\mathcal {C}^{S2}_{+-+}$ are as the sum over $\lambda , \mu , \nu , \lambda ',\mu ',\nu ',\iota _2$ of more elementary terms; see equation (5.46). In the present section, we will simply focus on one of them since all the corresponding estimates are identical, up to flipping the sign of various frequencies. Furthermore, we discard the complex conjugation signs over $\widetilde {f}$ since they do not play any role in the estimates. More precisely, we consider

(9.1) $$ \begin{align} \begin{aligned} \mathcal{C}^{S1}_{+-+}(f,f,f) = &\iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{p}(\xi,\eta,\zeta) \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \\ \mbox{where} \qquad & \Psi(\xi,\eta,\zeta) = \Phi_{+-+}(\xi,\xi-\eta,\xi-\eta-\zeta,\xi-\zeta) \\&\qquad \qquad = \langle \xi \rangle - \langle \xi - \eta \rangle + \langle \xi - \eta -\zeta \rangle - \langle \xi - \zeta\rangle \end{aligned} \end{align} $$

and

$$ \begin{align*} \mathcal{C}^{S2}_{+-+}(f,f,f) = & \iiint e^{is \Psi(\xi,\eta,\zeta,\theta)} \mathfrak{p}(\xi,\eta,\zeta,\theta) \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \,d\theta \\ \qquad \mbox{where} \quad & \Psi(\xi,\eta,\zeta,\theta) = \Phi_{+ - +}(\xi,\xi-\eta,\xi-\eta-\zeta-\theta,\xi-\zeta) \\ & \qquad \qquad = \langle \xi \rangle - \langle \xi - \eta \rangle + \langle \xi - \eta -\zeta -\theta \rangle - \langle \xi - \zeta\rangle. \end{align*} $$

We omit the $\mathrm {p.v.}$ sign for lighter notation and slightly abuse notation in denoting the symbols $\mathfrak {p}$ and the phases $\Psi $ with the same letter in the two different expressions above; the presence of the extra variable $\theta $ should resolve any confusion.

Let us say a word about the parametrisation of the frequencies chosen above. If we were dealing with the nonlinear Schrödinger equation, the phase resulting from the above parametrisation would be (say, for $\mathcal {C}^{S1}_{+-+}$ )

$$ \begin{align*}\xi^2 - (\xi-\eta)^2 + (\xi - \eta -\zeta)^2 - (\xi - \zeta)^2 = 2 \eta \zeta, \end{align*} $$

which does not depend on $\xi $ and is thus very favorable to deriving estimates. Of course, we are not dealing with the nonlinear Schrödinger equation, but close to interactions of the type $(\xi ,\xi ,\xi ) \to \xi $ , the above identity holds to leading order; this should be kept in mind in the estimates that follow.

Finally, we will assume in this section that the symbols $\mathfrak {p}$ satisfy

(9.2) $$ \begin{align} \begin{aligned} & \mathfrak{p}(\xi,\eta,\zeta) = \mathfrak{p}(\xi,\eta,\zeta) \varphi_{\leq -10}(|\xi-\sqrt{3}|+|\eta|+|\zeta|), \\ & \mathfrak{p}(\xi,\eta,\zeta,\theta) = \mathfrak{p}(\xi,\eta,\zeta,\theta) \varphi_{\leq -10}(|\xi-\sqrt{3}|+|\eta|+|\zeta|+|\theta|). \end{aligned} \end{align} $$

That is, the frequencies are localised to $|\xi -\sqrt {3}| \ll 1$ and $|\eta |, |\zeta |, |\theta | \ll 1$ , and they are in $\mathcal {C}_0^{\infty }$ with $O(1)$ bounds on their derivatives. This latter assumption is justified (in the current frequency configuration) in view of the explicit formula in equation (5.46) and the smoothness of the coefficients involved in it, and the estimate of Lemma 5.3.

9.2 The bound for $\mathcal {C}^{S1}_{+-+}$

First note that for $\tau (\xi ) = \langle \xi \rangle $ , one has $\tau '(\xi ) = \frac {\xi }{ \langle \xi \rangle }$ , $\tau ''(\xi ) = \frac {1}{\langle \xi \rangle ^3}$ and $\tau '''(\xi ) = - \frac {3\xi }{\langle \xi \rangle ^5}$ . Therefore, in the regime which interests us here ( $|\xi - \sqrt {3}| \ll 1$ and $|\eta |, |\zeta | \ll 1$ ), we have the expansions

(9.3) $$ \begin{align} \begin{aligned} & \Psi(\xi,\eta,\zeta) = \frac{1}{\langle \xi \rangle^3} 2 \eta \zeta + O(|\eta,\zeta|^3), \\ & \partial_{\xi} \Psi(\xi,\eta,\zeta) = - \frac{3\xi}{\langle \xi \rangle^5} \eta \zeta + O(|\eta,\zeta|^3), \\ & \partial_{\eta} \Psi(\xi,\eta,\zeta) = \frac{1}{\langle \xi -\eta \rangle^3} \zeta + O(|\zeta|^2), \\ & (\partial_{\eta} - \partial_{\zeta}) \Psi(\xi,\eta,\zeta) = \frac{1}{\langle \xi -\eta \rangle^3} (\zeta - \eta) + O( |\eta-\zeta|^2), \\ & \partial_{\eta}^2 \Psi(\xi,\eta,\zeta) =\frac{3(\xi-\eta)}{\langle \xi - \eta \rangle^5} \zeta + O(|\zeta|^2), \\ & \partial_{\eta} \partial_{\zeta} \Psi(\xi,\eta,\zeta) = \frac{1}{\langle \xi - \eta - \zeta \rangle^3}. \end{aligned} \end{align} $$

Applying $\partial _{\xi }$ to equation (9.1) gives

$$ \begin{align*}\mathcal{J}^1 + \mathcal{J}^2 + \mathcal{J}^3 + \{ \mbox{symmetrical or easier terms} \}, \end{align*} $$

where

$$ \begin{align*} &\mathcal{J}^1 = \iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{p}(\xi,\eta,\zeta) i s \partial_{\xi} \Psi(\xi,\eta,\zeta) \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta, \\ &\mathcal{J}^2 = \iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{p}(\xi,\eta,\zeta) \partial_{\xi} \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta, \\ &\mathcal{J}^3 = \iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{p}(\xi,\eta,\zeta) \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta. \end{align*} $$

First observe that $\mathcal {J}^1$ can be reduced to the other cases. Indeed, $\partial _{\xi } \Psi /\partial _{\eta } \Psi $ is a smooth function, and therefore, it is possible to integrate by parts in $\eta $ in $\mathcal {J}^1$ via the identity $\frac {1}{i s \partial _{\eta } \Psi } \partial _{\eta } e^{is \Psi } = e^{is \Psi }$ , obtaining terms similar to $\mathcal {J}^2$ and $\mathcal {J}^3$ . Therefore, it will be sufficient to treat $\mathcal {J}^2$ and $\mathcal {J}^3$ .

In what follows, we will localise the variables $\xi $ , $\xi -\eta $ , $\xi -\eta -\zeta $ , $\xi - \zeta $ and s, on the dyadic scales

(9.4) $$ \begin{align} \begin{aligned} & s \approx 2^m, \quad |\xi - \sqrt{3}| \approx 2^{\ell}, \\ & |\xi-\eta - \sqrt{3}| \approx 2^{j_1}, \quad |\xi-\eta-\zeta - \sqrt{3}| \approx 2^{j_2}, \quad |\xi-\zeta-\sqrt{3}| \approx 2^{j_3}. \end{aligned} \end{align} $$

Consistently with equation (2.30), our aim will be to show that under the a priori assumptions in equation (7.10), we have

(9.5) $$ \begin{align} \sup_{\ell \in \mathbb{Z} \cap [\lfloor -\gamma n \rfloor,0]} \left\|\tau_n(t) \varphi_{\ell}^{[-\gamma n,0]}(\xi-\sqrt{3}) \int_0^t \mathcal{J}^{2,3}(s,\xi) \, ds \right\|_{L^{\infty}_t([0,T]) L^2_{\xi}({\mathbb R})} \lesssim 2^{\alpha n} 2^{-\beta \ell} {\varepsilon}_1^3. \end{align} $$

9.2.1 Bound for $\mathcal {J}^2$

We add a localisation in time in the integrand and consider

$$ \begin{align*}\mathcal{J}_m^2 = \iint e^{is \Psi(\xi,\eta,\zeta)} \tau_m(s) \mathfrak{p}(\xi,\eta,\zeta) \partial_{\xi} \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta. \end{align*} $$

Case 1: $|\ell + \gamma n| \leq 5$ . By taking the inverse Fourier transform of this expression, using Plancherel’s equality, the a priori bounds in equations (7.19) and (7.25) and Lemma 6.5,

$$ \begin{align*} & \left\| \int_0^t \mathcal{J}_{m}^2(s,\xi) \, ds \right\|_{L^2} \lesssim \int_0^t \tau_m(s) \| \partial_{\xi} \widetilde{f} \|_{L^2} \| e^{is\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}}^2 \,ds \lesssim 2^{(\alpha + \beta \gamma)m} {\varepsilon}_1^3. \end{align*} $$

Therefore,

$$ \begin{align*}\sum_{m \leq n} \left\| \int_0^t \mathcal{J}_{m}^2(s,\xi) \, ds \right\|_{L^2} \lesssim 2^{(\alpha + \beta \gamma)n}{\varepsilon}_1^3. \end{align*} $$

Case 2: $-\gamma n \leq \ell \leq -\gamma m$ . Similarly to the previous case,

$$ \begin{align*} & \left\| \int_0^t \mathcal{J}_{m}^2(s,\xi) \, ds \right\|_{L^2} \lesssim \int_0^t \tau_m(s) \| \partial_{\xi} \widetilde{f} \|_{L^2} \| e^{is\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}}^2 \,ds \lesssim 2^{(\alpha + \beta \gamma)m} {\varepsilon}_1^3. \end{align*} $$

This suffices since if $-\gamma n \leq \ell \leq -\gamma m$ ,

$$ \begin{align*} \sum_{\substack{m<-\ell/\gamma \\ m\leq n}} \left\| \int_0^t \mathcal{J}_{m}^2(s,\xi) \, ds \right\|_{L^2} \lesssim \sum_{\substack{m \leq - {\ell}/{\gamma} \\ m \leq n}} 2^{(\alpha + \beta \gamma) m} {\varepsilon}_1^3 \lesssim 2^{\alpha n - \beta \ell} {\varepsilon}_1^3. \end{align*} $$

Case 3: $j_1> \ell - 100$ . We now localise in $\xi -\eta $ , by defining

$$ \begin{align*}\mathcal{J}_{m,\ell}^{2,(3)} = \iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{m}(\xi,\eta,\zeta) \partial_{\xi} \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta, \end{align*} $$

where

$$ \begin{align*}\mathfrak{m}(\xi,\eta,\zeta) = \mathfrak{m}_{m,\ell}^{\mathcal{J}^{2,(3)}} (\xi,\eta,\zeta) = \mathfrak{p}(\xi,\eta,\zeta) \varphi_{\ell}(\xi-\sqrt{3}) \varphi_{>\ell - 100}(\xi-\eta - \sqrt{3}) \tau_m(s). \end{align*} $$

Estimating as above, we have

$$ \begin{align*}\left\| \int_0^t \mathcal{J}_{m,\ell}^{2,(3)}(s,\xi) \,ds \right\|_{L^2} \lesssim \int_0^t \tau_m(s) \|\varphi_{> \ell - 100}(\cdot - \sqrt 3) \partial_{\xi} \widetilde{f}(\xi) \|_{L^2} \| e^{is\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}}^2\, ds \lesssim 2^{\alpha m} 2^{-\beta \ell} {\varepsilon}_1^3. \end{align*} $$

Therefore,

$$ \begin{align*}\sum_{m\leq n}\left\| \int_0^t \mathcal{J}_{m,\ell}^{2,(3)}(s,\xi) \,ds \right\|_{L^2} \lesssim 2^{\alpha n - \beta \ell} {\varepsilon}_1^3. \end{align*} $$

Case 4: $\ell> -\gamma m$ and $j_1 \leq \ell - 100$ . Let us now consider

$$ \begin{align*} & \mathcal{J}_{m,\ell}^{2,(4)} = \iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{m}(\xi,\eta,\zeta) \partial_{\xi} \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta, \end{align*} $$

where

$$ \begin{align*} & \mathfrak{m}(\xi,\eta,\zeta) = \mathfrak{m}_{m,\ell}^{\mathcal{J}^{2,(4)}} (\xi,\eta,\zeta) = \mathfrak{p}(\xi,\eta,\zeta)\varphi_{\ell}(\xi-\sqrt{3}) \varphi_{<\ell-100}(\xi-\eta - \sqrt{3}) \tau_m(s). \end{align*} $$

Observe that, on the support of the integrand, $|\eta | \sim 2^{\ell }$ , which implies (see equation (9.3))

$$ \begin{align*}\left| \frac{1}{\partial_{\zeta} \Psi} \right| \sim 2^{-\ell}, \qquad \left| \frac{\partial_{\zeta}^2 \Psi}{(\partial_{\zeta} \Psi)^2} \right| \sim 2^{-\ell}. \end{align*} $$

Integrating by parts in $\zeta $ , we obtain (we are omitting irrelevant numerical constants)

$$ \begin{align*} \mathcal{J}^{2,(4)}_{m,\ell}(s,\xi) & = \iint e^{is \Psi} \partial_{\zeta} \left[ \frac{\mathfrak{m}}{s \partial_{\zeta} \Psi} \right] \partial_{\xi} \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \\ & \quad + \iint e^{is \Psi} \frac{\mathfrak{m}}{s \partial_{\zeta} \Psi} \partial_{\xi} \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta + \{ \mbox{symmetrical term} \} \\ & = \mathcal{J}^{2,(4)\flat}_{m,\ell} + \mathcal{J}^{2,(4)\sharp}_{m,\ell} + \{ \mbox{symmetrical term} \}. \end{align*} $$

We notice first that the term $\mathcal {J}^{2,(4)\flat }_{m,\ell }$ is much simpler to estimate than $\mathcal {J}^{2,(4)\sharp }_{m,\ell }$ . Indeed, both symbols enjoy the same estimates, but two functions $\widetilde {f}$ are differentiated in the latter and only one in the former. Therefore, we only concentrate on $\mathcal {J}^{2,(4)\sharp }_{m,\ell }$ , for which we would like to apply Lemma 6.5, using that

(9.6) $$ \begin{align} \left\| \mathcal{F}\left( \frac{\mathfrak{m}}{ \partial_{\zeta} \Psi} \right) \right\|_{L^1} \lesssim 2^{-\ell}. \end{align} $$

To see why this is true, notice that, on the support of $\mathfrak {m}$ , the variables $\xi $ and $\eta $ enjoy the localisation $|\xi -\sqrt {3}| + |\eta | \lesssim 2^{\ell }$ , while for any $a,b,c$ ,

$$ \begin{align*} \left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \frac{1}{\partial_{\zeta} \Psi} \right| \lesssim 2^{-(b+1)\ell} \quad \mbox{and} \quad \left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \mathfrak{m} \right| \lesssim 2^{-(a+b)\ell}. \end{align*} $$

By Remark 6.6 following Lemma 6.5, we obtain equation (9.6).

Thus, we can apply Lemma 6.5, using the bounds in equations (7.19), (7.20) and (7.25), to obtain

(9.7) $$ \begin{align} \begin{aligned} \left\| \int_0^t\mathcal{J}^{2,(4)\flat}_{m,\ell} \,ds \right\|_{L^2} & \lesssim \int_0^t \left\| \mathcal{F}\left( \frac{\mathfrak{m}}{ \partial_{\zeta} \Psi} \right) \right\|_{L^1} \| \varphi_{<\ell}(\cdot - \sqrt 3) \partial_{\xi} \widetilde{f} \|_{L^1} \| \partial_{\xi} \widetilde{f} \|_{L^2} \| e^{is\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}} \frac{ds}{s} \\ & \lesssim 2^{-\ell} \| \varphi_{<\ell}(\cdot - \sqrt 3) \partial_{\xi} \widetilde{f} \|_{L^1} \| \partial_{\xi} \widetilde{f} \|_{L^2} \| e^{is\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}} \\ & \lesssim 2^{-\ell} \cdot 2^{\beta' \ell + \alpha m}{\varepsilon}_1 \cdot 2^{(\alpha + \beta \gamma)m} {\varepsilon}_1 \cdot 2^{-m/2} {\varepsilon}_1 \\ & \lesssim 2^{-\beta \ell + \alpha m} {\varepsilon}_1^3, \end{aligned} \end{align} $$

where we used that $\ell> -\gamma m$ and $\alpha + \beta \gamma < \frac {1}{4}$ . We abused notations slightly by simply denoting $L^{\infty }$ instead of $L^{\infty }_{s \approx 2^m} L^{\infty }_x$ ; we will use this shorthand repeatedly in the following.

9.2.2 Bound for $\mathcal {J}^3$

Cases 1,2,3: $\ell < -\gamma m$ or $j_2> \ell - 100$ . These cases are identical to cases 1, 2 and 3 of the estimate for $\mathcal {J}^2$ , except that the roles of $j_1$ and $j_2$ are exchanged.

Case 4: $\ell> -\gamma m$ and $j_2 < \ell - 100$ . Without loss of generality, we can assume that $j_1 \geq j_3$ . In the following, we will add an index $j_4$ to track the localisation of $\eta - \zeta $ :

$$ \begin{align*}|\eta - \zeta|\approx 2^{j_4}.\end{align*} $$

Due to the definitions of $\ell , j_1, j_2, j_3$ (see equation (9.4)), it suffices to consider three regions (up to the symmetry between $j_1$ and $j_3$ ):

• • Case 4.1: $2^{\ell } \approx 2^{j_1} \gtrsim 2^{j_3}$ and ${j_4}> {\ell - 100}$ ;

• • Case 4.2: $2^{\ell } \approx 2^{j_1} \approx 2^{j_3}$ and ${j_4} < {\ell - 100}$ ;

• • Case 4.3: $2^{j_1} \approx 2^{j_3} \approx 2^{j_4}\gg 2^{\ell }$ .

Case 4.1: $\ell> -\gamma m$ , $j_2 < \ell - 100$ , $2^{\ell } \approx 2^{j_1} \gtrsim 2^{j_3}$ and $j_4> \ell - 100$ . In other words, we are considering here

$$ \begin{align*}\mathcal{J}_{m,\ell}^{3,(1)} = \iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{m}(\xi,\eta,\zeta)\widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta, \end{align*} $$

where

$$ \begin{align*} \mathfrak{m}(\xi,\eta,\zeta) & = \mathfrak{m}_{m,\ell}^{\mathcal{J}^{3,(1)}}(\xi,\eta,\zeta) \\ & = \mathfrak{p}(\xi,\eta,\zeta) \varphi_{\ell}(\xi-\sqrt{3}) \varphi_{\sim \ell}(\xi-\eta - \sqrt{3}) \varphi_{<\ell-100}(\xi-\eta -\zeta- \sqrt{3}) \\ & \qquad \qquad \qquad \varphi_{\leq\ell}(\xi-\zeta-\sqrt{3}) \varphi_{>\ell - 100}(\eta-\zeta) \tau_m(s). \end{align*} $$

On the support of the symbol,

$$ \begin{align*}| (\partial_{\eta} - \partial_{\zeta}) \Psi | \sim |\eta - \zeta| \approx 2^{\ell}, \qquad | (\partial_{\eta} - \partial_{\zeta})^2 \Psi | \approx 1. \end{align*} $$

Integrating by parts using the identity $\frac {1}{is(\partial _{\eta } - \partial _{\zeta }) \Psi } (\partial _{\eta } - \partial _{\zeta }) e^{is\Psi } = e^{is\Psi }$ gives

$$ \begin{align*} \mathcal{J}^{3,(1)}_{m, \ell} & = \iint e^{is \Psi(\xi,\eta,\zeta)} (\partial_{\eta} - \partial_{\zeta}) \left[ \frac{\mathfrak{m}(\xi,\eta,\zeta)}{is(\partial_{\eta} - \partial_{\zeta}) \Psi)} \right] \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \\ & \quad + \iint e^{is \Psi(\xi,\eta,\zeta)}\frac{1}{is(\partial_{\eta} - \partial_{\zeta}) \Psi} \mathfrak{m}(\xi,\eta,\zeta) \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta) \partial_{\xi} \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \\ & \quad + \{ \mbox{symmetrical terms} \} \\ & = \mathcal{J}^{3,(1)\flat}_{m, \ell}+ \mathcal{J}^{3,(1)\sharp}_{m, \ell} + \{ \mbox{symmetrical terms} \}. \end{align*} $$

In order to estimate $\mathcal {J}^{3,(1)\flat }_{m, \ell }$ , we claim that

$$ \begin{align*}\left\| \mathcal{F} \left( (\partial_{\eta} - \partial_{\zeta}) \left[ \frac{\mathfrak{m}(\xi,\eta,\zeta)}{i(\partial_{\eta} - \partial_{\zeta}) \Psi)} \right] \right) \right\|_{L^1} \lesssim 2^{- 2 \ell}. \end{align*} $$

This follows from the remark after Lemma 6.5 since on the support of $\mathfrak {m}$ , the variables $\xi $ , $\eta $ and $\zeta $ are such that $|\xi |, |\eta |, |\zeta | \lesssim 2^{\ell }$ , and for any $a,b,c$ ,

$$ \begin{align*}\left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \frac{1}{(\partial_{\eta} - \partial_{\zeta}) \Psi} \right| \lesssim 2^{- \ell (1 + b + c)} \qquad \mbox{while} \qquad \left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \mathfrak{m} \right| \lesssim 2^{- \ell (a + b + c)}. \end{align*} $$

Thus we can apply Lemma 6.5 together with equations (7.18) and (7.20) to obtain

$$ \begin{align*} \left\| \int_0^t \mathcal{J}_{m,\ell}^{3,(1)\flat} \,ds \right\|_{L^2} & \lesssim 2^{-2 \ell} \| \varphi_{<\ell}(\cdot - \sqrt 3) \widetilde{f} \|_{L^1} \| \varphi_{<\ell}(\cdot - \sqrt 3) \partial_{\xi} \widetilde{f} \|_{L^1} \| \varphi_{<\ell}(\cdot - \sqrt 3) \widetilde{f} \|_{L^2} \\ & \lesssim 2^{-2\ell} \cdot 2^{\ell}{\varepsilon}_1 \cdot 2^{\beta' \ell + \alpha m}{\varepsilon}_1 \cdot 2^{\ell/2} {\varepsilon}_1 = 2^{-\beta \ell + \alpha m} {\varepsilon}_1^3. \end{align*} $$

Turning to $\mathcal {J}^{3,(1)\sharp }_{m, \ell }$ , by the arguments given above,

$$ \begin{align*}\left\| \mathcal{F} \left( \frac{\mathfrak{m}(\xi,\eta,\zeta) }{(\partial_{\eta} - \partial_{\zeta}) \Psi} \right) \right\|_{L^1} \lesssim 2^{-\ell}. \end{align*} $$

Thus we can apply Lemma 6.5 to obtain

$$ \begin{align*}\left\| \int_0^t \mathcal{J}_{m,\ell}^{3,(1)\sharp} \,ds \right\|_{L^2} \lesssim 2^{-\ell} \| e^{is\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}} \| \varphi_{<\ell}(\cdot - \sqrt 3) \partial_{\xi} \widetilde{f} \|_{L^1} \| \partial_{\xi} \widetilde{f}\|_{L^2}. \end{align*} $$

From here, the estimate proceeds just as for equation (9.7) above.

Case 4.2: $\ell> -\gamma m$ , $j_2 < \ell - 100$ , $2^{\ell } \approx 2^{j_1} \approx 2^{j_3}$ and $j_4 < \ell - 100$ . In other words, we are considering here

$$ \begin{align*}\mathcal{J}_{m,\ell}^{3,(2)} = \iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{m}(\xi,\eta,\zeta)\widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta, \end{align*} $$

where

$$ \begin{align*} \mathfrak{m}(\xi,\eta,\zeta) &= \mathfrak{m}_{m,\ell}^{\mathcal{J}^{3,(2)}}(\xi,\eta,\zeta) \\ & = \mathfrak{p}(\xi,\eta,\zeta) \varphi_{\ell}(\xi-\sqrt{3}) \varphi_{\sim \ell}(\xi-\eta - \sqrt{3}) \\ & \qquad \varphi_{<\ell-100}(\xi-\eta -\zeta- \sqrt{3})\varphi_{\sim \ell}(\xi-\zeta- \sqrt{3}) \varphi_{<\ell - 100}(\eta-\zeta) \tau_m(s). \end{align*} $$

Notice that, on the support of $\mathfrak {m}$ ,

$$ \begin{align*}|\xi - \eta - \sqrt 3| \approx |\xi - \zeta - \sqrt 3| \approx |\eta| \approx |\zeta| \sim 2^{\ell}, \end{align*} $$

so that

$$ \begin{align*}| \Psi| \approx |\partial_{\xi} \Psi| \approx 2^{2 \ell} \qquad \mbox{and} \qquad |\partial_{\eta} \Psi| \approx |\partial_{\zeta} \Psi| \approx 2^{\ell}. \end{align*} $$

In the expression above giving $\mathcal {J}_{m,\ell }^{3,(2)}$ , we write $\partial _{\xi } \widetilde {f}(\xi -\eta -\zeta ) = -\partial _{\eta } \widetilde {f}(\xi -\eta -\zeta )$ and integrate by parts in $\eta $ . This results in

$$ \begin{align*} \mathcal{J}_{m,\ell}^{3,(2)} & = \iint e^{is \Psi(\xi,\eta,\zeta)} \partial_{\eta} \mathfrak{m}(\xi,\eta,\zeta) \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \\ & \quad - \iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{m}(\xi,\eta,\zeta) \partial_{\xi} \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \\ & \quad + \iint e^{is \Psi(\xi,\eta,\zeta)} is\partial_{\eta} \Psi \mathfrak{m}(\xi,\eta,\zeta) \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \\ & = \mathcal{J}_{m,\ell}^{3,(2)\flat} + \mathcal{J}_{m,\ell}^{3,(2)\sharp} + \mathcal{J}_{m,\ell}^{3,(2)\natural}. \end{align*} $$

We claim that the first term in the above right-hand side, namely $\mathcal {J}_{m,\ell }^{3,(2)\flat }$ , is easier to treat than the third, $\mathcal {J}_{m,\ell }^{3,(2)\natural }$ , because $|\partial _{\eta } \mathfrak m | \approx 2^{-\ell } \lesssim 2^{m+\ell } \approx |s \partial _{\eta } \Psi |$ with corresponding bounds for the $L^1$ norm of their Fourier transform. The second term, $\mathcal {J}_{m,\ell }^{3,(2)\sharp }$ , can be treated like Case 3 for $\mathcal {J}^2$ ; thus we are left with analysing the third term. In order to bound it, we integrate by parts in s:

$$ \begin{align*} \int_0^t \mathcal{J}_{m,\ell}^{3,(2)\natural} \,ds & = \int_0^t \iint e^{is \Psi(\xi,\eta,\zeta)} \frac{\partial_{\eta} \Psi}{\Psi} s \mathfrak{m}(\xi,\eta,\zeta) \partial_s \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta\,ds \\ & \quad + \int_0^t \iint e^{is \Psi(\xi,\eta,\zeta)} \frac{\partial_{\eta} \Psi}{\Psi} \partial_s [s \mathfrak{m}(\xi,\eta,\zeta)] \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \,ds \\ & \quad + \{ \mbox{similar or easier terms} \}. \end{align*} $$

The ‘similar or easier’ terms here also include the boundary terms coming from the integration by parts, which can be estimated like the other two terms.

We show how to bound the first term in the right-hand side above, since the second term can be bounded the same way. First observe that Lemma 6.5 applies since on the support of $\mathfrak {m}$ , the variables are such that $|\xi -\sqrt 3| + |\eta | + |\zeta | \lesssim 2^{\ell }$ ; and for any $a,b,c$ ,

$$ \begin{align*}\displaystyle \left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \frac{\partial_{\eta} \Psi}{\Psi} \right| \lesssim 2^{-\ell (1 +b +c)}. \end{align*} $$

We write

(9.8) $$ \begin{align} \begin{aligned} & \int_0^t \iint e^{is \Psi(\xi,\eta,\zeta)} i \frac{\partial_{\eta} \Psi}{\Psi} s \mathfrak{m}(\xi,\eta,\zeta) \partial_s \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \,ds \\ & \quad = \sum_{\iota_1 \iota_2 \iota_3} \int_0^t \iiiint e^{is \Lambda_{\iota_1 \iota_2 \iota_3}(\xi,\eta,\zeta,\sigma,\rho)} i \frac{\partial_{\eta} \Psi}{\Psi} s \mathfrak{m}'(\xi,\eta,\zeta,\rho,\sigma) \\ & \qquad \times\, \widetilde{f}(\xi-\eta-\sigma-\rho) \widetilde{f}(\sigma) \widetilde{f}(\rho) \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \,d\sigma\,d\rho \, ds \\ &\qquad + \{ \mbox{similar terms} \}. \end{aligned} \end{align} $$

In the above equation, we denoted $\mathfrak {m}'$ for the 5-linear symbol arising when one replaces $\partial _s f$ by $\mathcal {C}^{S1}$ ; we omitted various indexes and complex conjugate signs to alleviate the notations, and denoted

$$ \begin{align*}\Lambda_{\iota_1 \iota_2 \iota_3}(\xi,\eta,\zeta,\sigma,\rho) = \langle \xi \rangle - \iota_1 \langle\xi-\eta-\sigma-\rho \rangle - \iota_2 \langle \sigma \rangle - \iota_3 \langle \rho \rangle - \langle \xi-\eta-\zeta \rangle + \langle \xi-\zeta \rangle. \end{align*} $$

By Lemma equation (6.13), the 5-linear term satisfies Hölder estimates and can be bounded by

$$ \begin{align*}\| \dots \|_{L^2} \lesssim 2^{-\ell} 2^{2m} \| e^{is\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}}^4 \| \varphi_{\sim \ell}(\cdot - \sqrt 3) \widetilde f \|_{L^2} \lesssim 2^{-\ell/2} {\varepsilon}_1^5 \lesssim 2^{-\beta \ell + \alpha m} {\varepsilon}_1^5, \end{align*} $$

where the last inequality holds since $\ell> -\gamma m$ and $\alpha> \beta ' \gamma $ .

The ‘similar terms’ in equation (9.8) are of various types: some involve principal value operators instead of $\delta $ , but these can be treated identically; other contain the regular quadratic term, which can be treated similarly using (see equation (11.45)):

$$ \begin{align*}\| \varphi_{\ell}(\cdot - \sqrt 3) \mathcal{Q}^R(f,f) \|_{L^2} \lesssim 2^{\ell/2} 2^{-m}. \end{align*} $$

Case 4.3: $\ell> -\gamma m$ , $j_2 < \ell - 100$ , $2^{j_1} \approx 2^{j_3} \gg 2^{\ell }$ . We would like to estimate here $\sum _{j_1 \gg \ell } \mathcal {J}_{m,\ell ,j_1}^{\kern2.2pt 3,(3)}$ , with

$$ \begin{align*}\mathcal{J}_{m,\ell,j_1}^{3,(3)} = \iint e^{is \Psi(\xi,\eta,\zeta)} \mathfrak{m}(\xi,\eta,\zeta)\widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta, \end{align*} $$

where

$$ \begin{align*} \mathfrak{m}(\xi,\eta,\zeta) & = \mathfrak{m}_{m,\ell,j_1}^{\mathcal{J}^{3,(3)}}(\xi,\eta,\zeta) \\ & = \mathfrak{p}(\xi,\eta,\zeta) \varphi_{\ell}(\xi-\sqrt{3}) \varphi_{j_1}(\xi-\eta - \sqrt{3}) \varphi_{<\ell-100}(\xi-\eta -\zeta- \sqrt{3}) \\ & \qquad \qquad \qquad \varphi_{\sim j_1}(\xi-\zeta-\sqrt{3}) \varphi_{\sim j_1}(\eta-\zeta) \tau_m(s). \end{align*} $$

On the support of this symbol,

$$ \begin{align*}| (\partial_{\eta} - \partial_{\zeta}) \Psi | \approx |\eta - \zeta| \approx 2^{j_1}, \qquad | (\partial_{\eta} - \partial_{\zeta})^2 \Psi | \approx 1.\end{align*} $$

Integrating by parts through the identity $\frac {1}{is(\partial _{\eta } - \partial _{\zeta }) \Psi } (\partial _{\eta } - \partial _{\zeta }) e^{is\Psi } = e^{is\Psi }$ gives

$$ \begin{align*} \mathcal{J}^{3,(3)}_{m, \ell,j_1} & = \iint e^{is \Psi(\xi,\eta,\zeta)} (\partial_{\eta} - \partial_{\zeta}) \left[ \frac{\mathfrak{m}(\xi,\eta,\zeta)}{is(\partial_{\eta} - \partial_{\zeta}) \Psi)} \right] \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta) \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \\ & \quad + \iint e^{is \Psi(\xi,\eta,\zeta)}\frac{1}{is(\partial_{\eta} - \partial_{\zeta}) \Psi} \mathfrak{m}(\xi,\eta,\zeta) \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta) \partial_{\xi} \widetilde{f}(\xi-\zeta) \, d\eta \,d\zeta \\ & \quad + \{ \mbox{symmetrical terms} \} \\ & = \mathcal{J}^{3,(3)\flat}_{m,\ell,j_1} + \mathcal{J}^{3,(3)\sharp}_{m,\ell,j_1} + \{ \mbox{symmetrical terms} \}. \end{align*} $$

Both of these terms can be estimated very similarly to the corresponding terms in Case 4.1; for completeness, we show how to bound $\mathcal {J}^{3,(3)\sharp }_{m,\ell ,j_1}$ .

We claim first that

(9.9) $$ \begin{align} \left\| \mathcal{F} \left[ \frac{\mathfrak{m}(\xi,\eta,\zeta)}{(\partial_{\eta} - \partial_{\zeta}) \Psi)} \right] \right\|_{L^1} \lesssim 2^{- j_1}. \end{align} $$

Indeed, we can write $ \mathfrak {m} = \mathfrak {n} \varphi _{< \ell - 100}(\xi -\eta -\zeta - \sqrt 3) $ with

$$ \begin{align*} \mathfrak{n}(\xi,\eta,\zeta) & = \mathfrak{p}(\xi,\eta,\zeta) \varphi_{\ell}(\xi-\sqrt{3}) \varphi_{j_1}(\xi-\eta - \sqrt{3}) \varphi_{\sim j_1}(\xi-\zeta-\sqrt{3}) \varphi_{\sim j_1}(\eta-\zeta) \varphi_{\gtrsim j_1}(\eta-\zeta) \tau_m(s). \end{align*} $$

On the support of $\mathfrak {n}$ , the variables are constrained by $|\xi - \sqrt 3| \sim 2^{\ell }$ , $|\eta | \lesssim 2^{j_1}$ and $|\zeta | \lesssim 2^{j_1}$ , and for any $a,b,c$ , we have

$$ \begin{align*}\left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \frac{1}{(\partial_{\eta} - \partial_{\zeta}) \Psi} \right| \lesssim 2^{- j_1 (1 + b + c)}, \qquad \left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \mathfrak{n} \right| \lesssim 2^{- a \ell - (b + c) j_1}. \end{align*} $$

From Remark 6.6 after Lemma 6.5, we deduce

$$ \begin{align*}\left\| \mathcal{F} \left[ \frac{\mathfrak{n}(\xi,\eta,\zeta)}{(\partial_{\eta} - \partial_{\zeta}) \Psi)} \right] \right\|_{L^1} \lesssim 2^{- j_1}, \end{align*} $$

hence equation (9.9).

Applying Lemma 6.5, we obtain

$$ \begin{align*}\left\| \int_0^t \mathcal{J}_{m,\ell,j_1}^{3,(1)\sharp} \,ds \right\|_{L^2} \lesssim 2^{-j_1} \| e^{is\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}} \| \varphi_{<\ell}(\cdot - \sqrt 3) \partial_{\xi} \widetilde{f} \|_{L^1} \| \partial_{\xi} \widetilde{f}\|_{L^2} , \end{align*} $$

from which, after summing in $j_1 \gg \ell $ , one can proceed as in equation (9.7).

9.3 The bound for $\mathcal {C}^{S2}_{+-+}$

We now look at the ‘ $\mathrm {p.v.}$ ’ contributions of the form

(9.10) $$ \begin{align} \begin{aligned} \iiint e^{is \Psi(\xi,\eta,\zeta,\theta)} \mathfrak{p}(\xi,\eta,\zeta,\theta) & \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \,d\theta \\ \Psi(\xi,\eta,\zeta,\theta) & : = \Phi_{+ - +}(\xi,\xi-\eta,\xi-\eta-\zeta-\theta,\xi-\zeta) \\ & = \langle \xi \rangle - \langle \xi - \eta \rangle + \langle \xi - \eta -\zeta -\theta \rangle - \langle \xi - \zeta\rangle. \end{aligned} \end{align} $$

In the regime that interests us here ( $|\xi - \sqrt {3}| \ll 1$ and $|\eta |, |\zeta |, |\theta | \ll 1$ ), we have the expansions

$$ \begin{align*} & \Psi(\xi,\eta,\zeta,\theta) = - \frac{\xi}{\langle \xi \rangle} \theta + \frac{1}{\langle \xi \rangle^3} \left(\frac{\theta^2}{2} + \eta \zeta + \eta \theta + \zeta \theta\right) + O(|\eta,\zeta,\theta|^3) = -\frac{\xi}{\langle \xi \rangle} \theta + O(|\eta,\zeta,\theta|^2), \\ & \partial_{\xi} \Psi (\xi,\eta,\zeta,\theta) = - \frac{1}{\langle \xi \rangle^3} \theta + O(|\eta,\zeta,\theta|^2), \\ & \partial_{\eta} \Psi (\xi,\eta,\zeta,\theta) = \frac{1}{\langle \xi -\eta \rangle^3} (\zeta + \theta) + O( |\zeta + \theta|^2), \\ & \partial_{\eta}^2 \Psi (\xi,\eta,\zeta,\theta) = \frac{3(\xi-\eta)}{\langle \xi - \eta \rangle^5} (\zeta + \theta) + O(|\zeta + \theta|^2), \\ & (\partial_{\eta} - \partial_{\zeta}) \Psi = \frac{1}{\langle \xi -\eta \rangle^3} (\zeta - \eta) + O( |\eta-\zeta|^2). \end{align*} $$

9.3.1 Commuting $\langle \xi \rangle \partial _{\xi }$ with equation (9.10)

In order to perform this commutation, it is convenient to adopt a new set of coordinates, namely write

$$ \begin{align*}(9.10) = \iiint e^{is \Phi_{+-+}(\xi,\eta,{\sigma},\theta)} \mathfrak{p}(\xi,\eta,{\sigma},\theta) \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \frac{\widehat{\phi}(p)}{p} \, d\eta \,d\sigma \,d\theta, \end{align*} $$

with $p = \xi - \eta - \sigma - \theta $ . In the expression above, we have abused notation slightly by also denoting $\mathfrak {p}$ the symbol in the new coordinates, and by omitting irrelevant sign changes. To commute $\langle \xi \rangle \partial _{\xi }$ with equation (9.10), we will rely on the following elegant identity: observe that

(9.11) $$ \begin{align} (\langle \xi \rangle \partial_{\xi} + X_{\eta,{\sigma},\theta}) \Phi_{+-+} = p, \qquad X_{\eta,{\sigma},\theta} := \langle \eta \rangle \partial_{\eta} - \langle \sigma \rangle \partial_{\sigma} + \langle \theta \rangle \partial_{\theta}. \end{align} $$

When applying $\langle \xi \rangle \partial _{\xi }$ to equation (9.10), we can use this identity to integrate by parts in $\eta ,\sigma $ and $\theta $ . Since the adjoint satisfies $X_{\eta ,{\sigma },\theta }^{\ast } = - X_{\eta ,{\sigma },\theta }$ , up to terms that are easier to estimate, we see that estimating $\langle \xi \rangle \partial _{\xi }$ of equation (9.10) reduces to bounding

(9.12a) $$ \begin{align} & it \iiint e^{it \Phi_{+-+}} \mathfrak{p}(\xi,\eta,\sigma,\theta) \, \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \widehat{\phi}(p) \, d\eta \, d\sigma \,d\theta \qquad\qquad\qquad\qquad\quad\end{align} $$

(9.12b) $$ \begin{align} & + \iiint e^{it \Phi_{+-+}} \mathfrak{p}(\xi,\eta,\sigma,\theta) X_{\eta,{\sigma},\theta} \big(\widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \big) \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta \qquad\qquad\quad\end{align} $$

(9.12c) $$ \begin{align} & + \iiint e^{it \Phi_{+-+}} \mathfrak{p}(\xi,\eta,\sigma,\theta) \, \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \, \big( \langle \xi \rangle \partial_{\xi} + X_{\eta,{\sigma},\theta} \big) \Big[ \frac{\widehat{\phi}(p)}{p}\Big] \, d\eta \, d\sigma \,d\theta \end{align} $$

(9.12d) $$ \begin{align} & + \iiint e^{it \Phi_{+-+}} X_{\eta,{\sigma},\theta} \, \mathfrak{p}(\xi,\eta,\sigma,\theta) \, \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \, \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta. \qquad\qquad\ \ \ \end{align} $$

Estimate of equation (9.12a). This term does not have a singularity and can be estimated by integrating by parts in the ‘uncorrelated’ variables $\eta ,\sigma $ and $\theta $ . Each of the three inputs would then give a gain of $\langle t \rangle ^{-3/4+\alpha }$ , which is sufficient to absorb the power of t in front and integrate over time. Similar (in fact, harder) terms have been treated in Section 8, so we can skip the details.

Estimate of equation (9.12c). For this term, we observe (see equation (11.71)) that

(9.13) $$ \begin{align} \big( \langle \xi \rangle \partial_{\xi} + X_{\eta,{\sigma},\theta} \big) \Big[ \frac{\widehat{\phi}(p)}{p}\Big] = \Phi_{+-+}(\xi,\eta,{\sigma},\theta) \partial_p \Big[ \frac{\widehat{\phi}(p)}{p}\Big]. \end{align} $$

Note that this identity is formal as it is written, since $\partial _p (1/p)$ does not converge (even in the $\mathrm {p.v.}$ sense); however, it can be made rigorous by localising a little away from $p=0$ and using the $\mathrm {p.v.}$ to deal with very small values of p.

From equation (9.13), we obtain, upon integration by parts in s, that

(9.14) $$ \begin{align} \int_0^t i (9.12c) \, ds & = \iiint e^{is \Phi_{+-+}} \mathfrak{p}(\xi,\eta,\sigma,\theta) \, \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \, \partial_p \frac{\widehat{\phi}(p)}{p}\, d\eta \, d\sigma \,d\theta \, \Big|_{s=0}^{s=t} \end{align} $$

(9.15) $$ \begin{align} & - \int_0^t \iiint e^{is \Phi_{+-+}} \mathfrak{p}(\xi,\eta,\sigma,\theta) \, \partial_s \Big[ \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \Big] \partial_p \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta \, ds. \end{align} $$

To estimate equation (9.14), we convert the $\partial _p$ into $\partial _{\eta }$ and integrate by parts in $\eta $ . The worst term is when $\partial _{\eta }$ hits the exponential; this causes a loss of t, but an $L^2\times L^{\infty }\times L^{\infty }$ Hölder estimate using Lemma 6.13 suffices to recover it.

The term in equation (9.15) is similar. We may assume that $\partial _s$ hits $\widetilde {f}(\sigma )$ . Again we convert $\partial _p$ into $\partial _{\eta }$ and integrate by parts in $\eta $ . This causes a loss of s when hitting the exponential phase, which is offset by an $L^{\infty }\times L^2\times L^{\infty }$ estimate with $\partial _s \widetilde {f}$ placed in $L^2$ and giving $\langle t \rangle ^{-1}$ decay using equation (7.56).

Estimate of equation (9.12d). This term can be estimated directly using the trilinear estimates from Lemma 6.13.

This leaves us with equation (9.12b), which, coming back to the original coordinates, and taking into account the symmetry between the $\eta $ and $\zeta $ variables, reduces to the two following terms

$$ \begin{align*} &\mathcal{H}^2 = \iiint e^{is \Psi(\xi,\eta,\zeta,\theta)} \mathfrak{p}(\xi,\eta,\zeta,\theta) \partial_{\xi} \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta}\, d\eta \,d\zeta\,d\theta, \\ &\mathcal{H}^3 = \iiint e^{is \Psi(\xi,\eta,\zeta,\theta)} \mathfrak{p}(\xi,\eta,\zeta,\theta) \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta}\, d\eta \,d\zeta\,d\theta. \end{align*} $$

In order to bound these terms, we will dyadically localise the variables in the problem as follows:

(9.16) $$ \begin{align} \begin{aligned} & s \approx 2^m, \quad |\xi - \sqrt{3}| \approx 2^{\ell}, \quad |\theta| \approx 2^h, \\ & |\xi-\eta - \sqrt{3}| \approx 2^{j_1}, \quad |\xi-\eta-\zeta -\theta- \sqrt{3}| \approx 2^{j_2}, \quad |\xi-\zeta-\sqrt{3}| \approx 2^{j_3}. \end{aligned} \end{align} $$

9.3.2 Bound for $\mathcal {H}^2$

Cases 1,2,3: $\ell < -\gamma m$ or $j_1> \ell - 100$ . These cases can be dealt with as in Section 9.2.1, relying on Lemma 6.7 instead of Lemma 6.5.

Case 4.1: $\ell> -\gamma m$ , $j_1 < \ell - 100$ and $|\theta +\xi -\sqrt 3| \geq 2^{\ell -10} $ . We want to bound here $\sum _{h> \ell - 10} \mathcal {H}^{2,(1)}_{m,\ell ,h}$ , where

$$ \begin{align*} \mathcal{H}^{2,(1)}_{m,\ell,h} := \iiint e^{is \Psi(\xi,\eta,\zeta,\theta)} \mathfrak{m}(\xi,\eta,\zeta,\theta) \partial_{\xi}\widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta}\, d\eta \,d\zeta \,d\theta \end{align*} $$

with

$$ \begin{align*} \mathfrak{m}(\xi,\eta,\zeta,\theta) & = \mathfrak{m}^{\mathcal{H}^{2,(1)}}_{m,\ell,h}(\xi,\eta,\zeta,\theta) \\ & = \mathfrak{p}(\xi,\eta,\zeta) \varphi_{\ell}(\xi - \sqrt{3}) \varphi_{<\ell-100}(\xi-\eta - \sqrt{3}) \varphi_{h} (\theta + \xi - \sqrt{3}) \tau_m(s). \end{align*} $$

On the support of $\mathfrak {m}(\xi ,\eta ,\zeta )$ , $|\partial _{\zeta } \Psi | \approx |\eta + \theta | \gtrsim |\eta |$ and $|\xi - \sqrt {3}|, |\eta | \sim 2^{\ell }$ and $|\theta | \lesssim 2^h$ ; moreover, for any a, b, c,

$$ \begin{align*}\left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \partial_{\theta}^d \frac{1}{\partial_{\zeta} \Psi} \right| \lesssim 2^{-h(1+b+d)}. \end{align*} $$

Therefore, Lemma 6.7 applies and we can proceed exactly as in Case 4 of Section 9.2.1, since the sum over $h> \ell $ of $2^{-h}$ gives the same factor of $2^{\ell }$ there.

Case 4.2: $\ell> -\gamma m$ , $j_1 < \ell - 100$ and $|\theta +\xi -\sqrt 3| < 2^{\ell - 10}$ . We want to bound here

$$ \begin{align*} \mathcal{H}^{2,(2)}_{m,\ell} = \iiint e^{is \Psi(\xi,\eta,\zeta,\theta)} \mathfrak{m}(\xi,\eta,\zeta)\partial_{\xi}\widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta}\, d\eta \,d\zeta \,d\theta, \end{align*} $$

where

$$ \begin{align*} \mathfrak{m}(\xi,\eta,\zeta) & = \mathfrak{m}^{\mathcal{H}^{2,(2)}}_{m,\ell}(\xi,\eta,\zeta) \\ & = \mathfrak{p}(\xi,\eta,\zeta) \varphi_{\ell}(\xi - \sqrt{3}) \varphi_{<\ell-100}(\xi-\eta - \sqrt{3}) \varphi_{<\ell - 10} (\theta + \xi - \sqrt{3}) \tau_m(s). \end{align*} $$

On the support of the integrand, $|\theta | \approx 2^{\ell }$ . Therefore, noticing that $\partial _{\theta } \Psi $ is smooth and bounded away from zero, we integrate by parts in $\theta $ to obtain

$$ \begin{align*} \mathcal{H}^{2,(2)}_{m,\ell} & = \iiint e^{is \Psi(\xi,\eta,\zeta,\theta)} \partial_{\xi}\widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \partial_{\theta} \left[ \frac{\mathfrak{m}}{s\partial_{\theta} \Psi} \frac{\widehat{\phi}(\theta)}{\theta} \right] \, d\eta \,d\zeta \,d\theta \\ & \quad + \iiint e^{is \Psi(\xi,\eta,\zeta,\theta)} \frac{\mathfrak{m}}{s\partial_{\theta} \Psi} \partial_{\xi}\widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta}\, d\eta \,d\zeta \,d\theta \\ & = \mathcal{H}^{2,(2) \flat}_{m,\ell} + \mathcal{H}^{2,(2) \sharp}_{m,\ell}. \end{align*} $$

Using that $|\xi |, |\eta |, |\theta | \lesssim 2^{\ell }$ and $| \partial _{\xi }^a \partial _{\eta }^b \partial _{\zeta }^c \partial _{\theta }^d \mathfrak {m}| \lesssim 2^{-\ell (a+b+d)}$ , we get by Lemma 6.7 equations (7.18), (7.20) and (7.25),

$$ \begin{align*} \int_0^t \left\| \mathcal{H}^{2,(2) \flat}_{m,\ell} \right\|_{L^2} \,ds & \lesssim 2^{-\ell} \| \varphi_{<\ell}(\cdot - \sqrt{3}) \partial_{\xi} \widetilde f \|_{L^1} \| \widetilde{f} \|_{L^2} \| e^{-it\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}} \\ & \lesssim 2^{-\ell} 2^{\beta' \ell + \alpha m} 2^{-m/2} {\varepsilon}_1^3 \lesssim 2^{-\beta \ell + \alpha m} {\varepsilon}_1^3. \end{align*} $$

Similarly, by Lemma 6.7, we get equations (7.19), (7.20) and (7.25),

$$ \begin{align*} \int_0^t \left\| \mathcal{H}^{2,(2) \sharp}_{m,\ell} \right\|_{L^2} \,ds & \lesssim \| \varphi_{<\ell}(\cdot - \sqrt{3}) \partial_{\xi} \widetilde f \|_{L^1} \| \partial_{\xi} \widetilde f \|_{L^2} \| e^{-it\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}} \\ & \lesssim 2^{\beta' \ell + \alpha m} 2^{(\alpha + \beta \gamma)m} 2^{-m/2} {\varepsilon}_1^3 \lesssim 2^{-\beta \ell + \alpha m} {\varepsilon}_1^3. \end{align*} $$

9.3.3 Bound for $\mathcal {H}^3$

Cases 1,2,3: $\ell < -\gamma m$ or $j_2> \ell - 100$ . With the help of Lemma 6.7 instead of Lemma 6.5, these cases are dealt with exactly as for $\mathcal {J}^3$ in Section 9.2.2. We introduce one further index to record the size of $|\eta - \zeta |$ :

$$ \begin{align*} & |\eta - \zeta| \approx 2^{j_4}. \end{align*} $$

From now on, we can assume that $\ell> -\gamma m$ and $j_1 < \ell - 100$ . The cases that remain to be distinguished are

• • Case 4.1: $2^{j_1},2^{j_3} \lesssim 2^{\ell }$ , $2^{j_4} \gtrsim 2^{\ell }$ ;

• • Case 4.2.1: $2^{j_1},2^{j_3} \lesssim 2^{\ell }$ , $2^{j_4} \ll 2^{\ell }$ , $2^{2\ell } \lesssim 2^h \lesssim 2^{\ell }$ ;

• • Case 4.2.2: $2^{j_1},2^{j_3} \lesssim 2^{\ell }$ , $2^{j_4} \ll 2^{\ell }$ , $2^h \ll 2^{2\ell }$ ;

• • Case 4.3.1: $2^{j_1} \approx 2^{j_3} \gg 2^{\ell }$ , $2^h \ll 2^{j_1}$ ;

• • Case 4.3.2: $2^{j_1} \gg 2^{\ell }$ , $2^h \gtrsim 2^{j_1}$ .

Case 4.1: $\ell> -\gamma m$ , $j_2 < \ell - 100$ , $2^{j_1}, 2^{j_3} \lesssim 2^{\ell }$ and $j_4> \ell -100$ . This corresponds to the symbol

$$ \begin{align*} \mathfrak{m}_{\ell,m}^{\mathcal{H}^{3,(1)}} & = \varphi_{\ell}(\xi - \sqrt{3}) \varphi_{< \ell +10}(\xi-\eta - \sqrt{3}) \varphi_{< \ell - 100}(\xi-\eta -\zeta - \theta -\sqrt{3}) \\ & \qquad \qquad \qquad \qquad \varphi_{< \ell+10}(\xi-\zeta- \sqrt{3}) \varphi_{>\ell-100}(\eta-\zeta). \end{align*} $$

On the support of this symbol, the frequency variables enjoy the localisations $|\xi -\sqrt {3}|, |\eta |, |\zeta |, |\theta | \lesssim 2^{\ell }$ , and the symbol satisfies the estimates

$$ \begin{align*}| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \partial_{\theta}^d \mathfrak{m} | \lesssim 2^{-(a+b+c+d) \ell}. \end{align*} $$

Furthermore, $|(\partial _{\eta } - \partial _{\zeta }) \Psi | \gtrsim 2^{\ell }$ , and therefore one can proceed as in Case 4.1 of Section 9.2.2. Indeed, $(\partial _{\eta } - \partial _{\zeta }) \Psi $ is independent of $\theta $ and, on the support of the symbol, $\left | \partial _{\xi }^a \partial _{\eta }^b \partial _{\zeta }^c \partial _{\theta }^d \frac {1}{(\partial _{\eta } - \partial _{\zeta }) \Psi } \right | \lesssim 2^{-\ell (1+b+c)}$ for any $a,b,c,d$ .

Case 4.2.1: $\ell> -\gamma m$ , $j_2 < \ell - 100$ , $2^{j_1}, 2^{j_3} \lesssim 2^{\ell }$ , $j_4 \leq \ell - 100$ and $h> 2\ell -100$ . After the change of variables $\eta ' = \eta + \theta $ , let

$$ \begin{align*}\mathcal{H}^{3,(2)}_{h,\ell,m} = \iiint e^{is \Phi(\xi,\eta',\zeta,\theta)} \mathfrak{m}(\xi,\eta',\zeta,\theta) \widetilde{f}(\xi-\eta'+\theta) \partial_{\xi}\overline{\widetilde{f}(\xi-\eta'-\zeta)} \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta}\, d\eta' \,d\zeta\,d\theta, \end{align*} $$

where

$$ \begin{align*} \Phi(\xi,\eta',\zeta,\theta) = \langle \xi \rangle - \langle \xi - \eta' + \theta \rangle + \langle \xi - \eta' -\zeta \rangle - \langle \xi - \zeta\rangle \end{align*} $$

and

$$ \begin{align*} \mathfrak{m}(\xi,\eta',\zeta) & = \mathfrak{m}^{\mathcal{H}^{3,(2)}}_{h,\ell,m}(\xi,\eta',\zeta) \\ & = \varphi_{\ell}(\xi - \sqrt{3}) \varphi_{<\ell-100}(\xi-\eta' -\zeta - \sqrt{3}) \varphi_{< \ell + 10}(\xi-\eta' + \theta -\sqrt{3})\varphi_{< \ell + 10}(\xi-\zeta- \sqrt{3}) \\ & \qquad \qquad \qquad \varphi_{<\ell-100} (\eta'-\theta-\zeta) \varphi_{h} (\theta) \tau_m(s) \mathfrak{p}(\xi,\eta' - \theta,\zeta). \end{align*} $$

On the support of this symbol, $2^h \lesssim 2^{\ell }$ ; therefore, in the following we will bound $\sum _{ 2\ell - 100 < h < \ell + 100} \mathcal {H}^{3,(2)}_{h,\ell ,m}$ . Noticing that $\partial _{\theta } \Phi = \frac { \xi - \eta ' - \theta }{\langle \xi - \eta ' - \theta \rangle }$ is smooth and $\gtrsim 1$ , we integrate by parts in $\theta $ to obtain

$$ \begin{align*} \mathcal{H}^{3,(2)}_{h,\ell,m} & = \iiint e^{is \Phi(\xi,\eta',\zeta,\theta)} \frac{\mathfrak{m}}{i s\partial_{\theta} \Phi} \partial_{\xi} \widetilde{f}(\xi-\eta'+\theta) \partial_{\xi} \widetilde{f}(\xi-\eta'-\zeta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta}\, d\eta' \,d\zeta\,d\theta \\ & \qquad - \iiint e^{is \Phi(\xi,\eta',\zeta,\theta)} \widetilde{f}(\xi-\eta'+\theta) \partial_{\xi} \widetilde{f}(\xi-\eta'-\zeta) \widetilde{f}(\xi-\zeta) \partial_{\theta} \left[ \frac{\mathfrak{m}}{i s\partial_{\theta} \Phi} \frac{\widehat{\phi}(\theta)}{\theta}\right]\, d\eta' \,d\zeta\,d\theta \\ & = \mathcal{H}^{3,(2)\flat}_{h,\ell,m} + \mathcal{H}^{3,(2)\sharp}_{h,\ell,m}. \end{align*} $$

Estimating $ \mathcal {H}^{3,(2)\flat }_{h,\ell ,m}$ is now straightforward, using that $|\xi -\sqrt 3|, |\eta '|, |\zeta | \lesssim 2^{\ell }$ , $|\theta | \approx 2^h$ and $|\partial _{\xi }^a \partial _{\eta '}^b \partial _{\zeta }^c \partial _{\theta }^d \mathfrak {m}| \lesssim 2^{-(a+b+c) \ell - dh}$ :

$$ \begin{align*} \int_0^t \sum_{ 2\ell-100 < h < \ell+100} \left\| \mathcal{H}^{3,(2)\flat}_{h,\ell,m} \right\|_{L^2}\,ds & \lesssim |\ell| {\| \varphi_{\sim \ell}(\cdot - \sqrt{3}) \partial_{\xi} \widetilde{f} \|}_{L^2} {\| \varphi_{<\ell} (\cdot - \sqrt{3}) \partial_{\xi} \widetilde{f} \|}_{L^1} {\| e^{-it\langle D \rangle} \mathcal{W}^* f \|}_{L^{\infty}} \\ & \lesssim |\ell| 2^{-\beta \ell + \alpha m} 2^{\beta' \ell + \alpha m} 2^{-m/2} {\varepsilon}_1^3 \lesssim 2^{-\beta \ell + \alpha m} {\varepsilon}_1^3. \end{align*} $$

To estimate $\mathcal {H}^{3,(2)\sharp }_{h,\ell ,m}$ , observe that

$$ \begin{align*}\left\| \mathcal{F} \left( \partial_{\theta} \left[ \frac{ \mathfrak{m}}{\partial_{\theta} \Phi} \frac{\widehat{\phi}(\theta)}{\theta} \right] \right) \right\|_{L^1} \lesssim 2^{-h} \end{align*} $$

and, therefore,

$$ \begin{align*} & \int_0^t \left\| \sum_{2\ell-100 < h <\ell+100} \mathcal{H}^{3,(2)\sharp}_{h,\ell,m} \right\|_{L^2}\,ds \\ & \qquad \lesssim \sum_{2\ell-100 < h <\ell+100} 2^{- h} \| \varphi_{<\ell} (\cdot - \sqrt 3) \widetilde{f} \|_{L^2} \| \varphi_{<\ell} (\cdot - \sqrt{3}) \partial_{\xi} \widetilde{f} \|_{L^1} \| e^{-it\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}} \\ & \qquad \lesssim \sum_{2\ell-100 < h <\ell+100} 2^{- h} 2^{\ell/2} 2^{\beta' \ell + \alpha m} 2^{-m/2} {\varepsilon}_1^3 \lesssim 2^{-\beta \ell + \alpha m} {\varepsilon}_1^3, \end{align*} $$

where we used that $\ell> -\gamma m > -m/2$ .

Case 4.2.2: $\ell> -\gamma m$ , $j_2 < \ell - 100$ , $2^{\ell } \sim 2^{j_1} \sim 2^{j_3}$ , $j_4 < \ell - 100$ and $h < 2\ell -100$ . In this case, $|\eta | , |\zeta | \approx \left | \xi - \sqrt 3 \right | \approx 2^{\ell }$ and $|\theta | \ll 2^{\ell }$ , so that $|\Psi | \approx 2^{2 \ell }$ , $|\partial _{\eta } \Psi | \approx 2^{\ell }$ , and, for any $a,b,c,d$ ,

$$ \begin{align*}\left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \partial_{\theta}^d \frac{\partial_{\eta} \Psi}{\Psi} \right| \lesssim 2^{-\ell(1+b+c)-2\ell d}. \end{align*} $$

Therefore, this case can be dealt with as in Case 4.2 of Section 9.2.2.

Case 4.3.1: $\ell> -\gamma m$ , $j_2 < \ell - 100$ , $2^{\ell } \ll 2^{j_1} \approx 2^{j_3}$ , $2^h \ll 2^{j_1}$ . This corresponds to the symbol

$$ \begin{align*} \mathfrak{m}(\xi,\eta,\zeta,\theta) = \mathfrak{m}_{\ell,j_1,m}^{\mathcal{H}^{3,(3)}}(\xi,\eta,\zeta,\theta) & = \varphi_{\ell}(\xi - \sqrt{3}) \varphi_{j_1}(\xi-\eta - \sqrt{3}) \varphi_{<\ell-100}(\xi-\eta -\zeta - \theta -\sqrt{3}) \\ & \qquad \qquad \qquad \qquad \varphi_{\sim j_1}(\xi-\zeta- \sqrt{3}) \varphi_{\sim j_1}(\eta - \zeta) \varphi_{<j_1 - 100} (\theta)\tau_m(s), \end{align*} $$

which is such that, on its support, $|\eta |,|\zeta |, |\eta - \zeta | \approx 2^{j_1}$ and $|\theta | \ll 2^{j_1}$ .

This case can mostly be treated like Case 4.3 in Section 9.2.2 since $(\partial _{\eta } - \partial _{\zeta }) \Psi $ is independent of $\theta $ . The only delicate point is that Lemma 6.7 and the remark following it do not directly apply here. For this reason, we let $ \mathfrak {m}(\xi ,\eta ,\zeta ,\theta ) = \mathfrak {n}(\xi ,\eta ,\zeta ,\theta ) \varphi _{<\ell -100}(\xi -\eta -\zeta - \theta -\sqrt {3}) $ and consider the symbol

$$ \begin{align*}\mathfrak{m}_1(\xi,\eta,\zeta,\theta) = \frac{\mathfrak{m}(\xi,\eta,\zeta,\theta)}{(\partial_{\eta} - \partial_{\zeta}) \Psi} = \frac{\mathfrak{n}(\xi,\eta,\zeta,\theta)}{(\partial_{\eta} - \partial_{\zeta}) \Psi} \varphi_{<\ell-100}(\xi-\eta -\zeta - \theta -\sqrt{3}), \end{align*} $$

which appears if one follows the proof of Case 4.3 in $\mathcal {J}^3$ . Following the same argument used to show equation (9.9), one can see that

$$ \begin{align*}\left| \mathcal{F} \left[\frac{\mathfrak{n}}{(\partial_{\eta} - \partial_{\zeta}) \Psi} \right](x,y,z,t) \right| \lesssim 2^{\ell + 2 j_1} F(2^{\ell} x) F(2^{j_1} (y,z,t)), \end{align*} $$

where we denote as F a generic rapidly decaying function of size $O(1)$ together with its derivatives. The Fourier transform of $\mathfrak {m}_1$ is bounded by the convolution of the above right-hand side with

$$ \begin{align*}\left| \mathcal{F} \varphi_{<\ell-100}(\xi-\eta -\zeta - \theta -\sqrt{3}) \right| = 2^{\ell} F(2^{\ell} x) \delta(-x = y = z = t): \end{align*} $$

that is,

$$ \begin{align*}| \widehat{\mathfrak{m}_1}(x,y,z,t) | \lesssim 2^{2\ell + j_1} F(2^{\ell} x) F(2^{\ell} y) F(2^{j_1}(y-z)) F(2^{j_1}(y-t)). \end{align*} $$

Therefore,

$$ \begin{align*}\left| \int \widehat{\mathfrak{m}_1} (x,y,z,t) \,dt \right| \lesssim 2^{2\ell} F(2^{\ell} x) F(2^{\ell} y) F(2^{j_1}(y-z)) \end{align*} $$

and Lemma 6.7 applies, giving that the norm of $V_{\mathfrak {m}_1}$ between Lebesgue spaces at the Hölder scaling is $\lesssim 2^{-j_1}$ .

Case 4.3.2: $\ell> -\gamma m$ , $j_2 < \ell - 100$ , $2^{\ell } \ll 2^{j_1}$ , $2^h \gtrsim 2^{j_1}$ . This corresponds to the symbol

$$ \begin{align*} \mathfrak{m}(\xi,\eta,\zeta,\theta) & = \mathfrak{m}_{\ell,j_1,m}^{\mathcal{H}^{3,(3)}}(\xi,\eta,\zeta,\theta) \\ & = \varphi_{\ell}(\xi - \sqrt{3}) \varphi_{j_1}(\xi-\eta - \sqrt{3}) \varphi_{<\ell-100}(\xi-\eta -\zeta - \theta -\sqrt{3}) \varphi_h (\theta)\tau_m(s). \end{align*} $$

In this case, it is possible to integrate by parts in $\theta $ and argue exactly as in Case 4.2.1. The only thing to check is that Lemma 6.7 applies; therefore, we need to bound the Fourier transform of $\mathfrak {m}$ . A computation reveals that

$$ \begin{align*}\left| \widehat{\mathfrak{m}}(x,y,z,t) \right| \lesssim 2^{2\ell + j_1 + h} F(2^{\ell} z) F(2^{\ell}(x+z)) F(2^{j_1}(y-z)) F(2^h(t-z)), \end{align*} $$

so that

$$ \begin{align*}\left| \int \widehat{\mathfrak{m}_1} (x,y,z,t) \,dt \right| \lesssim 2^{2\ell + j_1 } F(2^{\ell} z) F(2^{\ell}(x+z)) F(2^{j_1}(y-z)). \end{align*} $$

By Lemma 6.7, the norm of $V_{\mathfrak {m}}$ between Lebesgue spaces at the Hölder scaling is $\lesssim 1$ .

10 Pointwise estimates for the ‘singular’ part

The aim of this section is to prove the following proposition:

Proposition 10.1. Under the assumptions of Theorem 1.1, consider u solution of equation (KG) and assume the a priori bounds in equation (7.10) on the renormalised profile $\widetilde {f}$ . Let $\mathcal {C}^{S} = \mathcal {C}^{S1} + \mathcal {C}^{S2}$ be the cubic singular terms defined in equations (5.57)–(5.58) with equation (5.46).

Denote

(10.1) $$ \begin{align} X(\xi) = (X_+(\xi), X_-(\xi)) := (\widetilde{f}(\xi), \widetilde{f}(-\xi)), \qquad \xi>0. \end{align} $$

Then

• • There exists a real valued Hamiltonian $H = H(X_+,X_-)$ such that, for $\xi>0$ ,

  (10.2) $$ \begin{align} \begin{aligned} \mathcal{C}^{S}(f,f,f)(t,\xi) & = - \frac{i}{t} \, \frac{d}{d\overline{X_+}} H + R_+(t,\xi), \\ \mathcal{C}^{S}(f,f,f)(t,-\xi) & = - \frac{i}{t} \, \frac{d}{d\overline{X_-}} H + R_-(t,\xi), \end{aligned} \end{align} $$
  for all $t \geq 1$ ; see equation (10.27) for the exact formula for H.

• • There exists $\delta _0>0$ such that the remainders satisfy, for all $m=0,1,\dots $ ,

  (10.3) $$ \begin{align} {\Big\| \langle \xi \rangle^{3/2} \int_0^t R_\epsilon (s,\xi)\, \tau_m(s) ds \Big\|}_{L^{\infty}_{\xi}} \lesssim {\varepsilon}_1^3 2^{-\delta_0m}, \qquad \epsilon\in\{+,-\}. \end{align} $$

• • There exists an asymptotic profile $W^{\infty } = (W^{\infty }_+, W^{\infty }_-) \in \big (\langle \xi \rangle ^{-3/2}L^{\infty }_{\xi }\big )^2$ such that, for all $t\geq 0$ ,

  (10.4) $$ \begin{align} \langle \xi \rangle^{3/2} \Big| X(t,\xi) - S^{-1}(\xi) \exp\Big( -(5 i/12) \,(\log t) \, \mathrm{diag}\big( \ell_{+ \infty}^2\big| W^{\infty}_+ \big|^2, \ell_{- \infty}^2\big| W^{\infty}_- \big|^2 \big) \Big) \,W^{\infty}(\xi) \Big| \lesssim {\varepsilon}_1^3 \langle t \rangle^{-\delta_0}, \end{align} $$
  where $S(\xi )$ is the scattering matrix associated to the potential V defined in equation (3.12).

Here are a few remarks about the statement above and its consequences:

• • From the inequality in equation (10.9) appearing in the proof of equation (10.4), we deduce in particular the bound ${\| \langle \xi \rangle ^{3/2}\widetilde {f} \|}_{L^{\infty }} \leq {\varepsilon }_1$ ; this is one of the bounds needed for the main bootstrap Proposition 7.2.

• • The behaviour at negative times can be obtained by using time-reversal symmetry. In the context of our distorted Fourier space asymptotics, this ends up involving a conjugation by the scattering matrix S. We refer the reader to the explicit calculation in [7, Remark 1.2]. When applied to equation (10.4) this conjugation will simplify the formula and give asymptotics akin to the flat ones that do not involve S; see equation (10.25).

• • It is of course possible to derive asymptotics in physical space from the asymptotics in Fourier space, both in $L^{\infty }_x$ and $L^2_x$ . This can be done by putting together the linear asymptotics in equation (3.33) with equation (10.4), passing from f to g using equation (5.53) (note that $T(g,g)$ is a fast-decaying remainder in $L^{\infty }_x$ ) and eventually passing from g to u using equation (1.6). We refer the reader to [36] for the details of such an argument in the context of water waves and to [29] for the nonlinear Schrödinger equation.

Let us show first how to obtain the final asymptotic formula in equation (10.4) given equations (10.2) and (10.3). The argument is fairly standard as it appears in similar forms in [29, 39, 32, 24]. We refer the reader to these papers for more detailed presentations.

Proof of equation (10.4)

Recall that the evolution of $\widetilde {f}$ is given by equation (7.59). In Section 11.3, we show that all the terms on the right-hand side of equation (7.59), with the exception of the cubic terms $\mathcal {C}^S$ , satisfy bounds of the same type as the remainders in equation (10.3); see in particular Propositions 11.5 and 11.7. Then with the notation in equation (10.1), the asymptotics in equations (10.2)–(10.3) imply, for $\xi>0$ ,

(10.5) $$ \begin{align} \begin{aligned} \partial_t X_+ & = - \frac{i}{t} \, \frac{\partial}{\partial\overline{X_+}} H + R_1(t,\xi), \\ \partial_t X_- & = - \frac{i}{t} \, \frac{\partial}{\partial\overline{X_-}} H + R_2(t,\xi), \end{aligned} \end{align} $$

with $R_i$ satisfying bounds as in equation (10.3). In the rest of the proof of equation (10.4), we will denote just by $R=R(t,\xi )$ any generic remainder terms satisfying equation (10.3). This should not be confused with $R_+$ and $R_-$ , the transmission coefficients. Note that such a bound implies that $R(t)$ has a well defined anti-derivative that is uniformly bounded in time in $\langle \xi \rangle ^{-3/2}L^{\infty }_{\xi }$ .

Equation (10.5) with equation (10.27) can be written as

$$ \begin{align*} \begin{aligned} \partial_t X_+ = & - \frac{5i}{12 \, t} \Big[ \ell_{+ \infty}^2 \big| (S X)_1 \big|^2 (S X)_1 \overline{T}(\xi) + \ell_{- \infty}^2 \big| (S X)_2 \big|^2 (S X)_2 \overline{R_-}(\xi) \Big] + R(t,\xi), \\ \partial_t X_- = & - \frac{5i}{12 \, t} \Big[ \ell_{+ \infty}^2 \big| (S X)_1 \big|^2 (S X)_1 \overline{R_+}(\xi) + \ell_{- \infty}^2 \big| (S X)_2 \big|^2 (S X)_2 \overline{T}(\xi) \Big] + R(t,\xi), \end{aligned} \end{align*} $$

where S is the scattering matrix in equation (3.12). If we denote $(Z_+(\xi ),Z_-(\xi ))^t := S(\xi ) (X_+(\xi ), X_-(\xi ))^t$ and use equation (3.11), this simplifies to give

(10.6) $$ \begin{align} \begin{aligned} \partial_t Z_{\pm} = & - \frac{5i}{12\, t} \ell_{\pm \infty}^2 |Z_{\pm}|^2 Z_{\pm} + R(t,\xi). \end{aligned} \end{align} $$

Defining the modified profile $W=(W_+(\xi ),W_-(\xi ))^t$ by

(10.7) $$ \begin{align} \begin{aligned} & W_{\pm}(t,\xi) := \exp\Big( \frac{5i}{12} \ell_{\pm \infty}^2\int_0^t |Z_{\pm}(s,\xi)|^2 \, \frac{ds}{s+1} \Big) \, Z_\pm(t,\xi), \\ & |W_\pm(t,\xi)|=|Z_\pm(t,\xi)|, \end{aligned} \end{align} $$

we see that

(10.8) $$ \begin{align} \partial_t W_{\pm}(t,\xi) = \exp\Big( \frac{5i}{12} \ell_{\pm \infty}^2 \int_0^t |Z_{\pm}|^2\, \frac{ds}{s+1} \Big) \, R(t,\xi). \end{align} $$

In particular this implies that $\partial _t |W_{\pm }|^2 = 2\mathrm {Re}\big (R(t,\xi ) \overline {Z_{\pm }}\big )$ and therefore, since S is unitary,

(10.9) $$ \begin{align} \begin{aligned} \langle \xi \rangle^{3}\Big( |\widetilde{f}(t,\xi)|^2 - |\widetilde{f}(0,\xi)|^2 \Big) \lesssim \Big| \mathrm{Re} \int_0^t \langle \xi \rangle^{3/2} R(s,\xi) \cdot \langle \xi \rangle^{3/2}\overline{Z_{\pm}}(s,\xi) \, ds \Big| \lesssim {\varepsilon}_1^4. \end{aligned} \end{align} $$

For this last inequality, we have used the bounds in equation (10.3) (which in particular imply that R has a well-defined anti-derivative), integration by parts in s, equation (10.6) and the a priori assumption $|\langle \xi \rangle ^{3/2}Z_\pm (t,\xi )| \lesssim {\varepsilon }_1$ .

Similarly, from equation (10.8), using that the remainders satisfy estimates like equation (10.3), integrating by parts in s and using that the time derivative of the exponential factor is $O({\varepsilon }_1^2 \langle t \rangle ^{-1})$ , we can see that, for all $0<t_1<t_2$ ,

$$ \begin{align*} \langle \xi \rangle^{3/2} \big| W(t_1,\xi) - W(t_2,\xi) \big| \lesssim {\varepsilon}_1^3 \, t_1^{-\delta_0}. \end{align*} $$

By letting $W_\epsilon ^{\infty }(\xi ) := \lim _{t \rightarrow \infty } W_\epsilon (t,\xi )$ in the space $\langle \xi \rangle ^{-3/2}L^{\infty }$ , it follows that

(10.10) $$ \begin{align} \langle \xi \rangle^{3/2} \Big| |Z_\pm(t,\xi)| -|W_\pm^{\infty}(\xi)| \Big| \lesssim {\varepsilon}_1^3 \, \langle t \rangle^{-\delta_0}. \end{align} $$

The conclusion in equation (10.4) follows from equations (10.7) and (10.10), up to possibly redefining the asymptotic profile $W_\pm ^{\infty }$ by a constant phase.

The rest of this section is organised as follows. In Section 10.1, we provide asymptotic formulas for oscillatory integrals like those defining $\mathcal {C}^{S1,2}$ . These formulas are first obtained at a formal level by applying heuristic stationary phase type estimates. In Section 10.2, we use these formulas to derive the leading order of equation (10.2) with the proper Hamiltonian structure. The precise bounds needed to rigorously justify these formulas – that is, the error estimates in equation (10.3) – are proved in Section 10.3.

10.1 Heuristic asymptotics

Our first aim is to compute the asymptotics as $t \to \infty $ for the main model operators

(10.11) $$ \begin{align} & I_\delta(t) := \iiint e^{it \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',\sigma')} F(\xi,\eta,\eta',\sigma') \delta(p_*)\,d\eta\,d\eta' \,d\sigma', \end{align} $$

(10.12) $$ \begin{align} & I_{\operatorname{p.v.}}(t) := \iiint e^{it \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',\sigma')} F(\xi,\eta,\eta',\sigma') \frac{\widehat{\phi}(p_*)}{p_*}\,d\eta\,d\eta' \,d\sigma', \end{align} $$

where

(10.13) $$ \begin{align} p_* = \lambda_* \xi - \mu_* \eta - \mu^{\prime}_* \eta' - \nu^{\prime}_* \sigma', \end{align} $$

and

(10.14) $$ \begin{align} \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',\lambda_* \xi - \mu_* \eta - \mu^{\prime}_* \eta'-p_*) = \langle \xi \rangle -\kappa_1 \langle \eta \rangle - \kappa_2 \langle \eta' \rangle - \kappa_3 \langle \lambda_* \xi - \mu_* \eta - \mu^{\prime}_* \eta'-p_* \rangle. \end{align} $$

Note that the operators $\mathcal {C}^{S1,2}$ are of the form in equations (10.11)–(10.12) above.

We begin by examining the phase, which we sometimes denote just by $\Phi = \Phi (\xi ,\eta ,\eta ',{\sigma }')$ , keeping the dependence on the various parameters $ \kappa _1,\kappa _2, \kappa _3, \lambda _*,\mu _*,\mu ^{\prime }_*,\nu ^{\prime }_*$ implicit.

Observing that $\nabla _{\eta ,\eta '} \Phi = 0$ implies that $\eta ' = \kappa _1 \kappa _2 \mu ^{\prime }_* \mu _* \eta $ , a small computation shows that the stationary point with respect to $\eta $ and $\eta '$ is given by

(10.15) $$ \begin{align} \nabla_{\eta,\eta'} \Phi = 0 \qquad \Longleftrightarrow \qquad \left\{ \begin{array}{l} \eta = \eta_S = \kappa_3 \mu_*(\kappa_1 + \kappa_3 + \kappa_1 \kappa_2 \kappa_3)^{-1} (\lambda_* \xi - p_*). \\ \\ \eta' = \eta^{\prime}_S = \kappa_1 \kappa_2 \kappa_3 \mu_*'(\kappa_1 + \kappa_3 + \kappa_1 \kappa_2 \kappa_3)^{-1} (\lambda_* \xi - p_*), \\ \\ \sigma' = \sigma^{\prime}_S = \nu^{\prime}_* \kappa_1 (\kappa_1 + \kappa_3 + \kappa_1 \kappa_2 \kappa_3)^{-1} (\lambda_* \xi - p_*). \end{array} \right. \end{align} $$

Furthermore, at the stationary point,

(10.16) $$ \begin{align} \operatorname{Hess}_{\eta,\eta'} \Phi = \left( \begin{array}{ll} - \kappa_1 \tau''(\eta_S) - \kappa_3 \tau''(\sigma^{\prime}_S) \quad & - \kappa_3 \mu_* \mu^{\prime}_* \tau''(\sigma^{\prime}_S) \\ \\ - \kappa_3 \mu_* \mu^{\prime}_* \tau''(\sigma^{\prime}_S) & -\kappa_2 \tau''(\eta^{\prime}_S) - \kappa_3 \tau''(\sigma^{\prime}_S) \end{array} \right), \qquad \tau(x) := \langle x \rangle. \end{align} $$

Asymptotics for $I_\delta $

In this case, $p_*=0$ , and the stationary point is

(10.17) $$ \begin{align} \begin{array}{l} \eta = \eta_{S0} = \kappa_3 \mu_*(\kappa_1 + \kappa_3 + \kappa_1 \kappa_2 \kappa_3)^{-1} \lambda_* \xi, \\ \eta' = \eta^{\prime}_{S0} = \kappa_1 \kappa_2 \kappa_3 \mu_*'(\kappa_1 + \kappa_3 + \kappa_1 \kappa_2 \kappa_3)^{-1} \lambda_* \xi, \\ \sigma' = \sigma^{\prime}_{S0} = \nu^{\prime}_* \kappa_1 (\kappa_1 + \kappa_3 + \kappa_1 \kappa_2 \kappa_3)^{-1} \lambda_* \xi. \end{array} \end{align} $$

We distinguish two cases:

• • If $|\kappa _1 + \kappa _3 + \kappa _1 \kappa _2 \kappa _3| = 1$ , then $|\eta _{S0}| = |\eta ^{\prime }_{S0}| = |\sigma ^{\prime }_{S0} | = |\xi |$ and

  (10.18) $$ \begin{align} \begin{aligned} & \Phi(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}) = (1 - \kappa_1 - \kappa_2 - \kappa_3) \langle \xi \rangle, \\ & \operatorname{det} \operatorname{Hess} \Phi(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}) = [(\kappa_1 + \kappa_3)(\kappa_2 + \kappa_3) - 1 ] \tau''(\xi)^2 = - \tau''(\xi)^2, \\ & \operatorname{sign} \operatorname{Hess} \Phi(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}) = 0, \end{aligned} \end{align} $$
  where we denote by $\operatorname {sign}M$ the number of positive minus the number of negative eigenvalues of a matrix M.

• • If $|\kappa _1 + \kappa _3 + \kappa _1 \kappa _2 \kappa _3| = 3$ , then $|\eta _{S0}| = |\eta ^{\prime }_{S0}| = |\sigma ^{\prime }_{S0} | = |\xi |/3$ and

  $$ \begin{align*} & \Phi(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}) = \langle \xi \rangle - ( \kappa_1 + \kappa_2 + \kappa_3)\langle \xi /3 \rangle, \\ & \operatorname{det} \operatorname{Hess} \Phi(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}) = [(\kappa_1 + \kappa_3)(\kappa_2 + \kappa_3) - 1 ] \tau''(\xi/3)^2, \\ & \operatorname{Tr} \operatorname{Hess} \Phi(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}) =- (\kappa_1 + \kappa_2 + 2 \kappa_3) \tau''(\xi/3). \end{align*} $$

In both cases, by the stationary phase lemma,

$$ \begin{align*}I_\delta(t) \overset{t \to + \infty}{\sim} \frac{2\pi}{t} \frac{e^{i\frac{\pi}{4} \operatorname{sign} \operatorname{Hess} \Phi}}{| \operatorname{det} \operatorname{Hess} \Phi|^{1/2}} e^{it\Phi(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0})} F(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}). \end{align*} $$

If $\Phi = 0$ (hence $\{ \kappa _1,\kappa _2,\kappa _3 \} = \{+,+,-\}$ ),

(10.19) $$ \begin{align} I_\delta(t) \overset{t \to + \infty}{\sim} \frac{2\pi}{t} \frac{1}{\tau''(\xi)} F(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}). \end{align} $$

Asymptotics for $I_{\mathrm {p.v.}}$

Here $p_* \neq 0$ and, to leading order in $p_*$ small, $\Phi $ and $\operatorname {det} \operatorname {Hess} \Phi (\xi ,\eta _S,\eta ^{\prime }_S,\sigma ^{\prime }_S)$ agree with their value at $p_*=0$ computed above. We also compute the next order in $p_*$ of $\Phi $ :

• • If $|\kappa _1 + \kappa _3 + \kappa _1 \kappa _2 \kappa _3| = 1$ , then

  $$ \begin{align*}\Phi(\xi,\eta_S,\eta^{\prime}_S,\sigma^{\prime}_S) = \langle \xi \rangle - (\kappa_1 + \kappa_2 + \kappa_3) \left[ \langle \xi \rangle - \tau'(\lambda_* \xi) p_* \right] + O(p_*^2). \end{align*} $$

• • If $|\kappa _1 + \kappa _3 + \kappa _1 \kappa _2 \kappa _3| = 3$ , then

  $$ \begin{align*}\Phi(\xi,\eta_S,\eta^{\prime}_S,\sigma^{\prime}_S) = \langle \xi \rangle - (\kappa_1 + \kappa_2 + \kappa_3) \left[ \langle \xi /3\rangle - \frac{1}{3}\tau'\left( \frac{\lambda_* \xi}{3} \right) p_*\right] + O(p_*^2). \end{align*} $$

In order to give asymptotics, we focus on the former case ( $|\kappa _1 + \kappa _3 + \kappa _1 \kappa _2 \kappa _3| = 1$ ) since it is the most relevant. Applying the stationary phase lemma for $p_*$ fixed,

$$ \begin{align*}I_{\operatorname{p.v.}}(t) \overset{t \to + \infty}{\sim} \frac{2\pi}{t} \frac{1}{\tau''(\xi)} e^{it \langle \xi \rangle (1 - \kappa_1 - \kappa_2 - \kappa_3)} F(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}) \int e^{it \tau'(\lambda_* \xi) (\kappa_1 + \kappa_2 + \kappa_3) p_*} \frac{\widehat{\phi}(p_*)}{p_*}\,dp_*. \end{align*} $$

Since $\widehat {\mathcal {F}} \frac {\widehat {\phi }(x)}{x} = \frac {1}{\sqrt {2\pi }} \widehat {{\mathcal {F}}}(1/x) \ast \phi = - \frac {i}{2} \mbox {sign} \ast \phi $ (see equation (4.8)),

$$ \begin{align*}I_{\operatorname{p.v.}}(t) \overset{t \to + \infty}{\sim} i \frac{\pi \sqrt{2\pi}}{t} \frac{1}{\tau''(\xi)} e^{it \langle \xi \rangle (1 - \kappa_1 - \kappa_2 - \kappa_3)} F(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}) \mbox{sign} ( \tau'(\lambda_* \xi) (\kappa_1 + \kappa_2 + \kappa_3)). \end{align*} $$

If $\Phi =0$ ,

(10.20) $$ \begin{align} I_{\operatorname{p.v.}}(t) \overset{t \to + \infty}{\sim} i \frac{\pi \sqrt{2\pi}}{t} \frac{1}{\tau''(\xi)} F(\xi,\eta_{S0},\eta^{\prime}_{S0},\sigma^{\prime}_{S0}) \mbox{sign} (\lambda_* \xi ). \end{align} $$

Asymptotics for $\widetilde {f}$

We apply the above asymptotics to the situation that interests us to derive (formally, for the moment) asymptotics for $\partial _t\widetilde {f}$ ; see equation (7.59).

The only relevant terms in the expansion are equations (10.19) and (10.20) for which $\Phi = 0$ and that correspond to $\{ \kappa _1,\kappa _2, \kappa _3 \} = \{+,+,-\}$ . Comparing the definition of $p_\ast $ in equation (10.13) with equation (5.43), we obtain (recall $\kappa _1=\iota _1$ )

$$ \begin{align*}\lambda_* = \iota_2 \lambda \nu, \qquad \mu_* = \kappa_1 \iota_2 \mu \nu, \qquad \mu^{\prime}_* = \kappa_2 \iota_2 \lambda' \mu', \qquad \nu^{\prime}_* = \kappa_3 \iota_2 \lambda' \nu' \end{align*} $$

and find that

$$ \begin{align*} & \eta_{S0} = \lambda \mu \xi, \qquad \eta^{\prime}_{S0} = \lambda \nu \lambda' \mu' \xi, \qquad \sigma^{\prime}_{S0} = \lambda \nu \lambda' \nu' \xi. \end{align*} $$

Comparing with the definition of $\Sigma _0$ in equation (5.42), we get that the value of $\Sigma _0$ at these points is

(10.21) $$ \begin{align} \Sigma_0 = \left\{ \begin{array}{ll} 2 \iota_2 \nu \lambda \xi & \,\, \mbox{if } \,\, (\kappa_1,\kappa_2,\kappa_3) = (-,+,+), \\[3pt] 0 & \,\, \mbox{if } \,\, (\kappa_1,\kappa_2,\kappa_3) = (+,-,+)\ \mbox{or}\ (+,+,-). \end{array} \right. \end{align} $$

Recall the formula in equation (5.46) for the leading order symbol in the cubic terms appearing in equations (5.57)–(5.58). We can compute their asymptotics as $t\rightarrow \infty $ using equations (10.19) and (10.20), obtaining

$$ \begin{align*} & \mathcal{C}^S_{\kappa_1 \kappa_2 \kappa_3}(f,f,f)(\xi) \\ & \quad \sim - \frac{1}{32 i t} \langle \xi \rangle^3 \sum_{\substack{\epsilon,\epsilon',\iota_2 \\ \lambda,\mu,\nu,\lambda',\mu',\nu'}}\frac{1}{ \pi^2 ({(1-\kappa_1)\langle \xi \rangle - \iota_2\langle\Sigma_0\rangle}) \langle \xi \rangle^3 \langle \Sigma_0 \rangle } \big(A^{\epsilon,\epsilon'}_{\nu,\lambda'}(\Sigma_0)\big)_{\iota_2} \\ & \quad \quad \times \mathbf{a}_{\lambda,-}^{\epsilon}(\xi) \mathbf{a}_{\mu,\kappa_1}^{\epsilon}(\lambda \mu \xi) \mathbf{a}_{\mu',\kappa_2}^{\epsilon'}(\lambda \nu \lambda' \mu' \xi) \mathbf{a}_{\nu',\kappa_3}^{\epsilon'}(\lambda \nu \lambda' \nu' \xi) \widetilde{f}_{\kappa_1}(\lambda \mu \xi) \widetilde{f}_{\kappa_2}(\lambda \nu \lambda' \mu' \xi) \widetilde{f}_{\kappa_3}(\lambda \nu \lambda' \nu' \xi) \\ & \quad \quad \times \ell_{\epsilon \infty} \ell_{\epsilon' \infty} \left[ \pi^2 (1+\epsilon\epsilon'\nu \lambda' ) \iota_2 + \pi^2(\epsilon'\lambda'+\epsilon\nu) \operatorname{sign}(\iota_2 \lambda \nu \xi)\right]. \end{align*} $$

Changing $\lambda '$ to $\lambda \nu \lambda '$ , this becomes

(10.22) $$ \begin{align} \begin{aligned} \mathcal{C}^S_{\kappa_1 \kappa_2 \kappa_3}(f,f,f)(\xi) & \sim \frac{i}{32 t} \sum_{\substack{\epsilon,\epsilon',\iota_2 \\ \lambda,\mu,\nu, \lambda',\mu',\nu'}}\frac{\iota_2}{ ((1-\kappa_1)\langle \xi \rangle - \iota_2\langle\Sigma_0\rangle) \langle \Sigma_0 \rangle} \big(A^{\epsilon,\epsilon'}_{\nu,\lambda\nu\lambda'}(\Sigma_0)\big)_{\iota_2} \\ & \quad \times \mathbf{a}_{\lambda,-}^{\epsilon}(\xi) \mathbf{a}_{\mu,\kappa_1}^{\epsilon}(\lambda \mu \xi) \mathbf{a}_{\mu',\kappa_2}^{\epsilon'}( \lambda' \mu' \xi) \mathbf{a}_{\nu',\kappa_3}^{\epsilon'}(\lambda' \nu' \xi) \widetilde{f}_{\kappa_1}(\lambda \mu \xi) \widetilde{f}_{\kappa_2}( \lambda' \mu' \xi) \widetilde{f}_{\kappa_3}( \lambda' \nu' \xi) \\ & \quad \times \ell_{\epsilon \infty} \ell_{\epsilon' \infty} \big[1+\epsilon\epsilon'\lambda \lambda' + (\epsilon'\lambda'+ \epsilon{\lambda}) \operatorname{sign}(\xi)\big]. \end{aligned} \end{align} $$

10.2 Structure of modified scattering

In this subsection, we analyse the leading orders in the (resonant) asymptotic terms. In view of equation (10.22), we are interested in the structure of the term

(10.23) $$ \begin{align} \begin{aligned} & N_{{\kappa}_1{\kappa}_2{\kappa}_3}(f,f,f)(t,\xi) := \frac{1}{\langle \Sigma_0 \rangle} \sum_{\substack{\epsilon,\epsilon',\iota_2 \\ \lambda,\mu,\nu,\lambda',\mu',\nu'}} \frac{\iota_2}{(1-\kappa_1)\langle \xi \rangle - \iota_2 \langle\Sigma_0\rangle} \big(A^{\epsilon,\epsilon'}_{\nu,\lambda\nu\lambda'}(\Sigma_0)\big)_{\iota_2} \\ & \qquad \qquad \times \mathbf{a}_{\lambda,-}^{\epsilon}(\xi) \, \mathbf{a}_{\mu,\kappa_1}^{\epsilon}(\lambda \mu \xi) \, \mathbf{a}_{\mu',\kappa_2}^{\epsilon'}( \lambda' \mu' \xi) \, \mathbf{a}_{\nu',\kappa_3}^{\epsilon'}(\lambda' \nu' \xi) \\ & \qquad \qquad \times \widetilde{f}_{\kappa_1}(\lambda \mu \xi) \, \widetilde{f}_{\kappa_2}( \lambda' \mu' \xi) \, \widetilde{f}_{\kappa_3}( \lambda' \nu' \xi) \, \ell_{\epsilon \infty} \ell_{\epsilon' \infty} \big[1 + \epsilon\epsilon^{\prime}\lambda \lambda' + [ \epsilon\lambda + \epsilon^{\prime}\lambda'] \operatorname{sign}(\xi)\big]. \end{aligned} \end{align} $$

For the term $\big [1 + \epsilon \epsilon ^{\prime }\lambda \lambda ' + [\epsilon \lambda + \epsilon ^{\prime }\lambda '] \operatorname {sign}(\xi )\big ]$ to be nonzero, we need $\epsilon \lambda = \epsilon ' \lambda '$ . In view of the formulas in equation (5.41) for $A^{\epsilon ,\epsilon '}_{{\lambda },{\lambda }'}$ , this further imposes that $\epsilon = \epsilon '$ and $\lambda = \lambda '$ , in which case $A^{\epsilon , \epsilon '}_{\lambda , \lambda '} = 1/2$ . Finally, one can sum over $\nu $ , which does not appear in the expression, and equation (10.23) becomes

$$ \begin{align*} N_{{\kappa}_1{\kappa}_2{\kappa}_3}(f,f,f)(t,\xi) & := \frac{2}{\langle \Sigma_0 \rangle} \sum_{\substack{\epsilon,\iota_2 \\ \lambda,\mu,\mu',\nu'}} \frac{\iota_2}{(1-\kappa_1)\langle \xi \rangle - \iota_2 \langle\Sigma_0\rangle} \\ &\quad \times \mathbf{a}_{\lambda,-}^{\epsilon}(\xi) \, \mathbf{a}_{\mu,\kappa_1}^{\epsilon}(\lambda \mu \xi) \, \mathbf{a}_{\mu',\kappa_2}^{\epsilon}( \lambda \mu' \xi) \, \mathbf{a}_{\nu',\kappa_3}^{\epsilon}(\lambda \nu' \xi) \\ & \quad\times \widetilde{f}_{\kappa_1}(\lambda \mu \xi) \, \widetilde{f}_{\kappa_2}( \lambda \mu' \xi) \, \widetilde{f}_{\kappa_3}( \lambda \nu' \xi) \,\ell_{\epsilon \infty}^2 \big[1 + \epsilon\lambda \operatorname{sign}(\xi)\big]. \end{align*} $$

The flat case. For the reader’s convenience, we first look at the simpler case $V=0$ , for which $T\equiv 1$ , $R_\pm \equiv 0$ , so that equation (4.5) reads

$$ \begin{align*} \mathbf{a}^-_+(\xi) = \mathbf{a}^+_+(\xi) \equiv 1, \qquad \mathbf{a}^+_-(\xi) = \mathbf{a}^-_-(\xi) \equiv 0, \end{align*} $$

and $\ell _{+\infty } = -\ell _{-\infty }$ , which we set to $1$ without loss of generality. Then in equation (10.23), only the sum over $\lambda = \mu = \mu ' = \nu '=+$ survives. Moreover, summing over $\epsilon $ eliminates the contribution to the summand from the $\epsilon \lambda \operatorname {sign}(\xi )$ factor. Overall, this gives

(10.24) $$ \begin{align} \begin{aligned} N_{{\kappa}_1{\kappa}_2{\kappa}_3}(f,f,f)(t,\xi) & = \frac{4}{\langle \Sigma_0 \rangle} \sum_{\iota_2} \frac{\iota_2}{(1-\kappa_1)\langle \xi \rangle - \iota_2\langle\Sigma_0\rangle} \, \widetilde{f}_{\kappa_1}(\xi) \, \widetilde{f}_{\kappa_2}(\xi) \, \widetilde{f}_{\kappa_3}(\xi). \end{aligned} \end{align} $$

When ${\kappa }_1=+$ , so that ${\kappa }_2{\kappa }_3=-$ and $\Sigma _0 = 0$ , this is

$$ \begin{align*} \begin{aligned} - 8 \widetilde{f}(\xi) \, {\big| \widetilde{f}(\xi) \big|}^2. \end{aligned} \end{align*} $$

When $\kappa _1=-$ , so that $\langle \Sigma _0 \rangle =\langle 2 \xi \rangle $ , we get

$$ \begin{align*} \begin{aligned} \frac{4}{\langle 2 \xi \rangle} \sum_{\iota_2} \frac{\iota_2}{2 \langle \xi \rangle -\iota_2\langle 2 \xi \rangle } \, \overline{\widetilde{f}}(\xi) \, {\big( \widetilde{f}(\xi) \big)}^2 = \frac{8}{3} \, {|\widetilde{f}(\xi)|}^2 \, \widetilde{f}(\xi). \end{aligned} \end{align*} $$

Overall, we find that

$$ \begin{align*}\sum_{\substack{(\kappa_1,\kappa_2,\kappa_3) = (+,+,-), \\ (+,-,+), (-,+,+)}} N_{{\kappa}_1{\kappa}_2{\kappa}_3}(f,f,f)(t,\xi) =-\frac{40}{3} |\widetilde{f}(\xi)|^2 \widetilde{f}(\xi). \end{align*} $$

In particular, from equations (10.22)–(10.23) and the fact that all the other terms in equation (7.59) for $\partial _t \widetilde {f}$ are lower-orders (in the sense that they satisfy estimates like equation (10.3)), we can deduce

(10.25) $$ \begin{align} \partial_t \widetilde{f}(t,\xi) \approx -\frac{5i}{12t} |\widetilde{f}(\xi)|^2 \widetilde{f}(\xi). \end{align} $$

This leads to ‘standard’ modified scattering as in [30].

The general case. If $({\kappa }_1,{\kappa }_2,{\kappa }_3)=(+,+,-)$ (which is identical to $({\kappa }_1,{\kappa }_2,{\kappa }_3)=(+,-,+)$ ), $\Sigma _0=0$ and

$$ \begin{align*} \begin{aligned} N_{+--}(f,f,f)(t,\xi) & = -4\sum_{\substack{\epsilon, \\ \lambda,\mu,\mu',\nu'}} \overline{\mathbf{a}_{\lambda}^{\epsilon}(\xi)} \, \mathbf{a}_{\mu}^{\epsilon}(\lambda \mu \xi) \, \mathbf{a}_{\mu'}^{\epsilon}(\lambda \mu' \xi) \, \overline{\mathbf{a}_{\nu'}^{\epsilon}(\lambda \nu' \xi)} \\ & \qquad \qquad \qquad \, \times \widetilde{f}(\lambda \mu \xi) \, \widetilde{f}(\lambda \mu' \xi)\,\overline{\widetilde{f}(\lambda \nu' \xi)} \, \ell_{\epsilon \infty}^2 [1 + \epsilon \lambda \operatorname{sign}(\xi)]. \end{aligned} \end{align*} $$

If $({\kappa }_1,{\kappa }_2,{\kappa }_3)=(-,+,+)$ , $\Sigma _0=2\iota _2 \nu \lambda \xi $ , and we get

$$ \begin{align*} N_{-++}(f,f,f)(t,\xi) & = \frac{4}{3}\sum_{\substack{\epsilon, \\ \lambda,\mu,\mu',\nu'}} \overline{\mathbf{a}_{\lambda}^{\epsilon}(\xi)} \, \mathbf{a}_{\mu}^{\epsilon}(\lambda \mu \xi) \, \mathbf{a}_{\mu'}^{\epsilon}(\lambda \mu' \xi) \, \overline{\mathbf{a}_{\nu'}^{\epsilon}(\lambda \nu' \xi)} \\ & \qquad \qquad \qquad \,\times \widetilde{f}(\lambda \mu \xi) \, \widetilde{f}(\lambda \mu' \xi) \, \overline{\widetilde{f}(\lambda \nu' \xi)} \,\ell_{\epsilon \infty}^2 [1 + \epsilon \lambda \operatorname{sign}(\xi)]. \end{align*} $$

Therefore,

(10.26) $$ \begin{align} \begin{aligned} \sum_{\substack{(\kappa_1,\kappa_2,\kappa_3) = (+,+,-), \\ (+,-,+), (-,+,+)}} N_{{\kappa}_1{\kappa}_2{\kappa}_3}(f,f,f)(t,\xi)& = - \frac{20}{3} \sum_{\substack{\epsilon, \\ \lambda,\mu,\mu',\nu'}} \overline{\mathbf{a}_{\lambda}^{\epsilon}(\xi)} \, \mathbf{a}_{\mu}^{\epsilon}(\lambda \mu \xi) \, \mathbf{a}_{\mu'}^{\epsilon}(\lambda \mu' \xi) \, \overline{\mathbf{a}_{\nu'}^{\epsilon}(\lambda \nu' \xi)}\\ & \times \widetilde{f}(\lambda \mu \xi) \, \widetilde{f}(\lambda \mu' \xi) \, \overline{\widetilde{f}(\lambda \nu' \xi)} \, \ell_{\epsilon \infty}^2 [1 + \epsilon \lambda \operatorname{sign}(\xi)]. \end{aligned} \end{align} $$

Hamiltonian structure. Recall the evolution equation (7.59) for $\widetilde {f}$ . As we show in Section 11.3, all the terms on the right-hand side of equation (7.59), with the exception of $\mathcal {C}^{S1,2}$ , decay at an integrable-in-time rate. Then from equations (10.22), (10.23) and (10.26), and letting $t = \log t'$ , we see that the asymptotic evolution of $\widetilde {f}$ is governed to leading order by the ODE

$$ \begin{align*} \partial_{t'} \widetilde{f}(t',\xi) & = -\frac{5i}{24} \sum_{\substack{\epsilon, \\ \lambda,\mu,\mu',\nu'}} \overline{\mathbf{a}_{\lambda}^{\epsilon}(\xi)} \, \mathbf{a}_{\mu}^{\epsilon}(\lambda \mu \xi) \, \mathbf{a}_{\mu'}^{\epsilon}(\lambda \mu' \xi) \, \overline{\mathbf{a}_{\nu'}^{\epsilon}(\lambda \nu' \xi)} \\ &\quad \times \widetilde{f}(t',\lambda \mu \xi) \, \widetilde{f}(t',\lambda \mu' \xi) \, \overline{\widetilde{f}(t',\lambda \nu' \xi)} \, \ell_{\epsilon \infty}^2 [1 + \epsilon \lambda \operatorname{sign}(\xi) ]. \end{align*} $$

We now show how to view the joint evolution of $\widetilde {f}(t',\xi )$ and $\widetilde {f}(t',-\xi )$ into the form of an Hamiltonian system. For $\xi>0$ , we let

$$ \begin{align*}X_+(t') = \widetilde{f}(t',\xi), \qquad X_-(t') = \widetilde{f}(t',-\xi). \end{align*} $$

Then the evolution is

$$ \begin{align*} & \frac{d}{dt'} X_+ = -\frac{5}{12} i \sum_{\substack{\epsilon,\mu,\mu',\nu'}} \overline{\mathbf{a}_{\epsilon}^{\epsilon}(\xi)} \, \mathbf{a}_{\mu}^{\epsilon}(\epsilon \mu \xi) \, \mathbf{a}_{\mu'}^{\epsilon}(\epsilon \mu' \xi) \, \overline{\mathbf{a}_{\nu'}^{\epsilon}(\epsilon \nu' \xi)} \, X_{\epsilon \mu} \, X_{\epsilon \mu' } \, \overline{X_{\epsilon \nu'}} \, \ell_{\epsilon \infty}^2, \\ & \frac{d}{dt'} X_- = -\frac{5}{12} i \sum_{\substack{\epsilon,\mu,\mu',\nu'}} \overline{\mathbf{a}_{-\epsilon}^{\epsilon}(-\xi)} \, \mathbf{a}_{\mu}^{\epsilon}(\epsilon \mu \xi) \, \mathbf{a}_{\mu'}^{\epsilon}(\epsilon \mu' \xi) \, \overline{\mathbf{a}_{\nu'}^{\epsilon}(\epsilon \nu' \xi)} \, X_{\epsilon \mu} \, X_{\epsilon \mu' } \, \overline{X_{\epsilon \nu'}} \, \, \ell_{\epsilon \infty}^2. \end{align*} $$

The main observation is that this derives from the Hamiltonian

(10.27) $$ \begin{align} \begin{aligned} H(X) & = \frac{5}{24} \sum_{\epsilon} \left| \sum_{\mu} \mathbf{a}_{\mu}^{\epsilon}(\epsilon \mu \xi) X_{\epsilon \mu} \right|{}^4 \ell_{\epsilon \infty}^2 \\ &= \frac{5}{24} \left[ \ell_{+\infty}^2 |(S(\xi)X)_1|^4 + \ell_{-\infty}^2 |(S(\xi) X)_2|^4 \right], \end{aligned} \end{align} $$

where we regard $(X_+,X_-)$ as conjugate variables of $(\overline {X_+},\overline {X_-})$ and consider the standard (complex) symplectic form $J=-i$ ; in equation (10.27), S denotes the scattering matrix and X the vector $(X_+,X_-)$ . The evolution associated to H is

(10.28) $$ \begin{align} \begin{aligned} \frac{d}{dt'} X = - i \frac{\partial}{\partial \overline{X}} H. \end{aligned} \end{align} $$

Note that since H is invariant under phase rotations, the evolution equation (10.28) conserves $|X_+|^2 + |X_-|^2$ .

10.3 Rigorous asymptotics

Here we give the estimates necessary to justify the asymptotic formulas in equations (10.19) and (10.20) for the integrals in equations (10.11) and (10.12), thus obtaining a proof of the main asymptotics equations (10.2)–(10.3) in Proposition 10.1 We refer the reader to similar arguments in the literature, such as those in [32, 34] for fractional NLS equations and in [24, 7] for the NLS with a potential; see also references therein for other works that use different approaches, as well as [55] and the more recent [57].

In Sections 10.3.1 and 10.3.2, we look at the cases with $\{\kappa _1,\kappa _2,\kappa _3\} = \{+,+,-\}$ that give the leading order terms on the right-hand sides of equations (10.19) and (10.20) and, eventually, combined with the algebraic calculations of Section 10.2, the asymptotics in equation (10.2). In Section 10.3.3, we discuss how to handle all the other nonresonant and faster-decaying terms.

10.3.1 Asymptotics for equation (10.11) when $\{\kappa _1,\kappa _2,\kappa _3\} = \{+,+,-\}$

For simplicity, and without loss of generality, we may choose a single combination of the signs $\lambda ,\mu ,\dots $ , appearing in equation (10.13), and thus concentrate on the expression

(10.29) $$ \begin{align} \begin{aligned} & I_1(t,\xi) := \iint e^{it \Phi_1(\xi,\eta,\sigma)} F_1(t,\xi,\eta,{\sigma}) \,d\eta\,d{\sigma}, \\ & \Phi_1(\xi,\eta,{\sigma}) := \langle \xi \rangle -\langle \eta \rangle + \langle \sigma \rangle - \langle \xi - \eta + {\sigma} \rangle, \\ & F_1(t,\xi,\eta,{\sigma}) := \mathfrak{m}_1(\xi,\eta,{\sigma}) \, \widetilde{f}(t,\eta) \overline{\widetilde{f}(t,{\sigma})} \widetilde{f}(t,\xi-\eta+\sigma). \end{aligned} \end{align} $$

From the explicit formula in equation (5.46) and the bounds in Lemma 5.3 (see also the proofs of Lemmas 6.9 and 6.13), we can think that the symbol $\mathfrak {m}_1$ is smooth and satisfies

(10.30) $$ \begin{align} \left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\sigma}^c \mathfrak{m}_1(\xi,\eta,{\sigma}) \right| \lesssim \frac{1}{\langle \eta \rangle \langle \sigma \rangle \langle \xi - \eta + \sigma \rangle} \langle \mathrm{med}(|\eta|,|{\sigma}|,|\xi-\eta-\sigma|) \rangle^{a+b+c}. \end{align} $$

As we calculated earlier in the section (see equation (10.17)), the only (time-frequency) stationary point of the integral $I_1$ is at $(\eta ,\sigma ) = (\xi ,\xi )$ . Although one should think that the hardest case is when $|\xi | \approx \sqrt {3}$ , below we do not need to decompose in frequency space with respect to the distance to $\sqrt {3}$ , and it will suffice to use the bounds

(10.31) $$ \begin{align} {\| \varphi_{[-5,5]} \partial_{\xi} \widetilde{f} \|}_{L^2} \lesssim {\varepsilon}_1 \langle t \rangle^{\rho}, \qquad {\| \langle \xi \rangle (1-\varphi_{[-5,5]}) \partial_{\xi} \widetilde{f} \|}_{L^2} \lesssim {\varepsilon}_1 \langle t \rangle^{\alpha}, \end{align} $$

where $\rho := {\alpha } +{\beta }{\gamma }$ ; see equation (7.19).

We change variables so that the stationary point is at $(0,0)$ and look at

(10.32) $$ \begin{align} \begin{aligned} & I_1(t,\xi) = \iint e^{it \Phi_1(\xi,\xi+\eta,\xi+\eta+{\sigma})} \, F_1(t,\xi,\xi+\eta,\xi+\eta+{\sigma}) \,d\eta\,d{\sigma}, \\ & F_1(t,\xi,\xi+\eta,\xi+\eta+{\sigma}) = \mathfrak{m}_1(\xi,\xi+\eta,\xi+\eta+{\sigma}) \widetilde{f}(\xi+\eta) \overline{\widetilde{f}(\xi+\eta+{\sigma})} \widetilde{f}(\xi+{\sigma}). \end{aligned} \end{align} $$

To verify equation (10.19), we show that

(10.33) $$ \begin{align} \begin{aligned} \langle \xi \rangle^{3/2} \left| \int_0^t \Big[ I_1(s,\xi) - \frac{2\pi}{s} \, \langle \xi \rangle^3 \, F_1(s,\xi,\xi,\xi) \Big] \, \tau_m(s) ds \right| \lesssim {\varepsilon}_1^3 2^{-\delta_0 m}, \end{aligned} \end{align} $$

where $\delta _0>0$ small enough is to be chosen below. Notice that this is consistent with the estimates for the remainders in equations (10.2)–(10.3). Also notice that

$$ \begin{align*}F_1(t,\xi,\xi,\xi) = \mathfrak{m}_1(\xi,\xi,\xi)|\widetilde{f}(t,\xi)|^2\widetilde{f}(t,\xi),\end{align*} $$

where $\mathfrak {m}_1(\xi ,\xi ,\xi )$ coincides with the symbol appearing in the trilinear terms of Section 10.2.

Without loss of generality, we may assume that $|\eta |\geq |{\sigma }|$ . Moreover, we claim that it suffices to deal with

(10.34) $$ \begin{align} \langle t \rangle^{-2\alpha - 2\delta_0} \lesssim |\xi| \lesssim \langle t \rangle^{(1/2)(\alpha+p_0)+\delta_0}. \end{align} $$

To see this, we use the interpolation inequality

(10.35) $$ \begin{align} {\| \widetilde{f} \|}_{L^{\infty}} \lesssim {\big\|\widetilde{f}\big\|}_{L^2}^{1/2} {\big\|\partial_{\xi} \widetilde{f}\big\|}_{L^2}^{1/2}, \end{align} $$

which, for $k\geq 5$ , gives us

(10.36) $$ \begin{align} \begin{aligned} {\| \varphi_k \langle \xi \rangle^{3/2}\widetilde{f} \|}_{L^{\infty}} & \lesssim {\big\| \varphi_k\langle \xi \rangle^3 \widetilde{f}\big\|}_{L^2}^{1/2} \big( {\big\| \varphi_k' \widetilde{f}\big\|}_{L^2} + {\big\| \varphi_k \partial_{\xi} \widetilde{f}\big\|}_{L^2} \big)^{1/2} \\ & \lesssim 2^{-k}{\big\| \varphi_k\langle \xi \rangle^4 \widetilde{f}\big\|}_{L^2}^{1/2} \cdot ({\varepsilon}_1 \langle t \rangle^{\alpha})^{1/2} \lesssim 2^{-k} \cdot {\varepsilon}_1^2 \langle t \rangle^{(p_0+\alpha)/2}, \end{aligned} \end{align} $$

having used the a priori bounds in equation (7.10). Then if $2^k \geq \langle t \rangle ^{(\alpha +p_0)/2+\delta _0}$ , we already control uniformly in t and $\xi $ the quantity $\langle \xi \rangle ^{3/2}\widetilde {f}$ . For $k \leq -5$ instead, we have (see equation (7.22))

(10.37) $$ \begin{align} \begin{aligned} {\| \varphi_k \widetilde{f} \|}_{L^{\infty}} & \lesssim 2^{k/2} \langle t \rangle^{\alpha} \end{aligned} \end{align} $$

and therefore obtain the desired control whenever $2^k \lesssim \langle t \rangle ^{-2\alpha -2\delta _0}$ , as claimed.

We let $|\xi |\approx 2^k$ , with the constraints in equation (10.34), let $t \approx 2^m$ , $m=1,\dots $ , and split

(10.38) $$ \begin{align} \begin{aligned} & I_1(t,\xi) = \sum_{k_1 \geq k_2, \, k_1,k_2\in[k_0\infty)\cap {\mathbb Z}} I^{(1)}_{k_1,k_2}(t,\xi), \qquad k_0:= -m/2 + \delta m, \\ & I^{(1)}_{k_1,k_2}(t,\xi) := \iint e^{it \Phi_1} \, F_1(t) \,\varphi_{k_1}^{(k_0)}(\eta\langle \xi \rangle^{-3/2})\varphi_{k_2}^{(k_0)}({\sigma}\langle \xi \rangle^{-3/2}) \, d\eta\,d{\sigma}, \end{aligned} \end{align} $$

where $\delta $ will be chosen small enough, and we are omitting the arguments $(\xi ,\xi +\eta ,\xi +\eta +{\sigma })$ in $\Phi _1$ and $F_1$ for brevity. For simplicity we also restrict our attention to the main case when the size of all input frequencies are comparable to $2^k$ by looking at the case $|\eta |,|{\sigma }| \ll |\xi |$ : that is, $k_1,k_2\leq k - (3/2)k^+ - 10$ ; to simplify our notation, we omit the cutoffs induced by this restriction: that is, $\varphi _{\sim k} (\xi +\eta )$ , $\varphi _{\sim k} (\xi +\sigma +\eta )$ and $\varphi _{\sim k} (\xi +\sigma )$ . All other cases are simpler to handle.

Case $k_1=k_2=k_0$ . Note that from equation (10.31) under the restriction equation (10.34), we can infer (for $\alpha $ small enough)

(10.39) $$ \begin{align} {\| \varphi_k \partial_{\xi} \widetilde{f} \|}_{L^2} \lesssim {\varepsilon}_1 2^{-10k^+} \langle t \rangle^{\rho}. \end{align} $$

Then since $|\eta |,|\sigma | \ll |\xi |$ , from the a priori bounds in equations (7.10) and (10.30), we have

(10.40) $$ \begin{align} \begin{aligned} & |F_1(t,\xi,\xi+\eta,\xi+\eta+{\sigma})| \lesssim {\varepsilon}_1^3 2^{-9k^+/2}, \\ & {\| \partial_{\eta} F_1(t,\xi,\xi+\eta,\xi+\eta+{\sigma}) \|}_{L^2_{\eta}} \lesssim {\varepsilon}_1^3 \cdot 2^{-10k^+} \cdot \langle t \rangle^{\rho}, \\ & {\| \partial_{\sigma} F_1(t,\xi,\xi+\eta,\xi+\eta+{\sigma}) \|}_{L^2_{\sigma}} \lesssim {\varepsilon}_1^3 \cdot 2^{-10k^+} \cdot \langle t \rangle^{\rho}, \qquad \rho:=\alpha+\beta\gamma. \end{aligned} \end{align} $$

As a consequence,

(10.41) $$ \begin{align} \begin{aligned} & |F_1(t,\xi,\xi+\eta,\xi+\eta+{\sigma}) - F_1(t,\xi,\xi,{\sigma}+\xi)| \\ &\quad + |F_1(t,\xi,\xi,{\sigma}+\xi) - F_1(t,\xi,\xi,\xi)| \lesssim {\varepsilon}_1^3 2^{-10k^+}\langle t \rangle^{\rho} \cdot (|\eta| + |\sigma|)^{1/2}. \end{aligned} \end{align} $$

Using equation (10.41), we can see that the contribution close to the stationary points gives us the leading order term by arguing as follows. First, observe that

(10.42) $$ \begin{align} \begin{aligned} 2^{3k^+/2} & \Big| I^{(1)}_{k_0,k_0}(t,\xi) - F_1(t,\xi,\xi,\xi) \, \iint e^{it \Phi(\xi,\xi+\eta,\xi+\eta+{\sigma})} \,\varphi_{\leq k_0}(\eta\langle \xi \rangle^{-3/2})\varphi_{\leq k_0}({\sigma}\langle \xi \rangle^{-3/2}) \, d\eta\,d{\sigma} \Big| \\ & \lesssim 2^{3k^+/2} \cdot {\varepsilon}_1^3 2^{k_0/2} 2^{-10k^+} 2^{\rho m} \cdot 2^{2k_0 + 3k^+} = {\varepsilon}_1^3 \cdot 2^{(-5/4 + \rho + 5\delta/2)m}; \end{aligned} \end{align} $$

second, Taylor expanding, we have

(10.43) $$ \begin{align} \Phi_1(\xi,\xi+\eta,\xi+\eta+{\sigma}) = \frac{2\eta\sigma}{\langle \xi \rangle^3} + O\big((|\eta|+|{\sigma}|\big)^3 \langle \xi \rangle^{-4}) \end{align} $$

and therefore

(10.44) $$ \begin{align} \begin{aligned} 2^{3k^+/2} & \Big| F_1(t,\xi,\xi,\xi) \, \iint \Big[ e^{it \Phi(\xi,\xi+\eta,\xi+\eta+{\sigma})} - e^{2it \eta{\sigma} \langle \xi \rangle^{-3}} \Big] \,\varphi_{\leq k_0}(\eta\langle \xi \rangle^{-3/2})\varphi_{\leq k_0}({\sigma}\langle \xi \rangle^{-3/2}) \, d\eta\,d{\sigma} \Big| \\ & \lesssim {\varepsilon}_1^3 2^{-3k^+} \cdot 2^m 2^{3k_0} 2^{-4k^+} \cdot 2^{2k_0}2^{3k^+} \\ & \lesssim {\varepsilon}_1^3 2^{-3m/2 + 5\delta m}; \end{aligned} \end{align} $$

third, a calculation shows that

(10.45) $$ \begin{align} \iint e^{2it\eta{\sigma} \langle \xi \rangle^{-3}} \,\varphi_{\leq k_0}(\eta\langle \xi \rangle^{-3/2})\varphi_{\leq k_0}({\sigma}\langle \xi \rangle^{-3/2}) \, d\eta\,d{\sigma} = \langle \xi \rangle^3 \frac{\pi}{t} + O(|t|^{-5/4}). \end{align} $$

Finally, we need to ensure that we can choose $\delta>0$ so that equations (10.42)–(10.45) are consistent with the right-hand side of the desired bound in equation (10.33). According to equations (10.42) and (10.34), by making $\delta _0$ small enough, it suffices to pick $\delta $ such that

(10.46) $$ \begin{align} (5/2)\delta < 1/4-\rho; \end{align} $$

this is possible since (see equation (2.31))

(10.47) $$ \begin{align} 1/4-\rho = -\alpha +(1/2)({\beta}'+{\gamma}') - {\beta}'{\gamma}'> {\gamma}'\beta. \end{align} $$

Case $k_1> k_0$ . Since we are assuming $|\eta |\geq |{\sigma }|$ , we may restrict, without loss of generality, to $k_1\geq k_2$ ; for brevity, we will often omit writing this restriction. In the case $k_1>k_0$ , we want to exploit integration by parts in $\sigma $ through the identity $e^{it \Phi (\xi ,\xi +\eta ,\xi +\eta +{\sigma })} = (it\partial _{\sigma }\Phi )^{-1} \partial _{\sigma } e^{it \Phi (\xi ,\xi +\eta ,\xi +\eta +{\sigma })}$ using that, on the support of the integral $I^{(1)}_{k_1,k_2}$ ,

(10.48) $$ \begin{align} \begin{aligned} |\partial_{\sigma}\Phi(\xi,\xi+\eta,\xi+\eta+{\sigma})| = \Big| \frac{\xi+{\sigma}}{\langle \xi+\sigma \rangle} - \frac{\xi+{\sigma}+\eta}{\langle \xi+\sigma+\eta \rangle} \Big| & \gtrsim |\eta|\langle \xi \rangle^{-3} \approx 2^{k_1}2^{-(3/2)k^+}. \end{aligned} \end{align} $$

Note that, under our current frequencies restrictions, we have a bound on the norm of trilinear operators with symbol $(\partial _{\sigma }\Phi )^{-1}$ consistent with the (pointwise) bound from equation (10.48): that is, $2^{-k_1}2^{(3/2)k^+}$ . We treated similar terms multiple times in Section 9; see, for example, equations (9.6) and (9.9). We first use this fact to integrate by parts and estimate the $L^2$ norm of $I^{(1)}_{k_1,k_2}$ . Up to faster-decaying lower-orders (which include contributions from hitting the symbol $\mathfrak {m}_1$ or the cutoffs where one can repeat integration by parts), we have

(10.49) $$ \begin{align} \begin{aligned} \big| I^{(1)}_{k_1,k_2}(t,\xi) \big|& \lesssim \frac{1}{t} \, \Big| \iint e^{it \Phi(\xi,\xi+\eta,\xi+\eta+{\sigma})} \, \widetilde{f}(\eta+\xi) \partial_{\sigma}\Big( \overline{\widetilde{f}(t,\xi+\eta+{\sigma})} \widetilde{f}(t,\xi+\sigma) \Big) \\ \quad & \times \frac{1}{\partial_{\sigma}\Phi}\, \mathfrak{m}_1(\xi,\xi+\eta,\xi+\eta+{\sigma}) \,\varphi_{k_1}^{(k_0)}(\eta\langle \xi \rangle^{-3/2})\varphi_{k_2}^{(k_0)}({\sigma}\langle \xi \rangle^{-3/2}) \, d\eta\,d{\sigma} \Big|, \end{aligned} \end{align} $$

so that

(10.50) $$ \begin{align} \begin{aligned}\Big\| \langle \xi \rangle^2 \varphi_k(\xi) \sum_{k_1>k_0} I^{(1)}_{k_1,k_2}(t) \Big\|_{L^2} & \lesssim 2^{2k^+} \cdot 2^{-m} 2^{-k_1} 2^{(3/2)k^+} {\| P_k e^{-it\langle \partial_x \rangle} \mathcal{W}^* f(t) \|}_{L^{\infty}}^2 {\| \varphi_k \partial_{\xi} \widetilde{f} \|}_{L^2} \\ & \lesssim 2^{7k^+/2} \cdot 2^{-m} \cdot 2^{-k_0} \cdot ({\varepsilon}_1 2^{-m/2})^2 \cdot {\varepsilon}_1 2^{-10k^+} 2^{\rho m} \\ & \lesssim {\varepsilon}_1^3 2^{-3m/2} \cdot 2^{(\rho +\delta)m}, \end{aligned} \end{align} $$

having used equation (10.39) the linear decay estimate, and $k_0 = -m/2+\delta m$ .

Next, we estimate the $L^2$ norm of $\langle \xi \rangle \partial _{\xi } I^{(1)}_{k_1,k_2}$ and then will interpolate with the bound in equation (10.50). It is convenient to look back at the original integration variables as they appear in equation (10.29), so as to have simpler formulas. Let us write, for $k_1>k_0$ ,

(10.51) $$ \begin{align} \begin{aligned} & I^{(1)}_{k_1,k_2}(t,\xi) := \iint e^{it \Phi_1(\xi,\eta,\sigma)} F_1(t,\xi,\eta,{\sigma}) \varphi_{k_1}((\eta-\xi) \langle \xi \rangle^{3/2}) \varphi_{k_2}^{(k_0)}(({\sigma}-\eta)\langle \xi \rangle^{3/2}) \,d\eta\,d{\sigma}. \end{aligned} \end{align} $$

When applying $\langle \xi \rangle \partial _{\xi }$ to $I^{(1)}_{k_1,k_2}$ , we obtain one main term: that is,

$$ \begin{align*} & \iint t \, \langle \xi \rangle \partial_{\xi} \Phi_1(\xi,\eta,{\sigma}) \, e^{it \Phi_1(\xi,\eta,{\sigma})} \, \widetilde{f}(t,\eta) \overline{\widetilde{f}(t,\xi-\eta+{\sigma})} \widetilde{f}(t,\sigma) \\ & \qquad \times \mathfrak{m}_1(\xi,\eta,{\sigma}) \,\varphi_{k_1}((\eta-\xi)\langle \xi \rangle^{-3/2})\varphi_{k_2}^{(k_0)}(({\sigma}-\eta)\langle \xi \rangle^{-3/2}) \, d\eta\,d{\sigma}, \end{align*} $$

plus other lower-order terms that are easier to estimate. We then note that the following identity holds:

(10.52) $$ \begin{align} \big( \langle \xi \rangle\partial_{\xi} + \langle \eta \rangle \partial_{\eta} + \langle \sigma \rangle \partial_{\sigma} \big) \Phi_1 = - \frac{\xi-\eta+{\sigma}}{\langle \xi-\eta + {\sigma} \rangle}\Phi_1. \end{align} $$

Using equation (10.52), we can integrate by parts in $\eta ,{\sigma }$ and s and obtain

(10.53) $$ \begin{align} \begin{aligned} & \Big| \sum_{k_1>k_0} \int_0^t \langle \xi \rangle \partial_{\xi} I^{(1)}_{k_1,k_2}(s,\xi) \tau_m(s) \, ds \Big| \lesssim \Big| \int_0^t A(s,\xi) \tau_m(s) \, ds \Big| + \Big| \int_0^t B(s,\xi) \tau_m(s) \, ds \Big| + \cdots \\ & A(t,\xi) := \sum_{k_1>k_0} \iint e^{it \Phi_1(\xi,\eta,{\sigma})} \, \langle \eta \rangle \partial_{\eta} \widetilde{f}(t,\eta) \overline{\widetilde{f}(t,{\sigma})} \widetilde{f}(t,\xi-\eta+{\sigma}) \\ & \qquad \times \mathfrak{m}_1(\xi,\eta,{\sigma}) \,\varphi_{k_1}((\eta-\xi)\langle \xi \rangle^{-3/2})\varphi_{k_2}^{(k_0)}(({\sigma}-\eta)\langle \xi \rangle^{-3/2}) \, d\eta\,d{\sigma}, \\ &B(t,\xi) := \sum_{k_1>k_0} t \iint e^{it \Phi_1(\xi,\eta,{\sigma})} \frac{\xi-\eta+{\sigma}}{\langle \xi-\eta + {\sigma} \rangle} \, \partial_t \widetilde{f}(t,\eta) \overline{\widetilde{f}(t,{\sigma})} \widetilde{f}(t,\xi-\eta+{\sigma}) \\ & \qquad \times \mathfrak{m}_1(\xi,\eta,{\sigma}) \,\varphi_{k_1}((\eta-\xi)\langle \xi \rangle^{-3/2})\varphi_{k_2}^{(k_0)}(({\sigma}-\eta)\langle \xi \rangle^{-3/2}) \, d\eta\,d{\sigma}, \end{aligned} \end{align} $$

where, as usual, $`\cdots $ ’ denotes similar terms or faster-decaying remainders. Using an $L^2\times L^{\infty } \times L^{\infty }$ Hölder estimate for both terms in equation (10.53) gives

(10.54) $$ \begin{align} \begin{aligned} \Big\| \langle \xi \rangle \partial_{\xi} \sum_{k_1>k_0} \int_0^t I^{(1)}_{k_1,k_2}(s,\xi) \tau_m(s)\, ds \Big\|_{L^2} & \lesssim 2^m \sup_{s\approx 2^m }{\| \langle \xi \rangle \partial_{\xi} \widetilde{f}(s) \big\|}_{L^2} {\| P_k e^{is\langle \partial_x \rangle} \mathcal{W}^* f(s) \|}_{L^{\infty}}^2 \\ & \quad + 2^{2m} \sup_{s\approx 2^m }{\| \partial_s \widetilde{f}(s) \big\|}_{L^2} {\| P_k e^{is\langle \partial_x \rangle} \mathcal{W}^* f(s) \|}_{L^{\infty}}^2 \\ & \lesssim {\varepsilon}_1^3 2^{m \rho}, \end{aligned} \end{align} $$

having used equation (7.19), the a priori $L^{\infty }$ decay and equation (7.56).

Interpolating equations (10.50) and (10.54) through equation (10.35), and in view of our choice of parameters in equations (10.46)–(10.47) and (10.34), we obtain

$$ \begin{align*} 2^{(3/2)k^+} \Big| \sum_{k_1> k_0 } \int_0^t I^{(1)}_{k_1,k_2}(s,\xi) \tau_m(s)\,ds \Big| & \lesssim {\varepsilon}_1^3 2^{-m/4} 2^{(\rho + \delta/2) m}, \end{align*} $$

which suffices in view of equation (10.46).

10.3.2 Asymptotics for equation (10.12) when $\{\kappa _1,\kappa _2,\kappa _3\} = \{+,+,-\}$

Once again, without loss of generality, we may choose a single combination of the signs $\lambda ,\mu ,\dots $ , appearing in equation (10.13), and concentrate on the expression

(10.55) $$ \begin{align} \begin{aligned} & I_2(t,\xi) = \iiint e^{it \Phi_2(\xi,\eta,\sigma,p)} F_2(t,\xi,\eta,\eta',{\sigma}) \frac{\widehat{\phi}(p)}{p}\,d\eta\,d\eta'\,d\sigma, \\ & \Phi_2(\xi,\eta,\eta',{\sigma}) = \langle \xi \rangle -\langle \eta \rangle + \langle \eta' \rangle -\langle \sigma \rangle, \qquad p = \xi-\eta+\eta'-\sigma, \\ & F_2(t,\xi,\eta,\eta',{\sigma}) := \mathfrak{m}_2(\xi,\eta,\eta',{\sigma}) \, \widetilde{f}(t,\eta) \overline{\widetilde{f}(t,\eta')} \widetilde{f}(t,{\sigma}). \end{aligned} \end{align} $$

From the formula in equations (5.57)–(5.58) with equation (5.46) and the bounds in equation (5.26), we may assume that the symbol is smooth and satisfies

(10.56) $$ \begin{align} \left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\eta'}^c \partial_{\sigma}^d \mathfrak{m}_2(\xi,\eta,\eta',\sigma') \right| \lesssim \frac{1}{\langle \eta \rangle \langle \eta' \rangle \langle \sigma \rangle } \langle \mathrm{med}(|\eta|,|\eta'|,|{\sigma}|) \rangle^{a+b+c+d}. \end{align} $$

To obtain asymptotics for equation (10.55) and a rigorous proof of equation (10.20), we can use ideas similar to those used to treat equation (10.29) in Section 10.3.1 above; we will then follow similar steps and concentrate on the main differences, in particular on how to treat the $\mathrm {p.v.}$ , while skipping some of the other details.

Recall from equation (10.15) that the stationary points of the integral $I_2$ in equation (10.55) are $(\eta ,\eta ',\sigma ) = (\xi -p,\xi -p,\xi -p)$ . As in the treatment of equation (10.29), it is convenient to change variables by letting $\eta \mapsto \xi +\eta -p$ , $\eta '\mapsto \xi +\eta +{\sigma }-p$ and ${\sigma }\mapsto \xi +{\sigma }-p$ ; this centres the stationary points (in $(\eta ,{\sigma },p)$ ) at the origin and gives the expression

(10.57) $$ \begin{align} \begin{aligned} I_2(t,\xi) = \iiint & e^{it \Phi(\xi,\eta,\sigma,p)} F(t,\xi,\eta,{\sigma},p) \frac{\widehat{\phi}(p)}{p}\,d\eta\,d\sigma \,dp, \\ \Phi(\xi,\eta,{\sigma},p) & := \Phi_2(\xi,\xi+\eta-p,\xi+\eta+{\sigma}-p, \xi+{\sigma}-p) \\ \qquad \qquad \qquad & = \langle \xi \rangle - \langle \xi+\eta-p\rangle + \langle \xi+\eta+{\sigma} - p \rangle - \langle \xi+{\sigma} -p \rangle, \\ \mathfrak{m}(\xi,\eta,{\sigma},p) & := \mathfrak{m}_2(\xi,\xi+\eta-p,\xi+{\sigma}+\eta-p,\xi+{\sigma}-p), \\ F(t,\xi,\eta,{\sigma},p) & := \mathfrak{m}(\xi,\eta,{\sigma},p) \widetilde{f}(\xi+\eta-p) \overline{\widetilde{f}(\xi+\eta+{\sigma}-p)} \widetilde{f}(\xi+{\sigma}-p). \end{aligned} \end{align} $$

To verify equation (10.20) with a remainder estimate consistent with equation (10.3), we need to show that

(10.58) $$ \begin{align} \begin{aligned} \langle \xi \rangle^{3/2} \left| \int_0^t \Big[ I_2(s,\xi) - \frac{i\pi\sqrt{2\pi}}{t} \, \langle \xi \rangle^3 \, F(s,\xi,0,0,0) \, \mbox{sign} (\xi) \Big] \tau_m(s) ds \right| \lesssim {\varepsilon}_1^3 2^{-\delta_0 m} \end{aligned} \end{align} $$

for $\delta _0$ small enough. As per our usual notation, we let $|\xi | \approx 2^k$ and, in view of equation (10.34) (and the interpolation argument that follows it), we may restrict to $-2\alpha -2\delta _0 \leq k \leq (\alpha +p_0)/2 + \delta _0$ . We again restrict to the most difficult case when all input frequencies have sizes comparable to $2^k$ by assuming $|\eta |,|{\sigma }| \ll |\xi |$ ; we omit the corresponding cutoffs for lighter notation.

Step 1. The first step needed to deal with the $\mathrm {p.v.}$ singularity in equation (10.57) is to remove a neighbourhood of $p=0$ as follows. For very small p, say $|p|\lesssim 2^{-10m}$ , we may substitute $F(t,\xi ,\eta ,{\sigma },p)$ by $F(t,\xi ,\eta ,{\sigma },0)$ and $\Phi (\xi ,\eta ,{\sigma },p)$ by $\Phi (\xi ,\eta ,{\sigma },0)$ up to very fast-decaying remainders. The resulting integral vanishes by using the $\mathrm {p.v.}$ and the fact that $\phi $ is even.

This leaves us with the expression

(10.59) $$ \begin{align} & \iiint e^{it \Phi(\xi,\eta,\sigma,p)} F(t,\xi,\eta,{\sigma},p) \varphi_{\geq 0}(|p|\langle t \rangle^{10}) \frac{\widehat{\phi}(p)}{p}\,d\eta\,d\sigma \,dp. \end{align} $$

In what follows, we will omit the cutoff localising to $|p| \gtrsim \langle t \rangle ^{-10}$ for simplicity, since its presence does not cause any additional difficulty in the arguments.

Similar to equation (10.38), we define a localised version of $I_2$ by

(10.60) $$ \begin{align} I^{(2)}_{k_1,k_2}(t,\xi) := \iiint e^{it \Phi(\xi,\eta,\sigma,p)} F(t,\xi,\eta,{\sigma},p) \, \varphi_{k_1}^{(k_0)}(\eta\langle \xi \rangle^{-3/2}) \varphi_{k_2}^{(k_0)}({\sigma}\langle \xi \rangle^{-3/2}) \, \frac{\widehat{\phi}(p)}{p}\,d\eta\,d\sigma \,dp, \end{align} $$

where $k_0 := -m/2 + \delta m$ .

Step 2. We first look at the case $k_1=k_2=k_0$ , which gives the leading order term in the asymptotics.

Step 2.1. This contribution can be analysed similarly to how we did for the term $I^{(1)}_{k_0,k_0}$ before; see the definition in equation (10.38). The same exact argument used above leads to the following analogue of equation (10.42) (see equations (10.40)–(10.41)):

(10.61) $$ \begin{align} \begin{aligned} & 2^{3k^+/2} \left| I^{(2)}_{k_0,k_0}(t,\xi) - \iiint e^{it \Phi(\xi,\eta,\sigma,p)} F(t,\xi,0,0,p) \varphi_{\leq k_0}(\eta\langle \xi \rangle^{-3/2}) \varphi_{\leq k_0}({\sigma}\langle \xi \rangle^{-3/2}) \frac{\widehat{\phi}(p)}{p}\,d\eta\,d\sigma \,dp \right| \\ & \qquad \qquad \lesssim {\varepsilon}_1^3 \cdot 2^{(-5/4 + \rho + 5\delta/2)m} m. \end{aligned} \end{align} $$

Note that we have included an additional $\log t$ factor on the right-hand side above to take into account the integration of $\widehat {\phi }(p)/p$ over the region $|p|\gtrsim 2^{-10m}$ . This still gives an acceptable bound under the conditions in equation (10.46).

Step 2.2. To calculate the asymptotics for the integral in equation (10.61), we first notice that, if $|p| \gtrsim 2^{-3m/5}$ , we can use integration by parts in p since $|\partial _p \Phi |\approx 2^{k^-}$ . More precisely, when one of the profiles is differentiated, we estimate it in $L^2$ , put $1/p$ in $L^2$ as well and estimate the other two profiles in $L^{\infty }$ ; when instead $\partial _p$ hits $1/p$ (or the cutoff in p), we estimate this in $L^1$ and place all the profiles in $L^{\infty }_{\xi }$ ; we then obtain a contribution bounded by

(10.62) $$ \begin{align} C 2^{3k^+/2} \cdot 2^{-m} 2^{-k^-} \cdot {\varepsilon}_1 \big(2^{3m/10} 2^{\rho m} + 2^{3m/5} \big) \cdot ({\varepsilon}_1 2^{-3k^+/2})^2\cdot 2^{2k_0}, \end{align} $$

where $\rho = \alpha +\beta \gamma $ . This is a remainder term of the desired $O(2^{-m-\delta _0m})$ size for $\delta _0$ small enough. From now on, we assume $|p| \lesssim 2^{-3m/5}$ and will sometimes omit the cutoff for notational simplicity.

By Taylor expanding the phase,

(10.63) $$ \begin{align} \Phi(\xi,\eta,{\sigma},p) = \langle \xi \rangle - \langle \xi -p \rangle + \frac{2\eta\sigma}{\langle \xi \rangle^3} + O\big((|\eta|+|{\sigma}| + |p| \big)^3 \langle \xi \rangle^{-3}), \end{align} $$

and using $|\eta |+|{\sigma }| + |p|\lesssim 2^{k_0}$ , we obtain (see equation (10.43) and the estimate below) that

$$ \begin{align*} \begin{aligned} & 2^{(3/2)k^+} \Big| \iiint \Big[ e^{it \Phi(\xi,\eta,\sigma,p)} - e^{it(\langle \xi \rangle - \langle \xi-p\rangle + 2\eta\sigma\langle \xi \rangle^{-3} )} \Big] \\ &\qquad \qquad \times F(t,\xi,0,0,p) \varphi_{k_0}(\eta\langle \xi \rangle^{-3/2}) \varphi_{k_0}({\sigma}\langle \xi \rangle^{-3/2}) \frac{\widehat{\phi}(p)}{p}\,d\eta\,d\sigma \,dp \Big| \lesssim {\varepsilon}_1^3 \cdot 2^{(-3/2 + 5\delta)m} m. \end{aligned} \end{align*} $$

Performing the integral in $(\eta ,{\sigma })$ using equation (10.45), we see that, for $|t| \approx 2^m$ ,

(10.64) $$ \begin{align} \begin{aligned} & 2^{(3/2)k^+}\Big| I^{(2)}_{k_0,k_0}(t,\xi) - \langle \xi \rangle^3\frac{\pi}{t} L(t,\xi) \Big| \lesssim {\varepsilon}_1^3 2^{(-1-\delta_0)m}, \\ & L(t,\xi) := \int e^{it(\langle \xi \rangle - \langle \xi-p\rangle)} F(t,\xi,0,0,p) \varphi_{\leq -3m/5} (p) \frac{\widehat{\phi}(p)}{p} \,dp. \end{aligned} \end{align} $$

Step 2.3. Recall that $F(t,\xi ,0,0,p) = \mathfrak {m}_2(\xi ,\xi -p,\xi -p,\xi -p) |\widetilde {f}(\xi -p)|^2\widetilde {f}(\xi -p)$ . In order to obtain equation (10.20), we want to show that, for $|t| \approx 2^m$ , $|\xi |\approx 2^{k^+}$ ,

(10.65) $$ \begin{align} \begin{aligned} L(t,\xi) & = \int e^{it(\langle \xi \rangle - \langle \xi-p\rangle)}F(t,\xi,0,0,p) \varphi_{\leq -3m/5} (p) \frac{\widehat{\phi}(p)}{p} \,dp \\ & = i \sqrt{\frac{\pi}{2}} \, F(t,\xi,0,0,0) \, \mbox{sign} (t\xi) + O(2^{-9k^+/2} 2^{-\delta_0m}). \end{aligned} \end{align} $$

From the bounds on $\mathfrak {m}_2$ and the a priori assumptions on $\widetilde {f}$ , we have

$$ \begin{align*} \begin{aligned} & |F(t,\xi,0,0,p)-F(t,\xi,0,0,0)| \\ &\quad \lesssim \big| \mathfrak{m}_2(\xi,\xi-p,\xi-p,\xi-p) - \mathfrak{m}_2(\xi,\xi,\xi,\xi) \big| |\widetilde{f}(\xi-p)|^3 \\ & \qquad + \big|\mathfrak{m}_2(\xi,\xi,\xi,\xi) \big( |\widetilde{f}(\xi-p)|^2\widetilde{f}(\xi-p) - |\widetilde{f}(\xi)|^2\widetilde{f}(\xi) \big) \big| \\ &\quad \lesssim {\varepsilon}_1^3 \left[ 2^{-(13/2) k^+} |p| + 2^{-7 k^+} |p|^{1/2} 2^{\rho m} \right]. \end{aligned}\end{align*} $$

This allows us to replace $F(t,\xi ,0,0,p)$ by $F(t,\xi ,0,0,0)$ , and after Taylor expanding $\langle \xi \rangle - \langle \xi -p\rangle = p\xi \langle \xi \rangle ^{-1} + O(|p|^2)$ and using that $|p| \lesssim 2^{-3m/5}$ , we obtain

(10.66) $$ \begin{align} L(t,\xi) & = F(t,\xi,0,0,0) \, \int e^{it p \xi \langle \xi \rangle^{-1}} \, \varphi_{\leq -3m/5} (p) \frac{\widehat{\phi}(p)}{p} \,dp + O(2^{-9k^+/2} 2^{-\delta_0m}). \end{align} $$

In equation (10.66), we can further replace $\widehat {\phi }(p)$ by $\widehat {\phi }(0)$ and eventually dispense with the cutoff in p (again via integration by parts), arriving at

(10.67) $$ \begin{align} \begin{aligned} L(t,\xi) & = F(t,\xi,0,0,0) \, \widehat{\phi}(0) \, \int e^{it p \xi \langle \xi \rangle^{-1}} \mathrm{p.v.} \frac{1}{p} \,dp + O(2^{-9k^+/2} 2^{-\delta_0m}) \\ & = F(t,\xi,0,0,0) \widehat{(\mathrm{p.v.} 1/x)} (-t\xi\langle \xi \rangle^{-1}) + O(2^{-9k^+/2} 2^{-\delta_0m}). \end{aligned} \end{align} $$

Using the last identity in equation (4.8) gives us equation (10.65).

Step 3: Case $k_1>k_0$ . To conclude the rigorous derivation of the asymptotics equation (10.20), we need to show that the remaining contributions from $I^{(2)}_{k_1,k_2}(s,\xi )$ (see equation (10.60)) satisfy $O(2^{-\delta _0m})$ bounds when integrated over $|s|\approx 2^m$ and measured in $\langle \xi \rangle ^{-3/2}L^{\infty }$ . This can be done similarly to the analogous estimate for the integral $I^{(1)}_{k_1,k_2}$ ; see the argument starting from equation (10.48).

First, we observe that we may restrict to $|p| \ll 2^k $ . Indeed, if $|p| \gtrsim 2^k$ , the $\mathrm {p.v.}$ in equation (10.60) is not singular and contributes a very small loss in view of equation (10.34); moreover, we can integrate by parts both in p and, depending on which profile is hit by $\partial _p$ , integrate in one of the variables $\eta $ or ${\sigma }$ or $\eta -{\sigma }$ .

Under our assumption that all input frequencies have size about $2^k$ , we have the following analogue of equation (10.48):

(10.68) $$ \begin{align} \begin{aligned} |\partial_{\sigma}\Phi(\xi,\eta,{\sigma},p)| = \Big| \frac{\xi+{\sigma}-p}{\langle \xi+\sigma -p\rangle} - \frac{\xi+{\sigma}+\eta-p}{\langle \xi+\sigma+\eta-p \rangle} \Big| \gtrsim 2^{k_1}2^{-(3/2)k^+}; \end{aligned} \end{align} $$

see the definition of $\Phi $ in equation (10.57). Integrating by parts in ${\sigma }$ to obtain an inequality analogous to equation (10.49), and then using Lemma 6.7 to estimate similarly to equation (10.50), we obtain for $|t|\approx 2^m$

(10.69) $$ \begin{align} \begin{aligned} \Big\| \langle \xi \rangle^2 \sum_{k_1>k_0} I^{(2)}_{k_1,k_2}(t) \Big\|_{L^2} \lesssim {\varepsilon}_1^3 2^{-3m/2} \cdot 2^{(\rho +\delta)m}. \end{aligned} \end{align} $$

To obtain the desired pointwise bound in $\langle \xi \rangle ^{-3/2}L^{\infty }$ , it is enough to interpolate equation (10.69) with the weighted $L^2$ -bound

(10.70) $$ \begin{align} \begin{aligned} \Big\| \langle \xi \rangle \partial_{\xi} \int_0^t \sum_{k_1>k_0} I^{(2)}_{k_1,k_2}(s,\xi) \, \tau_m(s) ds \Big\|_{L^2} & \lesssim {\varepsilon}_1^3 2^{m \rho}, \end{aligned} \end{align} $$

which we now prove.

We first need an analogue of equation (10.52) for the phase $\Phi _2=\Phi _2(\xi ,\eta ,\eta ',{\sigma })$ (see equation (10.57)). By defining $X_{a} := \langle a \rangle \partial _a$ , we have

(10.71) $$ \begin{align} (X_{\xi} + X_{\eta} + X_{\eta'} + X_{\sigma} )\Phi_2 = \xi-\eta+\eta'-{\sigma} = p. \end{align} $$

Note that this is essentially the same identity appearing in equation (11.71) and that we use to establish a weighted $L^2$ bound for the singular cubic terms when the inputs are away from the degenerate frequencies $\pm \sqrt {3}$ .

The identity in equation (10.71) can be applied to the time integral of $\langle \xi \rangle \partial _{\xi } I^{(2)}_{k_1,k_2}$ – expressed in the original variables $(\eta ,\eta ',{\sigma })$ (see equation (10.55))) – to integrate by parts in $(\eta ,\eta ',{\sigma })$ . This procedure gives

(10.72) $$ \begin{align} & \Big| \int_0^t \langle \xi \rangle\partial_{\xi} I^{(2)}_{k_1,k_2}(s,\xi) \, ds \Big| \lesssim \Big| \int_0^t C(s,\xi) \tau_m(s) \, ds \Big| + \Big| \int_0^t D(s,\xi) \tau_m(s) \, ds \Big| + O({\varepsilon}_1^3 2^{m\rho}), \end{align} $$

(10.73) $$ \begin{align} & C(s,\xi) := \iiint s \, e^{is \Phi_2} F_2(t,\xi,\eta,\eta',{\sigma}) \varphi_{k_1}(\eta-\xi+p) \varphi_{k_2}^{(k_0)}({\sigma}-\xi+p) \widehat{\phi}(p) \,d\eta\,d\eta'\,d{\sigma}, \end{align} $$

(10.74) $$ \begin{align} & D(s,\xi) := \iiint e^{is \Phi_2} F_2(t,\xi,\eta,\eta',{\sigma}) \varphi_{k_1}(\eta-\xi+p) \varphi_{k_2}^{(k_0)}({\sigma}-\xi+p) \, X \frac{\widehat{\phi}(p)}{p} \,d\eta\,d\eta'\,d{\sigma}, \end{align} $$

where $p := \xi -\eta +\eta '-{\sigma }$ and $X := ( X_{\xi } + X_{\eta } + X_{\eta '} + X_{\sigma } )$ ; the $O({\varepsilon }_1^3 2^{m\rho })$ in equation (10.72) includes similar and lower-order terms, such as the three terms where the derivatives $X_a$ hit the profiles (these are similar to the first term in equation (10.53)) or the symbol and the various cutoffs.

The term in equation (10.73) comes from canceling the $\mathrm {p.v.} 1/p$ with the p factor in the right-hand side of equation (10.71); note the factor of s coming from differentiating the phase. Integrating by parts in all three variables $\eta ,\eta '$ and ${\sigma }$ , this can be estimated in $L^2$ by $2^{m} X_{k,m}^3 \lesssim 2^m({\varepsilon }_1 2^{-(3/4-)m})^3$ , where, recall, $X_{k,m}$ is the quantity defined in equations (8.16)–(8.17) for $k\leq 0$ and, more generally, in equations (11.11)–(11.12). Upon integration over time, this is an acceptable contribution for equation (10.70).

To estimate the time integral of equation (10.74), we note that

(10.75) $$ \begin{align} X \frac{\widehat{\phi}(p)}{p} = \Phi_2(\xi,\eta,\eta',{\sigma}) \, \partial_p \frac{\widehat{\phi}(p)}{p}. \end{align} $$

Using the $\Phi _2$ factor, we can then integrate by parts in s through the usual identity $e^{is\Phi _2} = (i\Phi _2)^{-1}\partial _s e^{is\Phi _2}$ and obtain boundary terms plus additional time-integrated terms; since these can all be treated similarly, we just look at the main time-integrated term: that is (recall the definition of F in equation (10.55)),

(10.76) $$ \begin{align} \begin{aligned} \int_0^t \iiint e^{is \Phi_2} \big[ \partial_s \widetilde{f}(\eta) \big] \widetilde{f}(\eta') \widetilde{f}({\sigma}) \, \varphi_{k_1} \varphi_{k_2}^{(k_0)} \, \mathfrak{m}_2(\xi,\eta,\eta',{\sigma}) \, \partial_p \frac{\widehat{\phi}(p)}{p} \,d\eta\,d\eta'\,d{\sigma} \, ds. \end{aligned} \end{align} $$

The main observation here is that we can write $\partial _p (1/p) = - \partial _{\sigma } (1/p)$ and integrate by parts in ${\sigma }$ . The worst term is the one where $\partial _{\sigma }$ hits the exponential factor that will cause an additional loss of $s\approx 2^m$ . Applying Lemma 6.7 and equation (7.56), we get

(10.77) $$ \begin{align} \begin{aligned} {\| equation\ (10.76) \|}_{L^2} \lesssim 2^{2m} {\| P_{\sim k} \partial_s f \|}_{L^2} {\| P_{\sim k} e^{-it\langle \partial_x \rangle} \mathcal{W}^* f(t) \|}_{L^{\infty}}^4 \lesssim {\varepsilon}_1^5. \end{aligned} \end{align} $$

A similar argument is also used and further detailed after equation (11.71). This concludes the proof of equation (10.70) and of the asymptotic formula in equation (10.20) in the main case $\{\kappa _1,\kappa _2,\kappa _3\}=\{+,+.-\}$ .

10.3.3 Estimates of equations (10.11)–(10.12) for $\{\kappa _1,\kappa _2,\kappa _3\}\neq \{+,+,-\}$

In the nonresonant cases $\{\kappa _1,\kappa _2,\kappa _3\}\neq \{+,+,-\}$ , we show how the integrals in equations (10.11) and (10.12) can be absorbed into the remainder term appearing in equations (10.2)–(10.3). For ease of reference, we recall the formulas for these integrals:

(10.78) $$ \begin{align} & I_\delta(t) := \iiint e^{it \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',\sigma)} F(t,\xi,\eta,\eta',\sigma) \delta(p)\,d\eta\,d\eta' \,dp, \end{align} $$

(10.79) $$ \begin{align} & I_{\operatorname{p.v.}}(t) := \iiint e^{it \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',\sigma)} F(t,\xi,\eta,\eta',\sigma) \frac{\widehat{\phi}(p)}{p}\,d\eta\,d\eta' \,dp, \end{align} $$

where

(10.80) $$ \begin{align} F(t,\xi,\eta,\eta',{\sigma}) = \mathfrak{m}(\xi,\eta,\eta',{\sigma}) \widetilde{f}(t,\eta)\widetilde{f}(t,\eta')\widetilde{f}(t,{\sigma}) \end{align} $$

and (see equations (10.13)–(10.14))

(10.81) $$ \begin{align} \begin{aligned} & \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta', {\sigma}) := \langle \xi \rangle -\kappa_1 \langle \eta \rangle - \kappa_2 \langle \eta' \rangle - \kappa_3 \langle {\sigma} \rangle, \qquad {\sigma} := \xi - \eta - \eta' - p, \end{aligned} \end{align} $$

having chosen, without loss of generality, a fixed combination of the the signs ${\lambda }_\ast ,\mu _\ast ,\dots $

The main idea to estimate in $\langle \xi \rangle ^{-3/2}L^{\infty }$ (the time integrals of) equations (10.78) and (10.79) is similar to the one used in the two previous paragraphs, based on interpolating the $\langle \xi \rangle ^{-2} L^2$ and $\langle \xi \rangle ^{-1}\dot {H}^1$ norms via equation (10.35).

Since the phase equation (10.81) does not have stationary points in $(\eta ,\eta ')$ at which it simultaneously vanishes, we will show below that one can obtain fast decay for the $L^2$ norm:

(10.82) $$ \begin{align} \Big\| \langle \xi \rangle^2 \int_0^t I(s) \, \tau_m(s) ds \Big\|_{L^2} & \lesssim {\varepsilon}_1^3 2^{-m/2} 2^{(\rho + 2\delta) m }, \qquad I \in \{I_{\delta}, I_{\mathrm{p.v.}}\}. \end{align} $$

Moreover, thanks to equation (11.67) in Proposition 11.8, we have that

(10.83) $$ \begin{align} \Big\| \langle \xi \rangle \partial_{\xi} \int_0^t I(s) \, \tau_m(s) ds \Big\|_{L^2} & \lesssim {\varepsilon}_1^3 2^{\alpha m} , \qquad I \in \{I_{\delta}, I_{\mathrm{p.v.}} \}. \end{align} $$

Interpolating equations (10.82) and (10.83), we arrive at a bound consistent with equation (10.3) for $\delta $ and $\delta _0$ small enough. We are just left with proving equation (10.82).

Proof of equation (10.82). The case $(\kappa _1,\kappa _2,\kappa _3)= (-,-,-)$ is the easiest since $|\Phi _{---}| \gtrsim 1$ . The cases $\{\kappa _1,\kappa _2,\kappa _3\} = \{-,-,+\}$ and $\{+,+,+\}$ are similar, so let us just concentrate on the latter sign combination. Moreover, it suffices to only look at the more complicated case of $I_{\mathrm {p.v.}}$ .

We start by recalling that

(10.84) $$ \begin{align} \begin{aligned} & \nabla_{\eta,\eta'}\Phi_{+++} = 0 \quad \Longleftrightarrow \quad \eta=\eta'={\sigma} = (1/3)(\xi-p) =: \xi_0, \\ & \Phi_{+++}(\xi,\xi_0,\xi_0,\xi_0) = \langle \xi \rangle - 3 \langle\xi_0\rangle \end{aligned} \end{align} $$

(see equation (10.15)). We let $|t|\approx 2^m$ and dyadically localise the frequencies into

(10.85) $$ \begin{align} |\xi|\approx 2^k, \quad |\eta| \approx 2^{k_1}, \quad |\eta'| \approx 2^{k_2}, \quad, |{\sigma}| \approx 2^{k_3}, \quad |p| \approx 2^q, \end{align} $$

denote by $\varphi _{\underline {k}}$ the standard smooth cutoff that localises to the region where equation (10.85) holds and define the localised version of the integral in equation (10.79) by

(10.86) $$ \begin{align} & I_{\underline{k}}(t) := \iiint e^{it \Phi_{+++}(\xi,\eta,\eta',\sigma)} F(t,\xi,\eta,\eta',\sigma) \frac{\widehat{\phi}(p)}{p}\, \varphi_{\underline{k}}(\xi,\eta,\eta',{\sigma}) \, d\eta\,d\eta' \,dp. \end{align} $$

By the usual arguments (including dealing with very small values of $|p|$ by using the $\mathrm {p.v.}$ ), we may reduce to prove a slightly stronger bound than equation (10.82) (with a factor of $\delta $ instead of $2\delta $ , say) for $I_{\underline {k}}$ . We split the proof into several cases:

Case $q \geq \mathrm {min}(k, -k)-10$ . Let us first look at the case $k \leq 0$ for which we have $|p| \gtrsim |\xi |$ . In this case, the $\mathrm {p.v.}$ is not singular, and equation (10.86) is a ‘regular’ cubic term, up to an additional factor of $2^{-k}$ coming from $1/p$ ; however, since $k \geq (-2\alpha -2\delta _0) m$ (see equation (10.34)), this represent a very small loss. When $k_3 \geq -m/3$ , an integration by parts in p suffices to obtain the desired bound. When instead $k_3 \leq -m/3$ , we can directly use an $L^{\infty } \times L^{\infty } \times L^2$ trilinear Hölder estimate (in physical space): the linear decay estimate applied to the $L^{\infty }$ norms gives two factors of ${\varepsilon }_12^{-m/2}$ , and equation (7.19) applied to the $L^2$ norm of the profile with frequency $\approx 2^{k_3}$ gives an additional factor of $2^{k_3} 2^{\alpha m}$ , yielding a stronger bound than the right-hand side of equation (10.82).

When $k\geq 0$ , we have $|p| \gtrsim |\xi |^{-1}$ , and we can use a similar argument. Notice that we do not need to worry about the loss of a possibly large factor of $|\xi |$ from $1/|p|$ thanks to the upper bound in equation (10.34). From now on, we may assume that $|p| \ll \mathrm {min}(|\xi | , |\xi |^{-1})$ .

Case $\mathrm {max}(|k_1-k_2|,|k_1-k_3|,|k_2-k_3|) \geq 5$ . Without loss of generality, we may assume $k_1 \geq k_2 + 5$ . We may also assume $k_1 \geq -m/3$ , for otherwise an $L^2\times L^{\infty }\times L^{\infty }$ estimate will give a bound of $C \cdot {\varepsilon }_1 2^{k_1} 2^{\alpha m} \cdot ({\varepsilon }_1 2^{-m/2})^2$ for the $L^2$ norm of equation (10.86), which is better than equation (10.82). Let us also assume that $k_1\leq 10$ since the complementary case is easier to treat.

Since $|\eta -\eta '| \gtrsim 2^{k_1}$ , we have

(10.87) $$ \begin{align} |\partial_{\eta} \Phi_{+++}| \gtrsim 2^{k_1^-}. \end{align} $$

Integrating by parts in $\eta $ in equation (10.86), we obtain one main term when the derivative hits the profiles: that is,

(10.88) $$ \begin{align} \iiint e^{it \Phi_{\kappa_1 \kappa_2 \kappa_3}(\xi,\eta,\eta',\sigma)} \frac{\mathfrak{m} \varphi_{\underline{k}}}{t \, \partial_{\eta} \Phi_{+++}}(\xi,\eta,\eta',\sigma) \, \partial_{\eta} \big[ \widetilde{f}(\eta) \widetilde{f}(\xi-\eta-\eta'-p) \big] \widetilde{f}(\eta') \, \frac{\widehat{\phi}(p)}{p}\,d\eta\,d\eta' \,dp, \end{align} $$

plus other faster-decaying terms when the derivative hits the symbol or the various cutoffs.

One can check that a bound of $C 2^{-k_1^-}$ holds for the norm of the trilinear operator associated to the (localisation of the) symbol $(\partial _{\eta } \Phi _{+++})^{-1}$ , consistently with equation (10.87). Then an $L^2 \times L^{\infty } \times L^{\infty }$ estimate, using equations (10.34) and (10.31), gives us

(10.89) $$ \begin{align} \begin{aligned} {\| \langle \xi \rangle^2 equation\ (10.88) \|}_{L^2} & \lesssim 2^{-m} 2^{2k} \cdot 2^{-k_1^-} \mathrm{max}\big( {\| \partial_{\eta} \varphi_{k_1} \widetilde{f} \|}_{L^2}, {\| \partial_{\eta} \varphi_{k_3} \widetilde{f} \|}_{L^2} \big) \cdot \big({\varepsilon}_1 2^{-m/2} \big)^2 \\ & \lesssim {\varepsilon}_1^3 2^{-2m} 2^{2(\alpha+\delta_0)m} 2^{m/3} \cdot 2^{\rho m}, \end{aligned} \end{align} $$

which suffices after time integration.

Case $\mathrm {max}(|k_1-k_2|,|k_1-k_3|,|k_2-k_3|) \leq 5$ . In particular, we must also have that $k \leq \mathrm {max}(k_1,k_2,k_3) + 20$ . Motivated by equation (10.84), we further decompose dyadically

$$ \begin{align*} |\xi-2\eta-\eta'-p| \approx 2^{n_1}, \qquad |\xi-\eta-2\eta'-p| \approx 2^{n_2}, \end{align*} $$

by inserting smooth cutoffs, that we implicitly include into $\varphi _{\underline {k}}$ .

Subcase $\mathrm {max}(n_1,n_2) \geq -m/2 + \delta m$ . Let us assume, without loss of generality, that $n_1\geq n_2$ , so that $|\xi -2\eta -\eta '-p| \gtrsim 2^{-m/2+\delta m}$ . Note that, in view of our restriction, we have $n_1 \leq k_1 + 10$ . In this case, we can integrate by parts in $\eta $ in the expression in equation (10.86) using that

$$ \begin{align*} |\partial_{\eta} \Phi_{+++}| \gtrsim 2^{-3k_1^+} 2^{n_1} \end{align*} $$

and that an estimate of $2^{-n_1+3k_1}$ holds for the norm of the trilinear operator associated to $(\partial _{\eta }\Phi _{+++})^{-1}$ . Up to easier and faster-decaying terms, this integration by parts gives us the same main term in equation (10.88) above. Estimating as in equation (10.89) gives

(10.90) $$ \begin{align} \begin{aligned} {\| \langle \xi \rangle^2 equation\ (10.88) \|}_{L^2} & \lesssim 2^{-m} \cdot 2^{-n_1} 2^{3k_1^+} \cdot \mathrm{max}\big( {\| \partial_{\eta} \varphi_{k_1} \widetilde{f} \|}_{L^2}, {\| \partial_{\eta} \varphi_{k_3} \widetilde{f} \|}_{L^2} \big) \cdot \big({\varepsilon}_1 2^{-m/2} \big)^2 \\ &\lesssim {\varepsilon}_1^3 2^{-2m} \cdot 2^{(1/2-\delta +\rho)m}. \end{aligned} \end{align} $$

Subcase $\mathrm {min}(n_1,n_2) \leq -m/2 + \delta m$ . Let us denote by $I_{\underline {k},0}$ the localisation of equation (10.86) to this region, and note that in this case, both $\eta $ and $\eta '$ are very close to $\xi _0:=(1/3)(\xi -p)$ , and so is ${\sigma }=\xi -\eta -\eta '-p$ . More precisely, we can see that

$$ \begin{align*} |\Phi_{+++}(\xi,\eta,\eta',{\sigma})| \gtrsim \big| \langle \xi \rangle - 3 \langle \xi_0 \rangle \big| + O(2^{-m/2 + \delta m}) \gtrsim \langle \xi \rangle^{-1}, \end{align*} $$

since $|p| \ll \langle \xi \rangle ^{-1}$ , and we have the upper bound in equation (10.34) for $|\xi |$ . It is then possible to integrate by parts in s in the time integral of $I_{\underline {k},0}$ , incurring a minimal loss of $2^{k^+}$ . Then from the usual trilinear Hölder estimates, using the bound in equation (7.56) for $\partial _t f$ the $H^4$ -type a priori bound in equation (7.10) and the $L^{\infty }_x$ decay, we can see that

$$ \begin{align*} \Big\| \langle \xi \rangle^2 \int_0^t I_{\underline{k},0}(s,\xi) \, \tau_m(s) ds \Big\|_{L^2} \lesssim {\varepsilon}_1^3 2^{-m+p_0m} + 2^{m} \cdot {\varepsilon}_1^5 2^{-2m+ p_0 m}. \end{align*} $$

This concludes the proof of equation (10.82) and the main Proposition 10.1.

11 Estimates of lower-order terms

This section contains estimates for all the terms that have not been treated in Sections 7–10:

• • In Section 11.1, we prove the weighted bound for all the quadratic interactions that are not covered in Section 8.

• • In Section 11.2, we complete the proof of the a priori bounds on the Sobolev-type component of our norm by estimating the regular quadratic terms $\mathcal {Q}^R(f,f)$ , which were left out of the proofs in Section 7; see Lemma 7.8 and the first line of equation (7.36).

• • In Section 11.3, we prove the Fourier- $L^{\infty }$ bound for the regular quadratic terms and all other terms that are not the main ones covered in Section 10.

• • Finally, Section 11.4 contains the estimates for the weighted norms of all the cubic interactions $\mathcal {C}^{S1,2}_{{\kappa }_1{\kappa }_2{\kappa }_3}$ (see equation (5.57)), which were left out of the analysis of Section 9; these are of two types: the interactions with $\{{\kappa }_1,{\kappa }_2,{\kappa }_3\}=\{++-\}$ with not all frequencies close to $\sqrt {3}$ (or $-\sqrt {3}$ ), and the interactions corresponding to all the other signs combinations.

11.1 Other quadratic interactions

Here we estimate the weighted norm of the regular quadratic term $\mathcal {Q}^{R}$ (see equation (5.15)) for all the interactions that are not the main ones considered in Section 8. These are:

• • The interactions with $(\iota _1\iota _2)=(++)$ that do not satisfy equation (8.2) or, more precisely, equations (8.26) and (8.29); with the notation from equations (8.32) and (8.35)–(8.36), these are interactions where we have either $\ell> -7\beta 'm$ or $k_1>-10$ .

• • The interactions with $(\iota _1\iota _2)\neq (++)$ .

By estimating these terms, we will complete the proof of the main Proposition 8.1. Several of the arguments that we will use below are along the same lines as in Section 8 and simpler in many cases, so we will omit some details.

11.1.1 Notation and preliminary reductions

Let us begin by recalling some definitions. Recall the notation in equations (8.7)–(8.8),

(11.1) $$ \begin{align} \begin{aligned} \mathcal{Q}^R_{\iota_1\iota_2}[a,b](t,\xi) & = -\iota_1\iota_2 \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})} \, \mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,{\sigma}) \, \widetilde{a}_{\iota_1}(\eta) \, \widetilde{b}_{\iota_2}({\sigma}) \, d\eta \, d{\sigma}, \\ \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma}) & := \langle \xi \rangle - \iota_1 \langle \eta \rangle - \iota_2 \langle \sigma \rangle, \end{aligned} \end{align} $$

where we omit the irrelevant signs $\kappa _1,\kappa _2$ and the indicator functions according to Remark 5.1; see also Remark 5.11 and Lemma 5.9. Recall the definition of the main localised operator from equation (8.28):

(11.2) $$ \begin{align} \begin{aligned} I^{p,k_1,k_2}_{\iota_1\iota_2}[a,b](t,\xi) & := \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})} \, \varphi_p^{(p_0)}\big(\Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})\big) \, \mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,{\sigma}) \, \\ & \qquad \times \varphi_{k_1}(\eta) \widetilde{a}_{\iota_1}(\eta) \, \varphi_{k_2}(\sigma) \widetilde{b}_{\iota_2}({\sigma}) \, d\eta \, d{\sigma}, \qquad p_0 = -m + {\delta} m, \\ \Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma}) & := \langle \xi \rangle - \iota_1 \langle \eta \rangle - \iota_2 \langle \sigma \rangle, \end{aligned} \end{align} $$

where $t\approx 2^m$ , $m=0,1,\dots $ ; also recall from the definition of $\mathfrak {q}_{\iota _1\iota _2}$ in equation (5.16), with $\mu _R$ as in equations (4.6)–(4.7), and Remark 5.1, which we may assume for all $a,b,c \geq 0$ and arbitrarily large N,

(11.3) $$ \begin{align} |\partial_{\xi}^a \partial_{\eta}^b \partial_{\sigma}^c \mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,\sigma) | \lesssim \frac{1}{\langle \eta \rangle\langle \sigma \rangle} \cdot \big[ 1 + \inf_{\mu,\nu}|\xi - \mu\eta-\nu\sigma| \big]^{-N} \cdot R(\eta,{\sigma})^{a+b+c+1}, \end{align} $$

where $R(\eta ,{\sigma }) \approx \mathrm {min}(\langle \eta \rangle ,\langle \sigma \rangle )$ ; see equation (5.13). Notice in particular that the symbol decays very fast when one of the frequencies $(\xi ,\eta ,{\sigma })$ is much larger than the other two; this will allow us to concentrate on ‘diagonal’ interactions where $\mathrm {max}(|\xi |,|\eta |,|{\sigma }|) \approx \mathrm {med}(|\xi |,|\eta |,|{\sigma }|)$ .

In view of the preliminary reductions made in Section 8 – see in particular the estimates leading to Lemma 8.4 – it suffices to obtain the two following estimates:

(11.4) $$ \begin{align} \begin{aligned} 2^m 2^k \left\| \varphi_k(\xi) \chi_{\ell,\sqrt{3}}(\xi) \int_{0}^t I^{p,k_1,k_2}_{++}(f,f)(\xi,s) \, \tau_m(s)\, ds \right\|_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{-\beta\ell} 2^{-2\beta'm}, \\ \ell> - 7\beta'm \qquad \mbox{or} \qquad k_1 > - 10, \end{aligned} \end{align} $$

and

(11.5) $$ \begin{align} \begin{aligned} 2^m 2^k \left\| \varphi_k(\xi) \chi_{\ell,\sqrt{3}}(\xi) \int_{0}^t I^{p,k_1,k_2}_{\iota_1\iota_2}(f,f)(s,\xi) \, \tau_m(s)\, ds \right\|_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{-\beta\ell} 2^{-2\beta'm}, \\ \mbox{with} \qquad (\iota_1\iota_2) \in \{ (+-), (-+), (--) \}. \end{aligned} \end{align} $$

We assume without loss of generality that

$$ \begin{align*}k_1 \geq k_2. \end{align*} $$

Notice that in addition to the localisations already present in Lemma 8.4, we have included here a localisation in $|\xi |\approx 2^k$ and a factor of $2^k$ on the left-hand sides of equations (11.4)–(11.5), which is consistent with the fact that $\langle \xi \rangle \nabla _{\xi }\Phi _{\iota _1\iota _2} = \xi $ ; see the formula in equation (8.10) and recall that this factor was disregarded in the estimates of Section 8 since there we were only looking at the case $|\xi |\approx \sqrt {3}$ . For small $\xi $ , this factor turns out to be helpful in the analysis of the signs combinations other than $(++)$ .

Notice also that in both equations (11.4) and (11.5), we have discarded the summations over $(k,k_1,k_2)$ (and p) and reduced ourselves to a bound for fixed triples $(k,k_1,k_2)$ . To justify this reduction, it suffices to show how to bound the sums over $\mathrm {max}(k,k_1,k_2)\geq 10m$ or $\mathrm {min}(k,k_1,k_2) \leq -10m$ , because then the sum over the remaining $O(m^3)$ terms ( $O(m^4)$ when we include p) can be accounted for by the factor of $2^{-2\beta ' m}$ (and the lack of the $2^{\alpha m}$ factor) as we did for the parameters $k_1,k_2$ and p before (see the paragraph after Lemma 8.4).

Let us briefly explain how to deal with the cases $\mathrm {max}(k,k_1)\geq 10m$ and $\mathrm {min}(k,k_2) \leq -10m$ . Observe that the pointwise bound on the symbol from equation (11.3) gives us, on the support of the integral,

(11.6) $$ \begin{align} |\mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,\sigma) | \lesssim 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \big[ 1 + \inf_{\mu,\nu}|\xi - \mu\eta-\nu\sigma| \big]^{-5}; \end{align} $$

then Young’s inequality yields

(11.7) $$ \begin{align} \begin{aligned} 2^m 2^k & \left\| \varphi_k(\xi) \chi_{\ell,\sqrt{3}}(\xi) \int_{0}^t I^{p,k_1,k_2}_{++}(f,f)(\xi,s) \, \tau_m(s)\, ds \right\|_{L^2_{\xi}} \\ & \lesssim 2^{2m} 2^k \cdot 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot {\| \varphi_{k_1} \widetilde{f} \|}_{L^2} {\| \varphi_{k_2} \widetilde{f} \|}_{L^1} \\ & \lesssim 2^{2m} 2^k \cdot 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot \mathrm{min}\big(2^{-4k_1},2^{k_1/2}\big) 2^{\alpha m} {\varepsilon}_1 \cdot \mathrm{min} \big(2^{k_2}, 2^{-7k_2/2}\big) 2^{\alpha m} {\varepsilon}_1, \end{aligned} \end{align} $$

having using the a priori bound on the $H^4$ Sobolev norm in the last inequality. If $\mathrm {max}(k,k_1)\geq 10m$ and $|k_1-k| <10$ , we can use the factor of $2^{-5k_1}$ in equation (11.7) to sum over k and $k_1$ (the sum over $k_2$ can be done independently) and obtain a stronger upper bound than the right-hand sides of equations (11.4)–(11.5); when instead $|k-k_1| \geq 10$ , we can use the decay of the symbol away from the diagonal, which results in the extra power of $2^{-20\mathrm {max}(k,k_1)}$ in equation (11.7).

In the case $k \leq -10m$ , the factor of $2^k$ in front of the estimate in equation (11.7) already allows one to sum over k and again obtain stronger bounds than equations (11.4)–(11.5). Similarly, equation (11.7) suffices if $k_2 \leq -10m$ .

Before proving equations (11.4) and (11.5), we show how to deal with relatively large input frequencies and, in particular, how to handle the nonstandard estimate for the symbol $\mathfrak {q}$ appearing in equation (11.3).

11.1.2 High frequencies

From the estimates for the symbol $\mathfrak {q}$ in equation (11.3), we see that $\mathfrak {q}$ is essentially smooth and fast decaying in the quantity $\inf _{\mu ,\nu }|\xi - \mu \eta -\nu \sigma |$ but has the nonstandard feature that its derivatives in $\xi ,\eta ,\sigma $ might grow for frequencies larger than $1$ . Therefore, in each of our integration by parts arguments, there is a potential loss of a factor of $R(\eta ,{\sigma })$ when derivatives hit the symbol. However, thanks to the $H^4$ control on our solution, we can comfortably handle this, using the following lemma:

Lemma 11.1 (High frequencies)

Assume $k_2\leq k_1$ . For all $s\approx 2^m$ , we have

(11.8) $$ \begin{align} \begin{aligned} & {\| \varphi_k (\xi) I^{p,k_1,k_2}_{\iota_1\iota_2}(f,f)(s,\xi) \|}_{L^2} \lesssim 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot {\| \varphi_{k_1} \widetilde{f} \|}_{L^2} \\ &\qquad \qquad \qquad \cdot \mathrm{min} \Big( {\| \varphi_{k_2} \widetilde{f} \|}_{L^1}, 2^{-m-k_2^-} \big( (2^{k_2^+}+2^{-k_2^-}) {\| \varphi_{k_2} \widetilde{f} \|}_{L^1} + {\| \partial_{\xi}(\varphi_{k_2} \widetilde{f}) \|}_{L^1} \big) \Big). \end{aligned} \end{align} $$

Proof. Bringing the absolute values inside the integral gives us the basic bound

$$ \begin{align*} |I^{p,k_1,k_2}_{\iota_1\iota_2}(f,f)(t,\xi)| \lesssim \iint |\mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,{\sigma})| \cdot \varphi_{k_1}(\eta) |\widetilde{f}_{\iota_1}(\eta)| \cdot \varphi_{k_2}(\sigma) |\widetilde{f}_{\iota_2}({\sigma})| \, d\eta \, d{\sigma}, \end{align*} $$

which, using equation (11.3) (with $a=b=c=0)$ , $R(\eta ,\sigma ) \approx 2^{k_2^+}$ and Young’s inequality, implies

(11.9) $$ \begin{align} {\| \varphi_k (\xi) I^{p,k_1,k_2}_{\iota_1\iota_2}(f,f)(s,\xi) \|}_{L^2} \lesssim 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot {\| \varphi_{k_1} \widetilde{f} \|}_{L^2} \cdot {\| \varphi_{k_2} \widetilde{f} \|}_{L^1}. \end{align} $$

To prove equation (11.8), we need to show, for $k_2 \geq -m/2$ , that

(11.10) $$ \begin{align} \begin{aligned} {\| \varphi_k (\cdot) I^{p,k_1,k_2}_{\iota_1\iota_2}[f,f](\cdot,s) \|}_{L^2} \lesssim 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot {\| \varphi_{k_1} \widetilde{f} \|}_{L^2} \cdot 2^{-m-k_2^-} \\ \cdot \big( {\| \partial_{\sigma}(\varphi_{k_2} \widetilde{f}) \|}_{L^1} + (2^{k_2^+}+2^{-k_2^-}) {\|\varphi_{k_2} \widetilde{f}\|}_{L^1} \big). \end{aligned} \end{align} $$

This is done by integrating by parts in ${\sigma }$ first and then estimating as in equation (11.9) above. More precisely, we look at the formula in equation (11.2) and note that $|\partial _{\sigma } \Phi _{\iota _1\iota _2}| \approx 2^{k_2^-}$ . Using this and the usual identity $(is\partial _{\sigma }\Phi _{\iota _1\iota _2})^{-1}\partial _{\sigma } e^{is\Phi _{\iota _1\iota _2}} = e^{is\Phi _{\iota _1\iota _2}}$ , we can integrate by parts in ${\sigma }$ , gaining the factor $2^{-m-k_2^-}$ . When $\partial _{\sigma }$ hits $\varphi _p^{(p_0)}$ , we use the argument that led to Remark 8.6 and repeat the integration by parts as needed. If $\partial _{\sigma }$ hits the symbol $\mathfrak {q}$ , we use equation (11.3) to deduce a bound of

$$ \begin{align*} C \sup_{|\eta|\approx2^{k_1},|{\sigma}|\approx2^{k_2}} R(\eta,{\sigma})^2 \cdot 2^{-k_1^+}{2^{-20| k^+ - k_1^+|}} \cdot {\| \varphi_{k_1} \widetilde{f} \|}_{L^2} \cdot 2^{-k_2^+} 2^{-m-k_2^-}{\| \varphi_{k_2} \widetilde{f} \|}_{L^1} \\ \lesssim 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot {\| \varphi_{k_1} \widetilde{f} \|}_{L^2} \cdot 2^{k_2^+} 2^{-m-k_2^-}{\| \varphi_{k_2} \widetilde{f} \|}_{L^1}. \end{align*} $$

If instead $\partial _{\sigma }$ falls on $\varphi _{k_2} \widetilde {f}$ , we estimate using Young’s and finally obtain equation (11.10).

Let us define, just for the purpose of the estimate in this section, the following variant of $X_{k,m}$ (see equation (8.16)), which we still denote in the same way, to also take into account frequencies $k\geq 0$ :

(11.11) $$ \begin{align} X_{k,m}(c) := \mathrm{min}\Big( {\| \varphi_k \widetilde{c} \|}_{L^1}, 2^{-m -k^-} \big({\| \partial_{\xi}(\varphi_k\widetilde{c}) \|}_{L^1} + (2^{k^+} + 2^{-k^-}) {\| \varphi_{[k-5,k+5]} \widetilde{c} \|}_{L^1}\big) \Big). \end{align} $$

Note that this coincides with equation (8.16) when $k \leq 0$ . Also note that this extended definition still satisfies the upper bound $X_{k,m}(f(t) \tau _m(t)) \lesssim {\varepsilon }_1 2^{-3m/4} 2^{\alpha m}$ (see equation (8.17)), which we used many times before; more precisely, using the a priori bounds in equation (7.10) (see also equations (7.21)–(7.24)), we can estimate

(11.12) $$ \begin{align} X_{k,m}(f(t)\tau_m(t)) \lesssim {\varepsilon}_1 \mathrm{min} \big(2^{-7k^+/2}, 2^{3k^-/2}, 2^{-m-k^-/2}, 2^{-m-k^+/2} \big) 2^{\alpha m}. \end{align} $$

As a consequence of Lemma 11.1, we see that

(11.13) $$ \begin{align} \begin{aligned} {\| \varphi_k (\xi) I^{p,k_1,k_2}_{\iota_1\iota_2}[f,f](s,\xi) \|}_{L^2} & \lesssim 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot {\| \varphi_{k_1} \widetilde{f} \|}_{L^2} \cdot X_{k_2,m}(f) \\ & \lesssim 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot 2^{-4k_1^+} {\| f \|}_{H^4} \cdot X_{k_2,m}(f). \end{aligned} \end{align} $$

Then we see that if $\mathrm {max}(k_1,k_2) =k_1 \geq m/3$ , by our a priori bounds, we get

(11.14) $$ \begin{align} \begin{aligned} 2^k {\| \varphi_k (\xi) I^{p,k_1,k_2}_{\iota_1\iota_2}[f,f](s,\xi) \|}_{L^2} & \lesssim 2^k 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot {\varepsilon}_1 2^{\alpha m} 2^{-4m/3} \cdot {\varepsilon}_1 2^{-3m/4} 2^{\alpha m} \\ & \lesssim {\varepsilon}_1^2 2^{-2m - 5\beta'm}. \end{aligned} \end{align} $$

This implies equations (11.4)–(11.5) in the large-frequencies regime $\mathrm {max}(k_1,k_2) \geq m/3$ .

Remark 11.2 (Handling the derivatives of $\mathfrak {q}$ for large frequencies)

Thanks to the above argument, we are only left with proving the main bounds in equations (11.4)–(11.5) for $\mathrm {max}(k,k_1) \leq m/3$ (and $\mathrm {min}(k,k_2) \geq -10m$ , say). In particular, this allows us to disregard all the terms in our integration by parts arguments in frequency space where derivatives fall on the symbol $\mathfrak {q}$ , despite the nonstandard growth of its derivatives for frequencies larger than $1$ ; see the factor of $R(\eta ,{\sigma })$ in equation (11.3). Indeed, on the support of equation (11.2), we have $R(\eta ,{\sigma }) \approx 2^{k_2^+}$ (recall that we also assume $k_2\leq k_1$ ) so that each derivative of $\mathfrak {q}$ can cost at most a factor of $2^{m/3}$ , while the gain from any integration by parts argument is always at least $2^{-m/2}$ . Therefore, a term where a derivative hits $\mathfrak {q}$ is always better behaved than terms where derivatives hit the profiles (or other cutoffs). We will then analyse only these latter types of terms.

11.1.3 Proof of equation (11.4)

Recall the relation between the parameters in equation (2.31) and that by symmetry we assume $k_1\geq k_2$ . Also, recall that we are assuming that at least one of the two conditions $\ell> -7\beta 'm$ or $k_1> -10$ holds true. As usual, we divide the proof into a few cases.

Step 1: $k \leq -5$ or $k_1 \leq -4\beta 'm-10$ . Let us first discuss the case $k\leq -5$ , where we have $|\xi | \ll 1$ and therefore $|\Phi _{++}| \geq 2 - \langle \xi \rangle \gtrsim 1$ . In this case, we can integrate by parts in s without introducing any loss and then analyse the resulting quartic terms (boundary terms are easy to handle) as done in Section 8 starting on page 100. Here we should take some care since the input frequencies $\eta $ and $\sigma $ could be close to $\pm \sqrt {3}$ ; then integration by parts in one of these frequencies could potentially introduce a loss, since, for example, the $L^2$ -norm of $\partial _{\eta }\widetilde {f}(\eta )$ degenerates for $\eta $ close to $\sqrt {3}$ . However, it suffices to observe that in this case the quantity $X_{k_1,m}$ (see equation (11.11)) satisfies for any $j_1 \in [-\gamma m, 0] \cap {\mathbb Z}$ (hence $|k_1|\leq 5$ )

(11.15) $$ \begin{align} \begin{aligned} X_{k_1,m}\big(\widetilde{{\mathcal{F}}}^{-1} (\chi_{j_1,\sqrt{3}} \widetilde{f}(t)) \tau_m(t) \big) & \approx \mathrm{min}\big( {\| \varphi_{[k_1-5,k_1+5]} \chi_{j_1,\sqrt{3}} \widetilde{f} \|}_{L^1}, 2^{-m} {\| \partial_{\xi}(\varphi_{k_1} \chi_{j_1,\sqrt{3}}\widetilde{f}) \|}_{L^1} \big) \\ & \lesssim 2^{-m} {\| \partial_{\xi}(\varphi_{k_1} \chi_{j_1,\sqrt{3}}\widetilde{f}) \|}_{L^1} \lesssim {\varepsilon}_1 2^{-m} 2^{\beta'j_1 + \alpha m}, \end{aligned} \end{align} $$

having used the consequence of the a priori bounds in equation (7.20). The estimate in equation (11.15) is substantially better than the general bound of $2^{-3m/4+\alpha m}$ used throughout Section 8, where we considered $k_1 < 0$ .

Next, let us discuss the case $k> -5$ and $k_1 \leq -4\beta 'm-10$ . In particular, since $k_1 \leq -10$ , we are under the assumption that $\ell> -7\beta 'm$ . Then we see that

$$ \begin{align*}|\Phi_{++}| \geq |2 - \langle \xi \rangle| - 2(\langle \eta \rangle-1) \approx 2^{\ell}\end{align*} $$

since $||\xi |-\sqrt {3}| \approx 2^{\ell } \gg 2^{2k_1} \approx \langle \eta \rangle -1$ . Therefore, we have the strong lower bound $|\Phi _{++}| \gtrsim 2^{\ell } \geq 2^{-7\beta 'm}$ , and integration by parts in time can be used to handle this case as well.

We can then assume

(11.16) $$ \begin{align} k> -5, \qquad k_1 > -4\beta'm-10, \qquad k_2 \leq k_1, \qquad p < 2k_1-10, \end{align} $$

where this last condition is just a consequence of restricting to the case $p < -8\beta 'm - 30$ (the complementary case being again easier to deal with by integration by parts in time).

Step 2: Decomposition in $||\eta | -\sqrt {3}| \approx 2^{j_1}$ . To proceed further, we need to decompose the integral in equation (11.4) by inserting cutoffs in the size of $||\eta |-\sqrt {3}|\approx 2^{j_1}$ . We first notice that if $j_1 \geq -10$ – that is, $\eta $ is away from $\pm \sqrt {3}$ – then we are in a situation similar to the one in Section 8, with the additional advantage that $|\eta |$ cannot be small (and is in fact almost lower bounded by $1$ ; see equation (11.16)). An application of equation (8.40) in Lemma 8.5, together with the bound in equation (11.6) for the symbol, would then give us

(11.17) $$ \begin{align} \begin{aligned} & 2^k {\big\| I^{p,k_1,k_2}_{++}\big[ \widetilde{{\mathcal{F}}}^{-1}(\chi_{j_1,\sqrt{3}}\widetilde{f}),f \big](\cdot,s) \big\|}_{L^2} \\ &\quad \lesssim 2^k 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot 2^{p-k_1/2} \cdot 2^{-m-k_1} {\| \partial_{\xi} (\chi_{j_1,\sqrt{3}}\widetilde{f}) \|}_{L^2} \cdot X_{k_2,m} \\ &\quad \lesssim {\varepsilon}_1^2 2^{p-3k_1/2} \cdot 2^{-m+\alpha m} \cdot 2^{-3m/4+\alpha m}. \end{aligned} \end{align} $$

This is enough, provided, for example, that $p\leq -m/4 - 10\beta ' m$ . In the complementary case $p> -m/4 - 10\beta ' m$ , we can efficiently integrate by parts in time and argue as in Sections 8.6 and 8.7. We may then reduce matters to the harder case $j_1 \leq -10$ .

We define

(11.18) $$ \begin{align} \begin{aligned} I^{p,k,j_1,k_2}[a,b](t,\xi) & := \varphi_k(\xi) \iint e^{it \Phi_{++}(\xi,\eta,{\sigma})} \, \varphi_p^{(p_0)}\big(\Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})\big) \, \mathfrak{q}^{\prime}(\xi,\eta,{\sigma}) \\ &\quad \times \chi_{j_1,\sqrt{3}}^{[-\gamma m,0]}(\eta) \, \widetilde{a}_{\iota_1}(\eta) \, \varphi_{k_2}(\sigma) \widetilde{b}_{\iota_2}({\sigma}) \, d\eta \, d{\sigma} \end{aligned} \end{align} $$

(note that in the notation, we have dispensed with the irrelevant parameter $k_1$ associated to the localisation in $|\eta |\approx 2^{k_1}\approx 1$ ), where

(11.19) $$ \begin{align} & \mathfrak{q}^{\prime}(\xi,\eta,{\sigma}) := \mathfrak{q}^{\prime}_{\iota_1\iota_2;k,k_1,k_2}(\xi,\eta,{\sigma}) := \varphi_{\sim k}(\xi)\varphi_{\sim k_1}(\eta)\varphi_{\sim k_2}({\sigma}) \mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,{\sigma}) \cdot 2^k. \end{align} $$

From equation (11.3), and since we are considering $|k_1| \leq 5$ and $k>-5$ , we have

(11.20) $$ \begin{align} & |\partial_{\eta}^b \partial_{\sigma}^c \mathfrak{q}^{\prime}_{\iota_1\iota_2}(\xi,\eta,{\sigma})| \lesssim 2^{(b+c)k_2^+} 2^{-20k^+}. \end{align} $$

To obtain equation (11.4), it then suffices to prove the following:

Lemma 11.3. With the definitions in equations (11.18)–(11.20), under our a priori assumptions, we have, for all $j_1\leq -10$ ,

(11.21) $$ \begin{align} \begin{aligned} 2^m \left\| \int_{0}^t I^{p,k,j_1,k_2}[f,f](\cdot,s) \, \tau_m(s)\, ds \right\|_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{-3\beta'm}. \end{aligned} \end{align} $$

Note that in equation (11.21), we have discarded the factor of $2^{-\beta \ell }$ on the right-hand side, which is of little help when $\ell $ is close to $0$ .

Before proceeding with the proof of Lemma 11.3, let us observe that the same argument used to prove equation (8.39) in Lemma 8.5 gives us (we can use the $L^2_{\xi }$ norm instead of the $L^{\infty }_{\xi }$ by Hölder and equation (11.20))

(11.22) $$ \begin{align} \begin{aligned} {\| I^{p,k,j_1,k_2}[f,f](s) \|}_{L^2} & \lesssim X_{k_1,m}\big(\widetilde{{\mathcal{F}}}^{-1}( \chi_{j_1,\sqrt{3}}\widetilde{f}(s)) \tau_m(s) \big) \cdot X_{k_2,m}(f) \\ & \lesssim {\varepsilon}_1^2 \cdot 2^{-m+\alpha m} 2^{\beta' j_1} \cdot {\varepsilon}_1 2^{3k_2/2} 2^{\alpha m}. \end{aligned} \end{align} $$

In particular, we have equation (11.21) when $3k_2/2 \leq -m-2\alpha -3\beta 'm$ . We may therefore assume from now on that

(11.23) $$ \begin{align} k_2 \geq - 2m/3 - 10\beta'm. \end{align} $$

For later use, we also record here the following analogue of the estimate in equation (8.40) applied to equation (11.18):

(11.24) $$ \begin{align} \begin{aligned} {\big\| I^{p,k,j_1,k_2}[f,f](s) \big\|}_{L^2} & \lesssim 2^{p} \cdot 2^{-m} {\big\| \partial_{\xi} (\chi_{j_1,\sqrt{3}}^{[-\gamma m,0]} \widetilde{f}) \big\|}_{L^2} \cdot X_{k_2,m}(f) \\ & \lesssim 2^{p} \cdot 2^{-m} {\varepsilon}_1 2^{\gamma \beta m + \alpha m} \cdot {\varepsilon}_1 \mathrm{min}(2^{3k_2/2},2^{-m + k_2/2})2^{\alpha m}. \end{aligned} \end{align} $$

Step 3: $p \leq -m/2 - 5\beta 'm$ . In this case, integration by parts in time is not efficient. However, since $\gamma \beta + 2\alpha \leq 1/4$ (see equation (2.31)), we see that equation (11.24) already suffices to give equation (11.21).

Step 4: $p \geq -m/2 - 5\beta 'm$ . This is the hardest case in the proof of equation (11.4). The basic idea is to integrate by parts as in Section 8.6 and analyse the resulting terms, which are similar to those in equations (8.57)–(8.60), with the notation in equation (8.56) and the identities in equations (8.66)–(8.69). In the present case, we have similar formulas, with a different localisation in $\eta $ at the scale $||\eta |-\sqrt {3}|\approx 2^{j_1} \ll 1$ instead of $|\eta |\approx 2^{k_1} \ll 1$ .

We define, similarly to equation (8.56),

(11.25) $$ \begin{align} \begin{aligned} \underline{I}^{p,k,j_1,k_2}[g,h](s,\xi) := \iint e^{is \Phi_{++}} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}'(\xi,\eta,{\sigma}) \, \chi_{j_1,\sqrt{3}}^{[-\gamma m,0]}(\eta) \widetilde{g}(\eta) \, \varphi_{k_2}(\sigma) \widetilde{h}({\sigma}) \, d\eta \, d{\sigma}, \end{aligned} \end{align} $$

where $\mathfrak {q}'$ satisfies equation (11.20). In particular, since $k_2\leq 5$ , we may think of this just as a smooth symbol that decays very fast in $\langle \xi \rangle $ and with $O(1)$ bounds on its derivatives.

Disregarding the boundary terms that come from the integration by parts in time that can be treated as before, we reduce matters to estimating

(11.26) $$ \begin{align} K^{S1,2}_{\iota_1\iota_2\iota_3}(t,\xi) & := \underline{I}^{p,k,j_1,k_2} \big[ \widetilde{{\mathcal{F}}}^{-1} \mathcal{C}^{S1,2}_{\iota_1\iota_2\iota_3}[f,f,f],f\big](s,\xi), \end{align} $$

(11.27) $$ \begin{align} L^{S1,2}_{\iota_1\iota_2\iota_3}(t,\xi) & := \underline{I}^{p,k,j_1,k_2} \big[f, \widetilde{{\mathcal{F}}}^{-1} \mathcal{C}_{\iota_1\iota_2\iota_3}^{S1,2}[f,f,f] \big](s,\xi), \end{align} $$

and

(11.28) $$ \begin{align} D^R(t,\xi) & := \underline{I}^{p,j_1,k_2}\big[ \widetilde{{\mathcal{F}}}^{-1} \mathcal{R},f\big](s,\xi) + \underline{I}^{p,j_1,k_2}\big[f, \widetilde{{\mathcal{F}}}^{-1} \mathcal{R} \big](s,\xi). \end{align} $$

For equation (11.21), it suffices to prove an upper bound of ${\varepsilon }_1^2 2^{-2m - 3\beta 'm}$ for the $L^2_{\xi }$ -norms of equations (11.26)–(11.28).

Estimate of equations (11.26)–(11.27 ). As in Section 8, since we are assuming $k_2 \leq k_1$ , the two terms in equations (11.26) and (11.27) are not symmetric; similar to before, it turns out that the second one is slightly harder to treat, so it will be the focus of our analysis. We concentrate on the $\mathcal {C}^{S1}$ contribution since the one with $\mathcal {C}^{S2}$ will differ only slightly; see, for example, the arguments on page 106.

Expanding out as in equation (8.106) and introducing frequency cutoffs for the new correlated variables, we reduce to estimating quartic terms of the form

(11.29) $$ \begin{align} \begin{aligned} & L_{\underline{k}} := \iiiint e^{it\Psi_{\iota_1\iota_2\iota_2}} \, \frac{\varphi_p\big(\Phi\big)}{\Phi} \, \mathfrak{q}\, \varphi_{\underline{k}}(\eta,\sigma,\rho,\zeta) \, \widetilde{f}(\eta) \widetilde{f}(\rho) \widetilde{f}(\zeta) \widetilde{f}({\sigma}-\rho-\zeta) \, d\eta \, d{\sigma} \, d\zeta \, d\rho, \\ & \Psi_{\iota_1\iota_2\iota_3} := \langle \xi \rangle - \langle \eta \rangle - \iota_1\langle \rho \rangle - \iota_2\langle\zeta\rangle - \iota_2\langle{\sigma}-\rho-\zeta\rangle, \qquad \iota_1,\iota_2,\iota_3 \in \{+,-\}, \\ & \varphi_{\underline{k}}(\eta,\sigma,\rho,\zeta) := \chi_{j_1,\sqrt{3}}(\eta)\varphi_{k_2}(\sigma) \varphi_{k_3}(\rho)\varphi_{k_4}(\zeta)\varphi_{k_5}(\sigma-\rho-\zeta), \end{aligned} \end{align} $$

for a smooth symbol $\mathfrak {q}$ . It suffices to show that for $|t| \approx 2^m$ and $|\mathrm {max}(k_2,k_3) - \mathrm {med}(k_2,k_3,k_4)|\leq 5, k_5 \leq k_4 \leq k_3 \leq 0$ , we have

(11.30) $$ \begin{align} & \big| L_{\underline{k}}(t,\xi) \big| \lesssim {\varepsilon}_1^3 2^{-2m} 2^{-4\beta'm}. \end{align} $$

Integration by parts in the uncorrelated variable $\eta $ , using that $|\eta | \approx 1$ and equation (11.15), gives the following analogue of equation (8.110):

(11.31) $$ \begin{align} \big| L_{\underline{k}}(t,\xi) \big| \lesssim {\varepsilon}_1^4 \cdot 2^{-p} \cdot 2^{-m+4\alpha m} \cdot 2^{k_5+k_4 + \mathrm{min}(k_2,k_3)} \cdot 2^{(1/2)(k_3+k_4+k_5)}. \end{align} $$

We want to combine equation (11.31) with exploiting the oscillations in the integral in equation (11.29) in the directions of $\partial _{\sigma }$ , $\partial _{\sigma } + \partial _\rho $ and $\partial _{\sigma } + \partial _{\zeta }$ whenever this is convenient, and proceed similarly to Case 2 on page 104. Before doing this, we need to show how to deal with the cases when integration by parts is not possible (see the analogous Case 1 of Step 3 on page 108. We fix $\delta \in (0,\alpha )$ .

Case 1: $\mathrm {min}(k_2,k_4) + k_4 \leq -m + \delta m$ . This is the case when integration by parts in $\partial _{\sigma } + \partial _{\zeta }$ is not possible, because $|(\partial _{\sigma } + \partial _{\zeta }) \Psi | \approx |\zeta | \approx 2^{k_4}$ and hitting cutoffs will cost $2^{-k_2} + 2^{-k_4}$ . From equation (11.31), we have

$$ \begin{align*} \big| L_{\underline{k}}(t,\xi) \big| \lesssim {\varepsilon}_1^4 2^{-p} \cdot 2^{-m + 4\alpha m} \cdot 2^{k_2+3k_4}. \end{align*} $$

Since we are assuming $k_2+k_4 \leq -m +\delta m$ , the above bound would suffice to obtain equation (11.30) if it were the case that $-p+2k_4 \leq -6\beta 'm$ . On the other hand, if $-p+2k_4 \geq -6\beta 'm$ , we would have $k_4 \geq -m/4 -9\beta 'm$ and therefore $k_2 \leq -3m/4 + 10\beta 'm$ , which is a contradiction to equation (11.23).

Case 2: $\mathrm {min}(k_2,k_4) + k_4 \geq -m + \delta m$ . In this case, we also have $k_2 + k_3 \geq -m + \delta m$ , and we can integrate by parts both in $\partial _{\sigma } + \partial _\rho $ and $\partial _{\sigma } + \partial _{\zeta }$ . We further distinguish between the case $\mathrm {min}(k_2,k_5) \geq -m/2$ and $\mathrm {min}(k_2,k_5) \leq -m/2$ . In the first case, we can integrate by parts in $\sigma $ to obtain, up to faster-decaying terms,

$$ \begin{align*} \big| L_{\underline{k}}(t,\xi) \big| \lesssim 2^{-p} \cdot {\varepsilon}_1 2^{-m + \alpha m} \cdot X_{k_3,m} \cdot X_{k_4,m} \cdot X_{k_5,m}, \end{align*} $$

which is more than sufficient since $ X_{k,m} \lesssim {\varepsilon }_1 2^{-3m/4+\alpha m}$ . In the case $\mathrm {min}(k_2,k_5) \leq -m/2$ , we estimate the profile $\varphi _{k_5}\widetilde {f}({\sigma }-\rho -\zeta )$ in $L^{\infty }$ (this gives ${\varepsilon }_12^{k_5/2}2^{\alpha m}$ ) and integrate $\varphi _{k_2}$ in $d{\sigma }$ (this gives a $2^{k_2}$ factor), thus obtaining, again up to faster-decaying terms,

$$ \begin{align*} \big| L_{\underline{k}}(t,\xi) \big| \lesssim 2^{-p} \cdot {\varepsilon}_1 2^{-m + \alpha m} \cdot X_{k_3,m} \cdot X_{k_4,m} \cdot 2^{k_2} \cdot {\varepsilon}_1 2^{k_5/2} 2^{\alpha m}; \end{align*} $$

this suffices in view of the lower bound on p.

Estimate of equation (11.28). Finally we estimate the terms in equation (11.28). A bound analogous to equation (8.128) (here $|k_1|\leq 5$ ) directly gives us what we want:

$$ \begin{align*} {\big\|\underline{I}^{p,k,j_1,k_2} \big[ \widetilde{{\mathcal{F}}}^{-1}\mathcal{R},f\big](s,\xi) \big\|}_{L^2} & \lesssim 2^{-k_1/2} {\|\mathcal{R}(s)\|}_{L^2} \cdot X_{k_2,m} \lesssim {\varepsilon}_1^3 2^{-3m/2 + 2\alpha m} \cdot {\varepsilon}_1 2^{-3m/4 + \alpha m}, \end{align*} $$

having used equation (7.54). With a similar estimate, also using equation (11.15), we can bound

$$ \begin{align*} {\big\|\underline{I}^{p,j_1,k_2}\big[f,\widetilde{{\mathcal{F}}}^{-1}\mathcal{R} \big](s,\xi)\big\|}_{L^2} &\lesssim X_{k_1,m}\big(\widetilde{{\mathcal{F}}}^{-1}( \chi_{j_1,\sqrt{3}}\widetilde{f}(s))\tau_m(s) \big) \cdot 2^{-k_2/2} {\|\mathcal{R}(s)\|}_{L^2} \\ &\lesssim {\varepsilon}_1 2^{-m+\alpha m} \cdot 2^{-k_2/2} {\varepsilon}_1^3 2^{-3m/2 + 2\alpha m}, \end{align*} $$

which, in view of equation (11.23), suffices.

11.1.4 Proof of equation (11.5)

To conclude the proof of Proposition 8.1, we show how to treat the other sign combinations. The main point here is that the phases satisfy

$$\begin{align*}\Phi_{\iota_1\iota_2}(\xi,0,0):= \langle \xi \rangle - \iota_1-\iota_2\end{align*}$$

and, therefore, are not completely resonant since $(\iota _1\iota _2)\neq (++)$ . On the other hand, we still need to pay some attention to the case when one of the inputs is close to the degenerate frequencies $\pm \sqrt {3}$ .

Step 1: Preliminary reductions. First, notice that if $(\iota _1\iota _2)=(--)$ , we have $|\Phi |\gtrsim 1$ . This case is then easily handled by integrating by parts in s. By symmetry, we can reduce matters to the case $\iota _1=+=-\iota _2$ (but we do not assume a relation between $k_1$ and $k_2$ ) and look at the integral in equation (11.2) with phase

(11.32) $$ \begin{align} \Phi_{+-}(\xi,\eta,{\sigma}) = \langle \xi \rangle-\langle \eta \rangle+\langle \sigma \rangle. \end{align} $$

Notice that if $|\eta |,|{\sigma }|\leq 1$ , then $|\Phi _{+-}|\gtrsim 1$ , and the bound in equation (11.5) would again be easy to prove. We may then assume $\mathrm {max}(k_1,k_2)\geq -5$ and, for a similar reason, $k_1\geq k_2$ .

We decompose into the size of $||\eta |-\sqrt {3}| \approx 2^{j_1}$ by letting

(11.33) $$ \begin{align} \begin{aligned} I^{p,k,k_1,k_2,j_1}(t,\xi) & := \iint e^{it \Phi_{+-}(\xi,\eta,{\sigma})} \, \varphi_p^{(p_0)}\big(\Phi_{\iota_1\iota_2}(\xi,\eta,{\sigma})\big) \, \mathfrak{q}_{\iota_1\iota_2}(\xi,\eta,{\sigma}) \, \chi_{j_1,\sqrt{3}}^{[-\gamma m,0]}(\eta) \, \\ &\quad \times\, \varphi_k(\xi) \varphi_{k_1}(\eta) \widetilde{a}_{\iota_1}(\eta) \, \varphi_{k_2}(\sigma) \widetilde{b}_{\iota_2}({\sigma}) \, d\eta \, d{\sigma} \end{aligned} \end{align} $$

(recall the definition in equation (2.28)) and aim to prove

(11.34) $$ \begin{align} \begin{aligned} 2^m 2^{k} \left\| \chi_{\ell,\sqrt{3}}(\cdot) \int_{0}^t I^{p,k,k_1,k_2,j_1}(\cdot,s) \, \tau_m(s)\, ds \right\|_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{-\beta\ell} 2^{-3\beta'm}. \end{aligned} \end{align} $$

First, we may only concentrate on the case $j_1 \leq -10$ , for otherwise there is no degeneracy of $\partial _{\eta } \widetilde {f}$ , Lemma 8.5 applies verbatim, and the proof can proceed as in Section 8; see also the argument following equation (11.17). We can then forget the localisation in $|\eta |\approx 1$ , eliminating the cutoff $\varphi _{k_1}$ from equation (11.33), and rename it as $I^{p,k,j_1,k_2}$ .

Moreover, when $j_1 \leq -10$ , we may also assume that $\ell \geq -5$ , for otherwise we would have $||\xi |-\sqrt {3}| \leq 2^{\ell +2}$ and therefore

$$ \begin{align*} |\Phi_{+-}(\xi,\eta,{\sigma})| = |\langle \xi \rangle-2 - (\langle \eta \rangle-2) + \langle \sigma \rangle| \geq \langle \sigma \rangle - 2^{\ell+2} - 2^{j_1+2} \gtrsim 1. \end{align*} $$

Similarly, we may assume $k\leq 5$ , for otherwise $|\Phi _{-+}| \gtrsim 2^k$ .

We have then reduced equation (11.34) to showing

(11.35) $$ \begin{align} \begin{aligned} 2^m 2^{k} \left\| \int_{0}^t I^{p,k,j_1,k_2}(\cdot,s) \, \tau_m(s)\, ds \right\|_{L^2_{\xi}} \lesssim {\varepsilon}_1^2 \, 2^{-3\beta'm}. \\ \mbox{with} \qquad j_1,p \leq -10, \quad k\leq 5. \end{aligned} \end{align} $$

For later reference, we write

(11.36) $$ \begin{align} \Phi_{+-}(\xi,\eta,{\sigma}) = \frac{\xi^2}{1+\langle \xi \rangle} + \frac{\sigma^2}{1+\langle \sigma \rangle} - \frac{\eta^2 - 3}{\langle \eta \rangle+2}. \end{align} $$

Step 2: Preliminary bounds. Following a similar approach to that of Section 8, we want to treat a few cases by some basic bilinear estimates like those in Lemma 8.5. In particular, under the parameter restrictions in equation (11.35), we have the following two analogues of equations (8.39) and (8.40): first, by estimating $L^2_{\xi } \mapsto L^{\infty }_{\xi }$ gaining a factor of $2^{k/2}$ and then integrating by parts in the two uncorrelated variables $\eta $ and ${\sigma }$ (as in the proof of equation (8.20)), we have

(11.37) $$ \begin{align} {\big\| I^{p,k,j_1,k_2}[f,f](s) \big\|}_{L^2} \lesssim 2^{k/2} \cdot {\varepsilon}_1 2^{-m} 2^{\beta'j_1} 2^{\alpha m} \cdot {\varepsilon}_1 \mathrm{min}(2^{-m-k_2/2},2^{3k_2/2}) 2^{\alpha m}, \end{align} $$

having used equation (11.15); second,

(11.38) $$ \begin{align} {\big\| I^{p,k,j_1,k_2}[f,f](s) \big\|}_{L^2} \lesssim 2^{p} \cdot {\varepsilon}_1 2^{-m} 2^{-\beta j_1} 2^{\alpha m} \cdot {\varepsilon}_1 \mathrm{min}(2^{-m-k_2/2},2^{3k_2/2}) 2^{\alpha m}, \end{align} $$

arguing as in the proof of Lemma 8.5 and using the a priori bound on ${\|\chi _{j_1,\sqrt {3}}\partial _{\eta }\widetilde {f}\|}_{L^2}$ .

Step 3: Case $k \leq -m/6 - 5\beta 'm$ . Applying equation (11.37), we see that

$$ \begin{align*} 2^k {\big\| I^{p,k,j_1,k_2}[f,f](s) \big\|}_{L^2} \lesssim {\varepsilon}_1^2 2^{3k/2} \cdot 2^{-m+\alpha m} \cdot 2^{-3m/4 +\alpha m}. \end{align*} $$

This implies equation (11.35) for k in the range under consideration.

Step 4: Case $2k \leq j_1 + 10$ . Using equation (11.38) and canceling the factor of $2^{-\beta j_1}$ by the factor of $2^k$ in front of the expression, we can bound

$$ \begin{align*} 2^k {\big\| I^{p,k,j_1,k_2}[f,f](s) \big\|}_{L^2} \lesssim {\varepsilon}_1^2 2^{p} \cdot 2^{-m+\alpha m} \cdot 2^{-3m/4 +\alpha m}.\end{align*} $$

When $p \leq -m/4-4\beta 'm$ , this already suffices. For $p \geq -m/4-4\beta 'm$ , we instead integrate by parts; the loss is only about $2^{m/4}$ and is a much smaller loss than what we had in Section 8.7, for example, so the analysis of the resulting quartic terms performed there suffices here too.

Step 5: Case $2k> j_1 + 10$ . In this case, $\xi ^2 \gg |\eta ^2-3|$ , and from equation (11.36), we see that

(11.39) $$ \begin{align} |\Phi_{+-}(\xi,\eta,{\sigma})| \gtrsim 2^{2k}. \end{align} $$

In particular, integration by parts in time is very efficient, especially by noticing that we have an extra factor of $2^k$ in front of the expression in equation (11.35). The loss incurred by dividing by $\Phi _{+-}$ is then bounded by $2^{-k} \lesssim 2^{m/6 + 5\beta 'm}$ , and the same arguments used in Section 8.7 apply here.

11.2 Sobolev estimates

Here we show how to bootstrap the Sobolev bound in Proposition 7.2 and obtain the bound on the first norm in equation (7.11).

Proposition 11.4. Under the bootstrap assumptions in equations (7.7) and (7.10), for all $t\in [0,T]$ , we have

(11.40) $$ \begin{align} {\| \langle \xi \rangle^{4} \widetilde{f}(t) \|}_{L^{2}} \leq C{\varepsilon}_{0} + C {\varepsilon}_1^2\langle t \rangle^{p_0}. \end{align} $$

Proof. From equations (5.55) and (5.53), and equation (7.36), we have

(11.41) $$ \begin{align} \partial_t \widetilde{f} & = \mathcal{Q}^R(g,g) + \mathcal{C}^{S,1}(g,g,g) + \mathcal{C}^{S,2}(g,g,g) \nonumber\\ & = \mathcal{Q}^R(f,f) + \mathcal{R}_H(f,g) + \mathcal{C}^{S,1}(g,g,g) + \mathcal{C}^{S,2}(g,g,g). \end{align} $$

It then suffices to show that that each term on the right-hand side of equation (11.41) is bounded in $L^2(\langle \xi \rangle ^8 d\xi )$ by $C {\varepsilon }_1^2\langle t \rangle ^{p_0-1}$ so that equation (11.40) follows from integration in time, also using the bound equation (7.4) at time $0$ .

The cubic terms can be treated directly using the trilinear estimates of Lemma 6.13 and the a priori Sobolev and decay assumptions in equation (7.7); the term $\mathcal {R}_H(f,g)$ is already estimated as desired in equation (7.37).

For the quadratic term in equation (11.41), we need an additional nontrivial argument that uses integration by parts in frequencies, the structure of the symbol, and Lemma 6.11. For convenience, let us rewrite here the expression for $\mathcal {Q}^R$ (see equation (5.56))

(11.42) $$ \begin{align} \mathcal{Q}_{\iota_1\iota_2}^R(a,b)(t,\xi) = \iint e^{it \Phi_{\iota_1\iota_2}(\xi,\eta,\sigma)} \, \mathfrak{q}(\xi,\eta,\sigma) \, \widetilde{a}_{\iota_1}(t,\eta) \widetilde{b}_{\iota_2}(t,\sigma) \, d\eta \, d\sigma \end{align} $$

and recall that the symbol $\mathfrak {q}$ is given as in equations (5.15)–(5.16) and (4.6)–(4.7) and the bilinear estimates of Lemma 6.11 hold. Without loss of generality, let us assume that the support of equation (11.42) is restricted to $|\eta |\geq |{\sigma }|$ . Also, we may assume that $|\xi |\geq 10$ . We look at three different cases depending on the size of $\xi $ and $\eta $ .

Case 1: $|\xi | \geq 5|\eta |$ . First we treat the case of $|\xi | \leq \langle t \rangle ^{p_0/10}$ . In this case, we use the estimate in equation (6.20) to obtain

$$ \begin{align*} {\| \langle \xi \rangle^4 \mathcal{Q}_{\iota_1\iota_2}^R(f,f)(t) \|}_{L^2} & \lesssim \langle t \rangle^{p_0/2} {\| \mathcal{Q}_{\iota_1\iota_2}^R(f,f)(t) \|}_{L^2} \\ & \lesssim \langle t \rangle^{p_0/2} {\| e^{i\iota_1t\langle \partial_x \rangle} \mathcal{W}^*f \|}_{L^{\infty-}} {\| e^{i\iota_2t\langle \partial_x \rangle} \mathcal{W}^*f \|}_{L^{\infty-}} \lesssim {\varepsilon}_1^2 \langle t \rangle^{-1+p_0}. \end{align*} $$

If instead $|\xi | \geq \langle t \rangle ^{p_0/10}$ , we use the decay property of $\mu _R$ in equation (4.7) and see that

$$ \begin{align*} {\big\| \langle \xi \rangle^4 \mathcal{Q}_{\iota_1\iota_2}^R(f,f)(t) \big\|}_{L^2} & \lesssim \sup_{\substack{|\xi| \geq 2(|\eta|+|{\sigma}|) \\ |\xi|> t^{p_0/10}}} \big| \langle \xi \rangle^6 \mu^R(\xi,\eta,{\sigma}) \big| {\| \widetilde{f} \|}_{L^2_{\eta}} {\| \widetilde{f} \|}_{L^2_{\sigma}} \\ & \lesssim \langle t \rangle^{-(N/2-6)p_0/10} {\varepsilon}_1^2, \end{align*} $$

which suffices since we can take N arbitrarily large.

Case 2: $|\xi | < 5|\eta |$ and $|\eta | \geq \langle t \rangle ^{1/3}$ . In this case, the first input of $\mathcal {Q}^R$ is projected to (distorted) frequencies greater than $\langle t \rangle ^{1/3}$ , and we denote it by $f_1$ , where $\widetilde {f_1} := \varphi _{\geq 0}(\eta \langle t \rangle ^{-1/3})\widetilde {f}$ .

We begin by integrating by parts in the uncorrelated variable ${\sigma }$ and notice that the term where the symbol $\mathfrak {q}$ is differentiated is lower-order. Then using that

$$ \begin{align*}|\mathfrak{q}(\xi,\eta,\sigma)| \lesssim \frac{1}{\langle \eta \rangle} (\inf_{{\lambda},\mu} \langle \xi \pm \eta \pm \sigma \rangle )^{-N} \end{align*} $$

together with Young’s inequality gives

$$ \begin{align*} {\| \langle \xi \rangle^4 \mathcal{Q}_{\iota_1\iota_2}^R\big(f,f)(t) \|}_{L^2} & \lesssim {\|\langle \eta \rangle^{3} \widetilde{f_1} \|}_{L^2} \cdot {\varepsilon}_1 \langle t \rangle^{-3/4+\alpha} \\ & \lesssim \langle t \rangle^{-1/3} {\| \langle \eta \rangle^4 \widetilde{f_1} \|}_{L^2} \cdot {\varepsilon}_1\langle t \rangle^{-3/4 + \alpha} \lesssim {\varepsilon}_1^2 \langle t \rangle^{-1}. \end{align*} $$

Case 3: $|\xi | < 5|\eta |$ and $|\eta | \leq \langle t \rangle ^{1/3}$ . In this last case we integrate by parts in $\eta $ as well. We denote the first input of $\mathcal {Q}^R$ by $f_2 := \varphi _{\leq 0}(\eta \langle t \rangle ^{-1/3})\widetilde {f}$ . Integrating by parts in $\eta $ gains a factor of $|t|^{-1}$ and differentiates the profile $\widetilde {f_2}(\eta )$ . By the same argument as above,

$$ \begin{align*} {\| \langle \xi \rangle^4 \mathcal{Q}_{\iota_1\iota_2}^R\big[f,f\big](t) \|}_{L^2} & \lesssim \langle t \rangle^{-1} {\| \langle \eta \rangle^{3} \partial_{\eta} \widetilde{f_2} \|}_{L^2} \cdot {\varepsilon}_1 \langle t \rangle^{-3/4+\alpha} \\ & \lesssim \langle t \rangle^{-1} \langle t \rangle^{2/3} {\| \langle \eta \rangle \partial_{\eta} \widetilde{f_2}\|}_{L^2} \cdot {\varepsilon}_1\langle t \rangle^{-3/4 + \alpha} \\ & \lesssim \langle t \rangle^{-1/3} \cdot {\varepsilon}_1 \langle t \rangle^{\alpha} \cdot {\varepsilon}_1 \langle t \rangle^{-3/4+\alpha}, \end{align*} $$

which suffices and concludes the proof of equation (11.40).

11.3 Pointwise estimates for the regular part and other higher-order terms

In this subsection, we first show that the regular part $\mathcal {Q}^R$ in equations (5.15)–(5.16) does not contribute to the pointwise asymptotic behaviour of the solution, or, in other words, that it is a remainder when measured in the $\langle \xi \rangle ^{-3/2}L^{\infty }_{\xi }$ norm. Then we control the $\langle \xi \rangle ^{-3/2}L^{\infty }_{\xi }$ norm of all the other terms that are not the singular cubic terms treated in Section 10; these include cubic terms that arise when passing from the original profile, g, to the renormalised profile, f, and quartic and higher-order terms. Along the way, we also establish bounds on the weighted norm of some cubic terms that are not already accounted for in Section 7. In particular, these estimates will conclude the proof of the bound on the last norm in equation (7.11) in the main bootstrap Proposition 7.2 and give the bounds on the remainders in equations (10.2)–(10.3) in Proposition 10.1.

11.3.1 Remainders from the quadratic regular part

We begin by recalling that from Lemma 7.8, we have

(11.43) $$ \begin{align} \begin{aligned} \mathcal{Q}^R(g,g) & = \mathcal{Q}^R(f,f) + \mathcal{Q}^R(f,T(f,f)) + \mathcal{Q}^R(T(f,f),f) + \mathcal{R}_2(f,g), \end{aligned} \end{align} $$

where $\mathcal {R}_2(f,g)$ is the quartic term defined in equation (7.39) and satisfies

(11.44) $$ \begin{align} \begin{aligned} {\| \langle \xi \rangle \partial_{\xi} \mathcal{R}_2(f,g)(t) \|}_{L^2}& \lesssim {\varepsilon}_2^2 \langle t \rangle^{-1+\alpha}. \end{aligned} \end{align} $$

We need to control in $\langle \xi \rangle ^{-3/2}L^{\infty }_{\xi }$ all the terms on the right-hand side of equation (11.43) (Proposition 11.5 below) and the weighted norms of the cubic terms $\mathcal {Q}^R(f,T(f,f)) + \mathcal {Q}^R(T(f,f),f)$ (Proposition 11.6 below), since the weighted norm of $\mathcal {Q}^R(f,f)$ was taken care of in Section 8 and Section 11.1.

Proposition 11.5 ( $L^{\infty }_{\xi }$ control for $\mathcal {Q}^R$ and remainders)

Under the assumptions of Theorem 1.1, consider the u solution of equation (KG) satisfying equations (2.32)–(2.33), and let f be the renormalised profile defined in equation (5.53). We have

(11.45) $$ \begin{align} {\| \langle \xi \rangle^{3/2} \mathcal{Q}^R(f,f)(t) \|}_{L^{\infty}_{\xi}} \lesssim {\varepsilon}_{1}^2 \langle t \rangle^{-3/2+2\alpha}. \end{align} $$

Moreover, for any $m=0,1,\dots $ we have

(11.46) $$ \begin{align} {\Big\| \langle \xi \rangle^{3/2} \int_{0}^{t} \mathcal{Q}^R[f,T(f,f)](s,\xi) \, \tau_m(s) \, ds \Big\|}_{L^{\infty}_{\xi}} \lesssim {\varepsilon}_1^3 2^{-m/20}. \end{align} $$

Finally,

(11.47) $$ \begin{align} {\big\| \langle \xi \rangle^{3/2} \mathcal{R}_2(f,g)(t) \|}_{L^{\infty}_{\xi}} \lesssim {\varepsilon}_2^2 \langle t \rangle^{-1-1/20}. \end{align} $$

Proof. Proof of equation (11.45). This bound is essentially already contained in the proof of Lemma 8.3 where, however, we only dealt with bounded frequencies. Using the same argument (integration by parts in the uncorrelated variables $\eta $ and ${\sigma }$ ), decomposing dyadically the input frequencies as usual and using the bound in equation (11.3) for the symbol $\mathfrak {q}$ , we get for all $t \approx 2^m$

$$ \begin{align*} {\| \langle \xi \rangle^{3/2} \varphi_k(\xi) \mathcal{Q}^R(f,f)(t) \|}_{L^{\infty}_{\xi}} \lesssim 2^{3k^+/2} \sum_{k_1,k_2} 2^{-k_1^+} {2^{-20| k^+ - k_1^+|}} \cdot X_{k_1,m} \cdot X_{k_2,m}. \end{align*} $$

Using the estimate $X_{k,m} \lesssim {\varepsilon }_1 \mathrm {min}(2^{3k^-/2}, 2^{-m-k^-/2}, 2^{-m-k^+/2})2^{\alpha m}$ (see equation (11.12)), we can perform the two sums over $k_1,k_2$ and obtain

$$ \begin{align*} {\| \langle \xi \rangle^{3/2} \varphi_k(\xi) \mathcal{Q}^R(f,f)(t) \|}_{L^{\infty}_{\xi}} \lesssim ({\varepsilon}_1 2^{-3m/4 + \alpha m})^2. \end{align*} $$

Proof of equations (11.46) and (11.47) We first claim that a strong bound in $L^2$ holds for the cubic terms: that is, for all $t\approx 2^m$ ,

(11.48) $$ \begin{align} {\big\| \langle \xi \rangle^2 \mathcal{Q}^R(f,T(f,f))(t) \|}_{L^2} + {\big\| \langle \xi \rangle^2 \mathcal{Q}^R(T(f,f),f)(t) \|}_{L^2} \lesssim {\varepsilon}_1^3 2^{-6m/5}. \end{align} $$

To see this, it suffices to use that, for p large enough,

$$ \begin{align*} {\big\| e^{-it\langle \partial_x \rangle} \langle \partial_x \rangle^{1+} \mathcal{W}^*f \big\|}_{L^p} \lesssim {\varepsilon}_1 \langle t \rangle^{-1/4}, \end{align*} $$

which follows from interpolating the a priori decay assumptions and the $H^4$ bound, and then apply equation (6.21) with $p_1,p_2$ large enough and equation (6.15).

Then using the inequality ${\| \langle \xi \rangle ^{3/2} f \|}_{L^{\infty }} \lesssim \big ( {\| \langle \xi \rangle \partial _{\xi } f \|}_{L^2} + {\| f \|}_{L^2}\big )^{1/2} {\| \langle \xi \rangle ^2 f \|}_{L^{\infty }}^{1/2}$ to interpolate between equation (11.48) and the weighted bound in equation (11.49) from Proposition 11.6 below, we obtain equation (11.46).

Using again equations (6.20) and (6.15) with the Sobolev norm bound and the decay for the linear evolution of g, it is easy to see that the quartic term $\mathcal {R}_2(f,g)$ in equation (7.39) satisfies

$$ \begin{align*} {\| \langle \xi \rangle^{2} \mathcal{R}_2(f,g)(t) \|}_{L^2} & \lesssim {\varepsilon}_2^3 \langle t \rangle^{-3/2}. \end{align*} $$

Interpolating this and the weighted bound in equation (11.44), we obtain equation (11.47).

Proposition 11.6 Weighted estimates for other remainders

For any $m=0,1 \dots $ , we have

(11.49) $$ \begin{align} {\Big\| \langle \xi \rangle \partial_{\xi} \int_{0}^{t} \mathcal{Q}^R[T(f,f),f](s,\xi) \, \tau_m(s) ds \Big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_1^3 2^{\alpha m}. \end{align} $$

Proof. These cubic terms are much easier to treat than the quadratic terms analysed in Section 8. For completeness, we briefly discuss how to estimate them.

For simplicity, we assume $|\xi |\leq 1$ ; this can be done in view of the estimate in equation (11.3) (see also equation (11.20)) for the symbol $\mathfrak {q}$ . We look at the formulas for $\mathcal {Q}^R$ (see equation (11.1)) and T (see equation (5.54)) and write out the term explicitly as a trilinear operator; after localising dyadically in the frequencies, and making the usual reductions, this leads us to consider a term of the form

(11.50) $$ \begin{align} \begin{aligned} & L^R_{\underline{k}}(s,\xi) := \iiint e^{is \Psi_{\iota_1\iota_2\iota_3}} \, \, \mathfrak{q}'(\xi,\eta,{\sigma},\rho) \, \varphi_{\underline{k}}'(\xi,\eta,\sigma,\rho) \, \widetilde{f}(\rho) \widetilde{f}(\rho-\eta) \widetilde{f}({\sigma})\, d\eta \, d{\sigma} \, d\rho, \\ & \Psi_{\iota_1\iota_2\iota_3}(\xi,\eta,{\sigma},\rho) = \langle \xi \rangle - \iota_1 \langle \rho \rangle - \iota_2 \langle \eta-\rho \rangle - \iota_3 \langle \sigma \rangle, \\ & \varphi_{\underline{k}}'(\xi,\eta,\sigma,\rho) := \varphi_k(\xi) \varphi_{k_2}(\sigma) \varphi_{k_3}(\rho)\varphi_{k_4}(\eta-\rho), \qquad k_4\leq k_3 \leq 0. \end{aligned} \end{align} $$

Here, we may assume that $\mathfrak {q}'$ is smooth, with uniform bounds on its derivatives, except at the points $\rho =0$ , $\rho -\eta =0$ , ${\sigma }=0$ and $\eta =0$ , where it can have $ \mbox {sign} $ -type singularities. Note that the boundedness property holds in view of equation (11.3) and the estimates on the symbol of T from Lemma 6.9, when we assume that all the frequencies involved are $\lesssim 1$ ; when frequencies are large, the estimate in equation (11.3) degenerates, but as discussed before, this case is not harder to treat than the case of frequencies less than $1$ and can be analysed using the bounds in equations (11.11)–(11.12) for the quantity $X_{k,m}$ when $k\geq 0$ . Also recall that the lack of smoothness when one of the three input variables is zero is not an issue; the singularity at $\eta $ is instead a potential issue that we will address below.

As usual, we localise time $s \approx 2^m$ . Since applying $\langle \xi \rangle \partial _{\xi }$ will cost at most a factor of $s \xi \approx 2^m 2^k$ , we can reduce matters to obtaining the estimate

(11.51) $$ \begin{align} 2^{k} {\Big\| \int_0^t L^R_{\underline{k}}(s,\xi) \, \tau_m(s) ds \Big\|}_{L^2} \lesssim {\varepsilon}_1^3 2^{-m}. \end{align} $$

This is implied by the stronger bound

(11.52) $$ \begin{align} 2^{3k/2} \big| L^R_{\underline{k}}(s,\xi) \big| \lesssim {\varepsilon}_1^3 2^{-2m}, \qquad s\approx 2^m. \end{align} $$

The arguments needed to show equation (11.52) are similar to those used in Section 8.6 to estimate the term $K_{\underline {k}}$ in equation (8.72) (see also equations (8.70)–(8.71)). Note that $K_{\underline {k}}$ is actually a quartic term while $L^R_{\underline {k}}$ is only cubic, but, on the other hand, $L^R_{\underline {k}}$ has a (smooth) bounded symbol, while the symbol of $K_{\underline {k}}$ has a large $1/\Phi $ factor, where $\Phi $ is only assumed to be approximately lower bounded by $2^{-m/2}$ .

Examining equation (11.50), we see that in fact all three input frequencies are uncorrelated, and we have the possibility of integrating by parts in each of them. However, we need to account for the singularity of the symbol in $\eta $ . For this, we introduce a decomposition in $|\eta |$ by inserting cutoffs $\varphi _{k_1}(\eta )$ , $k_1\in {\mathbb Z}$ . The sum over $|k_1| \geq 10m$ is easily dealt with using the a priori bounds in equation (7.10) on the $L^{\infty }_{\xi }$ and $H^4$ -type norm. It then suffices to estimate the contribution at each fixed $k_1$ , with $|k_1|\leq 10m$ of the terms (we are changing variables $\eta \mapsto \rho -\eta '$ )

(11.53) $$ \begin{align} \begin{aligned} L^R_{\underline{k},k_1}(s,\xi) & := \iiint e^{is \Psi_{\iota_1\iota_2\iota_3}(\xi,\rho-\eta',\rho,{\sigma})} \, \, \mathfrak{q}'(\xi,\rho-\eta',{\sigma},\rho) \, \varphi_{\underline{k}}'(\xi,\rho-\eta',\sigma,\rho) \varphi_{k_1}(\rho-\eta') \, \\ &\quad \times\, \widetilde{f}(\rho) \widetilde{f}(\eta') \widetilde{f}({\sigma})\, d\eta' \, d{\sigma} \, d\rho. \end{aligned} \end{align} $$

The sum over $k_1$ can be done at the expense of an $O(m)$ loss.

In equation (11.53), we integrate by parts in $\rho $ and/or $\eta '$ and/or ${\sigma }$ whenever any of these variables have size $\gtrsim 2^{-m/2}$ and use the a priori bounds in equation (7.22) when instead they are $\lesssim 2^{-m/2}$ ; this gives us the usual factor of ${\varepsilon }_1 2^{-3m/4 + \alpha m}$ for each of the three inputs. This suffices provided we do not differentiate the symbol or, better, the cutoff $\varphi _{k_1}$ when integrating by parts in $\rho $ or $\eta '$ .

Let us then consider the case when $|\rho |\gtrsim 2^{-m/2}$ and we hit the symbol with $\partial _\rho $ . This gives the contribution

$$ \begin{align*} \begin{aligned} &\iiint e^{is \Psi_{\iota_1\iota_2\iota_3}(\xi,\rho-\eta',\rho,{\sigma})} \, \frac{\langle\rho\rangle}{s\rho} \, \mathfrak{q}'(\xi,\rho-\eta',{\sigma},\rho) \, \varphi_{\underline{k}}'(\xi,\rho-\eta',\sigma,\rho) \varphi_{\sim k_1}(\rho-\eta') 2^{-k_1}\, \\ &\quad\times\, \widetilde{f}(\rho) \widetilde{f}(\eta') \widetilde{f}({\sigma})\, d\eta' \, d{\sigma} \, d\rho. \end{aligned} \end{align*} $$

Integrating by parts in ${\sigma }$ and $\eta '$ (again, we assume their sizes are $\gtrsim 2^{m/2}$ , the complementary arguments being similar) leads to a main term of the form

$$ \begin{align*} \begin{aligned} & \iiint e^{is \Psi_{\iota_1\iota_2\iota_3}(\xi,\rho-\eta',\rho,{\sigma})} \, \frac{\langle\rho\rangle \langle\eta'\rangle \langle \sigma \rangle}{s^3\rho \,\eta' {\sigma}} \, \mathfrak{q}'(\xi,\rho-\eta',{\sigma},\rho) \, \varphi_{\underline{k}}'(\xi,\rho-\eta',\sigma,\rho) \varphi_{\sim k_1}(\rho-\eta') 2^{-k_1}\, \\ &\quad\times \widetilde{f}(\rho) \, \partial_{\eta'} \widetilde{f}(\eta') \, \partial_{\sigma} \widetilde{f}({\sigma})\, d\eta' \, d{\sigma} \, d\rho. \end{aligned} \end{align*} $$

This is bounded by

$$ \begin{align*} & C 2^{-3m} \cdot 2^{-k_2-k_3-k_4} \cdot {\| \varphi_{k_3}\widetilde{f} \|}_{L^{\infty}} \cdot 2^{k_4/2} {\| \varphi_{k_4} \partial_{\eta'} \widetilde{f} \|}_{L^2} \cdot 2^{k_2/2} {\| \varphi_{k_2} \partial_{\sigma} \widetilde{f} \|}_{L^2} \\ \quad \lesssim 2^{-3m} \cdot 2^{-(k_2+k_3+k_4)/2} \cdot 2^{3\alpha m}. \end{align*} $$

Since $\mathrm {min}(k_2,k_3,k_4) \geq -m/2$ in our current scenario, this gives us the desired equation (11.52). Similar estimates hold true if $\partial _{\eta '}$ hits the symbol instead of the profile or if $\mathrm {min}(k_2,k_4) \leq -m/2$ .

11.3.2 Remainders from the cubic singular terms

From Lemma 7.9, we know that

(11.54) $$ \begin{align} \begin{aligned} & \mathcal{C}^{S}(g,g,g) - \mathcal{C}^{S}(f,f,f) \\ &\quad = \mathcal{C}^{S}(T(f,f),f,f) + \mathcal{C}^{S}(f,T(f,f),f) + \mathcal{C}^{S}(f,f,T(f,f)) + \mathcal{R}_3(f,g), \end{aligned} \end{align} $$

where $\mathcal {R}_3(f,g)$ is the quintic term that is defined in equation (7.48) and satisfies equation (7.46):

(11.55) $$ \begin{align} {\| \langle \xi \rangle \partial_{\xi} \mathcal{R}_3(f,g)(t) \|}_{L^2} & \lesssim {\varepsilon}_2^3 \langle t \rangle^{-1+\alpha}. \end{align} $$

We prove control of all the terms on the right-hand side of equation (11.54).

Proposition 11.7 Weighted estimates for remainder terms

Denote $\mathcal {C} = \mathcal {C}^{S}(T(f,f),f,f)$ , or $\mathcal {C}^{S}(f,T(f,f),f)$ or $\mathcal {C}^{S}(f,f,T(f,f))$ . Then we have

(11.56) $$ \begin{align} \begin{aligned} {\Big\| \langle \xi \rangle \partial_{\xi} \int_0^t \mathcal{C}(\xi,s) \, ds \Big\|}_{L^2_{\xi}} \lesssim {\varepsilon}_1^4. \end{aligned} \end{align} $$

Moreover, for $m=0,1,\dots $ ,

(11.57) $$ \begin{align} \begin{aligned} {\Big\| \langle \xi \rangle^{3/2} \int_0^t \mathcal{C}(\cdot,s) \, \tau_m(s) ds \Big\|}_{L^{\infty}_{\xi}} \lesssim {\varepsilon}_1^4 2^{-m/10}. \end{aligned} \end{align} $$

Finally,

(11.58) $$ \begin{align} {\| \langle \xi \rangle^{3/2} \mathcal{R}_3(f,g)(t) \|}_{L^{\infty}_{\xi}} & \lesssim {\varepsilon}_2^3 \langle t \rangle^{-1-\alpha}. \end{align} $$

Note that, as in Propositions 11.5 and equation (11.6), we need to use the time integral in equations (11.56) and (11.57) too.

Proof. Proof of equation (11.56). Let us consider the term $\mathcal {C} = \mathcal {C}^{S1}[T(f,f),f,f]$ and restrict our attention to the portion of T corresponding to the $\delta $ contribution of its symbol Z; see the formulas in equations (5.57), (5.46), (5.29) and (5.11). The slight modifications that are needed to deal with the other terms pf $\mathrm {p.v.}$ -type will be clear to the reader; compare also with the arguments in Section 11.4.1 (where we deal with a $\mathrm {p.v.}$ contribution) and the algebra following equation (11.71). Writing out explicitly the quartic term under consideration, and disregarding the irrelevant signs $\epsilon ,\epsilon ',{\lambda },\mu ,\nu \dots $ in the symbols in equations (5.46) and (5.11), we obtain an expression of the form

(11.59) $$ \begin{align} \begin{aligned} & \mathcal{C}(t,\xi) = \iiint e^{it \Phi_{\iota_1\iota_2\iota_3\iota_4}} \mathfrak{c} \, \widetilde{f}_{\iota_1}(\eta) \widetilde{f}_{\iota_2}({\sigma}) \widetilde{f}_{\iota_3}(\rho) \widetilde{f}_{\iota_4}(\xi-\eta-{\sigma}-\rho) \, d\eta \, d{\sigma} \,d\rho, \\ & \Phi_{\iota_1\iota_2\iota_3\iota_4}(\xi,\eta,\sigma,\theta) = - \langle \xi \rangle +\iota_1\langle \eta \rangle +\iota_2\langle \sigma \rangle + \iota_3 \langle \rho \rangle + \iota_4 \langle\xi-\eta-\sigma-\rho\rangle. \\ \end{aligned} \end{align} $$

Here, as usual, we can think of $\mathfrak {c}$ as a smooth symbol so that its associated $4$ -linear operator satisfies standard Hölder estimates.

To handle this term, the main idea is to use the following ‘commutation identity’ for $\langle \xi \rangle \partial _{\xi }$ and $\Phi := \Phi _{\iota _1\iota _2\iota _3\iota _4}$ : let $X_a := \langle a \rangle \partial _a$ ; then

(11.60) $$ \begin{align} (X_{\xi} + \iota_1 X_{\eta} + \iota_2 X_{\sigma} + \iota_3X_\rho) \Phi = -\iota_4 \frac{\xi-\eta-\sigma-\rho}{\langle \xi-\eta-\sigma-\rho\rangle} \Phi. \end{align} $$

Thanks to this, we can write $\langle \xi \rangle \partial _{\xi } \mathcal {C}$ as a linear combination of terms of the following two types, up to similar or easier ones:

(11.61) $$ \begin{align} & \mathcal{C}_a = \iiint e^{it \Phi} \mathfrak{c} \,\big( \langle \eta \rangle \partial_{\eta} \widetilde{f}_{\iota_1}(\eta) \big) \, \widetilde{f}_{\iota_2}({\sigma}) \widetilde{f}_{\iota_3}(\rho) \widetilde{f}_{\iota_4}(\xi-\eta-{\sigma}-\rho) \, d\eta \, d{\sigma} \,d\rho, \end{align} $$

(11.62) $$ \begin{align} & \mathcal{C}_b = \iiint e^{it \Phi} \, \big( i t\, \Phi \big) \mathfrak{c} \, \widetilde{f}_{\iota_1}(\eta) \widetilde{f}_{\iota_2}({\sigma}) \widetilde{f}_{\iota_3}(\rho) \widetilde{f}_{\iota_4}(\xi-\eta-{\sigma}-\rho) \, d\eta \, d{\sigma} \,d\rho. \end{align} $$

Note that the terms where the derivatives $X_a$ hit the symbol can be treated easily by an $L^2\times L^{\infty }\times L^{\infty }\times L^{\infty }$ -type estimate using the a priori $H^4$ bound and the linear decay estimate.

$\mathcal {C}_a$ is directly estimated using a $4$ -linear Hölder estimate, the a priori bound in equation (7.19) and the usual linear decay estimate:

$$ \begin{align*} {\| \mathcal{C}_a \|}_{L^2} \lesssim {\|\langle \xi \rangle \partial_{\xi} \widetilde{f}_{\iota_1} \|}_{L^2} \big( \langle t \rangle^{-1/2} {\| u \|}_{X_T} \big)^3 \lesssim {\varepsilon}_1^4 \langle t \rangle^{-5/4}. \end{align*} $$

The contribution from equation (11.62) is estimated integrating by parts in time:

$$ \begin{align*} \int_0^t \mathcal{C}_b \,ds = \mathcal{C}_{b_1}(t) + \int_0^t \mathcal{C}_{b_2}(s)\,ds, \end{align*} $$

where $C_{b_1}$ is like $\mathcal {C}_b$ without the factor of $\Phi $ , and $C_{b_2}$ is like $\mathcal {C}_{b_1}$ with one profile $\widetilde {f}$ replaced by $\partial _t\widetilde {f}$ . In particular, we can see that

$$ \begin{align*} {\| \mathcal{C}_{b_1}(t) \|}_{L^2} \lesssim t {\| \widetilde{f} \|}_{L^2} \big( \langle t \rangle^{-1/2} {\| u \|}_{X_T} \big)^3 \lesssim {\varepsilon}_1^4 \langle t \rangle^{-1/2} \end{align*} $$

and

$$ \begin{align*} {\| \mathcal{C}_{b_2}(s) \|}_{L^2} \lesssim {\big\| \partial_s \big(s \widetilde{f} \, \big) \big\|}_{L^2} \big( \langle s \rangle^{-1/2} {\| u \|}_{X_T} \big)^3 \lesssim {\varepsilon}_1^4 \langle s \rangle^{-5/4}, \end{align*} $$

having used equation (7.56). These give us equation (11.56).

Proof of equation (11.57). This follows by interpolating the $\langle \xi \rangle ^{-3/2}L^{\infty }_{\xi }$ norm between the $\langle \xi \rangle ^{-2}L^2$ and $\langle \xi \rangle ^{-1}\dot {H}^1$ and using that the $\langle \xi \rangle ^{-2}L^2$ norm of the quantity we are estimating is bounded at least by ${\varepsilon }_1^4 2^{-m/4}$ .

Proof of equation (11.58). From its definition, we see that $\mathcal {R}_3(f,g)$ is a quintic term in $(f,g)$ ; see equations (7.48) and (7.49). Then using the multilinear estimates from Lemmas 6.13 and 6.10 and the decay for the linear evolution of f and g, we can see that

(11.63) $$ \begin{align} {\| \langle \xi \rangle^2 \mathcal{R}_3(f,g)(t) \|}_{L^2} & \lesssim {\varepsilon}_2^3 \langle t \rangle^{-2+\alpha}. \end{align} $$

Interpolating this and equation (11.55), we obtain the pointwise bound in equation (11.58).

11.4 Other singular cubic interactions

In this subsection, we complete the analysis of the singular cubic terms $\mathcal {C}^{S1}_{\iota _1 \iota _2 \iota _3}$ and $\mathcal {C}^{S2}_{\iota _1 \iota _2 \iota _3}$ defined in equations (5.57)–(5.58). Section 9 was dedicated to the analysis of these terms when $(\iota _1,\iota _2,\iota _3) = (+,-,+)$ , in the fully resonant situation when all input frequencies are $\sqrt {3}$ ; this also covers the case when they are all $-\sqrt {3}$ . We now treat all the other interactions, which are, as was to be expected, relatively easier to deal with.

We will focus only on the $\mathcal {C}^{S2}_{\iota _1 \iota _2 \iota _3}$ terms for the sake of brevity, but the terms $\mathcal {C}^{S1}_{\iota _1 \iota _2 \iota _3}$ are amenable to a similar treatment. We make a convenient choice of the parameters $\lambda , \mu , \dots $ (which do not matter as far as estimates are concerned) and drop all irrelevant indexes as well as complex conjugation signs to obtain the following formula for $\mathcal {C}^{S2}_{\iota _1 \iota _2 \iota _3}$ :

(11.64) $$ \begin{align} \begin{aligned} & \mathcal{C}^{S2}_{\iota_1 \iota_2 \iota_3}[a,b,c](t,\xi) = \iiint e^{it \Phi_{\iota_1\iota_2 \iota_3}(\xi,\eta,{\sigma},\theta)} \mathfrak{c}^{S,2}(\xi,\eta,\sigma,\theta) \, \widetilde{a}(t,\eta) \widetilde{b}(t,{\sigma}) \widetilde{c}(t,\theta) \frac{\widehat{\phi}(p)}{p} \, d\eta \, d{\sigma} \,d\theta, \\ & \Phi_{\iota_1 \iota_2 \iota_3}(\xi,\eta,{\sigma},\theta) := \langle \xi \rangle - \iota_1 \langle \eta \rangle - \iota_2 \langle \sigma \rangle - \iota_3 \langle \theta \rangle, \qquad p = \xi - \eta - \sigma -\theta. \end{aligned} \end{align} $$

Recall that $\mathfrak {c}^{S,2}(\xi ,\eta ,\sigma ,\theta )$ satisfies the bound

$$ \begin{align*}\left| \mathfrak{c}^{S,2}(\xi,\eta,\sigma,\theta) \right| \lesssim \frac{1}{\langle \eta \rangle \langle \eta' \rangle \langle \sigma' \rangle}, \end{align*} $$

and the trilinear operator with this symbol enjoys the boundedness properties stated in Lemma 6.13.

We will distinguish different cases depending on whether $\eta $ , $\sigma $ and $\theta $ are close to or removed from $\pm \sqrt {3}$ . We define cutoff functions

(11.65) $$ \begin{align} \chi_{c}(\xi) = \chi \left( \frac{\xi - \sqrt 3}{r} \right) + \chi \left( \frac{\xi + \sqrt 3}{r} \right), \qquad \chi_{r}(\xi) = 1 - \chi \left( \frac{\xi - \sqrt 3}{4r} \right) - \chi \left( \frac{\xi + \sqrt 3}{4r} \right), \end{align} $$

where r is a sufficiently small positive number and $\chi =\varphi _{\leq 0}$ ; see the notation in Section 2.5.1. Notice that $\chi _c$ and $\chi _r$ do not add up to one, since it will be convenient in the estimates to have a separation between their supports. Since they can be treated with straightforward adaptations, we skip the estimates corresponding to $1 - \chi _c - \chi _r$ for the sake of brevity. According to equation (11.65), we define the frequency projections

(11.66) $$ \begin{align} P_\ast f := \widetilde{{\mathcal{F}}}^{-1} \big( \chi_\ast \, \widetilde{f} \, \big), \qquad \ast \in \{c,r\}.\end{align} $$

We will prove the following main proposition:

Proposition 11.8 (Weighted estimates for the singular cubic interactions)

Let $\mathcal {C}^{S} \in \{\mathcal {C}^{S1},\mathcal {C}^{S2}\}$ as defined in equation (5.57). With the a priori assumptions in equation (7.10), we have, for $t\in [0,T]$ ,

(11.67) $$ \begin{align} \Big\| \langle \xi \rangle\partial_{\xi} \int_0^t \mathcal{C}^{S}_{\iota_1 \iota_2 \iota_3}[a,b,c](s,\xi) \, ds \Big\|_{L^2} \lesssim {\varepsilon}_1^3 \langle t \rangle^{\alpha}, \end{align} $$

when

$$ \begin{align*} & \{\iota_1, \iota_2, \iota_3\} =\{+,+,-\} \quad \mbox{and} \quad \{a,b,c\} \in \{P_{p_1} f, P_{p_2}f, P_r f\}, \quad p_1,p_2 \in\{c,r\} \\ & \mbox{or when} \quad \{\iota_1, \iota_2, \iota_3\} \neq \{+,+,-\}. \end{align*} $$

Moreover, if $\{\iota _1, \iota _2, \iota _3\} =\{+,+,-\}$ and $a,b,c = P_c f$ , but their frequencies are not all equal to either $\sqrt {3}$ or - $\sqrt {3}$ , then

(11.68) $$ \begin{align} \Big\| \int_0^t \mathcal{C}^{S}_{\iota_1 \iota_2 \iota_3}[a,b,c](s,\xi) \, ds \Big\|_{W_T} \lesssim {\varepsilon}_1^3. \end{align} $$

The proof of Proposition 11.8 will complete the proof of the weighted bound in equation (7.11).

For a better organization of our exposition, we will prove equations (11.67)–(11.68) by distinguishing cases relative to whether the frequencies are close or not to $\pm \sqrt {3}$ , and subcases depending on the $\iota $ ’s signs combinations.

11.4.1 Three frequencies removed from $\pm \sqrt 3$

This case is similar to the cubic nonlinear Schrödinger equation, where the dispersion relation is $\Lambda = \xi ^2$ ; see [24, 7]. In [24], weighted estimates are proved under the assumption that the potential V is generic; here we provide a more general (and simpler) argument similar to the one in [7] that also applies to the case of exceptional potentials and any solution u such that $\widetilde {u}(0)=0$ .

As before, we simplify our notation by dropping some of the irrelevant indexes in our formulas. We look at the restriction of equation (11.64) to inputs with frequencies away from $\pm \sqrt {3}$ by defining

(11.69) $$ \begin{align} \begin{aligned} \mathcal{C}_{rrr}(a,b,c)(t,\xi) &:= \iiint e^{it \Phi_{\iota_1\iota_2 \iota_3}(\xi,\eta,\sigma,\theta)} \mathfrak{c}_{rrr}(\xi,\eta,\sigma,\theta) \widetilde{a}(t,\eta) \widetilde{b}(t,\sigma) \widetilde{c}(t,\theta) \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta, \\ \mathfrak{c}_{rrr} (\xi,\eta,\sigma,\theta) & := \mathfrak{c}^{S,2} (\xi,\eta,\sigma,\theta) \chi_r(\eta) \chi_r(\sigma) \chi_r(\theta), \end{aligned} \end{align} $$

and aim to show

(11.70) $$ \begin{align} {\Big\| \langle \xi \rangle \partial_{\xi} \int_0^t \mathcal{C}_{rrr}(f, f, f)(s) \, ds \Big\|}_{L^2} \lesssim {\varepsilon}_1^3 \langle t \rangle^{\alpha}. \end{align} $$

Observe that

(11.71) $$ \begin{align} (\langle \xi \rangle \partial_{\xi} + X_{\eta,{\sigma},\theta}) \Phi_{\iota_1, \iota_2 ,\iota_3} = p, \qquad X_{\eta,{\sigma},\theta} := \iota_1\langle \eta \rangle \partial_{\eta} + \iota_2\langle \sigma \rangle \partial_{\sigma} + \iota_3\langle \theta \rangle \partial_{\theta}. \end{align} $$

Then when applying $\langle \xi \rangle \partial _{\xi }$ to equation (11.69), we can use the above identity to integrate by parts in $\eta ,\sigma $ and $\theta $ . Since the adjoint satisfies $X_{\eta ,{\sigma },\theta }^{\ast } = - X_{\eta ,{\sigma },\theta }$ , we see that

(11.72a) $$ \begin{align} & \langle \xi \rangle \partial_{\xi}\mathcal{C}_{rrr}[f,f,f](t,\xi) = i t \iiint e^{it \Phi_{\iota_1\iota_2 \iota_3}} \mathfrak{c}_{rrr}(\xi,\eta,\sigma,\theta) \, \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \widehat{\phi}(p) \, d\eta \, d\sigma \,d\theta \end{align} $$

(11.72b) $$ \begin{align} & + \iiint e^{it \Phi_{\iota_1\iota_2 \iota_3}} \mathfrak{c}_{rrr}(\xi,\eta,\sigma,\theta) X_{\eta,{\sigma},\theta} \big(\widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \big) \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta \qquad\qquad \ \ \end{align} $$

(11.72c) $$ \begin{align} & + \iiint e^{it \Phi_{\iota_1\iota_2 \iota_3}} \mathfrak{c}_{rrr}(\xi,\eta,\sigma,\theta) \, \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \, \big( \langle \xi \rangle \partial_{\xi} + X_{\eta,{\sigma},\theta} \big) \Big[ \frac{\widehat{\phi}(p)}{p}\Big] \, d\eta \, d\sigma \,d\theta \end{align} $$

(11.72d) $$ \begin{align} & + \iiint e^{it \Phi_{\iota_1\iota_2 \iota_3}} X_{\eta,{\sigma},\theta} \, \mathfrak{c}_{rrr}(\xi,\eta,\sigma,\theta) \, \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \, \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta. \qquad\qquad \ \ \end{align} $$

Estimate of equation (11.72a). The first term in equation (11.72) does not have a singularity and can be estimated by integrating by parts in the ‘uncorrelated’ variables $\eta ,\sigma $ and $\theta $ . Each of the three inputs would then give a gain of $\langle t \rangle ^{-3/4+\alpha }$ , which is sufficient to absorb the power of t in front and integrate over time. Similar (in fact, harder) terms have been treated in Section 8, so we can skip the details.

Estimate of equation (11.72b). For this term, it suffices to use the Hölder-type estimate from Lemma 6.13, estimating in $L^2$ the profile that is hit by the derivative and the other two in $L^{\infty }_x$ .

Estimate of equation (11.72c). For this term, we observe (see equation (11.71)) that

(11.73) $$ \begin{align} \big( \langle \xi \rangle \partial_{\xi} + X_{\eta,{\sigma},\theta} \big) \Big[ \frac{\widehat{\phi}(p)}{p}\Big] = \Phi_{\iota_1,\iota_2,\iota_3}(\xi,\eta,{\sigma},\theta) \partial_p \Big[ \frac{\widehat{\phi}(p)}{p}\Big]. \end{align} $$

Note that this identity is formal as it is written, since $\partial _p (1/p)$ does not converge (even in the $\mathrm {p.v.}$ sense); however, it can be made rigorous by localising a little away from $p=0$ and using the $\mathrm {p.v.}$ to deal with very small values of p.

From equation (11.73), we obtain, upon integration by parts in s, that

(11.74) $$ \begin{align} \int_0^t i equation\ (11.72c) \, ds & = \iiint e^{is \Phi_{\iota_1\iota_2 \iota_3}} \mathfrak{c}_{rrr}(\xi,\eta,\sigma,\theta) \, \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \, \partial_p \frac{\widehat{\phi}(p)}{p}\, d\eta \, d\sigma \,d\theta \, \Big|_{s=0}^{s=t} \end{align} $$

(11.75) $$ \begin{align} & - \int_0^t \iiint e^{it \Phi_{\iota_1\iota_2 \iota_3}} \mathfrak{c}_{rrr}(\xi,\eta,\sigma,\theta) \, \partial_s \Big[ \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \Big] \partial_p \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta \, ds. \end{align} $$

To estimate equation (11.74), we convert the $\partial _p$ into $\partial _{\eta }$ and integrate by parts in $\eta $ . The worst term is when $\partial _{\eta }$ hits the exponential; this causes a loss of t, but an $L^2\times L^{\infty }\times L^{\infty }$ Hölder estimate using Lemma 6.13 suffices to recover it.

The term in equation (11.75) is similar. We may assume that $\partial _s$ hits $\widetilde {f}(\sigma )$ . Again we convert $\partial _p$ into $\partial _{\eta }$ and integrate by parts in $\eta $ . This causes a loss of s when hitting the exponential phase, which is offset by an $L^{\infty }\times L^2\times L^{\infty }$ estimate with $\partial _s \widetilde {f}$ placed in $L^2$ and giving $\langle t \rangle ^{-1}$ decay using equation (7.56).

Estimate of equation (11.72d). This term can be estimated directly using the trilinear estimates from Lemma 6.13. The only difficulty is the loss of one derivative resulting from the differentiation of the symbol, but this is easily recovered using the $H^4$ a priori bound from equation (7.10), and $p_0 < \alpha $ ; see equation (2.32).

11.4.2 One frequency close, two removed from $\pm \sqrt 3$

Let us now consider

$$ \begin{align*} \mathcal{C}_{crr}[a,b,c](t,\xi) & := \iiint e^{it \Phi_{\iota_1\iota_2 \iota_3}(\xi,\eta,\sigma,\theta)} \mathfrak{c}_{crr}(\xi,\eta,\sigma,\theta) \widetilde{a}(t,\eta) \widetilde{b}(t,\sigma) \widetilde{c}(t,\theta) \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta, \\ \mathfrak{c}_{crr} (\xi,\eta,\sigma,\theta) & := \mathfrak{c}^{S,2} (\xi,\eta,\sigma,\theta) \chi_c(\eta) \chi_r(\sigma) \chi_r(\theta). \end{align*} $$

One can proceed exactly as in the previous subsection, with the exception of the treatment of equation (11.72b), which must be modified due to the degeneracy of the weighted norm close to $\sqrt {3}$ . The only problematic term is the one where the first function (whose frequency is close to $\pm \sqrt {3}$ ) is differentiated. Thus, we are looking at

$$ \begin{align*}\iiint e^{it \Phi_{\iota_1\iota_2 \iota_3}} \mathfrak{c}_{crr}(\xi,\eta,\sigma,\theta) \langle \eta \rangle \partial_{\eta} \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta. \end{align*} $$

We need to distinguish cases depending on the $\iota $ signs.

The $+++$ case. Since only the first argument $\widetilde {f}(\eta )$ is differentiated, it is natural to try to integrate by parts in $\partial _{\sigma }-\partial _{\theta }$ . We thus need to look at frequencies for which

$$ \begin{align*}(\partial_{\sigma} - \partial_{\theta}) \Phi_{+++}(\xi,\eta,\sigma,\theta) = \Phi_{+++}(\xi,\eta,\sigma,\theta) = 0. \end{align*} $$

We will refer to these as ‘restricted (space-time) resonances’. The vanishing of $(\partial _{\sigma } - \partial _{\theta }) \Phi _{+++}$ imposes that $\sigma = \theta $ . Therefore, resonances are given by the zeros of

$$ \begin{align*}\Phi_{+++}(\xi,\eta,\sigma,\sigma) = \langle \eta + 2\sigma + p \rangle - \langle \eta \rangle - 2 \langle \sigma \rangle. \end{align*} $$

Squaring both sides of $ \langle \eta + 2\sigma + p \rangle = \langle \eta \rangle + 2 \langle \sigma \rangle $ results in $p^2 + 2p(\eta + 2\sigma ) + 4\eta \sigma = 4 + 4 \langle \eta \rangle \langle \sigma \rangle $ , which has no solutions if $|p| \ll 1$ and $(\xi ,\eta ,\sigma ,\theta ) \in \operatorname {Supp} (\mathfrak {c}_{2,crr})$ . Note that we may easily restrict to $|p| \ll 1$ , since interactions for which $|p| \gtrsim 1$ can be treated like regular cubic terms by integrating by parts in the uncorrelated variables ${\sigma }$ and $\theta $ .

Without loss of generality, we assume that $|\sigma | \geq |\theta |$ ; we then distinguish between the case where $|\sigma | \lesssim 1$ , and $|\sigma | \gg 1$ .

• • If $|\sigma | \lesssim 1$ , we resort either to integration by parts in $\partial _{\sigma } - \partial _{\theta }$ or to integration by parts in s, using that either $(\partial _{\sigma } - \partial _{\theta })\Phi _{+++}$ or $\Phi _{+++}$ can be bounded away from zero.In the former case, one finds (after adding a cutoff that we omit) the expression

  $$ \begin{align*}\iiint e^{it \Phi_{+++}} \frac{\mathfrak{c}_{crr}(\xi,\eta,\sigma,\theta) }{ is(\partial_{\theta}-\partial_{\eta}) \Phi_{+++}} \langle \eta \rangle \partial_{\eta} \widetilde{f}(\eta) \partial_{\sigma} \widetilde{f}(\sigma) \widetilde{f}(\theta) \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta + \{ \mbox{easier terms} \}, \end{align*} $$
  whose $L^2$ -norm can be bounded by
  $$ \begin{align*}C t^{-1} {\| \langle \eta \rangle \partial_{\eta} \widetilde{f} \|}_{L^2} {\| \partial_{\sigma} \widetilde{f} \|}_{L^1} {\| e^{-it\langle D \rangle} \mathcal{W}^* f\|}_{L^{\infty}} \lesssim {\varepsilon}_1^3 t^{-1}. \end{align*} $$
  In the latter case, one finds
  $$ \begin{align*}\int_0^t \iiint e^{it \Phi_{+++}} \frac{\mathfrak{c}_{crr}(\xi,\eta,\sigma,\theta) }{i \Phi_{+++}} \langle \eta \rangle\partial_s [ \partial_{\eta} \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) ]\frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta \,ds. \end{align*} $$
  The control of this expression is easy if the time derivative hits $\widetilde {f}(\sigma )$ or $\widetilde {f}(\theta )$ , by using a trilinear estimate and equation (7.56). If $\partial _t$ hits $ \widetilde {f}(\eta )$ , the $\partial _{\eta }$ derivative might result in an additional t factor. We use equation (7.59) and look at the two main contributions on its right-hand side: when we substitute $\mathcal {C}^S$ to $\partial _t f$ , we obtain a $5$ -linear expression in f, and estimating four inputs in $L^{\infty }$ , and one in $L^2$ suffices; when we substitute $\mathcal {Q}^R$ to $\partial _t \widetilde {f}$ , we can use the bound $\| \mathcal {Q}^R(f,f) \|_{L^2} \lesssim t^{-1+}$ , which follows from Lemma 6.11, and estimate the two other inputs in $L^{\infty }$ .

• • If $|\sigma | \gg 1$ , we have

  $$ \begin{align*}|\Phi_{+++}(\xi,\eta,\sigma,\theta)| \gtrsim \left\{ \begin{array}{ll} 1 & \mbox{ if}\ \sigma,\theta\ \mbox{have the same sign,} \\ \langle \theta \rangle & \mbox{ if}\ \sigma,\theta\ \mbox{have opposite signs,} \end{array} \right. \end{align*} $$
  as long as $|p| \ll 1$ . Indeed, this is obvious if $\sigma $ and $\theta $ have opposite signs; and if they do have the same sign,
  $$ \begin{align*} - \Phi_{+++}(\xi,\eta,\sigma,\theta) & = - \langle \eta + \sigma + \theta + p \rangle +\langle \eta \rangle + \langle \sigma \rangle + \langle \theta \rangle \\ & = - | \eta + \sigma + \theta + p| + \langle \eta \rangle + |\sigma| + \langle \theta \rangle + O\left(|\sigma|^{-1} \right) \gtrsim 1. \end{align*} $$
  Turning to estimates on derivatives, for any $p,\eta ,\sigma ,\theta $ such that $|p|,|\eta | \lesssim 1$ , $|\sigma | \gg 1$ , and $\sigma $ and $\theta $ have the same sign,
  $$ \begin{align*}\left| \partial_p^a \partial_{\eta}^b \partial_{\sigma}^c \partial_{\theta}^d \frac{1}{\Phi_{+++}(\eta,\sigma,\theta,p)} \right| \lesssim |\sigma|^{-c} \langle \theta \rangle^{-d}, \end{align*} $$
  so that Lemma 6.7 applies. In the case where $\sigma $ and $\theta $ have opposite signs, the above does not hold (think of the case where $\sigma + \theta =0$ ). Assuming for instance $\sigma>0$ , $\theta <0$ ( $|\sigma | \geq |\theta |$ ), let $\sigma ' = \sigma + \theta $ . Then the above derivative estimate holds for the variables $(p,\eta ,\sigma ',\theta )$ . In both cases, Lemma 6.7 applies, and an integration by parts in time suffices.

The $+--$ case. This can be dealt with similarly to the $+++$ case. First, we observe that there are again no restricted resonances

$$ \begin{align*}\sigma = \theta, \qquad \mbox{and} \qquad \langle \eta + 2\sigma + p \rangle - \langle \eta \rangle + 2 \langle \sigma \rangle = 0, \end{align*} $$

with $|p| \ll 1$ . This is clear if $|\sigma |\gg 1$ ; if instead $|\sigma | \lesssim 1$ , it suffices to treat the case $p=0$ and argue by continuity. In other words, it suffices to show that there are no solutions of $\langle \eta + 2\sigma \rangle = \langle \eta \rangle - 2 \langle \sigma \rangle $ . Squaring both sides leads to $\langle \eta \rangle \langle \sigma \rangle = 1 - \eta \sigma $ , whose only solution is $\eta = -\sigma $ , but this is not allowed on the support of $\mathfrak {c}_{crr}$ .

Therefore, as long as $|\sigma | + |\theta | \lesssim 1$ , the argument used for the $+++$ case applies. On the other hand, when $|\sigma | + |\theta | \gg 1$ , we have $|\Phi _{+--}(\xi ,\eta ,\sigma ,\theta )| \gtrsim \langle \sigma \rangle + \langle \theta \rangle $ , so that the argument used above also applies.

The $-++$ case. Once again we look at possible solutions of

$$ \begin{align*}\langle \eta + 2\sigma + p \rangle + \langle \eta \rangle - 2 \langle \sigma \rangle = 0 \end{align*} $$

for $|p| \ll 1$ , on the support of the integral. It is easy to verify that this equation does not have solutions for $|\sigma | \gg 1$ ; in the complementary case, it suffices to consider the case $p=0$ and notice that the only solution to $\langle \eta + 2\sigma \rangle = - \langle \eta \rangle + 2 \langle \sigma \rangle $ is $\eta = -\sigma $ , but this does not belong to $\,\mbox {supp}\,(\mathfrak {c}_{crr})$ .

We then distinguish different frequencies configurations:

• • If $|\sigma | + |\theta | \lesssim 1$ , the argument given in the previous cases apply.

• • If $|\sigma | \sim |\theta | \gg 1$ and $\sigma $ and $\theta $ have opposite signs, then $|\Phi _{-++}| \gtrsim \langle \eta \rangle \approx 1$ . If they have equal signs,

  $$ \begin{align*} \Phi_{-++}(\xi,\eta,\sigma,\theta) & = \langle p+ \eta + \sigma + \theta \rangle + \langle \eta \rangle - \langle \sigma \rangle - \langle \theta \rangle \\ & = |p + \eta + \sigma + \theta|+ \langle \eta \rangle - |\sigma| - |\theta| + O\left( {|\sigma|}^{-1} \right) \gtrsim 1 \end{align*} $$
  as long as $|p| \ll 1$ . The estimates on the derivatives are the natural ones, and an integration by parts in s suffices.

• • If $|\sigma | \gg |\theta | + 1 $ , we need a different argument. Observe that $\left | (\partial _{\sigma } - \partial _{\theta }) \Phi _{+--}(\xi ,\eta ,\sigma ,\theta ) \right | \gtrsim \langle \theta \rangle ^{-2}$ , and more precisely

  $$ \begin{align*}\left| \partial_{\sigma}^a \partial_{\theta}^b \frac{1}{(\partial_{\sigma} - \partial_{\theta}) \Phi_{-++}(\xi,\eta,\sigma,\theta)} \right| \lesssim \langle \theta \rangle^{2-b} |\sigma|^{-a}. \end{align*} $$
  Therefore, an integration by parts in $\partial _{\sigma } - \partial _{\theta }$ , followed by an application of (a small adaptation of) Lemma 6.13 gives (using $|\theta |\lesssim |{\sigma }|$ )
  $$ \begin{align*} {\| \mathcal{C}_{crr}(f,f,f) \|}_{L^2} & \lesssim t^{-1} \cdot {\| \chi_c(\eta) \partial_{\eta} \widetilde{f} \|}_{L^{2+}} {\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \widehat{{\mathcal{F}}}^{-1} \partial_{\sigma} \widetilde{f} \|}_{L^{\infty-}} \cdot {\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* f \|}_{L^{\infty-}} \\ & \lesssim t^{-1} {\| \chi_c(\eta) \partial_{\eta} \widetilde{f} \|}_{L^2} {\| \chi_r({\sigma}) \langle \sigma \rangle \partial_{\sigma} \widetilde{f} \|}_{L^2} {\| \langle \partial_x \rangle^{0+} e^{-it\langle \partial_x \rangle} \mathcal{W}^* f \|}_{L^{\infty-}} \\ & \lesssim t^{-1} \cdot {\varepsilon}_1 \langle t \rangle^{\alpha+\beta\gamma} \cdot {\varepsilon}_1 \langle t \rangle^{\alpha} \cdot {\varepsilon}_1 \langle t \rangle^{-1/2+} \\ & \lesssim \langle t \rangle^{-1} {\varepsilon}_1^3, \end{align*} $$
  having used Sobolev’s embedding theorem for the second inequality (recall $|\eta | \approx \sqrt {3}$ , $|{\sigma }| \not \approx \sqrt {3}$ ), interpolation between the linear decay and the $H^4$ -norm, the a priori bounds (see in particular equation (7.19)) and $\alpha + \beta \gamma < 1/4$ .

The $-+-$ case. For this case, it is obvious here that there are no restricted space-time resonances since, when $\sigma = -\theta $ , the phase is $\Phi _{-+-}(\xi ,\eta ,\sigma ,\theta ) = \langle \eta + p \rangle + \langle \eta \rangle $ . Once again,

• • If $|\sigma | + |\theta | \lesssim 1$ , one can resort to integration by parts in $\partial _s$ or $\partial _{\sigma } - \partial _{\theta }$ .

• • If $|\sigma | + |\theta | \gg 1$ ,

  $$ \begin{align*} \Phi_{-+-}(\xi,\eta,\sigma,\theta) & = \langle p+ \eta + \sigma + \theta \rangle + \langle \eta \rangle - \langle \sigma \rangle + \langle \theta \rangle \gtrsim 1 \end{align*} $$
  as long as $|p| \ll 1$ .

The $---$ case. This is the easiest case since $\Phi _{---}(\xi ,\eta ,\sigma ,\theta ) \gtrsim 1$ for all $\xi ,\eta ,\sigma ,\theta $ .

The $+-+$ case. This is the hardest case, since restricted space-time resonances are present; the phase vanishes when ${\sigma }=-\theta $ and $p=0$ . The case $|\theta | + |\sigma | \lesssim 1$ is essentially treated in Section 9; therefore we can assume that $|\sigma | \gg 1$ and $|\sigma | \geq |\theta |$ . If $|\sigma | \gg |\theta |$ or $\sigma \approx \theta $ , then an integration by parts in $\partial _{\sigma } - \partial _{\theta }$ suffices; therefore, we will only focus on the case where $\sigma \approx - \theta $ .

It is convenient to adopt the same parametrisation of the frequency variables as in Section 9, which, after replacing the second $\widetilde {f}$ by $\widetilde {f}(-\cdot )$ , leads to the question of bounding

(11.76) $$ \begin{align} \begin{aligned} & \sum_{n\geq 10} \iiint e^{is\Psi(\xi,\eta,\zeta,\theta)} \mathfrak{m}_n(\xi,\eta,\sigma,\theta) \partial_{\xi} \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \,d\theta, \\ & \Psi(\xi,\eta,\zeta,\theta) = \langle \xi \rangle - \langle \xi - \eta \rangle + \langle \xi - \eta -\zeta -\theta \rangle - \langle \xi - \zeta\rangle, \end{aligned} \end{align} $$

where, slightly abusing notations by letting $\mathfrak {c}_{crr}$ be the symbol expressed both in the $(\eta ,\sigma ,\theta )$ and $(\xi -\eta ,\xi -\eta -\zeta -\theta ,\xi -\zeta )$ variables, we define

$$ \begin{align*} \mathfrak{m}_n(\xi,\eta,\sigma,\theta) = \mathfrak{c}_{crr} (\xi,\eta,\sigma,\theta) \langle \xi -\eta \rangle \varphi_{n}(\xi-\eta-\zeta-\theta) \varphi_{\sim n}(\xi-\zeta). \end{align*} $$

Using the a priori $H^4$ bound, Cauchy-Schwarz’s inequality and Lemma 6.13, we can estimate the $L^2$ norm of each element in the sum in equation (11.76) by

$$ \begin{align*} C 2^{-(2-)n} \| \partial_{\xi} \widetilde{f} \|_{L^2} \| \varphi_n \widetilde{f} \|_{L^1} \| \varphi_{\sim n} \widetilde{f} \|_{L^1} \lesssim {\varepsilon}_1 \langle s \rangle^{\alpha + \beta \gamma} 2^{-(9-)n} \| f \|_{H^4}^2. \end{align*} $$

This bound suffices as long as $2^n \gtrsim \langle s \rangle ^{1/6}$ .

If, on the other hand, $2^n \lesssim \langle s \rangle ^{1/6}$ , we can now follow the skeleton of the estimate of $\mathcal {H}^2$ in Section 9.3.2. Cases 1, 2 and 3 are identical, simply relying on the easy generalisation of Lemma 6.13 to the symbol $\mathfrak {m}_n$ above.

Let us then consider the analogue of Case 4.1, which corresponds to the localisations $|\xi - \sqrt {3}| \approx 2^{\ell }$ , $|\xi - \eta - \sqrt 3| \leq 2^{\ell -100}$ , $|\theta +\xi -\sqrt {3}| \approx 2^h \geq 2^{\ell -10}$ . To these we add $|\zeta | \approx 2^n$ , in correspondence with the nth summand in equation (11.76) Under these conditions, the absolute value of the $\zeta $ derivative of $\Psi $ is

$$ \begin{align*}|\partial_{\zeta} \Psi(\xi,\eta,\zeta,\theta)| = |- \tau'(\xi-\eta-\zeta-\theta) + \tau'(\xi -\zeta)| \approx | \tau''(\xi-\zeta) (\eta + \theta)| \gtrsim 2^{-3n} 2^h. \end{align*} $$

More precisely, we have

$$ \begin{align*}\left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \partial_{\theta}^d \frac{1}{\partial_{\zeta} \Psi(\xi,\eta,\zeta,\theta)} \right| \lesssim 2^{3n-h} 2^{-(a+c)n} 2^{-h(b+d)}, \end{align*} $$

so that, recalling the bounds on $\mathfrak {c}^{S,2}$ , we get

$$ \begin{align*}{\Big\| \widehat{{\mathcal{F}}} \frac{\mathfrak{m}(\xi,\eta,\zeta,\theta)}{\partial_{\zeta} \Psi(\xi,\eta,\zeta,\theta) } \Big\|}_{L^1} \lesssim 2^{n-h}. \end{align*} $$

Integrating by parts in $\zeta $ gives several terms; the leading one is given by

$$ \begin{align*}\iiint e^{is\Psi(\xi,\eta,\zeta,\theta)} \frac{\mathfrak{m}_n(\xi,\eta,\sigma,\theta)}{s \partial_{\zeta} \Psi(\xi,\eta,\zeta,\theta)} \partial_{\xi} \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-\eta-\zeta-\theta) \widetilde{f}(\xi-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \,d\theta. \end{align*} $$

This can be bounded in $L^2$ by

$$ \begin{align*} C s^{-1} \cdot 2^{n-h} \| \varphi_{< \ell-100} \partial_{\xi} \widetilde{f} \|_{L^1} \|\varphi_n \partial_{\xi} \widetilde{f} \|_{L^2} \| e^{-it\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}} \lesssim {\varepsilon}_1^3 2^{n-h} 2^{\beta'\ell} \langle s \rangle^{-3/2 + 2\alpha}. \end{align*} $$

Summing over $2^n \lesssim \langle s \rangle ^{1/6}$ and $h \geq \ell - 10$ , using that $2^{\ell } \gtrsim \langle s \rangle ^{-\gamma }$ , with equation (2.31), gives the desired bound.

Finally, there remains Case 4.2 in Section 9.3.2, which corresponds to $|\theta | \approx 2^{\ell }$ . Here we can integrate by parts in $\theta $ using that, for all $a,b,c,d$ (not all equal to zero),

$$ \begin{align*}\left| \partial_{\xi}^a \partial_{\eta}^b \partial_{\zeta}^c \partial_{\theta}^d \frac{1}{\partial_{\theta} \Psi(\xi,\eta,\zeta,\theta)} \right| \lesssim 2^{-n(1+a+b+c+d)}. \end{align*} $$

11.4.3 Two frequencies close, one removed from $\pm \sqrt {3}$

Defining $\mathcal {C}_{ccr}$ through the symbol

$$ \begin{align*}\mathfrak{c}_{ccr}(\xi,\eta,\sigma,\theta) = \mathfrak{c}^{2,S} (\xi,\eta,\sigma,\theta) \chi_c(\eta) \chi_c(\sigma) \chi_r(\theta), \end{align*} $$

we follow once again the approach of Section 11.4.1 and see that the only problematic term is

$$ \begin{align*}\iiint e^{is \Phi_{\iota_1\iota_2 \iota_3}} \mathfrak{c}_{ccr}(\xi,\eta,\sigma,\theta) \langle \eta \rangle \partial_{\eta} \widetilde{f}(\eta) \widetilde{f}(\sigma) \widetilde{f}(\theta) \frac{\widehat{\phi}(p)}{p} \, d\eta \, d\sigma \,d\theta \end{align*} $$

(and, symmetrically, the term where the derivative hits the second function). On the support of $\mathfrak {c}_{2,ccr}$

$$ \begin{align*}\left| (\partial_{\sigma} - \partial_{\theta}) \Phi_{\iota_1 \iota_2 \iota_3} \right| \gtrsim 1, \end{align*} $$

so that we can integrate by parts in $\partial _{\sigma } - \partial _{\theta }$ . The worst term resulting from this is

$$ \begin{align*}\iiint \frac{1}{t(\partial_{\sigma} - \partial_{\theta}) \Phi_{\iota_1 \iota_2 \iota_3}} e^{it \Phi_{\iota_1\iota_2 \iota_3}} \mathfrak{c}_{2,ccr}(\xi,\eta,\sigma,\theta) \langle \eta \rangle \partial_{\eta} \widetilde{f}(\eta) \partial_{\sigma} \widetilde{f}(\sigma) \widetilde{f}(\theta) \frac{\varphi_{<0}(p)}{p} \, d\eta \, d\sigma \,d\theta. \end{align*} $$

Using a slight adaptation of Lemma 6.13, this expression can be bounded in $L^2$ by

$$ \begin{align*}C s^{-1} {\| \partial_{\xi} \widetilde{f} \|}_{L^2} {\| \partial_{\xi} \widetilde{f} \|}_{L^1} {\| e^{-it\langle D \rangle} \mathcal{W}^* f \|}_{L^{\infty}} \lesssim \langle s \rangle^{-3/2 + 2 \alpha + \beta \gamma} {\varepsilon}_1^3, \end{align*} $$

and since $\alpha + \beta \gamma <1/4$ , we can integrate in time and close the estimate.

11.4.4 Three frequencies close to $\pm \sqrt {3}$

Examining the phase in equation (11.64), we see that if $\xi ,\eta ,\sigma ,\theta $ are all close to $\pm \sqrt {3}$ , then $|\Phi _{\iota _1 \iota _2 \iota _3}| \gtrsim 1$ unless $(\iota _1 ,\iota _2 ,\iota _3) = (+,-,+)$ up to a permutation. We can thus restrict the discussion to the case $(\iota _1 ,\iota _2 ,\iota _3) = (+,-,+)$ . This case was already the focus of Section 9, where it was furthermore assumed that $(\eta ,\theta ,\sigma )$ was close to $(\sqrt {3},-\sqrt {3},\sqrt {3})$ ; notice the different sign due to the particular choice of p in equation (11.64). While the interaction analysed in Section 9 is the worst one, we also need to consider another partially resonant scenario where the phase can vanish but not its gradient, namely, $(\eta ,\theta ,\sigma )$ close to $(\sqrt {3},-\sqrt {3},-\sqrt {3})$ , and prove the corresponding estimate in equation (11.68).

Since the approach followed is very close to that introduced in Section 9, we adopt a similar parametrization of the integration variables and consider the trilinear expression

(11.77) $$ \begin{align} \begin{aligned} \iiint e^{is \Psi(\xi,\eta,\zeta,\theta)} \mathfrak{p}(\xi,\eta,\zeta) & \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-2\sqrt{3}-\eta-\zeta-\theta) \widetilde{f}(\xi-2\sqrt{3}-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \, d\theta, \\ \mbox{where} \qquad \Psi(\xi,\eta,\zeta,\theta) & = \Phi_{+-+}(\xi,\xi-\eta,\xi-2\sqrt{3}-\eta-\zeta-\theta,\xi-2\sqrt{3}-\zeta) \\ & = \langle \xi \rangle- \langle \xi - \eta \rangle + \langle \xi -2\sqrt{3} - \eta -\zeta -\theta \rangle - \langle \xi -2\sqrt{3}- \zeta\rangle, \end{aligned} \end{align} $$

where it is understood that $\mathfrak {p}$ is smooth and such that, on its support, $\xi $ is close to $\sqrt {3}$ and $\eta ,\zeta $ (and $\theta $ ) to zero. Denoting $\tau (\xi ) = \langle \xi \rangle $ , we start by recording a few estimates on the phase function:

$$ \begin{align*} & \Psi(\xi,\eta,\zeta) = \tau'(\xi)\eta - \tau'(\xi - 2 \sqrt{3} - \zeta) (\eta + \theta) + O(\eta^2 + \theta^2), \\ & \partial_{\xi} \Psi(\xi,\eta,\zeta) = \tau''(\xi)\eta - \tau''(\xi - 2 \sqrt{3} - \zeta) (\eta + \theta) + O(\eta^2 + \theta^2), \\ & \partial_{\eta} \Psi(\xi,\eta,\zeta) = \tau'(\xi - \eta) - \tau'(\xi- 2 \sqrt{3} - \eta - \zeta -\theta), \\ & (\partial_{\eta} - \partial_{\zeta}) \Psi(\xi,\eta,\zeta) = \tau'(\xi - \eta) - \tau'(\xi- 2 \sqrt{3} - \zeta), \\ & \partial_{\zeta} \Psi(\xi,\eta,\zeta) = \tau''(\xi - 2 \sqrt{3} - \zeta)( \eta + \theta) + O(\eta^2 + \theta^2), \\ & \partial_{\zeta}^2 \Psi(\xi,\eta,\zeta) = - \tau'''(\xi - 2 \sqrt{3} - \zeta)( \eta + \theta)+ O(\eta^2 + \theta^2). \end{align*} $$

As a consequence,

$$ \begin{align*}|\Psi|, |\partial_{\xi} \Psi|, |\partial_{\zeta} \Psi|, |\partial_{\zeta}^2 \Psi| \approx |\eta| \qquad \mbox{and} \qquad | \partial_{\eta} \Psi|, |(\partial_{\eta} - \partial_{\zeta}) \Psi| \gtrsim 1. \end{align*} $$

Applying $\partial _{\xi }$ to equation (11.77), one obtains several terms, which can be reduced to the following main ones:

(11.78a) $$ \begin{align} & \iiint e^{is \Psi} \mathfrak{p}(\xi,\eta,\zeta) \partial_{\xi} \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-2\sqrt{3}-\eta-\zeta-\theta) \widetilde{f}(\xi-2\sqrt{3}-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \, d\theta, \end{align} $$

(11.78b) $$ \begin{align} & \iiint e^{is \Psi} \mathfrak{p}(\xi,\eta,\zeta) \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-2\sqrt{3}-\eta-\zeta-\theta) \widetilde{f}(\xi-2\sqrt{3}-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \, d\theta, \end{align} $$

(11.78c) $$ \begin{align} & \iiint e^{is \Psi} \mathfrak{p}(\xi,\eta,\zeta) \widetilde{f}(\xi-\eta) \widetilde{f}(\xi-2\sqrt{3}-\eta-\zeta-\theta)\partial_{\xi} \widetilde{f}(\xi-2\sqrt{3}-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \, d\theta. \end{align} $$

The term in equation (11.78b) can be estimated in a straightforward way by integrating by parts using the vector field $\partial _{\eta } - \partial _{\zeta }$ , since $|(\partial _{\eta } - \partial _{\zeta }) \Psi | \gtrsim 1$ ; the same applies to equation (11.78c) with the vector field $\partial _{\eta }$ . We illustrate this estimate for equation (11.78b). After integrating by parts, the worst term is of the form

$$ \begin{align*}\iiint e^{is \Psi} \frac{\mathfrak{p}(\xi,\eta,\zeta)}{(\partial_{\eta}-\partial_{\zeta}) \Psi} \partial_{\xi} \widetilde{f}(\xi-\eta) \partial_{\xi} \widetilde{f}(\xi-2\sqrt{3}-\eta-\zeta-\theta) \widetilde{f}(\xi-2\sqrt{3}-\zeta) \frac{\widehat{\phi}(\theta)}{\theta} \, d\eta \,d\zeta \, d\theta. \end{align*} $$

In $L^2$ , this can be estimated by

$$ \begin{align*}C s^{-1} \| \partial_{\xi} \widetilde{f} \|_{L^2} \| \partial_{\xi} \widetilde{f} \|_{L^1} \| e^{-it\langle D \rangle} \mathcal{W}^* f \|_{L^{\infty}} \lesssim {\varepsilon}_1^3 \langle s \rangle^{-3/2+2\alpha + \beta \gamma}, \end{align*} $$

which suffices.

This leaves us with equation (11.78a), which can be treated as $\mathcal {H}_2$ in Section 9.3.2. Following the notation and the approach taken there, we localise dyadically $\xi - \sqrt {3}$ , $\xi - \eta - \sqrt {3}$ and $\theta + \xi - \sqrt {3}$ to the scales $2^{\ell }$ , $2^{j_1}$ , and $2^h$ , respectively. Since $|\partial _{\zeta } \Psi | \approx |\partial _{\zeta }^2 \Psi | \approx |\eta + \theta |$ , the approach in Section 9.3.2 can be followed almost verbatim, and we can skip the details.

With this, the proof of Proposition 9.1 is completed. In particular, we have obtained the improvement on the weighted a priori bound in equation (7.11). This in turn completes the proof of Proposition 7.2 and therefore of Theorem 1.1.