Published online by Cambridge University Press: 12 February 2018
Let 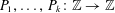 $P_{1},\ldots ,P_{k}:\mathbb{Z}\rightarrow \mathbb{Z}$ be polynomials of degree at most
$P_{1},\ldots ,P_{k}:\mathbb{Z}\rightarrow \mathbb{Z}$ be polynomials of degree at most 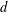 $d$ for some
$d$ for some 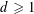 $d\geqslant 1$, with the degree
$d\geqslant 1$, with the degree 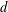 $d$ coefficients all distinct, and admissible in the sense that for every prime
$d$ coefficients all distinct, and admissible in the sense that for every prime 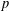 $p$, there exists integers
$p$, there exists integers 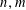 $n,m$ such that
$n,m$ such that 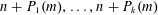 $n+P_{1}(m),\ldots ,n+P_{k}(m)$ are all not divisible by
$n+P_{1}(m),\ldots ,n+P_{k}(m)$ are all not divisible by 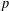 $p$. We show that there exist infinitely many natural numbers
$p$. We show that there exist infinitely many natural numbers 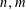 $n,m$ such that
$n,m$ such that 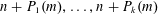 $n+P_{1}(m),\ldots ,n+P_{k}(m)$ are simultaneously prime, generalizing a previous result of the authors, which was restricted to the special case
$n+P_{1}(m),\ldots ,n+P_{k}(m)$ are simultaneously prime, generalizing a previous result of the authors, which was restricted to the special case 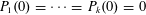 $P_{1}(0)=\cdots =P_{k}(0)=0$ (though it allowed for the top degree coefficients to coincide). Furthermore, we obtain an asymptotic for the number of such prime pairs
$P_{1}(0)=\cdots =P_{k}(0)=0$ (though it allowed for the top degree coefficients to coincide). Furthermore, we obtain an asymptotic for the number of such prime pairs 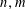 $n,m$ with
$n,m$ with 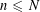 $n\leqslant N$ and
$n\leqslant N$ and 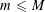 $m\leqslant M$ with
$m\leqslant M$ with 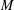 $M$ slightly less than
$M$ slightly less than 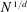 $N^{1/d}$. This asymptotic is already new in general in the homogeneous case
$N^{1/d}$. This asymptotic is already new in general in the homogeneous case 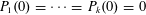 $P_{1}(0)=\cdots =P_{k}(0)=0$. Our arguments rely on four ingredients. The first is a (slightly modified) generalized von Neumann theorem of the authors, reducing matters to controlling certain averaged local Gowers norms of (suitable normalizations of) the von Mangoldt function. The second is a more recent concatenation theorem of the authors, controlling these averaged local Gowers norms by global Gowers norms. The third ingredient is the work of Green and the authors on linear equations in primes, allowing one to compute these global Gowers norms for the normalized von Mangoldt functions. Finally, we use the Conlon–Fox–Zhao densification approach to the transference principle to combine the preceding three ingredients together. In the special case
$P_{1}(0)=\cdots =P_{k}(0)=0$. Our arguments rely on four ingredients. The first is a (slightly modified) generalized von Neumann theorem of the authors, reducing matters to controlling certain averaged local Gowers norms of (suitable normalizations of) the von Mangoldt function. The second is a more recent concatenation theorem of the authors, controlling these averaged local Gowers norms by global Gowers norms. The third ingredient is the work of Green and the authors on linear equations in primes, allowing one to compute these global Gowers norms for the normalized von Mangoldt functions. Finally, we use the Conlon–Fox–Zhao densification approach to the transference principle to combine the preceding three ingredients together. In the special case 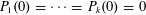 $P_{1}(0)=\cdots =P_{k}(0)=0$, our methods also give infinitely many
$P_{1}(0)=\cdots =P_{k}(0)=0$, our methods also give infinitely many 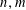 $n,m$ with
$n,m$ with 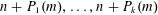 $n+P_{1}(m),\ldots ,n+P_{k}(m)$ in a specified set primes of positive relative density
$n+P_{1}(m),\ldots ,n+P_{k}(m)$ in a specified set primes of positive relative density 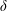 $\unicode[STIX]{x1D6FF}$, with
$\unicode[STIX]{x1D6FF}$, with 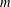 $m$ bounded by
$m$ bounded by 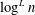 $\log ^{L}n$ for some
$\log ^{L}n$ for some 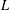 $L$ independent of the density
$L$ independent of the density 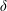 $\unicode[STIX]{x1D6FF}$. This improves slightly on a result from our previous paper, in which
$\unicode[STIX]{x1D6FF}$. This improves slightly on a result from our previous paper, in which 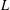 $L$ was allowed to depend on
$L$ was allowed to depend on 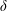 $\unicode[STIX]{x1D6FF}$.
$\unicode[STIX]{x1D6FF}$.