Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T20:33:34.869Z Has data issue: false hasContentIssue false
  • English
  • Français

Young-Measure approximations for elastodynamics with non-monotone stress-strain relations

Published online by Cambridge University Press:  15 June 2004

Carsten Carstensen  and
Marc Oliver Rieger
Carsten Carstensen
Affiliation:
Department of Mathematics, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. [email protected].
Marc Oliver Rieger
Affiliation:
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56100 Pisa, Italy. [email protected].
Get access

Abstract

Microstructures in phase-transitions of alloys are modeled by the energy minimization of a nonconvex energy density ϕ. Their time-evolution leads to a nonlinear wave equation $u_{tt}=\mbox{div}\:S(Du)$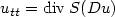 with the non-monotone stress-strain relation $S=D\phi$ 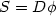plus proper boundary and initial conditions. This hyperbolic-elliptic initial-boundary value problem of changing types allows, in general, solely Young-measure solutions. This paper introduces a fully-numerical time-space discretization of this equation in a corresponding very weak sense. It is shown that discrete solutions exist and generate weakly convergent subsequences whose limit is a Young-measure solution. Numerical examples in one space dimension illustrate the time-evolving phase transitions and microstructures of a nonlinearly vibrating string.

Keywords

Non-monotone evolutionnonlinear elastodynamicsYoung-measure approximationnonlinear wave equation.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 38 , Issue 3 , May 2004 , pp. 397 - 418
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, J.M. and James, R.D., Fine phase mixtures as minimizers of energy. Arch. Rational Mech. Anal. 100 (1987) 13–52. CrossRef
Ball, J.M., Kirchheim, B. and Kristensen, J., Regularity of quasiconvex envelopes. Calc. Var. Partial Differential Equations 11 (2000) 333–359. CrossRef
Berliocchi, H. and Lasry, J.-M., Intégrandes normales et mesures paramétrées en calcul des variations. Bull. Soc. Math. France 101 (1973) 129–184. CrossRef
C. Carstensen, Numerical analysis of microstructure, in Theory and numerics of differential equations (Durham, 2000), Universitext, Springer Verlag, Berlin (2001) 59–126.
Carstensen, C. and Plecháč, P., Numerical solution of the scalar double-well problem allowing microstructure. Math. Comp. 66 (1997) 997–1026. CrossRef
Carstensen, C. and Roubíček, T., Numerical approximation of Young measures in non-convex variational problems. Numer. Math. 84 (2000) 395–415. CrossRef
Carstensen, C. and Dolzmann, G., Time-space discretization of the nonlinear hyperbolic system $u_{tt}=div(\sigma ({D}u)+{D}u_{t})$ . SIAM J. Numer. Anal. 42 (2004) 75–89. CrossRef
Chipot, M., Collins, C. and Kinderlehrer, D., Numerical analysis of oscillations in multiple well problems. Numer. Math. 70 (1995) 259–282. CrossRef
Collins, C. and Luskin, M., Optimal-order error estimates for the finite element approximation of the solution of a nonconvex variational problem. Math. Comp. 57 (1991) 621–637. CrossRef
Collins, C., Kinderlehrer, D. and Luskin, M., Numerical approximation of the solution of a variational problem with a double well potential. SIAM J. Numer. Anal. 28 (1991) 321–332. CrossRef
Dafermos, C.M. and Hrusa, W.J., Energy methods for quasilinear hyperbolic initial-boundary value problems. Applications to elastodynamics. Arch. Rational Mech. Anal. 87 (1985) 267–292. CrossRef
Demoulini, S., Young-measure solutions for a nonlinear parabolic equation of forward-backward type. SIAM J. Math. Anal. 27 (1996) 376–403. CrossRef
Demoulini, S., Young-measure solutions for nonlinear evolutionary systems of mixed type. Ann. Inst. H. Poincaré Anal. Non Linéaire 14 (1997) 143–162. CrossRef
Friesecke, G. and Dolzmann, G., Implicit time discretization and global existence for a quasi-linear evolution equation with nonconvex energy. SIAM J. Math. Anal. 28 (1997) 363–380. CrossRef
Kinderlehrer, D. and Pedregal, P., Weak convergence of integrands and the Young measure representation. SIAM J. Math. Anal. 23 (1992) 1–19. CrossRef
Klouček, P. and Luskin, M., The computation of the dynamics of the martensitic transformation. Contin. Mech. Thermodyn. 6 (1994) 209–240. CrossRef
M. Luskin, On the computation of crystalline microstructure, in Acta numerica, Cambridge Univ. Press, Cambridge (1996) 191–257.
S. Müller, Variational models for microstructure and phase transition, in Calculus of Variations and Geometric Evolution Problems, S. Hildebrandt and M. Struwe Eds., Lect. Notes Math. 1713, Springer-Verlag, Berlin (1999).
R.A. Nicolaides and N.J. Walkington, Computation of microstructure utilizing Young measure representations, in Transactions of the Tenth Army Conference on Applied Mathematics and Computing (West Point, NY, 1992), US Army Res. Office, Research Triangle Park, NC (1993) 57–68.
P. Pedregal, Parametrized measures and variational principles. Birkhäuser (1997).
M.O. Rieger, Time dependent Young measure solutions for an elasticity equation with diffusion, in International Conference on Differential Equations, Vol. 2 (Berlin, 1999), World Sci. Publishing, River Edge, NJ 1 (2000) 457–459.
Rieger, M.O., Young-measure solutions for nonconvex elastodynamics. SIAM J. Math. Anal. 34 (2003) 1380–1398. CrossRef
M.O. Rieger and J. Zimmer, Global existence for nonconvex thermoelasticity. Preprint 30/2002, Center for Nonlinear Analysis, Carnegie Mellon University, Pittsburgh, USA (2002).
T. Roubíček, Relaxation in optimization theory and variational calculus. Walter de Gruyter & Co., Berlin (1997).
Slemrod, M., Dynamics of measured valued solutions to a backward-forward heat equation. J. Dynam. Differ. Equations 3 (1991) 1–28. CrossRef
L. Tartar, Compensated compactness and applications to partial differential equations, in Nonlinear analysis and mechanics: Heriot-Watt Symposium. Pitman, Boston, Mass. IV (1979) 136–212.
M.E. Taylor, Partial Differential Equations III. Appl. Math. Sciences. Springer-Verlag, 117 (1996).
L.C. Young, Generalized curves and the existence of an attained absolute minimum in the calculus variations, volume classe III. (1937).
L.C. Young, Lectures on the calculus of variations and optimal control theory. W.B. Saunders Co., Philadelphia (1969).
Zhang, K., On some semiconvex envelopes. NoDEA. Nonlinear Differential Equations Appl. 9 (2002) 37–44. CrossRef