Published online by Cambridge University Press: 15 August 2002
A control system of the second order in time with control
$u=u(t) \in L^2([0,T];U)$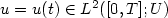 is considered. If the
system is controllable in a strong sense and
uT is the control
steering the system to the rest at time
T,
then the L2–norm of uT decreases as $1/\sqrt T$
is considered. If the
system is controllable in a strong sense and
uT is the control
steering the system to the rest at time
T,
then the L2–norm of uT decreases as $1/\sqrt T$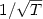 while the $L^1([0,T];U)$
while the $L^1([0,T];U)$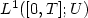 –norm of uT is approximately constant.
The proof is based on the moment approach
and properties of the relevant exponential family. Results are
applied to the wave equation with boundary or distributed controls.
–norm of uT is approximately constant.
The proof is based on the moment approach
and properties of the relevant exponential family. Results are
applied to the wave equation with boundary or distributed controls.