Article contents
Upper bounds for a class of energies containinga non-local term
Published online by Cambridge University Press: 31 July 2009
Abstract
In this paper we construct upper bounds for families offunctionals of the form
$$E_\varepsilon(\phi):=\int_\Omega\Big(\varepsilon |\nabla\phi|^2+\frac{1}{\varepsilon }W(\phi)\Big){\rm d}x+\frac{1}{\varepsilon }\int_{{\mathbb{R}}^N}|\nabla \bar H_{F(\phi)}|^2{\rm d}x$$ 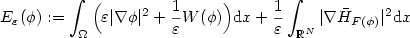
where Δ $\bar H_u$ 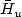 = div { $\chi_\Omega$
= div { $\chi_\Omega$ 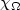 u}. Particular cases of such functionals arise inMicromagnetics. We also use our technique to construct upper boundsfor functionals that appear in a variational formulation ofthe method of vanishing viscosity for conservation laws.
u}. Particular cases of such functionals arise inMicromagnetics. We also use our technique to construct upper boundsfor functionals that appear in a variational formulation ofthe method of vanishing viscosity for conservation laws.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 16 , Issue 4 , October 2010 , pp. 856 - 886
- Copyright
- © EDP Sciences, SMAI, 2009
References
- 2
- Cited by


