Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T03:55:18.415Z Has data issue: false hasContentIssue false
  • English
  • Français

Variations on a central limit theorem in infinite ergodic theory

Published online by Cambridge University Press:  04 June 2014

DAMIEN THOMINE
DAMIEN THOMINE*
Affiliation:
Université de Rennes 1, Rennes, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In a previous paper the author proved a distributional convergence for the Birkhoff sums of functions of null average defined over a dynamical system with an infinite, invariant, ergodic measure, akin to a central limit theorem. Here we extend this result to larger classes of observables, with milder smoothness conditions, and to larger classes of dynamical systems, which may no longer be mixing. A special emphasis is given to continuous time systems: semi-flows, flows, and 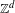$\mathbb{Z}^{d}$-extensions of flows. The latter generalization is applied to the geodesic flow on 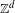$\mathbb{Z}^{d}$-periodic manifolds of negative sectional curvature.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 5 , August 2015 , pp. 1610 - 1657
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory. American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
Aaronson, J. and Denker, M.. A local limit theorem for stationary processes in the domain of attraction of a normal distribution. Asymptotic Methods in Probability and Statistics with Applications (St. Petersburg, 1998). Birkhäuser, Boston, 2001, pp. 215–223.CrossRefGoogle Scholar
Aaronson, J. and Denker, M.. Local limit theorems for partial sums of stationary sequences generated by Gibbs–Markov maps. Stoch. Dyn. 1 (2001), 193–237.CrossRefGoogle Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L.. Regular Variation (Encyclopedia of Mathematics and its Applications, 27). Cambridge University Press, Cambridge, 1987.CrossRefGoogle Scholar
Bowen, R.. Symbolic dynamics for hyperbolic flows. Amer. J. Math. 95 (1973), 429–460.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 1975.CrossRefGoogle Scholar
Burkholder, D. L.. Distribution function inequalities for martingales. Ann. Probab. 1 (1973), 19–42.CrossRefGoogle Scholar
Csáki, E. and Földes, A.. On asymptotic independence and partial sums. Asymptotic Methods in Probability and Statistics, A Volume in Honour of Miklós Csörgő. Elsevier, Amsterdam, 1998, pp. 373–381.Google Scholar
Csáki, E. and Földes, A.. Asymptotic independence and additive functionals. J. Theoret. Probab. 13 (2000), 1123–1144.CrossRefGoogle Scholar
Dobrushin, R. L.. Two limit theorems for the simplest random walk on a line (in Russian). Uspekhi Mat. Nauk 10 (1955), 139–146.Google Scholar
Gouëzel, S.. Sharp polynomial estimates for the decay of correlations. Israel J. Math. 139 (2004), 29–65.CrossRefGoogle Scholar
Jakubowski, A.. Tightness criteria for random measures with application to the principle of conditioning in Hilbert spaces. Probab. Math. Statist. 9 (1988), 95–114.Google Scholar
Pisier, G.. Martingales in Hilbert spaces (in connection with type and cotype),http://people.math.jussieu.fr/∼pisier/ihp-pisier.pdf (February 9, 2011). Lecture Notes for Winter School on ‘Type, cotype and martingales on Banach Spaces’, Institut Henri Poincaré, 2–8 February, 2011.Google Scholar
Pollicott, M. and Sharp, R.. Orbit counting for some discrete groups acting on simply connected manifolds with negative curvature. Invent. Math. 117 (1994), 275–302.CrossRefGoogle Scholar
Schweiger, F.. Numbertheoretical endomorphisms with 𝜎-finite invariant measure. Israel J. Math. 21 (1975), 308–318.CrossRefGoogle Scholar
Serfling, R. J.. Moment inequalities for the maximum cumulative sum. Ann. Math. Stat. 41 (1970), 1227–1234.CrossRefGoogle Scholar
Thomine, D.. A generalized central limit theorem in infinite ergodic theory. Probab. Theory Related Fields to appear, http://link.springer.com/journal/440/online first/page/3.Google Scholar
Zweimüller, R.. Mixing limit theorems for ergodic transformations. J. Theoret. Probab. 20 (2007), 1059–1071.CrossRefGoogle Scholar
Zweimüller, R.. Infinite measure preserving transformations with compact first regeneration. J. Anal. Math. 103 (2007), 93–131.CrossRefGoogle Scholar