Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-21T11:41:18.197Z Has data issue: false hasContentIssue false
  • English
  • Français

Support stability of maximizing measures for shifts of finite type

Part of: Dynamical systems with hyperbolic behavior Topological dynamics

Published online by Cambridge University Press:  09 October 2019

JULIANO S. GONSCHOROWSKI ,
ANTHONY QUAS  and
JASON SIEFKEN
JULIANO S. GONSCHOROWSKI
Affiliation:
Universidade Tecnológica Federal do Paraná, Av. Prof. Laura Pacheco Bastos, 800, CEP 85053-525, Guarapuava, PR, Brasil email [email protected]
ANTHONY QUAS
Affiliation:
Department of Mathematics and Statistics, University of Victoria, Victoria BC, CanadaV8W 3R4 email [email protected]
JASON SIEFKEN
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, CanadaM5S 2E4 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper establishes a fundamental difference between $\mathbb{Z}$ subshifts of finite type and 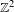$\mathbb{Z}^{2}$ subshifts of finite type in the context of ergodic optimization. Specifically, we consider a subshift of finite type 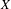$X$ as a subset of a full shift $F$. We then introduce a natural penalty function 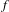$f$, defined on $F$, which is 0 if the local configuration near the origin is legal and 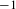$-1$ otherwise. We show that in the case of $\mathbb{Z}$ subshifts, for all sufficiently small perturbations, $g$, of 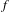$f$, the $g$-maximizing invariant probability measures are supported on 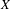$X$ (that is, the set 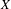$X$ is stably maximized by 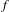$f$). However, in the two-dimensional case, we show that the well-known Robinson tiling fails to have this property: there exist arbitrarily small perturbations, $g$, of 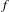$f$ for which the $g$-maximizing invariant probability measures are supported on 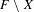$F\setminus X$.

Keywords

symbolic dynamicstilingsclassical ergodic theory

MSC classification

Primary: 37D35: Thermodynamic formalism, variational principles, equilibrium states 37B50: Multi-dimensional shifts of finite type, tiling dynamics 37B10: Symbolic dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 3 , March 2021 , pp. 869 - 880
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chazottes, J. R., Gambaudo, J. M., Hochman, M. and Ugalde, E.. On the finite-dimensional marginals of shift-invariant measures. Ergod. Th. & Dynam. Sys. 32 (2012), 1485–1500.CrossRefGoogle Scholar
Contreras, G.. Ground states are generically a periodic orbit. Invent. Math. 205 (2016), 383–412.CrossRefGoogle Scholar
Cortez, M.-I.. ℤ d Toeplitz arrays. Discrete Contin. Dyn. Syst. 15 (2006), 859–881.CrossRefGoogle Scholar
Hochman, M.. On the dynamics and recursive properties of multidimensional symbolic systems. Invent. Math. 176(1) (2009), 131–167.CrossRefGoogle Scholar
Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. 15 (2006), 197–224.CrossRefGoogle Scholar
Jenkinson, O.. Every ergodic measure is uniquely maximizing. Discrete Contin. Dyn. Syst. 16 (2006), 383–392.CrossRefGoogle Scholar
Jenkinson, O.. A partial order on × 2-invariant measures. Math. Res. Lett. 15 (2008), 893–900.CrossRefGoogle Scholar
Johnson, A. and Madden, K.. Putting the pieces together: understanding Robinson’s nonperiodic tilings. College Math. J. 28 (1997), 172–181.CrossRefGoogle Scholar
Quas, A.. Coupling and splicing. Lecture Notes available at http://www.math.uvic.ca/faculty/aquas/CoupleSplice.pdf.Google Scholar
Robinson, R. M.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.CrossRefGoogle Scholar
Wang, H.. Proving theorems by pattern recognition. Part 2. Bell Syst. Tech. J. 40 (1961), 1–41.CrossRefGoogle Scholar
Yuan, G. and Hunt, B. R.. Optimal orbits of hyperbolic systems. Nonlinearity 12 (1999), 1207–1224.CrossRefGoogle Scholar