Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Li, Shi Hai
1992.
Relations between chain recurrent points and turning points on the interval.
Proceedings of the American Mathematical Society,
Vol. 115,
Issue. 1,
p.
265.
Brucks, Karen M.
Otero-Espinar, Maria Victoria
and
Tresser, Charles
1992.
Homeomorphic restrictions of smooth endomorphisms of an interval.
Ergodic Theory and Dynamical Systems,
Vol. 12,
Issue. 3,
p.
429.
Li, Shihai
1992.
Dynamical properties of the shift maps on the inverse limit spaces.
Ergodic Theory and Dynamical Systems,
Vol. 12,
Issue. 1,
p.
95.
Hero, Michael W.
1992.
Special 𝛼-limit points for maps of the interval.
Proceedings of the American Mathematical Society,
Vol. 116,
Issue. 4,
p.
1015.
Bruckner, A. M.
and
Smítal, J.
1993.
A characterization of ω-limit sets of maps of the interval with zero topological entropy.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 1,
p.
7.
Blokh, Alexander M.
1995.
Dynamics Reported.
Vol. 4,
Issue. ,
p.
1.
Buescu, Jorge
and
Stewart, Ian
1995.
Liapunov stability and adding machines.
Ergodic Theory and Dynamical Systems,
Vol. 15,
Issue. 2,
p.
271.
D’Aniello, Emma
and
Steele, T.
2003.
A 𝐶¹ function for which the 𝜔-limit points are not contained in the closure of the periodic points.
Transactions of the American Mathematical Society,
Vol. 355,
Issue. 6,
p.
2545.
Mai, Jiehua
and
Sun, Taixiang
2007.
The ω-limit set of a graph map.
Topology and its Applications,
Vol. 154,
Issue. 11,
p.
2306.
Hofbauer, Franz
Raith, Peter
and
Smítal, Jaroslav
2010.
The space of ω-limit sets of piecewise continuous maps of the interval.
Journal of Difference Equations and Applications,
Vol. 16,
Issue. 2-3,
p.
275.
Sun, Taixiang
Tao, Chunyan
Xi, Hongjian
and
Qin, Bin
2014.
Topological Limits andω-Limit Sets of the Dendrite Maps.
Journal of Dynamical Systems and Geometric Theories,
Vol. 12,
Issue. 2,
p.
165.
Hantáková, Jana
and
Roth, Samuel
2021.
On backward attractors of interval maps*
.
Nonlinearity,
Vol. 34,
Issue. 11,
p.
7415.


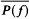 ⊆Λ(
⊆Λ(