Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ward, Thomas
1996.
Ergodic Theory of ℤd-ActionsEd.M. Pollicott and K. Schmidt. Proceedings of the Warwick Symposium 1993–94. L.M.S. Lecture Notes series, 228, C.U.P..
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 5,
p.
1105.
Старков, Александр Николаевич
and
Starkov, Aleksandr Nikolaevich
1997.
Новый прогресс в теории однородных потоков.
Успехи математических наук,
Vol. 52,
Issue. 4,
p.
87.
Manning, Anthony
and
Schmidt, Klaus
1999.
Common homoclinic points of commuting toral automorphisms.
Israel Journal of Mathematics,
Vol. 114,
Issue. 1,
p.
289.
Schmidt, Klaus
2001.
European Congress of Mathematics.
p.
543.
Lindenstrauss, Elon
2001.
p-adic foliation and equidistribution.
Israel Journal of Mathematics,
Vol. 122,
Issue. 1,
p.
29.
Lind, Douglas
and
Schmidt, Klaus
2002.
Vol. 1,
Issue. ,
p.
765.
Feres, Renato
and
Katok, Anatole
2002.
Vol. 1,
Issue. ,
p.
665.
Kleinbock, Dmitry
Shah, Nimish
and
Starkov, Alexander
2002.
Vol. 1,
Issue. ,
p.
813.
Tomanov, George
2002.
Rigidity in Dynamics and Geometry.
p.
407.
Sarnak, Peter
2003.
Spectra of hyperbolic surfaces.
Bulletin of the American Mathematical Society,
Vol. 40,
Issue. 4,
p.
441.
Einsiedler, Manfred
and
Katok, Anatole
2003.
Invariant measures on G/Γ for split simple Lie groups G.
Communications on Pure and Applied Mathematics,
Vol. 56,
Issue. 8,
p.
1184.
Einsiedler, Manfred
and
Lindenstrauss, Elon
2003.
Rigidity properties of ℤ^{𝕕}-actions on tori and solenoids.
Electronic Research Announcements of the American Mathematical Society,
Vol. 9,
Issue. 13,
p.
99.
Lindenstrauss, Elon
2004.
Dynamics and Randomness II.
Vol. 10,
Issue. ,
p.
123.
Lindenstrauss, Elon
and
Schmidt, Klaus
2004.
Invariant sets and measures of nonexpansive group automorphisms.
Israel Journal of Mathematics,
Vol. 144,
Issue. 1,
p.
29.
Einsiedler, Manfred
and
Ward, Thomas
2005.
Isomorphism rigidity in entropy rank two.
Israel Journal of Mathematics,
Vol. 147,
Issue. 1,
p.
269.
Lindenstrauss, Elon
2005.
Rigidity of multiparameter actions.
Israel Journal of Mathematics,
Vol. 149,
Issue. 1,
p.
199.
Einsiedler, Manfred
and
Katok, Anatole
2005.
Rigidity of measures—The high entropy case and non-commuting foliations.
Israel Journal of Mathematics,
Vol. 148,
Issue. 1,
p.
169.
Lindenstrauss, Elon
2006.
Equidistribution in Number Theory, An Introduction.
Vol. 237,
Issue. ,
p.
261.
Kalinin, Boris
and
Sadovskaya, Victoria
2007.
On classification of resonance-free Anosov ℤk actions.
Michigan Mathematical Journal,
Vol. 55,
Issue. 3,
Bourgain, Jean
Furman, Alex
Lindenstrauss, Elon
and
Mozes, Shahar
2007.
Invariant measures and stiffness for non-Abelian groups of toral automorphisms
.
Comptes Rendus. Mathématique,
Vol. 344,
Issue. 12,
p.
737.


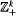 We show that they are either Haar measures or that every element of the action has zero metric entropy.
We show that they are either Haar measures or that every element of the action has zero metric entropy.