Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T04:06:34.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Hölder continuity of the Lyapunov exponent for analytic quasiperiodic Schrödinger cocycle with weak Liouville frequency

Published online by Cambridge University Press:  20 March 2013

JIANGONG YOU  and
SHIWEN ZHANG
JIANGONG YOU
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China email [email protected]@163.com
SHIWEN ZHANG
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China email [email protected]@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

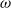For analytic quasiperiodic Schrödinger cocycles, Goldshtein and Schlag [Hölder continuity of the integrated density of states for quasi-periodic Schrödinger equations and averages of shifts of subharmonic functions. Ann. of Math. (2) 154 (2001), 155–203] proved that the Lyapunov exponent is Hölder continuous provided that the base frequency $\omega $ satisfies a strong Diophantine condition. In this paper, we give a refined large deviation theorem, which implies the Hölder continuity of the Lyapunov exponent for all Diophantine frequencies 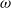$\omega $, even for weak Liouville 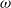$\omega $, which improves the result of Goldshtein and Schlag.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 4 , August 2014 , pp. 1395 - 1408
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A.. Global theory of one-frequency Schrodinger operators I: Stratified analyticity of the Lyapunov exponent and the boundary of nonuniform hyperbolicity. Preprint, 2009, http://arxiv.org/abs/0905.3902v1[math.DS].Google Scholar
Avila, A. and Jitomirskaya, S.. The ten martini problem. Ann. of Math. (2) 170 (2009), 303–342.Google Scholar
Avila, A. and Jitomirskaya, S.. Almost localization and almost reducibility. J. Eur. Math. Soc. 12 (2010), 93–131.Google Scholar
Avron, J. and Simon, B.. Almost periodic Schrödinger operators, II. The integrated density of states. Duke Math. J. 50 (1983), 369–391.Google Scholar
Bourgain, J.. Green’s Function Estimates for Lattice Schrödinger Operators and Applications (Annals of Mathematics Studies, 158). Princeton University Press, Princeton, NJ, 2005, p. 173.Google Scholar
Bourgain, J.. Hölder regularity of integrated density of states for the almost Mathieu operator in a perturbative regime. Lett. Math. Phys. 18 (2000), 51–83.Google Scholar
Bourgain, J.. Positivity and continuity of the Lyapunov exponent for shifts on Td with arbitrary frequency vector and real analytic potential. J. Anal. Math. 96 (2005), 313–355.CrossRefGoogle Scholar
Bourgain, J. and Goldshtein, M.. On nonperturbative localization with quasi-periodic potential. Ann. of Math. (2) 152 (2000), 835–879.Google Scholar
Bourgain, J. and Jitomirskaya, S.. Continuity of the Lyapunov exponent for quasiperiodic operators with analytic potential. J. Stat. Phys. 108 (5/6) (2002), 1028–1218.Google Scholar
Bochi, J.. Genericity of zero Lyapunov exponents. Ergod. Th. & Dynam. Sys. 22 (6) (2002), 1667–1696.CrossRefGoogle Scholar
Craig, W. and Simon, B.. Log Hölder continuity of the integrated density of states for stochastic Jacobi matrices. Commun. Math. Phys. 90 (1983), 207–218.Google Scholar
Furman, A.. On the multiplicative ergodic theorem for the uniquely ergodic systems. Ann. Inst. Henri Poincaré 33 (1997), 797–815.Google Scholar
Goldshtein, M. and Schlag, W.. Hölder continuity of the integrated density of states for quasi-periodic Schrödinger equations and averages of shifts of subharmonic functions. Ann. of Math. (2) 154 (2001), 155–203.Google Scholar
Goldshtein, M. and Schlag, W.. Fine properties of the integrated density of states and a quantitative separation property of the Dirichlet eigenvalues. Geom. Funct. Anal. 18 (2008), 755–869.Google Scholar
Jitomirskaya, S.. Ergodic Schrödinger operator (on one foot). Proc. Sympos. Pure Math. 76 (2) (2007), 613–647.Google Scholar
Jitomirskaya, S., Koslover, D. and Schulteis, M.. Continuity of the Lyapunov exponent for general analytic quasiperiodic cocycles. Ergod. Th. & Dynam. Sys. 29 (2009), 1881–1905.Google Scholar
Sorets, E. and Spencer, T.. Positive Lyapunov exponents for Schrodinger operators with quasi-periodic potentials. Comm. Math. Phys. 142 (1991), 543–566.CrossRefGoogle Scholar
Wang, Y. and You, J.. Examples of discontinuity of Lyapunov exponent in smooth quasi-periodic cocycles. Preprint, 2012, http://arxiv.org/abs/1202.0580[math.DS].Google Scholar
You, J. and Zhou, Q.. Embedding of analytic quasi-periodic cocycles into analytic quasi-periodic linear systems and its applications. Comm. Math. Phys. to appear.Google Scholar