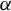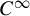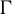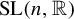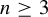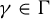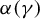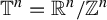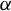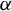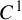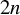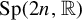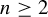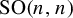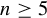Global rigidity of higher rank lattice actions with dominated splitting

Abstract

Let $\alpha $ be a $C^{\infty }$ volume-preserving action on a closed n-manifold M by a lattice $\Gamma $ in $\mathrm {SL}(n,\mathbb {R})$, $n\ge 3$. Assume that there is an element $\gamma \in \Gamma $ such that $\alpha (\gamma )$ admits a dominated splitting. We prove that the manifold M is diffeomorphic to the torus ${{\mathbb T}^{n}={\mathbb R}^{n}/{\mathbb Z}^{n}}$ and $\alpha $ is smoothly conjugate to an affine action. Anosov diffeomorphisms and partial hyperbolic diffeomorphisms admit a dominated splitting. We obtained a topological global rigidity when $\alpha $ is $C^{1}$. We also prove similar theorems for actions on $2n$-manifolds by lattices in $\textrm {Sp}(2n,{\mathbb R})$ with $n\ge 2$ and $\mathrm {SO}(n,n)$ with $n\ge 5$.

1 Introduction

In this paper, we study topological and smooth global rigidity of higher rank lattice actions on specific dimensional manifolds under weak hyperbolicity assumptions. Throughout the paper, a manifold stands for a compact connected smooth Riemannian manifold without boundary. We can state one simple corollary of our result as the following corollary.

Corollary 1.1. Let $\Gamma <\mathrm {SL}(n,{\mathbb R})$ be a lattice for $n\ge 3$ and $\alpha \colon \Gamma \to \mathrm {Diff}^{1}(M^{n})$ be a volume-preserving $C^{1}\ \Gamma $ action on a closed smooth n-dimensional manifold M. Assume that there is a $\gamma _{0}\in \Gamma $ such that $\alpha (\gamma _{0})$ admits a dominated splitting.

Then the manifold M is homeomorphic to the n-torus ${\mathbb T}^{n}={\mathbb R}^{n}/{\mathbb Z}^{n}$ . Moreover, the action $\alpha $ is topologically conjugate to an affine action on the n-torus. If the action $\alpha $ is a $C^{\infty }$ action, then the topological conjugacy is smooth.

The conclusion says that, up to finite index, the action $\alpha $ is conjugate to the action of a finite index subgroup of $\mathrm {SL}(n,{\mathbb Z})$ by automorphisms on ${\mathbb T}^{n}$ .

Recall that Anosov diffeomorphisms and partial hyperbolic diffeomorphisms admit a dominated splitting. Even in the case where $\alpha (\gamma _{0})$ is an Anosov diffeomorphism, Corollary 1.8 gives a new rigidity result.

The existence of $C^{0}$ conjugacy implies that there is a finite index subgroup $\Gamma _{1}<\Gamma $ such that there is an unbounded group homomorphism from $\Gamma _{1}$ to $\mathrm {SL}(n,{\mathbb Z})$ . For instance, if $\Gamma $ is a cocompact, then such an action $\alpha $ cannot exist. In other words, in that case, $\Gamma $ cannot act on n-manifolds smoothly with an element which admits a dominated splitting.

The main motivations of this paper are twofold.

1. (1) Recently Brown, Fisher, and Hurtado proved that for a lattice $\Gamma $ in $\mathrm {SL}(n,{\mathbb R})$ , $n\ge 3$ , any volume-preserving smooth $\Gamma $ action on an $(n-1)$ -dimensional manifold should factor through finite group action [BFH16, BFH20, BFH21]. The above Corollary 1.1 says that in an n-dimensional case, which is right after the critical dimension, if your action has a uniform hyperbolic phenomenon, then the action should be a standard action.

2. (2) Conjecturally, a smooth lattice action with a uniform hyperbolic diffeomorphism is smoothly conjugate to an algebraic action, see [Gor07, Fis11]. Corollary 1.1 gives an evidence for the conjecture.

The rigidity of higher rank lattice actions on manifolds with hyperbolicity is studied by many authors under various assumptions. We indicate some previous results related to this paper. For these works, $n\ge 3$ .

First, without specifying the base manifold, Feres proved that $C^{\infty }$ global rigidity for actions on n-manifolds by lattices in $\mathrm {SL}(n,{\mathbb R})$ assuming that the action preserves a connection, is non-isometric, and is ergodic volume-preserving [Fer95]. In [FL98], Feres and Labourie proved the $C^{\infty }$ global rigidity result for a lattice in $\mathrm {SL}(n,{\mathbb R})$ action on a n-manifold under certain assumptions including an Anosov property of the induced action on the suspension space. In [GS99], Goetze and Spatzier proved $C^{\infty }$ global rigidity of higher rank lattice volume-preserving Cartan actions on manifolds without assuming dimension assumptions.

Assuming the manifold is a torus, Katok and Lewis proved that topological and smooth global rigidity of actions on the n-torus by finite index subgroup of $\mathrm {SL}(n,{\mathbb Z})$ under certain assumptions including the existence of one Anosov element [KL96]. In [KLZ96], Katok, Lewis, and Zimmer proved the smooth global rigidity of actions on the n-torus by $\mathrm {SL}(n,{\mathbb Z})$ assuming that the action has an ergodic fully supported probability measure and has one Anosov element. In [MQ01], Margulis and Qian proved topological global rigidity of higher rank lattice actions on tori or nilmanifolds assuming that the action lifts to the universal cover, has an invariant measure, and has one Anosov element. Recently, Brown, Rodriguez Hertz, and Wang proved both topological and smooth global rigidity of higher rank lattice actions on nilmanifolds only assuming a certain lifting condition and the existence of an Anosov element [BRHW17].

1.1 Statement of main theorem

In this paper, we study the global rigidity of $\Gamma $ actions on M in the cases SL, Sp, and SO. Roughly speaking, the main theorem says that in these cases, if there is a uniform hyperbolicity from one element, then the entire group action should be algebraic. Throughout the paper, we use the following notation.

Notation 1.2. (Cases SL, Sp, and SO)

${}$

• SL. Let $n\ge 3$ , $G=\mathrm {SL}(n,{\mathbb R})$ , and M be a closed n-dimensional manifold. Let $d=n$ .

• Sp. Let $n\ge 2$ , $G=\mathrm {Sp}(2n,{\mathbb R})$ , and M be a closed $2n$ -dimensional manifold. Let ${d=2n}$ .

• SO. Let $n\ge 5$ , $G=\mathrm {SO}(n,n)$ , and M be a closed $2n$ -dimensional manifold. Let ${d=2n}$ .

In the above cases, let $\Gamma <G$ be a lattice in G.

Recall that the symplectic group $\mathrm {Sp}(2n,{\mathbb R})$ and the indefinite orthogonal group $\mathrm {SO}(n,n)$ are defined as

$$ \begin{align*}\mathrm{Sp}(2n,{\mathbb R})=\{g\in \mathrm{SL}(2n,{\mathbb R}): g^{tr}Jg=J\},\quad J=\begin{bmatrix} 0_{n} & I_{n} \\ -I_{n} &0_{n} \end{bmatrix}, \end{align*} $$

$$ \begin{align*}\mathrm{SO}(n,n)=\{g\in\mathrm{SL}(2n,{\mathbb R}): g^{tr}I_{n,n}g=I_{n,n}\},\quad I_{n,n}=\begin{bmatrix} 0_{n}& I_{n} \\ I_{n} & 0_{n} \end{bmatrix},\end{align*} $$

where $I_{n}$ is an $n\times n$ identity matrix and $0_{n}$ is an $n\times n$ zero matrix.

Remark 1.3. In the case of SO, we require that $n\ge 5$ although $n\ge 2$ is enough to get higher rank. When $n=2,3$ , we have isomorphisms

$$ \begin{align*}\mathfrak{so}(2,2)\simeq \mathfrak{sl}(2,{\mathbb R})\times \mathfrak{sl}(2,{\mathbb R}),\mathfrak{so}(3,3)\simeq \mathfrak{sl}(4,{\mathbb R}).\end{align*} $$

Therefore, in those cases, either the group is not simple or does not fit into the dimension condition. When $n=4$ , $\textrm {Spin}(8,\mathbb {C})$ (or $\mathfrak {so}(8,\mathbb {C})$ ) admits three non-trivial $8$ -dimensional representations, a defining and two half-spin representations, so-called triality (e.g. [FH91, §20.3]). We avoid this case for simplicity.

Recall that we say that $C^{1}$ diffeomorphism f on M admits a dominated splitting if there is an f-invariant continuous non-trivial splitting $TM=E\oplus F$ , and constants $C,\unicode{x3bb}>0$ such that for all $x\in M$ and $n\ge 0$ , we have

$$ \begin{align*}\frac{\|D_{x}f^{n}(v)\|}{\|D_{x}f^{n}(w)\|}<Ce^{-\unicode{x3bb} n}, \end{align*} $$

for all $v\in E$ , $w\in F$ with $\|v\|=\|w\|=1$ .

Example 1.4. Recall that $f\in \mathrm {Diff}^{1}(M)$ is called an Anosov diffeomorphism if there is an f-invariant continuous non-trivial splitting $TM=E_{s}\oplus E_{u}$ , and constants $C>0,\unicode{x3bb} <1$ such that for all $x\in M$ and $n\ge 0$ ,

$$ \begin{align*}\|D_{x}f^{n}(v)\| \le C\unicode{x3bb}^{n} \|v\|, \|D_{x}f^{-n}(w)\|\le C\unicode{x3bb}^{n}\|w\|,\end{align*} $$

for all $v\in E_{s}$ and $w\in E_{u}$ . The subbundles $E_{s}$ and $E_{u}$ are called the stable and unstable distribution, respectively.

All Anosov diffeomorphisms admit a dominated splitting. More generally, partially hyperbolic diffeomorphisms (for definition, see [Pes04]) admit a dominated splitting.

Now the main result in this paper is the following theorem.

Theorem 1.5. (Main theorem)

Let G, $\Gamma $ , M, and d be as in Notation 1.2. Let ${\alpha \colon \Gamma \to \mathrm {Diff}^{1}_{\mathrm {Vol}}(M)}$ be a $C^{1}$ volume-preserving action. Assume that there is an element $\gamma _{0}\in \Gamma $ such that $\alpha (\gamma _{0})$ admits a dominated splitting. Then the action has an Anosov element, that is,

$$ \begin{align*}\text{ there exists } \gamma_{0}'\in\Gamma \textrm{ such that } \alpha(\gamma_{0}')\textrm{ is an Anosov diffeomorphism.}\end{align*} $$

Furthermore, in the case of SL, the manifold M is homeomorphic to a torus. In the cases of Sp and SO, the manifold M is homeomorphic to a torus or an infra-torus.

Remark 1.6. In Theorem 1.5, we actually prove that $\alpha (\gamma )$ is an Anosov diffeomorphism on M for all hyperbolic elements $\gamma \in \Gamma $ . An element $g\in G$ is said to be hyperbolic if there is no eigenvalue (over $\mathbb {C}$ ) of g with modulus $1$ . This will allow us to prove that the manifold is a torus or an infra-torus.

Remark 1.7. In this paper, the only use of the volume-preserving condition is to make sure that the cocycle $L\colon \Gamma \times M \to {\mathbb R}$ , $L(\gamma ,x)= \ln |\det D_{x}(\alpha (\gamma ))|$ is trivial in Proposition 4.6. Actually, if L is continuously cohomologous to the constant cocycle $(\gamma ,x)\mapsto 0$ , then the same arguments still hold. In [KLZ96, Lemma 2.5] and the paragraph before their lemma, the same conclusions were deduced as in our Proposition 4.6. In our proof of Proposition 4.6, L being trivial is used to promote continuous equivariant projective framing to continuous framing up to sign. Therefore, we can prove that $\alpha (\gamma )$ is an Anosov diffeomorphism if $\gamma \in \Gamma $ is hyperbolic. Presumably, in [KLZ96], they construct a continuous conjugacy between L and the trivial cocycle to deduce the same conclusion. We, however, could not see how they construct a continuous conjugacy between L and the constant cocycle using a fully supported $\Gamma $ -invariant ergodic measure $\mu $ in [KLZ96]. We note though that, in [BRHW17], they build a continuous conjugacy between $\Gamma $ actions ( $\alpha $ and its linear data) and then prove that L is continuously cohomologous to the trivial cocycle using the conjugacy, when we have an Anosov action on the torus. This shows that the measure assumption is redundant in the setting of [KLZ96].

In our setting, even we assumed the Anosov $\Gamma $ action, we stick with the volume- preserving assumption since we could not see how to produce a continuous conjugacy using a general fully supported $\Gamma $ -invariant measure $\mu $ . When we assumed the action is Anosov, then a slightly weaker assumption on the measure is enough. For instance, if the Anosov $\Gamma $ action has a fully supported invariant measure $\mu $ which has a local product structure for the Anosov element (for instance, when $\mu $ is a measure of maximal entropy for the Anosov element), then one can deduce that there is a $\Gamma $ -invariant smooth measure using Livšic’s theorem. In this case, we can conclude that the cocycle $\Gamma \times M \to {\mathbb R}$ , $(\gamma ,x)\mapsto \ln |\det D_{x}(\gamma )|$ is continuously cohomologous with the constant cocycle $(\gamma ,x)\mapsto 0$ , and hence the same conclusion as in our theorems hold.

1.2 Global rigidity of the action

The main theorem implies that the action is indeed algebraic under a lifting assumption.

Corollary 1.8. Assume the same settings as in Theorem 1.5. In the cases of Sp and SO, we further assume that there is a finite index subgroup $\Gamma _{0}$ in $\Gamma $ such that the action $\alpha |_{\Gamma _{0}}$ lifts to the finite cover $M_{0}$ of M that is homeomorphic to a torus. Denote the lifted action of $\Gamma _{1}$ on $M_{0}$ as $\alpha _{0}$ . In the case of SL, simply denote $\Gamma _{0}=\Gamma $ and $M_{0}=M$ .

Then, there is a finite subgroup $\Gamma _{1}<\Gamma _{0}$ such that the lifted action $\alpha _{0}$ of $\Gamma _{1}$ on $M_{0}$ is topologically conjugate to its linear data $\rho _{0}$ . More precisely, there is a finite index subgroup $\Gamma _{1}<\Gamma _{0}$ and a homeomorphism $h\colon M_{0}\to M_{0}$ such that

$$ \begin{align*}\rho_{0}(\gamma)\circ h=\alpha_{0}(\gamma)\circ h\quad \text{for all } \gamma\in\Gamma_{1},\end{align*} $$

where $\rho _{0}\colon \Gamma _{1}\to \operatorname {\mathrm {Aut}}(M_{0})\simeq \mathrm {SL}(d,{\mathbb Z})$ is the associated linear data of $\alpha _{0}$ . If $\alpha $ is a $C^{\infty }$ action, then the conjugacy h is indeed $C^{\infty }$ as well.

As we discussed earlier, Corollary 1.8 also says that such $\alpha $ cannot exist unless the unbounded group homomorphism $\rho _{0}$ exists. This implies that $\Gamma $ is commensurable to $G({\mathbb Z})$ due to Margulis’ normal subgroup theorem as in [Zim84, Ch. 7]. Here, $G({\mathbb Z})$ is $\mathrm {SL}(n,{\mathbb Z})$ , $\mathrm {Sp}(2n,{\mathbb Z})$ , or $\mathrm {SO}(n,n,{\mathbb Z})$ in the cases of SL, Sp, or SO, respectively.

In Corollary 1.8, h intertwines the entire $\alpha _{0}(\Gamma _{0})$ action on $M_{0}$ with an affine action on $M_{0}$ (see for instance [MQ01, Lemma 6.8.]). In particular, in the case of SL, the entire $\Gamma $ action is conjugate to an affine action. This shows Corollary 1.1.

1.3 Organization of the paper

The paper is organized as follows. In §2, we provide some settings and preliminaries for the proof. In §3, we prove some algebraic properties of G and $\Gamma $ that we need. We prove that we can arrange any two subspaces into general position using G on one subspace. This will be used in the proof of Theorem 1.5. In §4, we prove Theorem 1.5. The main idea is a comparison between the continuous data from dominated splittings and the measurable data from the superrigidity. We extend and modify the idea in [KLZ96]. In §5, we prove Corollary 1.8 based on [BRHW17].

2 Preliminaries

Throughout the paper, we fix a vector space $V={\mathbb R}^{d}$ with the standard inner product. Also, M stands for a d-dimensional manifold. Here, d is the number in Notation 1.2.

In the cases of Sp and SO, we will put additional structures on it.

2.1 Settings

We fix some notation which will be used throughout the paper.

In all cases, there are at most three homomorphisms from G to $\mathrm {GL}(V)$ , up to conjugation, namely the trivial, defining, and contragredient representations due to the dimension condition. Throughout the paper, we denote trivial, defining, and contragredient representation as $\pi _{0}$ , $\pi _{1}$ , and $\pi _{2}$ , respectively.

In the case of SL, $\pi _{1}$ and $\pi _{2}$ are not an isomorphic representation. Nevertheless, we may assume that $\pi _{1}(G)=\pi _{2}(G)=\mathrm {SL}(V)$ as $\mathrm { SL}(n,{\mathbb R})$ is invariant under transpose.

In the case of Sp, $\pi _{1}$ and $\pi _{2}$ are isomorphic as a representation. We put the symplectic form $\omega $ and the symplectic basis $ {\mathcal B}$ on V. More precisely, we fix basis $ {\mathcal B}$ and a symplectic form $\omega $ on V as

$$ \begin{align*} {\mathcal B}=\{e_{1},\ldots, e_{n}, f_{1},\ldots,f_{n}\},\end{align*} $$

$$ \begin{align*}\omega(e_{i},f_{j})=\delta_{ij}, \quad \omega(e_{i},e_{j})=\omega(f_{i},f_{j})=0\end{align*} $$

for all $i,j\in \{1,\ldots , n\}$ . Here, $\delta _{ij}$ is the Kronecker delta symbol. Without loss of generality, we may assume that $\pi _{1}=\pi _{2}$ and

$$ \begin{align*}\pi_{1}(G)=\pi_{2}(G)=\textrm{Sp}(V,\omega),\end{align*} $$

where

$$ \begin{align*}\textrm{Sp}(V,\omega)=\{A\in\mathrm{SL}(V): \omega(Av,Aw)=\omega(v,w)\textrm{ for all } v,w\in V\}.\end{align*} $$

In the case of SO, $\pi _{1}$ and $\pi _{2}$ are isomorphic as a representation again. We can define a signature $(n,n)$ quadratic form Q and a basis $ {\mathcal C}$ on V as

$$ \begin{align*} {\mathcal C}=\{x_{1},\ldots, x_{n},y_{1},\ldots, y_{n}\},\end{align*} $$

$$ \begin{align*}Q\bigg(\sum_{i=1}^{n}( a_{i}x_{i}+b_{i}y_{i})\bigg)=\sum_{i=1}^{n}a_{i}^{2}-\sum_{i=1}^{n}b_{i}^{2}.\end{align*} $$

Without loss of generality, we may assume that

$$ \begin{align*}\pi_{1}(G)=\pi_{2}(G)=\mathrm{SO}(V,Q),\end{align*} $$

where

$$ \begin{align*}\mathrm{SO}(V,Q)=\{A\in\mathrm{SL}(V): Q(Av)=Q(v)\textrm{ for all } v\in V\}.\end{align*} $$

Note that in all cases, $\pi _{1}$ and $\pi _{2}$ are irreducible.

2.2 Cocycle superrigidity theorem

On a d-dimensional manifold M, we denote the frame bundle P on M. We identify the fibers of the frame bundle P at $x\in M$ as the set of linear isomorphisms $V\to T_{x}M$ .

First, $\mathrm {SL}_{n}$ and $\textrm {Sp}_{2n}$ are algebraically simply connected. For the case of SO, the algebraically universal cover is $\textrm {Spin}_{2n}$ . As we assume that $n\ge 5$ , there is a unique (complex) non-trivial $2n$ -dimensional representation of $\textrm {Spin}_{2n}$ up to conjugation which is the defining representation of $\textrm {Spin}_{2n}(\mathbb {C})$ . The defining representation factors through $\mathrm {SO}(2n,\mathbb {C})$ . Therefore, we can restate the non-ergodic version of the cocycle superrigidity theorem [FMW04, Theorem 4.5] as follows.

Theorem 2.1. (Cocycle superrigidity, non-ergodic case [FMW04])

Let $\Gamma $ , G, and M be as in the cases of SL, Sp, or SO. Let P be the frame bundle on M.

Then there is:

1. (1) a measurable section $\sigma \colon M\to P$ ;

2. (2) a measurable $\Gamma $ -invariant map $\iota \colon M\to \{0,1,2\}$ ;

3. (3) compact subgroups $\kappa _{i}\subset \mathrm {GL}(V)$ ; and

4. (4) measurable cocycles $K_{i}\colon \Gamma \times \iota ^{-1}(i)\to \kappa _{i}$ for $i=0,1,2$ ,

such that:

1. (1) for $\mu $ almost every x and every $\gamma \in \Gamma $ ,

   $$ \begin{align*}D_{x}(\gamma)\sigma(x)= \sigma(\alpha(\gamma)(x))\pi_{\iota(x)}(\gamma)K_{\iota(x)}(\gamma,x); \end{align*} $$

2. (2) $\pi _{i}(G)$ commutes with $\kappa _{i}$ for $i=0,1,2$ .

If we denote by $\{\mu _{i}\}_{i\in I}$ the ergodic decomposition of $\mu $ with respect to the $\Gamma $ action, then we have a partition of I into $I_{0}$ , $I_{1}$ , and $I_{2}$ such that, for $\mu _{i}$ almost every x, we have $\iota (x)=i$ if and only if $i\in I_{i}$ for $i\in \{0,1,2\}$ . Note that $\iota ^{-1}(i)$ is an $\alpha (\Gamma )$ invariant measurable set for all $i\in \{0,1,2\}$ . For each $i\in \{1,2,3\}$ , let us denote by $\mu _{i}$ the integration of ergodic components in $I_{i}$ ,

$$ \begin{align*}\mu_{i}=\int_{j\in I_{i}} \mu_{j}.\end{align*} $$

Then we can decompose $\mu $ as

$$ \begin{align*}\mu=\mu_{0}+\mu_{1}+\mu_{2}.\end{align*} $$

Let us denote by $X_{i}$ the support of $\mu _{i}$ . Here, $X_{i}$ is a compact $\Gamma $ -invariant subset in M for all $i\in \{0,1,2\}$ .

In all cases, by Schur’s lemma and dimension considerations, we have

$$ \begin{align*}Z_{\mathrm{GL}(d,{\mathbb R})}(\pi_{1}(G))=Z_{\mathrm{GL}(d,{\mathbb R})}(\pi_{2}(G))={\mathbb R}^{\times}\cdot I_{V}.\end{align*} $$

Therefore, $\kappa _{1}$ and $\kappa _{2}$ are compact subgroups of ${\mathbb R}^{\times }\cdot I_{V}$ so that they are subgroups of $\{\pm I_{V}\}$ . In particular, $K_{1}$ and $K_{2}$ take values in $\{\pm I_{V}\}$ .

In [FMW04, Theorem 4.5], the statement is not written in the bundle theoretic form. However, Theorem 2.1 can be directly deduced from it.

2.3 Franks–Newhouse and Brin–Manning theorems

In this section, we recall some facts on Anosov diffeomorphisms. An Anosov diffeomorphism is said to be codimension  $1$ if the dimension of stable or unstable distribution is $1$ . The first theorem due to the Franks–Newhouse theorem states that if a manifold M admits a codimension $\textrm{1}$ Anosov diffeomorphism, then the manifold is homeomorphic to the torus ${\mathbb R}^{d}/{\mathbb Z}^{d}$ (See [Hir01, New70, Fra70]).

Theorem 2.2. (The Franks–Newhouse theorem)

If $f\colon M\to M$ is a codimension 1 Anosov diffeomorphism, then M is homeomorphic to the torus ${\mathbb T}^{d}={\mathbb R}^{d}/{\mathbb Z}^{d}$ .

If we can control the dilation on the stable and unstable distribution, then we can use the Brin–Manning theorem as follows. Let M be a manifold and $f\colon M\to M$ be an Anosov diffeomorphism. The map f induces a bounded linear operator $f_{*}$ on the Banach space of a continuous vector field on M as

$$ \begin{align*}f_{*}X(x)=D_{f^{-1}(x)}(X(f^{-1}(x)))\end{align*} $$

for a continuous vector field X on M. Then the spectrum of $f_{*}$ is contained in the interior of two annuli with the radius $0<\unicode{x3bb} _{1}<\unicode{x3bb} _{2}<1$ and $1<\mu _{2}<\mu _{1}<\infty $ .

Theorem 2.3. (The Brin–Manning theorem, see [BM81])

Let $f\colon M\to M$ be an Anosov diffeomorphism on M. Let $\mu _{1},\mu _{2}$ and $\unicode{x3bb} _{1},\unicode{x3bb} _{2}$ be as above. Assume that

$$ \begin{align*}1+\frac{\log\mu_{2}}{\log\mu_{1}}>\frac{\log\unicode{x3bb}_{1}}{\log\unicode{x3bb}_{2}},\end{align*} $$

and

$$ \begin{align*}1+\frac{\log\unicode{x3bb}_{2}}{\log\unicode{x3bb}_{1}}>\frac{\log\mu_{1}}{\log\mu_{2}}.\end{align*} $$

Then, M is homeomorphic to a torus or a flat manifold.

Note that if M is a flat manifold, then M is an infra-torus or torus by Bieberbach’s theorem [Bie11, Bie12].

3 Auxiliary lemmas for SL, Sp, and SO

The proof of the main theorem requires some properties of $\mathrm {SL}(V)$ , $\mathrm { Sp}(V,\omega )$ , and $\mathrm {SO}(V,Q)$ . In this section, we will prove such facts. We retain the notation in the previous section.

First, we will use the following fact that is about the normalizer in $\mathrm { GL}(V)$ which is a special case of [Fer95, Lemma 2.5].

Lemma 3.1. Let $H\subset \mathrm {GL}(V)$ be an real algebraic subgroup in $\mathrm {GL}(V)$ . Let G be either $\mathrm {SL}(V)$ , $\mathrm {Sp}(V,\omega )$ , or $\mathrm {SO}(V,Q)$ . Assume that H is normalized by G. Then H contains G or is contained in ${\mathbb R}^{\times }\cdot \{I_{V}\}$ .

In all cases, G is a $\mathbb {R}$ -split group. Denote the ${\mathbb R}$ -rank of G as $\textrm {rk}_{{\mathbb R}}(G)$ . Note that

$$ \begin{align*}\textrm{rk}_{{\mathbb R}}(\mathrm{SL}(n,{\mathbb R}))=n-1,\quad\textrm{and}\quad \textrm{rk}_{{\mathbb R}}(\mathrm{Sp}(2n,{\mathbb R}))=\textrm{rk}_{{\mathbb R}}(\mathrm{SO}(n,n))=n.\end{align*} $$

The following theorem in [PR01] ensures the existence of higher rank free abelian subgroup ${\mathbb Z}^{n-1}$ in $\Gamma $ .

Theorem 3.2. (Prasad and Rapinchuk [PR01])

In all cases in Notation 1.2, there is a subgroup $\Gamma _{0}< \Gamma $ and a maximal ${\mathbb R}$ -split torus $A\simeq {\mathbb R}^{\textrm {rk}_{{\mathbb R}}(G)}$ in G such that $ {\mathcal A}=A\cap \Gamma _{0}\simeq {\mathbb Z}^{\textrm {rk}_{{\mathbb R}}(G)}$ is a lattice in A.

In following subsections, we prove that for any two subspaces $W_{1}$ and $W_{2}$ in V, there is $g\in G$ such that the subspaces $gW_{1}$ and $W_{2}$ are in general position (Corollaries 3.7 and 3.11). Recall that two subspaces $W_{1}$ and $W_{2}$ are in general position if

$$ \begin{align*}\dim(W_{1}\cap W_{2})=\max\{0,\dim W_{1}+\dim W_{2}-\dim V\}.\end{align*} $$

Note that this can be checked easily in the case of $\mathrm { SL}(V)$ as $\mathrm {SL}(V)$ acts transitively on the space of all k-dimensional subspaces of V for all k.

3.1 Properties of Sp

Throughout this subsection, we always denote $(V,\omega )$ to be a ${d=2n}$ -dimensional symplectic vector space as in the case of Sp in §2.1. Recall that we put the symplectic form $\omega $ and the symplectic basis

$$ \begin{align*} {\mathcal B}=\{e_{1},\ldots, e_{n},f_{1},\ldots, f_{n}\}\end{align*} $$

on V. Also, $\textrm {Sp}(V,\omega )$ is denoted by the symplectic group for the symplectic form $\omega $ on V.

For any subspace $W<V$ , let

$$ \begin{align*}W^{\perp}=\{v\in V: \omega(v,w)=0\textrm{ for all } w\in W\}\end{align*} $$

and $\omega _{W}$ be the bilinear form on W induced by the restriction of $\omega $ .

Recall that a subspace $W<V$ is said to be:

1. (1) symplectic if $W\cap W^{\perp }=\{0\}$ (equivalently, $\omega _{W}$ is symplectic form);

2. (2) Lagrangian if $W^{\perp }=W$ (equivalently, $\omega _{W}=\omega _{W^{\perp }}=0$ );

3. (3) isotropic if $W\subset W^{\perp }$ (equivalently, $\omega _{W}=0$ ); and

4. (4) coisotropic if $W^{\perp }\subset W$ (equivalently, $\omega _{W^{\perp }}=0$ ).

The following decomposition will be useful (for the proof, see for instance [RS13, Theorem 7.3.3]).

Lemma 3.3. (Witt–Artin decomposition)

Let $(V,\omega )$ be a symplectic space. For any subspace W in V, if subspaces H and J satisfy

$$ \begin{align*}W= H\oplus(W\cap W^{\perp}),\quad W^{\perp}=J\oplus (W\cap W^{\perp}),\end{align*} $$

then H and J are symplectic. Furthermore, V can be decomposed into an $\omega $ -orthogonal direct sum

$$ \begin{align*}V=H\oplus J\oplus (H\oplus J)^{\perp}\end{align*} $$

and $W\cap W^{\perp }$ is a Lagrangian subspace in $(H\oplus J)^{\perp }$ .

From the definition and Lemma 3.3, the following lemma can be deduced directly.

Lemma 3.4. Let $W<V$ be a subspace. Let $r=\dim (W\cap W^{\perp })$ and $p=\dim W$ . Then:

1. (1) $r\le p$ ;

2. (2) $r\le n$ ;

3. (3) $r\le 2n-p$ ;

4. (4) $p-r$ is even.

The following is also an application of Lemma 3.3.

Lemma 3.5. For any two subspaces $W_{1}, W_{2}<V$ , if

$$ \begin{align*}\dim W_{1}=\dim W_{2}\quad\textrm{and}\quad \dim(W_{1}\cap W_{1}^{\perp})=\dim(W_{2}\cap W_{2}^{\perp}),\end{align*} $$

then there is an $h\in \textrm {Sp}(V,\omega )$ such that

$$ \begin{align*}hW_{1}=W_{2}.\end{align*} $$

Proof. Assume that two subspaces $W_{1},W_{2}<V$ satisfy $\dim W_{1}=\dim W_{2}$ and $ \dim (W_{1}\cap W_{1}^{\perp })=\dim (W_{2}\cap W_{2}^{\perp })$ . Using Lemma 3.3, we know that if subspaces $H_{1}$ and $J_{1}$ satisfy

$$ \begin{align*}W_{1}= H_{1}\oplus(W_{1}\cap W_{1}^{\perp}),\quad W_{1}^{\perp}=J_{1}\oplus (W_{1}\cap W_{1}^{\perp}),\end{align*} $$

then $H_{1}$ and $J_{1}$ are symplectic. Furthermore, V can be decomposed into an $\omega $ -orthogonal direct sum

$$ \begin{align*}V=H_{1}\oplus J_{1}\oplus (H_{1}\oplus J_{1})^{\perp}\end{align*} $$

and $W_{1}\cap W_{1}^{\perp }$ is a Lagrangian subspace in $(H_{1}\oplus J_{1})^{\perp }$ .

Similarly, for subspaces $H_{2}$ and $J_{2}$ that satisfy

$$ \begin{align*}W_{2}= H_{2}\oplus(W_{2}\cap W_{2}^{\perp}),\quad W_{2}^{\perp}=J_{2}\oplus (W_{2}\cap W_{2}^{\perp}),\end{align*} $$

then $H_{2}$ and $J_{2}$ are symplectic. Furthermore, V can be decomposed into an $\omega $ -orthogonal direct sum

$$ \begin{align*}V=H_{2}\oplus J_{2}\oplus (H_{2}\oplus J_{2})^{\perp}.\end{align*} $$

Moreover, $W_{2}\cap W_{2}^{\perp }$ is a Lagrangian subspace in $(H_{2}\oplus J_{2})^{\perp }$ .

Note that the above decomposition shows that we can decompose $\omega $ as

$$ \begin{align*}\omega=\omega_{H_{1}}+\omega_{J_{1}}+\omega_{(H_{1}\oplus J_{1})^{\perp}} = \omega_{H_{2}}+\omega_{J_{2}}+\omega_{(H_{2}\oplus J_{2})^{\perp}}.\end{align*} $$

Furthermore, by our assumptions about dimension,

$$ \begin{align*}\dim H_{1}=\dim H_{2}, \dim J_{1}=\dim J_{2}, \dim (W_{1}\cap W_{1}^{\perp})= \dim (W_{2}\cap W_{2}^{\perp}).\end{align*} $$

This implies that, as each direct summand is symplectic, we can find linear maps ${h_{1}:H_{1}\to H_{2}}$ , $h_{2}:J_{1}\to J_{2}$ , and $h_{3}:(H_{1}\oplus J_{1})^{\perp }\to (H_{2}\oplus J_{2})^{\perp }$ so that they satisfy the following:

1. (1) $h_{1}$ maps $\omega _{H_{1}}$ to $\omega _{H_{2}}$ ;

2. (2) $h_{2}$ maps $\omega _{J_{1}}$ to $\omega _{J_{2}}$ ;

3. (3) $h_{3}$ maps $\omega _{(H_{1}\oplus )^{\perp }}$ to $\omega _{(H_{2}\oplus J_{2})^{\perp }}$ .

Furthermore, as $W_{1}\cap W_{1}^{\perp }$ and $W_{2}\cap W_{2}^{\perp }$ are Lagrangians in $(H_{1}\oplus J_{1})^{\perp }$ and $(H_{2}\oplus J_{2})^{\perp }$ , respectively, we can further require that $h_{3}$ satisfies

$$ \begin{align*}h_{3}(W_{1}\cap W_{1}^{\perp})=W_{2}\cap W_{2}^{\perp}.\end{align*} $$

Combining $h_{1},h_{2}$ , and $h_{3}$ , we can find a $h\in \textrm {Sp}(V, \omega )$ such that

$$ \begin{align*}h(H_{1})=H_{2},\quad h(J_{1})=J_{2},\quad h((H_{1}\oplus J_{1})^{\perp})=(H_{2}\oplus J_{2})^{\perp},\quad \textrm{ and}\end{align*} $$

$$ \begin{align*}h(W_{1}\cap W_{1}^{\perp})=W_{2}\cap W_{2}^{\perp}.\end{align*} $$

This implies that $h(W_{1})=W_{2}$ for some $h\in \textrm {Sp}(V,\omega )$ .

Lemma 3.6. With the above notation, let $W_{1}$ and $W_{2}$ be subspaces in V such that $\dim W_{1}+\dim W_{2}=\dim V=2n$ . Then there is a $h\in {\textrm {Sp}}(V,\omega )$ such that ${hW_{1}\cap W_{2}=\{0\}}$ .

Proof. First, we claim that there are subspaces $Y_{1}$ and $Y_{2}$ such that

$$ \begin{align*}Y_{1}\cap Y_{2}=\{0\}, \quad \dim W_{i}=\dim Y_{i}, \quad\textrm{and}\quad \dim (W_{i}\cap W_{i}^{\perp})=\dim (Y_{i}\cap W_{i}^{\perp})\end{align*} $$

for all $i=1,2$ . If we can find such $Y_{1}$ and $Y_{2}$ , then we can prove the lemma using Lemma 3.4 to each $W_{i}$ .

We will find $Y_{1}$ and $Y_{2}$ explicitly. Let

$$ \begin{align*}\dim W_{1}=p, \quad\dim W_{2}=q,\quad \dim(W_{1}\cap W_{1}^{\perp})=r, \quad\textrm{and}\quad \dim(W_{2}\cap W_{2}^{\perp})=s.\end{align*} $$

Note that

$$ \begin{align*}p+q=2n, \max(r,s)\le \min(p,q), \quad\textrm{and}\quad 2|(p-r), 2|(q-s).\end{align*} $$

We may assume that $p\ge q$ without loss of generality.

Case 1: r is even. In this case, $r,s,p$ , and q are all even. Let

$$ \begin{align*} {\mathcal B}_{1}=&\,\{e_{1}^{1},\ldots, e_{(p-r)/2}^{1},e_{1}^{2},\ldots,e_{(q-s)/2}^{2},e_{1}^{3},\ldots, e_{(r+s-2)/2}^{3}\} \cup\{e_{1}^{4}\} \\ &\cup \{f_{1}^{1},\ldots, f_{(p-r)/2}^{1},f_{1}^{2},\ldots,f_{(q-s)/2}^{2},f_{1}^{3},\ldots, f_{(r+s-2)/2}^{3}\}\cup \{f_{1}^{4}\} \end{align*} $$

be a symplectic basis on V that satisfies $\omega (e_{i}^{j},e_{k}^{l})=\omega (f_{i}^{j},f_{k}^{l})=0$ and $\omega (e_{i}^{j},f_{k}^{l})=\delta _{ik}\delta _{jl}$ for all $i,j,k,l$ . We can find $Y_{1}$ and $Y_{2}$ in the claim as follows.

1. (1) Case 1-1.  $r+s \le q+1$ :

   $$ \begin{align*} Y_{1}=&\,\textrm{span}( \{e_{1}^{1},\ldots,e_{(p-r)/2}^{1}\}\cup \{f_{1}^{1},\ldots,f_{(p-r)/2}^{1}\}\cup\{e_{1}^{4}\}\\&\cup \{(e_{(s+1)/2}^{3}+f_{1}^{2}),\ldots, (e_{(r+s-2)/2}^{3}+f_{(r-1)/2}^{2})\}\\& \cup\{(f_{(s+1)/2}^{3}+e_{1}^{2}),\ldots,(f_{(r+s-2)/2}^{3}+e_{(r-1)/2}^{2})\} ),\\Y_{2}=&\,\textrm{span}(\{e_{1}^{2},\ldots, e_{(q-s)/2}^{2}\}\cup \{f_{1}^{2},\ldots, f_{(q-s)/2}^{2}\}\cup\{f_{1}^{4}\}\\&\cup \{(e_{1}^{3}+f_{1}^{1}),\ldots, (e_{(s-1)/2}^{3}+f_{(s-1)/2}^{2})\}\\&\cup \{(f_{1}^{3}+e_{1}^{1}),\ldots, f_{(s-1)/2}^{3}+e_{(s-1)/2}^{1}\}). \end{align*} $$

2. (2) Case 1-2.  $q+1\le r+s \le p+1$ :

   $$ \begin{align*} Y_{1}=&\,\textrm{span}( \{e_{1}^{1},\ldots,e_{(p-r)/2}^{1}\}\cup \{f_{1}^{1},\ldots,f_{(p-r)/2}^{1}\}\cup\{e_{1}^{4}\}\\&\cup \{(e_{(s+1)/2+1}^{3}+f_{1}^{2}),\ldots, (e_{(q-1)/2}^{3}+f_{(q-s)/2}^{2})\}\\& \cup\{(f_{(s+1)/2}^{3}+e_{1}^{2}),\ldots,(f_{(q-1)/2}^{3}+e_{(q-s)/2}^{2})\}\\&\cup \{(e_{(q+1)/2}^{3}+f_{1}^{3}),\ldots,(e_{(r+s-2)/2}^{3}+f_{(r+s-q-1)/2}^{3})\}\\&\cup\{(f_{(q+1)/2}^{3}+e_{1}^{3}),\ldots, (f_{(r+s-2)/2}^{3}+e_{(r+s-q-1)2}^{3})\}),\\Y_{2}=&\,\textrm{span}(\{e_{1}^{2},\ldots, e_{(q-s)/2}^{2}\}\cup \{f_{1}^{2},\ldots, f_{(q-s)/2}^{2}\}\cup\{f_{1}^{4}\}\\&\cup \{(e_{1}^{3}+f_{1}^{1}),\ldots, (e_{(s-1)/2}^{3}+f_{(s-1)/2}^{2})\}\\&\cup \{(f_{1}^{3}+e_{1}^{1}),\ldots, (f_{(s-1)/2}^{3}+e_{(s-1)/2}^{1})\}). \end{align*} $$

3. (3) Case 1-3.  $p+1< r+s$ :

   $$ \begin{align*} Y_{1}=&\,\textrm{span}( \{e_{1}^{1},\ldots,e_{(p-r)/2}^{1}\}\cup \{f_{1}^{1},\ldots,f_{(p-r)/2}^{1}\}\cup\{e_{1}^{4}\}\\&\cup \{(e_{1}^{3}+f_{1}^{2}),\ldots, (e_{(q-s)/2}^{3}+f_{(q-s)/2}^{2})\}\\& \cup\{(f_{1}^{3}+e_{1}^{2}),\ldots,(f_{(q-s)/2}^{3}+e_{(q-s)/2}^{2})\}\\&\cup \{(e_{(q-s+2)/2}^{3}+f_{(q-s+2)/2}^{2}),\ldots, (e_{(2r+s-q-2)/2}^{3}+f_{(2r+s-q-2)/2}^{3})\},\\Y_{2}=&\,\textrm{span}(\{e_{1}^{2},\ldots, e_{(q-s)/2}^{2}\}\cup \{f_{1}^{2},\ldots, f_{(q-s)/2}^{2}\}\cup\{f_{1}^{4}\}\\&\cup \{(e_{(2r+s-q)/2}^{3}+f_{1}^{1}),\ldots, (e^{3}_{(r+s-2)/2}+f_{(q-r)/2}^{1})\})\\&\cup \{(f_{(2r+s-q)/2}^{3}+e_{1}^{1}),\ldots, (f^{3}_{(r+s-2)/2}+e_{(q-r)/2}^{1})\})\\&\cup \{(e_{(q-s+2)/2}^{3}-f_{(q-s+2)/2}^{3}),\ldots, (e_{(2r+s-q-2)/2}^{3}-f_{(2r+s-q-2)/2}^{3})\}). \end{align*} $$

Case 2. r is odd: In this case, $r,s,p$ , and q are all odd. Let

$$ \begin{align*} {\mathcal B}_{2}=&\,\{e_{1}^{1},\ldots, e_{(p-r)/2}^{1},e_{1}^{2},\ldots,e_{(q-s)/2}^{2},e_{1}^{3},\ldots, e_{(r+s)/2}^{3}\} \\&\cup \{f_{1}^{1},\ldots, f_{(p-r)/2}^{1},f_{1}^{2},\ldots,f_{(q-s)/2}^{2},f_{1}^{3},\ldots, f_{(r+s)/2}^{3}\} \end{align*} $$

be a symplectic basis on V that satisfies $\omega (e_{i}^{j},e_{k}^{l})=\omega (f_{i}^{j},f_{k}^{l})=0$ and $\omega (e_{i}^{j},f_{k}^{l})=\delta _{ik}\delta _{jl}$ for all $i,j,k,l$ . We can find $Y_{1}$ and $Y_{2}$ in the claim as follows.

1. (1) Case 2-1.  $r+s \le q$ :

   $$ \begin{align*} Y_{1}=&\,\textrm{span}( \{e_{1}^{1},\ldots,e_{(p-r)/2}^{1}\}\cup \{f_{1}^{1},\ldots,f_{(p-r)/2}^{1}\}\\&\cup \{(e_{(s+2)/2}^{3}+f_{1}^{2}),\ldots, (e_{q/2}^{3}+f_{r/2}^{2})\} \cup\{(f_{(s+2)}^{3}+e_{1}^{2}),\ldots,(f_{q/2}^{3}+e_{r/2}^{2})\} ),\\Y_{2}=&\,\textrm{span}(\{e_{1}^{2},\ldots, e_{(q-s)/2}^{2}\}\cup \{f_{1}^{2},\ldots, f_{(q-s)/2}^{2}\}\\&\cup \{(e_{1}^{3}+f_{1}^{1}),\ldots, (e_{s/2}^{3}+f_{s/2}^{2})\}\cup \{(f_{1}^{3}+e_{1}^{1}),\ldots, f_{s/2}^{3}+e_{s/2}^{1}\}). \end{align*} $$

2. (2) Case 2-2.  $q\le r+s\le p$ :

   $$ \begin{align*} Y_{1}=&\,\textrm{span}( \{e_{1}^{1},\ldots,e_{(p-r)/2}^{1}\}\cup \{f_{1}^{1},\ldots,f_{(p-r)/2}^{1}\}\\&\cup \{(e_{(s+2)/2+1}^{3}+f_{1}^{2}),\ldots, (e_{q/2}^{3}+f_{(q-s)/2}^{2})\}\\& \cup\{(f_{(s+2)/2}^{3}+e_{1}^{2}),\ldots,(f_{q/2}^{3}+e_{(q-s)/2}^{2})\}\\&\cup \{(e_{(q+2)/2}^{3}+f_{1}^{3}),\ldots,(e_{(r+s)/2}^{3}+f_{(r+s-q-1)/2}^{3})\}\\&\cup\{(f_{(q+2)/2}^{3}+e_{1}^{3}),\ldots, (f_{(r+s)/2}^{3}+e_{(r+s-q-1)/2}^{3})\}),\\Y_{2}=&\,\textrm{span}(\{e_{1}^{2},\ldots, e_{(q-s)/2}^{2}\}\cup \{f_{1}^{2},\ldots, f_{(q-s)/2}^{2}\}\\&\cup \{(e_{1}^{3}+f_{1}^{1}),\ldots, (e_{s/2}^{3}+f_{s/2}^{2})\}\\&\cup \{(f_{1}^{3}+e_{1}^{1}),\ldots, (f_{s/2}^{3}+e_{s/2}^{1})\}). \end{align*} $$

3. (3) Case 2-3.  $p\le r+s$ :

   $$ \begin{align*} Y_{1}=&\,\textrm{span}( \{e_{1}^{1},\ldots,e_{(p-r)/2}^{1}\}\cup \{f_{1}^{1},\ldots,f_{(p-r)/2}^{1}\}\\&\cup \{(e_{1}^{3}+f_{1}^{2}),\ldots, (e_{(q-s)/2}^{3}+f_{(q-s)/2}^{2})\}\\& \cup\{(f_{1}^{3}+e_{1}^{2}),\ldots,(f_{(q-s)/2}^{3}+e_{(q-s)/2}^{2})\}\\&\cup \{(e_{(q-s+2)/2}^{3}+f_{(q-s+2)/2}^{2}),\ldots, (e_{(2r+s-q)/2}^{3}+f_{(2r+s-q)/2}^{3})\},\\Y_{2}=&\,\textrm{span}(\{e_{1}^{2},\ldots, e_{(q-s)/2}^{2}\}\cup \{f_{1}^{2},\ldots, f_{(q-s)/2}^{2}\}\\&\cup \{(e_{(2r+s-q)/2}^{3}+f_{1}^{1}),\ldots, (e^{3}_{(r+s-2)/2}+f_{(q-r)/2}^{1})\})\\ &\cup \{(f_{(2r+s-q)/2}^{3}+e_{1}^{1}),\ldots, (f^{3}_{(r+s-2)/2}+e_{(q-r)/2}^{1})\})\\ &\cup \{(e_{(q-s+2)/2}^{3}-f_{(q-s+2)/2}^{3}),\ldots, (e_{(2r+s-q)/2}^{3}-f_{(2r+s-q)/2}^{3})\}). \end{align*} $$

Finally, we can deduce the following corollary from Lemma 3.6.

Corollary 3.7. For any two subspaces $W_{1},W_{2}<V$ , there is an element $h\in \textrm {Sp}(V,\omega )$ such that $hW_{1}$ and $W_{2}$ are in general position. In particular:

1. (1) $hW_{1}\cap W_{2}=0$ if $\dim W_{1}+\dim W_{2}\le 2n$ ;

2. (2) $V=hW_{1}+W_{2}$ if $\dim W_{1}+\dim W_{2} \ge 2n$ .

Proof. Denote $\dim W_{1}=s$ and $\dim W_{2}=k$ .

If $k,s \ge n$ , then we can find n-dimensional subspaces $X_{1}$ and $X_{2}$ such that $X_{1}<W_{1}$ and $X_{2}<W_{2}$ . If $k,s\le n$ , then we can find n-dimensional subspaces $X_{1}$ and $X_{2}$ such that $X_{1}>W_{1}$ and $X_{2}>W_{2}$ . If $k\le n\le s$ and $k+s \ge 2n$ , then we can find n-dimensional subspaces $X_{1}$ and $X_{2}$ such that $X_{1}<W_{1}$ and $X_{2}>W_{2}$ . Finally, if $k\le n\le s$ and ${k+s \le 2n}$ , then we define $X_{1}=W_{2}$ and find a $(2n-k)$ -dimensional subspace $X_{2}$ such that $X_{2}>W_{1}$ . For the $s\le n\le k$ case, we take $X_{1}$ and $X_{2}$ similarly.

In all cases, using Lemmas 3.5 and 3.6, one can find $h\in \textrm {Sp}(V,\omega )$ such that $hX_{1}$ and $X_{2}$ are in general position. This implies that $hW_{1}$ and $W_{2}$ are in general position.

3.2 Properties of SO

Throughout this subsection, let $(V,Q)$ be a $d=2n$ -dimensional vector space V with a quadratic form Q as in the case SO. Recall that we put a basis

$$ \begin{align*} {\mathcal C}=\{x_{1},\ldots, x_{n},y_{1},\ldots, y_{n}\}\end{align*} $$

and a quadratic form

$$ \begin{align*}Q\bigg(\sum_{i=1}^{n}( a_{i}x_{i}+b_{i}y_{i})\bigg)=\sum_{i=1}^{n}a_{i}^{2}-\sum_{i=1}^{n}b_{i}^{2}\end{align*} $$

on V. Also, $\mathrm {SO}(V,Q)$ is denoted by the group of linear isomorphisms on V that preserves Q. The elements of $\mathrm {SO}(V,Q)$ are called an isometry.

For any subspace $W<V$ , we define the signature of the restricted quadratic form $Q|_{W}$ on W as

$$ \begin{align*}\textrm{sign}(W)=(l,p,q)\end{align*} $$

if $Q|_{W}$ admits orthogonal diagonalization

$$ \begin{align*}Q|_{W}\bigg(\sum_{i=1}^{l+p+q} c_{i}z_{i}\bigg)= c_{l+1}^{2}+\cdots+c_{l+p}^{2}-c_{l+p+1}^{2}-\cdots - c_{l+p+q}^{2}\end{align*} $$

for some basis $\{z_{1},\ldots ,z_{l+p+q}\}$ in W. For instance,

$$ \begin{align*}\textrm{sign}(V)=(0,n,n).\end{align*} $$

Note that Sylvester’s law of inertia says that the signature is well defined for every subspace. (See [Jac85, Theorem 6.8].)

Recall that the quadratic form Q gives bilinear symmetric form B on V as

$$ \begin{align*}B(x,y)=Q(x+y)-Q(x)-Q(y)\end{align*} $$

for all $x,y\in V$ . For any subspace W in V, define the orthogonal complement of W as

$$ \begin{align*}W^{\perp}=\{v\in V: B(v,w)=0\textrm{ for all } w\in W\}.\end{align*} $$

The subspace $W\cap W^{\perp }$ is called the radical of W and we will denote $\textrm {rad}(W)=W\cap W^{\perp }$ .

Also, we denote orthogonal direct sum of two subspaces $W_{1}$ and $W_{2}$ in V as

$$ \begin{align*}W_{1}\oplus W_{2}=W_{1}\perp W_{2}\end{align*} $$

when $B(w_{1},w_{2})=0$ for all $w_{1}\in W_{1}$ and $w_{2}\in W_{2}$ . The following lemma characterizes possible signatures.

Lemma 3.8. Let $W<V$ be a subspace of V. Let $\mathrm {sign}(W)=(l,p,q)$ . Then:

1. (1) $l+p\le n$ , $l+q\le n$ ; and

2. (2) $\dim W=l+p+q$ .

Conversely, assume that a triple of numbers $(l,p,q)$ satisfies $l,p,q \ge 0$ , $l+p\le n$ , $l+q \le n$ , and $l+p+q \le 2n$ . Then we can find a subspace W in V such that $\mathrm {sign}(W)=(l,p,q)$ .

Proof. Let $W<V$ be a subspace with $\mathrm {sign}(W)=(l,p,q)$ . If $l=0$ and $p>n$ , then we can find $(n+1)$ linearly independent vectors $w_{1},\ldots , w_{n+1}\in W$ such that $Q(w_{i})=1$ . However, as $\mathrm {sign}(V)=(0,n,n)$ , this gives a contradiction. The same arguments hold for q.

When $l \ge 1$ , the radical of W is non-tirvial. Let $r=\dim (W\cap W^{\perp })\ge 1$ . Fix a basis $\{w_{1},\ldots , w_{r}\}$ of $\textrm {rad}(W)$ . Write $W=W'\oplus \textrm {rad}(W)$ for some $W'$ . Then we can find a subspace U and a basis $z_{1},\ldots , z_{r}$ of U satisfies the following conditions (see [Jac85, Theorem 6.11]):

1. (1) the restricted quadratic form $Q|_{W\oplus U}$ is non-degenerate;

2. (2) $\dim \textrm {rad}(W)=\dim U=r$ ;

3. (3) for each $i\in \{1,\ldots ,r\}$ , a pair $(z_{i},w_{i})$ spans hyperbolic plane $H_{i}$ , and

   $$ \begin{align*}W\oplus U=W'\perp H_{1}\perp\cdots \perp H_{r}.\end{align*} $$

Recall that a two-dimensional subspace is called a hyperbolic plane if the restriction of Q on it is non-degenerate and it contains a vector u so that $Q(u)=0$ . This implies that

$$ \begin{align*}\mathrm{sign}(W\oplus U)= (0,l+p,l+q).\end{align*} $$

As $W\oplus U$ is a subspace of V, the arguments for the $l=0$ case can be applied for $W\oplus U$ so that we can deduce $l+p, l+q \le n$ .

Conversely, if we have triple numbers $(l,p,q)$ as in the statement, then we can just take subspace W as

$$ \begin{align*}W=\textrm{span}\{x_{1}+y_{1},\ldots, x_{l}+y_{l},x_{l+1},\ldots, x_{l+p},y_{l+1},\ldots, y_{l+q}\}.\end{align*} $$

The next lemma says that if two subspaces have the same signature, then we can find an element in $\mathrm {SO}(V,Q)$ so that it transforms one subspace to the other subspace.

Lemma 3.9. For any two subspaces $W_{1}, W_{2}<V$ , if

$$ \begin{align*}\mathrm{sign}(W_{1})=\mathrm{sign}(W_{2}),\end{align*} $$

then there is an element $h\in \mathrm {SO}(V,\omega )$ such that

$$ \begin{align*}hW_{1}=W_{2}.\end{align*} $$

Proof. Let $W_{1}$ and $W_{2}$ be subspaces in V with the same signature. As they have the same signature, there is a linear isometry h between $W_{1}$ and $W_{2}$ . Witt’s extension theorem says that h can be extended to an element in $\mathrm { SO}(V,Q)$ . See [Jac85, p. 369]. That means that there is an element $h\in \mathrm {SO}(V,Q)$ such that $hW_{1}=W_{2}$ as we desired.

Next, we see that if there are two subspaces, then we can find subspaces that are in general position with the same signatures respectively.

Lemma 3.10. Assume that $l_{1},p_{1},q_{1}, l_{2}, p_{2},q_{2}\in {\mathbb N}_{>0}$ satisfies the following conditions:

1. (1) $l_{1}+p_{1}, l_{1}+q_{1}\le n$ ;

2. (2) $l_{2}+p_{2}, l_{2}+q_{2}\le n$ ; and

3. (3) $l_{1}+p_{1}+q_{1}+l_{2}+p_{2}+q_{2}=2n$ .

Then there are two subspaces $Y_{1},Y_{2}<V$ such that:

1. (1) $Y_{1}$ and $Y_{2}$ satisfy

   $$ \begin{align*}\mathrm{sign}(Y_{1})=(l_{1},p_{1},q_{1}), \quad \mathrm{sign}(Y_{2})=(l_{2},p_{2},q_{2});\quad\textrm{and}\end{align*} $$

2. (2) $Y_{1}$ and $Y_{2}$ are in general position.

Proof. We fix a basis $ {\mathcal C}=\{x_{1},\ldots , x_{n},y_{1},\ldots , y_{n}\}$ on V such that $Q(x_{i})=1, Q(y_{i})=-1$ for all $i\in \{1,\ldots , n\}$ . We construct $Y_{1}$ and $Y_{2}$ explicitly. Without loss of generality, we need to construct $Y_{1}$ and $Y_{2}$ in the following two cases.

1. (1) Case I. $p_{1}\ge q_{1}$ and $p_{2}\le q_{2}$ .

2. (2) Case II. $p_{1}\le q_{1}$ and $p_{2}\le q_{2}$ .

When $p_{1}\ge q_{1}$ and $p_{2}\ge q_{2}$ , one can change the role of x and y from Case II.

Case I. $p_{1}\ge q_{1}$ and $p_{2}\le q_{2}$ : Without loss of generality, we may assume

$$ \begin{align*}p_{1}-q_{1}\le q_{2}-p_{2}.\end{align*} $$

Indeed, we can change roles of x and y from below for the other case.

Case I-1. $p_{1}+p_{2}, q_{1}+q_{2} \le n$ :

1. (1) if $0\le l_{1}-n+q_{1}+q_{2}, 0\le l_{2}-n+q_{1}+q_{2}$ , then we can take $Y_{1}$ and $Y_{2}$ as

   $$ \begin{align*} Y_{1}&=\textrm{span}\{ x_{p_{1}+p_{2}+1}+y_{q_{1}+1},\ldots, x_{n-l_{2}}+y_{2q_{1}+l_{1}-n+q_{2}}\}\\ &\perp \textrm{span}\{ x_{q_{1}+q_{2}+1}+y_{q_{1}+q_{2}+1},\ldots, x_{n}+y_{n}\}\\ &\perp \underbrace{\textrm{span}\{x_{1},\ldots, x_{q_{1}},x_{q_{1}+p_{2}+1},\ldots, x_{p_{2}+p_{1}}\}}_{\textrm{positive definite}}\\ &\perp \underbrace{\textrm{span}\{y_{1},\ldots, y_{q_{1}}\}}_{\textrm{negative definite}}\\ Y_{2}&= \textrm{span}\{x_{n-l_{2}+1}+y_{1},\ldots, x_{q_{1}+q_{2}}+y_{q_{1}+q_{2}+l_{2}-n}\}\\ &\perp \textrm{span}\{ x_{q_{1}+q_{2}+1}-y_{q_{1}+q_{2}+1},\ldots, x_{n}-y_{n}\}\\ &\perp \underbrace{\textrm{span}\{y_{q_{1}+1},\ldots,y_{p_{2}+q_{2}}\}}_{\textrm{negative definite}}\\ &\perp \underbrace{\textrm{span}\{x_{q_{1}+1},\ldots, x_{q_{1}+p_{2}}\}}_{\textrm{positive definite}}; \end{align*} $$

2. (2) if $l_{1}-n+q_{1}+q_{2}\le 0\le l_{2}-n+q_{1}+q_{2}$ , then we can take $Y_{1}$ and $Y_{2}$ as

   $$ \begin{align*} Y_{1}&=\textrm{span}\{x_{n-(l_{1}-1)}+y_{n-(l_{1}-1)},\ldots, x_{n}+y_{n}\}\\ &\perp\underbrace{\textrm{span}\{x_{q_{1}+p_{2}+1},\ldots, x_{p_{1}+p_{2}},x_{1},\ldots, x_{q_{1}}\}}_{\textrm{positive definite}}\\ &\perp\underbrace{\textrm{span}\{y_{1},\ldots, y_{q_{1}}\}}_{\textrm{negative definite}}\\ Y_{2}&=\textrm{span}\{ x_{p_{1}+p_{2}+1}+y_{1},\ldots, x_{n-l_{1}}+y_{n-(l_{1}+p_{1}+p_{2})}\}\\ &\perp \textrm{span}\{x_{1}+y_{q_{1}+q_{2}+1},\ldots, x_{n-(l_{1}+q_{1}+q_{2})}+y_{n-l_{1}}\}\\ &\perp\textrm{span}\{x_{n-(l_{1}-1)}-y_{n-(l_{1}-1)},\ldots, x_{n}-y_{n}\}\\ &\perp\underbrace{\textrm{span}\{x_{q_{1}+1},\ldots, x_{q_{1}+p_{2}}\}}_{\textrm{positive definite}}\\ &\perp\underbrace{\textrm{span}\{y_{q_{1}+1},\ldots, y_{q_{1}+p_{2}}\}}_{\textrm{negative definite}}; \end{align*} $$

3. (3) if $l_{2}-n+q_{1}+q_{2}\le 0\le l_{1}-n+q_{1}+q_{2}$ , then we can take $Y_{1}$ and $Y_{2}$ as

   $$ \begin{align*} Y_{1}&= \textrm{span}\{x_{n-(l_{2}-1)}+y_{n-(l_{2}-1)},\ldots, x_{n}+y_{n}\}\\ &\perp \textrm{span}\{x_{p_{1}+p_{2}+1}+y_{q_{1}+1},\ldots, x_{n-l_{2}}+y_{n-l_{2}-p_{2}-p_{1}}\}\\ &\perp\textrm{span}\{x_{q_{1}+1}+y_{q_{1}+q_{2}+1},\ldots, x_{n-l_{2}-q_{2}}+y_{n-l_{2}}\}\\ &\perp \underbrace{\textrm{span}\{x_{q_{1}+p_{2}+1},\ldots, x_{p_{1}+p_{2}},x_{1},\ldots, x_{q_{1}}\}}_{\textrm{positive definite}}\\ &\perp \underbrace{\textrm{span}\{y_{1},\ldots, y_{q_{1}}\}}_{\textrm{negative definite}}\\ Y_{2}&=\textrm{span}\{x_{n-(l_{2}-1)}-y_{n-(l_{2}-1)},\ldots, x_{n}-y_{n}\}\\ &\perp \underbrace{\textrm{span}\{x_{q_{1}+1},\ldots, x_{q_{1}+p_{2}}\}}_{\textrm{positive definite}}\\ &\perp \underbrace{\textrm{span}\{y_{q_{1}+1},\ldots, y_{q_{1}+q_{2}}\}}_{\textrm{negative definite}}. \end{align*} $$

Case I-2. $q_{1}+q_{2}\le n\le p_{1}+p_{2}$ : We can take $Y_{1}$ and $Y_{2}$ as

$$ \begin{align*} Y_{1}&=\textrm{span}\{ x_{p_{1}+p_{2}+q_{1}+q_{2}+l_{2}-n+1}+y_{q_{1}+1},\ldots, x_{n}+y_{q_{1}+l_{1}}\}\\ &\perp\underbrace{\textrm{span}\{x_{1},\ldots, x_{q_{1}},x_{q_{1}+p_{2}+1},\ldots, x_{p_{1}+q_{2}}\}}_{\textrm{positive definite}}\\ &\perp \underbrace{\textrm{span} \{y_{1},\ldots, y_{q}\}}_{\textrm{negative definite}}\\ Y_{2}&=\textrm{span}\{x_{p_{1}+p_{2}+q_{1}+q_{2}-n+1}+y_{q_{1}+q_{2}-n+1},\ldots, x_{p_{1}+p_{2}+q_{1}+q_{2}-n+l_{2}}+y_{q_{1}+q_{2}+l_{2}-n}\} \\ &\perp \underbrace{\textrm{span}\{x_{q_{1}+1},\ldots, x_{q_{1}+p_{2}}\}}_{\textrm{positive definite}}\\ &\perp\underbrace{\textrm{span}\{x_{p_{1}+q_{2}+1}+\sqrt{2}y_{1},\ldots, x_{p_{1}+p_{2}+q_{1}+q_{2}-n}+\sqrt{2}y_{q_{1}+q_{2}-n}\}}_{\textrm{negative definite}}\\ &\perp \underbrace{\textrm{span}\{y_{q_{1}+1},\ldots, y_{n}\}}_{\textrm{negative definite}}. \end{align*} $$

Case I-3. $q_{1}+q_{2}\ge n\ge p_{1}+p_{2}$ : one can construct desired $Y_{1}$ and $Y_{2}$ from case I-2 after changing the role of x and y.

Case II. $p_{1}\le q_{1}$ , $p_{2}\le q_{2}$ : without loss of generality, we may assume that $l_{1}\le l_{2}$ . We divide into two cases.

Case II-1. $p_{1}+p_{2}\le n$ :

1. (1) if $n-p_{1}-p_{2}\le l_{1}$ and $n-p_{1}-p_{2}\le l_{2}$ , then we can take $Y_{1}$ and $Y_{2}$ as

   $$ \begin{align*} Y_{1}&=\textrm{span}\{ x_{p_{1}+p_{2}+1}+y_{p_{1}+p_{2}+1},\ldots, x_{n}+y_{n}\}\\ &\perp \textrm{span}\{x_{p_{1}+1}+y_{q_{1}+q_{2}+1},\ldots, x_{p_{1}+l_{1}-n+p_{1}+p_{2}}+y_{q_{1}+q_{2}+l_{1}-n+p_{1}+p_{2}}\}\\ &\perp\underbrace{\textrm{span}\{x_{1},\ldots, x_{p_{1}}\}}_{\textrm{positive definite}}\\ &\perp \underbrace{\textrm{span} \{y_{1},\ldots, y_{q_{1}}\}}_{\textrm{negative definite}}\\ Y_{2}&=\textrm{span}\{x_{p_{1}+p_{2}+1}-y_{p_{1}+p_{2}+1},\ldots, x_{n}-y_{n}\}\\ &\perp\textrm{span}\{x_{1}+y_{q_{1}+q_{2}+l_{1}-n+p_{1}+p_{2}+1},\ldots, x_{l_{2}-n+p_{1}+p_{2}}+y_{p_{1}+p_{2}}\}\\ &\perp\underbrace{\textrm{span}\{x_{p_{1}+1},\ldots, x_{p_{1}+p_{2}}\}}_{\textrm{positive definite}}\\ &\perp\underbrace{\textrm{span}\{y_{q_{1}+1},\ldots, y_{q_{1}+q_{2}}\}}_{\textrm{negative definite}}; \end{align*} $$

2. (2) if $l_{1}\le n-p_{1}-p_{2}\le l_{2}$ , then we can take $Y_{1}$ and $Y_{2}$ as

   $$ \begin{align*} Y_{1}&=\textrm{span}\{x_{n-(l_{1}-1)}+y_{n-(l_{1}-1)},\ldots, x_{n}+y_{n}\}\\ &\perp \underbrace{\textrm{span}\{x_{1},\ldots, x_{p_{1}}\}}_{\textrm{positive definite}}\\ &\perp \underbrace{\textrm{span}\{y_{1},\ldots, y_{q_{1}}\}}_{\textrm{negative definite}}\\ Y_{2}&=\textrm{span}\{x_{n-(l_{1}-1)}-y_{n-(l_{1}-1)},\ldots, x_{n}-y_{n}\}\\ &\perp\textrm{span}\{x_{p_{1}+p_{2}+1}+y_{1},\ldots, x_{n-l_{1}}+y_{n-l_{1}-p_{1}-p_{2}}\}\\ &\perp\textrm{span}\{x_{1}+y_{q_{1}+q_{2}+1},\ldots, x_{n-l_{1}-q_{1}-q_{2}}+y_{n-l_{1}}\}\\ &\perp\underbrace{\textrm{span}\{x_{p_{1}+1},\ldots, x_{p_{1}+p_{2}}\}}_{\textrm{positive definite}}\\ &\perp\underbrace{\textrm{span}\{y_{q_{1}+1},\ldots, y_{q_{1}+q_{2}}\}}_{\textrm{negative definite}}. \end{align*} $$

Case II-2. $p_{1}+p_{2}\ge n$ : we can take $Y_{1}$ and $Y_{2}$ as

$$ \begin{align*} Y_{1}&=\textrm{span}\{x_{p_{1}+1}+y_{p_{1}+p_{2}+q_{1}+q_{2}-n+1},\ldots, x_{l_{1}+p_{1}}+y_{l_{1}+p_{1}+p_{2}+q_{1}+q_{2}-n}\}\\ &\perp\underbrace{\textrm{span}\{x_{1},\ldots,x_{p_{1}}\}}_{\textrm{positive definite}}\\ &\perp\underbrace{\textrm{span}\{y_{1},\ldots, y_{q_{1}}\}}_{\textrm{negative definite}}\\ Y_{2}&=\textrm{span}\{x_{1}+y_{l_{1}+p_{1}+p_{2}+q_{1}+q_{2}-n+1},\ldots, x_{l_{2}}+y_{n}\}\\ &\perp\underbrace{\textrm{span}\{x_{p_{1}+1},\ldots,x_{n}\}}_{\textrm{positive definite}}\\ &\perp\underbrace{\textrm{span}\{\sqrt{2}x_{1}+y_{q_{1}+q_{2}+1},\ldots, \sqrt{2}x_{p_{1}+p_{2}-n}+y_{p_{1}+p_{2}+q_{1}+q_{2}-n}\}}_{\textrm{positive definite}}\\ &\perp\underbrace{\textrm{span}\{y_{q_{1}+1},\ldots, y_{q_{1}+q_{2}}\}}_{\textrm{negative definite}}. \end{align*} $$

The above case by case constructions show that we can find desired subspaces $Y_{1}$ and  $Y_{2}$ .

As a result, we can deduce the following corollary that is analogous to Corollary 3.7. The proof is the same as Corollary 3.7 using Lemmas 3.9 and 3.10 instead of Lemmas 3.5 and 3.6.

Corollary 3.11. For any two subspaces $W_{1},W_{2}<V$ , there is an element $h\in \mathrm {SO}(V,Q)$ such that $hW_{1}$ and $W_{2}$ are in general position. In particular:

1. (1) $hW_{1}\cap W_{2}=0$ if $\dim W_{1}+\dim W_{2}\le 2n$ ;

2. (2) $V=hW_{1}+W_{2}$ if $\dim W_{1}+\dim W_{2} \ge 2n$ .

4 Proof of Theorem 1.5

We follow the notation of Notation 1.2 and the previous sections. Throughout this section, $V={\mathbb R}^{d}$ is the fixed vector space and M is a d-dimensional manifold.

Recall that we identified the fiber of frame bundle P at $x\in M$ with the group of linear isomorphisms $V\to T_{x}M$ .

Let $\alpha \colon \Gamma \to \mathrm {Diff}^{1}(M)$ be a $C^{1}$ action. In Theorem 1.5, we assumed the following hold.

1. (1) There is a $\gamma _{0}\in \Gamma $ so that $\alpha (\gamma _{0})$ admits dominated splitting. We can find continuous $\alpha (\gamma _{0})$ invariant subbundles E and F, some constant $C,\unicode{x3bb}>0$ so that

   $$ \begin{align*}TM=E\oplus F, \quad \frac{\|D_{x}\alpha(\gamma_{0}^{n})(v)\|}{\|D_{x}\alpha(\gamma_{0}^{n})(w)\|}<Ce^{-\unicode{x3bb} n} \quad \text{for all } n>0\end{align*} $$

   for any unit vectors $v\in E$ and $w\in F$ .

2. (2) $\alpha $ is a volume-preserving action, so we have an $\alpha $ invariant probability measure $\mu $ on M that is fully supported.

As in §2.2, let $\pi _{0}$ , $\pi _{1}$ , and $\pi _{2}$ be the trivial, defining, and contragredient representations of G on V, respectively. If $\pi _{1}$ is isomorphic to $\pi _{2}$ , then we assumed $\pi _{1}=\pi _{2}$ after a conjugation. Without loss of generality, in all cases, we also assumed that the image of $\pi _{1}$ and $\pi _{2}$ is the same, $\pi _{1}(G)=\pi _{2}(G)$ , after conjugation. In §2.2, we showed that there is a measurable section $\sigma \colon M\to P$ , measurable map $\iota \colon M\to \{0,1,2\}$ , a compact subgroup $\kappa _{i}\subset \mathrm {GL}(V)$ , and measurable cocycle $K_{i}\colon \Gamma \times \iota ^{-1}(i)\to \kappa _{i}$ for $i=0,1,2$ such that:

1. (1) for $\mu $ almost every $x\in M$ and for every $\gamma \in \Gamma $ ,

   $$ \begin{align*}D_{x}(\gamma)\sigma(x)= \sigma(\alpha(\gamma)(x))\pi_{\iota(x)}(\gamma)K_{\iota(x)}(\gamma,x) \end{align*} $$

   with respect to the measurable framing $\sigma $ ;

2. (2) $\pi _{i}(G)$ commutes with $\kappa _{i}$ for $i=0,1,2$ ;

3. (3) $K_{1}$ , $K_{2}\subset \{\pm I_{V}\}$ .

The proof will be divided into the following steps. In §4.1, we prove that $\iota ^{-1}(0)$ is a $\mu $ -measure zero set using the dominated splitting. This allows us to focus on non-trivial representations $\pi _{1}$ and $\pi _{2}$ . In §4.2, we prove that, after projectivization, the measurable section is the same as the continuous section almost everywhere using a comparison between the measurable data from the superrigidity theorem and the continuous data from dominated splittings. Until this point, every proof works under the existence of a fully supported invariant Borel probability measure $\mu $ assumption instead of a volume-preserving assumption. Under the volume-preserving assumption, we conclude that, for all hyperbolic elements $\gamma \in \Gamma $ , $\alpha (\gamma )$ is an Anosov diffeomorphism. In §4.3, using the Franks–Newhouse theorem in the case of SL and the Brin–Manning theorem in the cases of Sp and SO, we deduce that M is a torus or infra-torus. This gives a proof of Theorem 1.5.

4.1 Nullity of $\iota ^{-1}(0)$

The following lemma says the set $\iota ^{-1}(0)$ is a null set under our assumptions so that we can assume that there is no $\pi _{0}$ and $\kappa _{0}$ .

Lemma 4.1. Under the same notation and assumptions as in Theorem 1.5, we can find a measurable section $\sigma \colon M\to P$ and a measurable map $\iota \colon M\to \{1,2\}$ such that for $\mu $ almost every x, every $\gamma \in \Gamma $ ,

$$ \begin{align*}D_{x}(\alpha(\gamma))\sigma(x)=\pm \sigma(\alpha(\gamma)(x))\pi_{\iota(x)}(\gamma)\end{align*} $$

for $\mu $ almost every $x\in M$ and every $\gamma \in \Gamma $ .

Proof. We fixed a standard inner product on $V={\mathbb R}^{d}$ . To obtain a contradiction, suppose that $\iota ^{-1}(0)$ has positive $\mu $ measure.

As $\pi _{0}$ is the trivial representation, for any $n\ge 0$ and $\mu $ -almost every $x\in \iota ^{-1}(0)$ , we have

(1) $$ \begin{align} D_{x}(\alpha(\gamma_{0}^{n}))\sigma(x)=\sigma(\alpha(\gamma_{0}^{n})(x))K_{0}(\gamma_{0}^{n},x),\end{align} $$

where $K_{0}: \Gamma \times \iota ^{-1}(0)\to \kappa _{0}$ is the compact group valued cocycle.

For any $c>0$ , define

$$ \begin{align*}\mathcal{S}_{c}=\{x\in \iota^{-}(0): x\textrm{ satisfies equation~(1) and } \|\sigma(x)\|, \|\sigma(x)^{-1}\| <c\},\end{align*} $$

where $\|\sigma (x)\|$ is the operator norm of $\sigma (x):V\to T_{x}M$ with respect to standard norm on V and the Riemannian metric on $T_{x}M$ . Note that $\mathcal {S}_{c}\subset M$ is measurable. Since we assumed that $\mu (\iota ^{-1}(0))$ has positive measure, we can find sufficiently large number $C_{0}>0$ such that

$$ \begin{align*}\mu(\mathcal{S}_{C_{0}})>0.\end{align*} $$

Using the Poincaré recurrence theorem for the measure-preserving transformation $\alpha (\gamma _{0})$ , for $\mu $ -almost every $x_{0}\in S_{C_{0}}$ , one can find a sequence $\{n_{k}\}_{k\in {\mathbb N}}\subset {\mathbb N}$ such that:

1. (1) $n_{0}=0$ , $n_{k}\to \infty $ as $k\to \infty $ ;

2. (2) equation (1) holds; and

3. (3) for all $k\ge 0$ ,

   $$ \begin{align*}\|\sigma(\alpha(\gamma_{0}^{n_{k}})(x_{0}))\|<C_{0} \quad\textrm{and}\quad \|\sigma(\alpha(\gamma_{0}^{n_{k}})(x_{0}))^{-1}\|<C_{0}.\end{align*} $$

Fix $x_{0}\in S_{C_{0}}$ and the sequence $\{n_{k}\}$ as above.

For any unit vector $v\in E$ , set $v_{V}=\sigma (x)^{-1}(v)\in V$ . Using equation (1) and the bound of $\sigma $ , we get

$$ \begin{align*}\frac{1}{C_{0}}\|v_{V}\|<\|D_{x_{0}}(\alpha(\gamma_{0}^{n_{k}})(v)\|=\|\sigma(\alpha(\gamma_{0}^{n_{k}})(x_{0}))K_{0}(\gamma_{0}^{n_{k}},x_{0})(v_{V})\|<C_{0}\|v_{V}\|.\end{align*} $$

This implies

$$ \begin{align*}\lim_{k\to\infty}\frac{1}{n_{k}}\ln\|D_{x_{0}}(\alpha(\gamma_{0}^{n_{k}}))(v)\|=0.\end{align*} $$

Similar arguments can be applied for all unit vectors in F so that we have

$$ \begin{align*}\lim_{k\to\infty}\frac{1}{n_{k}}\ln\|D_{x_{0}}(\alpha(\gamma_{0}^{n_{k}}))(v)\|=\lim_{k\to\infty}\frac{1}{n_{k}}\ln\|D_{x_{0}}(\alpha(\gamma_{0}^{n_{k}})(w)\| =0\end{align*} $$

for any unit vector $v\in E_{x_{0}}$ and for all $w\in F_{x_{0}}$ .

However, as $\gamma _{0}\in \Gamma $ admits a dominated splitting, for all $x\in M$ , there is a positive $\unicode{x3bb}>0$ such that

$$ \begin{align*}\bigg[\lim_{k\to\infty}\frac{1}{n_{k}}\ln\|D_{x}(\alpha(\gamma_{0}^{n_{k}}))(v)\|\bigg] -\bigg[\lim_{k\to\infty}\frac{1}{n_{k}}\ln\|D_{x}(\alpha(\gamma_{0}^{n_{k}})(w)\| \bigg]<-\unicode{x3bb}.\end{align*} $$

This gives a contradiction.

4.2 Continuity of the projectivized measurable framing

In this section, we modify and extend ideas in [KLZ96] (see also [BRHW17, §8.3]). We continue to use the same notation as in the previous section. We fixed $V={\mathbb R}^{d}$ and identified the fiber of the frame bundle P over M at x with the set of linear isomorphisms from V to $T_{x}M$ . Let us denote by $\overline {P}$ the projective frame bundle over M. Each fiber is naturally identified with $\operatorname {\mathrm {PGL}}(V)$ . We will use the bracket notation $[-]$ for the projectivization of a linear map.

As we discussed in §2.2, $\pi _{1}$ is not isomorphic to $\pi _{2}$ only in the case of SL. In this case, the measure $\mu $ can be decomposed into $\mu =\mu _{1}+\mu _{2}$ where $\mu _{1}(\iota ^{-1}(1))=1$ and $ \mu _{2}(\iota ^{-1}(2))=1$ unless $\mu =\mu _{1}$ or $\mu =\mu _{2}$ . We denote by $X_{1}$ and $X_{2}$ the support of $\mu _{1}$ and $\mu _{2}$ , respectively. Note that $X_{1}$ and $X_{2}$ are $\alpha (\Gamma )$ invariant compact set with $M=X_{1}\cup X_{2}$ since $\mu $ is fully supported on the compact manifold M. When $\mu =\mu _{1}$ or $\mu =\mu _{2}$ , set $X_{2}=\emptyset $ or $X_{1}=\emptyset $ , respectively. When $\pi _{1}=\pi _{2}$ , set $X_{1}=M$ and $X_{2}=\emptyset $ .

Proposition 4.2. (Continuity of the projectivized measurable framing)

Let G, $\Gamma $ , M, and d be as in Notation 1.2. Let $\alpha \colon \Gamma \to \mathrm {Diff}^{1}(M)$ be a $C^{1}$ action and $\mu $ be a $\alpha (\Gamma )$ invariant fully supported Borel probability measure on M. Assume that there is an element $\gamma \in \Gamma $ such that $\alpha (\gamma )$ admits a dominated splitting. Then, there are continuous sections $ {\mathcal C}_{i}\colon X_{i}\to \overline {P}$ to the projective frame bundle over M on each $X_{i}$ for $i\in \{1,2\}$ such that

$$ \begin{align*}[D_{x}\alpha(\gamma)] {\mathcal C}_{i}(x)= {\mathcal C}_{i}(\alpha(\gamma)(x))[\pi_{i}(\gamma)]\end{align*} $$

for any $x\in X_{i}$ and $\gamma \in \Gamma $ .

Enumerate elements of $\Gamma $ into $\Gamma =\{\gamma _{0},\gamma _{1},\ldots \}$ , where $\gamma _{0}$ is the distinguished element where $\alpha (\gamma _{0})$ admits dominated splitting. Then, for all $\gamma _{j}\in \Gamma $ , $\alpha (\gamma _{j}\gamma _{0}\gamma _{j}^{-1})$ also admits dominated splitting. More precisely, there is $C_{j}>0$ and $\unicode{x3bb}>0$ such that

$$ \begin{align*}TM=E^{j}\oplus F^{j},\quad \frac{\|D_{x}(\alpha(\gamma_{j}\gamma_{0}^{n}\gamma_{j}^{-1}))(v)\|}{\|D_{x}(\alpha(\gamma_{j}\gamma_{0}^{n}\gamma_{j}^{-1}))(w)\|}< C_{j}e^{-\unicode{x3bb}},\end{align*} $$

for all $x\in M$ , unit vectors $ v\in E^{j}, w\in F^{j}$ , and $n\ge 0$ . Note that $E_{j}=\alpha (\gamma _{j})E \textrm { and } F_{j}=\alpha (\gamma _{j})F$ . In particular, $\dim E^{j}$ and $\dim F^{j}$ do not depend on j. Let us denote $\dim E^{j}=s$ and $\dim F^{j}=u$ .

Let $C\colon M\to \overline {P}$ denote the projectivization of the measurable section $\sigma $ in Lemma 4.1. Note that the map C is just measurable a priori. Lemma 4.1 says that the derivative is (measurably) conjugate to the representation $\pi _{1}$ or $\pi _{2}$ up to $\pm I_{V}$ . Therefore, there are non-trivial subspaces $W_{E,1}^{j}, W_{E,2}^{j}, W_{F,1}^{j}$ , and $W_{F,2}^{j}$ in V such that, for $\mu $ -almost every (a.e.) $x\in M$ , we have

$$ \begin{align*}C(x)W_{E,1}^{j}=E_{x}^{j}, \quad C(x)W_{F,1}^{j}=F_{x}^{j} \quad\textrm{for a.e } x\in \iota^{-1}(1)\end{align*} $$

and

$$ \begin{align*}C(x)W_{E,2}^{j}=E_{x}^{j}, \quad C(x)W_{F,2}^{j}=F_{x}^{j} \quad\textrm{for a.e. } x\in \iota^{-1}(2).\end{align*} $$

Furthermore, $W_{E,*}^{j}$ and $W_{F,*}^{j}$ are corresponding subspaces for the dominated splitting of the linear map $\pi _{*}(\gamma _{j}\gamma _{0}\gamma _{j}^{-1})$ on V for $*\in \{1,2\}$ . Therefore, $W_{E,*}^{j}=\pi _{*}(\gamma _{j})W_{E,*}^{0}$ and $W_{F,*}^{j}=\pi _{*}(\gamma _{j})W_{F,*}^{0}$ for any j and $*$ . Note that for all j, we have $\dim W_{E,1}^{j}=\dim W_{E,2}^{j}=s$ and $\dim W_{F,1}^{j}=\dim W_{F,2}^{j}=u.$

Let $\textrm {Gr}(V,s)$ and $\textrm {Gr}(V,u)$ denote the Grassmannian varieties of dimension s and u subspaces in V, respectively. We have the standard algebraic $\mathrm {GL}(V)$ actions on $\textrm {Gr}(V,s)$ and $\textrm {Gr}(V,u)$ .

Lemma 4.3. We can find $m\ge 0$ such that

$$ \begin{align*}\bigcap_{j=0}^{m-1}\mathrm{ Stab}_{\mathrm{GL}(V)}(W_{E,*}^{j})\subset{\mathbb R}^{\times}\cdot\{I_{V}\}\quad\textrm{and}\quad \bigcap_{j=0}^{m-1}\mathrm{ Stab}_{\mathrm{GL}(V)}(W_{F,*}^{j})\subset{\mathbb R}^{\times}\cdot\{I_{V}\}\end{align*} $$

for each $*\in \{1,2\}$ . Here, for a subspace W in V, $\mathrm {Stab}_{\mathrm {GL}(V)}(W)$ is the stabilizer of W in $\mathrm {GL}(V)$ for the linear action on V by $\mathrm {GL}(V)$ . When we define $\mathrm {Stab}_{\operatorname {\mathrm {PGL}}(V)}(W)$ similarly,

$$ \begin{align*}\bigcap_{j=0}^{m-1}\mathrm{Stab}_{\operatorname{\mathrm{PGL}}(V)}(W_{E,*}^{j})= \bigcap_{j=0}^{m-1}\mathrm{Stab}_{\operatorname{\mathrm{PGL}}(V)}(W_{F,*}^{j})=\{[I_{V}]\}.\end{align*} $$

Proof of Lemma 4.3

For simplicity, denote $\mathrm {Stab}$ for $\mathrm {Stab}_{\mathrm {GL}(V)}$ . Define for each $*\in \{1,2\}$ ,

$$ \begin{align*}S_{E,*}=\bigcap_{j=0}^{\infty} \mathrm{ Stab}(W_{E,*}^{j})=\bigcap_{j=0}^{\infty}\mathrm{ Stab}(\pi_{*}(\gamma_{j})W_{E,*}^{0})=\bigcap_{j=0}^{\infty}\pi_{*}(\gamma_{j})\mathrm{ Stab}(W_{E,*}^{0})\pi_{*}(\gamma_{j})^{-1}.\end{align*} $$

We first claim that $S_{E,*}$ is contained in ${\mathbb R}^{\times }\cdot \{I_{V}\}$ . Since $\Gamma $ is Zariski dense in G by Borel density theorem [Bor60], we have

$$ \begin{align*}S_{E,*}=\bigcap_{g \in G}\pi_{*}(g)\mathrm{ Stab}(W_{E,*}^{0})\pi_{*}(g)^{-1}.\end{align*} $$

This implies that $S_{E,*}$ is normalized by $\pi _{*}(G)$ . Note that $S_{E,*}$ is an algebraic group defined over ${\mathbb R}$ as it is defined by intersection of stabilizers of the algebraic action. Recall that for the case SL, we assumed that

$$ \begin{align*}\pi_{1}(G)=\pi_{2}(G)=\mathrm{SL}(V).\end{align*} $$

For the case Sp, as in §2.1, we put the symplectic form $\omega $ on V so that

$$ \begin{align*}\pi_{1}(G)=\pi_{2}(G)=\textrm{Sp}(V,\omega).\end{align*} $$

Finally, for the case SO, as in §2.1, we put the quadratic form Q with signature $(0,n,n)$ on V so that

$$ \begin{align*}\pi_{1}(G)=\pi_{2}(G)=\mathrm{SO}(V,Q).\end{align*} $$

By Lemma 3.1, $S_{E,*}$ contains $\pi _{*}(G)$ or is contained in ${\mathbb R}^{\times }\cdot \{I_{V}\}$ . As $\pi _{*}$ is irreducible, because of dimension considerations, $S_{E,*}$ should be contained in ${\mathbb R}^{\times }\cdot \{I_{V}\}$ . This proves the claim. We can define and argue similarly for $S_{F,*}$ so that we have

$$ \begin{align*}S_{F,*}=\bigcap_{j=0}^{\infty} \mathrm{ Stab}(W_{F,*}^{j})\subset{\mathbb R}^{\times}\cdot\{I_{V}\}.\end{align*} $$

Here, $\mathrm {Stab}(W_{E,*}^{j})$ , $\mathrm {Stab}(W_{F,*}^{j})$ , $S_{E,*}$ , and $S_{F,*}$ are all real algebraic groups as they are defined by the stabilizer or the intersection of stabilizers of the algebraic action. By Noetherian property, in all cases, we can find $m\ge 1$ such that

$$ \begin{align*}S_{E,*}=\bigcap_{j=0}^{m-1}\mathrm{Stab}(W_{E,*}^{j}), \quad S_{F,*}=\bigcap_{j=0}^{m-1}\mathrm{Stab}(W_{F,*}^{j})\end{align*} $$

for each $*\in \{1,2\}$ .

From now on, we fix m as in Lemma 4.3. Let $\textrm {Gr}(s)$ and $\textrm {Gr}(u)$ be the Grassmannian bundle over M that consists of dimension s and u subspaces of the tangent space, respectively. Let $\textrm {Gr}(T_{x}M,s)$ be the fiber of $\textrm {Gr}(s)$ at $x\in M$ . We have the linear action of $\operatorname {\mathrm {PGL}}(T_{x}M)$ on $\textrm {Gr}(T_{x}M,s)^{m}\times \textrm {Gr}(T_{x}M,u)^{m}$ for each $x\in M$ . Recall that we identify the fiber of $\overline {P}$ at x as $\operatorname {\mathrm {PGL}}(T_{x}M)$ . This leads to defining maps $\Phi ^{0}_{*}$ for each $*\in \{1,2\}$ as

$$ \begin{align*}\Phi^{0}_{*}\colon \overline{P} \to ((\textrm{Gr}(s)^{m})\times (\textrm{Gr}(u)^{m}))\end{align*} $$

$$ \begin{align*}\Phi^{0}_{*}(x,[p_{x}])= (x,([p_{x}](W_{E,*}^{0}),\ldots, [p_{x}](W_{E,*}^{m-1})), ([p_{x}](W_{F,*}^{0}), \ldots, [p_{x}](W_{F,*}^{m-1}))).\end{align*} $$

Lemma 4.4. With the above notation, $\Phi ^{0}_{*}$ is a smooth injective local embedding. Furthermore, the inverse map $(\Phi ^{0}_{*})^{-1}$ defined on $\Phi ^{0}_{*}(\overline {P})$ is continuous.

Proof of Lemma 4.4

This appears in [KLZ96, Proof of Lemma 2.3] and [BRHW17, p. 953]. For the convenience of the reader, we sketch the proof here.

Note that $\operatorname {\mathrm {PGL}}(T_{x}M)$ actions on $\textrm {Gr}(T_{x}M,s)$ and $\textrm {Gr}(T_{x}M,u)$ are algebraic, so that the map $\Phi _{*}^{0}$ is an algebraic map between fibers. As $\Phi _{*}^{0}$ is identity on the base, it is smooth.

For linear $\operatorname {\mathrm {PGL}}(V)$ actions on $\textrm {Gr}(V,s)$ and $\textrm {Gr}(V,u)$ , Lemma 4.3 implies that the common stabilizer of $\{W_{E,*}^{j}\}_{j}$ is trivial as well as for the common stabilizer of $\{W_{F,*}^{j}\}_{j}$ . Furthermore, the orbit of $\operatorname {\mathrm {PGL}}(V)$ is locally closed as the action is algebraic. Combining these facts with the inverse function theorem, the map $\Phi ^{0}_{*}$ is injective local embedding and the inverse map is continuous on $\Phi ^{0}_{*}(\overline {P})$ .

Now we are ready to prove Proposition 4.2.

Proof of Proposition 4.2

Recall that we denoted m as in Lemma 4.3.

Define the map

$$ \begin{align*}\tau\colon M\to ((\textrm{Gr}(s)^{m})\times (\textrm{Gr}(u)^{m}))\end{align*} $$

$$ \begin{align*}\tau(x)=(x,(E^{0}_{x},\ldots, E^{m-1}_{x}),(F^{0}_{x},\ldots, F^{m-1}_{x})).\end{align*} $$

As the splitting is continuous, we know that the map $\tau $ is continuous.

Let us denote by $U_{*}$ the image of $\Phi ^{0}_{*}$ for each $*\in \{1,2\}$ and $U=\bigcup _{*\in \{1,2\}}U_{*}$ . We denoted the measurable section $C:M\to \overline {P}$ as the projection of $\sigma $ that comes from Lemma 4.1. For $\mu $ -almost every point $x\in \tau ^{-1}(U)$ , we have

$$ \begin{align*}\tau(x)=\Phi^{0}_{*}(C(x)),\end{align*} $$

where $\iota (x)=*$ . As $\mu $ is fully supported, there is $M^{0}\subset \tau ^{-1}(U)$ so that:

1. (1) $\mu (M^{0})=1$ (in particular, $M^{0}$ is dense in M); and

2. (2) for all $x\in M^{0}$ , we have

   $$ \begin{align*}\tau(x)=\Phi^{0}_{*}(C(x)), \end{align*} $$

   where $\iota (x)=*\in \{1,2\}$ .

First, we claim that $\tau (M)\subset U$ . To get a contradiction, assume that $M\neq \tau ^{-1}(U)$ . Then, for any $x_{0}\in M\setminus \tau ^{-1}(U)$ , we can find a sequence $\{x_{n}\}_{n\in {\mathbb N}}\subset M^{0}$ so that $x_{n}\to x_{0}$ as $n\to \infty $ . We may assume that $\iota (x_{n})=1$ or $2$ for all n after passing to a subsequence. For simplicity of notation, denote $\iota (x_{n})=*$ for all n.

As $x_{n}\in M^{0}$ for any n, we have

$$ \begin{align*}\tau(x_{n})=\Phi^{0}_{*}(C(x_{n})).\end{align*} $$

We use a local trivialization of the fiber bundle P at $x_{0}$ . That is, there is an open neighborhood $ {\mathcal O}$ of $x_{0}$ and a homeomorphism $\varphi \colon {\mathcal O}\times \mathrm {GL}(V) \to P|_{ {\mathcal O}}$ , such that $\varphi (x,\cdot )$ is identity, using the trivialization $T {\mathcal O}\simeq {\mathcal O} \times V$ , for each $x\in {\mathcal O}$ . Here, $\varphi $ induces the trivialization of the projective fiber bundle over $ {\mathcal O}$ as $\overline {\varphi }: {\mathcal O}\times \operatorname {\mathrm {PGL}}(V)\to \overline {P}|_{ {\mathcal O}}$ that is a homeomorphism and the identity map from $\operatorname {\mathrm {PGL}}(V)$ to $\overline {P}_{x}$ for all $x\in {\mathcal O}$ the same as $\varphi $ . Let us denote by $\varphi _{y}$ the linear isomorphism $\varphi _{y}=\varphi (y,\cdot )\colon \mathrm {GL}(V)\to P_{y}$ for $y\in {\mathcal O}$ .

For sufficiently large n, we may assume that $x_{n}\in {\mathcal O}$ . Then we can find sequence $g_{n}\in \mathrm {GL}(V)$ such that:

1. (1) $\{\|g_{n}\|\}_{n\in {\mathbb N}}$ is bounded; and

2. (2) $\overline {\varphi }(x_{n},[g_{n}])=C(x_{n})$ .

Passing to a subsequence, we can find an endomorphism L on V, or equivalently, matrix $L\in M_{V}({\mathbb R})$ so that $g_{n}\to L$ as $n\to \infty $ . If $L\in \mathrm {GL}(V)$ , then using continuity of $\tau $ and $\Phi ^{0}_{*}$ ,

$$ \begin{align*} \tau(x_{0})&=\lim_{n\to\infty}\tau(x_{n})\\ &=\lim_{n\to\infty}\Phi^{0}_{*}(C(x_{n}))=\lim_{n\to\infty}\Phi^{0}_{*}(\overline{\varphi}(x_{n},[g_{n}]))\\ &=\Phi^{0}_{*}(\overline{\varphi}(x_{0},[L])).\end{align*} $$

This contradicts our assumption that $x_{0}\in M\setminus \tau ^{-1}(U)$ . Therefore, $L\notin \mathrm {GL}(V)$ so that we will denote by K and R the non-trivial subspaces

$$ \begin{align*}K=\ker L \quad\textrm{and}\quad R=L(V)\subset V\end{align*} $$

in V.

The following lemma allows us to make $W_{E,*}^{l}$ and $W_{F,*}^{l}$ be in general position with K.

Lemma 4.5. There is a $\gamma _{l}\in \Gamma $ so that

$$ \begin{align*}\pi_{*}(\gamma_{l})W_{E,*}^{0}=W_{E,*}^{l}\quad \textrm{and}\quad \pi_{*}(\gamma_{l})W_{F,*}^{0}=W_{F,*}^{l}\end{align*} $$

are in general position with K.

We will prove Lemma 4.5 later. As a Grassmannian variety is compact, passing to a subsequence, we may assume that

$$ \begin{align*}g_{n}W_{E,*}^{l} \to Q_{E}, \quad g_{n}W_{F,*}^{l}\to Q_{F}\quad \textrm{as } n\to \infty\end{align*} $$

for some $Q_{E}\in \textrm {Gr}(V,s)$ and $Q_{F}\in \textrm {Gr}(V,u)$ .

Let W be the subspace of $V={\mathbb R}^{d}$ which is in general position with respect to K and $g_{n}W$ converges to $W_{0}$ in the appropriate Grassmannian variety. Then, if ${\dim W+\dim K <d}$ , then $W\cap K=\{0\}$ and $W_{0}=\lim _{n\to \infty } g_{n}W=L(W)\subset L(V)=R$ . Otherwise, we have $\dim W+\dim K\ge d$ , in which case, $K+W\simeq V={\mathbb R}^{d}$ , and hence ${W_{0}=\lim _{n\to \infty }g_{n}W \supset L(V)=R}$ . We can apply these arguments to $Q_{E}=\lim _{n\to \infty } g_{n}W_{E,*}^{l}$ and $Q_{F}=\lim _{n\to \infty } g_{n}W_{F,*}^{l}$ since, by Lemma 4.5, $W_{E,*}^{l}$ and $W_{F,*}^{l}$ are in general position with respect to K. Then, either $Q_{E},Q_{F}\subset R$ , $Q_{E}\subset R\subset Q_{F}$ , $Q_{F}\subset R\subset Q_{E}$ , or ${R\subset Q_{E},Q_{F}}$ . In any case, $Q_{E}$ and $Q_{F}$ are not transversal.

Let continuous maps $\tau _{E}\colon M\to \textrm {Gr}(s)$ and $\tau _{F}\colon M\to \textrm {Gr}(u)$ be given by

$$ \begin{align*}\tau_{E}(x)=E_{x}^{l}, \tau_{F}(x)=F_{x}^{l}\end{align*} $$

using the existence of the dominated splitting of $\alpha (\gamma _{l}\gamma _{0}\gamma _{l}^{-1})$ and the continuity of the splitting $T_{x}M=E_{x}^{l}\oplus F_{x}^{l}$ . By construction, we have

$$ \begin{align*}\tau_{E}(x_{n})=\varphi_{x_{n}}^{-1}(g_{n}W_{E,*}^{l}), \tau_{F}(x_{n})=\varphi_{x_{n}}^{-1}(g_{n}W_{F,*}^{l}).\end{align*} $$

Using continuity of $\tau _{E}$ and $\tau _{F}$ , we can deduce that

$$ \begin{align*} \tau_{E}(x_{0})=\varphi_{x_{0}}^{-1}(Q_{E}),\quad \tau_{F}(x_{0})=\varphi_{x_{0}}^{-1}(Q_{F}).\end{align*} $$

In particular, $Q_{E}$ and $Q_{F}$ are transversal since $T_{x}M=E_{x_{0}}^{l}\oplus F_{x_{0}}^{l}$ . This contradicts the fact that $Q_{E}$ and $Q_{F}$ are not transversal. Therefore, if $x\in M$ is the limit of a sequence $\{x_{n}\}_{n=1}^{\infty }\subset \iota ^{-1}(i)\cap M^{0}$ , then $\tau (x)\in U_{i}$ for all $i\in \{1,2\}$ . As M is connected, we prove that $M=\tau ^{-1}(U)$ .

Recall that $\mu $ can be decomposed into $\mu =\mu _{1}+\mu _{2}$ , where $\mu _{1}(\iota ^{-1}(1))=1$ , $\mu _{2}(\iota ^{-1}(2))=1$ unless $\mu =\mu _{1}$ or $\mu =\mu _{2}$ . We denoted $X_{1}$ and $X_{2}$ by the support of $\mu _{1}$ and $\mu _{2}$ , respectively. As $\mu $ is fully supported, $M=X_{1}\cup X_{2}$ .

Define the map $ {\mathcal C}_{1}:X_{1}\to \overline {P}$ and $ {\mathcal C}_{2}:X_{2}\to \overline {P}$ ,

$$ \begin{align*} {\mathcal C}_{1}(x)=(\Phi_{1}^{0})^{-1}\circ \tau (x), \quad {\mathcal C}_{2}(y)=(\Phi_{2}^{0})^{-1}\circ \tau(y)\end{align*} $$

for all $x\in X_{1}$ or $y\in X_{2}$ , respectively. In the above discussions, we proved not only ${M=\tau ^{-1}(U)}$ but also $ {\mathcal C}_{1}$ and $ {\mathcal C}_{2}$ is well defined on $X_{1}$ and $X_{2}$ , respectively. Furthermore, $ {\mathcal C}_{1}$ and $ {\mathcal C}_{2}$ are continuous by Lemma 4.4 and

$$ \begin{align*}C(x)= {\mathcal C}_{1}(x)=(\Phi_{1}^{0})^{-1}\circ\tau(x),\end{align*} $$

$$ \begin{align*}C(y)= {\mathcal C}_{2}(y)=(\Phi_{2}^{0})^{-1}\circ\tau(y)\end{align*} $$

for all $x\in \iota ^{-1}(1)\cap M^{0}$ and $y\in \iota ^{-1}(2)\cap M^{0}$ . Therefore,

$$ \begin{align*}[D_{x}\alpha(\gamma)] {\mathcal C}_{i}(x)= {\mathcal C}_{i}(\alpha(\gamma)(x))[\pi_{i}(\gamma)]\end{align*} $$

for all $\gamma \in \Gamma $ , for all $x\in X_{i}$ , and for all $i\in \{1,2\}$ . This proves the proposition.

We prove Lemma 4.5 here.

Proof of Lemma 4.5

Note that

$$ \begin{align*}U_{E,*}=\{g\in \pi_{*}(G): gW_{E,*}^{0} \textrm{ is in general position with }K\}, \end{align*} $$

and

$$ \begin{align*}U_{F,*}=\{g\in \pi_{*}(G): gW_{F,*}^{0} \textrm{ is in general position with }K\}\end{align*} $$

are Zariski open subsets for any $*\in \{1,2\}$ .

In the case of SL, as $\mathrm {SL}(V)$ acts transitively on $\textrm {Gr}(s)$ and $\textrm {Gr}(u)$ , $U_{E,*}$ and $U_{F,*}$ are non-empty Zariski open subsets. Therefore, the intersection $U_{E,*}\cap U_{F,*}$ is also a non-empty Zariski open subset as $\mathrm {SL}(V)$ is an irreducible variety. As $\Gamma $ is Zariski dense in G, by the Borel density theorem, we can find $\gamma _{l}\in \Gamma $ so that $\pi _{*}(\gamma _{l})W_{E,*}^{0}=W_{E,*}^{l}$ and $\pi _{*}(\gamma _{l})W_{F,*}^{0}=W_{F,*}^{l}$ are in general position with K.

In the cases of Sp and SO, using Corollaries 3.7 and 3.11, respectively, we have

$$ \begin{align*}U_{E,*}=\{g\in \pi_{*}(G): gW_{E,*}^{0} \textrm{ is in general position with }K\}\neq\emptyset. \end{align*} $$

Therefore, $U_{E,*}^{0}$ is non-empty Zariski open in $\pi _{*}(G)$ . Similarly,

$$ \begin{align*}U_{F,*}=\{g\in \pi_{*}(G): gW_{F,*}^{0} \textrm{ is in general position with }K\}\end{align*} $$

is a non-empty Zariski open subset in $\pi _{*}(G)$ . Using irreducibility of $\pi _{*}(G)$ , we know that $U_{E,*}^{0}\cap U_{F,*}^{0}$ is also a non-empty Zariski open subset. Again using the fact that $\Gamma $ is Zariski dense in G, there is $\gamma _{l}\in \Gamma $ such that $\pi _{*}(\gamma _{l})W_{E,*}^{0}=W_{E,*}^{l}$ and $\pi _{*}(\gamma _{l})W_{F,*}^{0}=W_{F,*}^{l}$ are in general position with K.

Now, using the volume-preserving assumption, we can find lots of Anosov diffeomorphims. Recall that, using Theorem 3.2, we can find a finite index subgroup $\Gamma _{0}$ in $\Gamma $ and a maximal ${\mathbb R}$ -split torus A in G such that $ {\mathcal A}=A\cap \Gamma _{0}$ is a cocompact lattice in A.

Proposition 4.6. (Abundance of Anosov diffeomorphisms)

Let G, $\Gamma $ , M, and d be as in Notation 1.2. Let $\alpha \colon \Gamma \to \mathrm {Diff}^{1}_{\mathrm {Vol}}(M)$ be a $C^{1}$ volume-preserving action. Assume that there is $\gamma _{0}\in \Gamma $ such that $\alpha (\gamma _{0})$ admits dominated splitting. Then every hyperbolic element $\gamma \in \Gamma $ , especially $\gamma \in {\mathcal A}$ , is an Anosov diffeomorphism.

Proof. Using Proposition 4.2 for the measure with positive density, we can find continuous sections to projective frame bundle over M on each $X_{i}$ , $ {\mathcal C}_{i}\colon X_{i}\to \overline {P}$ for $i\in \{1,2\}$ such that

$$ \begin{align*}[D_{x}\alpha(\gamma)] {\mathcal C}_{i}(x)= {\mathcal C}_{i}(\alpha(\gamma)(x))[\pi_{i}(\gamma)]\end{align*} $$

for any $x\in X_{i}$ and $\gamma \in \Gamma $ . As we assumed $\alpha (\Gamma )$ preserves volume, for any $\gamma \in \Gamma $ and for each $i\in \{1,2\}$ , there is a continuous map $\widetilde { {\mathcal C}_{i}}:X_{i}\to [P/\{\pm I\}]|_{X_{i}}$ such that for all $x\in X_{i}$ ,

(2) $$ \begin{align} D_{x}\alpha(\gamma)\widetilde{ {\mathcal C}_{i}}(x)= \widetilde{ {\mathcal C}_{i}}(\alpha(\gamma)(x))\pi_{i}(\gamma).\end{align} $$

Here, we use the facts that the Jacobian determinant of $D_{x}\alpha (\gamma )$ is $\pm 1$ and the determinant of $\pi _{i}(\gamma )$ is always $1$ .

For any hyperbolic element $\gamma \in \Gamma $ , denote $E_{\pi _{1}(\gamma )}^{s}$ and $E_{\pi _{1}(\gamma )}^{u}$ by the direct sum of generalized eigenspaces corresponding to an eigenvalue less than $1$ and bigger than $1$ of $\pi _{1}(\gamma )$ , respectively. Here, $E_{\pi _{2}(\gamma )}^{u}$ and $E_{\pi _{2}(\gamma )}^{u}$ can be defined similarly. We have decomposition

$$ \begin{align*}V=E_{\pi_{1}(\gamma)}^{s}\oplus E_{\pi_{1}(\gamma)}^{u}=E_{\pi_{2}(\gamma)}^{s}\oplus E_{\pi_{2}(\gamma)}^{u}\end{align*} $$

with respect to $\pi _{1}(\gamma )$ and $\pi _{2}(\gamma )$ , respectively. Then, we can define a splitting

$$ \begin{align*}T_{x}M|_{X_{1}}= {\mathcal C}_{1}E_{\pi_{1}(\gamma)}^{s}\oplus {\mathcal C}_{1}E_{\pi_{1}(\gamma)}^{u},\end{align*} $$

$$ \begin{align*}T_{x}M|_{X_{2}}= {\mathcal C}_{2}E_{\pi_{2}(\gamma)}^{s}\oplus {\mathcal C}_{2}E_{\pi_{2}(\gamma)}^{u}\end{align*} $$

which is continuous on $X_{1}$ and $X_{2}$ , respectively.

Using equation (2), we know that exponential growth of $D_{x}\alpha (\gamma ^{n})$ and $\pi _{i}(\gamma ^{n})$ is compatible so that there are constants $C'>0$ , $0<\unicode{x3bb} <1$ such that

$$ \begin{align*}\|D_{x}\alpha(\gamma^{n})v_{i}^{s}\|<C'\unicode{x3bb}^{n}, \quad \|D_{x}\alpha(\gamma^{-n})v_{i}^{u}\|<C'\unicode{x3bb}^{n}\end{align*} $$

for all $x\in X_{i}$ , $v_{i}^{s}\in {\mathcal C}_{i}E_{\pi _{i}(\gamma )}^{s}$ , $v_{i}^{u}\in {\mathcal C}_{i}E_{\pi _{i}(\gamma )}^{u}$ , and $n>0$ . This shows that $\alpha (\gamma )$ is an Anosov diffeomorphism.

Remark 4.7. The proof shows that the dimension of stable distribution for $\alpha (\gamma )$ is the same as the dimension of $E_{\pi _{1}(\gamma )}^{s}$ or $E_{\pi _{2}(\gamma )}^{s}$ . The same holds for the unstable distribution.

Remark 4.8. As the referee pointed out, even if we assumed the existence of a fully supported invariant Borel probability measure instead of the volume-preserving assumption for instance, we still conclude the following with the similar argument with the proof of Proposition 4.6. Under the same assumptions, let $\gamma \in \Gamma $ be an element so that, in the standard representation, it has simple eigenvalues. That is, it is $\mathbb {C}$ diagonalizable and every eigenspace is a one-dimensional subspace. Then, $\alpha (\gamma )$ admits a fine dominated splitting into one-dimensional distributions.

4.3 Characterizing the manifold M

We characterize M in this subsection. We prove that M is a torus or a flat manifold in the cases of SL, Sp, and SO under the assumptions in the theorem.

4.3.1 Case SL

Theorem 3.2 implies that there is a subgroup $\Gamma _{0}$ and a maximal ${\mathbb R}$ -split torus A such that $ {\mathcal A}=A\cap \Gamma _{0}\simeq {\mathbb Z}^{n-1}$ is a lattice in $A\simeq {\mathbb R}^{n-1}$ . Up to conjugacy, we may assume that the maximal ${\mathbb R}$ -split torus A in the Theorem 3.2 is of the form:

$$ \begin{align*}A=\{\textrm{diag}(e^{\unicode{x3bb}_{1}},\ldots,e^{\unicode{x3bb}_{n}})\colon \unicode{x3bb}_{1},\ldots,\unicode{x3bb}_{n}\in{\mathbb R}, \unicode{x3bb}_{1}+\cdots+\unicode{x3bb}_{n}=0\}.\end{align*} $$

We define a one-parameter subgroup $\{a_{\unicode{x3bb} }\}=\{\textrm {diag}(e^{(n-1)\unicode{x3bb} },e^{-\unicode{x3bb} },\ldots ,e^{-\unicode{x3bb} }):\unicode{x3bb} \in {\mathbb R}\}$ which makes a line in $A\simeq \mathbb {R}^{n-1}$ .

We know that in the torus $A/ {\mathcal A}\simeq {\mathbb R}^{n-1}/{\mathbb Z}^{n-1}$ , the image of irrational line is dense. Therefore, there are elements of $ {\mathcal A}\simeq {\mathbb Z}^{n-1}$ either on the line $\{a_{\unicode{x3bb} }\}$ (when the line is rational) or arbitrarily close to it (when the line is irrational). This implies that we can find $\gamma \in {\mathcal A}=A\cap \Gamma _{0}$ such that $\gamma $ is a semisimple hyperbolic element such that every eigenvalue is a positive real number and only one eigenvalue is bigger than $1$ . Proposition 4.6 implies that $\alpha (\gamma )$ is a codimension one Anosov diffeomorphism. Therefore, the manifold M is homeomorphic to the torus due to the Franks–Newhouse Theorem 2.2. This proves Theorem 1.5 in the case of SL.

4.3.2 Cases Sp and SO

Up to conjugacy, we may assume that the maximal ${\mathbb R}$ -split torus A in the Theorem 3.2 is of the form:

$$ \begin{align*}A=\{\textrm{diag}(e^{\unicode{x3bb}_{1}},\ldots,e^{\unicode{x3bb}_{n}}, e^{-\unicode{x3bb}_{n}},\ldots,e^{-\unicode{x3bb}_{1}})\colon \unicode{x3bb}_{1},\ldots,\unicode{x3bb}_{n}\in{\mathbb R}_{\ge0} \}.\end{align*} $$

We can give a metric on A so that A is isometric to ${\mathbb R}^{n}$ using the similar argument as in the case of SL.

For each positive real number $\unicode{x3bb} \in {\mathbb R}_{>0}$ , define an element $a_{\unicode{x3bb} }\in A$ as

$$ \begin{align*}a_{\unicode{x3bb}}=\textrm{diag}(\underbrace{\unicode{x3bb},\ldots, \unicode{x3bb}}_{n},\underbrace{\unicode{x3bb}^{-1},\ldots, \unicode{x3bb}^{-1}}_{n}).\end{align*} $$

Again, note that $ {\mathcal A}=A\cap \Gamma _{0}\simeq {\mathbb Z}^{n}$ is a lattice in $A\simeq {\mathbb R}^{n}$ . Using the same arguments as above, there are elements of $ {\mathcal A}\simeq {\mathbb Z}^{n}$ either on the line $\{a_{\unicode{x3bb} }\}$ or arbitrarily close to it. Therefore, we can find $\gamma \in {\mathcal A}=A\cap \Gamma _{0}$ such that eigenvalues $e^{\unicode{x3bb} _{1}}>e^{\unicode{x3bb} _{2}}>\cdots >e^{\unicode{x3bb} _{n}}>1>e^{-\unicode{x3bb} _{n}}>\cdots >e^{-\unicode{x3bb} _{1}}$ of $\gamma \in \Gamma _{0}$ satisfy the inequality

$$ \begin{align*}1+\frac{\unicode{x3bb}_{n}}{\unicode{x3bb}_{1}}>\frac{\unicode{x3bb}_{1}}{\unicode{x3bb}_{n}},\quad1+\frac{\unicode{x3bb}_{n}}{\unicode{x3bb}_{1}}>\frac{\unicode{x3bb}_{1}}{\unicode{x3bb}_{n}}\end{align*} $$

as the above inequality holds if all $\unicode{x3bb} _{i}$ are close to each other.

For such $\gamma \in \Gamma _{0}$ , Proposition 4.6 says that $\alpha (\gamma )$ is an Anosov diffeomorphism. Furthermore, the above inequalities show that it satisfies conditions in the Brin–Manning Theorem 2.3. Therefore, M is homeomorphic to a torus or a flat manifold. In particular, there is a finite cover $M_{0}$ of M so that $M_{0}$ is homeomorphic to a torus. This proves Theorem 1.5 in the cases of Sp and SO.

5 Proof of Corollary 1.8

In this section, we prove Corollary 1.8, topological rigidity and smooth rigidity. Retaining the notation in the Corollary 1.8, Theorem 1.5 says that there is a finite cover $M_{0}$ of M, so that $M_{0}$ is homeomorphic to the d-dimensional torus ${\mathbb T}^{d}={\mathbb R}^{d}/{\mathbb Z}^{d}$ . Recall that we assumed that there is a finite index subgroup $\Gamma _{0}<\Gamma $ such that we can lift $\Gamma _{0}$ action to $M_{0}$ .

To see that there is a $C^{0}$ conjugacy, we will use the theorems in [BRHW17] for $M_{0}$ . We denote the lifted $\Gamma _{0}$ action on $M_{0}$ as $\alpha _{1}$ . Note that $\Gamma _{0}$ is still a lattice in G. We can find a hyperbolic element $\gamma \in \Gamma _{0}$ . As we assumed the action is volume preserving, there is a fully supported Borel probability measure $\mu _{0}$ on $M_{0}$ that is preserved by $\alpha _{1}(\Gamma _{0})$ . The [BRHW17, Proposition 9.7] implies that the action $\alpha _{1}$ lifts to the universal cover of $\widetilde {M}$ . Using [BRHW17, Theorem 1.3], we can deduce that there is finite index subgroup $\Gamma _{1}<\Gamma _{0}$ so that $\alpha _{1}|_{\Gamma _{1}}$ is topologically conjugate to its linear data $\rho _{1}$ of $\alpha _{1}$ . Indeed, the $\alpha _{1}(\gamma )$ is an Anosov diffeomorphism so that we have topological conjugacy h, that is,

$$ \begin{align*}\rho_{1}(\gamma)\circ h=h\circ \alpha_{1}(\gamma)\end{align*} $$

for all $\gamma \in \Gamma _{1}$ . This proves that there is a $C^{0}$ conjugacy between $\alpha _{1}$ and $\rho _{1}$ as in Corollary 1.8.

Remark 5.1. After we know that the $M_{0}$ is homeomorphic to the torus and the action lifts to the universal cover, one can also use [MQ01, Theorem 1.3] to get a topological conjugacy.

For the smooth conjugacy, we need to use the theorems in [RHW14]. Now, we assumed $\alpha $ is $C^{\infty }$ . We will prove the $C^{0}$ conjugacy that we already found as above is indeed smooth. We know that for every non-identity hyperbolic element in $\gamma \in \Gamma _{2}$ , $\alpha _{1}(\gamma )$ is an Anosov diffeomorphism. Again, using [PR01], we can find free abelian subgroup Z of rank $2$ in $\Gamma _{2}$ such that every non-identity element $z\in Z$ is hyperbolic. This implies that the linear data $\rho _{1}|_{Z}$ does not have rank one factor. (See [RHW14, Lemma 2.9].) So we can deduce that the h is indeed smooth due to [FKS13] or [RHW14]. This proves smoothness of the conjugacy so that completes the proof of Corollary 1.8.