 $3$-manifolds: the surgeries and the foliations
$3$-manifolds: the surgeries and the foliationsPublished online by Cambridge University Press: 27 April 2022
Every Anosov flow on a 3-manifold is associated to a bifoliated plane (a plane endowed with two transverse foliations
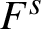 $F^s$
and
$F^s$
and
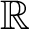 $F^u$
) which reflects the normal structure of the flow endowed with the center-stable and center-unstable foliations. A flow is
$F^u$
) which reflects the normal structure of the flow endowed with the center-stable and center-unstable foliations. A flow is
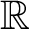 $\mathbb{R}$
-covered if
$\mathbb{R}$
-covered if
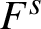 $F^s$
(or equivalently
$F^s$
(or equivalently
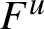 $F^u$
) is trivial. On the other hand, from any Anosov flow one can build infinitely many others by Dehn–Goodman–Fried surgeries. This paper investigates how these surgeries modify the bifoliated plane. We first observe that surgeries along orbits corresponding to disjoint simple closed geodesics do not affect the bifoliated plane of the geodesic flow of a hyperbolic surface (Theorem 1). Analogously, for any non-
$F^u$
) is trivial. On the other hand, from any Anosov flow one can build infinitely many others by Dehn–Goodman–Fried surgeries. This paper investigates how these surgeries modify the bifoliated plane. We first observe that surgeries along orbits corresponding to disjoint simple closed geodesics do not affect the bifoliated plane of the geodesic flow of a hyperbolic surface (Theorem 1). Analogously, for any non-
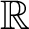 $\mathbb{R}$
-covered Anosov flow, surgeries along pivot periodic orbits do not affect the branching structure of its bifoliated plane (Theorem 2). Next, we consider the set
$\mathbb{R}$
-covered Anosov flow, surgeries along pivot periodic orbits do not affect the branching structure of its bifoliated plane (Theorem 2). Next, we consider the set
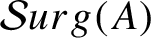 $\mathcal{S}urg(A)$
of Anosov flows obtained by Dehn–Goodman–Fried surgeries from the suspension flow
$\mathcal{S}urg(A)$
of Anosov flows obtained by Dehn–Goodman–Fried surgeries from the suspension flow
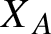 $X_A$
of any hyperbolic matrix
$X_A$
of any hyperbolic matrix
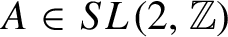 $A \in SL(2,\mathbb{Z})$
. Fenley proved that performing only positive (or negative) surgeries on
$A \in SL(2,\mathbb{Z})$
. Fenley proved that performing only positive (or negative) surgeries on
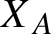 $X_A$
leads to
$X_A$
leads to
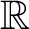 $\mathbb{R}$
-covered Anosov flows. We study here Anosov flows obtained by a combination of positive and negative surgeries on
$\mathbb{R}$
-covered Anosov flows. We study here Anosov flows obtained by a combination of positive and negative surgeries on
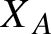 $X_A$
. Among other results, we build non-
$X_A$
. Among other results, we build non-
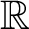 $\mathbb{R}$
-covered Anosov flows on hyperbolic manifolds. Furthermore, we show that given any flow
$\mathbb{R}$
-covered Anosov flows on hyperbolic manifolds. Furthermore, we show that given any flow
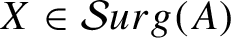 $X\in \mathcal{S}urg(A)$
there exists
$X\in \mathcal{S}urg(A)$
there exists
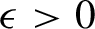 $\epsilon>0$
such that every flow obtained from
$\epsilon>0$
such that every flow obtained from
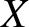 $X$
by a non-trivial surgery along any
$X$
by a non-trivial surgery along any
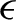 $\epsilon$
-dense periodic orbit
$\epsilon$
-dense periodic orbit
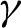 $\gamma$
is
$\gamma$
is
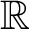 $\mathbb{R}$
-covered (Theorem 4). Analogously, for any flow
$\mathbb{R}$
-covered (Theorem 4). Analogously, for any flow
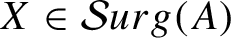 $X \in \mathcal{S}urg(A)$
there exist periodic orbits
$X \in \mathcal{S}urg(A)$
there exist periodic orbits
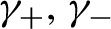 $\gamma_+,\gamma_-$
such that every flow obtained from
$\gamma_+,\gamma_-$
such that every flow obtained from
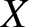 $X$
by surgeries with distinct signs on
$X$
by surgeries with distinct signs on
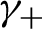 $\gamma_+$
and
$\gamma_+$
and
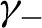 $\gamma_-$
is non-
$\gamma_-$
is non-
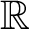 $\mathbb{R}$
-covered (Theorem 5).
$\mathbb{R}$
-covered (Theorem 5).