Hostname: page-component-77c89778f8-5wvtr Total loading time: 0 Render date: 2024-07-21T09:12:13.632Z Has data issue: false hasContentIssue false
  • English
  • Français

Mœglin’s theorem and Goldie rank polynomials in Cartan type A

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  09 November 2011

Jonathan Brundan
Jonathan Brundan*
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR 97403, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

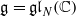We use the theory of finite W-algebras associated to nilpotent orbits in the Lie algebra to give another proof of Mœglin’s theorem about completely prime primitive ideals in the enveloping algebra U(𝔤). We also make some new observations about Joseph’s Goldie rank polynomials in Cartan type A.

Keywords

primitive idealsfinite W-algebrasGoldie rank polynomials

MSC classification

Secondary: 17B35: Universal enveloping (super)algebras
Type
Research Article
Information
Compositio Mathematica , Volume 147 , Issue 6 , November 2011 , pp. 1741 - 1771
Copyright
Copyright © Foundation Compositio Mathematica 2011

References

[BB81]Beilinson, A. and Bernstein, J., Localisation de 𝔤-modules, C. R. Acad. Sci. Paris Ser. I Math. 292 (1981), 15–18.Google Scholar
[BG10]Brown, J. and Goodwin, S., Finite dimensional representations for finite W-algebras associated to even multiplicity nilpotent orbits in classical Lie algebras, arXiv:1009.3869.Google Scholar
[BG07]Brundan, J. and Goodwin, S., Good grading polytopes, Proc. Lond. Math. Soc. 94 (2007), 155–180.CrossRefGoogle Scholar
[BGK08]Brundan, J., Goodwin, S. and Kleshchev, A., Highest weight theory for finite W-algebras, Int. Math. Res. Not. 2008 (2008), doi:10.1093/imrn/rnn051.CrossRefGoogle Scholar
[BK06]Brundan, J. and Kleshchev, A., Shifted Yangians and finite W-algebras, Adv. Math. 200 (2006), 136–195.CrossRefGoogle Scholar
[BK08a]Brundan, J. and Kleshchev, A., Representations of shifted Yangians and finite W-algebras, Mem. Amer. Math. Soc. 196 (2008).Google Scholar
[BK08b]Brundan, J. and Kleshchev, A., Schur–Weyl duality for higher levels, Selecta Math. 14 (2008), 1–57.CrossRefGoogle Scholar
[BK81]Brylinksi, J.-L. and Kashiwara, M., Kazhdan–Lusztig conjecture and holonomic systems, Invent. Math. 64 (1981), 387–410.Google Scholar
[CD77]Conze-Berline, N. and Duflo, M., Sur les représentations induites des groupes semi-simples complexes, Compositio Math. 34 (1977), 307–336.Google Scholar
[dVvD95]de Vos, K. and van Driel, P., The Kazhdan–Lusztig conjecture for finite W-algebras, Lett. Math. Phys. 35 (1995), 333–344.CrossRefGoogle Scholar
[Dix96]Dixmier, J., Enveloping algebras, Graduate Studies in Mathematics, vol. 11 (American Mathematical Society, Providence, RI, 1996).Google Scholar
[Duf77]Duflo, M., Sur la classification des idéaux primitifs dans l’algèbre enveloppante d’une algèbre de Lie semi-simple, Ann. of Math. (2) 105 (1977), 107–120.CrossRefGoogle Scholar
[Ful97]Fulton, W., Young tableaux, London Mathematical Society Student Texts, vol. 35 (London Mathematical Society, London, 1997).Google Scholar
[GG02]Gan, W. L. and Ginzburg, V., Quantization of Slodowy slices, Int. Math. Res. Not. 5 (2002), 243–255.CrossRefGoogle Scholar
[Gin09]Ginzburg, V., Harish-Chandra bimodules for quantized Slodowy slices, Represent. Theory 13 (2009), 236–271.CrossRefGoogle Scholar
[Irv85]Irving, R., Projective modules in the category 𝒪S: self-duality, Trans. Amer. Math. Soc. 291 (1985), 701–732.Google Scholar
[Jan83]Jantzen, J. C., Einhüllende Algebren halbeinfacher Lie-Algebren, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 3 (Springer, Berlin, 1983).CrossRefGoogle Scholar
[Jan04]Jantzen, J. C., Nilpotent orbits in representation theory, Progress in Mathematics, vol. 228 (Birkhäuser, Basel, 2004).CrossRefGoogle Scholar
[Jos78a]Joseph, A., Sur la classification des idéaux primitifs dans l’algèbre enveloppante de , C. R. Acad. Sci. Paris 287 (1978), A303–A306.Google Scholar
[Jos78b]Joseph, A., Gelfand–Kirillov dimension for the annihilators of simple quotients of Verma modules, J. Lond. Math. Soc. 18 (1978), 50–60.CrossRefGoogle Scholar
[Jos80a]Joseph, A., Towards the Jantzen conjecture, Compositio Math. 40 (1980), 35–67.Google Scholar
[Jos80b]Joseph, A., Kostant’s problem, Goldie rank and the Gelfand–Kirillov conjecture, Invent. Math. 56 (1980), 191–213.CrossRefGoogle Scholar
[Jos80c]Joseph, A., Goldie rank in the enveloping algebra of a semisimple Lie algebra I, J. Algebra 65 (1980), 269–283.CrossRefGoogle Scholar
[Jos80d]Joseph, A., Goldie rank in the enveloping algebra of a semisimple Lie algebra II, J. Algebra 65 (1980), 284–306.CrossRefGoogle Scholar
[Jos81a]Joseph, A., Towards the Jantzen conjecture III, Compositio Math. 41 (1981), 23–30.Google Scholar
[Jos81b]Joseph, A., Goldie rank in the enveloping algebra of a semisimple Lie algebra III, J. Algebra 73 (1981), 295–326.CrossRefGoogle Scholar
[Jos85]Joseph, A., On the associated variety of a primitive ideal, J. Algebra 93 (1985), 509–523.CrossRefGoogle Scholar
[Jos87]Joseph, A., On the cyclicity of vectors associated with Duflo involutions, in Noncommutative harmonic analysis and Lie groups, Lecture Notes in Mathematics, vol. 1243 (Springer, New York, 1987), 144–188.CrossRefGoogle Scholar
[Jos88]Joseph, A., A surjectivity theorem for rigid highest weight modules, Invent. Math. 92 (1988), 567–596.CrossRefGoogle Scholar
[KRW03]Kac, V., Roan, S. and Wakimoto, M., Quantum reduction for affine superalgebras, Comm. Math. Phys. 241 (2003), 307–342, math-ph/0302015.CrossRefGoogle Scholar
[KL79]Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras, Invent. Math. 53 (1979), 165–184.CrossRefGoogle Scholar
[Kos78]Kostant, B., On Whittaker modules and representation theory, Invent. Math. 48 (1978), 101–184.CrossRefGoogle Scholar
[Los10a]Losev, I., Quantized symplectic actions and W-algebras, J. Amer. Math. Soc. 23 (2010), 35–59.CrossRefGoogle Scholar
[Los10b]Losev, I., On the structure of category 𝒪 for W-algebras, Sémin. Congr. 25 (2010), 351–368.Google Scholar
[Los11a]Losev, I., 1-dimensional representations and parabolic induction for W-algebras, Adv. Math. 226 (2011), 4841–4883.CrossRefGoogle Scholar
[Los11b]Losev, I., Finite-dimensional representations of W-algebras, Duke Math. J. 159 (2011), 99–143.CrossRefGoogle Scholar
[Lyn79]Lynch, T. E., Generalized Whittaker vectors and representation theory, PhD thesis, MIT (1979).Google Scholar
[M\OT1\oe 87]Mœglin, C., Idéaux complètement premiers de l’algèbre enveloppante de , J. Algebra 106 (1987), 287–366.CrossRefGoogle Scholar
[M\OT1\oe 88]Mœglin, C., Modèle de Whittaker et idéaux primitifs complètement premiers dans les algèbres enveloppantes des algèbres de Lie semisimples complexes II, Math. Scand. 63 (1988), 5–35.CrossRefGoogle Scholar
[Pre02]Premet, A., Special transverse slices and their enveloping algebras, Adv. Math. 170 (2002), 1–55.CrossRefGoogle Scholar
[Pre07a]Premet, A., Enveloping algebras of Slodowy slices and the Joseph ideal, J. Eur. Math. Soc. 9 (2007), 487–543.CrossRefGoogle Scholar
[Pre07b]Premet, A., Primitive ideals, non-restricted representations and finite W-algebras, Mosc. Math. J. 7 (2007), 743–762.CrossRefGoogle Scholar
[Pre10]Premet, A., Commutative quotients of finite W-algebras, Adv. Math. 225 (2010), 269–306.CrossRefGoogle Scholar
[Pre11]Premet, A., Enveloping algebras of Slodowy slices and Goldie rank, Transform. Groups 16 (2011), 857–888.CrossRefGoogle Scholar
[Skr02]Skryabin, S., A category equivalence, appendix to [Pre02].Google Scholar
[Vog91]Vogan, D., Associated varieties and unipotent representations, in Harmonic analysis on reductive groups, Progress in Mathematics, vol. 101 (Birkhäuser, Basel, 1991), 315–388.CrossRefGoogle Scholar