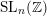Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
André, Simon
and
Fruchter, Jonathan
2022.
Formal solutions and the first‐order theory of acylindrically hyperbolic groups.
Journal of the London Mathematical Society,
Vol. 105,
Issue. 2,
p.
1012.
Kunyavskiĭ, Boris
Plotkin, Eugene
and
Vavilov, Nikolai
2023.
Bounded generation and commutator width of Chevalley groups: function case.
European Journal of Mathematics,
Vol. 9,
Issue. 3,
Avni, Nir
and
Meiri, Chen
2023.
On the model theory of higher rank arithmetic groups.
Duke Mathematical Journal,
Vol. 172,
Issue. 13,
Glazer, Itay
and
Hendel, Yotam
2024.
On Singularity Properties of Word Maps and Applications to Probabilistic Waring Type Problems.
Memoirs of the American Mathematical Society,
Vol. 299,
Issue. 1497,