No CrossRef data available.
Article contents
Improved algebraic fibrings
Published online by Cambridge University Press: 13 September 2024
Abstract
We show that a virtually residually finite rationally solvable (RFRS) group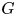 
$G$ of type 
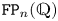$\mathtt {FP}_n(\mathbb {Q})$ virtually algebraically fibres with kernel of type 
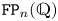$\mathtt {FP}_n(\mathbb {Q})$ if and only if the first 
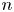$n$ 
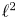$\ell ^2$-Betti numbers of 
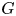$G$ vanish, that is, 
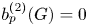$b_p^{(2)}(G) = 0$ for 
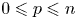$0 \leqslant p \leqslant n$. This confirms a conjecture of Kielak. We also offer a variant of this result over other fields, in particular in positive characteristic. As an application of the main result, we show that amenable virtually RFRS groups of type 
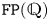$\mathtt {FP}(\mathbb {Q})$ are virtually Abelian. It then follows that if 
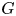$G$ is a virtually RFRS group of type 
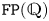$\mathtt {FP}(\mathbb {Q})$ such that 
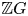$\mathbb {Z} G$ is Noetherian, then 
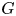$G$ is virtually Abelian. This confirms a conjecture of Baer for the class of virtually RFRS groups of type 
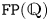$\mathtt {FP}(\mathbb {Q})$, which includes (for instance) the class of virtually compact special groups.
MSC classification
Primary:
20F65: Geometric group theory
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
Agol, I., The virtual Haken conjecture, Doc. Math. 18 (2013), 1045–1087, with an appendix by I. Agol, Daniel Groves, and Jason Manning.Google Scholar
Bartholdi, L., Amenability of groups is characterized by Myhill's theorem, J. Eur. Math. Soc. (JEMS) 21 (2019), 3191–3197, with an appendix by Dawid Kielak.Google Scholar
Bergeron, N., Haglund, F. and Wise, D. T., Hyperplane sections in arithmetic hyperbolic manifolds, J. Lond. Math. Soc. (2) 83 (2011), 431–448.Google Scholar
Bieri, R., Normal subgroups in duality groups and in groups of cohomological dimension 
$2$, J. Pure Appl. Algebra 7 (1976), 35–51.Google Scholar
$2$, J. Pure Appl. Algebra 7 (1976), 35–51.Google ScholarBieri, R., Deficiency and the geometric invariants of a group, J. Pure Appl. Algebra 208 (2007), 951–959, with an appendix by Pascal Schweitzer.Google Scholar
Bieri, R. and Eckmann, B., Finiteness properties of duality groups, Comment. Math. Helv. 49 (1974), 74–83.Google Scholar
Bieri, R., Neumann, W. D. and Strebel, R., A geometric invariant of discrete groups, Invent. Math. 90 (1987), 451–477.Google Scholar
Bieri, R. and Renz, B., Valuations on free resolutions and higher geometric invariants of groups, Comment. Math. Helv. 63 (1988), 464–497.Google Scholar
Brady, N., Branched coverings of cubical complexes and subgroups of hyperbolic groups, J. Lond. Math. Soc. (2) 60 (1999), 461–480.Google Scholar
Bridson, M. R. and Haefliger, A., Metric spaces of non-positive curvature, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 319 (Springer, Berlin, 1999).Google Scholar
Brown, K. S., Cohomology of groups, Graduate Texts in Mathematics, vol. 87 (Springer, New York, 1994). Corrected reprint of the 1982 original.Google Scholar
Cohn, P. M., Skew fields: Theory of general division rings, Encyclopedia of Mathematics and its Applications, vol. 57 (Cambridge University Press, Cambridge, 1995).Google Scholar
Degrijse, D., Amenable groups of finite cohomological dimension and the zero divisor conjecture, Preprint (2016), arXiv:1609.07635.Google Scholar
Fel'dman, G. L., The homological dimension of group algebras of solvable groups, Izv. Akad. Nauk SSSR Ser. Mat. 35 (1971), 1225–1236.Google Scholar
Gräter, J., Free division rings of fractions of crossed products of groups with Conradian left-orders, Forum Math. 32 (2020), 739–772.Google Scholar
Grigorčuk, R. I., On Burnside's problem on periodic groups, Funktsional. Anal. i Prilozhen. 14 (1980), 53–54.Google Scholar
Hall, P., On the finiteness of certain soluble groups, Proc. Lond. Math. Soc. (3) 9 (1959), 595–622.Google Scholar
Hillman, J. A., Elementary amenable groups and $4$-manifolds with Euler characteristic $0$, J. Aust. Math. Soc. Ser. A 50 (1991), 160–170.Google Scholar
$4$-manifolds with Euler characteristic 
$0$, J. Aust. Math. Soc. Ser. A 50 (1991), 160–170.Google ScholarHillman, J. A. and Linnell, P. A., Elementary amenable groups of finite Hirsch length are locally-finite by virtually-solvable, J. Aust. Math. Soc. Ser. A 52 (1992), 237–241.Google Scholar
Hughes, I., Division rings of fractions for group rings, Comm. Pure Appl. Math. 23 (1970), 181–188.Google Scholar
Italiano, G., Martelli, B. and Migliorini, M., Hyperbolic 5-manifolds that fiber over $S^1$, Invent. Math. 231 (2023), 1–38.Google Scholar
$S^1$, Invent. Math. 231 (2023), 1–38.Google ScholarJaikin-Zapirain, A., The universality of Hughes-free division rings, Selecta Math. (N.S.) 27 (2021), article 74.Google Scholar
Juschenko, K., Non-elementary amenable subgroups of automata groups, J. Topol. Anal. 10 (2018), 35–45.Google Scholar
Kammeyer, H., $L^2$-invariants of nonuniform lattices in semisimple Lie groups, Algebr. Geom. Topol. 14 (2014), 2475–2509.Google Scholar
$L^2$-invariants of nonuniform lattices in semisimple Lie groups, Algebr. Geom. Topol. 14 (2014), 2475–2509.Google ScholarKielak, D., The Bieri-Neumann-Strebel invariants via Newton polytopes, Invent. Math. 219 (2020), 1009–1068.Google Scholar
Kielak, D., Fibring over the circle via group homology, in Manifolds and groups, Oberwolfach Reports, vol. 17 (European Mathematical Society, 2020), 428–431.Google Scholar
Kielak, D., Residually finite rationally solvable groups and virtual fibring, J. Amer. Math. Soc. 33 (2020), 451–486.Google Scholar
Koberda, T. and Suciu, A. I., Residually finite rationally $p$ groups, Commun. Contemp. Math. 22 (2020), 1950016.Google Scholar
$p$ groups, Commun. Contemp. Math. 22 (2020), 1950016.Google ScholarKropholler, P. and Lorensen, K., Group-graded rings satisfying the strong rank condition, J. Algebra 539 (2019), 326–338.Google Scholar
Kropholler, R., Hyperbolic groups with finitely presented subgroups not of type $F_3$, Geom. Dedicata 213 (2021), 589–619.Google Scholar
$F_3$, Geom. Dedicata 213 (2021), 589–619.Google ScholarLinnell, P. A., Division rings and group von Neumann algebras, Forum Math. 5 (1993), 561–576.Google Scholar
Llosa Isenrich, C., Martelli, B. and Py, P., Hyperbolic groups containing subgroups of type $\mathscr {F}_{3}$ not $\mathscr {F}_{4}$, J. Differential Geom. 127 (2024), 1121–1147.Google Scholar
$\mathscr {F}_{3}$ not 
$\mathscr {F}_{4}$, J. Differential Geom. 127 (2024), 1121–1147.Google ScholarLlosa Isenrich, C. and Py, P., Subgroups of hyperbolic groups, finiteness properties and complex hyperbolic lattices, Invent. Math. 235 (2024), 233–254.Google Scholar
Lodha, Y., A hyperbolic group with a finitely presented subgroup that is not of type FP3, in Geometric and cohomological group theory, London Mathematical Society Lecture Note series, vol. 444 (Cambridge University Press, Cambridge, 2018), 67–81.Google Scholar
Lück, W., $L^2$-invariants: theory and applications to geometry and K-theory (Springer, Berlin, 2002).Google Scholar
$L^2$-invariants: theory and applications to geometry and K-theory (Springer, Berlin, 2002).Google ScholarMcConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings, revised edition, Graduate Studies in Mathematics, vol. 30 (American Mathematical Society, Providence, RI, 2001), with the cooperation of L. W. Small.Google Scholar
Minasyan, A., Virtual retraction properties in groups, Int. Math. Res. Not. IMRN 2021 (2021), 13434–13477.Google Scholar
Passman, D. S., The algebraic structure of group rings, Pure and Applied Mathematics (Wiley, 1977).Google Scholar
Rips, E., Subgroups of small cancellation groups, Bull. Lond. Math. Soc. 14 (1982), 45–47.Google Scholar
Sikorav, J.-C., Homologie de Novikov associée à une classe de cohomologie de degré un, Thèse d’État, Université Paris-Sud (Orsay) (1987).Google Scholar
Stallings, J., On fibering certain 3-manifolds, in Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961) (Prentice-Hall, Englewood Cliffs, NJ, 1962), 95–100.Google Scholar