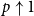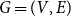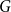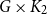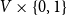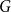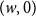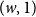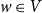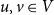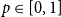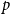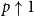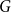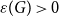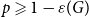The bunkbed conjecture holds in the $p\uparrow 1$ limit

Abstract

Let $G=(V,E)$ be a countable graph. The Bunkbed graph of $G$ is the product graph $G \times K_2$ , which has vertex set $V\times \{0,1\}$ with “horizontal” edges inherited from $G$ and additional “vertical” edges connecting $(w,0)$ and $(w,1)$ for each $w \in V$ . Kasteleyn’s Bunkbed conjecture states that for each $u,v \in V$ and $p\in [0,1]$ , the vertex $(u,0)$ is at least as likely to be connected to $(v,0)$ as to $(v,1)$ under Bernoulli- $p$ bond percolation on the bunkbed graph. We prove that the conjecture holds in the $p \uparrow 1$ limit in the sense that for each finite graph $G$ there exists $\varepsilon (G)\gt 0$ such that the bunkbed conjecture holds for $p \geqslant 1-\varepsilon (G)$ .

1. Introduction

In Bernoulli bond percolation, the edges of a countable graph $G=(V,E)$ (which we allow to contain self-loops and/or multiple edges) are each deleted or retained independently at random with retention probability $p\in [0,1]$ . We call retained edges open, deleted edges closed, and write ${\mathbb{P}}_p={\mathbb{P}}^G_p$ for the law of the resulting random subgraph. Percolation theorists seek to understand the geometry of the connected components of the random subgraph that remains, and how this geometry depends on the parameter $p$ . Despite the simplicity of the model, this is a rich subject with many connections to other topics in mathematics, physics, and computer science; see e.g. [5, 6] for background and overview.

When studying percolation, it is often important to understand the behaviour of connection probabilities between vertices, also known as the two-point function. Situations often arise in which it is easier to bound averages of the two-point function (e.g. over a box in the hypercubic lattice) than it is to prove pointwise bounds; see for instance the thirteen-year gap between Hara and Slade’s proof of mean-field behaviour for the Fourier transform of the two-point function for high-dimensional percolation in 1990 [9] and the subsequent proof of pointwise bounds by Hara, van der Hofstad, and Slade in 2003 [10]. As such, it would be very useful to have general techniques to convert averaged bounds into pointwise bounds. Such a conversion would be straightforward if one knew that the connection probability from the origin to $x=(x_1,\ldots,x_d)$ on the hypercubic lattice $\mathbb{Z}^d$ is a decreasing function of $|x_i|$ for each $i=1,\ldots,d$ . Unfortunately, this intuitively plausible statement seems to be out of reach of present methods, although an analogous statement is known to hold for the Ising model [15].

These considerations lend motivation to the bunkbed conjecture, which was first formulated by Kasteleyn in the mid 1980s [2, Remark 5]. Given a graph $G=(V,E)$ , the bunkbed graph is defined to be the Cartesian product $G\times K_2$ of $G$ and the graph with one edge (sometimes known as the box product and denoted $G{\Box } K_2$ ), which has vertex set $V\times \{0,1\}$ with “horizontal” edges inherited from $G$ and additional “vertical” edges connecting $(w,0)$ and $(w,1)$ for each $w \in V$ (Figure 1). We refer to Bernoulli percolation on $G \times K_2$ as the bunkbed model and write ${\mathbb{P}}_p^{\text{bb}}={\mathbb{P}}_p^{G\times{K}_2}$ for its law. To lighten notation, we will often write $v_i=(v,i)$ for $v\in V$ and $i\in \{0,1\}$ .

Figure 1. A graph $G$ (top) and the bunkbed model on $G$ (bottom).

Conjecture 1. (Bunkbed conjecture). Let $G=(V,E)$ be a finite graph. Then ${\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( u_0 \leftrightarrow v_0 \right )$ $\geqslant$ ${\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( u_0 \leftrightarrow v_1 \right )$ for every $p \in \left [ 0,1 \right ]$ and $u,v\in V$ .

(In fact Kastelyn may have conjectured the stronger statement that this inequality remains true after conditioning on which vertical edges are present (Figure 2); see Theorem 2 below.) Despite its simple and intuitive statement, and proofs of analogous statements for the Ising model and simple random walk by Häggström [7, 8], the bunkbed conjecture has so far evaded resolution. Indeed, even the case in which $G$ is the complete graph was verified only in the recent work of Van Hintum and Lammers [11] following partial results of De Buyer [3, 4]. Further special cases of the conjecture have been studied by Leander [12] and Linusson [13], ¹ and interesting related correlation inequalities inspired by the bunkbed conjecture have been developed in the work of Van den Berg, Häggström, and Kahn [1, 2].

Figure 2. The bunkbed model after conditioning on vertical edges.

The goal of this paper is to prove that the bunkbed conjecture holds (with strict inequality) in the limit as $p \uparrow 1$ . We have not attempted to optimize the resulting constants.

Theorem 1. Let $G=(V,E)$ be a finite, connected graph. Then ${\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( u_0 \leftrightarrow v_0 \right )$ $\gt{\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( u_0 \leftrightarrow v_1 \right )$ for every $u,v\in V$ and $1-2^{-(\left \lvert E \right \rvert +4)/2} \leqslant p\lt 1$ .

The complementary fact that the conjecture holds in the limit as $p \downarrow 0$ holds for trivial reasons. Indeed, if we consider Bernoulli bond percolation between any two vertices $u$ and $v$ on a finite graph $G=(V,E)$ , then one can easily see that

\begin{align*}{\mathbb{P}}^G_p(u \leftrightarrow v) & = \sum _{\omega \in \Omega } \mathbb{1}\left [ u \overset{\omega }{\leftrightarrow } v \right ] p^{\#\text{open}}\left ( 1-p \right )^{\#\text{closed}} \\ & = \#\{\text{geodesics from $u$ to $v$}\} \cdot p^{d(u,v)} \pm O\left ( p^{d\left ( u, v \right )+1} \right ) \end{align*}

where $d(u,v)$ is the graph distance between $u$ and $v$ , i.e., the length of the shortest path connecting $u$ to $v$ . Since the graph distances in the bunkbed graph satisfy $d(u_0,v_1)=d(u_0,v_0)+1$ for every $u,v\in V$ , the conjecture holds in the $p\downarrow 0$ limit as claimed.

In contrast, analysis of simple examples shows that it is not possible to deduce Theorem 1 by expanding to a bounded number of terms in powers of $(1-p)$ . Indeed, if $G_n$ is the path of length $n$ with vertices $\{0,1,\ldots,n\}$ , one can solve the associated linear recursion to compute that the probabilities ${\mathbb{P}}^{\text{bb}}_{1-\varepsilon }(0_0\leftrightarrow n_0)$ and ${\mathbb{P}}^{\text{bb}}_{1-\varepsilon }(0_0\leftrightarrow n_1)$ both share the first $n+1$ terms of their expansion in powers of $\varepsilon$

\begin{align*}{\mathbb{P}}^{\text{bb}}_{p}(0_0\leftrightarrow n_0) & = 1 - (n+2)(1-p)^2 - 2(n-1)(1-p)^3 \\ & \quad + \frac{1}{2}(n^2+7n+10)(1-p)^4+ \cdots \pm O((1-p)^{n+1}) \end{align*}

while ${\mathbb{P}}^{\text{bb}}_{p}(0_0\leftrightarrow n_0) -{\mathbb{P}}^{\text{bb}}_{p}(0_0\leftrightarrow n_1) = \varepsilon ^{n+1}(1-\varepsilon )^n$ . Thus, in this example the bunkbed inequality ${\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( 0_0 \nleftrightarrow n_0 \right )$ $\geqslant{\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( 0_0 \nleftrightarrow n_1 \right )$ is not detected when expanding to any bounded number of terms in powers of $(1-p)$ .

Note that if one could find a single value of $p$ such that the bunkbed conjecture held for every finite graph at $p$ , then the bunkbed conjecture would hold for every graph $G$ and every $p$ by a theorem of Rudzinski and Smyth [16].

2. Proof

We write $T$ for the set of $w\in V$ such that the vertical edge connecting $w_0$ and $w_1$ is open. One can deduce Theorem 1 from the following theorem by taking expectations over $T$ .

Theorem 2. Let $G=(V,E)$ be a finite graph. Then ${\mathbb{P}}^{{\text{bb}}}_{p}$ $\left ( u_0 \leftrightarrow v_0 \mid T=t \right )$ $ \geqslant{\mathbb{P}}^{{\text{bb}}}_{p}\left ( u_0 \leftrightarrow v_1 \mid T=t \right )$ for every $u,v\in V$ , $t \subseteq V$ , and $1-2^{-(\left \lvert E \right \rvert +4)/2}\leqslant p\lt 1$ , with strict inequality if and only if $u$ and $v$ are connected in $V \setminus t$ .

Here, the condition that $u$ and $v$ are connected in $V \setminus t$ includes the condition that $u,v \notin t$ .

The proof of Theorem 2 will rely on a relationship between percolation on the bunkbed graph and another model due to Linusson [13], which we call the alternative bunkbed model (Figure 3).

Figure 3. A tripartition $s = (s_0,s_1,s_2)$ (top) and its induced alternative bunkbed model (bottom).

Let $G=(V,E)$ be a finite graph, let $t \subseteq V$ be a set of vertices, and let $p\in (0,1)$ . If we condition on the event $T=t$ , the horizontal edges of the bunkbed graph are still i.i.d., each with probability $p$ of being open.

We call a partition of $E$ into three disjoint (possibly empty) sets a tripartition of $E$ , and write $\mathcal{S}$ for the set of tripartitions of $E$ . Let $S=(S_0,S_1,S_2)$ be the random tripartition of the edge set of $G$ into those edges that have zero, one, or two corresponding open horizontal edges in the bunkbed graph. We can sample from the conditional distribution of percolation on the bunkbed graph given $T=t$ and $S=s=(s_0,s_1,s_2)$ by choosing for each edge $e\in s_1$ exactly one of the two corresponding horizontal bunkbed edges to be open, each with probability $1/2$ , independently at random for each $e\in s_1$ ; if $e \in s_0$ then both corresponding horizontal bunkbed edges are closed while if $e \in s_2$ then both corresponding bunkbed edges are open.

Given a tripartition $s=(s_0,s_1,s_2)$ of the edge set of $G$ , we write $G(s)=(V(s),E(s))$ for the graph formed by deleting the edges of $s_0$ and contracting every edge of $s_2$ , and write $\pi _s:V\to V(s)$ for the resulting projection map (where each vertex of $v$ is identified with its connected component in $s_2$ ). Note that $G(s)$ may contain self-loops and multiple edges even if the original graph $G$ did not.

These considerations lead to the definition of the alternative bunkbed model, which we now introduce. Let $G=(V,E)$ be a finite graph and let $t\subseteq V$ be a distinguished set of vertices. Let ${\mathbb{Q}}_G^t$ be the law of the random subgraph of the bunkbed graph $G \times K_2$ in which we include a vertical edge $\{u_0,u_1\}$ if and only if $u\in t$ , and for each edge of $G$ choose exactly one of the two corresponding horizontal edges of $G\times K_2$ to be open, independently at random with probability $1/2$ each. Given a random variable with law ${\mathbb{Q}}_G^t$ , we say that an edge $e$ of $G$ is up if the upper of its two corresponding horizontal edges is open (i.e., the horizontal edge connecting two vertices of the form $u_1$ and $v_1$ ), and down otherwise.

The description of the conditional distribution of the bunkbed model given $T=t$ and $S=s$ discussed above leads to the identity

(1) \begin{align} &{\mathbb{P}}^{{\text{bb}}}_{p}\left ( u_0 \leftrightarrow v_0 \mid T=t \right ) -{\mathbb{P}}^{{\text{bb}}}_{p}\left ( u_0 \leftrightarrow v_1 \mid T=t \right )\nonumber \\[5pt] & \quad= \sum _{s \in \mathcal{S}} \left [{\mathbb{Q}}_{G(s)}^{\pi _s(t)}\left (\pi _s(u)_0 \leftrightarrow \pi _s(v)_0\right ) -{\mathbb{Q}}_{G(s)}^{\pi _s(t)}\left (\pi _s(u)_0 \leftrightarrow \pi _s(v)_1\right )\right ]{\mathbb{P}}^{{\text{bb}}}_{p}\left ( S=s \right ). \end{align}

Note also that we have the equality

(2) \begin{equation} {\mathbb{P}}^{{\text{bb}}}_{p}\left ( S=s \right ) = (1-p)^{2\left \lvert s_0 \right \rvert } (2p(1-p))^{\left \lvert s_1 \right \rvert } p^{2\left \lvert s_2 \right \rvert } \end{equation}

for each tripartition $s\in \mathcal{S}$ . Linusson has conjectured [13, Conjecture 2.5] that

\begin{align*}{\mathbb{Q}}_{G}^{t}(u_0 \leftrightarrow v_0) \geqslant{\mathbb{Q}}_{G}^{t}(u_0 \leftrightarrow v_1) \end{align*}

for every finite graph $G=(V,E)$ , $t\subseteq V$ , and $u,v \in V$ ; it follows from (1) that this conjecture implies Conjecture 1. We will instead use (1) to probe the validity of the bunkbed conjecture when $p$ is close to $1$ , the main idea being that $G(s)$ is typically very small in this regime since most edges will be contracted.

Fix a finite graph $G=(V,E)$ , a set $t\subseteq V$ , two vertices $u,v\in V$ and a tripartition $s\in \mathcal{S}$ . We say that a path in $G(s)$ from $\pi _s(u)$ to $\pi _s(v)$ is vertical-free if all vertices on that path (including the endpoints) are not in $\pi _s(t)$ . Let $d(s)$ be the length of the shortest vertical-free path if such a path exists, and $\infty$ otherwise. We also define

\begin{align*} F(s) \;:\!=\;{\mathbb{Q}}_{G(s)}^{\pi _s(t)}\!\left (\pi _s(u)_0 \leftrightarrow \pi _s(v)_0\right ) -{\mathbb{Q}}_{G(s)}^{\pi _s(t)}\!\left (\pi _s(u)_0 \leftrightarrow \pi _s(v)_1\right ). \end{align*}

The idea is to partition $\mathcal{S}$ into several classes according to the value of $d(s)$ as follows:

\begin{align*} \mathcal{S}_{\infty } = \left \{ s \in \mathcal{S} \colon d(s) = \infty \right \} \qquad \mathcal{S}_{\leqslant 1} = \left \{ s \in \mathcal{S} \colon d(s) \leqslant 1 \right \} \qquad \mathcal{S}_{\geqslant 2} = \left \{ s \in \mathcal{S} \colon d(s) \geqslant 2 \right \}. \end{align*}

We will show that $F$ vanishes on $\mathcal{S}_{\infty }$ and that it is uniformly positive on $\mathcal{S}_{\leqslant 1}$ . The contribution of the final set $\mathcal{S}_{\geqslant 2}$ will be controlled using the trivial inequality $F(s) \geqslant -1$ .

We recall the following argument of Linusson [13, Lemma 2.3], which we include a proof of for completeness.

Lemma 1. (Mirroring argument). If $s \in \mathcal{S}_{\infty }$ then $F(s) = 0$ .

Proof. Fix $s\in \mathcal{S}_{\infty }$ . To lighten notation we write $\pi =\pi _s$ . The claim is trivial if $\pi (u)$ or $\pi (v)$ belongs to $\pi (t)$ , so suppose not. Note that $\pi (u) \neq \pi (v)$ as otherwise $d(s) = 0$ .

Let $U$ be the set of vertices in $G(s)$ that have a vertical-free path to $\pi (u)$ , $E_u$ be the set of edges of $G(s)$ that have at least one endpoint in $U$ and $E_v=E(s)\setminus E_u$ . The partition $\left \{ E_u, E_v \right \}$ has the properties that any vertex that is an endpoint both of an edge in $E_u$ and an edge in $E_v$ must belong to $\pi (t)$ , that every edge incident to $\pi (u)$ belongs to $E_u$ , and that every edge incident to $\pi (v)$ belongs to $E_v$ .

Let $\omega$ be a sample from ${\mathbb{Q}}^{\pi (t)}_{G(s)}$ , and let $f_{uv}$ be the random variable

\begin{align*} f_{uv}(\omega ) = \frac{1}{2}\left \{ \mathbb{1}\left [ \pi (u)_0 \leftrightarrow \pi (v)_0 \right ] + \mathbb{1}\left [ \pi (u)_1 \leftrightarrow \pi (v)_1 \right ] - \mathbb{1}\left [ \pi (u)_0 \leftrightarrow \pi (v)_1 \right ] - \mathbb{1}\left [ \pi (u)_1 \leftrightarrow \pi (v)_0 \right ] \right \}, \end{align*}

where connections are defined in $\omega$ . Note that by symmetry $f_{uv}(\omega )$ has expectation $F(s)$ . If we define $\omega '$ by flipping the value of each edge in $E_v$ (i.e., replacing each up edge with a down edge and vice versa) then we see that $\omega '$ has the same distribution as $\omega$ and that $f_{uv}(\omega ')=-f_{uv}(\omega )$ as depicted in Figure 4: If there is a path from $u_0$ to $v_0$ in $\omega$ then there is a path from $u_0$ to $v_1$ in $\omega '$ and vice versa. It follows that $f_{uv}(\omega )$ has expectation zero.

Figure 4. The mirroring argument.

Next we establish a uniform positive lower bound on $\mathcal{S}_{\leqslant 1}$ .

Lemma 2. If $ s\in \mathcal{S}_{\leqslant 1}$ then $F(s) \geqslant 2^{-\left \lvert s_1 \right \rvert } \geqslant 2^{-\left \lvert E \right \rvert }$ .

Proof. Fix $s\in \mathcal{S}_{\leqslant 1}$ and write $\pi =\pi _s$ . Let $\omega$ and $f_{uv}$ be as above. First observe that $f_{uv}(\omega ) \geqslant 0$ deterministically. Indeed, since either $u_0 \leftrightarrow v_0$ or $u_1 \leftrightarrow v_1$ , we have that the sum of the first two indicators is at least $1$ . Thus, for $f_{uv}$ to be negative we would require both of the latter two indicators to be $1$ , but in this case at least one of the two events $\{\pi (u)_0 \leftrightarrow \pi (v)_1 \leftrightarrow \pi (v)_0 \leftrightarrow \pi (u)_1\}$ or $\{\pi (v)_0 \leftrightarrow \pi (u)_1 \leftrightarrow \pi (u)_0 \leftrightarrow \pi (v)_1\}$ must hold, so that the vertices $\{\pi (u)_0,\pi (u)_1,\pi (v)_0,\pi (v)_1\}$ all belong to the same connected component of $\omega$ and $f_{uv}(\omega )=0$ .

To conclude, we note that if every edge of $G(s)$ is up or every edge of $G(s)$ is down then $f_{uv} = 1$ (if $d(s) = 0$ ) or $f_{uv} = 1/2$ (if $d(s) = 1$ ), and this happens with probability $2^{1-\left \lvert s_1 \right \rvert }$ .

We are now ready to complete the proof of Theorem 2.

Proof of Theorem 2. It follows from (1) and Lemma 1 that

\begin{align*}{\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( u_0 \leftrightarrow v_0 \mid T=t \right ) -{\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( u_0 \leftrightarrow v_1 \mid T=t \right ) = \sum _{s\not \in \mathcal{S}_\infty }{\mathbb{P}}^{\text{bb}}_p(S=s\mid T=t) F(s). \end{align*}

If $u$ and $v$ are not connected in $V \setminus t$ then $\mathcal{S}=\mathcal{S}_\infty$ and the right hand side is zero as claimed. It remains to prove that the right hand side is positive when $u$ and $v$ are connected in $V \setminus t$ and $p\geqslant 1-2^{-(\left \lvert E \right \rvert +4)/2}$ .

Observe that if $ s\in \mathcal{S}_{\geqslant 2}$ then there exists a set $A = \left \{ e_1, \ldots, e_k \right \} \subseteq s_1$ such that $\pi _s(A)$ is a vertical-free path in $G(s)$ connecting $\pi _s(u)$ and $\pi _s(v)$ with $k\geqslant 2$ . As such, if we pick one such $A=A(s)$ for each $s\in \mathcal{S}_{\geqslant 2}$ and define a tripartition $g(s)$ by $g(s) = \left ( s_0, s_1 \setminus A, s'_{\!\!2} = s_2 \cup A \right )$ then $g(s) \in \mathcal{S}_{\leqslant 1}$ . Note that the construction of the function $g\;:\;\mathcal{S}_{\geqslant 2}\to \mathcal{S}_{\leqslant 1}$ depends on the choice of set $A(s)$ for each $s\in \mathcal{S}_{\geqslant 2}$ and may not be unique. The function $g$ has the following properties:

1. 1. Since $|g(s)_2|-|s_2|=|s_1|-|g(s)_1| \geqslant 2$ for every $s\in \mathcal{S}_{\geqslant 2}$ , it follows from (2) that

   (3) \begin{equation} {\mathbb{P}}^{\text{bb}}_p(S=s) \leqslant \frac{4(1-p)^2}{p^{2}}{\mathbb{P}}^{\text{bb}}_p(S=g(s)) \end{equation}
   for every $s\in \mathcal{S}_{\geqslant 2}$ and $p \geqslant 2/3$ .

2. 2. Since each $s\in \mathcal{S}_{\geqslant 2}$ can be written $s=(g(s)_0,g(s)_1\cup A(s), g(s)_2 \setminus A(s))$ where $A(s)$ is a non-empty subset of $g(s)_2$ , we have that if $s'\in \mathcal{S}_{\leqslant 1}$ then the preimage $g^{-1}(s')$ satisfies

   (4) \begin{equation} |g^{-1}(s')| \leqslant 2^{|s'_{\!\!2}|} \leqslant 2^{|E|}. \end{equation}

These properties together with the trivial inequality $F(s) \geqslant -1$ allow us to bound

(5) \begin{align} \sum _{s\notin \mathcal{S}_\infty }{\mathbb{P}}^{\text{bb}}_p(S=s \mid T=t)F(s) &= \sum _{s'\in \mathcal{S}_{\leqslant 1}} \left [{\mathbb{P}}^{\text{bb}}_p(S=s'\mid T=t)F(s')+\sum _{s \in g^{-1}(s')}{\mathbb{P}}^{\text{bb}}_p(S=s \mid T=t)F(s)\right ] \nonumber \\[5pt] &\geqslant \sum _{s'\in \mathcal{S}_{\leqslant 1}} \left [{\mathbb{P}}^{\text{bb}}_p(S=s' \mid T=t)\left (F(s')-\frac{4(1-p)^2}{p^2}2^{|s'_{\!\!2}|}\right )\right ] \nonumber \\[5pt] &\geqslant \sum _{s'\in \mathcal{S}_{\leqslant 1}} \left [{\mathbb{P}}^{\text{bb}}_p(S=s' \mid T=t)\left (2^{-|s'_{\!\!1}|}-\frac{4(1-p)^2}{p^2}2^{|s'_{\!\!2}|}\right )\right ], \end{align}

where we used (3) and (4) in the first inequality and Lemma 2 in the second. If $(1-p)^2 \leqslant 2^{-|E|-4}$ then $p\geqslant 2/3$ , $p^2 \geqslant 1/2$ , and

\begin{equation*}2^{-|s'_{\!\!1}|}-\frac {4{(1-p)}^2}{p^2}2^{|s'_{\!\!2}|} \geqslant 2^{-|s'_{\!\!1}|} - 2^{|s'_{\!\!2}|-|E|-1} \geqslant 2^{-|s'_{\!\!1}|-1} \geqslant 2^{-|E|-1}\end{equation*}

where we used that $|s'_{\!\!1}|+|s'_{\!\!2}|\leqslant |E|$ in the penultimate inequality. Substituting this estimate into (5) yields that

(6) \begin{equation} \sum _{s\notin \mathcal{S}_\infty }{\mathbb{P}}^{\text{bb}}_p(S=s \mid T=t)F(s) \geqslant 2^{-|E|-1}{\mathbb{P}}^{\text{bb}}_p(S \in \mathcal{S}_{\leqslant 1}\mid T=t). \end{equation}

whenever $(1-p)^2 \leqslant 2^{-|E|-4}$ . If $u$ and $v$ are connected by some simple path in $V \setminus t$ then we can form a tripartition $s \in \mathcal{S}_{\leqslant 1}$ by taking all the edges of this path to belong to $s_2$ and taking every other edge to belong to $s_1$ , so that $s_0$ is empty. When $p \geqslant 2/3$ we have that ${\mathbb{P}}^{\text{bb}}(S\in \mathcal{S}_{\leqslant 1}\mid T=t) \geqslant{\mathbb{P}}^{\text{bb}}(S=s\mid T=t) \geqslant (2(1-p)p)^{|E|}$ and hence by (6) that

\begin{align*}{\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( u_0 \leftrightarrow v_0 \mid T=t \right ) -{\mathbb{P}}^{{\text{bb}}}_{p}\!\left ( u_0 \leftrightarrow v_1 \mid T=t \right ) \geqslant \frac{1}{2}p^{|E|}(1-p)^{|E|} \end{align*}

whenever ${(1-p)}^{2} \leqslant{2}^{-|E|-4}$ and $u$ and $v$ are connected in $V\setminus t$ .