Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kang, Mihyun
and
Panagiotou, Konstantinos
2013.
On the connectivity of random graphs from addable classes.
Journal of Combinatorial Theory, Series B,
Vol. 103,
Issue. 2,
p.
306.
BOUSQUET-MÉLOU, MIREILLE
and
WELLER, KERSTIN
2014.
Asymptotic Properties of Some Minor-Closed Classes of Graphs.
Combinatorics, Probability and Computing,
Vol. 23,
Issue. 5,
p.
749.
McDiarmid, Colin
and
Weller, Kerstin
2014.
LATIN 2014: Theoretical Informatics.
Vol. 8392,
Issue. ,
p.
391.
McDiarmid, Colin
2016.
Connectivity for bridge-alterable graph classes.
European Journal of Combinatorics,
Vol. 56,
Issue. ,
p.
33.
McDiarmid, Colin
and
Scott, Alex
2016.
Random graphs from a block-stable class.
European Journal of Combinatorics,
Vol. 58,
Issue. ,
p.
96.
McDIARMID, COLIN
and
WELLER, KERSTIN
2017.
Bridge-Addability, Edge-Expansion and Connectivity.
Combinatorics, Probability and Computing,
Vol. 26,
Issue. 5,
p.
697.
Heinig, Peter
Müller, Tobias
Noy, Marc
and
Taraz, Anusch
2018.
Logical limit laws for minor-closed classes of graphs.
Journal of Combinatorial Theory, Series B,
Vol. 130,
Issue. ,
p.
158.
Dowden, Chris
Kang, Mihyun
and
Sprüssel, Philipp
2018.
The Evolution of Random Graphs on Surfaces.
SIAM Journal on Discrete Mathematics,
Vol. 32,
Issue. 1,
p.
695.
Chapuy, Guillaume
and
Perarnau, Guillem
2019.
Connectivity in bridge-addable graph classes: The McDiarmid–Steger–Welsh conjecture.
Journal of Combinatorial Theory, Series B,
Vol. 136,
Issue. ,
p.
44.
Chapuy, G.
and
Perarnau, G.
2020.
Local Convergence and Stability of Tight Bridge-addable Classes.
Canadian Journal of Mathematics,
Vol. 72,
Issue. 3,
p.
563.
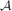 of labelled graphs is bridge-addable if, for all graphs G in
of labelled graphs is bridge-addable if, for all graphs G in 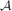 and all vertices u and v in distinct connected components of G, the graph obtained by adding an edge between u and v is also in
and all vertices u and v in distinct connected components of G, the graph obtained by adding an edge between u and v is also in 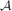 ; the class
; the class 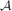 is monotone if, for all G ∈
is monotone if, for all G ∈ 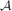 and all subgraphs H of G, we have H ∈
and all subgraphs H of G, we have H ∈ 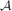 . We show that for any bridge-addable, monotone class
. We show that for any bridge-addable, monotone class 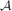 whose elements have vertex set {1,. . .,n}, the probability that a graph chosen uniformly at random from
whose elements have vertex set {1,. . .,n}, the probability that a graph chosen uniformly at random from 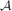 is connected is at least (1−on(1))e−½, where on(1) → 0 as n → ∞. This establishes the special case of the conjecture of McDiarmid, Steger and Welsh when the condition of monotonicity is added. This result has also been obtained independently by Kang and Panagiotou.
is connected is at least (1−on(1))e−½, where on(1) → 0 as n → ∞. This establishes the special case of the conjecture of McDiarmid, Steger and Welsh when the condition of monotonicity is added. This result has also been obtained independently by Kang and Panagiotou.