Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T06:57:45.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Perturbation Analysis of Orthogonal Least Squares

Part of: Numerical approximation and computational geometry Numerical analysis in abstract spaces Algorithms - Computer Science

Published online by Cambridge University Press:  22 March 2019

Pengbo Geng ,
Wengu Chen  and
Huanmin Ge
Pengbo Geng
Affiliation:
Graduate School, China Academy of Engineering Physics, Beijing 100088, China Email: [email protected]
Wengu Chen
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, 100088, China Email: [email protected]
Huanmin Ge
Affiliation:
Sports Engineering College, Beijing Sport University, Beijing, 100088, China Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Orthogonal Least Squares (OLS) algorithm is an efficient sparse recovery algorithm that has received much attention in recent years. On one hand, this paper considers that the OLS algorithm recovers the supports of sparse signals in the noisy case. We show that the OLS algorithm exactly recovers the support of 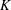$K$-sparse signal $\boldsymbol{x}$ from 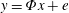$\boldsymbol{y}=\boldsymbol{\unicode[STIX]{x1D6F7}}\boldsymbol{x}+\boldsymbol{e}$ in 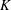$K$ iterations, provided that the sensing matrix 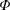$\boldsymbol{\unicode[STIX]{x1D6F7}}$ satisfies the restricted isometry property (RIP) with restricted isometry constant (RIC) 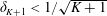$\unicode[STIX]{x1D6FF}_{K+1}<1/\sqrt{K+1}$, and the minimum magnitude of the nonzero elements of $\boldsymbol{x}$ satisfies some constraint. On the other hand, this paper demonstrates that the OLS algorithm exactly recovers the support of the best 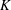$K$-term approximation of an almost sparse signal $\boldsymbol{x}$ in the general perturbations case, which means both 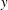$\boldsymbol{y}$ and 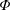$\boldsymbol{\unicode[STIX]{x1D6F7}}$ are perturbed. We show that the support of the best 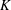$K$-term approximation of $\boldsymbol{x}$ can be recovered under reasonable conditions based on the restricted isometry property (RIP).

Keywords

orthogonal least square (OLS)sparse signalrestricted isometry property (RIP)general perturbation

MSC classification

Primary: 65D15: Algorithms for functional approximation
Secondary: 65J22: Inverse problems 68W40: Analysis of algorithms
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 780 - 797
Copyright
© Canadian Mathematical Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

W. Chen is the corresponding author. This work was supported by the NSF of China (No. 11871109) and NSAF (Grant No. U1830107).

References

Blumensath, T. and Davies, M., Compressed sensing and source separation . In: Int. Conf. on Independent Component Analysis and Signal Separation , Springer-Verlag Berlin, Heidelberg, 2007, pp. 341–348.Google Scholar
Candès, E. J. and Tao, T., Decoding by linear programming . IEEE Trans. Inform. Theory 51(2005), no. 12, 4203–4215. https://doi.org/10.1109/TIT.2005.858979 Google Scholar
Candès, E. J. and Tao, T., Near-optimal signal recovery from random projections: Universal encoding strategies . IEEE Trans. Inform. Theory 52(2006), no. 12, 5406–5425. https://doi.org/10.1109/TIT.2006.885507 Google Scholar
Candès, E. J., Romberg, J., and Tao, T., Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information . IEEE Trans. Inform. Theory 52(2006), no. 2, 489–509. https://doi.org/10.1109/TIT.2005.862083 Google Scholar
Chen, S., Billings, S. A., and Luo, W., Orthogonal least squares methods and their application to non-linear system identification . Internat. J. Control. 50(1989), no. 5, 1873–1896. https://doi.org/10.1080/00207178908953472 Google Scholar
Chen, S. S., Donoho, D. L., and Saunders, M. A., Atomic decomposition by basis pursuit . SIAM J. Sci. Comput. 20(1998), 33–61. https://doi.org/10.1137/S1064827596304010 Google Scholar
Chen, W. and Ge, H., A sharp bound on RIC in generalized orthogonal maching pursuit . Canad. Math. Bull. 61(2017), no. 1, 40–54. https://doi.org/10.4153/CMB-2017-009-6 Google Scholar
Ding, J., Chen, L., and Gu, Y., Perturbation analysis of orthogonal matching pursuit . IEEE Trans. Signal Process. 61(2013), no. 2, 398–410. https://doi.org/10.1109/TSP.2012.2222377 Google Scholar
Donoho, D. L., Compressed sensing . IEEE Trans. Inform. Theory 56(2006), no. 4, 1289–1306. https://doi.org/10.1109/TIT.2006.871582 Google Scholar
Fannjiang, A. C., Strohmer, T., and Yan, P., Compressed remote sensing of sparse objects . SIAM J. Imaging Sci. 3(2010), no. 3, 595–618. https://doi.org/10.1137/090757034 Google Scholar
Foucart, S., Stability and robustness of weak orthogonal matching pursuits . In: Recent advances in harmonic analysis and applications , Springer Proc. Math. Stat., 25, Springer, New York, 2013. https://doi.org/10.1007/978-1-4614-4565-4_30 Google Scholar
Herman, M. A. and Needell, D., Mixed operators in compressed sensing . In: Proceedings IEEE 44th Ann. Conf. Inf. Sci. Syst. , Princeton, NJ, 2010, pp. 1–6.Google Scholar
Herman, M. A. and Strohmer, T., High-resolution radar via compressed sensing . IEEE Trans. Signal Process. 57(2009), no. 6, 2275–2284. https://doi.org/10.1109/TSP.2009.2014277 Google Scholar
Herman, M. A. and Strohmer, T., General deviants: An analysis of perturbations in compressed sensing . IEEE J. Sel. Topics Signal Process. 4(2010), no. 2, 342–349.Google Scholar
Herzet, C., Soussen, C., Idier, J., and Gribonval, R., Exact recovery conditions for sparse representations with partial support information . IEEE Trans. Inform. Theory 59(2013), no. 11, 7509–7524.Google Scholar
Li, H. and Liu, G., An improved analysis for support recovery with orthogonal matching pursuit under general perturbations . IEEE Access. 99(2018), no. 6, 18856–18867.Google Scholar
Mo, Q., A sharp restricted isometry constant bound of orthogonal matching pursuit. 2015. arxiv:1501.01708 Google Scholar
Needell, D. and Troop, J. A., CoSaMP: Iterative signal recovery from incomplete and inaccurate samples . Appl. Comput. Harmon. Anal. 26(2009), no. 3, 301–321. https://doi.org/10.1016/j.acha.2008.07.002 Google Scholar
Shen, Y., Li, B., Pan, W., and Li, J., Analysis of generalized orthogonal matching pursuit using restricted constant . Electron. Lett. 50(2014), no. 14, 1020–1022.Google Scholar
Soussen, C., Gribonval, R., Idier, J., and Herzet, C., Joint k-step analysis of orthogonal matching pursuit and orthogonal least squares . IEEE Trans. Inform. Theory 59(2013), no. 5, 3158–3174. https://doi.org/10.1109/TIT.2013.2238606 Google Scholar
Tropp, J. A. and Gilbert, A. C., Signal recovery from random measurements via orthogonal matching pursuit . IEEE Trans. Inform. Theory 53(2007), no. 12, 4655–4666. https://doi.org/10.1109/TIT.2007.909108 Google Scholar
Wang, J., Support recovery With orthogonal matching pursuit in the presence of noise . IEEE Trans. Signal Process. 63(2015), no. 21, 5868–5877. https://doi.org/10.1109/TSP.2015.2468676 Google Scholar
Wang, J., Kwon, S., Li, P, and Shim, B., Recovery of sparse signals via generalized orthogonal matching pursuit: a new analysis . IEEE Trans. Signal Process. 64(2015), no. 4, 1076–1089. https://doi.org/10.1109/TSP.2015.2498132 Google Scholar
Wang, J., Kwon, S., and Shim, B., Generalized orthogonal matching pursuit . IEEE Trans. Singnal Process. 60(2012), no. 12, 6202–6216.Google Scholar
Wang, J. and Li, P., Recovery of sparse signals using multiple orthogonal least squares . IEEE Trans. Signal Process. 65(2017), no. 8, 2049–2062. https://doi.org/10.1109/TSP.2016.2639467 Google Scholar
Wang, J. and Shim, B., On the recovery limit of sparse signals using orthogonal matching pursuit . IEEE Trans. Signal Process. 60(2012), no. 9, 4973–4976. https://doi.org/10.1109/TSP.2012.2203124 Google Scholar
Wen, J., Zhou, Z., Li, D., and Tang, X., A novel sufficient condition for generalized orthogonal matching pursuit . IEEE Comm. Lett. 21(2017), no. 4, 805–808.Google Scholar
Wen, J., Zhou, Z., Wang, J., Tang, X., and Mo, Q., A sharp condition for exact support recovery of sparse signals with orthogonal matching pursuit . IEEE Trans. Signal Process. 65(2017), 1370–1382. https://doi.org/10.1109/TSP.2016.2634550 Google Scholar
Wen, J., Wang, J., and Zhang, Q., Nearly optimal bounds for orthogonal least squares . IEEE Trans. Signal Proces. 65(2017), no. 20, 5347–5356. https://doi.org/10.1109/TSP.2017.2728502 Google Scholar