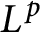 $L^p$-algebras
$L^p$-algebrasPublished online by Cambridge University Press: 30 October 2020
Let G be a locally compact group and let
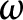 $\omega $
be a continuous weight on G. In this paper, we first characterize bicontinuous biseparating algebra isomorphisms between weighted
$\omega $
be a continuous weight on G. In this paper, we first characterize bicontinuous biseparating algebra isomorphisms between weighted
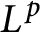 $L^p$
-algebras. As a result, we extend previous results of Edwards, Parrott, and Strichartz on algebra isomorphisms between
$L^p$
-algebras. As a result, we extend previous results of Edwards, Parrott, and Strichartz on algebra isomorphisms between
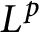 $L^p$
-algebras to the setting of weighted
$L^p$
-algebras to the setting of weighted
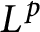 $L^p$
-algebras. We then study the automorphisms of certain weighted
$L^p$
-algebras. We then study the automorphisms of certain weighted
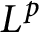 $L^p$
-algebras on integers, applying known results on composition operators to classical function spaces.
$L^p$
-algebras on integers, applying known results on composition operators to classical function spaces.
Y.K. is supported by the French “Investissements d'Avenir” program, project ISITE-BFC (contract ANR-15-IDEX-03). S.Z. is supported by the mobility program of the region of Bourgogne-Franche-Comté, France.
 ${L}_p^w(G)$
. Math. Notes 84(2008), nos. 3–4, 529–537. http://dx.doi.org/10.1134/S0001434608090241
CrossRefGoogle Scholar
${L}_p^w(G)$
. Math. Notes 84(2008), nos. 3–4, 529–537. http://dx.doi.org/10.1134/S0001434608090241
CrossRefGoogle Scholar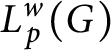 ${L}_p^w(G)$
. Mat. Sbornik 200(2009), 75–88. http://dx.doi.org/10.1070/SM2009v200n02ABEH00993
Google Scholar
${L}_p^w(G)$
. Mat. Sbornik 200(2009), 75–88. http://dx.doi.org/10.1070/SM2009v200n02ABEH00993
Google Scholar