Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T17:39:30.185Z Has data issue: false hasContentIssue false
  • English
  • Français

Representation of Groups by Generalized Normal Multiplication Tables

Published online by Cambridge University Press:  20 November 2018

A. Ginzburg
A. Ginzburg*
Affiliation:
Carnegie Institute of Technology, Pittsburgh, Pennsylvania, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

G will denote a finite (or infinite) group of order n. In a normal multiplication table (n.m.t.) of G (7, 8, 9, 12) all entries in one diagonal are equal to e (the identity of G), and if the entry on the intersection of the ith column and jth row is gi,j ∈ G, then

The following is a n.m.t. of Z6 = {0, 1, 2, 3, 4, 5}:

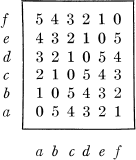
Remark. The cyclic groups Zn will always be written in additive notation. The table is uniquely defined by every one of its columns, in particular by the first.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 774 - 791
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Erdös, P. and Ginzburg, A., On a combinatorial problem in latin squares, Publ. Math. Inst. Hungar. Acad. Sci., Ser. A, 8 (1963), 407–411.Google Scholar
2. Ginzburg, A., Multiplicative systems as homomorphic images of square sets, thesis, Technion, Israel Institute of Technology, Haifa, 1959.Google Scholar
3. Ginzburg, A., Systèmes multiplicatifs de relations. Boucles quasiassociatives, C. R. Acad. Sci. Paris, 250 (1960), 1413–1416.Google Scholar
4. Ginzburg, A., A note on Cayley loops, Can. J. Math., 16 (1964), 77–81.Google Scholar
5. Ginzburg, A. and Tamari, D., Representation of binary systems by families of binary relations, submitted for publication.Google Scholar
6. Higman, B., Applied group-theoretic and matrix methods (Oxford, 1955).Google Scholar
7. Tamari, D., Monoïdes préordonnés et chaînes de Malcev, Bull. Soc. Math. France, 82 (1954), 53–96, and additional stencils with the original manuscript of this thesis.Google Scholar
8. Tamari, D., Les images homomorphes des grotipoïdes de Brandt et Vimmersion des semi-groupes, C. R. Acad. Sci. Paris, 229 (1949), 1291–1293.Google Scholar
9. Tamari, D., Représentations isomorphes par de systèmes de relations. Systèmes associatifs, C. R. Acad. Sci. Paris, 232 (1951), 1332–1334.Google Scholar
10. Tamari, D., “Near groups” as generalized normal multiplication tables, Not. Amer. Math. Soc., 7 (1960), 77.Google Scholar
11. Tamari, D. and Ginzburg, A., Representation of multiplicative systems by families of binary relations (I), J. London Math. Soc., 37 (1962), 410–423.Google Scholar
12. Zassenhaus, H. J., The theory of groups (Chelsea, 1958).Google Scholar