Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T17:32:30.153Z Has data issue: false hasContentIssue false
  • English
  • Français

On S2-Groups and Groups of Moebius Transformations

Published online by Cambridge University Press:  20 November 2018

P. J. Lorimer
P. J. Lorimer*
Affiliation:
University of Auckland, Auckland, New Zealand
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let PGL(2, ƒ) denote the group of all Moebius transformations

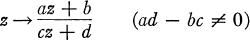
over a field F. The object of this paper is to prove the following theorem.

Theorem 1. G is an S2-group and the centre of G is trivial if and only if G is isomorphic to a group PGL(2, ƒ), char ƒ ≠ 2.

This theorem was proved for finite groups in (1). The present paper extends the result to infinite groups and also improves the method of proof used in that paper. Many of the theorems given there were proved for infinite groups and are used here with appropriate references.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 484 - 485
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Lorimer, P. J., Ti-groups and a characterization of the finite groups of Moebius transformations, Can. J. Math., 17 (1965), 353–366.Google Scholar
2. Lorimer, P. J., A characterization of the Moebius and similarity groups, J. Austral. Math. Soc. 5, Pt. 2 (1965), 237–240.Google Scholar
3. Schwerdtfeger, H. W. E., On a property of the Moebius group, Ann. di Mat. (4), 54 (1961), 23–32.Google Scholar
4. Schwerdtfeger, H. W. E., Uber eine spezielle Klasse Frobeniusscher Gruppen, Archiv der Math., 13 (1962), 283–289.Google Scholar
5. Zassenhaus, H., Kennzeichnung endlicher linear er Gruppen als Permutations gruppen, Abh. Math. Sem. Univ. Hamburg, 11 (1936), 17–40.Google Scholar