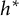1 Introduction
1.1 Overview
In the present article, we will focus on the integer point enumeration of certain polytopes that arise as a result of slicing a rectangular prism. To be precise, if
![]() $\textbf {c}=(c_1,\ldots ,c_n)$
is a vector of positive integers, we define the n-dimensional rectangular prism
$\textbf {c}=(c_1,\ldots ,c_n)$
is a vector of positive integers, we define the n-dimensional rectangular prism
This is of course a lattice polytope in
![]() $\mathbb {R}^n$
. We will be dealing with certain slices of rectangular prisms. More precisely, we define for each
$\mathbb {R}^n$
. We will be dealing with certain slices of rectangular prisms. More precisely, we define for each
![]() $k\in \mathbb {Z}_{>0}$
and
$k\in \mathbb {Z}_{>0}$
and
![]() $\textbf {c}$
as before:
$\textbf {c}$
as before:
 $$ \begin{align} \mathscr{R}_{k,\textbf{c}} := \left\{ x\in \mathscr{R}_{\textbf{c}} : \sum_{i=1}^n x_i = k\right\}. \end{align} $$
$$ \begin{align} \mathscr{R}_{k,\textbf{c}} := \left\{ x\in \mathscr{R}_{\textbf{c}} : \sum_{i=1}^n x_i = k\right\}. \end{align} $$
The problem of enumerating the lattice points lying inside a convex polytope
![]() $\mathscr {P}\subseteq \mathbb {R}^n$
with integral vertices is of fundamental importance in several areas within mathematics and has been systematically approached under different perspectives. Whenever a lattice polytope
$\mathscr {P}\subseteq \mathbb {R}^n$
with integral vertices is of fundamental importance in several areas within mathematics and has been systematically approached under different perspectives. Whenever a lattice polytope
![]() $\mathscr {P}$
is fixed, the function that associates to each positive integer t the number of integral points lying in the dilation
$\mathscr {P}$
is fixed, the function that associates to each positive integer t the number of integral points lying in the dilation
![]() $t\mathscr {P}$
, namely,
$t\mathscr {P}$
, namely,
happens to be a polynomial of degree
![]() $d = \dim \mathscr {P}$
. This polynomial, first studied by Ehrhart [Reference Ehrhart13], is known as the Ehrhart polynomial of the polytope
$d = \dim \mathscr {P}$
. This polynomial, first studied by Ehrhart [Reference Ehrhart13], is known as the Ehrhart polynomial of the polytope
![]() $\mathscr {P}$
.
$\mathscr {P}$
.
Ehrhart polynomials have proven to be a remarkably useful tool in different problems within discrete geometry and algebraic combinatorics, especially due to their connection with chromatic polynomials of graphs, order polynomials of posets, solutions of certain linear diophantine equations, Hilbert functions in commutative algebra, and toric varieties in algebraic geometry.
For some specific classes of polytopes such as regular simplices, hypercubes, cross-polytopes, and zonotopes, it is possible to determine explicitly the Ehrhart polynomial and, more specifically, its coefficients. For example, the Ehrhart polynomial of a rectangular prism admits a quite easy expression:
 $$ \begin{align} \operatorname{\mathrm{ehr}}(\mathscr{R}_{\textbf{c}}, t) = \prod_{i=1}^n (c_it+1).\end{align} $$
$$ \begin{align} \operatorname{\mathrm{ehr}}(\mathscr{R}_{\textbf{c}}, t) = \prod_{i=1}^n (c_it+1).\end{align} $$
A classical result in the theory of Ehrhart polynomials is that for every lattice polytope
![]() $\mathscr {P}$
of dimension d, if we write
$\mathscr {P}$
of dimension d, if we write
then some of the coefficients are easy to understand, i.e.,
![]() $a_0 = 1$
,
$a_0 = 1$
,
![]() $a_{d} = \operatorname {vol}(\mathscr {P})$
, and
$a_{d} = \operatorname {vol}(\mathscr {P})$
, and
![]() $a_{d-1} = \frac {1}{2} \operatorname {vol}(\partial \mathscr {P})$
; see [Reference Beck and Robins1] for detailed proofs of this fact and further exploration on the connections mentioned above. In particular, from this, we see that the Ehrhart polynomial of a polytope as an invariant is a vast generalization of the volume.
$a_{d-1} = \frac {1}{2} \operatorname {vol}(\partial \mathscr {P})$
; see [Reference Beck and Robins1] for detailed proofs of this fact and further exploration on the connections mentioned above. In particular, from this, we see that the Ehrhart polynomial of a polytope as an invariant is a vast generalization of the volume.
It is our belief that the study in this paper will be of interest and relevance in all of the following frameworks:
-
• Ehrhart positivity.
-
• Refinements and generalizations of the (flag) Eulerian numbers.
-
• Polymatroids satisfying the strong exchange property and polypositroids.
-
• Combinatorial interpretations of
 $h^*$
-polynomials.
$h^*$
-polynomials. -
• Hilbert functions of arbitrary algebras of Veronese type.
In what follows, we expand on the relation of our work with each of the above points.
1.1.1 Ehrhart positivity
By looking at equation (1.3), we see that the coefficients of the terms of degree d,
![]() $d-1$
, and
$d-1$
, and
![]() $0$
are positive for every lattice polytope. However, the remaining coefficients can be negative in general. Although there are some general formulas for computing them [Reference McMullen35], they are quite intricate. One of the major questions in the study of Ehrhart theory is to determine classes of polytopes having the property that all of the coefficients of
$0$
are positive for every lattice polytope. However, the remaining coefficients can be negative in general. Although there are some general formulas for computing them [Reference McMullen35], they are quite intricate. One of the major questions in the study of Ehrhart theory is to determine classes of polytopes having the property that all of the coefficients of
![]() $\operatorname {\mathrm{ehr}}(\mathscr {P}, t)$
are positive; such polytopes are said to be Ehrhart positive. See [Reference Liu32] for a thorough exposition regarding positivity of Ehrhart polynomials.
$\operatorname {\mathrm{ehr}}(\mathscr {P}, t)$
are positive; such polytopes are said to be Ehrhart positive. See [Reference Liu32] for a thorough exposition regarding positivity of Ehrhart polynomials.
Theorem 1.1 All slices of prisms
![]() $\mathscr {R}_{k,\textbf {c}}$
are Ehrhart positive.
$\mathscr {R}_{k,\textbf {c}}$
are Ehrhart positive.
Sometimes we informally refer to the polytopes
![]() $\mathscr {R}_{k,\textbf {c}}$
as “thin” slices of prisms. This is because if we fix
$\mathscr {R}_{k,\textbf {c}}$
as “thin” slices of prisms. This is because if we fix
![]() $\textbf {c}=(c_1,\ldots ,c_n)$
and two nonnegative integers
$\textbf {c}=(c_1,\ldots ,c_n)$
and two nonnegative integers
![]() $a < b$
, by defining
$a < b$
, by defining
 $$ \begin{align} \mathscr{R}^{\prime}_{a,b,\textbf{c}} := \left\{ x\in \mathscr{R}_{\textbf{c}} : a \leq \sum_{i=1}^n x_i \leq b\right\},\end{align} $$
$$ \begin{align} \mathscr{R}^{\prime}_{a,b,\textbf{c}} := \left\{ x\in \mathscr{R}_{\textbf{c}} : a \leq \sum_{i=1}^n x_i \leq b\right\},\end{align} $$
we obtain another type of slice of a prism. We usually refer to them as “fat” slices of a prism. The difference between these two types of slices will not be of much relevance; we will see explicitly how it is possible to transform one into the other while preserving the Ehrhart polynomials. In particular, we will also prove that fat slices of prisms are Ehrhart positive.
In fact, the Ehrhart positivity will be deduced via a combinatorial formula for each of the coefficients that reveals positivity. To formulate this statement, we introduce the notion of “
![]() $\textbf {c}$
-compatible weighted permutations” (defined in Section 3.3), where
$\textbf {c}$
-compatible weighted permutations” (defined in Section 3.3), where
![]() $\textbf {c}=(c_1,\ldots ,c_n)$
is a vector of positive integers. We define
$\textbf {c}=(c_1,\ldots ,c_n)$
is a vector of positive integers. We define
Theorem 1.2 Let
![]() $\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
and
$\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
and
![]() $0 < k < c_1+\cdots +c_n$
. For each
$0 < k < c_1+\cdots +c_n$
. For each
![]() $0\leq m\leq n-1$
, the coefficient of
$0\leq m\leq n-1$
, the coefficient of
![]() $t^m$
in
$t^m$
in
![]() $\operatorname {\mathrm{ehr}}(\mathscr {R}_{k,\textbf {c}},t)$
is given by
$\operatorname {\mathrm{ehr}}(\mathscr {R}_{k,\textbf {c}},t)$
is given by
 $$\begin{align*}[t^m]\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) = \frac{1}{(n-1)!}\sum_{\ell = 0}^{k-1}W(\ell,n,m+1,\textbf{c})A(m,k-\ell-1). \end{align*}$$
$$\begin{align*}[t^m]\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) = \frac{1}{(n-1)!}\sum_{\ell = 0}^{k-1}W(\ell,n,m+1,\textbf{c})A(m,k-\ell-1). \end{align*}$$
In particular, Theorem 1.1 holds.
Here,
![]() $A(n,k)$
stands for the Eulerian numbers, i.e., the number of permutations
$A(n,k)$
stands for the Eulerian numbers, i.e., the number of permutations
![]() $\sigma \in \mathfrak {S}_n$
having exactly k descents.
$\sigma \in \mathfrak {S}_n$
having exactly k descents.
Part of the intuition on how to properly define the notion of weights and compatibility comes from [Reference Ferroni14, Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22]. In the first of these papers, a rather easy particular case of the above description yields the Ehrhart positivity of
![]() $\Delta _{k,n} = \mathscr {R}_{k,(1,\ldots ,1)}$
, and the role of
$\Delta _{k,n} = \mathscr {R}_{k,(1,\ldots ,1)}$
, and the role of
![]() $W(\ell ,n,m+1,\textbf {c})$
in Theorem 1.2 is played by the “weighted Lah numbers”
$W(\ell ,n,m+1,\textbf {c})$
in Theorem 1.2 is played by the “weighted Lah numbers”
![]() $W(\ell ,n,m+1)$
. That explains much of the terminology and the notation that we use in the present paper. On the other hand, in [Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22], a different proof for the Ehrhart positivity of hypersimplices is outlined, the main advantage being that it does not rely on generating function identities but only on an inclusion–exclusion argument which is applied to a family of cleverly defined sets. Recently, the ideas used in the Ehrhart positivity results of these papers have also been extended and adapted in [Reference McGinnis34] to establish the Ehrhart positivity of different classes of polytopes.
$W(\ell ,n,m+1)$
. That explains much of the terminology and the notation that we use in the present paper. On the other hand, in [Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22], a different proof for the Ehrhart positivity of hypersimplices is outlined, the main advantage being that it does not rely on generating function identities but only on an inclusion–exclusion argument which is applied to a family of cleverly defined sets. Recently, the ideas used in the Ehrhart positivity results of these papers have also been extended and adapted in [Reference McGinnis34] to establish the Ehrhart positivity of different classes of polytopes.
1.1.2 Flag Eulerian numbers
Notice that a priori it is not clear what the volume of a slice of a prism will look like. A famous result attributed in [Reference Stanley39] to Laplace states that if we slice the n-dimensional unit cube, which is just
![]() $\mathscr {R}_{\textbf {c}}$
for
$\mathscr {R}_{\textbf {c}}$
for
![]() $\textbf {c} = (1,\ldots ,1)\in \mathbb {Z}^n$
, with the hyperplane
$\textbf {c} = (1,\ldots ,1)\in \mathbb {Z}^n$
, with the hyperplane
![]() $\sum _{i=1}^{n} x_i= k$
, the normalized volume of the resulting polytope is precisely the Eulerian number
$\sum _{i=1}^{n} x_i= k$
, the normalized volume of the resulting polytope is precisely the Eulerian number
![]() $A(n-1,k-1)$
, that is, the number of permutations
$A(n-1,k-1)$
, that is, the number of permutations
![]() $\sigma \in \mathfrak {S}_{n-1}$
that have exactly
$\sigma \in \mathfrak {S}_{n-1}$
that have exactly
![]() $k-1$
descents. In the literature, the set of points in the n-dimensional unit cube having sum of coordinates equal to k is known as the hypersimplex
$k-1$
descents. In the literature, the set of points in the n-dimensional unit cube having sum of coordinates equal to k is known as the hypersimplex
![]() $\Delta _{k,n}$
.
$\Delta _{k,n}$
.
We introduce the following generalization of the notion of flag Eulerian numbers in [Reference Han and Josuat-Vergès21].
Definition 1.3 The flag Eulerian number
![]() $A_{n,k}^{(\textbf {c})}$
is defined as the number of
$A_{n,k}^{(\textbf {c})}$
is defined as the number of
![]() $\textbf {c}$
-colored permutations having k flag descents.
$\textbf {c}$
-colored permutations having k flag descents.
(The notions of
![]() $\textbf {c}$
-colored permutations and flag descents will be explained later, in Section 6.) In analogy to the case of the classical Eulerian numbers, we will realize these numbers as volumes of polytopes.
$\textbf {c}$
-colored permutations and flag descents will be explained later, in Section 6.) In analogy to the case of the classical Eulerian numbers, we will realize these numbers as volumes of polytopes.
Theorem 1.4 Let
![]() $\textbf {c}=(c_1,\dots , c_{n})\in \mathbb {Z}^n_{>0}$
, and let
$\textbf {c}=(c_1,\dots , c_{n})\in \mathbb {Z}^n_{>0}$
, and let
![]() $\textbf {c}'=(c_1,\dots ,c_{n},1)$
. The normalized volume of
$\textbf {c}'=(c_1,\dots ,c_{n},1)$
. The normalized volume of
![]() $\mathscr {R}_{k+1,\textbf {c}'}$
equals the flag Eulerian number
$\mathscr {R}_{k+1,\textbf {c}'}$
equals the flag Eulerian number
![]() $A_{n,k}^{(\textbf {c})}$
.
$A_{n,k}^{(\textbf {c})}$
.
In particular, this extends some results by Han and Josuat-Vergès [Reference Han and Josuat-Vergès21] which were valid for vectors
![]() $\textbf {c}$
of the form
$\textbf {c}$
of the form
![]() $(r,\ldots ,r)$
. Since the volume is also captured as the leading coefficient of the Ehrhart polynomial, as a consequence of Theorem 1.2, we can conclude a handy formula for the volume of
$(r,\ldots ,r)$
. Since the volume is also captured as the leading coefficient of the Ehrhart polynomial, as a consequence of Theorem 1.2, we can conclude a handy formula for the volume of
![]() $\mathscr {R}_{k,\textbf {c}}$
, and thus for the flag Eulerian numbers.
$\mathscr {R}_{k,\textbf {c}}$
, and thus for the flag Eulerian numbers.
Corollary 1.5 Let
![]() $\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
. Then the volume of
$\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
. Then the volume of
![]() $\mathscr {R}_{k,\textbf {c}}$
is given by
$\mathscr {R}_{k,\textbf {c}}$
is given by
 $$\begin{align*}\operatorname{vol}(\mathscr{R}_{k,\textbf{c}}) = \frac{1}{(n-1)!}\sum_{\ell = 0}^{k-1} B(\ell,\textbf{c})A(n-1,k-\ell-1),\end{align*}$$
$$\begin{align*}\operatorname{vol}(\mathscr{R}_{k,\textbf{c}}) = \frac{1}{(n-1)!}\sum_{\ell = 0}^{k-1} B(\ell,\textbf{c})A(n-1,k-\ell-1),\end{align*}$$
where
![]() $B(\ell ,\textbf {c})$
is defined as the number of ways of placing
$B(\ell ,\textbf {c})$
is defined as the number of ways of placing
![]() $\ell $
indistinguishable balls into n boxes of capacities
$\ell $
indistinguishable balls into n boxes of capacities
![]() $c_1-1, \ldots , c_n-1$
, respectively.
$c_1-1, \ldots , c_n-1$
, respectively.
In particular, when combining the preceding two results, we obtain a combinatorial identity relating the flag Eulerian numbers with the classical Eulerian numbers.
Corollary 1.6 The flag Eulerian number
![]() $A_{n,k}^{(\textbf {c})}$
is given by
$A_{n,k}^{(\textbf {c})}$
is given by
 $$\begin{align*}A_{n,k}^{(\textbf{c})} = \sum_{\ell = 0}^{k} B(\ell, \textbf{c}) A(n, k-\ell),\end{align*}$$
$$\begin{align*}A_{n,k}^{(\textbf{c})} = \sum_{\ell = 0}^{k} B(\ell, \textbf{c}) A(n, k-\ell),\end{align*}$$
where
![]() $B(\ell ,\textbf {c})$
is defined as in Corollary 1.5.
$B(\ell ,\textbf {c})$
is defined as in Corollary 1.5.
1.1.3 Polymatroids and polypositroids
The study of the volume of the hypersimplex has been a leit motiv for several important developments in combinatorics. For instance, the hypersimplex
![]() $\Delta _{k,n}$
admits a regular unimodular triangulation as was proved by Stanley in [Reference Stanley39] (see also [Reference Sturmfels43]). Generalizing such triangulations, in [Reference Lam and Postnikov29], Lam and Postnikov introduced the notion of alcoved polytope, a family that essentially contains all hypersimplices and, more importantly, all the polytopes of the form
$\Delta _{k,n}$
admits a regular unimodular triangulation as was proved by Stanley in [Reference Stanley39] (see also [Reference Sturmfels43]). Generalizing such triangulations, in [Reference Lam and Postnikov29], Lam and Postnikov introduced the notion of alcoved polytope, a family that essentially contains all hypersimplices and, more importantly, all the polytopes of the form
![]() $\mathscr {R}_{k,\textbf {c}}$
. They proved that all alcoved polytopes possess a regular unimodular triangulation and therefore their volume can be recovered by counting the number of simplices of the triangulation (see [Reference Lam and Postnikov29, Theorem 3.2]).
$\mathscr {R}_{k,\textbf {c}}$
. They proved that all alcoved polytopes possess a regular unimodular triangulation and therefore their volume can be recovered by counting the number of simplices of the triangulation (see [Reference Lam and Postnikov29, Theorem 3.2]).
The edges of a polytope of the form
![]() $\mathscr {R}_{k,\textbf {c}}$
are parallel to some vector of the form
$\mathscr {R}_{k,\textbf {c}}$
are parallel to some vector of the form
![]() ${e_i-e_j}$
; hence, they are particular instances of generalized permutohedra or polymatroids. Actually, in the influential paper [Reference Herzog and Hibi23], these polytopes are coined “polymatroids of Veronese type.” The main result of Herzog, Hibi, and Vladoiu in [Reference Herzog, Hibi and Vladoiu24] characterizes them (up to an affinity) as the polymatroids satisfying the strong exchange property.
${e_i-e_j}$
; hence, they are particular instances of generalized permutohedra or polymatroids. Actually, in the influential paper [Reference Herzog and Hibi23], these polytopes are coined “polymatroids of Veronese type.” The main result of Herzog, Hibi, and Vladoiu in [Reference Herzog, Hibi and Vladoiu24] characterizes them (up to an affinity) as the polymatroids satisfying the strong exchange property.
More recently, Lam and Postnikov studied in [Reference Lam and Postnikov30] the class of polypositroids, the family of all polytopes that are simultaneously polymatroids and alcoved polytopes. The polytopes
![]() $\mathscr {R}_{k,\textbf {c}}$
are polypositroids; hence, an additional combinatorial toolbox is at disposal for their study. In the past two decades, the Ehrhart theory of the hypersimplex and other alcoved polytopes and polymatroids has been matter of intensive research, motivated in part due to the conjectures posed by De Loera, Haws, and Köppe in [Reference De Loera, Haws and Köppe9]. In [Reference Postnikov37], Postnikov proved the Ehrhart positivity of certain polymatroids arising as Minkowski sums of simplices. In [Reference Ferroni14], Ferroni gave a combinatorial formula for the Ehrhart coefficients of the hypersimplex
$\mathscr {R}_{k,\textbf {c}}$
are polypositroids; hence, an additional combinatorial toolbox is at disposal for their study. In the past two decades, the Ehrhart theory of the hypersimplex and other alcoved polytopes and polymatroids has been matter of intensive research, motivated in part due to the conjectures posed by De Loera, Haws, and Köppe in [Reference De Loera, Haws and Köppe9]. In [Reference Postnikov37], Postnikov proved the Ehrhart positivity of certain polymatroids arising as Minkowski sums of simplices. In [Reference Ferroni14], Ferroni gave a combinatorial formula for the Ehrhart coefficients of the hypersimplex
![]() $\Delta _{k,n}$
(see also [Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22]). In [Reference Castillo and Liu6, Reference Castillo and Liu7], Castillo and Liu proved the positivity of the Ehrhart coefficients of high degree and the linear term for arbitrary polymatroids; the latter was also proved in [Reference Jochemko and Ravichandran26]. Although arbitrary polymatroids can have negative Ehrhart coefficients [Reference Ferroni16], it is conjectured in [Reference Ferroni, Jochemko and Schröter18] that positroids are indeed Ehrhart positive. We remark that it is not true that general alcoved polytopes are Ehrhart positive, as in fact the class of order polytopes fails to be Ehrhart positive as was shown by Stanley (see [Reference Liu and Tsuchiya33]). For a more detailed state of the art, we refer to a recent survey by Ferroni and Higashitani [Reference Ferroni and Higashitani17].
$\Delta _{k,n}$
(see also [Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22]). In [Reference Castillo and Liu6, Reference Castillo and Liu7], Castillo and Liu proved the positivity of the Ehrhart coefficients of high degree and the linear term for arbitrary polymatroids; the latter was also proved in [Reference Jochemko and Ravichandran26]. Although arbitrary polymatroids can have negative Ehrhart coefficients [Reference Ferroni16], it is conjectured in [Reference Ferroni, Jochemko and Schröter18] that positroids are indeed Ehrhart positive. We remark that it is not true that general alcoved polytopes are Ehrhart positive, as in fact the class of order polytopes fails to be Ehrhart positive as was shown by Stanley (see [Reference Liu and Tsuchiya33]). For a more detailed state of the art, we refer to a recent survey by Ferroni and Higashitani [Reference Ferroni and Higashitani17].
1.1.4 Combinatorial interpretations for
 $h^*$
-polynomial-vectors
$h^*$
-polynomial-vectors
The study of the
![]() $h^*$
-polynomial (which encodes the same information as the usual Ehrhart polynomial) of alcoved polytopes is an intriguing and very active area of research (see, for instance, recent work [Reference Ferroni, Jochemko and Schröter18, Reference Sinn and Sjöberg38]). The
$h^*$
-polynomial (which encodes the same information as the usual Ehrhart polynomial) of alcoved polytopes is an intriguing and very active area of research (see, for instance, recent work [Reference Ferroni, Jochemko and Schröter18, Reference Sinn and Sjöberg38]). The
![]() $h^*$
-polynomial of
$h^*$
-polynomial of
![]() $\Delta _{k,n}$
exhibits remarkable combinatorial properties, and has been described by Li [Reference Li31] and by Early [Reference Early12] and Kim [Reference Kim28] using different approaches. This problem had also been studied by Katzman in [Reference Katzman27], where the problem of giving a combinatorial interpretation for this remained widely open.
$\Delta _{k,n}$
exhibits remarkable combinatorial properties, and has been described by Li [Reference Li31] and by Early [Reference Early12] and Kim [Reference Kim28] using different approaches. This problem had also been studied by Katzman in [Reference Katzman27], where the problem of giving a combinatorial interpretation for this remained widely open.
Due to Stanley’s result [Reference Stanley40] that shows that the coefficients of the
![]() $h^*$
-polynomial of a polytope always are nonnegative integers, it is highly desirable to provide combinatorial interpretations for these numbers. The second main result of this paper consists of such a combinatorial interpretation for the polytopes
$h^*$
-polynomial of a polytope always are nonnegative integers, it is highly desirable to provide combinatorial interpretations for these numbers. The second main result of this paper consists of such a combinatorial interpretation for the polytopes
![]() $\mathscr {R}_{k,\textbf {c}}$
. We will generalize Kim’s result to all slices of prisms.
$\mathscr {R}_{k,\textbf {c}}$
. We will generalize Kim’s result to all slices of prisms.
Theorem 1.7 Let
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and
![]() $0<k<c_1+\cdots +c_n$
. For each
$0<k<c_1+\cdots +c_n$
. For each
![]() $0\leq i\leq n$
, the coefficient
$0\leq i\leq n$
, the coefficient
![]() $[x^i]h^*(\mathscr {R}_{k,\textbf {c}},x)$
equals the number of
$[x^i]h^*(\mathscr {R}_{k,\textbf {c}},x)$
equals the number of
![]() $\textbf {c}$
-compatible decorated ordered set partitions of type
$\textbf {c}$
-compatible decorated ordered set partitions of type
![]() $(k,n)$
having winding number i.
$(k,n)$
having winding number i.
Again, we defer to Section 5 the definitions and the terminology for the above statement. On the other hand, since the sum of the entries of the
![]() $h^*$
-vector of a polytope equals the normalized volume, then each of the above coefficients provides a refinement for the flag Eulerian numbers.
$h^*$
-vector of a polytope equals the normalized volume, then each of the above coefficients provides a refinement for the flag Eulerian numbers.
1.1.5 Hilbert functions and algebras of Veronese type
Our results admit an interesting interpretation from the perspective of commutative algebra. Let us fix a field
![]() $\mathbb {F}$
, a vector
$\mathbb {F}$
, a vector
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}^n_{>0}$
, and a positive integer
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}^n_{>0}$
, and a positive integer
![]() $k<c_1+\cdots +c_n$
. Consider
$k<c_1+\cdots +c_n$
. Consider
![]() $\mathscr {V}(\textbf {c},k)$
, the graded subalgebra of
$\mathscr {V}(\textbf {c},k)$
, the graded subalgebra of
![]() $\mathbb {F}[x_1,\ldots ,x_n]$
generated by all the monomials
$\mathbb {F}[x_1,\ldots ,x_n]$
generated by all the monomials
![]() $x_1^{\alpha _1}\cdots x_n^{\alpha _n}$
where
$x_1^{\alpha _1}\cdots x_n^{\alpha _n}$
where
![]() $\alpha _1+\cdots +\alpha _n=k$
and
$\alpha _1+\cdots +\alpha _n=k$
and
![]() $\alpha _i\leq c_i$
for each
$\alpha _i\leq c_i$
for each
![]() $1\leq i\leq n$
. We say that the algebra
$1\leq i\leq n$
. We say that the algebra
![]() $\mathscr {V}(\textbf {c},k)$
is of Veronese type. There is considerable literature on this topic, including [Reference Bruns, Vasconcelos and Villarreal5, Reference De Negri and Hibi10, Reference Katzman27, Reference Herzog and Zhu25].
$\mathscr {V}(\textbf {c},k)$
is of Veronese type. There is considerable literature on this topic, including [Reference Bruns, Vasconcelos and Villarreal5, Reference De Negri and Hibi10, Reference Katzman27, Reference Herzog and Zhu25].
Since
![]() $\mathscr {A}:=\mathscr {V}(\textbf {c},k)$
is isomorphic to the Ehrhart ring of
$\mathscr {A}:=\mathscr {V}(\textbf {c},k)$
is isomorphic to the Ehrhart ring of
![]() $\mathscr {R}_{k,\textbf {c}}$
, we can relate the Ehrhart polynomial with the Hilbert function, i.e.,
$\mathscr {R}_{k,\textbf {c}}$
, we can relate the Ehrhart polynomial with the Hilbert function, i.e.,
where
![]() $\mathscr {A}^m$
is the graded component of degree m of
$\mathscr {A}^m$
is the graded component of degree m of
![]() $\mathscr {A}$
.
$\mathscr {A}$
.
Corollary 1.8 Let
![]() $\mathscr {A}$
be an arbitrary algebra of Veronese type. Then the Hilbert function of
$\mathscr {A}$
be an arbitrary algebra of Veronese type. Then the Hilbert function of
![]() $\mathscr {A}$
is a polynomial with positive coefficients.
$\mathscr {A}$
is a polynomial with positive coefficients.
In addition to the positivity of the coefficients, of course we get the combinatorial interpretation provided by Theorem 1.2. On the other hand, we also obtain an interpretation for the coefficients of their h-vectors, i.e., the numerators of the Hilbert series.
Corollary 1.9 The ith entry of the h-vector of the algebra of Veronese type
![]() $\mathscr {V}(\textbf {c},k)$
over the field
$\mathscr {V}(\textbf {c},k)$
over the field
![]() $\mathbb {F}$
counts the number of
$\mathbb {F}$
counts the number of
![]() $\textbf {c}$
-compatible decorated ordered partitions of type
$\textbf {c}$
-compatible decorated ordered partitions of type
![]() $(k,n)$
and winding number i.
$(k,n)$
and winding number i.
1.2 Outline
The paper is structured as follows. In Section 2, we describe the basics of the Ehrhart theory of both “thin” and “fat” slices of prisms and provide a first explicit formula for the Ehrhart polynomial. Although this formula, stated in Theorem 2.5, does not reveal the positivity of the coefficients, it happens to be interesting on its own. In Section 3, we introduce the notion of “
![]() $\textbf {c}$
-compatible weighted permutations” following [Reference Ferroni14, Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22], which allows us to define the numbers
$\textbf {c}$
-compatible weighted permutations” following [Reference Ferroni14, Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22], which allows us to define the numbers
![]() $W(\ell ,n,m+1,\textbf {c})$
appearing in Theorem 1.2. The definition is somewhat involved, and the enumeration of such objects, achieved in Theorem 3.11, is arguably the most technical part of the paper. In Section 4, we state and prove Theorem 1.2. In Section 5, we approach the
$W(\ell ,n,m+1,\textbf {c})$
appearing in Theorem 1.2. The definition is somewhat involved, and the enumeration of such objects, achieved in Theorem 3.11, is arguably the most technical part of the paper. In Section 4, we state and prove Theorem 1.2. In Section 5, we approach the
![]() $h^*$
-polynomials of
$h^*$
-polynomials of
![]() $\mathscr {R}_{k,\textbf {c}}$
inspired by [Reference Early12, Reference Kim28]; the main difficulty with this section is coming up with the right definitions, but once this is done, Kim’s techniques can be applied in a rather direct manner. Finally, in Section 6, we discuss some applications, in particular we prove Corollary 1.5 and discuss Corollary 1.9; we extend results by Han and Josuat-Vergès [Reference Han and Josuat-Vergès21] by combining our results and a generalized version of their notion of flag Eulerian number; finally, also in Section 6, we give a short proof of the Ehrhart positivity of the independence polytope of all uniform matroids.
$\mathscr {R}_{k,\textbf {c}}$
inspired by [Reference Early12, Reference Kim28]; the main difficulty with this section is coming up with the right definitions, but once this is done, Kim’s techniques can be applied in a rather direct manner. Finally, in Section 6, we discuss some applications, in particular we prove Corollary 1.5 and discuss Corollary 1.9; we extend results by Han and Josuat-Vergès [Reference Han and Josuat-Vergès21] by combining our results and a generalized version of their notion of flag Eulerian number; finally, also in Section 6, we give a short proof of the Ehrhart positivity of the independence polytope of all uniform matroids.
2 Slices of prisms
The main goal in this section is to provide a handy expression for the Ehrhart polynomial of the slices of prisms. This is done in Theorem 2.5. The main drawback is that we cannot see the coefficients directly and we cannot even be sure that they are positive. Nevertheless, this concrete expression will allow us to unveil a nice factorization in Section 4 that provides us with the combinatorial formula of Theorem 1.2.
2.1 Thin and fat slices
By definition, the polytope
![]() $\mathscr {R}_{k,\textbf {c}}$
introduced in equation (1.1) is the intersection between an n-dimensional rectangular prism and a hyperplane. It is an
$\mathscr {R}_{k,\textbf {c}}$
introduced in equation (1.1) is the intersection between an n-dimensional rectangular prism and a hyperplane. It is an
![]() $(n-1)$
-dimensional polytope, unless
$(n-1)$
-dimensional polytope, unless
![]() $k = 0$
or
$k = 0$
or
![]() $k = c_1+\cdots +c_n$
: in these two cases, it collapses to a point; also, it will be certainly empty if
$k = c_1+\cdots +c_n$
: in these two cases, it collapses to a point; also, it will be certainly empty if
![]() $k> c_1+\cdots +c_n$
. The combinatorics of slices of prisms, i.e., their face lattices, are much richer than for hypersimplices. For an elementary treatment of the face enumeration of certain slices of cubes, we refer to a beautiful article by Chakerian and Logothetti [Reference Chakerian and Logothetti8].
$k> c_1+\cdots +c_n$
. The combinatorics of slices of prisms, i.e., their face lattices, are much richer than for hypersimplices. For an elementary treatment of the face enumeration of certain slices of cubes, we refer to a beautiful article by Chakerian and Logothetti [Reference Chakerian and Logothetti8].
Example 2.1 Consider the vector
![]() $\textbf {c}=(6,3,4)$
and take
$\textbf {c}=(6,3,4)$
and take
![]() $k = 7$
. The polytope
$k = 7$
. The polytope
![]() $\mathscr {R}_{k,\textbf {c}}$
is obtained as the intersection of a rectangular prism in
$\mathscr {R}_{k,\textbf {c}}$
is obtained as the intersection of a rectangular prism in
![]() $\mathbb {R}^3$
and the hyperplane
$\mathbb {R}^3$
and the hyperplane
![]() $x+y+z=7$
, as depicted on the left in Figure 1. We can see that it corresponds to a pentagon in
$x+y+z=7$
, as depicted on the left in Figure 1. We can see that it corresponds to a pentagon in
![]() $\mathbb {R}^3$
with vertices
$\mathbb {R}^3$
with vertices
![]() $(6,0,1)$
,
$(6,0,1)$
,
![]() $(6,1,0)$
,
$(6,1,0)$
,
![]() $(4,3,0)$
,
$(4,3,0)$
,
![]() $(0,3,4)$
, and
$(0,3,4)$
, and
![]() $(3,0,4)$
, shown on the right of Figure 1. Furthermore, notice that the combinatorics of this polytope is genuinely different to that of all hypersimplices having dimension 2 (no hypersimplex is a pentagon).
$(3,0,4)$
, shown on the right of Figure 1. Furthermore, notice that the combinatorics of this polytope is genuinely different to that of all hypersimplices having dimension 2 (no hypersimplex is a pentagon).

Figure 1: The polytope
![]() $\mathscr {R}_{7,(6,3,4)}$
.
$\mathscr {R}_{7,(6,3,4)}$
.
We will sometimes restrict to the case in which
![]() $0 < k < c_1+\cdots +c_n$
; under this assumption, the Ehrhart polynomial has degree
$0 < k < c_1+\cdots +c_n$
; under this assumption, the Ehrhart polynomial has degree
![]() $n-1$
. Slices of prisms are always integral polytopes because they are discrete polymatroids (see Proposition 2.3 below).
$n-1$
. Slices of prisms are always integral polytopes because they are discrete polymatroids (see Proposition 2.3 below).
As we mentioned in the Introduction, the Ehrhart theory of the “thin” slices
![]() $\mathscr {R}_{k,\textbf {c}}$
defined in (1.1) and the “fat” slices
$\mathscr {R}_{k,\textbf {c}}$
defined in (1.1) and the “fat” slices
![]() $\mathscr {R}^{\prime }_{a,b,\textbf {c}}$
defined in (1.4) is essentially the same. Let us state this more precisely. Two lattice polytopes
$\mathscr {R}^{\prime }_{a,b,\textbf {c}}$
defined in (1.4) is essentially the same. Let us state this more precisely. Two lattice polytopes
![]() $\mathscr {P}_1\subseteq {\mathbb {R}}^n$
and
$\mathscr {P}_1\subseteq {\mathbb {R}}^n$
and
![]() $\mathscr {P}_2\subseteq {\mathbb {R}}^m$
are said to be integrally equivalent when there is an affine map
$\mathscr {P}_2\subseteq {\mathbb {R}}^m$
are said to be integrally equivalent when there is an affine map
![]() $\varphi :{\mathbb {R}}^n\to {\mathbb {R}}^m$
such that its restriction to
$\varphi :{\mathbb {R}}^n\to {\mathbb {R}}^m$
such that its restriction to
![]() $\mathscr {P}_1$
induces a bijection
$\mathscr {P}_1$
induces a bijection
![]() $\varphi :\mathscr {P}_1\to \mathscr {P}_2$
which preserves the lattice, i.e., the image under
$\varphi :\mathscr {P}_1\to \mathscr {P}_2$
which preserves the lattice, i.e., the image under
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbb {Z}^n \cap \operatorname {aff}\mathscr {P}_1$
is
$\mathbb {Z}^n \cap \operatorname {aff}\mathscr {P}_1$
is
![]() $\mathbb {Z}^m \cap \operatorname {aff}\mathscr {P}_2$
, where
$\mathbb {Z}^m \cap \operatorname {aff}\mathscr {P}_2$
, where
![]() $\operatorname {aff}\mathscr {P}_1$
denotes the affine space spanned by
$\operatorname {aff}\mathscr {P}_1$
denotes the affine space spanned by
![]() $\mathscr {P}_1$
and analogously for
$\mathscr {P}_1$
and analogously for
![]() $\mathscr {P}_2$
. Something immediate from the definitions is that integrally equivalent polytopes have the same Ehrhart polynomial.
$\mathscr {P}_2$
. Something immediate from the definitions is that integrally equivalent polytopes have the same Ehrhart polynomial.
Proposition 2.2 Let
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and
![]() $0\leq a < b$
. There is an integral equivalence between
$0\leq a < b$
. There is an integral equivalence between
![]() $\mathscr {R}^{\prime }_{a,b,\textbf {c}}$
(cf. equation (1.4)) and
$\mathscr {R}^{\prime }_{a,b,\textbf {c}}$
(cf. equation (1.4)) and
![]() $\mathscr {R}_{b,\textbf {c}'}$
, where
$\mathscr {R}_{b,\textbf {c}'}$
, where
![]() $\textbf {c}'\in \mathbb {Z}_{>0}^{n+1}$
is given by
$\textbf {c}'\in \mathbb {Z}_{>0}^{n+1}$
is given by
![]() $\textbf {c}' = (\textbf {c}, b-a)$
. In particular,
$\textbf {c}' = (\textbf {c}, b-a)$
. In particular,
Proof Let us prove that, using the notation of the statement, the two polytopes
![]() $\mathscr {R}^{\prime }_{a,b,\textbf {c}}$
and
$\mathscr {R}^{\prime }_{a,b,\textbf {c}}$
and
![]() $\mathscr {R}_{b,\textbf {c}'}$
are integrally equivalent. Notice that the polytope
$\mathscr {R}_{b,\textbf {c}'}$
are integrally equivalent. Notice that the polytope
![]() $\mathscr {R}_{b,\textbf {c}'}$
lies in
$\mathscr {R}_{b,\textbf {c}'}$
lies in
![]() $\mathbb {R}^{n+1}$
, whereas
$\mathbb {R}^{n+1}$
, whereas
![]() $\mathscr {R}^{\prime }_{a,b,\textbf {c}}\subseteq \mathbb {R}^n$
. Let us consider the map
$\mathscr {R}^{\prime }_{a,b,\textbf {c}}\subseteq \mathbb {R}^n$
. Let us consider the map
![]() $\pi : \mathbb {R}^{n+1}\to \mathbb {R}^n$
that forgets the last coordinate. The image of the polytope
$\pi : \mathbb {R}^{n+1}\to \mathbb {R}^n$
that forgets the last coordinate. The image of the polytope
![]() $\mathscr {R}_{b,\textbf {c}'}\subseteq \mathbb {R}^{n+1}$
is given by
$\mathscr {R}_{b,\textbf {c}'}\subseteq \mathbb {R}^{n+1}$
is given by
 $$\begin{align*}\pi(\mathscr{R}_{b,\textbf{c}'}) = \left\{ x\in \mathscr{R}_{\textbf{c}} : a\leq \sum_{i=1}^{n} x_i \leq b \right\} = \mathscr{R}^{\prime}_{a,b,\textbf{c}}.\end{align*}$$
$$\begin{align*}\pi(\mathscr{R}_{b,\textbf{c}'}) = \left\{ x\in \mathscr{R}_{\textbf{c}} : a\leq \sum_{i=1}^{n} x_i \leq b \right\} = \mathscr{R}^{\prime}_{a,b,\textbf{c}}.\end{align*}$$
Moreover, the restriction of
![]() $\pi $
to
$\pi $
to
![]() $\mathscr {R}_{b,\textbf {c}'}$
is in fact a bijection which preserves the lattice. To see this, notice that every lattice point in
$\mathscr {R}_{b,\textbf {c}'}$
is in fact a bijection which preserves the lattice. To see this, notice that every lattice point in
![]() $\mathbb {R}^{n+1}$
having sum of coordinates equal to b can be recovered by knowing the first n coordinates, and its preimage has to be a lattice point.
$\mathbb {R}^{n+1}$
having sum of coordinates equal to b can be recovered by knowing the first n coordinates, and its preimage has to be a lattice point.
It is because of this property that we will focus only on the Ehrhart theory of the “thin” slices of prisms.
2.2 Polymatroids with the strong exchange property
In [Reference Herzog and Hibi23], Herzog and Hibi introduced the notion of polymatroid of Veronese type. For the necessary background on polymatroids, we refer to their article, in particular [Reference Herzog and Hibi23, Example 2.6].
Proposition 2.3 Base polytopes of discrete polymatroids of Veronese type are slices of prisms. Conversely, every slice of a prism arises in this way.
In particular, since base polytopes of polymatroids are generalized permutohedra, we obtain that the edge directions of any slice of a prism is of the form
![]() $e_i-e_j$
. On the other hand, in light of the form of the inequalities that describe a slice of a prism, it follows that they are alcoved polytopes (as in [Reference Lam and Postnikov30]), hence:
$e_i-e_j$
. On the other hand, in light of the form of the inequalities that describe a slice of a prism, it follows that they are alcoved polytopes (as in [Reference Lam and Postnikov30]), hence:
Corollary 2.4 Slices of prisms are polypositroids.
Undertaking the discussion on polymatroids of Veronese type, as we mentioned in the Introduction, they admit a very neat characterization. They are (up to an affinity) precisely the discrete polymatroids that satisfy the strong exchange property (we refer to [Reference Herzog, Hibi and Vladoiu24] for the details).
2.3 The Ehrhart polynomial explicitly
Toward a proof of Theorem 1.2, the first step is to give a somewhat explicit expression for the Ehrhart polynomial of
![]() $\mathscr {R}_{k,\textbf {c}}$
. To simplify the statement, we introduce some notation. From now on, whenever
$\mathscr {R}_{k,\textbf {c}}$
. To simplify the statement, we introduce some notation. From now on, whenever
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{> 0}^n$
is fixed, for each
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{> 0}^n$
is fixed, for each
![]() $0\leq j \leq n$
, we will denote
$0\leq j \leq n$
, we will denote
 $$ \begin{align} \rho_{\textbf{c},j}(s) := \#\left\{ I\in \binom{[n]}{j} : \sum_{i \in I} c_i = s\right\}.\end{align} $$
$$ \begin{align} \rho_{\textbf{c},j}(s) := \#\left\{ I\in \binom{[n]}{j} : \sum_{i \in I} c_i = s\right\}.\end{align} $$
In other words,
![]() $\rho _{\textbf {c},j}(s)$
is the number of ways of choosing exactly j of the
$\rho _{\textbf {c},j}(s)$
is the number of ways of choosing exactly j of the
![]() $c_i$
’s in such a way that their sum is exactly s. If
$c_i$
’s in such a way that their sum is exactly s. If
![]() $j=0$
, we define
$j=0$
, we define
![]() $\rho _{\textbf {c},j}(s)$
to be
$\rho _{\textbf {c},j}(s)$
to be
![]() $1$
if
$1$
if
![]() $s=0$
and
$s=0$
and
![]() $0$
otherwise. The following result, also appearing in [Reference Katzman27, Theorem 2.1], is only a preliminary step toward the main proofs of this article.
$0$
otherwise. The following result, also appearing in [Reference Katzman27, Theorem 2.1], is only a preliminary step toward the main proofs of this article.
Theorem 2.5 Let
![]() $\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
. For each positive integer k, the Ehrhart polynomial of the polytope
$\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
. For each positive integer k, the Ehrhart polynomial of the polytope
![]() $\mathscr {R}_{k,\textbf {c}}$
is given by
$\mathscr {R}_{k,\textbf {c}}$
is given by
 $$\begin{align*}\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t)= \sum_{j=0}^{k-1}(-1)^j\sum_{v=0}^{k-1} \binom{t(k-v)+n-1-j}{n-1} \rho_{\textbf{c},j}(v). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t)= \sum_{j=0}^{k-1}(-1)^j\sum_{v=0}^{k-1} \binom{t(k-v)+n-1-j}{n-1} \rho_{\textbf{c},j}(v). \end{align*}$$
Proof By using the definition, we can write
 $$\begin{align*}\mathscr{R}_{k,\textbf{c}} = \left\{ x\in \mathbb{R}^n_{\geq 0} : \sum_{i=1}^n x_i = k \text{ and } x_i \leq c_i \text{ for all }1\leq i \leq n \right\}.\end{align*}$$
$$\begin{align*}\mathscr{R}_{k,\textbf{c}} = \left\{ x\in \mathbb{R}^n_{\geq 0} : \sum_{i=1}^n x_i = k \text{ and } x_i \leq c_i \text{ for all }1\leq i \leq n \right\}.\end{align*}$$
Therefore, it follows that
 $$ \begin{align*} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}}, t) &= \#(t \mathscr{R}_{k,\textbf{c}} \cap \mathbb{Z}^n)\\ &= \# \left\{ x\in \mathbb{Z}_{\geq 0}^n: \sum_{i=1}^n x_i = kt \text{ and } x_i \leq c_it \text{ for all }1\leq i \leq n \right\}\\ &= [x^{kt}] \prod_{i=1}^n (1+x+x^2+\cdots+x^{c_it}). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}}, t) &= \#(t \mathscr{R}_{k,\textbf{c}} \cap \mathbb{Z}^n)\\ &= \# \left\{ x\in \mathbb{Z}_{\geq 0}^n: \sum_{i=1}^n x_i = kt \text{ and } x_i \leq c_it \text{ for all }1\leq i \leq n \right\}\\ &= [x^{kt}] \prod_{i=1}^n (1+x+x^2+\cdots+x^{c_it}). \end{align*} $$
Using the identity
![]() $1+x+\cdots +x^{c_it} = \dfrac {1-x^{c_it+1}}{1-x}$
, we can further reduce
$1+x+\cdots +x^{c_it} = \dfrac {1-x^{c_it+1}}{1-x}$
, we can further reduce
 $$ \begin{align} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) = [x^{kt}] \left( \frac{1}{(1-x)^n} \prod_{i=1}^n (1-x^{c_it+1})\right). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) = [x^{kt}] \left( \frac{1}{(1-x)^n} \prod_{i=1}^n (1-x^{c_it+1})\right). \end{align} $$
Now, let us consider a generic coefficient of the factor
![]() $\prod _{i=1}^n (1-x^{c_it+1})$
; we can write
$\prod _{i=1}^n (1-x^{c_it+1})$
; we can write
 $$ \begin{align} [x^u] \prod_{i=1}^n (1-x^{c_it+1}) = \sum_{j=0}^n(-1)^j\#\left\{i_1<\cdots<i_j : \sum_{\ell=1}^j (c_{i_\ell}t+1) = u\right\}. \end{align} $$
$$ \begin{align} [x^u] \prod_{i=1}^n (1-x^{c_it+1}) = \sum_{j=0}^n(-1)^j\#\left\{i_1<\cdots<i_j : \sum_{\ell=1}^j (c_{i_\ell}t+1) = u\right\}. \end{align} $$
Thus, we can use what we obtained in equation (2.3) to simplify our formula in (2.2). Recall the classical generating function identity:
![]() $\frac {1}{(1-x)^n} = \sum _{i=0}^{\infty } \binom {n-1+i}{n-1} x^i$
.
$\frac {1}{(1-x)^n} = \sum _{i=0}^{\infty } \binom {n-1+i}{n-1} x^i$
.
 $$ \begin{align*} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) &= [x^{kt}] \left( \frac{1}{(1-x)^n} \prod_{i=1}^n (1-x^{c_it+1})\right)\\ &= [x^{kt}] \left( \sum_{i=0}^{\infty} \binom{n-1+i}{n-1}x^i \cdot \prod_{i=1}^n (1-x^{c_it+1})\right)\\ &= \sum_{u=0}^{kt} \binom{n-1+kt-u}{n-1}\left([x^u] \prod_{i=1}^n (1-x^{c_it+1})\right)\\ &= \sum_{u=0}^{kt} \binom{n-1+kt-u}{n-1} \sum_{j=0}^{k-1}(-1)^j\#\left\{i_1<\cdots<i_j : \sum_{\ell=1}^j (c_{i_\ell}t+1) = u\right\}\\ &= \sum_{j=0}^{k-1} (-1)^j \underbrace{\sum_{u=0}^{kt} \binom{n-1+kt-u}{n-1}\#\left\{i_1<\cdots<i_j : \sum_{\ell=1}^j (c_{i_\ell}t+1) = u\right\}}_{(\star)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) &= [x^{kt}] \left( \frac{1}{(1-x)^n} \prod_{i=1}^n (1-x^{c_it+1})\right)\\ &= [x^{kt}] \left( \sum_{i=0}^{\infty} \binom{n-1+i}{n-1}x^i \cdot \prod_{i=1}^n (1-x^{c_it+1})\right)\\ &= \sum_{u=0}^{kt} \binom{n-1+kt-u}{n-1}\left([x^u] \prod_{i=1}^n (1-x^{c_it+1})\right)\\ &= \sum_{u=0}^{kt} \binom{n-1+kt-u}{n-1} \sum_{j=0}^{k-1}(-1)^j\#\left\{i_1<\cdots<i_j : \sum_{\ell=1}^j (c_{i_\ell}t+1) = u\right\}\\ &= \sum_{j=0}^{k-1} (-1)^j \underbrace{\sum_{u=0}^{kt} \binom{n-1+kt-u}{n-1}\#\left\{i_1<\cdots<i_j : \sum_{\ell=1}^j (c_{i_\ell}t+1) = u\right\}}_{(\star)}. \end{align*} $$
Let us focus on the sum labeled by
![]() $(\star )$
. If
$(\star )$
. If
![]() $j=0$
, then it reduces to
$j=0$
, then it reduces to
![]() $\binom {n-1+kt}{n-1}$
, since only
$\binom {n-1+kt}{n-1}$
, since only
![]() $u=0$
contributes, as the sum of the “empty choice” of
$u=0$
contributes, as the sum of the “empty choice” of
![]() $c_i$
’s is zero by definition. On the other hand, if we assume that
$c_i$
’s is zero by definition. On the other hand, if we assume that
![]() $j\geq 1$
, then the condition
$j\geq 1$
, then the condition
![]() $\sum _{\ell =1}^j (c_{i_\ell }t+1) = u$
implies that
$\sum _{\ell =1}^j (c_{i_\ell }t+1) = u$
implies that
![]() $(c_{i_1}+\cdots +c_{i_j})t + j = u$
, and hence
$(c_{i_1}+\cdots +c_{i_j})t + j = u$
, and hence
![]() $u\equiv j\pmod {t}$
. Therefore, since
$u\equiv j\pmod {t}$
. Therefore, since
![]() $0\leq u\leq kt$
, we look only at the values
$0\leq u\leq kt$
, we look only at the values
![]() $u = j$
,
$u = j$
,
![]() $u=t+j$
,
$u=t+j$
,
![]() $u=2t+j$
, …,
$u=2t+j$
, …,
![]() $u = (k-1)t+j$
. Namely,
$u = (k-1)t+j$
. Namely,
 $$ \begin{align*} (\star) &= \sum_{v=0}^{k-1} \binom{n-1+kt-(vt+j)}{n-1} \# \left\{i_1<\cdots<i_j : c_{i_1}+\cdots+c_{i_j} = v\right\}\\ &= \sum_{v=0}^{k-1} \binom{t(k-v)+n-1-j}{n-1} \rho_{\textbf{c},j}(v). \end{align*} $$
$$ \begin{align*} (\star) &= \sum_{v=0}^{k-1} \binom{n-1+kt-(vt+j)}{n-1} \# \left\{i_1<\cdots<i_j : c_{i_1}+\cdots+c_{i_j} = v\right\}\\ &= \sum_{v=0}^{k-1} \binom{t(k-v)+n-1-j}{n-1} \rho_{\textbf{c},j}(v). \end{align*} $$
Thus, we obtain
 $$\begin{align*}\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) = \sum_{j=0}^{k-1}(-1)^j \sum_{v=0}^{k-1}\binom{t(k-v)+n-1-j}{n-1}\rho_{\textbf{c},j}(v), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) = \sum_{j=0}^{k-1}(-1)^j \sum_{v=0}^{k-1}\binom{t(k-v)+n-1-j}{n-1}\rho_{\textbf{c},j}(v), \end{align*}$$
and the proof is complete.
As Katzman notes in [Reference Katzman27], the particular case
![]() $\textbf {c} = (1,\ldots ,1)$
yields
$\textbf {c} = (1,\ldots ,1)$
yields
 $$\begin{align*}\rho_{\textbf{c},j}(v) = \left\{ \begin{matrix} \binom{n}{j}, & \text{ if }v=j,\\ 0, & \text{ if }v\neq j,\end{matrix} \right.\end{align*}$$
$$\begin{align*}\rho_{\textbf{c},j}(v) = \left\{ \begin{matrix} \binom{n}{j}, & \text{ if }v=j,\\ 0, & \text{ if }v\neq j,\end{matrix} \right.\end{align*}$$
and the formula reduces to
 $$\begin{align*}\operatorname{\mathrm{ehr}}(\Delta_{k,n}, t) = \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,(1,\ldots,1)},t)= \sum_{j=0}^{k-1}(-1)^j \binom{n}{j}\binom{t(k-j)+n-1-j}{n-1},\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ehr}}(\Delta_{k,n}, t) = \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,(1,\ldots,1)},t)= \sum_{j=0}^{k-1}(-1)^j \binom{n}{j}\binom{t(k-j)+n-1-j}{n-1},\end{align*}$$
which is the well-known formula for the Ehrhart polynomial of the hypersimplex appearing in Stanley’s book [Reference Stanley41, Exercise 4.62]. Notice that even in this very particular case this sum is alternating in sign and that the variable t appears inside a binomial coefficient, which is actually a polynomial with some negative coefficients when
![]() $j\geq 2$
. The positivity of the coefficients for hypersimplices was classified as an open problem in Stanley’s book, and was settled in [Reference Ferroni14].
$j\geq 2$
. The positivity of the coefficients for hypersimplices was classified as an open problem in Stanley’s book, and was settled in [Reference Ferroni14].
3 Weighted permutations
As the statement of Theorem 1.2 anticipates, the role played by the numbers
![]() $W(\ell ,n,m+1,\textbf {c})$
is fundamental. Its definition is slightly involved and cumbersome. The main motivation comes from the papers [Reference Ferroni14, Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22]. Nevertheless, we let the reader know that this section is completely self-contained. The technical part is the proof of Theorem 3.11, which provides an explicit (but rather complicated) formula for
$W(\ell ,n,m+1,\textbf {c})$
is fundamental. Its definition is slightly involved and cumbersome. The main motivation comes from the papers [Reference Ferroni14, Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22]. Nevertheless, we let the reader know that this section is completely self-contained. The technical part is the proof of Theorem 3.11, which provides an explicit (but rather complicated) formula for
![]() $W(\ell ,n,m+1,\textbf {c})$
. This will play a crucial role in the proof of Theorem 1.2.
$W(\ell ,n,m+1,\textbf {c})$
. This will play a crucial role in the proof of Theorem 1.2.
When dealing with permutations
![]() $\sigma \in \mathfrak {S}_n$
, we will denote
$\sigma \in \mathfrak {S}_n$
, we will denote
![]() $C(\sigma )$
the set of all its cycles.
$C(\sigma )$
the set of all its cycles.
3.1 Weighted Lah Numbers Revisited
First, recall that the Lah number
![]() $L(n,m)$
is defined as the number of ways of partitioning
$L(n,m)$
is defined as the number of ways of partitioning
![]() $[n]$
into a set of exactly m blocks, each of which is internally ordered. For example, if we partition the set
$[n]$
into a set of exactly m blocks, each of which is internally ordered. For example, if we partition the set
![]() $[4]$
into two blocks, then we distinguish between
$[4]$
into two blocks, then we distinguish between
![]() $\{(1,3),(2,4)\}$
and
$\{(1,3),(2,4)\}$
and
![]() $\{(1,3),(4,2)\}$
. Let us denote by
$\{(1,3),(4,2)\}$
. Let us denote by
![]() $\mathscr {L}(n,m)$
the set of all such partitions. It is not difficult to show that
$\mathscr {L}(n,m)$
the set of all such partitions. It is not difficult to show that
![]() $L(n,m)=|\mathscr {L}(n,m)| = \frac {n!}{m!}\binom {n-1}{m-1}$
.
$L(n,m)=|\mathscr {L}(n,m)| = \frac {n!}{m!}\binom {n-1}{m-1}$
.
Definition 3.1 [Reference Ferroni14]
Let
![]() $\pi \in \mathscr {L}(n,m)$
. We define the weight of
$\pi \in \mathscr {L}(n,m)$
. We define the weight of
![]() $\pi $
by
$\pi $
by
where
![]() $w(b)$
is the number of elements in the block b that are smaller (as positive integers) than the first element in b.
$w(b)$
is the number of elements in the block b that are smaller (as positive integers) than the first element in b.
As a quick example, consider the partition
![]() $\pi =\{(5,3,7),(6,2,4,1)\}\in \mathscr {L}(7,2)$
, which has weight
$\pi =\{(5,3,7),(6,2,4,1)\}\in \mathscr {L}(7,2)$
, which has weight
![]() $w(\pi )=1+3=4$
.
$w(\pi )=1+3=4$
.
Definition 3.2 [Reference Ferroni14]
We define the weighted Lah Numbers
![]() $W(\ell ,n,m)$
as the number of partitions
$W(\ell ,n,m)$
as the number of partitions
![]() $\pi \in \mathscr {L}(n,m)$
such that
$\pi \in \mathscr {L}(n,m)$
such that
![]() $w(\pi ) = \ell $
. The set of all such
$w(\pi ) = \ell $
. The set of all such
![]() $\pi $
is denoted by
$\pi $
is denoted by
![]() $\mathscr {W}(\ell ,n,m)$
.
$\mathscr {W}(\ell ,n,m)$
.
In [Reference Ferroni14, Remark 3.11], it is provided a linear recurrence that the weighted Lah numbers satisfy and that may be used to compute them.
The reason why they are relevant in this paper is because we are going to provide a vast generalization for them. Essentially, apart from the three parameters
![]() $\ell $
, n, and m, we will introduce an additional input
$\ell $
, n, and m, we will introduce an additional input
![]() $\textbf {c}$
consisting of n integer numbers. When all the entries of the vector
$\textbf {c}$
consisting of n integer numbers. When all the entries of the vector
![]() $\textbf {c}$
are ones, we will recover the weighted Lah numbers.
$\textbf {c}$
are ones, we will recover the weighted Lah numbers.
3.2 Weights for permutations
In [Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22], a different approach to the weighted Lah numbers is provided. We will review that version of their definition here. One particular advantage that it has is that these numbers can be thought as the quantity of “weighted permutations” satisfying a certain property. This suggests how to provide the right generalization for the main result of this section.
Definition 3.3 [Reference Hanely, Martin, McGinnis, Miyata, Nasr, Vindas-Meléndez and Yin22]
Let
![]() $\sigma \in \mathfrak {S}_n$
. A weight for
$\sigma \in \mathfrak {S}_n$
. A weight for
![]() $\sigma $
is a map
$\sigma $
is a map
![]() $w:C(\sigma ) \to \mathbb {Z}_{\geq 0}$
. The total weight of
$w:C(\sigma ) \to \mathbb {Z}_{\geq 0}$
. The total weight of
![]() $\sigma $
with respect to w, denoted by
$\sigma $
with respect to w, denoted by
![]() $w(\sigma )$
, is defined by
$w(\sigma )$
, is defined by
The pair
![]() $(\sigma ,w)$
will be called a weighted permutation.
$(\sigma ,w)$
will be called a weighted permutation.
Example 3.4 Assume that for every
![]() $\sigma \in \mathfrak {S}_5$
, we consider the weight induced by
$\sigma \in \mathfrak {S}_5$
, we consider the weight induced by
![]() $w(\mathfrak {c}) = \max \{i : i\in \mathfrak {c}\}$
. If we consider the permutation
$w(\mathfrak {c}) = \max \{i : i\in \mathfrak {c}\}$
. If we consider the permutation
![]() $(2,1,5,4,3)\in \mathfrak {S}_5$
, written as the product of the cycles
$(2,1,5,4,3)\in \mathfrak {S}_5$
, written as the product of the cycles
![]() $(1\; 2)(3\; 5)(4)$
, its total weight is
$(1\; 2)(3\; 5)(4)$
, its total weight is
![]() $2 + 5 + 4 = 11$
.
$2 + 5 + 4 = 11$
.
Proposition 3.5 There is a bijection between
![]() $\mathscr {L}(n,m)$
and the set of all weighted permutations
$\mathscr {L}(n,m)$
and the set of all weighted permutations
![]() $(\sigma ,w)$
where
$(\sigma ,w)$
where
![]() $\sigma \in \mathfrak {S}_n$
has exactly m cycles and
$\sigma \in \mathfrak {S}_n$
has exactly m cycles and
![]() $w(\mathfrak {c}) < |\mathfrak {c}|$
for all
$w(\mathfrak {c}) < |\mathfrak {c}|$
for all
![]() $\mathfrak {c}\in C(\sigma )$
.
$\mathfrak {c}\in C(\sigma )$
.
Proof The bijection is constructed explicitly as follows. Take
![]() $(\sigma ,w)$
as in the statement. To each cycle
$(\sigma ,w)$
as in the statement. To each cycle
![]() $\mathfrak {c}\in C(\sigma )$
, we assign a linearly ordered set b consisting of the elements of
$\mathfrak {c}\in C(\sigma )$
, we assign a linearly ordered set b consisting of the elements of
![]() $\mathfrak {c}$
as follows: choose the first element of b to be the
$\mathfrak {c}$
as follows: choose the first element of b to be the
![]() $(w(\mathfrak {c})+1)$
th smallest element in
$(w(\mathfrak {c})+1)$
th smallest element in
![]() $\mathfrak {c}$
and complete the ordering of b according to the order induced by the cycle
$\mathfrak {c}$
and complete the ordering of b according to the order induced by the cycle
![]() $\mathfrak {c}$
. For example, if
$\mathfrak {c}$
. For example, if
where
![]() $w((1\; 2\; 6)) = 1$
,
$w((1\; 2\; 6)) = 1$
,
![]() $w((3\; 5\; 7))=2$
and
$w((3\; 5\; 7))=2$
and
![]() $w((4\; 8)) = 0$
, then we take the partition
$w((4\; 8)) = 0$
, then we take the partition
It is straightforward to verify that this is indeed a bijection.
Remark 3.6 As a consequence of the preceding result, if we fix
![]() $0\leq \ell \leq n-m$
and restrict ourselves to the stratum
$0\leq \ell \leq n-m$
and restrict ourselves to the stratum
![]() $\mathscr {W}(\ell ,n,m) \hookrightarrow \mathscr {L}(n,m)$
, we see that it is in one-to-one correspondence with the family of all the weighted permutations
$\mathscr {W}(\ell ,n,m) \hookrightarrow \mathscr {L}(n,m)$
, we see that it is in one-to-one correspondence with the family of all the weighted permutations
![]() $(\sigma , w)$
such that
$(\sigma , w)$
such that
![]() $\sigma \in \mathfrak {S}_n$
has m cycles,
$\sigma \in \mathfrak {S}_n$
has m cycles,
![]() $w(\mathfrak {c}) < |\mathfrak {c}|$
for every
$w(\mathfrak {c}) < |\mathfrak {c}|$
for every
![]() $\mathfrak {c}\in C(\sigma )$
and
$\mathfrak {c}\in C(\sigma )$
and
![]() $w(\sigma ) = \ell $
.
$w(\sigma ) = \ell $
.
3.3 Compatibility
The bijection mentioned in Remark 3.6 suggests the following definition. Essentially, we use a certain bound for the weight of the cycles that depends on the elements that the cycles contain and not on their lengths as in Proposition 3.5.
Definition 3.7 Let
![]() $(\sigma , w)$
be a weighted permutation,
$(\sigma , w)$
be a weighted permutation,
![]() $\sigma \in \mathfrak {S}_n$
. Let us fix the vector
$\sigma \in \mathfrak {S}_n$
. Let us fix the vector
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
. We say that
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
. We say that
![]() $(\sigma ,w)$
is
$(\sigma ,w)$
is
![]() $\textbf {c}$
-compatible if
$\textbf {c}$
-compatible if
for every cycle
![]() $\mathfrak {c}\in C(\sigma )$
.
$\mathfrak {c}\in C(\sigma )$
.
Example 3.8 Consider the permutation
![]() $\sigma = (2,1,5,4,3)\in \mathfrak {S}_5$
with the weight w given in Example 3.4. If we consider the vector
$\sigma = (2,1,5,4,3)\in \mathfrak {S}_5$
with the weight w given in Example 3.4. If we consider the vector
![]() $\textbf {c} = (8,10,7,8,8)$
, then
$\textbf {c} = (8,10,7,8,8)$
, then
![]() $(\sigma ,w)$
is
$(\sigma ,w)$
is
![]() $\textbf {c}$
-compatible. However, if we take the vector
$\textbf {c}$
-compatible. However, if we take the vector
![]() $\textbf {c}=(3,3,3,3,3)$
, then
$\textbf {c}=(3,3,3,3,3)$
, then
![]() $(\sigma ,w)$
is not
$(\sigma ,w)$
is not
![]() $\textbf {c}$
-compatible.
$\textbf {c}$
-compatible.
Let us consider
![]() $\textbf {c} = \textbf {1} = (1,\ldots ,1)\in \mathbb {Z}_{> 0}^n$
. A weighted permutation
$\textbf {c} = \textbf {1} = (1,\ldots ,1)\in \mathbb {Z}_{> 0}^n$
. A weighted permutation
![]() $\sigma \in \mathfrak {S}_n$
is
$\sigma \in \mathfrak {S}_n$
is
![]() $\textbf {1}$
-compatible if and only if each cycle of
$\textbf {1}$
-compatible if and only if each cycle of
![]() $\sigma $
is assigned a number smaller than its length. In other words, by Proposition 3.5, we have that
$\sigma $
is assigned a number smaller than its length. In other words, by Proposition 3.5, we have that
![]() $\mathscr {L}(n,m)$
is in bijection with the set of all
$\mathscr {L}(n,m)$
is in bijection with the set of all
![]() $\textbf {1}$
-compatible weighted permutations
$\textbf {1}$
-compatible weighted permutations
![]() $(\sigma ,w)$
such that
$(\sigma ,w)$
such that
![]() $\sigma \in \mathfrak {S}_n$
has exactly m cycles.
$\sigma \in \mathfrak {S}_n$
has exactly m cycles.
Definition 3.9 For
![]() $\textbf {c}\in \mathbb {Z}_{> 0}^n$
, let us denote by
$\textbf {c}\in \mathbb {Z}_{> 0}^n$
, let us denote by
![]() $\mathscr {L}(n,m,\textbf {c})$
the set of all
$\mathscr {L}(n,m,\textbf {c})$
the set of all
![]() $\textbf {c}$
-compatible weighted permutations
$\textbf {c}$
-compatible weighted permutations
![]() $(\sigma ,w)$
where
$(\sigma ,w)$
where
![]() $\sigma \in \mathfrak {S}_n$
has m cycles. Let us denote by
$\sigma \in \mathfrak {S}_n$
has m cycles. Let us denote by
![]() $\mathscr {W}(\ell ,n,m,\textbf {c})$
the family of all
$\mathscr {W}(\ell ,n,m,\textbf {c})$
the family of all
![]() $(\sigma ,w)\in \mathscr {L}(n,m,\textbf {c})$
with total weight
$(\sigma ,w)\in \mathscr {L}(n,m,\textbf {c})$
with total weight
![]() $w(\sigma ) = \ell $
.
$w(\sigma ) = \ell $
.
If we use the notation
 $$ \begin{align*} L(n,m,\textbf{c}) &:= |\mathscr{L}(n,m,\textbf{c})|,\\ W(\ell,n,m,\textbf{c}) &:= |\mathscr{W}(\ell,n,m,\textbf{c})|, \end{align*} $$
$$ \begin{align*} L(n,m,\textbf{c}) &:= |\mathscr{L}(n,m,\textbf{c})|,\\ W(\ell,n,m,\textbf{c}) &:= |\mathscr{W}(\ell,n,m,\textbf{c})|, \end{align*} $$
then by taking
![]() $\textbf {c} = \textbf {1}$
, we have that
$\textbf {c} = \textbf {1}$
, we have that
![]() $L(n,m,\textbf {1}) = L(n,m)$
and
$L(n,m,\textbf {1}) = L(n,m)$
and
![]() $W(\ell ,n,m,\textbf {1}) = W(\ell ,n,m)$
.
$W(\ell ,n,m,\textbf {1}) = W(\ell ,n,m)$
.
3.4 A counting formula for weighted permutations
The main goal now is to provide a formula for
![]() $W(\ell ,n,m,\textbf {c})$
that is as concrete as possible. We introduce some notation that will be useful not only in this section but later in the paper.
$W(\ell ,n,m,\textbf {c})$
that is as concrete as possible. We introduce some notation that will be useful not only in this section but later in the paper.
If
![]() $[a,b]$
is an interval of (possibly negative) integers, we will denote
$[a,b]$
is an interval of (possibly negative) integers, we will denote
This is the sth elementary symmetric polynomial in
![]() $b-a+1$
variables, evaluated in the integers of the interval
$b-a+1$
variables, evaluated in the integers of the interval
![]() $[a,b]$
.
$[a,b]$
.
Remark 3.10 Observe that when
![]() $a=1$
, the number
$a=1$
, the number
![]() $P_{a,b}^s$
reduces to a Stirling number of the first kind,
$P_{a,b}^s$
reduces to a Stirling number of the first kind,
 $$\begin{align*}P_{1,b}^s = \biggl[\genfrac{}{}{0pt}{}{b+1}{b+1-s}\biggr],\end{align*}$$
$$\begin{align*}P_{1,b}^s = \biggl[\genfrac{}{}{0pt}{}{b+1}{b+1-s}\biggr],\end{align*}$$
that is, the number of permutations in
![]() $\mathfrak {S}_{b+1}$
with
$\mathfrak {S}_{b+1}$
with
![]() $b+1-s$
cycles. Also, if
$b+1-s$
cycles. Also, if
![]() $a> 0$
and
$a> 0$
and
![]() $b> 0$
, we have
$b> 0$
, we have
 $$ \begin{align} P_{-a,b}^s &= \sum_{j=0}^s P_{-a,-1}^j P_{1,b}^{s-j}\nonumber\\ &= \sum_{j=0}^s (-1)^j P_{1,a}^j P_{1,b}^{s-j}\nonumber\\ &= \sum_{j=0}^s (-1)^j \biggl[\genfrac{}{}{0pt}{}{a+1}{a+1-j}\biggr]\biggl[\genfrac{}{}{0pt}{}{b+1}{b+1-s+j}\biggr]. \end{align} $$
$$ \begin{align} P_{-a,b}^s &= \sum_{j=0}^s P_{-a,-1}^j P_{1,b}^{s-j}\nonumber\\ &= \sum_{j=0}^s (-1)^j P_{1,a}^j P_{1,b}^{s-j}\nonumber\\ &= \sum_{j=0}^s (-1)^j \biggl[\genfrac{}{}{0pt}{}{a+1}{a+1-j}\biggr]\biggl[\genfrac{}{}{0pt}{}{b+1}{b+1-s+j}\biggr]. \end{align} $$
Theorem 3.11 For every
![]() $\textbf {c}\in \mathbb {Z}_{> 0}^n$
, the following formula holds:
$\textbf {c}\in \mathbb {Z}_{> 0}^n$
, the following formula holds:
 $$\begin{align*}W(\ell,n,m+1,\textbf{c}) = \sum_{j=0}^{n}(-1)^jP^{n-1-m}_{-j+1,n-1-j}\sum_{i=0}^\ell\rho_{\textbf{c},j}(i)\binom{m+\ell-i}{m}. \end{align*}$$
$$\begin{align*}W(\ell,n,m+1,\textbf{c}) = \sum_{j=0}^{n}(-1)^jP^{n-1-m}_{-j+1,n-1-j}\sum_{i=0}^\ell\rho_{\textbf{c},j}(i)\binom{m+\ell-i}{m}. \end{align*}$$
Proof First, by using (3.1), we can rewrite the expression on the right as follows:
 $$ \begin{align*} &\sum_{j=0}^{n}\sum_{u=0}^j(-1)^{j-u} \biggl[\genfrac{}{}{0pt}{}{j}{j-u}\biggr]\biggl[\genfrac{}{}{0pt}{}{n-j}{m+1+u-j}\biggr]\sum_{i=0}^\ell\rho_{\textbf{c},j}(i)\binom{m+\ell-i}{m}\\ &=\sum_{j=0}^{n}\sum_{u=0}^j(-1)^{j-u} \biggl[\genfrac{}{}{0pt}{}{j}{j-u}\biggr]\biggl[\genfrac{}{}{0pt}{}{n-j}{m+1+u-j}\biggr]\sum_{i=0}^\ell\sum_{\substack{A\in \binom{[n]}{j}\\ \sum_{a\in A} c_a=i}}\binom{m+\ell-i}{m}\\ &=\sum_{j=0}^{n}\sum_{u=0}^j\sum_{i=0}^\ell\sum_{\substack{A\in \binom{[n]}{j}\\ \sum_{a\in A} c_a=i}}(-1)^{j-u} \biggl[\genfrac{}{}{0pt}{}{j}{j-u}\biggr]\biggl[\genfrac{}{}{0pt}{}{n-j}{m+1+u-j}\biggr]\binom{m+\ell-i}{m}. \end{align*} $$
$$ \begin{align*} &\sum_{j=0}^{n}\sum_{u=0}^j(-1)^{j-u} \biggl[\genfrac{}{}{0pt}{}{j}{j-u}\biggr]\biggl[\genfrac{}{}{0pt}{}{n-j}{m+1+u-j}\biggr]\sum_{i=0}^\ell\rho_{\textbf{c},j}(i)\binom{m+\ell-i}{m}\\ &=\sum_{j=0}^{n}\sum_{u=0}^j(-1)^{j-u} \biggl[\genfrac{}{}{0pt}{}{j}{j-u}\biggr]\biggl[\genfrac{}{}{0pt}{}{n-j}{m+1+u-j}\biggr]\sum_{i=0}^\ell\sum_{\substack{A\in \binom{[n]}{j}\\ \sum_{a\in A} c_a=i}}\binom{m+\ell-i}{m}\\ &=\sum_{j=0}^{n}\sum_{u=0}^j\sum_{i=0}^\ell\sum_{\substack{A\in \binom{[n]}{j}\\ \sum_{a\in A} c_a=i}}(-1)^{j-u} \biggl[\genfrac{}{}{0pt}{}{j}{j-u}\biggr]\biggl[\genfrac{}{}{0pt}{}{n-j}{m+1+u-j}\biggr]\binom{m+\ell-i}{m}. \end{align*} $$
If we look at a fixed
![]() $A\in \binom {[n]}{j}$
such that
$A\in \binom {[n]}{j}$
such that
![]() $\sum _{a\in A}c_a=i$
, the quantity
$\sum _{a\in A}c_a=i$
, the quantity
 $$\begin{align*}\biggl[\genfrac{}{}{0pt}{}{j}{j-u}\biggr]\biggl[\genfrac{}{}{0pt}{}{n-j}{m+1+u-j}\biggr]\binom{m+\ell-i}{m}\end{align*}$$
$$\begin{align*}\biggl[\genfrac{}{}{0pt}{}{j}{j-u}\biggr]\biggl[\genfrac{}{}{0pt}{}{n-j}{m+1+u-j}\biggr]\binom{m+\ell-i}{m}\end{align*}$$
can be seen as the number of weighted permutations
![]() $(\sigma ,w)$
that simultaneously satisfy the following properties:
$(\sigma ,w)$
that simultaneously satisfy the following properties:
-
•
 $\sigma \in \mathfrak {S}_n$
has exactly
$\sigma \in \mathfrak {S}_n$
has exactly
 $m+1$
cycles.
$m+1$
cycles. -
•
 $w(\sigma ) =\ell $
.
$w(\sigma ) =\ell $
. -
• Exactly
 $j-u$
of the cycles consist only of elements that are contained in A.
$j-u$
of the cycles consist only of elements that are contained in A. -
• The remaining
 $m+1-j+u$
cycles consist only of elements that are contained in
$m+1-j+u$
cycles consist only of elements that are contained in
 $[n]\smallsetminus A$
.
$[n]\smallsetminus A$
. -
•
 $w(\mathfrak {c}) \geq \sum _{h \in \mathfrak {c}} c_h$
for each of the
$w(\mathfrak {c}) \geq \sum _{h \in \mathfrak {c}} c_h$
for each of the
 $j-u$
cycles
$j-u$
cycles
 $\mathfrak {c}\in C(\sigma )$
that consist only of elements contained in A.
$\mathfrak {c}\in C(\sigma )$
that consist only of elements contained in A.
The last condition explains the factor
![]() $\binom {m+\ell -i}{m}$
, which is exactly the number of ways of putting
$\binom {m+\ell -i}{m}$
, which is exactly the number of ways of putting
![]() $\ell -i$
balls into
$\ell -i$
balls into
![]() $m+1$
boxes. This is because we put at least
$m+1$
boxes. This is because we put at least
![]() $i = \sum _{a\in A} c_a$
weight in the cycles consisting of elements in A, and then we can assign the remaining weight
$i = \sum _{a\in A} c_a$
weight in the cycles consisting of elements in A, and then we can assign the remaining weight
![]() $\ell - i$
in
$\ell - i$
in
![]() $\binom {m+\ell -i}{m}$
different ways.
$\binom {m+\ell -i}{m}$
different ways.
Let us call
![]() $\widehat {\mathscr {W}}(n,m+1,\ell ,A,j-u,\textbf {c})$
the set of all weighted permutations
$\widehat {\mathscr {W}}(n,m+1,\ell ,A,j-u,\textbf {c})$
the set of all weighted permutations
![]() $(\sigma , w)$
satisfying the five conditions above (recall that i is determined from A and
$(\sigma , w)$
satisfying the five conditions above (recall that i is determined from A and
![]() $\textbf {c}$
). Further, notice that
$\textbf {c}$
). Further, notice that
which is a direct consequence of the definitions.
The statement that we want to prove is therefore equivalent to showing that
 $$\begin{align*}|\mathscr{W}(\ell,n,m+1,\textbf{c})| =\sum_{j=0}^{n}\sum_{u=0}^j\sum_{i=0}^\ell\sum_{\substack{A\in \binom{[n]}{j}\\ \sum_{a\in A} c_a=i}}(-1)^{j-u} |\widehat{\mathscr{W}}(\ell,n,m+1,A,j-u,\textbf{c})|.\end{align*}$$
$$\begin{align*}|\mathscr{W}(\ell,n,m+1,\textbf{c})| =\sum_{j=0}^{n}\sum_{u=0}^j\sum_{i=0}^\ell\sum_{\substack{A\in \binom{[n]}{j}\\ \sum_{a\in A} c_a=i}}(-1)^{j-u} |\widehat{\mathscr{W}}(\ell,n,m+1,A,j-u,\textbf{c})|.\end{align*}$$
This equality is rather a consequence of an inclusion–exclusion argument that we explain now. In what follows, whenever
![]() $\mathscr {S}$
is a set, we use the notation
$\mathscr {S}$
is a set, we use the notation
![]() $\mathscr {S}[x]$
to denote
$\mathscr {S}[x]$
to denote
![]() $0$
or
$0$
or
![]() $1$
according to whether
$1$
according to whether
![]() $x\notin \mathscr {S}$
or
$x\notin \mathscr {S}$
or
![]() $x\in \mathscr {S}$
, respectively.
$x\in \mathscr {S}$
, respectively.
If
![]() $(\sigma ,w)\in \mathscr {W}(\ell ,n,m+1,\textbf {c})$
, then
$(\sigma ,w)\in \mathscr {W}(\ell ,n,m+1,\textbf {c})$
, then
![]() $(\sigma ,w)$
is present only in the set
$(\sigma ,w)$
is present only in the set
![]() $\widehat {\mathscr {W}}(\ell ,n,m+1, \varnothing ,0,\textbf {c})$
, which corresponds to the case in which
$\widehat {\mathscr {W}}(\ell ,n,m+1, \varnothing ,0,\textbf {c})$
, which corresponds to the case in which
![]() $u = j = 0$
, and appears with a plus sign.
$u = j = 0$
, and appears with a plus sign.
On the contrary, let us fix some weighted permutation in
![]() $\mathfrak {S}_n$
, with
$\mathfrak {S}_n$
, with
![]() $m+1$
cycles and total weight
$m+1$
cycles and total weight
![]() $\ell $
but is not
$\ell $
but is not
![]() $\textbf {c}$
-compatible; in other words,
$\textbf {c}$
-compatible; in other words,
![]() $(\sigma ,w)\notin \mathscr {W}(\ell ,n,m+1,\textbf {c})$
. Let
$(\sigma ,w)\notin \mathscr {W}(\ell ,n,m+1,\textbf {c})$
. Let
![]() $\mathfrak {c}_1,\dots ,\mathfrak {c}_b$
be the cycles
$\mathfrak {c}_1,\dots ,\mathfrak {c}_b$
be the cycles
![]() $\mathfrak {c}\in C(\sigma )$
for which
$\mathfrak {c}\in C(\sigma )$
for which
![]() $w(\mathfrak {c})\geq \sum _{h\in \mathfrak {c}} c_h$
. For
$w(\mathfrak {c})\geq \sum _{h\in \mathfrak {c}} c_h$
. For
![]() $B\subseteq [b]$
, let
$B\subseteq [b]$
, let
![]() $A_B:= \bigcup _{s\in B} \mathfrak {c}_s$
(where we are regarding the cycles
$A_B:= \bigcup _{s\in B} \mathfrak {c}_s$
(where we are regarding the cycles
![]() $\mathfrak {c}_s$
as sets). Then
$\mathfrak {c}_s$
as sets). Then
![]() $(\sigma ,w)$
is contained in precisely the sets
$(\sigma ,w)$
is contained in precisely the sets
![]() $\widehat {\mathscr {W}}(\ell ,n,m+1,A_B,|B|,\textbf {c})$
for
$\widehat {\mathscr {W}}(\ell ,n,m+1,A_B,|B|,\textbf {c})$
for
![]() $B\subseteq [b]$
. Therefore,
$B\subseteq [b]$
. Therefore,
 $$ \begin{align*} &\sum_{j=0}^{n}\sum_{u=0}^j\sum_{i=0}^\ell\sum_{\substack{A\in \binom{[n]}{j}\\ \sum_{a\in A} c_a=i}}(-1)^{j-u}\cdot \widehat{\mathscr{W}}(\ell,n,m+1,A,j-u,\textbf{c})[(\sigma,w)]\\ &=\sum_{B\subseteq [b]} (-1)^{|B|}\cdot \widehat{\mathscr{W}}(n,m+1,\ell,A_B,|B|,\textbf{c})[(\sigma,w)]\\ &=\sum_{B\subseteq [b]}(-1)^{|B|}=0. \end{align*} $$
$$ \begin{align*} &\sum_{j=0}^{n}\sum_{u=0}^j\sum_{i=0}^\ell\sum_{\substack{A\in \binom{[n]}{j}\\ \sum_{a\in A} c_a=i}}(-1)^{j-u}\cdot \widehat{\mathscr{W}}(\ell,n,m+1,A,j-u,\textbf{c})[(\sigma,w)]\\ &=\sum_{B\subseteq [b]} (-1)^{|B|}\cdot \widehat{\mathscr{W}}(n,m+1,\ell,A_B,|B|,\textbf{c})[(\sigma,w)]\\ &=\sum_{B\subseteq [b]}(-1)^{|B|}=0. \end{align*} $$
Hence, the proof is complete.
4 Ehrhart coefficients
In this section, we will prove Theorem 1.2 and then comment briefly about a conjecture that arose in the study of these polynomials.
4.1 The proof of Theorem 1.2
We start with a lemma that will be used later.
Lemma 4.1 The following equality holds:
 $$\begin{align*}[t^m] \binom{t(k-v)+n-1-j}{n-1} =\frac{1}{(n-1)!} \, (k-v)^m P_{-j+1,n-1-j}^{n-1-m}. \end{align*}$$
$$\begin{align*}[t^m] \binom{t(k-v)+n-1-j}{n-1} =\frac{1}{(n-1)!} \, (k-v)^m P_{-j+1,n-1-j}^{n-1-m}. \end{align*}$$
Proof By definition, we have that
 $$\begin{align*}\binom{t(k-v)+n-1-j}{n-1} = \frac{1}{(n-1)!} \prod_{s=1}^{n-1} \left(t(k-v)+n-j-s\right).\end{align*}$$
$$\begin{align*}\binom{t(k-v)+n-1-j}{n-1} = \frac{1}{(n-1)!} \prod_{s=1}^{n-1} \left(t(k-v)+n-j-s\right).\end{align*}$$
Therefore, apart from the factor
![]() $\frac {1}{(n-1)!}$
, we see that the coefficient of degree m consists of the product between
$\frac {1}{(n-1)!}$
, we see that the coefficient of degree m consists of the product between
![]() $(k-v)^m$
and the sum of all products of
$(k-v)^m$
and the sum of all products of
![]() $n-m-1$
numbers chosen in the interval of integers
$n-m-1$
numbers chosen in the interval of integers
![]() $[-j+1, n-1-j]$
, namely
$[-j+1, n-1-j]$
, namely
![]() $P_{-j+1,n-1-j}^{n-1-m}$
.
$P_{-j+1,n-1-j}^{n-1-m}$
.
We are now ready to prove Theorem 1.2.
Theorem 4.2 (Theorem 1.2)
Let
![]() $\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
. Let
$\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
. Let
![]() $0\leq m\leq n-1$
. The coefficient of
$0\leq m\leq n-1$
. The coefficient of
![]() $t^m$
in
$t^m$
in
![]() $\operatorname {\mathrm{ehr}}(\mathscr {R}_{k,\textbf {c}},t)$
is given by
$\operatorname {\mathrm{ehr}}(\mathscr {R}_{k,\textbf {c}},t)$
is given by
 $$\begin{align*}[t^m]\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) = \frac{1}{(n-1)!}\sum_{\ell = 0}^{k-1}W(\ell,n,m+1,\textbf{c})A(m,k-\ell-1). \end{align*}$$
$$\begin{align*}[t^m]\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) = \frac{1}{(n-1)!}\sum_{\ell = 0}^{k-1}W(\ell,n,m+1,\textbf{c})A(m,k-\ell-1). \end{align*}$$
Proof By using the formula that we obtained in Theorem 2.5 and Lemma 4.1, we have the following chain of equalities:
 $$ \begin{align*} [t^m]\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) &= \sum_{j=0}^{k-1}(-1)^j\sum_{v=0}^{k-1} [t^m]\binom{t(k-v)+n-1-j}{n-1} \rho_{\textbf{c},j}(v)\\ &=\frac{1}{(n-1)!}\sum_{j=0}^{k-1}\sum_{v=0}^{k-1}(-1)^{j} \,(k-v)^m\, P^{n-1-m}_{-j+1,n-1-j}\, \rho_{\textbf{c},j}(v)\\ &=\frac{1}{(n-1)!}\sum_{v=0}^k (k-v)^m\, \sum_{j=0}^{k-1}(-1)^j\, P^{n-1-m}_{-j+1,n-1-j} \,\rho_{\textbf{c},j}(v)\\ &=\frac{1}{(n-1)!}\sum_{v=0}^k (k-v)^m\, \sum_{j=0}^{n}(-1)^j\, P^{n-1-m}_{-j+1,n-1-j} \,\rho_{\textbf{c},j}(v), \end{align*} $$
$$ \begin{align*} [t^m]\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) &= \sum_{j=0}^{k-1}(-1)^j\sum_{v=0}^{k-1} [t^m]\binom{t(k-v)+n-1-j}{n-1} \rho_{\textbf{c},j}(v)\\ &=\frac{1}{(n-1)!}\sum_{j=0}^{k-1}\sum_{v=0}^{k-1}(-1)^{j} \,(k-v)^m\, P^{n-1-m}_{-j+1,n-1-j}\, \rho_{\textbf{c},j}(v)\\ &=\frac{1}{(n-1)!}\sum_{v=0}^k (k-v)^m\, \sum_{j=0}^{k-1}(-1)^j\, P^{n-1-m}_{-j+1,n-1-j} \,\rho_{\textbf{c},j}(v)\\ &=\frac{1}{(n-1)!}\sum_{v=0}^k (k-v)^m\, \sum_{j=0}^{n}(-1)^j\, P^{n-1-m}_{-j+1,n-1-j} \,\rho_{\textbf{c},j}(v), \end{align*} $$
where in the second to last step we changed the summation order and the upper limit for v because for
![]() $v=k$
we are just adding a zero due to the factor
$v=k$
we are just adding a zero due to the factor
![]() $(k-v)^m$
, and in the last step we changed the upper limit for j, as
$(k-v)^m$
, and in the last step we changed the upper limit for j, as
![]() $\rho _{\textbf {c},j}(v)$
is zero whenever
$\rho _{\textbf {c},j}(v)$
is zero whenever
![]() $j\geq k$
, as v is always at most k and the
$j\geq k$
, as v is always at most k and the
![]() $c_i$
’s are strictly positive. Let us introduce the following notation:
$c_i$
’s are strictly positive. Let us introduce the following notation:
 $$ \begin{align*} F_{n,m}(x) &:= \sum_{v=0}^{\infty} \left( \sum_{j=0}^{n}(-1)^j P^{n-1-m}_{-j+1,n-1-j} \rho_{\textbf{c},j}(v)\right) x^v,\\ G_{m}(x) &:= \sum_{v = 0}^{\infty} v^m \cdot x^v. \end{align*} $$
$$ \begin{align*} F_{n,m}(x) &:= \sum_{v=0}^{\infty} \left( \sum_{j=0}^{n}(-1)^j P^{n-1-m}_{-j+1,n-1-j} \rho_{\textbf{c},j}(v)\right) x^v,\\ G_{m}(x) &:= \sum_{v = 0}^{\infty} v^m \cdot x^v. \end{align*} $$
Using these names, the preceding chain of equalities reduces to
It is well known that
![]() $G_m(x)$
satisfies the following identity:
$G_m(x)$
satisfies the following identity:
 $$ \begin{align} G_m(x) = \frac{1}{(1-x)^{m+1}} \sum_{i=0}^{m} A(m,i) x^{i+1},\end{align} $$
$$ \begin{align} G_m(x) = \frac{1}{(1-x)^{m+1}} \sum_{i=0}^{m} A(m,i) x^{i+1},\end{align} $$
where
![]() $A(m,i)$
is an Eulerian number (see [Reference Stanley41, p. 40] for instance). On the other hand, notice that
$A(m,i)$
is an Eulerian number (see [Reference Stanley41, p. 40] for instance). On the other hand, notice that
 $$ \begin{align} \frac{1}{(1-x)^{m+1}} F_{n,m}(x) &= \sum_{\ell=0}^{\infty} \left(\sum_{i=0}^{\ell} \sum_{j=0}^{n}(-1)^j P^{n-1-m}_{-j+1,n-1-j} \rho_{\textbf{c},j}(i) \binom{m+\ell-i}{m}\right) x^{\ell}\nonumber \\ &= \sum_{\ell = 0}^{\infty} W(\ell,n,m+1,\textbf{c}) x^{\ell}, \end{align} $$
$$ \begin{align} \frac{1}{(1-x)^{m+1}} F_{n,m}(x) &= \sum_{\ell=0}^{\infty} \left(\sum_{i=0}^{\ell} \sum_{j=0}^{n}(-1)^j P^{n-1-m}_{-j+1,n-1-j} \rho_{\textbf{c},j}(i) \binom{m+\ell-i}{m}\right) x^{\ell}\nonumber \\ &= \sum_{\ell = 0}^{\infty} W(\ell,n,m+1,\textbf{c}) x^{\ell}, \end{align} $$
where in the last step we used Theorem 2.5. Now the equality of the statement follows from equations 4.1–4.3, just by writing
 $$ \begin{align*} [t^m]\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) &=\frac{1}{(n-1)!} [x^k] \left(\sum_{\ell=0}^{\infty} W(\ell,n,m+1,\textbf{c}) x^{\ell} \cdot \sum_{i=1}^m A(m,i-1) x^i\right)\\ &= \frac{1}{(n-1)!}\sum_{\ell = 0}^{k-1}W(\ell,n,m+1,\textbf{c})A(m,k-\ell-1).\\[-36pt] \end{align*} $$
$$ \begin{align*} [t^m]\operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t) &=\frac{1}{(n-1)!} [x^k] \left(\sum_{\ell=0}^{\infty} W(\ell,n,m+1,\textbf{c}) x^{\ell} \cdot \sum_{i=1}^m A(m,i-1) x^i\right)\\ &= \frac{1}{(n-1)!}\sum_{\ell = 0}^{k-1}W(\ell,n,m+1,\textbf{c})A(m,k-\ell-1).\\[-36pt] \end{align*} $$
Remark 4.3 If we change the last coordinate of
![]() $\textbf {c}=(c_1,\ldots ,c_{n-1},c_n)$
by
$\textbf {c}=(c_1,\ldots ,c_{n-1},c_n)$
by
![]() $\textbf {c}'=(c_1,\ldots ,c_{n-1},c_n+1)$
, it is immediate by definition that
$\textbf {c}'=(c_1,\ldots ,c_{n-1},c_n+1)$
, it is immediate by definition that
![]() $\mathscr {W}(\ell ,n,m+1,\textbf {c})\subseteq \mathscr {W}(\ell ,n,m+1,\textbf {c}')$
. More generally, by induction, it follows that whenever the vector
$\mathscr {W}(\ell ,n,m+1,\textbf {c})\subseteq \mathscr {W}(\ell ,n,m+1,\textbf {c}')$
. More generally, by induction, it follows that whenever the vector
![]() $\textbf {c}'-\textbf {c}$
has nonnegative coefficients, one has that
$\textbf {c}'-\textbf {c}$
has nonnegative coefficients, one has that
Due to the preceding result, this monotonicity property has a counterpart for the Ehrhart polynomials.
Corollary 4.4 If
![]() $\textbf {c},\textbf {c}'\in \mathbb {Z}^n_{>0}$
are vectors such that
$\textbf {c},\textbf {c}'\in \mathbb {Z}^n_{>0}$
are vectors such that
![]() $\textbf {c}'-\textbf {c}\in \mathbb {Z}^n_{\geq 0}$
, then
$\textbf {c}'-\textbf {c}\in \mathbb {Z}^n_{\geq 0}$
, then
where
![]() $\preceq $
denotes coefficientwise inequality.
$\preceq $
denotes coefficientwise inequality.
4.2 A unit-circle-rootedness conjecture
While verifying computationally the main results of the present paper, the following intriguing problem, that we pose here as a conjecture, arose.
Conjecture 4.5 For each
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and each
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and each
![]() $0\leq m\leq n - 1$
, the polynomial defined by
$0\leq m\leq n - 1$
, the polynomial defined by
 $$\begin{align*}p_{n,m,\textbf{c}}(x) = \sum_{\ell = 0}^{\infty} W(\ell,n,m+1,\textbf{c})\, x^{\ell},\end{align*}$$
$$\begin{align*}p_{n,m,\textbf{c}}(x) = \sum_{\ell = 0}^{\infty} W(\ell,n,m+1,\textbf{c})\, x^{\ell},\end{align*}$$
has all of its complex roots lying on the unit circle
![]() $|z| = 1$
.
$|z| = 1$
.
Notice that although we used the upper limit
![]() $\infty $
in the sum, it actually yields a polynomial, as for
$\infty $
in the sum, it actually yields a polynomial, as for
![]() $\ell> c_1+\cdots +c_n$
, one will certainly have
$\ell> c_1+\cdots +c_n$
, one will certainly have
![]() $W(\ell ,n,m+1,\textbf {c}) = 0$
. A reasonable question is whether some techniques regarding
$W(\ell ,n,m+1,\textbf {c}) = 0$
. A reasonable question is whether some techniques regarding
![]() $h^*$
-polynomials having roots on the unit circle can be applied to these particular polynomials (notice that they may not be the
$h^*$
-polynomials having roots on the unit circle can be applied to these particular polynomials (notice that they may not be the
![]() $h^*$
-polynomial of a polytope, as they can have a constant term larger than
$h^*$
-polynomial of a polytope, as they can have a constant term larger than
![]() $1$
). See [Reference Braun and Liu3] for results regarding polytopes having a unit-circle-rooted
$1$
). See [Reference Braun and Liu3] for results regarding polytopes having a unit-circle-rooted
![]() $h^*$
-polynomial.
$h^*$
-polynomial.
5 The
 $h^*$
-polynomial
$h^*$
-polynomial
Recall that the
![]() $h^*$
-polynomial of a lattice polytope
$h^*$
-polynomial of a lattice polytope
![]() $\mathscr {P}$
of dimension d is defined as the numerator of the generating function of its Ehrhart polynomial. Namely, it is defined as the only polynomial satisfying
$\mathscr {P}$
of dimension d is defined as the numerator of the generating function of its Ehrhart polynomial. Namely, it is defined as the only polynomial satisfying
 $$\begin{align*}\sum_{j=0}^{\infty} \operatorname{\mathrm{ehr}}(\mathscr{P}, j) \, x^j = \frac{h^*(\mathscr{P},x)}{(1-x)^{d+1}}.\end{align*}$$
$$\begin{align*}\sum_{j=0}^{\infty} \operatorname{\mathrm{ehr}}(\mathscr{P}, j) \, x^j = \frac{h^*(\mathscr{P},x)}{(1-x)^{d+1}}.\end{align*}$$
A classical result due to Stanley [Reference Stanley40] shows that
![]() $h^*(\mathscr {P},x)$
is a polynomial with nonnegative integer coefficients and has degree at most d. A basic property of
$h^*(\mathscr {P},x)$
is a polynomial with nonnegative integer coefficients and has degree at most d. A basic property of
![]() $h^*$
-polynomials is that
$h^*$
-polynomials is that
![]() $h^*(\mathscr {P},1)$
is equal to the normalized volume of the polytope
$h^*(\mathscr {P},1)$
is equal to the normalized volume of the polytope
![]() $\mathscr {P}$
.
$\mathscr {P}$
.
In [Reference Early12], Early conjectured a combinatorial formula for the coefficients of the
![]() $h^*$
-polynomial of the hypersimplex and, more generally, for the
$h^*$
-polynomial of the hypersimplex and, more generally, for the
![]() $h^*$
-polynomial of the polytopes of the form
$h^*$
-polynomial of the polytopes of the form
![]() $\mathscr {R}_{k,\textbf {c}}$
where
$\mathscr {R}_{k,\textbf {c}}$
where
![]() $\textbf {c}=(r,\ldots ,r)\in \mathbb {Z}_{>0}^n$
. In [Reference Kim28], Kim provided a proof of Early’s conjectures. The aim of this section is to provide the right generalization of the conjecture posed by Early for all the polytopes of the form
$\textbf {c}=(r,\ldots ,r)\in \mathbb {Z}_{>0}^n$
. In [Reference Kim28], Kim provided a proof of Early’s conjectures. The aim of this section is to provide the right generalization of the conjecture posed by Early for all the polytopes of the form
![]() $\mathscr {R}_{k,\textbf {c}}$
and then outline a proof that extends Kim’s procedure.
$\mathscr {R}_{k,\textbf {c}}$
and then outline a proof that extends Kim’s procedure.
5.1 A review of terminology
In the same way that the
![]() $\textbf {c}$
-compatible weighted permutations play a key role in the description of the coefficients of the Ehrhart polynomial of
$\textbf {c}$
-compatible weighted permutations play a key role in the description of the coefficients of the Ehrhart polynomial of
![]() $\mathscr {R}_{k,\textbf {c}}$
, for the
$\mathscr {R}_{k,\textbf {c}}$
, for the
![]() $h^*$
-polynomial, we have to introduce a different object, already studied in both [Reference Early12, Reference Kim28] and endow it with an extra condition that we call again “
$h^*$
-polynomial, we have to introduce a different object, already studied in both [Reference Early12, Reference Kim28] and endow it with an extra condition that we call again “
![]() $\textbf {c}$
-compatibility.”
$\textbf {c}$
-compatibility.”
Recall that a cyclically ordered partition of
![]() $[n]$
is a partition of
$[n]$
is a partition of
![]() $[n]$
into disjoint blocks that are ordered cyclically. For example, the partitions of
$[n]$
into disjoint blocks that are ordered cyclically. For example, the partitions of
![]() $[5]$
given by
$[5]$
given by
![]() $(\{1,2\}, \{3,5\}, \{4\})$
and
$(\{1,2\}, \{3,5\}, \{4\})$
and
![]() $(\{3,5\}, \{4\}, \{1,2\})$
are considered as equal. The set of blocks of such a partition
$(\{3,5\}, \{4\}, \{1,2\})$
are considered as equal. The set of blocks of such a partition
![]() $\xi $
will be customarily denoted by
$\xi $
will be customarily denoted by
![]() $P(\xi )$
.
$P(\xi )$
.
Definition 5.1 A decorated ordered set partition of type
![]() $(k,n)$
consists of a cyclically ordered partition
$(k,n)$
consists of a cyclically ordered partition
![]() $\xi $
of
$\xi $
of
![]() $[n]$
and a function
$[n]$
and a function
![]() $w:P(\xi ) \to \mathbb {Z}_{\geq 0}$
such that
$w:P(\xi ) \to \mathbb {Z}_{\geq 0}$
such that
For a vector
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
, we say that a decorated ordered set partition
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
, we say that a decorated ordered set partition
![]() $\xi $
is
$\xi $
is
![]() $\textbf {c}$
-compatible if
$\textbf {c}$
-compatible if
for all
![]() $\mathfrak {p}\in P(\xi )$
.
$\mathfrak {p}\in P(\xi )$
.
A decorated ordered set partition of type
![]() $(k,n)$
,
$(k,n)$
,
![]() $\xi =(L_1,\ldots ,L_m)$
, can be represented as a set of k points in a circle ordered in a clockwise fashion. The blocks
$\xi =(L_1,\ldots ,L_m)$
, can be represented as a set of k points in a circle ordered in a clockwise fashion. The blocks
![]() $L_i$
are placed among these points in such a way that the clockwise distance between
$L_i$
are placed among these points in such a way that the clockwise distance between
![]() $L_i$
and
$L_i$
and
![]() $L_{i+1}$
is
$L_{i+1}$
is
![]() $w(L_i)$
. Observe that this only depends on the cyclic order and not in the particular choice of the first block
$w(L_i)$
. Observe that this only depends on the cyclic order and not in the particular choice of the first block
![]() $L_1$
.
$L_1$
.
Notice that in the case in which
![]() $\textbf {c}=(1,\ldots ,1)$
the notion of being
$\textbf {c}=(1,\ldots ,1)$
the notion of being
![]() $\textbf {c}$
-compatible was named as “hypersimplicial” in [Reference Early12], whereas in the case
$\textbf {c}$
-compatible was named as “hypersimplicial” in [Reference Early12], whereas in the case
![]() $\textbf {c}=(r,\ldots ,r)$
it was called “r-hypersimplicial” in [Reference Kim28].
$\textbf {c}=(r,\ldots ,r)$
it was called “r-hypersimplicial” in [Reference Kim28].
Definition 5.2 The winding number of a decorated ordered set partition of type
![]() $(k,n)$
is defined as the only number d such that
$(k,n)$
is defined as the only number d such that
where
![]() $\lambda _i$
denotes the clockwise distance between the block containing i and the block containing
$\lambda _i$
denotes the clockwise distance between the block containing i and the block containing
![]() $i+1$
(modulo n).
$i+1$
(modulo n).
Having set all these names and notations, we are ready to state the main result of this section. The proof is carried out in the next subsection.
Theorem 5.3 Let
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and
![]() $0<k<c_1+\cdots +c_n$
. For each
$0<k<c_1+\cdots +c_n$
. For each
![]() $0\leq i\leq n$
, the coefficient
$0\leq i\leq n$
, the coefficient
![]() $[x^i]h^*(\mathscr {R}_{k,\textbf {c}},x)$
equals the number of
$[x^i]h^*(\mathscr {R}_{k,\textbf {c}},x)$
equals the number of
![]() $\textbf {c}$
-compatible decorated ordered set partitions of type
$\textbf {c}$
-compatible decorated ordered set partitions of type
![]() $(k,n)$
having winding number i.
$(k,n)$
having winding number i.
5.2 A proof à la Kim
We will outline a proof of Theorem 1.7. Some details are omitted as the proofs are carried out verbatim from [Reference Kim28]; in particular, to improve readability, we have decided to use the same (if not, very similar) notation.
The family of all the partitions of a set A will be henceforth denoted by
![]() $\Pi (A)$
. Also, we will use the notation
$\Pi (A)$
. Also, we will use the notation
so that in particular when
![]() $b=2$
, we recover the classical binomial numbers.
$b=2$
, we recover the classical binomial numbers.
Lemma 5.4 The following formula holds:
 $$\begin{align*}\binom{n}{a}_b = \sum_{j=0}^{\lfloor\frac{a}{b}\rfloor} (-1)^j \binom{n}{j}\binom{n-1+a-bj}{n-1}.\end{align*}$$
$$\begin{align*}\binom{n}{a}_b = \sum_{j=0}^{\lfloor\frac{a}{b}\rfloor} (-1)^j \binom{n}{j}\binom{n-1+a-bj}{n-1}.\end{align*}$$
Proof The proof is a standard argument with generating functions.
 $$ \begin{align*} \binom{n}{a}_b &= [x^a]\left(\sum_{i=0}^{b-1} x^i\right)^n\\ &= [x^a]\frac{(1-x^b)^n}{(1-x)^n}\\ &= [x^a]\left(\sum_{j=0}^n (-1)^j \binom{n}{j} x^{bj} \right)\left(\sum_{j=0}^{\infty}\binom{n-1+j}{n-1} x^j\right)\\ &= \sum_{j=0}^{\lfloor\frac{a}{b}\rfloor} (-1)^j\binom{n}{j}\binom{n-1+a-bj}{n-1}.\\[-34pt] \end{align*} $$
$$ \begin{align*} \binom{n}{a}_b &= [x^a]\left(\sum_{i=0}^{b-1} x^i\right)^n\\ &= [x^a]\frac{(1-x^b)^n}{(1-x)^n}\\ &= [x^a]\left(\sum_{j=0}^n (-1)^j \binom{n}{j} x^{bj} \right)\left(\sum_{j=0}^{\infty}\binom{n-1+j}{n-1} x^j\right)\\ &= \sum_{j=0}^{\lfloor\frac{a}{b}\rfloor} (-1)^j\binom{n}{j}\binom{n-1+a-bj}{n-1}.\\[-34pt] \end{align*} $$
Definition 5.5 Let
![]() $\xi $
be a decorated ordered set partition of type
$\xi $
be a decorated ordered set partition of type
![]() $(k,n)$
, and let
$(k,n)$
, and let
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
. The set of
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
. The set of
![]() $\textbf {c}$
-bad blocks of
$\textbf {c}$
-bad blocks of
![]() $\xi $
is the family
$\xi $
is the family
 $$\begin{align*}I_{\textbf{c}}(\xi) = \left\{ \mathfrak{p}\in P(\xi) : w(\mathfrak{p}) \geq \sum_{i\in \mathfrak{p}} c_i\right\}.\end{align*}$$
$$\begin{align*}I_{\textbf{c}}(\xi) = \left\{ \mathfrak{p}\in P(\xi) : w(\mathfrak{p}) \geq \sum_{i\in \mathfrak{p}} c_i\right\}.\end{align*}$$
If S is a family of pairwise disjoint subsets of
![]() $[n]$
, we define
$[n]$
, we define
and
Proposition 5.6 The number of
![]() $\textbf {c}$
-compatible decorated ordered set partitions of type
$\textbf {c}$
-compatible decorated ordered set partitions of type
![]() $(k,n)$
with winding number d is given by
$(k,n)$
with winding number d is given by
Proof The proof follows mutatis mutandis from [Reference Kim28, Proposition 2.11].
From now on, if we consider a cyclically ordered partition
![]() $\xi = (L_1,\ldots ,L_m)$
, we will consider the indices of the blocks modulo m. For instance,
$\xi = (L_1,\ldots ,L_m)$
, we will consider the indices of the blocks modulo m. For instance,
![]() $L_0=L_m$
and
$L_0=L_m$
and
![]() $L_{m+2} = L_{2}$
.
$L_{m+2} = L_{2}$
.
Definition 5.7 Let
![]() $T\subseteq [n]$
with
$T\subseteq [n]$
with
![]() $n\notin T$
.
$n\notin T$
.
-
• A T-singlet block is a singleton
 $\{t\}\subseteq T$
.
$\{t\}\subseteq T$
. -
• A sequence of T-singlet blocks
 $(L_i,\dots ,L_{i+j})$
where
$(L_i,\dots ,L_{i+j})$
where
 $L_{i+u}=\{t_{i+u}\}$
occurring in a decorated ordered set partition
$L_{i+u}=\{t_{i+u}\}$
occurring in a decorated ordered set partition
 $\xi $
is
$\xi $
is
 $\textbf {c}$
-packed if
$\textbf {c}$
-packed if
 $w(L_{i+u}) = c_{t_{i+u}}$
for all
$w(L_{i+u}) = c_{t_{i+u}}$
for all
 $0\leq u\leq j-1$
and
$0\leq u\leq j-1$
and
 $w(L_{i+j})\geq c_{t_{i+j}}$
.
$w(L_{i+j})\geq c_{t_{i+j}}$
. -
• A
 $\textbf {c}$
-packed sequence is increasing
$\textbf {c}$
-packed sequence is increasing
 $\textbf {c}$
-packed if
$\textbf {c}$
-packed if
 $t_i<t_{i+1}<\cdots <t_{i+j}$
.
$t_i<t_{i+1}<\cdots <t_{i+j}$
. -
• An increasing
 $\textbf {c}$
-packed sequence is maximal if it is not contained in a larger increasing
$\textbf {c}$
-packed sequence is maximal if it is not contained in a larger increasing
 $\textbf {c}$
-packed sequence.
$\textbf {c}$
-packed sequence.
Lemma 5.8 Let
![]() $S=\{B_1,\dots ,B_u\}\in \Pi (T)$
where
$S=\{B_1,\dots ,B_u\}\in \Pi (T)$
where
![]() $n\notin T$
and
$n\notin T$
and
![]() $T=\{t_1<\cdots <t_m\}$
. Write the elements of
$T=\{t_1<\cdots <t_m\}$
. Write the elements of
![]() $B_i$
in increasing order as
$B_i$
in increasing order as
![]() $B_i=\{t_{j_1}<t_{j_2}<\cdots <t_{j_{u_i}}\}$
. Then
$B_i=\{t_{j_1}<t_{j_2}<\cdots <t_{j_{u_i}}\}$
. Then
![]() $K_{\textbf {c}}(S)$
is in bijection with set of elements of
$K_{\textbf {c}}(S)$
is in bijection with set of elements of
![]() $K_{\textbf {c}}(\{\{t_1\},\dots ,\{t_m\}\})$
that have an increasing
$K_{\textbf {c}}(\{\{t_1\},\dots ,\{t_m\}\})$
that have an increasing
![]() $\textbf {c}$
-packed sequence
$\textbf {c}$
-packed sequence
![]() $(\{t_{j_1}\},\{t_{j_2}\},\dots ,\{t_{j_{u_i}}\})$
for all i.
$(\{t_{j_1}\},\{t_{j_2}\},\dots ,\{t_{j_{u_i}}\})$
for all i.
Proof See [Reference Kim28, Lemma 2.14].
Fix
![]() $T=\{t_1<\cdots <t_m\}\subseteq [n]$
with
$T=\{t_1<\cdots <t_m\}\subseteq [n]$
with
![]() $n\notin T$
. For each
$n\notin T$
. For each
![]() $S\in \Pi (T)$
, Lemma 5.8 provides a map
$S\in \Pi (T)$
, Lemma 5.8 provides a map
If we name
![]() $\chi _S$
the characteristic map of
$\chi _S$
the characteristic map of
![]() $i_S(K_{\textbf {c}}(S))$
, in other words,
$i_S(K_{\textbf {c}}(S))$
, in other words,
 $$\begin{align*}\chi_s(\xi) = \left\{ \begin{matrix} 1, & \text{ if }\xi\in i_S(K_{\textbf{c}}(S)),\\ 0, & \text{ if }\xi\notin i_S(K_{\textbf{c}}(S)), \end{matrix} \right.\end{align*}$$
$$\begin{align*}\chi_s(\xi) = \left\{ \begin{matrix} 1, & \text{ if }\xi\in i_S(K_{\textbf{c}}(S)),\\ 0, & \text{ if }\xi\notin i_S(K_{\textbf{c}}(S)), \end{matrix} \right.\end{align*}$$
then we have that
 $$ \begin{align*} H_{\textbf{c}}(T) &= \sum_{S\in \Pi(T)}(-1)^{|S|} |K_{\textbf{c}}(S)| = \sum_{S\in \Pi(T)}(-1)^{|S|} |i_S(K_{\textbf{c}}(S))|\\ &=\sum_{S\in \Pi(T)}(-1)^{|S|} \sum_{\xi\in K_{\textbf{c}}(\{\{t_1\},\dots,\{t_m\}\})}\chi_S(\xi)\\ &=\sum_{\xi\in K_{\textbf{c}}(\{\{t_1\},\dots,\{t_m\}\})}\sum_{S\in \Pi(T)}(-1)^{|S|}\chi_S(\xi). \end{align*} $$
$$ \begin{align*} H_{\textbf{c}}(T) &= \sum_{S\in \Pi(T)}(-1)^{|S|} |K_{\textbf{c}}(S)| = \sum_{S\in \Pi(T)}(-1)^{|S|} |i_S(K_{\textbf{c}}(S))|\\ &=\sum_{S\in \Pi(T)}(-1)^{|S|} \sum_{\xi\in K_{\textbf{c}}(\{\{t_1\},\dots,\{t_m\}\})}\chi_S(\xi)\\ &=\sum_{\xi\in K_{\textbf{c}}(\{\{t_1\},\dots,\{t_m\}\})}\sum_{S\in \Pi(T)}(-1)^{|S|}\chi_S(\xi). \end{align*} $$
Proposition 5.9 Fix
![]() $T\subseteq [n]$
with
$T\subseteq [n]$
with
![]() $n\notin T$
. If
$n\notin T$
. If
![]() $\xi \in K_{\textbf {c}}(T)$
does not have an increasing
$\xi \in K_{\textbf {c}}(T)$
does not have an increasing
![]() $\textbf {c}$
-packed sequence of length greater than 1, then the sum
$\textbf {c}$
-packed sequence of length greater than 1, then the sum
![]() $\sum _{S\in \Pi (T)}(-1)^{|S|}\chi _S(\xi )$
is equal to
$\sum _{S\in \Pi (T)}(-1)^{|S|}\chi _S(\xi )$
is equal to
![]() $(-1)^{|T|}$
. Otherwise, this sum is zero.
$(-1)^{|T|}$
. Otherwise, this sum is zero.
Proof This can be obtained by a reasoning entirely analogous to that of [Reference Kim28, Proposition 2.17].
Proposition 5.9 motivates the following definition.
Definition 5.10 For a fixed
![]() $T=\{t_1<\cdots <t_m\}\subseteq [n]$
with
$T=\{t_1<\cdots <t_m\}\subseteq [n]$
with
![]() $n\notin T$
, define
$n\notin T$
, define
![]() $\hat {K}_{\textbf {c}}(T)$
to be the decorated ordered set partitions of
$\hat {K}_{\textbf {c}}(T)$
to be the decorated ordered set partitions of
![]() $K_{\textbf {c}}(T)$
that do not contain an increasing
$K_{\textbf {c}}(T)$
that do not contain an increasing
![]() $\textbf {c}$
-packed sequence of length greater than
$\textbf {c}$
-packed sequence of length greater than
![]() $1$
.
$1$
.
Notice by Proposition 5.9 and the short calculation preceding it, we have that
Proposition 5.11 The set
![]() $\hat {K}_{\textbf {c}}(T)$
is in bijection with the following set:
$\hat {K}_{\textbf {c}}(T)$
is in bijection with the following set:
 $$\begin{align*}\left\{(v_1,\ldots,v_n)\in \mathbb{Z}^n : \sum_{i=1}^n v_i = (k-c_T)d \text{ and }\; \begin{matrix} 0&\leq v_i\leq& k-c_T-1 & \text{for each }i\notin T\\ 1&\leq v_i\leq &k-c_T & \text{for each }i\in T \end{matrix}\right\}, \end{align*}$$
$$\begin{align*}\left\{(v_1,\ldots,v_n)\in \mathbb{Z}^n : \sum_{i=1}^n v_i = (k-c_T)d \text{ and }\; \begin{matrix} 0&\leq v_i\leq& k-c_T-1 & \text{for each }i\notin T\\ 1&\leq v_i\leq &k-c_T & \text{for each }i\in T \end{matrix}\right\}, \end{align*}$$
where we use the notation
![]() $c_T:=\sum _{i\in T} c_i$
.
$c_T:=\sum _{i\in T} c_i$
.
Proof See [Reference Kim28, Proposition 2.22].
The idea is to provide a formula for
![]() $H_{\textbf {c}}$
. Since
$H_{\textbf {c}}$
. Since
![]() $H_{\textbf {c}} = (-1)^{|T|} \hat {K}_{\textbf {c}}(T)$
, it is enough to enumerate the elements in the set of Proposition 5.11. Its size can be calculated as follows. Let us consider new variables
$H_{\textbf {c}} = (-1)^{|T|} \hat {K}_{\textbf {c}}(T)$
, it is enough to enumerate the elements in the set of Proposition 5.11. Its size can be calculated as follows. Let us consider new variables
![]() $v^{\prime }_1,\ldots ,v^{\prime }_n$
. For each
$v^{\prime }_1,\ldots ,v^{\prime }_n$
. For each
![]() $i\notin T$
, we set
$i\notin T$
, we set
![]() $v_i'=v_i$
; otherwise, we put
$v_i'=v_i$
; otherwise, we put
![]() $v_i'=v_i-1$
. Then the cardinality of the set in Proposition 5.11 can be seen as the number of nonnegative integer solutions to
$v_i'=v_i-1$
. Then the cardinality of the set in Proposition 5.11 can be seen as the number of nonnegative integer solutions to
![]() $v^{\prime }_1+\cdots +v^{\prime }_n=(k-c_T)d-|T|$
under the constraints
$v^{\prime }_1+\cdots +v^{\prime }_n=(k-c_T)d-|T|$
under the constraints
![]() $0\leq v_i'\leq k-c_T-1$
for each
$0\leq v_i'\leq k-c_T-1$
for each
![]() $1\leq i\leq n$
. This coincides with the coefficient of
$1\leq i\leq n$
. This coincides with the coefficient of
![]() $x^{(k-c_T)d-|T|}$
in
$x^{(k-c_T)d-|T|}$
in
![]() $(1+x+\cdots +x^{k-c_T-1})^n$
, which is the number
$(1+x+\cdots +x^{k-c_T-1})^n$
, which is the number
![]() $\binom {n}{(k-c_T)d-|T|}_{k-c_T}$
.
$\binom {n}{(k-c_T)d-|T|}_{k-c_T}$
.
Putting all the pieces together, we obtain
 $$ \begin{align} \sum_{T\subseteq [n]}H_{\textbf{c}}(T) &=\sum_{T\subseteq [n]}(-1)^{|T|}|\hat{K}_{\textbf{c}}(T)|\nonumber\\ &=\sum_{T\subseteq [n]}(-1)^{|T|}\binom{n}{(k-c_T)d-|T|}_{k-c_T}\nonumber\\ &=\sum_{m=0}^n\sum_{|T|=m}(-1)^{|T|}\binom{n}{(k-c_T)d-|T|}_{k-c_T}\nonumber\\ &=\sum_{m=0}^{k-1}\sum_{|T|=m}(-1)^{m}\binom{n}{(k-c_T)d-m}_{k-c_T}\nonumber\\ &=\sum_{m=0}^{k-1}\sum_{v=0}^{k-1}\sum_{\substack{|T|=m\nonumber\\ c_T=v}}(-1)^{m}\binom{n}{(k-v)d-m}_{k-v}\nonumber\\ &=\sum_{m=0}^{k-1}\sum_{v=0}^{k-1}(-1)^{m}\rho_{\textbf{c},m}(v)\binom{n}{(k-v)d-m}_{k-v} \nonumber\\ &=\sum_{m=0}^{k-1}\sum_{v=0}^{k-1}(-1)^{m}\rho_{\textbf{c},m}(v)\sum_{i=0}^{d}(-1)^i\binom{n}{i}\binom{n-1+(k-v)(d-i)-m}{n-1} \end{align} $$
$$ \begin{align} \sum_{T\subseteq [n]}H_{\textbf{c}}(T) &=\sum_{T\subseteq [n]}(-1)^{|T|}|\hat{K}_{\textbf{c}}(T)|\nonumber\\ &=\sum_{T\subseteq [n]}(-1)^{|T|}\binom{n}{(k-c_T)d-|T|}_{k-c_T}\nonumber\\ &=\sum_{m=0}^n\sum_{|T|=m}(-1)^{|T|}\binom{n}{(k-c_T)d-|T|}_{k-c_T}\nonumber\\ &=\sum_{m=0}^{k-1}\sum_{|T|=m}(-1)^{m}\binom{n}{(k-c_T)d-m}_{k-c_T}\nonumber\\ &=\sum_{m=0}^{k-1}\sum_{v=0}^{k-1}\sum_{\substack{|T|=m\nonumber\\ c_T=v}}(-1)^{m}\binom{n}{(k-v)d-m}_{k-v}\nonumber\\ &=\sum_{m=0}^{k-1}\sum_{v=0}^{k-1}(-1)^{m}\rho_{\textbf{c},m}(v)\binom{n}{(k-v)d-m}_{k-v} \nonumber\\ &=\sum_{m=0}^{k-1}\sum_{v=0}^{k-1}(-1)^{m}\rho_{\textbf{c},m}(v)\sum_{i=0}^{d}(-1)^i\binom{n}{i}\binom{n-1+(k-v)(d-i)-m}{n-1} \end{align} $$
 $$ \begin{align} &=\sum_{i=0}^{d}(-1)^i \binom{n}{i} \left(\sum_{m=0}^{k-1}\sum_{v=0}^{k-1}(-1)^{m}\rho_{\textbf{c},m}(v)\binom{n-1+(k-v)(d-i)-m}{n-1}\right)\nonumber\\ &=\sum_{i=0}^{d}(-1)^i \binom{n}{i} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},d-i) \end{align} $$
$$ \begin{align} &=\sum_{i=0}^{d}(-1)^i \binom{n}{i} \left(\sum_{m=0}^{k-1}\sum_{v=0}^{k-1}(-1)^{m}\rho_{\textbf{c},m}(v)\binom{n-1+(k-v)(d-i)-m}{n-1}\right)\nonumber\\ &=\sum_{i=0}^{d}(-1)^i \binom{n}{i} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},d-i) \end{align} $$
 $$ \begin{align} &= [x^d] \left((1-x)^n\, \sum_{j=0}^{\infty} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}}, j) x^j\right)\nonumber\\ &=[x^d] h^*(\mathscr{R}_{k,\textbf{c}},x), \end{align} $$
$$ \begin{align} &= [x^d] \left((1-x)^n\, \sum_{j=0}^{\infty} \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}}, j) x^j\right)\nonumber\\ &=[x^d] h^*(\mathscr{R}_{k,\textbf{c}},x), \end{align} $$
where in (5.1) we used Lemma 5.4, in (5.2) we leveraged the formula of Theorem 2.5, and in (5.2) we just used the definition of the
![]() $h^*$
-polynomial. Now, combining this with Proposition 5.6, we have proved Theorem 1.7.
$h^*$
-polynomial. Now, combining this with Proposition 5.6, we have proved Theorem 1.7.
5.3 A real-rootedness conjecture
In the context of the study of the
![]() $h^*$
-polynomials of the polytopes
$h^*$
-polynomials of the polytopes
![]() $\mathscr {R}_{k,\textbf {c}}$
, we pose the following conjecture.
$\mathscr {R}_{k,\textbf {c}}$
, we pose the following conjecture.
Conjecture 5.12 Let
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}_{>0}^n$
and
![]() $k>0$
. Then
$k>0$
. Then
![]() $h^*(\mathscr {R}_{k,\textbf {c}},x)$
is real-rooted. Moreover, if
$h^*(\mathscr {R}_{k,\textbf {c}},x)$
is real-rooted. Moreover, if
![]() $c_n\geq 2$
, define
$c_n\geq 2$
, define
![]() $\textbf {c}'=(c_1,\ldots ,c_{n-1},c_n-1,1)\in \mathbb {Z}^{n+1}_{>0}$
, then the roots of
$\textbf {c}'=(c_1,\ldots ,c_{n-1},c_n-1,1)\in \mathbb {Z}^{n+1}_{>0}$
, then the roots of
![]() $h^*(\mathscr {R}_{k,\textbf {c}},x)$
and
$h^*(\mathscr {R}_{k,\textbf {c}},x)$
and
![]() $h^*(\mathscr {R}_{k,\textbf {c}'},x)$
interlace.
$h^*(\mathscr {R}_{k,\textbf {c}'},x)$
interlace.
Observe that this would automatically provide a proof for the unimodality of the coefficients of the
![]() $h^*$
-polynomial of all hypersimplices, a long-standing open problem regarding the combinatorics of the hypersimplex (see [Reference Braun2]). In particular, if we use the notation
$h^*$
-polynomial of all hypersimplices, a long-standing open problem regarding the combinatorics of the hypersimplex (see [Reference Braun2]). In particular, if we use the notation
![]() $p(x)\lessdot q(x)$
to denote that p and q interlace, after fixing k and n, our conjecture implies that one can produce the sequence of polynomials
$p(x)\lessdot q(x)$
to denote that p and q interlace, after fixing k and n, our conjecture implies that one can produce the sequence of polynomials
and
![]() $h^*(\mathscr {R}_{k,(1,\ldots ,1)},x)=h^*(\Delta _{k,n},x)$
. It is reasonable to search for recurrences that these polynomials satisfy and use techniques as those used in [Reference Haglund and Zhang20] or [Reference Gustafsson and Solus19].
$h^*(\mathscr {R}_{k,(1,\ldots ,1)},x)=h^*(\Delta _{k,n},x)$
. It is reasonable to search for recurrences that these polynomials satisfy and use techniques as those used in [Reference Haglund and Zhang20] or [Reference Gustafsson and Solus19].
6 Some applications
In this section, we discuss some applications that are of independent interest. In some cases, we omit details and definitions, and we advise to look at the references mentioned correspondingly.
6.1 Volumes
As we mentioned in the Introduction, the leading coefficient of
![]() $\operatorname {\mathrm{ehr}}(\mathscr {P},t)$
is
$\operatorname {\mathrm{ehr}}(\mathscr {P},t)$
is
![]() $\operatorname {vol}(\mathscr {P})$
. In particular, by using the formula of Theorem 1.2, for
$\operatorname {vol}(\mathscr {P})$
. In particular, by using the formula of Theorem 1.2, for
![]() $m=n-1$
, we obtain Corollary 1.5. We restate it and prove it now.
$m=n-1$
, we obtain Corollary 1.5. We restate it and prove it now.
Corollary 6.1 Let
![]() $\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
and
$\textbf {c}=(c_1,\dots ,c_n)\in \mathbb {Z}_{>0}^n$
and
![]() $0 < k < c_1+\cdots +c_n$
. Then the volume of
$0 < k < c_1+\cdots +c_n$
. Then the volume of
![]() $\mathscr {R}_{k,\textbf {c}}$
is given by
$\mathscr {R}_{k,\textbf {c}}$
is given by
 $$\begin{align*}\operatorname{vol}(\mathscr{R}_{k,\textbf{c}}) = \frac{1}{(n-1)!} \sum_{\ell = 0}^{k-1} B(\ell,\textbf{c})A(n-1,k-\ell-1),\end{align*}$$
$$\begin{align*}\operatorname{vol}(\mathscr{R}_{k,\textbf{c}}) = \frac{1}{(n-1)!} \sum_{\ell = 0}^{k-1} B(\ell,\textbf{c})A(n-1,k-\ell-1),\end{align*}$$
where
![]() $B(\ell ,\textbf {c})$
is defined as the number of ways of placing
$B(\ell ,\textbf {c})$
is defined as the number of ways of placing
![]() $\ell $
indistinguishable balls into n boxes of capacities
$\ell $
indistinguishable balls into n boxes of capacities
![]() $c_1-1, \ldots , c_n-1$
, respectively.
$c_1-1, \ldots , c_n-1$
, respectively.
Proof Given that we assume that
![]() $0 < k < c_1+\cdots +c_n$
, the Ehrhart polynomial has degree
$0 < k < c_1+\cdots +c_n$
, the Ehrhart polynomial has degree
![]() $n-1$
and hence the volume is obtained by taking
$n-1$
and hence the volume is obtained by taking
![]() $m=n-1$
in the statement of our main theorem.
$m=n-1$
in the statement of our main theorem.
 $$ \begin{align*} \operatorname{vol}(\mathscr{R}_{k,\textbf{c}}) &= [t^{n-1}] \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t)\\ &= \frac{1}{(n-1)!} \sum_{\ell = 0}^{k-1} W(\ell, n,n, \textbf{c}) A(n-1,k-\ell-1). \end{align*} $$
$$ \begin{align*} \operatorname{vol}(\mathscr{R}_{k,\textbf{c}}) &= [t^{n-1}] \operatorname{\mathrm{ehr}}(\mathscr{R}_{k,\textbf{c}},t)\\ &= \frac{1}{(n-1)!} \sum_{\ell = 0}^{k-1} W(\ell, n,n, \textbf{c}) A(n-1,k-\ell-1). \end{align*} $$
Notice that we have a factor
![]() $W(\ell ,n,n,\textbf {c})$
in each summand. The only permutation
$W(\ell ,n,n,\textbf {c})$
in each summand. The only permutation
![]() $\sigma \in \mathfrak {S}_n$
with n cycles is the identity. Therefore, in order for the permutation to admit a
$\sigma \in \mathfrak {S}_n$
with n cycles is the identity. Therefore, in order for the permutation to admit a
![]() $\textbf {c}$
-compatible weight, we have to ensure that each of the numbers
$\textbf {c}$
-compatible weight, we have to ensure that each of the numbers
![]() $i\in [n]$
is assigned a value between
$i\in [n]$
is assigned a value between
![]() $0$
and
$0$
and
![]() $c_i-1$
. To guarantee that the total weight is
$c_i-1$
. To guarantee that the total weight is
![]() $\ell $
, we can think that we are putting
$\ell $
, we can think that we are putting
![]() $\ell $
balls inside boxes with capacities
$\ell $
balls inside boxes with capacities
![]() $c_1-1,\ldots , c_n-1$
, as is described in the statement.
$c_1-1,\ldots , c_n-1$
, as is described in the statement.
6.2 Flag Eulerian numbers
In this subsection, we will extend and generalize some of the results of [Reference Han and Josuat-Vergès21]. Let
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}^n_{>0}$
. In what follows, we will define objects that coincide with those defined in [Reference Han and Josuat-Vergès21] when
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}^n_{>0}$
. In what follows, we will define objects that coincide with those defined in [Reference Han and Josuat-Vergès21] when
![]() $c_1=\cdots =c_n=r$
. A
$c_1=\cdots =c_n=r$
. A
![]() $\textbf {c}$
-colored permutation on
$\textbf {c}$
-colored permutation on
![]() $[n]$
consists of a permutation
$[n]$
consists of a permutation
![]() $\sigma \in \mathfrak {S}_n$
and a function
$\sigma \in \mathfrak {S}_n$
and a function
![]() $\textbf {s}:[n]\to \mathbb {Z}_{\geq 0}$
such that
$\textbf {s}:[n]\to \mathbb {Z}_{\geq 0}$
such that
![]() $s_i:=\textbf {s}(i) \leq c_i-1$
for each
$s_i:=\textbf {s}(i) \leq c_i-1$
for each
![]() $i\in [n]$
. The set of all
$i\in [n]$
. The set of all
![]() $\textbf {c}$
-colored permutations for a fixed value of n is denoted by
$\textbf {c}$
-colored permutations for a fixed value of n is denoted by
![]() $\mathfrak {S}_n^{(\textbf {c})}$
. The descent number of a
$\mathfrak {S}_n^{(\textbf {c})}$
. The descent number of a
![]() $\textbf {c}$
-colored permutation
$\textbf {c}$
-colored permutation
![]() $(\sigma , \textbf {s})\in \mathfrak {S}_n^{(\textbf {c})}$
is defined as
$(\sigma , \textbf {s})\in \mathfrak {S}_n^{(\textbf {c})}$
is defined as
![]() $\operatorname {des}(\sigma ,\textbf {s}) := \#\operatorname {Des}(\sigma ,\textbf {s})$
where
$\operatorname {des}(\sigma ,\textbf {s}) := \#\operatorname {Des}(\sigma ,\textbf {s})$
where
The flag descent number of a
![]() $\textbf {c}$
-colored permutation
$\textbf {c}$
-colored permutation
![]() $(\sigma ,\textbf {s})\in \mathfrak {S}_n^{(\textbf {c})}$
is defined by
$(\sigma ,\textbf {s})\in \mathfrak {S}_n^{(\textbf {c})}$
is defined by
The flag Eulerian numbers are defined by
In [Reference Han and Josuat-Vergès21], Han and Josuat-Vergès approached the case in which
![]() $c_1=\cdots =c_n=r$
Footnote
1
. They provided formulas and interpretations for
$c_1=\cdots =c_n=r$
Footnote
1
. They provided formulas and interpretations for
![]() $A_{n,k}^{(r,\ldots ,r)}$
. In particular, to obtain an explicit formula for such numbers, they studied certain half-open polytopes having these numbers as their volumes. We can extend this technique to arbitrary vectors
$A_{n,k}^{(r,\ldots ,r)}$
. In particular, to obtain an explicit formula for such numbers, they studied certain half-open polytopes having these numbers as their volumes. We can extend this technique to arbitrary vectors
![]() $\textbf {c}=(c_1,\ldots ,c_n)$
.
$\textbf {c}=(c_1,\ldots ,c_n)$
.
First, for each
![]() $v=(v_1,\ldots ,v_n)\in \mathbb {R}^n$
, we call
$v=(v_1,\ldots ,v_n)\in \mathbb {R}^n$
, we call
![]() $\operatorname {Des}(v)=\{i\in [n-1]:v_i>v_{i+1}\}$
. Let us use the name
$\operatorname {Des}(v)=\{i\in [n-1]:v_i>v_{i+1}\}$
. Let us use the name
and define the following two (half-open) polytopes:
 $$ \begin{align*} \mathcal{F}_{n,k}^{(\textbf{c})} &:= \left\{v\in\mathscr{R}_{\textbf{c}} : k \leq \operatorname{fdes}_{\textbf{c}}(v) < k+1\right\},\\ \mathcal{A}_{n,k}^{(\textbf{c})} &:= \left\{ v\in \mathscr{R}_{\textbf{c}} : k \leq \sum_{i=1}^n v_i < k+1 \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{F}_{n,k}^{(\textbf{c})} &:= \left\{v\in\mathscr{R}_{\textbf{c}} : k \leq \operatorname{fdes}_{\textbf{c}}(v) < k+1\right\},\\ \mathcal{A}_{n,k}^{(\textbf{c})} &:= \left\{ v\in \mathscr{R}_{\textbf{c}} : k \leq \sum_{i=1}^n v_i < k+1 \right\}. \end{align*} $$
The key observation is that the above two (half-open) polytopes have the same volume, as there is a measure-preserving map between them that we shall describe. In [Reference Stanley39], Stanley studied the case
![]() $c_1=\cdots =c_n=1$
, and in [Reference Han and Josuat-Vergès21], Han and Josuat-Vergès extended this to the case
$c_1=\cdots =c_n=1$
, and in [Reference Han and Josuat-Vergès21], Han and Josuat-Vergès extended this to the case
![]() $c_1=\cdots =c_n=r$
. The latter case had also been approached before by Steingrímsson in [Reference Steingrímsson42, Section 4.4]. We outline here how to show it for an arbitrary vector
$c_1=\cdots =c_n=r$
. The latter case had also been approached before by Steingrímsson in [Reference Steingrímsson42, Section 4.4]. We outline here how to show it for an arbitrary vector
![]() $\textbf {c}$
. Consider the map
$\textbf {c}$
. Consider the map
![]() $\varphi :[0,c_1)\times \cdots \times [0,c_n)\to [0,c_1)\times \cdots \times [0,c_n)$
defined everywhere, except in a measure zero set, by
$\varphi :[0,c_1)\times \cdots \times [0,c_n)\to [0,c_1)\times \cdots \times [0,c_n)$
defined everywhere, except in a measure zero set, by
![]() $(a_1,\ldots ,a_n)\mapsto (b_1,\ldots ,b_n)$
where for each
$(a_1,\ldots ,a_n)\mapsto (b_1,\ldots ,b_n)$
where for each
![]() $1\leq i\leq n$
we have
$1\leq i\leq n$
we have
 $$\begin{align*}b_i := \left\{ \begin{matrix} a_i - a_{i-1}, & \text{ if }a_{i-1}< a_i,\\ a_i - a_{i-1} + c_i, & \text{ if }a_{i-1}>a_i, \end{matrix} \right.\end{align*}$$
$$\begin{align*}b_i := \left\{ \begin{matrix} a_i - a_{i-1}, & \text{ if }a_{i-1}< a_i,\\ a_i - a_{i-1} + c_i, & \text{ if }a_{i-1}>a_i, \end{matrix} \right.\end{align*}$$
where we use the convention
![]() $a_0:=0$
. This map is injective where defined, as if we assume that
$a_0:=0$
. This map is injective where defined, as if we assume that
![]() $(a_1,\ldots ,a_n)$
and
$(a_1,\ldots ,a_n)$
and
![]() $(a_1',\ldots ,a_n')$
map to the same vector
$(a_1',\ldots ,a_n')$
map to the same vector
![]() $(b_1,\ldots ,b_n)$
, then looking at the first coordinates yields
$(b_1,\ldots ,b_n)$
, then looking at the first coordinates yields
![]() $a_1=a_1'$
. Next, looking at the second coordinates, we must have
$a_1=a_1'$
. Next, looking at the second coordinates, we must have
where
![]() $\varepsilon , \varepsilon '\in \{0,1\}$
depend on how
$\varepsilon , \varepsilon '\in \{0,1\}$
depend on how
![]() $a_1$
and
$a_1$
and
![]() $a_2$
compare (resp.
$a_2$
compare (resp.
![]() $a_1'$
and
$a_1'$
and
![]() $a_2'$
). Canceling the summand
$a_2'$
). Canceling the summand
![]() $a_1=a_1'$
from both sides gives
$a_1=a_1'$
from both sides gives
![]() $a_2 = a_2' + (\varepsilon '-\varepsilon ) c_2$
. Since we are assuming that both vectors
$a_2 = a_2' + (\varepsilon '-\varepsilon ) c_2$
. Since we are assuming that both vectors
![]() $(a_1,\ldots ,a_n)$
and
$(a_1,\ldots ,a_n)$
and
![]() $(a_1',\ldots ,a_n')$
lie in
$(a_1',\ldots ,a_n')$
lie in
![]() $[0,c_1)\times \cdots \times [0,c_n)$
, the only possibility is that
$[0,c_1)\times \cdots \times [0,c_n)$
, the only possibility is that
![]() $\varepsilon =\varepsilon '$
and that
$\varepsilon =\varepsilon '$
and that
![]() $a_2=a_2'$
. Inductively we can continue using the same reasoning.
$a_2=a_2'$
. Inductively we can continue using the same reasoning.
Notice that the map
![]() $\varphi $
is indeed measure-preserving, as if we consider for each
$\varphi $
is indeed measure-preserving, as if we consider for each
![]() $\sigma \in \mathfrak {S}_n$
the subset of
$\sigma \in \mathfrak {S}_n$
the subset of
![]() $\mathscr {R}_{\textbf {c}}$
defined by
$\mathscr {R}_{\textbf {c}}$
defined by
thenFootnote
2
![]() $\varphi |_{\mathscr {R}_{\textbf {c},\sigma }}$
is just a map of the form
$\varphi |_{\mathscr {R}_{\textbf {c},\sigma }}$
is just a map of the form
![]() $\varphi (\textbf {x}) = A\textbf {x} + \boldsymbol {\varepsilon }$
, where A is a matrix with
$\varphi (\textbf {x}) = A\textbf {x} + \boldsymbol {\varepsilon }$
, where A is a matrix with
![]() $1$
’s in the main diagonal and
$1$
’s in the main diagonal and
![]() $-1$
’s in second diagonal, whereas
$-1$
’s in second diagonal, whereas
![]() $\boldsymbol {\varepsilon }$
is a vector having
$\boldsymbol {\varepsilon }$
is a vector having
![]() $c_i$
’s or zeros as entries.
$c_i$
’s or zeros as entries.
Moreover, if we take a vector
![]() $v\in \mathcal {F}_{n,k}^{(\textbf {c})}$
having distinct coordinates and we call
$v\in \mathcal {F}_{n,k}^{(\textbf {c})}$
having distinct coordinates and we call
![]() $(v_1',\ldots ,v_n'):=\varphi (v)$
, we have that
$(v_1',\ldots ,v_n'):=\varphi (v)$
, we have that
and hence
![]() $\varphi $
maps (up to a measure zero subset) all of
$\varphi $
maps (up to a measure zero subset) all of
![]() $\mathcal {F}_{n,k}^{(\textbf {c})}$
to
$\mathcal {F}_{n,k}^{(\textbf {c})}$
to
![]() $\mathcal {A}_{n,k}^{(\textbf {c})}$
, and hence the volumes of these two (half-
$\mathcal {A}_{n,k}^{(\textbf {c})}$
, and hence the volumes of these two (half-
On one hand, we have that
![]() $\operatorname {vol}(\mathcal {A}_{n,k}^{(\textbf {c})})=\operatorname {vol}(\mathcal {F}_{n,k}^{(\textbf {c})})$
, whereas, on the other hand, it is not difficult to show that
$\operatorname {vol}(\mathcal {A}_{n,k}^{(\textbf {c})})=\operatorname {vol}(\mathcal {F}_{n,k}^{(\textbf {c})})$
, whereas, on the other hand, it is not difficult to show that
![]() $\operatorname {vol}(\mathcal {F}^{(\textbf {c})}_{n,k}) = \frac {1}{n!}A_{n,k}^{(\textbf {c})}$
. In other words,
$\operatorname {vol}(\mathcal {F}^{(\textbf {c})}_{n,k}) = \frac {1}{n!}A_{n,k}^{(\textbf {c})}$
. In other words,
We can use that
![]() $\mathcal {A}_{n,k}^{(\textbf {c})}$
is a slice of a prism with some missing facets. In particular, its volume will not change if we add these facets. This trick leads to a proof of the following result.
$\mathcal {A}_{n,k}^{(\textbf {c})}$
is a slice of a prism with some missing facets. In particular, its volume will not change if we add these facets. This trick leads to a proof of the following result.
Corollary 6.2 The flag Eulerian number
![]() $A_{n,k}^{(\textbf {c})}$
is given by
$A_{n,k}^{(\textbf {c})}$
is given by
 $$\begin{align*}A_{n,k}^{(\textbf{c})} = \sum_{\ell = 0}^{k} B(\ell, \textbf{c}) A(n, k-\ell),\end{align*}$$
$$\begin{align*}A_{n,k}^{(\textbf{c})} = \sum_{\ell = 0}^{k} B(\ell, \textbf{c}) A(n, k-\ell),\end{align*}$$
where
![]() $B(\ell ,\textbf {c})$
is defined as in Corollary 1.5.
$B(\ell ,\textbf {c})$
is defined as in Corollary 1.5.
Proof Consider the polytope
![]() $\mathscr {R}_{k+1, \textbf {c}'}$
for
$\mathscr {R}_{k+1, \textbf {c}'}$
for
![]() $\textbf {c}' = (c_1,\ldots ,c_n, 1)\in \mathbb {Z}_{>0}^{n+1}$
. By Corollary 1.5, we obtain
$\textbf {c}' = (c_1,\ldots ,c_n, 1)\in \mathbb {Z}_{>0}^{n+1}$
. By Corollary 1.5, we obtain
 $$ \begin{align} A_{n,k}^{(\textbf{c})} = n! \operatorname{vol}\left(\mathcal{A}^{(\textbf{c})}_{n,k}\right) = n! \operatorname{vol}\left(\mathscr{R}_{k+1,\textbf{c}'}\right) =\sum_{\ell = 0}^{k} B(\ell, \textbf{c}') A(n, k-\ell),\end{align} $$
$$ \begin{align} A_{n,k}^{(\textbf{c})} = n! \operatorname{vol}\left(\mathcal{A}^{(\textbf{c})}_{n,k}\right) = n! \operatorname{vol}\left(\mathscr{R}_{k+1,\textbf{c}'}\right) =\sum_{\ell = 0}^{k} B(\ell, \textbf{c}') A(n, k-\ell),\end{align} $$
where
![]() $B(\ell , \textbf {c}')$
is in this case the number of ways of placing
$B(\ell , \textbf {c}')$
is in this case the number of ways of placing
![]() $\ell $
balls into
$\ell $
balls into
![]() $n+1$
boxes of capacities
$n+1$
boxes of capacities
![]() $c_1-1,\ldots ,c_n-1$
and
$c_1-1,\ldots ,c_n-1$
and
![]() $0$
or, in other words,
$0$
or, in other words,
![]() $B(\ell ,\textbf {c}')=B(\ell ,\textbf {c})$
, which completes the proof.
$B(\ell ,\textbf {c}')=B(\ell ,\textbf {c})$
, which completes the proof.
The identity in the preceding corollary provides a new combinatorial formula for the version of the flag Eulerian numbers studied in [Reference Han and Josuat-Vergès21], by just particularizing
![]() $c_1=\cdots =c_n=r$
. We do not know of a direct combinatorial way of deriving the preceding equality.
$c_1=\cdots =c_n=r$
. We do not know of a direct combinatorial way of deriving the preceding equality.
Additionally, since the (normalized) volume of a polytope can be obtained by evaluating the
![]() $h^*$
-polynomial in
$h^*$
-polynomial in
![]() $x=1$
, we have a refinement of
$x=1$
, we have a refinement of
![]() $A_{n,k}^{(\textbf {c})}$
by considering the coefficients of the
$A_{n,k}^{(\textbf {c})}$
by considering the coefficients of the
![]() $h^*$
-polynomial of the polytope
$h^*$
-polynomial of the polytope
![]() $\mathscr {R}_{k+1,\textbf {c}'}$
by considering the winding numbers.
$\mathscr {R}_{k+1,\textbf {c}'}$
by considering the winding numbers.
Corollary 6.3 The flag Eulerian number
![]() $A_{n,k}^{(\textbf {c})}$
is given by
$A_{n,k}^{(\textbf {c})}$
is given by
where
![]() $\textbf {c}'=(\textbf {c},1)\in \mathbb {Z}^{n+1}_{>0}$
.
$\textbf {c}'=(\textbf {c},1)\in \mathbb {Z}^{n+1}_{>0}$
.
Compare this result to [Reference Kim28, Remark 1.2]. A version of this fact for hypersimplicial permutations (i.e.,
![]() $\textbf {c}=(1,\ldots ,1)$
) appeared also in [Reference Ocneanu36].
$\textbf {c}=(1,\ldots ,1)$
) appeared also in [Reference Ocneanu36].
6.3 Independence polytopes of uniform matroids
The uniform matroid
![]() $\mathsf{U}_{k,n}$
of rank k and cardinality n has the hypersimplex
$\mathsf{U}_{k,n}$
of rank k and cardinality n has the hypersimplex
![]() $\Delta _{k,n}$
as its base polytope. Its independence polytope, namely, the convex hull of the indicator vectors of all the independent subsets, denoted
$\Delta _{k,n}$
as its base polytope. Its independence polytope, namely, the convex hull of the indicator vectors of all the independent subsets, denoted
![]() $\mathscr {P}_I(\mathsf{U}_{k,n})$
is given by
$\mathscr {P}_I(\mathsf{U}_{k,n})$
is given by
 $$ \begin{align} \mathscr{P}_I(\mathsf{U}_{k,n}) = \left\{ x\in [0,1]^n : \sum_{i=1}^n x_i \leq k\right\}. \end{align} $$
$$ \begin{align} \mathscr{P}_I(\mathsf{U}_{k,n}) = \left\{ x\in [0,1]^n : \sum_{i=1}^n x_i \leq k\right\}. \end{align} $$
In his Ph.D. thesis [Reference Duna11], Duna conjectured that these polytopes are Ehrhart positive, and he proved that they indeed are when
![]() $k=2$
. Later, Ferroni proved in [Reference Ferroni15] that Ehrhart positivity holds for all k and n, but relies on complicated inequalities.
$k=2$
. Later, Ferroni proved in [Reference Ferroni15] that Ehrhart positivity holds for all k and n, but relies on complicated inequalities.
Observe that this polytope is a fat slice of the unit cube. Therefore, using Proposition 2.2, we see that
where
![]() $\textbf {c}' = (1,\ldots , 1, k)$
. This provides an alternative and much more conceptual proof of the Ehrhart positivity of these polytopes. Moreover, we can retrieve an explicit formula for their Ehrhart polynomial, also described in [Reference Duna11, Theorem 4.9].
$\textbf {c}' = (1,\ldots , 1, k)$
. This provides an alternative and much more conceptual proof of the Ehrhart positivity of these polytopes. Moreover, we can retrieve an explicit formula for their Ehrhart polynomial, also described in [Reference Duna11, Theorem 4.9].
Corollary 6.4 The Ehrhart polynomial of
![]() $\mathscr {P}_I(\mathsf{U}_{k,n})$
is given by
$\mathscr {P}_I(\mathsf{U}_{k,n})$
is given by
 $$\begin{align*}\operatorname{\mathrm{ehr}}(\mathscr{P}_I(\mathsf{U}_{k,n}), t) = \sum_{j=0}^{k-1}(-1)^j \binom{n}{j} \binom{(k-j)t+n-j}{n}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ehr}}(\mathscr{P}_I(\mathsf{U}_{k,n}), t) = \sum_{j=0}^{k-1}(-1)^j \binom{n}{j} \binom{(k-j)t+n-j}{n}.\end{align*}$$
This polynomial has positive coefficients.
Proof Since our polytope is integrally equivalent to
![]() $\mathscr {R}_{k,\textbf {c}'}$
for
$\mathscr {R}_{k,\textbf {c}'}$
for
![]() $\textbf {c}'=(1,\ldots ,1,k)\in \mathbb {Z}_{>0}^{n+1}$
, using Theorem 2.5, we have
$\textbf {c}'=(1,\ldots ,1,k)\in \mathbb {Z}_{>0}^{n+1}$
, using Theorem 2.5, we have
 $$\begin{align*}\operatorname{\mathrm{ehr}}(\mathscr{P}_I(\mathsf{U}_{k,n}), t) = \sum_{j=0}^{k-1}(-1)^j \sum_{v=0}^{k-1} \binom{(k-v)t+(n+1)-1-j}{(n+1)-1}\rho_{\textbf{c},j}(v).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ehr}}(\mathscr{P}_I(\mathsf{U}_{k,n}), t) = \sum_{j=0}^{k-1}(-1)^j \sum_{v=0}^{k-1} \binom{(k-v)t+(n+1)-1-j}{(n+1)-1}\rho_{\textbf{c},j}(v).\end{align*}$$
Recalling from equation (2.1) the definition of
![]() $\rho _{\textbf {c},j}(v)$
, we have that it is the number of ways of summing v using exactly j numbers among the
$\rho _{\textbf {c},j}(v)$
, we have that it is the number of ways of summing v using exactly j numbers among the
![]() $c_i$
’s. However, the only number v that can be obtained as the sum of j values among the
$c_i$
’s. However, the only number v that can be obtained as the sum of j values among the
![]() $c_i$
’s is just
$c_i$
’s is just
![]() $v=j$
, in exactly
$v=j$
, in exactly
![]() $\binom {n}{j}$
ways. In other words,
$\binom {n}{j}$
ways. In other words,
![]() $\rho _{\textbf {c},j}(v) = \binom {n}{j}$
if
$\rho _{\textbf {c},j}(v) = \binom {n}{j}$
if
![]() $j=v$
, and it is zero otherwise. This yields the result.
$j=v$
, and it is zero otherwise. This yields the result.
6.4 Hilbert series of algebras of Veronese type
The following algebraic structures arise naturally in combinatorics and commutative algebra.
Definition 6.5 Let
![]() $\mathbb {F}$
be a field, and fix a vector
$\mathbb {F}$
be a field, and fix a vector
![]() $\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}^n_{>0}$
and a positive integer
$\textbf {c}=(c_1,\ldots ,c_n)\in \mathbb {Z}^n_{>0}$
and a positive integer
![]() $k<c_1+\cdots +c_n$
. The graded subalgebra of
$k<c_1+\cdots +c_n$
. The graded subalgebra of
![]() $\mathbb {F}[x_1,\ldots ,x_n]$
generated by all the monomials
$\mathbb {F}[x_1,\ldots ,x_n]$
generated by all the monomials
![]() $x_1^{\alpha _1}\cdots x_n^{\alpha _n}$
where
$x_1^{\alpha _1}\cdots x_n^{\alpha _n}$
where
![]() $\alpha _1+\cdots +\alpha _n=k$
and
$\alpha _1+\cdots +\alpha _n=k$
and
![]() $\alpha _i\leq c_i$
for each
$\alpha _i\leq c_i$
for each
![]() $1\leq i\leq n$
is said to be of Veronese type and is denoted by
$1\leq i\leq n$
is said to be of Veronese type and is denoted by
![]() $\mathscr {V}(\textbf {c},k)$
.
$\mathscr {V}(\textbf {c},k)$
.
In [Reference De Negri and Hibi10], De Negri and Hibi studied the algebras of Veronese type and characterized the scenarios in which they are Gorenstein. In particular, in [Reference De Negri and Hibi10, Corollary 2.2], they prove that these algebras are Cohen–Macaulay and normal. An important step in such proofs consists of showing that there is an isomorphism between
![]() $\mathscr {V}(\textbf {c},k)$
and the Ehrhart ring of
$\mathscr {V}(\textbf {c},k)$
and the Ehrhart ring of
![]() $\mathscr {R}_{k,\textbf {c}}$
(see [Reference Bruns and Herzog4] for detailed definitions on Ehrhart rings of polytopes). In particular, we obtain as a consequence of Theorem 1.2 the following result.
$\mathscr {R}_{k,\textbf {c}}$
(see [Reference Bruns and Herzog4] for detailed definitions on Ehrhart rings of polytopes). In particular, we obtain as a consequence of Theorem 1.2 the following result.
Corollary 6.6 The Hilbert function of an algebra of Veronese type
![]() $\mathscr {A}$
is a polynomial having positive coefficients.
$\mathscr {A}$
is a polynomial having positive coefficients.
Proof By definition, the Hilbert function of
![]() $\mathscr {A}=\mathscr {V}(\textbf {c},k)$
is the map:
$\mathscr {A}=\mathscr {V}(\textbf {c},k)$
is the map:
By the discussion above, the dimension of the graded component
![]() $\mathscr {A}^m$
equals
$\mathscr {A}^m$
equals
![]() $\operatorname {\mathrm{ehr}}(\mathscr {R}_{k,\textbf {c}},m)$
, which we know has positive coefficients.
$\operatorname {\mathrm{ehr}}(\mathscr {R}_{k,\textbf {c}},m)$
, which we know has positive coefficients.
Notice that Hilbert functions very rarely possess such property. In [Reference Katzman27, p. 1145], Katzman referred to the combinatorial descriptions of the h-vector of
![]() $\mathscr {V}(\textbf {c},k)$
as “forbidding.” As a consequence of Theorem 1.7, we now state an interpretation for each of these entries.
$\mathscr {V}(\textbf {c},k)$
as “forbidding.” As a consequence of Theorem 1.7, we now state an interpretation for each of these entries.
Corollary 6.7 The ith entry of the h-vector of
![]() $\mathscr {V}(\textbf {c},k)$
counts the number of
$\mathscr {V}(\textbf {c},k)$
counts the number of
![]() $\textbf {c}$
-compatible decorated ordered permutations of type
$\textbf {c}$
-compatible decorated ordered permutations of type
![]() $(k,n)$
and winding number i.
$(k,n)$
and winding number i.
Acknowledgements
The first author wants to thank Katharina Jochemko for valuable suggestions that improved some aspects of this article. He also wants to thank the organizers and participants of the Workshops “Characteristic Polynomials of Hyperplane Arrangements and Ehrhart Polynomials of Convex Polytopes” at RIMS Kyoto, and “Combinatorial and Algebraic Aspects of Lattice Polytopes” at the Kwansei Gakuin University, both held in February 2023 for several enlightening discussions.