Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-02T21:50:42.959Z Has data issue: false hasContentIssue false
  • English
  • Français

An Integral Over Function Space

Published online by Cambridge University Press:  20 November 2018

W. F. Eberlein
W. F. Eberlein*
Affiliation:
University of Rochester
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Real functions

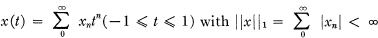
may be identified with elements x = (x0, x1, x2, … ) of the sequence space l1 Since the unit sphere S∞ of l1 is compact under the weak* topology = topology of co-ordinatewise convergence, a countably additive measure on S∞ is induced by a positive linear functional E (integral) on C(S∞), the weak* continuous real-valued functions on S∞. There exists a natural integral over S∞ reducing to

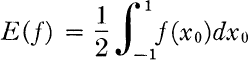
when f is a function of x0 alone. The partial sums Sn = Sn(x) of the power series for x(t) then form a martingale and zero-or-one phenomena appear. In particular, if R(x) is the radius of convergence of the series and e is the base of the natural logarithms, it turns out that R(x) = e for almost all x in S∞. Applications of the integral to the theory of numerical integration, the original motivation, will appear in a later paper.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 379 - 384
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Banach, S., The Lebesgue integral in abstract spaces, note to S. Saks, Theory of the integral (Warsaw, 1933).Google Scholar
2. Doob, J. L., Stochastic processes (New York, 1953).Google Scholar
3. Dunford, N. and Schwartz, J. T., Linear operators (New York, 1958).Google Scholar