No CrossRef data available.
Published online by Cambridge University Press: 11 November 2022
A partition 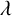 $\lambda $ of n is said to be nearly self-conjugate if the Ferrers graph of
$\lambda $ of n is said to be nearly self-conjugate if the Ferrers graph of 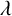 $\lambda $ and its transpose have exactly
$\lambda $ and its transpose have exactly 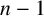 $n-1$ cells in common. The generating function of the number of such partitions was first conjectured by Campbell and recently confirmed by Campbell and Chern (‘Nearly self-conjugate integer partitions’, submitted for publication). We present a simple and direct analytic proof and a combinatorial proof of an equivalent statement.
$n-1$ cells in common. The generating function of the number of such partitions was first conjectured by Campbell and recently confirmed by Campbell and Chern (‘Nearly self-conjugate integer partitions’, submitted for publication). We present a simple and direct analytic proof and a combinatorial proof of an equivalent statement.
This work was supported by the National Natural Science Foundation of China (No. 11871246).