Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T01:56:19.976Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON FRAGMENTS OF UNIFORM REFLECTION IN SECOND ORDER ARITHMETIC

Part of: General logic Proof theory and constructive mathematics

Published online by Cambridge University Press:  09 June 2022

EMANUELE FRITTAION Open the ORCID record for EMANUELE FRITTAION [Opens in a new window]
EMANUELE FRITTAION*
Affiliation:
DEPARTMENT OF MATHEMATICS TECHNISCHE UNIVERSITÄTDARMSTADT, GERMANYE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider fragments of uniform reflection for formulas in the analytic hierarchy over theories of second order arithmetic. The main result is that for any second order arithmetic theory 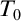$T_0$ extending $\mathsf {RCA}_0$ and axiomatizable by a 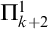$\Pi ^1_{k+2}$ sentence, and for any 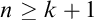$n\geq k+1$ ,

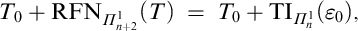$$\begin{align*}T_0+ \mathrm{RFN}_{\varPi^1_{n+2}}(T) \ = \ T_0 + \mathrm{TI}_{\varPi^1_n}(\varepsilon_0), \end{align*}$$
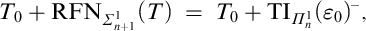$$\begin{align*}T_0+ \mathrm{RFN}_{\varSigma^1_{n+1}}(T) \ = \ T_0+ \mathrm{TI}_{\varPi^1_n}(\varepsilon_0)^{-}, \end{align*}$$
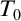where T is $T_0$ augmented with full induction, and 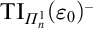$\mathrm {TI}_{\varPi ^1_n}(\varepsilon _0)^{-}$ denotes the schema of transfinite induction up to 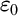$\varepsilon _0$ for 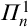$\varPi ^1_n$ formulas without set parameters.

Keywords

second order arithmeticuniform reflectionω-arithmeticpredicative cut elimination

MSC classification

Primary: 03F03: Proof theory, general
Secondary: 03F05: Cut-elimination and normal-form theorems 03F30: First-order arithmetic and fragments 03F35: Second- and higher-order arithmetic and fragments 03B30: Foundations of classical theories (including reverse mathematics)
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 28 , Issue 3 , September 2022 , pp. 451 - 465
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arai, T., Ordinal Analysis with an Introduction to Proof Theory , Logic in Asia: Studia Logica Library, Springer, Singapore, 2020.CrossRefGoogle Scholar
Beklemishev, L. D., Induction rules, reflection principles, and provably recursive functions . Annals of Pure and Applied Logic , vol. 85 (1997), no. 3, pp. 193–242.CrossRefGoogle Scholar
Beklemishev, L. D., Parameter free induction and provably total computable functions , Logical Foundations of Computer Science: Proceedings of the 4th International Symposium (LFCS’97) (S. Adian and A. Nerode, editors), Lecture Notes in Computer Science, vol. 224, Elsevier, Amsterdam, 1999, pp. 13–33.Google Scholar
Buchholz, W., Notation systems for infinitary derivations . Archive for Mathematical Logic , vol. 30 (1991), no. 5, pp. 277–296.CrossRefGoogle Scholar
Feferman, S., Arithmetization of metamathematics in a general setting . Fundamenta Mathematicae , vol. 49 (1960), no. 1, pp. 35–92.CrossRefGoogle Scholar
Feferman, S., Transfinite recursive progressions of axiomatic theories . The Journal of Symbolic Logic , vol. 27 (1962), no. 3, pp. 259–316.CrossRefGoogle Scholar
Friedman, H. and Sheard, M., Elementary descent recursion and proof theory . Annals of Pure and Applied Logic , vol. 71 (1995), no. 1, pp. 1–45.CrossRefGoogle Scholar
Gentzen, G., The Collected Papers of Gerhard Gentzen (M. E. Szabo, editor), Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam–London, 1969.Google Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Perspectives in Mathematical Logic, Springer, Berlin, 1998 (second printing).Google Scholar
Howard, W. A. and Kreisel, G., Transfinite induction and bar induction of types zero and one, and the role of continuity in intuitionistic analysis . The Journal of Symbolic Logic , vol. 31 (1966), no. 3, pp. 325–358.CrossRefGoogle Scholar
Kaye, R., Paris, J., and Dimitracopoulos, C., On parameter free induction schemas . The Journal of Symbolic Logic , vol. 53 (1988), no. 4, pp. 1082–1097.CrossRefGoogle Scholar
Kreisel, G. and Lévy, A., Reflection principles and their use for establishing the complexity of axiomatic systems . Mathematical Logic Quarterly , vol. 14 (1968), nos. 7–12, pp. 97–142.CrossRefGoogle Scholar
Leivant, D., The optimality of induction as an axiomatization of arithmetic . The Journal of Symbolic Logic , vol. 48 (1983), no. 1, pp. 182–184.CrossRefGoogle Scholar
Mints, G., Finite investigations of transfinite derivations . Journal of Soviet mathematics , vol. 10 (1978), no. 4, pp. 548–596.CrossRefGoogle Scholar
Ono, H., Reflection principles in fragments of Peano arithmetic . Zeitschrift fur mathematische Logik und Grundlagen der Mathematik , vol. 33 (1987), no. 4, pp. 317–333.CrossRefGoogle Scholar
Pakhomov, F. and Walsh, J., Reflection ranks and ordinal analysis. The Journal of Symbolic Logic, vol. 86 (2021), no. 4, pp. 1350–1384.CrossRefGoogle Scholar
Pakhomov, F. and Walsh, J., Reducing $\omega$ -model reflection to iterated syntactic reflection. Journal of Mathematical Logic, forthcoming.Google Scholar
Rathjen, M., The realm of ordinal analysis , Sets and Proofs (Leeds, 1997) (S. B. Cooper and J. K. Truss, editors), London Mathematical Society Lecture Note Series, vol. 258, Cambridge University Press, Cambridge, 1999, pp. 219–279.CrossRefGoogle Scholar
Schütte, K., Proof Theory , Springer, Berlin–New York, 1977 (Translated from the revised German edition by J. N. Crossley, Grundlehren der Mathematischen Wissenschaften, Band 225).CrossRefGoogle Scholar
Schwichtenberg, H., Proof Theory: Some Applications of Cut-Elimination, Handbook of Mathematical Logic (J. Barwise, editor), Studies in Logic and the Foundations of Mathematics, vol. 90, Elsevier, Amsterdam, 1977, pp. 867–895.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic , second ed., Perspectives in Logic, Cambridge University Press, Cambridge; Association for Symbolic Logic, Poughkeepsie, 2009.CrossRefGoogle Scholar
Troelstra, A. S., Metamathematical Investigation of Intuitionistic Arithmetic and Analysis, Lecture Notes in Mathematics, vol. 344, Springer, Berlin, 1973.CrossRefGoogle Scholar
Troelstra, A. S. and Schwichtenberg, H., Basic Proof Theory, second ed., Cambridge Tracts in Theoretical Computer Science, vol. 43, Cambridge University Press, Cambridge, 2000.CrossRefGoogle Scholar