Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T23:57:15.037Z Has data issue: false hasContentIssue false
  • English
  • Français

CRITICAL LENGTH FOR THE SPREADING–VANISHING DICHOTOMY IN HIGHER DIMENSIONS

Part of: Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  19 June 2020

MATTHEW J. SIMPSON Open the ORCID record for MATTHEW J. SIMPSON [Opens in a new window]
MATTHEW J. SIMPSON*
Affiliation:
School of Mathematical Sciences, Queensland University of Technology, Brisbane, Queensland 4001, Australia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider an extension of the classical Fisher–Kolmogorov equation, called the “Fisher–Stefan” model, which is a moving boundary problem on 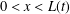$0<x<L(t)$. A key property of the Fisher–Stefan model is the “spreading–vanishing dichotomy”, where solutions with 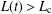$L(t)>L_{\text{c}}$ will eventually spread as 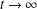$t\rightarrow \infty$, whereas solutions where 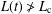$L(t)\ngtr L_{\text{c}}$ will vanish as 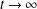$t\rightarrow \infty$. In one dimension it is well known that the critical length is 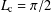$L_{\text{c}}=\unicode[STIX]{x1D70B}/2$. In this work, we re-formulate the Fisher–Stefan model in higher dimensions and calculate 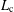$L_{\text{c}}$ as a function of spatial dimensions in a radially symmetric coordinate system. Our results show how 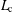$L_{\text{c}}$ depends upon the dimension of the problem, and numerical solutions of the governing partial differential equation are consistent with our calculations.

Keywords

reaction–diffusionFisher–Kolmogorov modelFisher’s equationStefan conditionmoving boundary problemtravelling wavesinvasionextinction

MSC classification

Primary: 35Q79: PDEs in connection with classical thermodynamics and heat transfer
Type
Research Article
Information
The ANZIAM Journal , Volume 62 , Issue 1 , January 2020 , pp. 3 - 17
Copyright
© 2020 Australian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

This is a contribution to the series of invited papers by past Tuck medallists (Editorial, Issue 62(1)). Matthew J. Simpson was awarded the 2020 Tuck medal.

References

Baker, R. E. and Simpson, M. J., “Models of collective cell motion for cell populations with different aspect ratio: diffusion, proliferation and travelling waves”, Physica A 391 (2012) 3729–3750; doi: 10.1016/j.physa.2012.01.009.CrossRefGoogle Scholar
Barenblatt, G. I., Scaling, self-similarity, and intermediate asymptotics (Cambridge University Press, Cambridge, 1996); doi: 10.1017/CBO9781107050242.CrossRefGoogle Scholar
Bradshaw-Hajek, B. H. and Broadbridge, P., “A robust cubic reaction–diffusion system for gene propagation”, Math. Comput. Modelling 39 (2004) 1151–1163; doi: 10.1016/S0895-7177(04)90537-7.CrossRefGoogle Scholar
Broadbridge, P., Bradshaw, B. H., Fulford, G. R. and Aldis, G. K., “Huxley and Fisher equations for gene propagation: an exact solution”, ANZIAM J. 44 (2002) 11–20; doi: 10.1017/S1446181100007860.CrossRefGoogle Scholar
Browning, A., Haridas, P. and Simpson, M. J., “A Bayesian sequential learning framework to parameterise continuum models of melanoma invasion into human skin”, Bull. Math. Biol. 81 676–698; doi: 10.1007/s11538-018-0532-1.CrossRefGoogle Scholar
Bunting, G., Du, Y. and Krakowski, K., “Spreading speed revisited: analysis of a free boundary model”, Netw. Heterog. Media 7 (2012) 583–603; doi: 10.3934/nhm.2012.7.583.CrossRefGoogle Scholar
Canosa, J., “On a nonlinear diffusion equation describing population growth”, IBM J. Res. Dev. 17 (1973) 307–313; doi: 10.1147/rd.174.0307.CrossRefGoogle Scholar
Crank, J., Free and moving boundary problems (Oxford University Press, Oxford, 1987).Google Scholar
Du, Y. and Guo, Z., “Spreading–vanishing dichotomy in a diffusive logistic model with a free boundary, II”, J. Differential Equations 250 (2011) 4336–4366; doi: 10.1016/j.jde.2011.02.011.CrossRefGoogle Scholar
Du, Y. and Guo, Z., “The Stefan problem for the Fisher–KPP equation”, J. Differential Equations 253 (2012) 996–1035; doi: 10.1016/j.jde.2012.04.014.CrossRefGoogle Scholar
Du, Y. and Lin, Z., “Spreading–vanishing dichotomy in the diffusive logistic model with a free boundary”, SIAM J. Math. Anal. 42 (2010) 377–405; doi: 10.1137/090771089.CrossRefGoogle Scholar
Du, Y. and Lou, B., “Spreading and vanishing in nonlinear diffusion problems with free boundaries”, J. Eur. Math. Soc. 17 (2015) 2673–2724; doi: 10.4171/JEMS/568.CrossRefGoogle Scholar
Du, Y., Matano, H. and Wang, K., “Regularity and asymptotic behavior of nonlinear Stefan problems”, Arch. Ration. Mech. Anal. 212 (2014) 957–1010; doi: 10.1007/s00205-013-0710-0.CrossRefGoogle Scholar
Du, Y., Matsuzawa, H. and Zhou, M., “Sharp estimate of the spreading speed determined by nonlinear free boundary problems”, SIAM J. Math. Anal. 46 (2014) 375–396; doi: 10.1137/130908063.CrossRefGoogle Scholar
El-Hachem, M., McCue, S. W., Jin, W., Du, Y. and Simpson, M. J., “Revisiting the Fisher–Kolmogorov–Petrovsky–Piskunov equation to interpret the spreading–extinction dichotomy”, Proc. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci. 475 (2019) 20190378; doi: 10.1098/rspa.2019.0378.Google ScholarPubMed
Fadai, N. T. and Simpson, M. J., “New travelling wave solutions for the porous-Fisher model with a moving boundary”, J. Phys. A: Math. Theor. 53 (2020) 095601; doi: 10.1088/1751-8121/ab6d3c.CrossRefGoogle Scholar
Fisher, R. A., “The wave of advance of advantageous genes”, Ann. Eugen. 7 (1937) 355–369; doi: 10.1111/j.1469-1809.1937.tb02153.x.CrossRefGoogle Scholar
Forbes, L. K., “A two-dimensional model for large-scale bushfire spread”, J. Aust. Math. Soc. Ser. B: Appl. Math. (currently, ANZIAM J.) 39 (1997) 171–194; doi: 10.1017/S0334270000008791.CrossRefGoogle Scholar
Gatenby, R. A. and Gawlinski, E. T., “A reaction–diffusion model of cancer invasion”, Cancer Res. 56 (1996) 5745–5753; https://cancerres.aacrjournals.org/content/56/24/5745.article-info.Google ScholarPubMed
Grindrod, P., Patterns and waves (Oxford University Press, Oxford, 2007); doi: 10.1137/1035173.Google Scholar
Gupta, S. C., The classical Stefan problem. Basic concepts, modelling and analysis with quasi-analytical solutions and methods. 2nd edn (Elsevier, Amsterdam, 2017); doi: 10.1016/C2017-0-02306-6.Google Scholar
Haridas, P., Penington, C. J., McGovern, J. A., McElwain, D. L. S. and Simpson, M. J., “Quantifying rates of cell migration and cell proliferation in co-culture barrier assays reveals how skin and melanoma cells interact during melanoma spreading and invasion”, J. Theoret. Biol. 423 (2017) 13–25; doi: 10.1016/j.jtbi.2017.04.017.CrossRefGoogle ScholarPubMed
Harris, S., “Fisher equation with density-dependent diffusion: special solutions”, J. Phys. A: Math. Theor. 37 (2004) 6267–6268; doi: 10.1088/0305-4470/37/24/005.CrossRefGoogle Scholar
Hickson, R. I., Barry, S. I. and Mercer, G. N., “Critical times in multilayer diffusion. Part 1: Exact solutions”, Int. J. Heat Mass Transfer 52 (2009) 5776–5783; doi: 10.1016/j.ijheatmasstransfer.2009.08.013.CrossRefGoogle Scholar
Hickson, R. I., Barry, S. I. and Mercer, G. N., “Critical times in multilayer diffusion. Part 2: Approximate solutions”, Int. J. Heat Mass Transfer 52 (2009) 5784–5791; doi: 10.1016/j.ijheatmasstransfer.2009.08.012.CrossRefGoogle Scholar
Jin, W., Shah, E. T., Penington, C. J., McCue, S. W., Chopin, L. K. and Simpson, M. J., “Reproducibility of scratch assays is affected by the initial degree of confluence: experiments, modelling and model selection”, J. Theoret. Biol. 390 (2016) 136–145; doi: 10.1016/j.jtbi.2015.10.040.CrossRefGoogle ScholarPubMed
Johnston, S. T., Ross, J. V., Binder, B. J., McElwain, D. L. S., Haridas, P. and Simpson, M. J., “Quantifying the effect of experimental design choices for in vitro scratch assays”, J. Theoret. Biol. 400 (2016) 19–31; doi: 10.1016/j.jtbi.2016.04.012.CrossRefGoogle ScholarPubMed
Johnston, S. T., Shah, E. T., Chopin, L. K., McElwain, D. L. S. and Simpson, M. J., “Estimating cell diffusivity and cell proliferation rate by interpreting IncuCyte ZOOM$^{\text{TM}}$ assay data using the Fisher–Kolmogorov model”, BMC Syst. Biol. 9 (2015) 38, 1–12; doi: 10.1186/s12918-015-0182-y.CrossRefGoogle ScholarPubMed
Kolmogorov, A. N., Petrovskii, I. G. and Piskunov, N. S., “A study of the diffusion equation with increase in the amount of substance, and its application to a biological problem”, Moscow Univ. Math. Bull. 1 (1937) 1–26.Google Scholar
Maini, P. K., McElwain, D. L. S. and Leavesley, D. I., “Traveling wave model to interpret a wound-healing cell migration assay for human peritoneal mesothelial cells”, Tissue Eng. 10 (2004) 475–482; doi: 10.1089/107632704323061834.CrossRefGoogle ScholarPubMed
Maini, P. K., McElwain, D. L. S. and Leavesley, D., “Travelling waves in a wound healing assay”, Appl. Math. Lett. 17 (2004) 575–580; doi: 10.1016/S0893-9659(04)90128-0.CrossRefGoogle Scholar
McCue, S. W., Jin, W., Moroney, T. J., Lo, K.-Y., Chou, S. E. and Simpson, M. J., “Hole-closing model reveals exponents for nonlinear degenerate diffusivity functions in cell biology”, Physica D 398 (2019) 130–140; doi: 10.1016/j.physd.2019.06.005.CrossRefGoogle Scholar
McCue, S. W., King, J. R. and Riley, D. S., “Extinction behaviour for two-dimensional inward-solidification problems”, Proc. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci. 459 (2003) 977–999; doi: 10.1098/rspa.2002.1059.CrossRefGoogle Scholar
McCue, S. W., King, J. R. and Riley, D. S., “The extinction problem for three-dimensional inward solidification”, J. Engrg. Math. 52 (2005) 389–409; doi: 10.1007/s10665-005-3501-2.CrossRefGoogle Scholar
McCue, S. W., Wu, B. and Hill, J. M., “Classical two-phase Stefan problem for spheres”, Proc. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci. 464 (2008) 2055–2076; doi: 10.1098/rspa.2007.0315.CrossRefGoogle Scholar
Murray, J. D., Mathematical biology I. An introduction (Springer, New York, 2002); doi: 10.1007/b98868.CrossRefGoogle Scholar
Nardini, J. T., Chapnick, D. A., Liu, X. and Bortz, D. M., “Modeling keratinocyte wound healing dynamics: cell–cell adhesion promotes sustained collective migration”, J. Theoret. Biol. 400 (2016) 103–117; doi: 10.1016/j.jtbi.2016.04.015.CrossRefGoogle ScholarPubMed
Painter, K. J. and Sherratt, J. A., “Modelling the movement of interacting cell populations”, J. Theoret. Biol. 225 (2003) 327–339; doi: 10.1016/S0022-5193(03)00258-3.CrossRefGoogle ScholarPubMed
Sánchez Garduno, F. and Maini, P. K., “An approximation to a sharp type solution of a density-dependent reaction diffusion equation”, Appl. Math. Lett. 7 (1994) 47–51; doi: 10.1016/0893-9659(94)90051-5.CrossRefGoogle Scholar
Sánchez Garduno, F. and Maini, P. K., “Traveling wave phenomena in some degenerate reaction diffusion equations”, J. Differential Equations 117 (1994) 281–319; doi: 10.1006/jdeq.1995.1055.CrossRefGoogle Scholar
Sengers, B. G., Please, C. P. and Oreffo, R. O. C., “Experimental characterization and computational modelling of two-dimensional cell spreading for skeletal regeneration”, J. R. Soc. Interface 4 (2007) 1107–1117; doi: 10.1098/rsif.2007.0233.CrossRefGoogle ScholarPubMed
Sherratt, J. A. and Marchant, B. P., “Nonsharp travelling wave fronts in the Fisher equation with degenerate nonlinear diffusion”, Appl. Math. Lett. 9 (1996) 33–38; doi: 10.1016/0893-9659(96)00069-9.CrossRefGoogle Scholar
Sherratt, J. A. and Murray, J. D., “Models of epidermal wound healing”, Proc. R. Soc. Lond. Ser. B 241 (1990) 29–36; doi: 10.1098/rspb.1990.0061.Google ScholarPubMed
Shigesada, N., Kawasaki, K. and Takeda, Y., “Modeling stratified diffusion in biological invasions”, American Naturalist 146 (1995) 229–251; doi: 10.1086/285796.CrossRefGoogle Scholar
Simpson, M. J. and Baker, R. E., “Exact calculations of survival probability for diffusion on growing lines, disks and spheres: the role of dimension”, J. Chem. Phys. 143 (2015) 094109; doi: 10.1063/1.4929993.CrossRefGoogle ScholarPubMed
Simpson, M. J., Baker, R. E. and McCue, S. W., “Models of collective cell spreading with variable cell aspect ratio: a motivation for degenerate diffusion models”, Phys. Rev. E 83 (2011) 021901; doi: 10.1103/PhysRevE.83.021901.CrossRefGoogle ScholarPubMed
Simpson, M. J., Landman, K. A. and Clement, T. P., “Assessment of a non-traditional operator split algorithm for simulation of reactive transport”, Math. Comput. Simul. 70 (2005) 44–60; doi: 10.1016/j.matcom.2005.03.019.CrossRefGoogle Scholar
Simpson, M. J., Landman, K. A., Hughes, B. D. and Newgreen, D. F., “Looking inside an invasion wave of cells using continuum models: proliferation is the key”, J. Theoret. Biol. 243 (2006) 343–360; doi: 10.1016/j.jtbi.2006.06.021.CrossRefGoogle ScholarPubMed
Simpson, M. J., Treloar, K. K., Binder, B. J., Haridas, P., Manton, K. J., Leavesley, D. I., McElwain, D. L. S. and Baker, R. E., “Quantifying the roles of motility and proliferation in a circular barrier assay”, J. R. Soc. Interface 10 (2013) 20130007; doi: 10.1098/rsif.2013.0007.CrossRefGoogle Scholar
Simpson, M. J., Zhang, D. C., Mariani, M., Landman, K. A. and Newgreen, D. F., “Cell proliferation drives neural crest cell invasion of the intestine”, Dev. Biol. 302 (2007) 553–568; doi: 10.1016/j.ydbio.2006.10.017.CrossRefGoogle ScholarPubMed
Skellam, J. G., “Random dispersal in theoretical populations”, Biometrika 38 (1951) 196–218; doi: 10.2307/2332328.CrossRefGoogle ScholarPubMed
Steele, J., Adams, J. and Sluckin, T., “Modelling paleoindian dispersals”, World Archaeol. 30 (1998) 286–305; doi: 10.1080/00438243.1998.9980411.CrossRefGoogle Scholar
Swanson, K. R., Bridge, C., Murray, J. D. and Alvord, E. C. Jr, “Virtual and real brain tumors: using mathematical modeling to quantify glioma growth and invasion”, J. Neurol. Sci. 216 (2003) 1–10; doi: 10.1016/j.jns.2003.06.001.CrossRefGoogle ScholarPubMed
Swanson, K. R., Rostomily, R. C. and Alvord, E. C. Jr, “A mathematical modelling tool for predicting survival of individual patients following resection of glioblastoma: a proof of principle”, Br. J. Cancer 98 (2008) 113–119; doi: 10.1038/sj.bjc.6604125.CrossRefGoogle ScholarPubMed
Treloar, K. K., Simpson, M. J., McElwain, D. L. S. and Baker, R. E., “Are in vitro estimates of cell diffusivity and cell proliferation rate sensitive to assay geometry?”, J. Theoret. Biol. 356 (2014) 71–84; doi: 10.1016/j.jtbi.2014.04.026.CrossRefGoogle ScholarPubMed
Vázquez, J. L., The porous medium equation (Oxford University Press, Oxford, 2007); doi: 10.1093/acprof:oso/9780198569039.001.0001.Google Scholar
Vittadello, S. T., McCue, S. W., Gunasingh, G., Haass, N. K. and Simpson, M. J., “Mathematical models for cell migration with real-time cell cycle dynamics”, Biophys. J. 114 (2018) 1241–1253; doi: 10.1016/j.bpj.2017.12.041.CrossRefGoogle ScholarPubMed
Vo, B. N., Drovandi, C. C., Pettitt, A. N. and Simpson, M. J., “Quantifying uncertainty in parameter estimates for stochastic models of collective cell spreading using approximate Bayesian computation”, Math. Biosci. 263 (2015) 133–142; doi: 10.1016/j.mbs.2015.02.010.CrossRefGoogle ScholarPubMed
Warne, D. J., Baker, R. E. and Simpson, M. J., “Using experimental data and information criteria to guide model selection for reaction–diffusion problems in mathematical biology”, Bull. Math. Biol. 81 (2019) 1760–1804; doi: 10.1007/s11538-019-00589-x.CrossRefGoogle ScholarPubMed
Witelski, T. P., “Merging traveling waves for the porous-Fisher’s equation”, Appl. Math. Lett. 8 (1995) 57–62; doi: 10.1016/0893-9659(95)00047-T.CrossRefGoogle Scholar