Spatial variability of new snow amounts derived from a dense network of Alpine automatic stations

Abstract

Since 1996, a dense network of Alpine automatic weather and snow-measurement (Interkantonales Mess- und Informationssystem (IMIS)) stations has been in operational use for local and regional avalanche warning. The measurements of the IMIS stations are assumed to be representative for spatially extended regions around the measuring sites for applications in avalanche risk management. In this study, the regional representativeness of these stations with regard to the daily amount of new snow is investigated. The results show that the amount of daily new snow is spatially correlated in a range of ∼5–55 km. Regarding simultaneous observations of daily new snow measurements, which are ∼5–10 km apart, the probability of detection (POD) is given as 0.5±0.03. In this paper, the POD of an automatic warning network is introduced as an indicator of the representativeness of point measurement information for avalanche warning applications. The results of this study may mark a reference value for verification of spatially distributed Alpine meteorological models which evaluate the amount of daily new snow in the Swiss Alps.

Introduction

In 1996, the Swiss mountain cantons began to set up a network of Alpine automatic weather Interkantonales Mess- und Informationssystem (IMIS) stations supervised by the Swiss Federal Institute for Snow and Avalanche Research (SLF) (Russi and others, 2003). At present, 90 automatic snow and 61 automatic wind-measuring units are in operational use for local and regional avalanche warning. The automatic stations are spread over an area of about 100 km ×300 km in the Swiss Alps. The current density of the network is based on the requirements of local and regional avalanche warning (Fig. 1). The amount of new snow and wind speed are the most interesting parameters for the estimation of avalanche hazard (McClung and Schaerer, 1993).

Fig. 1. The 75 IMIS snow-measuring stations covering the Swiss Alps in 2001. The stations are placed at altitudes ranging from 1610 to 2990 m, with a median altitude of 2270 m.

The point measurements of the IMIS stations are taken to be representative of spatially extended regions around the measuring sites. The SLF followed the concept of ‘index stations’, which means that the meteorological information registered by the IMIS stations is considered to be an index of the avalanche hazard risk situation for an entire region around the station. It is therefore crucial to quantify this regional representativeness of the IMIS stations. The main question is: how distant can a critical avalanche zone be from an IMIS index station in order for the point measurement information to be reliable for avalanche risk management?

This study focuses on the investigation of the regional representativeness concerning the daily amount of new snow, considered to be the most important factor for avalanche warning and avalanche hazard risk forecast. Further, daily new snow is also an important input parameter for artificial avalanche release expertise, snow hydrological modelling and general snow science research for which the IMIS index stations are used more frequently.

The first aim of this paper is to investigate a general statistical result regarding the spatial correlation of daily new snow events over the entire Swiss Alps, including all microclimatologic regions. The second goal is to provide the first numerical quantification of the statistical reliability of the IMIS new snow information as a function of increasing distance from an IMIS station for local avalanche risk management.

Data and Model

Since November 2001, 75 automatic snow-measurement stations have been in continuous operational use in the IMIS network. Data from all 75 stations, for the winter period 1 November to 30 April from 2001 to 2007, are chosen for the following geostatistical analysis of daily new snow variation between IMIS sites (Fig. 1). The stations are placed at altitudes ranging between 1610 and 2990 m, with a median altitude of 2270 m.

In the avalanche-warning community, new snow is commonly measured as the depth of snow fallen during a defined period. Regarding the importance of this study for other applications than avalanche warning, new snow is quantified here by the amount of daily new snow water equivalent (HNW) which describes the mass of snow fallen per day in millimetres of water content. The statistical results of the study can be pragmatically applied to avalanche warning by assuming that 1 mm HNW is equivalent to 1 cm height of new snow with an approximate density of 0.1 kgm ^{− 3}.

Owing to the influence of settling, HNW cannot be measured directly with an automatic measuring station. The settling of the snow cover has been calculated using the numerical model Snowpack, the snow-cover model developed at the SLF (Bartelt and Lehning, 2002). This multilayermodel is used to describe the physical properties of the snow cover, enabling the estimation of HNW, among other parameters. The Snowpack output is based on the input data registered every 30 min at the IMIS stations. All output parameters are therefore given in time-steps of 30 min. For this study, the amount of HNW at 0600 h is chosen. In the application of HNW estimation, the HNW value is determined by a combination of settling and snow height, where the density of the new snow is modelled with air temperature and relative humidity. The full features of Snowpack are documented in Bartelt and Lehning (2002) and Lehning and others (2002a,b).

To ensure the regional representativeness of the index station, it is important to define a standard of measuring site where the information is collected. The most important parameter for the HNW estimation is snow depth (H _S) which is measured automatically with an ultrasonic sensor (SR50, Campbell Scientific Inc.). Because H _S and its local spatial variation is strongly dependent upon the surrounding topography and the impact of wind, the site of the automatic measurement has to be carefully evaluated. The standard for an IMIS snow-measurement site with representative H _S for a region is defined as a flat alpine field with as little wind influence as possible. By selecting the sites according to this standard, the influence of wind has been minimized. However, the small effect of topography on snow depth can never be excluded. This additional condition is a characteristic of HNW measurement and is not relevant for many other meteorological parameters (e.g. air temperature). It is assumed here that most of the station sites are ideal snow-measuring sites following the defined IMIS standard.

Methodology

Comparison over the Swiss Alps

The geostatistical analysis of HNW variation among IMIS stations over the Swiss Alps is carried out by comparing the HNW estimation of pairs of IMIS stations. The HNW value at a single IMIS snow station at day t is defined as HNWi (t), i = 1, . . . ,N, where i represents an IMIS station and N = 75 is the total number of IMIS snow stations considered.

For comparison, HNW _i (t ) and HNW _j (t) for i= j are set in relation to each other at the same time t . Pairs of HNW _i (t ) and HNW _j (t ) are selected if HNW _i (t ) > 0 or HNW _j (t ) > 0, with the additional condition that the difference in geographical altitude within HNW pairs (HNW _ij ) is less than 300 m. The distance of the compared IMIS station pairs is given by the Euclidean distance d_ij of the site’s geographical positions.

Calculation of parameters for comparison

To quantify the relationship between two IMIS snow stations, the following parameters are chosen to indicate the correlation.

Variance function

The variance function γ is defined as

(1)

N(d) denotes a set of pairs of observations between classes of distance, where represents the mean value of all distances d_ij of IMIS stations between the distance classes [5, 10], [10, 15], . . . , [205, 210] km. As γ is symmetric with regard to a permutation of i and j, only pairs where i > j are selected.

Parameters derived from forecast theory

Since daily new snow information from an IMIS station is used for avalanche risk management, the theory of forecast interpretation is adapted for the analysis of the regional representativeness of the IMIS stations. As in forecast theory, the term ‘prediction’ is used as a forecast in time. Referring to the IMIS representativeness analysis, the prediction is meant as an extrapolation of the information in space at the same time.

Several parameters to estimate the quality of a forecast have been developed by Murphy and Winkler (1987), such as probability of detection (POD), false alarm rate, threat score and true skill score. Only the parameter POD is used here. Correctly quantifying detected HNW events is important in avalanche warning and artificial avalanche release.

To calculate the POD, we use contingency tables in which the relation between observed and forecast values is counted (Table 1). Here, HNW _i is assumed to be the observed value and HNW _j the forecast measurement. The POD therefore denotes the percentage of HNW observations at IMIS station i which are also observed at station j.

Table 1. Contingency table of forecast verification and its adaption to IMIS representativeness study

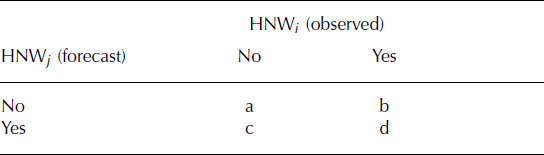
As the contingency table only compares ‘yes‘ or ‘no‘ information, the HNW _i values are separated into three classes for avalanche risk management applications:

1. 1. low: 5–15mm of HNW;

2. 2. medium: 15–30mm of HNW; and

3. 3. high: >30mm of HNW.

The POD value is calculated for each class using the equation

(2)

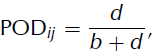
where b and d are derived from the contingency table (Table 1) and POD _ij is a value between 0 and 1. POD _ij is calculated for each selected pair. Analogous to the variogram, are averaged within the same distance classes POD _ij∈ [5, 10], [10, 15], . . . , [205, 210] km.

The statistical POD is defined as

(3)

It is important to remark that, in general, the POD of HNW _i vsHNW _j =HNW _j vsHNW _i . Here, several pairs ofHNW _i vs HNW _j in a distance class are compared, and vice versa. From a statistical point of view, HNW _i vs HNW _j is approximately equal to HNW _j vs HNW _i in this case.

The aim of this paper is to determine a statistical value of the POD and its variation with distance between two measurements. The statistically evaluated quantity of POD for daily snow precipitation estimations is quantified for the first time in this study, and may prove a very useful value in avalanche risk management.

Results and Discussion

Variogram

Variance γ is plotted on a double logarithmic scale in Figure 2, as a function of the distance between IMIS stations. The points represent the average of the γ value of all selected HNW _ij pairs within the 5 km distance classes, where ∈ [5, 10], [10, 15], . . . , [205, 210] km.

Fig. 2. Variance against distance on a double logarithmic scale. The points represent the average of γ over all selected IMIS HNW _ij pairs within the 5 km distance classes d. On the upper x axis, the number of selected pairs is indicated. Three different curves are depicted: (1) the two-point linear fit (dashed curve); (2) the two-point linear fit on logarithmic-transformed values (solid curve); and (3) a single exponential fit (dotted curve).

The error bars in Figure 2 denote the standard error referring to the mean value. The number of compared pairs is indicated on the upper x axis, which corresponds to the number of independent measurements of HNW _ij relations where i > j. The error bars show a significant variation of γ for all pairs of HNW _ij in the same distance class of ∼±30mm². This is due to the fact that two neighbouring IMIS stations can be positioned close together but within different microclimatological regions; alternatively, two stations might have similar regional climatic conditions but be positioned relatively far apart. Also, one measuring site may be exposed to a stronger wind influence than the other. Therefore, the local variance of HNW _ij is high.

To investigate the influence of systematically disturbed measuring sites on γ, about 50% of the stations were classified as more representative than the remainder and were selected for the calculation of γ. The selection of these particular stations is based on the personal experience of members of the Swiss National Avalanche Warning team who work with the IMIS HNWmeasurements daily during winter. The result using these selected stations is essentially the same as shown in Figure 2 but, as expected, with a smaller absolute value of γ. The form of the curve, especially the point where the values of γ saturate (inflection point), is similar to Figure 2. Note that this selection procedure does not include a comprehensive scientific method of classifying the stations according to their quality, which means that it is not possible to determine if the observed signal of γ is caused only by the nature of HNW events or also by the selection procedure. The statistical method applied here and the calculations using the selected stations lead to the conclusion that HNW events are not correlated for distances of >55 km from an IMIS station.However, the absolute value of γ, which changes with distance, is more influenced by the selection of the measuring sites.

In order to define the point where γ reaches saturation with increasing distance, a two-point linear fit on the regular values and on logarithmic-transformed values of both axes is calculated using a least-squares method. This method determines the minimum of the sum of the squared residuals (SSR) of the entire fitted two-point curve. The development of the SSR is shown in Figure 3, where the solid line indicates the regular linear fit and the dashed line shows the fit on logarithmic-transformed values. The values of the SSR are normalized to the maximum value. Considering both curves, the minimum is reached at ∼50–60 km which can be interpreted as the range of the variogram. This is equal to the statistical correlation length of HNW in the Swiss Alps.

Fig. 3. Development of the sum of squared residuals with varying distance of the inflection point. The minimum of the curves defines the optimal inflection point of the two-point fit. The solid curve represents the development of a linear two-point fit on non-transformed values (minimum at 48 km). The dashed curve is the development of a two-point fit on logarithmic-transformed values of γ and classes of distance (minimum 59 km).

This result indicates that a microclimatological region regarding HNW events in mountainous environments may generally have a magnitude of about 55 km. Laternser (2002) divided the Swiss Alps into 14 microclimatological regions for avalanche warning using clustering methods based on daily H _S data. The regions are ∼50–100 km long and ∼20– 50 km wide, which is the same magnitude as the correlation length of HNW derived in this study.

Furthermore, in Figure 2 three different curves are fitted to the averaged values of γ within distance classes: (1) the two-point linear fit on logarithmic-transformed values (solidcurve); (2) the two-point linear fit (dashed curve); and (3) a single exponential fit (dotted curve). The parameterization of these fits is summarized in Table 2. In order to compare the quality of the fits, the coefficient of determination R ² is calculated for all three curves over the entire range. As the quality of the fit is similar for all three curves, they represent the points equally.

Table 2. Three different fits for the variogram curve

It is important to determine if the spatial distribution of HNW shows a correlation in the range ∼5–55 km, which may be a sign of coherent snow precipitation cells with a correlated internal structure on this scale. The results in this study may indicate reference values for the verification of spatially distributed meteorological models such as the Alpine model (ALMO), the meteorological physical forecast model used by MeteoSwiss (Kaufmann and others, 2003). If the model reproduces the internal structure of HNW events in the Swiss Alps correctly, the correlation length of the modelled HNW must be similar to 55 km. This means that the model accurately describes the sizes of the precipitation cells and the microclimatological regions of the Alps. If this assumption is accurate, the HNW information between IMIS stations could be improved using spatially distributed models such as aLMo, and thus point measurements from the index station might be better extrapolated to avalanche risk regions.

Probability of detection (POD)

POD is plotted against the distance between IMIS stations for all three HNW classes in Figure 4. As in the variogram, the number of compared HNW pairs is indicated along the upper x axis, and the error bars signify the standard error of this number of measurements per distance class. As the statistical POD is calculated by POD _ij of HNW _j vs HNW _i and vice versa, the number of pairs is double that of the variogram.

Fig. 4. Statistical POD of HNW for three classes of daily snow precipitation intensity on a linear scale.

The results show that about 60% of HNW>30mmd ^{− 1} occurring at an IMIS station are correctly predicted to occur at another IMIS station ∼5–10 km away. POD saturates to an almost constant value at about 50 km, similar to the variogram. Due to the existence of snowfall in the entire region of the Swiss Alps, the POD of HNW is not zero even for long distances between IMIS stations.

Large daily snowfall events show a significantly higher POD for shorter distances than HNW events with a smaller daily intensity (HNW<30mmd ^{− 1}). This indicates that snowfall with a high daily intensity has a larger spatial dimension than smaller HNW. This means that it is more likely to detect a large snowfall event in a neighbouring local valley than a small event of less than 30 mmHNW. This is consistent with the author’s personal experience during the last 4 years concerning the performance of an IMIS station in local avalanche risk management.

The IMIS stations are more useful in predicting large daily snowfall events for neighbouring avalanche zones than they are for measuring smaller daily precipitation. This is a speciality of winter precipitation in the Alps, where it is mainly dominated by orographic precipitation and less by convective precipitation. During the summer, however, when convective precipitation is more likely in the form of storms, large precipitation can be very local and the POD for such intensities may decrease rapidly with distance. For this reason, an automatic warning system for natural hazards produced by large precipitation during the summer should have a higher spatial density than systems for snow avalanche warning such as IMIS. It is believed that the numerical quantification of the POD for precipitation during summer has not yet been published. For avalanche warning, Schneebeli and Laternser (2004) investigated similar results by developing a probabilistic model to evaluate the optimal density of stations measuring snowfall. The range of correlation and its dependence on intensity of HNW can also be demonstrated here by the analysis of the statistical POD value.

The decay of the POD to a value of approximate saturation occurs at about 50 km and indicates that the POD plot contains the same information as the variogram, but allows a different interpretation for practical use. As the variogram can be interpreted as the error of spatial measurement of HNW which increases with distance, the POD gives a probability of successfully detected HNW events which are distant from the measuring site. The declaration of the ratio of true to false detections within a HNW class may be useful for the specifications of automatic warning systems. For various applications in natural risk management, different dimensions of probability of detection are required. In this sense, the IMIS network cannot be considered as an automatic alarm system but rather as a warning system requiring a competent interpretation of the information.

Conclusion and Outlook

This study suggests that the correlation length of daily snowfall in the Swiss Alps, a high mountainous region, is about 55 km. For a statistical analysis (e.g. climatology) of HNW events, a minimum distance of about 55 km between measuring stations is recommended. The error of similar distant measuring pairs is about ±30mm². This indicates that the local variance of HNW between neighbouring IMIS stations 5–10 km apart is about ±25% of the mean value, which is very high. Thus, for daily avalanche warning and artificial avalanche release, the statistical interpretation may not be helpful. The POD of HNW events is about 0.5±0.03 for distances of 5–10 km between HNW measurements and decreases rapidly with increasing distance. This supports the conclusion that the measuring site must be placed as close to the critical hazard zone as possible, but still under the consideration of the standard for snow-measuring sites.

The propagation of the variance γ with distance can be interpreted as the error of HNW measurement and its spatial distribution. This result can be taken into account for spatial modelling in the sense of the variation of the model input parameters. For these reasons, the investigation of the variation of HNW on smaller scales such as 1 m to 1 km may be interesting for future scientific efforts. The results of this study may mark a potential reference value for the verification of spatially distributed Alpine weather models in terms of their internal structure of daily new snow precipitation cells.