Published online by Cambridge University Press: 08 February 2023
We consider a dual risk model with constant expense rate and i.i.d. exponentially distributed gains
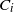 $C_i$
(
$C_i$
(
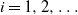 $i=1,2,\dots$
) that arrive according to a renewal process with general interarrival times. We add to this classical dual risk model the proportional gain feature; that is, if the surplus process just before the ith arrival is at level u, then for
$i=1,2,\dots$
) that arrive according to a renewal process with general interarrival times. We add to this classical dual risk model the proportional gain feature; that is, if the surplus process just before the ith arrival is at level u, then for
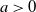 $a>0$
the capital jumps up to the level
$a>0$
the capital jumps up to the level
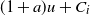 $(1+a)u+C_i$
. The ruin probability and the distribution of the time to ruin are determined. We furthermore identify the value of discounted cumulative dividend payments, for the case of a Poisson arrival process of proportional gains. In the dividend calculations, we also consider a random perturbation of our basic risk process modeled by an independent Brownian motion with drift.
$(1+a)u+C_i$
. The ruin probability and the distribution of the time to ruin are determined. We furthermore identify the value of discounted cumulative dividend payments, for the case of a Poisson arrival process of proportional gains. In the dividend calculations, we also consider a random perturbation of our basic risk process modeled by an independent Brownian motion with drift.