We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give a valuation theoretic characterization for a real closed field to be recursively saturated. This builds on work in [9], where the authors gave such a characterization for κ-saturation, for a cardinal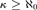 
$\kappa \ge \aleph _0 $. Our result extends the characterization of Harnik and Ressayre [7] for a divisible ordered abelian group to be recursively saturated.
