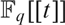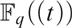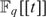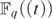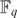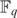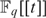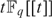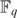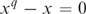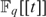4 results
DEFINABILITY OF HENSELIAN VALUATIONS BY CONDITIONS ON THE VALUE GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1064-1082
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Defining Coarsenings of Valuations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 665-687
-
- Article
- Export citation
DEFINABLE HENSELIAN VALUATIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 13 March 2015, pp. 85-99
- Print publication:
- March 2015
-
- Article
- Export citation
AN EXISTENTIAL ∅-DEFINITION OF
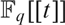 $F_q [[t]]$ IN
$F_q [[t]]$ IN 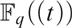 $F_q \left( t \right)$
$F_q \left( t \right)$
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 12 December 2014, pp. 1336-1343
- Print publication:
- December 2014
-
- Article
- Export citation

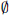 -definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
-definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.