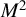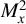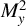A 172 mJ, high-energy picosecond 355 nm ultraviolet laser system at 100 Hz

Abstract

A high-energy picosecond 355 nm ultraviolet (UV) laser operating at 100 Hz was demonstrated. A 352 mJ, 69 ps, 1064 nm laser at 100 Hz was realized firstly by cascaded regenerative, laser diode end-pumped single-pass and side-pumped main amplifiers. The stimulated Raman scattering-based beam shaping technique, thermally induced birefringence compensation and 4f spatial filter-image relaying systems were used to maintain a relatively homogeneous beam intensity distribution during the amplification process. By using lithium triborate crystals for second- and third-harmonic generation (THG), a 172 mJ, approximately 56 ps, 355 nm UV laser was achieved with a THG conversion efficiency of 49%. To the best of our knowledge, it is the highest pulse energy of a picosecond 355 nm UV laser so far. The beam quality factor ${M}^2$ and pulse energy stability were ${M}_x^2$=3.92, ${M}_y^2$=3.71 and root mean square of 1.48%@3 hours. This laser system could play significant roles in applications including photoconductive switch excitation, laser drilling and laser micro-fabrication.

1 Introduction

High-energy, high-peak-power picosecond ultraviolet (UV) laser sources play important roles in applications including multiplexed and wide-field micromachining, photolithography, thin-film patterning, remote laser-induced breakdown spectroscopy and nonlinear optical measurement^{[ 1 – 6 ]}. Compared with conventional excimer lasers^{[ 7 ]}, solid-state UV lasers based on nonlinear frequency conversion (third-harmonic generation (THG) from a 1.06 μm near-infrared (NIR) laser) have the advantages of a long lifetime, compact structure, high stability, high repetition rate and low cost^{[ 8 , 9 ]}, and have been considered as the most efficient technique for UV laser generation. In recent years, the development of high-energy solid-state NIR laser sources, typically generated by the master oscillator power amplifier (MOPA) configuration, has directly facilitated the advancement of high-energy solid-state UV lasers. However, the damage of optical elements and the small-scale self-focusing (SF) effect induced by high-peak-power density are identified as the main obstacles for enhancing the pulse energy of picosecond NIR lasers^{[ 10 – 13 ]}. Chirped pulse amplification (CPA) can effectively decrease the peak power of the laser pulse during the amplification process, thereby enabling the development of ultrashort pulse laser systems with unprecedented performance. In 2020, Herkommer et al. ^{[ 14 ]} reported a CPA-based 1030 nm ytterbium-doped yttrium aluminum garnet (Yb:YAG) laser system with a regenerative amplifier (RA) and four thin-disk based multi-pass amplifiers, generating a pulse energy of 720 mJ and a pulse duration of 920 fs at a repetition rate of 1 kHz. In 2022, Andral et al. ^{[ 15 ]} conducted further research on frequency conversion based on the above NIR laser source, in which a 343 nm UV laser was generated with a pulse energy of 113 mJ and a peak power of 122 GW, corresponding to the THG conversion efficiency of 26%. CPA has been considered as the most effective method for high-energy ultrafast laser amplification, but the system is very complicated and costly.

By employing the stimulated Brillouin scattering (SBS) compression technique, the neodymium-doped yttrium aluminum garnet (Nd:YAG) laser system can achieve high-energy, high-peak-power laser pulses by direct compression of nanosecond-duration pulses to hundreds of picoseconds. In 2017, Bai et al. ^{[ 16 ]} reported a picosecond 355 nm UV laser system with the amplified NIR laser pulses compressed from 6.3 ns to 420 ps by an SBS compressor, in which the highest pulse energy of 100 mJ with a pulse width of 168 ps was obtained, corresponding to the THG conversion efficiency of 35.7%. However, the thermal effects and the optical damage threshold of the SBS medium limit the repetition rate of such systems (typically operating below 50 Hz)^{[ 17 – 19 ]}.

In addition, applying a seeder with a pulse duration at the tens or even hundreds of picoseconds level and using laser diode (LD)-pumped amplifiers is another effective way for generating high-energy picosecond NIR and 355 nm UV lasers. In 2021, Lü et al. ^{[ 20 ]} demonstrated a 91 mJ, 470 ps sub-nanosecond 355 nm UV laser system based on an LD-pumped Nd:YAG laser amplifier with a flat-top distribution of the NIR laser beam profile, corresponding to an extremely high THG conversion efficiency of 76%. However, the soft-edge aperture in this system caused almost 50% energy loss, as only the central part of the initial beam was used to form the flat-top beam distribution. Although the energy loss caused by the soft aperture, which is placed into the front end of the laser system, can be compensated by increasing the pump power of subsequent side-pumped modules, this approach also introduces additional thermal effects that worsen laser beam quality, and results in higher system cost. In addition, some efficient beam shaping techniques, such as using two aspherical lenses or grade-index lenses ^{[ 21 – 23 ]}, faced the challenges of meticulous manufacturing and precise assembling of optical components. Hence, we proposed a simple and high-efficiency technique based on the stimulated Raman scattering (SRS) effect in the Nd:YVO₄ crystal, which enabled simultaneous achievement of fundamental beam shaping and amplification, and only required a separator to remove the Raman component in the amplification system. This relies on the principle that the central part of the fundamental beam with higher intensity could experience more efficient Raman frequency conversion in the Raman crystal during the amplification process, resulting in a weakening of intensity at the center of the initial fundamental beam. However, no report has been found to date on this beam shaping technique and its application within amplification systems.

In this paper, we present a high-energy, high-peak-power and high-repetition-rate picosecond 355 nm UV laser system, where the SRS-based beam shaping technique was employed. The 1064 nm fundamental NIR laser source with the highest pulse energy of 352 mJ and pulse duration of 69 ps at 100 Hz was realized firstly. By utilizing two lithium triborate (LBO) crystals for cascading second-harmonic generation (SHG) and THG, a 355 nm UV laser with the highest pulse energy of 172 mJ and pulse duration of approximately 56 ps was realized, corresponding to the peak power of approximately 3 GW and the THG conversion efficiency from NIR to UV of 49%. The obtained pulse energy represented the highest pulse energy ever achieved of a picosecond 355 nm UV laser so far. This as-obtained UV laser system could play significant roles in applications including photoconductive switch excitation, laser drilling, laser micro-fabrication and so on.

2 Experimental setup

Figure 1 shows the schematic setup of the high-energy picosecond 355 nm UV laser system, including a master oscillator (MO), an RA, an LD end-pumped single-pass amplifier (SA), a side-pumped main amplifier (MA) and a harmonic generation unit. The MO was a mode-locked fiber laser that provided about 2 nJ, 100 ps seed pulses at a repetition rate of 25 MHz with the central wavelength of 1064.3 nm. An acousto-optic modulator was used as a pulse picker, selecting output pulses at a repetition rate of 100 Hz. After being collimated by an aspherical lens, the seed laser beam passed through an optical isolator (OI) to ensure extra protection of the MO. To match the fundamental mode of the RA cavity, the seed laser beam was expanded and aligned to 2.1 mm by the beam expander (BE). Inside the RA, a 5 mm × 5 mm × 20 mm, a-cut Nd:YVO₄ crystal with 0.15% (atomic fraction) Nd³⁺ doping and anti-reflection (AR) coating at 808 and 1064 nm on both end surfaces was end-pumped by a quasi-continuous wave (QCW) LD at 808 nm, which had a peak power of 200 W, a pump duration of 100 μs and a core diameter of 400 μm (numerical aperture (NA) = 0.22). The pump light was focused into the Nd:YVO₄ crystal by coupler 1 with an image ratio of 1:5.8. A thin-film polarizer (TFP2), a quarter-wave plate (QWP1) and a barium borate (BBO)-based Pockels cell (PC) were used to form a pulse selector. The PC was switched on at a quarter-wave voltage and a duration of 145 ns to amplify the seed laser in the RA cavity for seven round trips. Once the PC was switched off, the output pulses of the RA were reflected by TFP1, and then entered into the LD end-pumped SA.

Figure 1 Schematic setup of the high-energy picosecond 355 nm UV laser system. HWP, half-wave plate; OI, optical isolator; BE, beam expander; TFP, thin-film polarizer; FR, Faraday rotator; QWP, quarter-wave plate; PC, Pockels cell; HR, high-reflection mirror; LD, laser diode; DM, dichroic mirror; VT, vacuum tube; MD, Nd:YAG module; CL, compensating lens; QR, 90° quartz rotator.

The LD end-pumped SA consisted of a BE (BE2), a QCW LD, a Nd:YVO₄ crystal and a dichroic mirror (DM1). In order to minimize the risk of optical damage and optimize the energy extraction during the subsequent amplification, the initial Gaussian beam profile was shaped into a saddle-shaped concave intensity distribution based on the SRS effect of the Nd:YVO₄ crystal during the amplification process. The fundamental and Raman lights were separated by DM1 with high-reflection (HR) coating at 1064 nm and high-transmission (HT) coating at 1176 nm. The same as for the RA, an 808 nm fiber-coupled QCW LD with a pump pulse duration of 100 μs and a core diameter of 400 μm was used in the SA. The pump light with a peak power of 300 W was focused into the Nd:YVO₄ crystal (the same as that in the RA) by coupler 2 with an image ratio of 1:6.

After passing through the OI (OI2), the laser pulses were injected into the MA comprising three amplification stages with two double-pass single-module (MD1, MD2) amplifiers and a single-pass double-module (MD3+MD4) amplifier. All the main amplification stages used 808 nm QCW LD side-pumped laser modules with Nd:YAG crystals. The pump pulse duration of each module was set to approximately 230 μs at 100 Hz. The peak pump powers of MD1, MD2 and MD3/MD4 were 4500, 5200 and 5600 W, respectively. Each pumping module contained a Nd:YAG crystal rod with Nd³⁺-doping concentration of 0.6% (atomic fraction), parallel wedged angle of 2° and the dimensions of φ7 mm × 122 mm, φ11 mm × 127 mm, φ15 mm × 140 mm and φ15 mm × 140 mm, sequentially. Both the pump LD arrays and crystal rod were cooled by a water circulation system. Five 4f image relay Kepler telescopes were used during the main amplification. At the focuses in the telescopes, 2 mm diameter hard apertures were adopted to filter spatial high-frequency radiation and block back reflections. The telescopes incorporate vacuum tubes (VTs) that were applied to prevent air breakdown at the focuses. The laser polarization inside the double-pass amplifier was converted from linear polarization to circular polarization by using a QWP, allowing for the elimination of parasitic lasing on optical surfaces and mitigation of nonlinear interaction in optical elements^{[ 24 ]}. After passing through the same QWP plate for the second time, the circular laser polarization was converted back to linear polarization and reflected out by the TFP. A 45° Faraday rotator (FR) was introduced in each stage of the two double-pass amplifiers to ensure that the laser beam traversed through the crystal rod twice along the same path with a 90° polarization rotation, compensating the thermally induced birefringence effects. In the single-pass amplification stage, depolarization compensation was implemented through a 90° quartz rotator (QR) between MD3 and MD4.

After being amplified through the MA, the laser pulse energy was tuned by an optical attenuator consisting of a half-wave plate (HWP) and a TFP before entering into the harmonic generation unit. The incident fundamental picosecond laser beam was adjusted in size and was relay-imaged by a relay-imaging system. The frequency conversion was achieved by cascading the SHG with LBO1 and the THG with LBO2. The LBO1 had the dimensions of 15 mm × 15 mm × 8 mm and was cut at θ = 90° and φ = 10.8° for type-I phase matching. Both end faces of LBO1 were AR coated at 532 and 1064 nm. LBO2 had the dimensions of 15 mm × 15 mm × 10 mm and was cut at θ = 43.4° and φ = 90° for type-II phase matching. The front surface of LBO2 was AR coated at 532 and 1064 nm, while the rear surface was only AR coated at 355 nm. Both LBO crystals were mounted in constant temperature ovens individually. The temperature control accuracy of the oven was ±0.01°C at the lower injection powers, and it would decrease with the increasing injection powers due to more heat production inside the crystal, finally changing to ±0.25°C at the highest injection fundamental power in this experiment. Two DMs (DM2 and DM3) with HR coating at 355 nm and HT coating at 532/1064 nm were used to separate the 355 nm UV laser.

3 Results and discussion

The output pulse energy of each amplification stage is shown in Figure 2(a). The seed picosecond pulse with an energy of 2 nJ at 100 Hz was firstly amplified to 5 mJ after seven extraction cycles in the RA, corresponding to a gain value of about 2.5 × 10⁶. The beam quality factors of the RA output were measured to be ${M}_x^2$ = 1.04 and ${M}_y^2$ = 1.05, as shown in Figure 2(b). The inset color image in Figure 2(b) shows the output laser beam intensity profile, indicating a perfect Gaussian distribution with TEM₀₀ mode. Note that the axis orientation was set to auto-orientation along the major and minor axes of the elliptical beam during the measurements of laser beam profiles and ${M}^2$ values in this work. The axis closer to the horizontal direction was defined as the x-direction, while the other one was defined as the y-direction. In comparison to previous works that used Nd:YAG crystals in the RA process^{[ 25 , 26 ]}, the better beam quality obtained might be attributed to the natural birefringence of the Nd:YVO₄ crystal^{[ 27 , 28 ]}, which exhibits a significantly lower depolarization ratio than Nd:YAG crystals^{[ 29 ]}, helping to effectively mitigate the adverse impact of thermal depolarization on beam quality.

Figure 2 (a) Output energies of the master oscillator (MO), regenerative amplifier (RA), single-pass amplifier (SA), first stage of the main amplifier (MA.1), second stage of the main amplifier (MA.2), and third stage of the main amplifier (MA.3). (b) Output beam quality ${M}^2$ from the RA. The inset shows the near-field beam intensity distribution.

The beam intensity profile of the Gaussian beam from the RA was shaped during the single-pass amplification process based on the SRS effect. The peak power of the amplified pulses can reach the level of 100 MW, and the SRS effect is easily induced in the Nd:YVO₄ crystal^{[ 30 , 31 ]}. The growth expression for the first Stokes wave of Raman scattering near the threshold can be described as follows^{[ 32 ]}:

(1) $$\begin{align}{I}_\mathrm{st1}(l)={I}_\mathrm{SN}\exp \left({g}_\mathrm{R} Il\right),\end{align}$$

where I _st1(l) denotes the intensity of the first Stokes wavelength, I _SN is the spontaneous Raman scattering intensity of the first Stokes wavelength, g _R is the Raman gain coefficient, I is the fundamental light intensity and l is the length of the Raman medium. From Equation (1), I _st1(l) demonstrates a positive correlation with I. Thus, by utilizing BE2 for beam size control to adjust the fundamental laser intensity, the center part of the beam with higher intensity could experience more efficient Raman frequency conversion. This resulted in a weakening of the intensity at the center of the fundamental beam, allowing for the transformation of the initial Gaussian beam into a flat-top center or even a saddle-shaped concave center intensity distribution, as shown in Figures 3(a) and 3(b). The beam with the saddle-shaped concave center intensity distribution was selected for subsequent amplification to compensate for the higher central gain of the MA.

Figure 3 Intensity distributions of (a) the flat-top center beam and (b) the saddle-shaped concave center beam after being shaped by the single-pass amplifier. (c) Output laser spectra of the flat-top center beam (blue line) and the saddle-shaped concave center beam (red line) from the single-pass amplifier.

Figure 3(c) shows the output laser spectra of the flat-top center beam and the saddle-shaped concave center beam from the LD end-pumped SA. Dual-wavelength operations were achieved with the fundamental laser at 1064.3 nm and a Raman laser at 1175.7 nm (first Stokes wave). The frequency shift ω_R between the two wavelengths was about 890 cm^–1, corresponding to the Raman shift of the YVO₄ crystal. A DM (DM1) was utilized for beam separation. The pulse energy of approximately 800 μJ was measured for the 1175.7 nm Raman light, while the energy of the 1064.3 nm fundamental laser increased from 5 to 11 mJ when it was amplified and shaped into a saddle-shaped concave center intensity distribution.

The re-shaped fundamental picosecond pulse laser was amplified from 11 to 66, 182 and 352 mJ from the three amplification stages of the MA, as shown in Figure 2(a), corresponding to the gain values of 6, 2.8 and 1.9, respectively. No optical damage or beam breakup was observed at the highest output energy. Furthermore, the energy stability for 3 hours of operation was measured with an energy fluctuation of root mean square (RMS) 1.17%, as shown in Figure 4(a). Based on the precise thermally induced depolarization compensation in the MA, the depolarization losses in all three main amplification stages remained below 3%. The beam quality factors were measured to be ${M}_x^2$ = 2.86 and ${M}_y^2$ = 2.73 at the highest output pulse energy of 352 mJ, as shown in Figure 4(b). The inset color image in Figure 4(b) shows the intensity distribution of the amplified fundamental laser beam, exhibiting a Gaussian profile with relatively homogeneous beam intensity distribution after the main amplification process. This was the result of compensating for the inhomogeneous gain in the MA by the pre-shaped saddle-shaped beam, which was beneficial to avoid optical damage of the optical elements during the amplification process. As shown in Figure 4(c), the 3 dB spectral bandwidth of 0.18 nm of the seed laser was broadened to 0.29 nm and the spectrum was slightly red-shifted after passing the amplification stages. The spectral broadening was due to the new spectral components induced by the self-phase modulation (SPM) effect, and the spectral red shift arising from an imperfect gain matching between the central wavelength of seed laser and the gain spectra of amplifiers. Using a photo-detector (EOT, ET-3500F) with a bandwidth of more than 15 GHz and a digital oscilloscope (Tektronix, DSA72004) with a bandwidth of 20 GHz, the pulse widths of the seed and amplified lasers were measured to be 100 and 69 ps, respectively, as shown in Figure 4(d). Although the obtained pulse widths were within the measurable range, they were close to the bandwidth limit supported by the instruments. Therefore, the pulse widths were derived by separately averaging 30 sets of test data, and both fluctuations were less than ±2 ps. The shortening of the pulse width from 100 to 69 ps can be attributed to the gain saturation effects of the amplifiers^{[ 20 , 33 ]}, which also resulted in a steeper front edge compared to the back edge of the laser pulse.

Figure 4 (a) Energy stability of the 1064 nm fundamental laser pulse. (b) Measured beam quality factor ${M}^2$ at an output energy of 352 mJ. The inset shows the near-field beam intensity distribution. (c) Laser spectra of the seed pulses at an output energy of 2 nJ (black line) and the amplified pulses at an output energy of 352 mJ (red line). (d) Temporal profiles of the seed pulses at an output energy of 2 nJ (black line) and the amplified pulses at an output energy of 352 mJ (red line).

The amplified fundamental laser was collimated with a small divergence angle into the frequency conversion unit through a relay-imaging system. The dependences of the output pulse energy and the optical–optical conversion efficiency at 532 nm on the incident 1064 nm fundamental laser energy are shown in Figure 5(a), where each point was optimized by tuning the angle of LBO1 to achieve the optimal SHG. The maximum achievable green light energy was 211 mJ, corresponding to the SHG conversion efficiency of 60%.

Figure 5 (a) Dependence of the 532 nm green laser pulse energy and SHG efficiency on the incident 1064 nm laser pulse energy. (b) Energy stability of the 532 nm green laser pulse. (c) Dependence of the 355 nm UV laser pulse energy and THG efficiency on the incident 1064 nm laser pulse energy. (d) Energy stability of the 355 nm UV laser pulse.

For THG, the angles of two LBO crystals were tuned at different pulse energy of 1064 nm, as shown in Figure 5(c), to obtain the optimal output performances. It should be noted that the phase matching setting (angular tuning) of the frequency-doubling crystal in THG was different from the optimal SHG condition mentioned above. The highest THG conversion efficiency of 55% was obtained with 355 nm UV output energy of 66 mJ, and the maximum output energy of 172 mJ was obtained with the SHG and THG conversion efficiencies of approximately 45% and 49%, respectively. However, the SHG and THG efficiencies did not increase monotonically as the incident 1064 nm pump energy increased. The highest SHG (62%) and THG (55%) conversion efficiencies were obtained under the incident 1064 nm pump energies of 210 and 120 mJ, respectively. Subsequently, the declines in both the SHG and THG efficiencies were observed with further increments of the pump energy, indicating that the conversion efficiencies reached the saturation states, which might be due to the inverse conversion, thermal phase-mismatch and absorption-related effects. As shown in Figures 5(b) and 5(d), the energy stabilities over a period of 3 hours were measured to be RMS of 1.37% and 1.48% at the maximum output energies of the 532 nm green and 355 nm UV lasers, respectively. These periodic energy fluctuations might be attributed to the periodic temperature variations occurring in the two LBO crystals.

Figure 6(a) shows the beam quality factors of the UV laser of ${M}_x^2$ = 3.92 and ${M}_y^2$ = 3.71, and the inset color image illustrates the beam intensity distribution profile. Limited by the bandwidth of the UV photo-detector, the pulse duration of the UV laser cannot be measured accurately. However, an estimation of the pulse duration can be derived from the oscilloscope traces of the UV laser pulse as follows^{[ 34 ]}:

(2) $$\begin{align}{t}_\mathrm{real}=\sqrt{t_\mathrm{measure}^2-{t}_\mathrm{probe}^2-{t}_\mathrm{oscilloscope}^2},\end{align}$$

where t _real denotes the real rise time, t _measure denotes the measured rise time and t _probe and t _oscilloscope represent the rise times of the photo-detector and the oscilloscope, respectively. All these rise times are defined as the times between 20% and 80% of the peak values. Here, t _probe and t _oscilloscope are 150 and 17 ps given by a fast photo-detector (Thorlabs, DET025A/M) and a 20 GHz bandwidth oscilloscope (Tektronix, DSA 72004), respectively. Considering that the values of t _measure we obtained were higher than but close to 150.96 ps (Equation (2) works only if t _measure is larger than this value), and were affected by some parasitic oscillations or noise, we consequently determined the fluctuation range of t _measure as 154.6 ± 2 ps by conducting 30 sets of test data. According to the definition of rise time and the approximately symmetric shape of the UV laser pulse, the pulse duration of the UV laser can be assumed as 1.67 times that of t _real, so that the pulse duration was calculated in the range of 37–70 ps. By using the average value of t _measure, which was 154.6 ps, as shown in Figure 6(b), the pulse duration of the UV laser was estimated to be 56 ps (full width at half maximum, FWHM), corresponding to the peak power of approximately 3 GW. Table 1 lists the representative results of the high-energy picosecond 355 nm UV lasers. Our results represent the highest output energy of picosecond 355 nm UV lasers.

Figure 6 (a) Measured beam quality factor ${M}^2$ of the 355 nm UV laser at a pulse energy of 172 mJ. The inset shows the near-field beam intensity distribution. (b) Measured temporal pulse profile of the 355 nm UV laser.

Table 1 Representative results of the high-energy picosecond 355 nm UV laser.

4 Conclusion

In summary, a high-energy, picosecond 355 nm UV laser system operating at 100 Hz was realized. The 1064 nm fundamental laser pulses with the pulse energy of 352 mJ and pulse duration of 69 ps at 100 Hz were obtained firstly by cascaded RA, QCW LD end-pumped SA and side-pumped MA. In particular, the beam profile output from the RA was shaped from a Gaussian beam into a saddle-shaped concave center beam based on the SRS effect of the Nd:YVO₄ crystal in the LD end-pumped single-pass amplification, minimizing the risk of optical damage and optimizing the energy extraction during the subsequent amplification. Combined with multiple thermally induced birefringence compensation and 4f spatial filter-image relaying systems in the MA, a relatively homogeneous beam intensity distribution was obtained. Finally, a 172 mJ, approximately 56 ps, 100 Hz, 355 nm UV laser was obtained, corresponding to the peak power of approximately 3 GW and the THG conversion efficiency of 49% from NIR to UV. To the best of our knowledge, this is the highest pulse energy 355 nm picosecond UV laser reported to date. Our results provide a high-energy 355 nm UV laser system for applications including photoconductive switch excitation, laser drilling, laser micro-fabrication and so on.