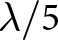Introduction
Microstrip patch antennas (MPAs) are inherently low gain, normally limited to 5–8 dBi, and narrow impedance matching bandwidth (IMBW), usually less than 4%, antennas [Reference Lee, Dahele, James and Hall1, Reference Garg, Bhartia, Bahl and Itapexiboon2]. More attention has been paid to enhancing the IMBW, as obvious from the published dedicated books [Reference Chen and Chia3, Reference Kumar and Ray4]. However, recently attention has also been paid to methods for increasing the gain of the MPA above 7 dBi to meet the need for high-data-rate communications and compensate for the propagation loss. The rectangular or circular patches are generally preferred due to their simple and regular geometry. On the other hand, the triangular MPA is more compact than the rectangular and circular MPA for a fixed resonance frequency [Reference Lee, Dahele, James and Hall1]. The linearly and circularly polarized equilateral triangular patch antenna (ETPA) and ETPA slot antenna are reported with the directive gain 3.07–9.3 dBi and IMBW 4.8%–50% in the frequency range 1.26–10.5 GHz on substrates of ![]() ${\varepsilon _r} = 1,2.2,2.5,3.38,3.55,4.4$ [Reference Chen5–Reference Luo, Gao, Sobhy, Sumantyo, Li, Wei, Xu and Wu12]. The low permittivity and thick substrates provide higher gain and wider IMBW. However, several innovative methods are employed to enhance the gain of the MPA above 8 dBi. Normally, the gain of the MPA could be enhanced by enlarging the radiating aperture area with a more uniform electric field distribution and suppressing surface waves on the conductor-backed dielectric sheet. The horizontal and vertical arraying of patches also increases the gain; however, at the cost of larger size and more complex feeding arrangement. The amplifier-incorporated active patches also provide higher gain [Reference Song and Bialkowski13]. The general concepts to get high-gain MPAs are implemented through the following methods: In the first method, the high permittivity superstrate under the resonance gain condition provides the gain enhancement [Reference Alexopoulos and Jackson14, Reference Jackson and Alexopoulos15]. In the second method, one or more supplementary parasitic or stacked patches are placed in proximity to the primary radiating patch to increase gain [Reference Yang, Zhang, Ye and Rahmat-Samii16–Reference Egashira and Nishiyama18]. It has a large separation between patches, 0.3λ–0.5λ, and the use of several parasitic patches results in a complex design process and fabrication. In the third method, a periodic structure is used to improve the patch antenna gain, namely partially reflective surfaces, metasurfaces, and electromagnetic band gaps. These periodic structures are in the form of a metallic screen with a periodic pattern [Reference Feresidis and Vardaxoglou19–Reference Kumar, Chaudhary and Mittra22]. In the fourth method, the patch-fed surface-mounted short pyramidal horn; short conical horn, and substrate-integrated waveguide (SIW), forming an H-plane horn, are suggested to enhance the gain [Reference Nasimuddin and Verma23–Reference Bhagwat and Raikwar27]. The SIW is a microstrip line-fed long antenna. In the fifth method, circular and rectangular patch antennas, operating in higher-order modes, are used to enhance the gain. The patches working in the higher-order modes are electrically large. The side-lobe level (SLL) of such a patch radiator is normally high. A special method is used to improve the SLL. In the case of a circular patch, combined TM11 and TM13 modes are used to get the gain of 13.06 dBi with 1.2% IMBW at 9.94 GHz [Reference Juyal and Shafai28]. The TM12 mode circular patch, with a non-resonant slot, on the air substrate, has also provided 11 dBi gain with a low SLL [Reference Juyal and Shafai29, Reference Juyal and Shafai30]. However, it is difficult to get air substrate. The shorted rectangular patch resonating in the TM30 mode has also been used to get 9–10 dBi gain. However, it has a large E-plane cross-polarization (XP) [Reference Wang, Bo Ng, Chan and Wong31].
${\varepsilon _r} = 1,2.2,2.5,3.38,3.55,4.4$ [Reference Chen5–Reference Luo, Gao, Sobhy, Sumantyo, Li, Wei, Xu and Wu12]. The low permittivity and thick substrates provide higher gain and wider IMBW. However, several innovative methods are employed to enhance the gain of the MPA above 8 dBi. Normally, the gain of the MPA could be enhanced by enlarging the radiating aperture area with a more uniform electric field distribution and suppressing surface waves on the conductor-backed dielectric sheet. The horizontal and vertical arraying of patches also increases the gain; however, at the cost of larger size and more complex feeding arrangement. The amplifier-incorporated active patches also provide higher gain [Reference Song and Bialkowski13]. The general concepts to get high-gain MPAs are implemented through the following methods: In the first method, the high permittivity superstrate under the resonance gain condition provides the gain enhancement [Reference Alexopoulos and Jackson14, Reference Jackson and Alexopoulos15]. In the second method, one or more supplementary parasitic or stacked patches are placed in proximity to the primary radiating patch to increase gain [Reference Yang, Zhang, Ye and Rahmat-Samii16–Reference Egashira and Nishiyama18]. It has a large separation between patches, 0.3λ–0.5λ, and the use of several parasitic patches results in a complex design process and fabrication. In the third method, a periodic structure is used to improve the patch antenna gain, namely partially reflective surfaces, metasurfaces, and electromagnetic band gaps. These periodic structures are in the form of a metallic screen with a periodic pattern [Reference Feresidis and Vardaxoglou19–Reference Kumar, Chaudhary and Mittra22]. In the fourth method, the patch-fed surface-mounted short pyramidal horn; short conical horn, and substrate-integrated waveguide (SIW), forming an H-plane horn, are suggested to enhance the gain [Reference Nasimuddin and Verma23–Reference Bhagwat and Raikwar27]. The SIW is a microstrip line-fed long antenna. In the fifth method, circular and rectangular patch antennas, operating in higher-order modes, are used to enhance the gain. The patches working in the higher-order modes are electrically large. The side-lobe level (SLL) of such a patch radiator is normally high. A special method is used to improve the SLL. In the case of a circular patch, combined TM11 and TM13 modes are used to get the gain of 13.06 dBi with 1.2% IMBW at 9.94 GHz [Reference Juyal and Shafai28]. The TM12 mode circular patch, with a non-resonant slot, on the air substrate, has also provided 11 dBi gain with a low SLL [Reference Juyal and Shafai29, Reference Juyal and Shafai30]. However, it is difficult to get air substrate. The shorted rectangular patch resonating in the TM30 mode has also been used to get 9–10 dBi gain. However, it has a large E-plane cross-polarization (XP) [Reference Wang, Bo Ng, Chan and Wong31].
The shorting pins have been investigated to control the frequency and polarization of microstrip antennas [Reference Schaubert, Farrar, Sindoris and Hayes32, Reference Gao, Sambell and Zhong33], to design dual band antennas [Reference Zhong and Lo34, Reference Waterhouse and Shuley35], and to enhance the IMBW [Reference Row and Liou7]. The shorting pins are also reported to increase the gain of the annular-ring patch antenna to 12 dBi at 2.425 GHz with IMBW 80 MHz. The inner radius of the annular ring is shorted to the ground with pins so that the outer radius can be increased to optimize the patch for high gain [Reference Arnieri, Boccia, Amendola and Di Massa36]. The shorting pins are also used to improve the gain of a rectangular patch. The loading of pins increases the resonance frequency of the patch from 1.614 to 2.546 GHz. It increases the electrical size of the patch, thus enhancing the gain to 10.3 dBi [Reference Zhang and Zhu37].
To the best of our knowledge gain of a compact ETPA has not been enhanced by using the shorting pins. The present work reports the use of three shorting pins to increase the gain of ETPA from −10.75 to 12.4 dBi at 5.43 GHz. The gain has been further enhanced to 14.2 dBi at 5.43 GHz by using an surface-mounted short horn (SMSH) of height ![]() $\lambda /5$. The enhanced gain ETPA does not operate in the usual fundamental TM10 mode, rather, it operates in radiating higher order deformed TM11 mode [Reference Lee, Luk and Dahele38]. By suitably placing three pins on three bisectors near the apex, using a probe feed, the Ez-field is redistributed to get radiating deformed TM11 mode.
$\lambda /5$. The enhanced gain ETPA does not operate in the usual fundamental TM10 mode, rather, it operates in radiating higher order deformed TM11 mode [Reference Lee, Luk and Dahele38]. By suitably placing three pins on three bisectors near the apex, using a probe feed, the Ez-field is redistributed to get radiating deformed TM11 mode.
The work is organized as follows. The “Modes of EPTA” section investigates the nature of modes of ETPA using HFSS and characteristic mode analysis (CMA) available with Computer Simulation Technology (CST). The “High-gain TM11 mode ETPA with shorting pins” section discusses loading of ETPA with shorting pins to get high-gain TM11 mode antenna. The “Design process of high-gain TM11 mode ETPA with three shorting pins” section suggests the design process of the three shorting pins loaded high-gain ETPA. The “High-gain TM11 mode ETPA with SMSH” section incorporates a triangular SMSH with ETPA to realize 14.2 dBi gain. The “Experimental validation of high-gain TM11 mode ETPA” section experimentally validates the design of ETPA antenna 1 and combined ETPA + SMSH antenna 2. This section also compares the performance of both antenna 1 and antenna 2 with reported high-gain, above 8 dBi, antennas. Finally, The “Conclusion” section concludes the investigation and design of the present high-gain ETPA.
Modes of ETPA
Figure 1 shows an ETPA on the Rogers 5880 substrate of the relative permittivity (![]() ${\varepsilon _r} = 2.2$) and thickness (h = 3.175). The coordinate system of the patch is located at the centroid of the triangle. The probe feed is located at distance F d, along the x-axis, from the base of the triangle. The length of the perpendicular bisector is D. The patch antenna is considered at 3.2 GHz. The side length of the patch is a = 3.8 cm. Using the cavity model, five modes – TM10, TM11, TM20, TM21, and TM30, are examined in literature [Reference Lee, Dahele, James and Hall1, Reference Lee, Luk and Dahele38]. The fundamental mode TM10 and higher order modes TM20 and TM21 are observed as the radiating modes, whereas the modes TM11 and TM30 are non-radiating modes. An ETPA operating in the TM21 mode provides a maximum gain of about 8 dBi, not one operating in the fundamental TM10 mode [Reference Lee, Dahele, James and Hall1]. The resonance frequencies of TMmn modes of ETPA could be computed by the following expression [Reference Olaimat and Nihad39]:
${\varepsilon _r} = 2.2$) and thickness (h = 3.175). The coordinate system of the patch is located at the centroid of the triangle. The probe feed is located at distance F d, along the x-axis, from the base of the triangle. The length of the perpendicular bisector is D. The patch antenna is considered at 3.2 GHz. The side length of the patch is a = 3.8 cm. Using the cavity model, five modes – TM10, TM11, TM20, TM21, and TM30, are examined in literature [Reference Lee, Dahele, James and Hall1, Reference Lee, Luk and Dahele38]. The fundamental mode TM10 and higher order modes TM20 and TM21 are observed as the radiating modes, whereas the modes TM11 and TM30 are non-radiating modes. An ETPA operating in the TM21 mode provides a maximum gain of about 8 dBi, not one operating in the fundamental TM10 mode [Reference Lee, Dahele, James and Hall1]. The resonance frequencies of TMmn modes of ETPA could be computed by the following expression [Reference Olaimat and Nihad39]:
 \begin{equation}\begin{gathered}
{f_{mn\ell }} = \frac{{2c}}{{3{a_{eff,mn}}\sqrt {{\varepsilon _r}} }}\left( {{m^2} + mn + {n^2}} \right)\,\,\,\,\,\,\,\left( a \right) \hfill \\
where,m + n + \ell = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( b \right) \hfill \\
\end{gathered} \end{equation}
\begin{equation}\begin{gathered}
{f_{mn\ell }} = \frac{{2c}}{{3{a_{eff,mn}}\sqrt {{\varepsilon _r}} }}\left( {{m^2} + mn + {n^2}} \right)\,\,\,\,\,\,\,\left( a \right) \hfill \\
where,m + n + \ell = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( b \right) \hfill \\
\end{gathered} \end{equation}
Figure 1. Equilateral triangular patch antenna. (a) ETPA without shorting pins. (b) ETPA with three shorting pins.
In the above equation ![]() ${f_{mn\ell }}$ is the modal resonance frequency of the mnth mode. It is computed under the condition given by equation (1b) for integers
${f_{mn\ell }}$ is the modal resonance frequency of the mnth mode. It is computed under the condition given by equation (1b) for integers ![]() $\,m,n,\ell $. As the integer
$\,m,n,\ell $. As the integer ![]() $\ell $ is not an independent quantity, the modal frequency is usually written as
$\ell $ is not an independent quantity, the modal frequency is usually written as ![]() ${f_{mn}}$. The mode-dependent effective side length of the equilateral triangle is given the following expression [Reference Olaimat and Nihad39]:
${f_{mn}}$. The mode-dependent effective side length of the equilateral triangle is given the following expression [Reference Olaimat and Nihad39]:
 \begin{equation}{a_{eff,mn}} = a + 2\sqrt m \frac{h}{{\sqrt {{\varepsilon _r}} }} - 2\sqrt {mn} \frac{h}{{\sqrt {{\varepsilon _r}} }} + 19.71\frac{{n{h^2}}}{{a{\varepsilon _r}}}\end{equation}
\begin{equation}{a_{eff,mn}} = a + 2\sqrt m \frac{h}{{\sqrt {{\varepsilon _r}} }} - 2\sqrt {mn} \frac{h}{{\sqrt {{\varepsilon _r}} }} + 19.71\frac{{n{h^2}}}{{a{\varepsilon _r}}}\end{equation} The referred paper [Reference Olaimat and Nihad39] has a typographical error for the constant that is corrected in the above equation as 19.71. The integers m and n could be exchanged without any change in resonance frequency. Therefore, modes TMmn and TMnm ![]() $\,\,\left( {m \ne n} \right)$ form pairs of degenerate modes with identical frequency and orthogonal field components. It shows that modes TM10, TM20, TM21, and TM30 have degenerate modes forming eight numbers of modes, and TM11 has no degeneracy.
$\,\,\left( {m \ne n} \right)$ form pairs of degenerate modes with identical frequency and orthogonal field components. It shows that modes TM10, TM20, TM21, and TM30 have degenerate modes forming eight numbers of modes, and TM11 has no degeneracy.
All nine modes for the ETPA could be generated using the CMA technique available with CST EM-Simulator. The CMA is a very effective technique extensively used that provides the solution of supported modes on a resonating structure without exciting the structure [Reference Harrington and Mautz40]. The computed eigenvalues provide information about the supported modes. The characteristic parameters, modal significance  $MS = 1/\sqrt {1 + {{\left| {{\lambda _n}} \right|}^2}} $, and characteristic angle
$MS = 1/\sqrt {1 + {{\left| {{\lambda _n}} \right|}^2}} $, and characteristic angle ![]() ${\alpha _n} = 180 + {\tan ^{ - 1}}({\lambda _n})$ are related to the eigenvalues
${\alpha _n} = 180 + {\tan ^{ - 1}}({\lambda _n})$ are related to the eigenvalues ![]() ${\lambda _n}$ [Reference Harrington and Mautz40]. In this work, only the modal significance (MS) parameter is used to get the modal frequencies for nine modes shown in Fig. 2. Figure 2 also indicates the S11-response from the EM-Simulator HFSS, giving modal resonance frequencies. It clearly shows five distinct modes. Figure 2 shows that the TM10, TM20, TM21, and TM30 modes have degeneracy, shown as the modal pairs obtained from CMA. The mode 3, corresponding to TM11 has no degeneracy. Table 1 shows the modal resonance frequencies obtained from both the CMA and HFSS. It also shows the modal frequencies computed using closed-form models [Reference Olaimat and Nihad39, Reference Karaboga, Guney, Kaplan and Akdagli41, Reference Nasimuddin and Verma42]. Usually, the modal resonance frequency obtained from HFSS is less than the modal resonance frequency obtained from CMA. The probe excitation is not used in CMA, whereas a probe is used to excite modes in HFSS. The presence of the probe changes the path of the surface current causing a change in resonance frequency [Reference Dey and Mittra43]. The influence of the probe is different at different modes, as the surface current distribution is mode-dependent. For TM10, TM20, and TM30 modes, the resonance frequency obtained from HFSS is lower than that of the CMA. For the TM21 mode, the resonance frequency obtained from HFSS is higher than that of the CMA. However, for the TM11 mode, both frequencies obtained from the CMA and HFSS are almost identical.
${\lambda _n}$ [Reference Harrington and Mautz40]. In this work, only the modal significance (MS) parameter is used to get the modal frequencies for nine modes shown in Fig. 2. Figure 2 also indicates the S11-response from the EM-Simulator HFSS, giving modal resonance frequencies. It clearly shows five distinct modes. Figure 2 shows that the TM10, TM20, TM21, and TM30 modes have degeneracy, shown as the modal pairs obtained from CMA. The mode 3, corresponding to TM11 has no degeneracy. Table 1 shows the modal resonance frequencies obtained from both the CMA and HFSS. It also shows the modal frequencies computed using closed-form models [Reference Olaimat and Nihad39, Reference Karaboga, Guney, Kaplan and Akdagli41, Reference Nasimuddin and Verma42]. Usually, the modal resonance frequency obtained from HFSS is less than the modal resonance frequency obtained from CMA. The probe excitation is not used in CMA, whereas a probe is used to excite modes in HFSS. The presence of the probe changes the path of the surface current causing a change in resonance frequency [Reference Dey and Mittra43]. The influence of the probe is different at different modes, as the surface current distribution is mode-dependent. For TM10, TM20, and TM30 modes, the resonance frequency obtained from HFSS is lower than that of the CMA. For the TM21 mode, the resonance frequency obtained from HFSS is higher than that of the CMA. However, for the TM11 mode, both frequencies obtained from the CMA and HFSS are almost identical.
Table 1. Resonance frequency for various modes


Figure 2. S11 and CMA results showing various modes.
Figure 2 further shows that the modes (6,7) and (8,9) overlap at MS value 0.8, creating (10.60%) wideband within 10 dB return-loss at 9 GHz. Modes 3 and (4,5) can also create a wideband with proper matching. At present, the overlap MS is 0.6, which is not sufficient for proper excitation of the modal pairs 3 and (4,5) to create a wideband. The distinct E-field and surface current of modes with degeneracy for ETPA could be obtained from CMA. Using CMA, these patterns are generated in the absence of the exciting coaxial probe. Figure 3(a–f) shows the E-field and surface current patterns only for the fundamental radiating mode TM10 and the non-radiating TM11 mode. The patterns for other modes are not presented and discussed for the sake of brevity. The HFSS provides these E-field and surface current patterns, shown in Fig. 4(a–f), in the presence of an exciting coaxial probe, only for mode 2, not for the degenerate mode 1. The similarity of the E-field patterns of CMA and HFSS shows that the fundamental mode 2 of the CMA is excited by HFSS, not mode 1.

Figure 3. CMA simulated E-field and surface current patterns without an exciting probe of TM10 and TM11 modes at 3.24 GHz and 5.75 GHz, respectively. (a) Electric field of mode 1 (TM10) at 3.24 GHz. (b) Electric field of mode 2 (TM10) at 3.24 GHz. (c) Surface current of mode 1 (TM10) at 3.24 GHz. (d) Surface current of mode 2 (TM10) at 3.24 GHz. (e) Electric field of mode 3 (TM11) at 5.75 GHz. (f) Surface current of mode 3 (TM11) at 5.75 GHz.
Figure 3(a, b) shows the orthogonal E-field patterns of mode 1 and mode 2 at 3.24 GHz, corresponding to TM10 mode. The vectors of the surface current density of modes 1 and 2, shown in Fig. 3(c, d), further demonstrate their orthogonality. Figure 3(b) for mode 2 shows that the apertures of slanted arms support minima in the Ez-field creating a null at boresight in the H-plane. The vertical aperture along the Y-axis, shown in Fig. 3(b), has a more uniform Ez-field. The vertical aperture provides primary radiation. HFSS further confirms the field distribution by simulating the probe-fed ETPA shown in Fig. 1(b). The probe feed is located at a distance F d = 18 mm from the base of the antenna. Figure 4(a, b) shows more uniform Ez in the vertical aperture. Figure 4(e) also confirms that the surface current is more uniformly distributed at the vertical edge. The x-components of the Ez-field around the apex of the triangle further add to radiation. The presence of an exciting coaxial probe disturbs the symmetry of the field at a slightly reduced resonance frequency of 3.21 GHz. A small decrease in resonance frequency is due to a little increase in the surface current path shown in Fig. 4(e) [Reference Dey and Mittra43]. The disturbed symmetry also causes a small XP level in the radiation patterns, shown in Fig. 5(a, b).

Figure 4. HFSS simulated E-field and surface current patterns, with an exciting coaxial probe, for TM10 and TM11 modes at 3.21 GHz and 5.75 GHz, respectively. (a) Electric field of mode-2 (TM10) at 3.21 GHz. (b) Electric field of mode-2 (TM10) at 3.21 GHz. (c) Electric field of mode-3 (TM11) at5.75 GHz. (d) Electric field of mode-3 (TM11) at 5.75 GHz. (e) Surface current of mode-2 (TM10) at 3.21 GHz. (f) Surface current of mode-3 (TM11) at 5.75 GHz.

Figure 5. HFSS simulated co- and cross-polarization E- and H-plane of ETPA without pin. (a) E-plane patterns at 3.21 GHz for TM10 mode. (b) H-plane patterns at 3.21 GHz for TM10 mode. (c) E-plane patterns at 5.75 GHz for TM11 mode. (d) H-plane patterns at 5.75 GHz for TM11 mode.
Figure 3(e, f) shows the Ez-field and surface current distribution of the mode 3 (TM11) at 5.75 GHz using CMA. The TM11 mode is a symmetric and in-phase mode. So, each aperture of the ETPA has two nulls in the Ez-field, corresponding to the surface current distribution, at three edges. The effective radiation from the ETPA at boresight is zero. Thus, the unperturbed TM11 mode is non-radiating, as predicted by the cavity model [Reference Lee, Dahele, James and Hall1, Reference Karaboga, Guney, Kaplan and Akdagli41]. Figure 4(c, d, and f), obtained from the HFSS, again shows the Ez-field and surface current distribution at 5.75 GHz for the TM11 mode. The presence of probe feed redistributes the aperture Ez-field and surface current. However, the aperture Ez-field is very weak, and the surface current distribution is symmetrical with a null in the center. The overall effect is to create a null at boresight in the radiation pattern, both in the E- and H-planes, for the TM11 mode. Figure 5(a–d) shows the HFSS-generated E- and H-plane radiation patterns of the ETPA at 3.21 GHz for TM10 mode and 5.75 GHz for TM11 mode. The (x–z) plane, i.e. ![]() $\,\,\varphi = {0^{\circ}}$ plane is the E-plane, and the (y–z) plane, i.e.
$\,\,\varphi = {0^{\circ}}$ plane is the E-plane, and the (y–z) plane, i.e. ![]() $\varphi = 90^\circ $ plane is the H-plane. The ETPA is a symmetrical structure relative to the E-plane. However, it is asymmetrical relative to the H-plane. Apart from the effect of the modal distribution of the aperture field, the geometrical symmetry and asymmetry of the ETPA also influence the radiation patterns in both the E- and H-planes. The boresight gain of TM10 mode ETPA is about 7.1 dBi at the resonating frequency of 3.21 GHz with a XP better than −25 dB in both the E- and H-planes. However, Fig. 5(c, d) shows that for the TM11 mode radiation at 5.75 GHz, the ETPA has co-polarization nulls in both the E- and H-planes at the boresight. The E-plane shows a −40 dB XP level. However, the XP level in H-plane is high, about −15 dB, at boresight with two adjacent nulls, −40 dBi and −31 dBi, at about
$\varphi = 90^\circ $ plane is the H-plane. The ETPA is a symmetrical structure relative to the E-plane. However, it is asymmetrical relative to the H-plane. Apart from the effect of the modal distribution of the aperture field, the geometrical symmetry and asymmetry of the ETPA also influence the radiation patterns in both the E- and H-planes. The boresight gain of TM10 mode ETPA is about 7.1 dBi at the resonating frequency of 3.21 GHz with a XP better than −25 dB in both the E- and H-planes. However, Fig. 5(c, d) shows that for the TM11 mode radiation at 5.75 GHz, the ETPA has co-polarization nulls in both the E- and H-planes at the boresight. The E-plane shows a −40 dB XP level. However, the XP level in H-plane is high, about −15 dB, at boresight with two adjacent nulls, −40 dBi and −31 dBi, at about ![]() $\theta = \pm 45^\circ $. The TM11 mode ETPA has a −10.75 dBi gain. The radiation characteristic of the ETPA at 3.21 GHz and 5.75 GHz follows the general discussion of aperture Ez-field and surface current distribution discussed above. The next section III discusses the process of converting the non-radiating TM11 mode into a radiating deformed TM11 mode.
$\theta = \pm 45^\circ $. The TM11 mode ETPA has a −10.75 dBi gain. The radiation characteristic of the ETPA at 3.21 GHz and 5.75 GHz follows the general discussion of aperture Ez-field and surface current distribution discussed above. The next section III discusses the process of converting the non-radiating TM11 mode into a radiating deformed TM11 mode.
High-gain TM11 mode ETPA with shorting pins
In the above discussion, HFSS simulation has provided a −10.75 dBi gain for the ETPA operating in unperturbed TM11 at 5.75 GHz. The non-radiating TM11 mode of the ETPA has to be converted to a radiating TM11 mode by shifting the Ez-field from the apex of the ETPA, shown in Fig. 3(e), to the radiating aperture. The Ez-field in the radiating aperture should be nearly uniform without null. In the process of converting the non-radiating mode to the radiating mode, the field structure of the unperturbed TM11 mode is deformed. The useful deformed TM11 mode is generated to get high-gain ETPA. The shifting of the Ez-field from the apex of the ETPA to the radiating aperture is a two-step process. In step 1, the Ez-fields concentrated at three apexes of the ETPA are shifted to the center of the patch by using three symmetrically located shorting pins at the three bisectors (bis 1, bis 2, and bis 3). The shorting pins redistribute the surface current to shift the Ez-field and generate the deformed TM11 mode. In step 2, the Ez-field of the deformed TM11 mode, located at the center of the ETPA, moved to the radiating aperture with the help of the probe feed, located suitably at the bisector near the apex. Figure 1(b) shows the ETPA with three shorting pins and probe feed. Both the steps are discussed below to realize the high-gain TM11 mode ETPA.
Step-1: Shifting of apex-located Ez-field to the center of ETPA
The Ez-field components distribution for the fundamental radiating TM10 mode and the next non-radiating TM11 mode are given by the following expressions obtained from the cavity model [Reference Zhang and Zhu44]:
 \begin{align}
{E_{z,10}}\left( {z,y} \right) & = {C_{10}}\left[ 2\cos \left( {\frac{{2\pi }}{{\sqrt 3 a}}x + \frac{{2\pi }}{3}} \right)\cos \left( {\frac{{2\pi }}{{3a}}y} \right) \right. \nonumber \\ & \qquad + \left. \cos \left( {\frac{{4\pi }}{{3a}}y} \right) \right]\,\,\,\,\,\,\,\left( a \right)\nonumber\\
{E_{z,11}}\left( {z,y} \right) & = {C_{11}}\left[ \cos 2\left( {\frac{{2\pi }}{{\sqrt 3 a}}x + \frac{{2\pi }}{3}} \right) + 2\cos \left( {\frac{{2\pi }}{{\sqrt 3 a}}x + \frac{{2\pi }}{3}} \right) \right. \nonumber \\ & \qquad \left. \cos \left( {\frac{{2\pi }}{a}y} \right) \right]\left( b \right)
\end{align}
\begin{align}
{E_{z,10}}\left( {z,y} \right) & = {C_{10}}\left[ 2\cos \left( {\frac{{2\pi }}{{\sqrt 3 a}}x + \frac{{2\pi }}{3}} \right)\cos \left( {\frac{{2\pi }}{{3a}}y} \right) \right. \nonumber \\ & \qquad + \left. \cos \left( {\frac{{4\pi }}{{3a}}y} \right) \right]\,\,\,\,\,\,\,\left( a \right)\nonumber\\
{E_{z,11}}\left( {z,y} \right) & = {C_{11}}\left[ \cos 2\left( {\frac{{2\pi }}{{\sqrt 3 a}}x + \frac{{2\pi }}{3}} \right) + 2\cos \left( {\frac{{2\pi }}{{\sqrt 3 a}}x + \frac{{2\pi }}{3}} \right) \right. \nonumber \\ & \qquad \left. \cos \left( {\frac{{2\pi }}{a}y} \right) \right]\left( b \right)
\end{align} where C10 and C11 are modal amplitude constants. At the perpendicular bisector (bis) located y = 0, the variation of the Ez,10 and Ez,11 along the x-axis could be plotted. For the TM10 mode, Ez,10 is zero (minima) at a distance  $d = \frac{2}{3}\,of\,bisector\,\left( D \right)$ of ETPA. Where d is the distance from the base of ETPA and D is the length of the bisector (bis). At distance d, the real part of the input impedance of the TM10 mode is also zero. Furthermore, at this distance d, the Ez,11-field of the TM11 mode is maximum [Reference Lee, Dahele, James and Hall1]. The normalized Ez-field distributions of the TM10 and TM11 modes at 3.21 GHz and 5.75 GHz, respectively, could also be obtained from HFSS. HFSS further accounts for the effect of probe feed on the Ez-field distribution. Figure 6 shows the unperturbed Ez-field distribution on bisectors 2 and 3 in the absence of probe feed on these bisectors. The probe feed is located at the bisector 1. So, at the bisector 1, the Ez-field of both modes is zero at the probe feed location F d/D = 0.52. The minimum of the TM10 mode and the maximum of the TM11 mode is moved to d/D = 0.34. The location of three pins at three bisectors is determined from the nearly undisturbed null of the Ez-field at either bisector 2 or 3 at d/D = 0.68. For side length a = 38 mm, the length of the bisector is
$d = \frac{2}{3}\,of\,bisector\,\left( D \right)$ of ETPA. Where d is the distance from the base of ETPA and D is the length of the bisector (bis). At distance d, the real part of the input impedance of the TM10 mode is also zero. Furthermore, at this distance d, the Ez,11-field of the TM11 mode is maximum [Reference Lee, Dahele, James and Hall1]. The normalized Ez-field distributions of the TM10 and TM11 modes at 3.21 GHz and 5.75 GHz, respectively, could also be obtained from HFSS. HFSS further accounts for the effect of probe feed on the Ez-field distribution. Figure 6 shows the unperturbed Ez-field distribution on bisectors 2 and 3 in the absence of probe feed on these bisectors. The probe feed is located at the bisector 1. So, at the bisector 1, the Ez-field of both modes is zero at the probe feed location F d/D = 0.52. The minimum of the TM10 mode and the maximum of the TM11 mode is moved to d/D = 0.34. The location of three pins at three bisectors is determined from the nearly undisturbed null of the Ez-field at either bisector 2 or 3 at d/D = 0.68. For side length a = 38 mm, the length of the bisector is ![]() $D = \sqrt 3 a/2 = 32.91{\text{mm}}$. Thus, the pins could be located at d = 22.4 mm on three bisectors of the ETPA, shown in Fig. 1(b).
$D = \sqrt 3 a/2 = 32.91{\text{mm}}$. Thus, the pins could be located at d = 22.4 mm on three bisectors of the ETPA, shown in Fig. 1(b).

Figure 6. EZ-field distributions at three bisectors of ETPA.
The three shorting pins at bisectors, without probe feed, move the Ez-field of the original unperturbed TM11 mode from the apex, shown in Fig. 3(e), to the center and mid of the apertures shown in Fig. 7(a). Figure 7(a), obtained using CMA, shows that aperture fields are still symmetrical, i.e. the deformed TM11 mode retains the symmetry of the unperturbed TM11 without shorting pins. However, the resonance frequency of the deformed TM11 mode is reduced to 5.43 GHz from 5.75 GHz. It is due to the longer current path, shown in Fig. 4(f), increasing the path length and inductance of the equivalent LC-resonator [Reference Dey and Mittra43]. Further, the symmetrical nature of the Ez aperture field of the deformed TM11 mode shows a null at boresight in both the E- and H-planes of the ETPA operating at 5.43 GHz. It is shown in Fig. 8(a, b). However, the maxima of the beam in E- and H-planes are shifted to −49° and 47°, respectively, with the beam level at 5.3 dBi and 4.42 dBi.

Figure 7. CMA and HFSS simulated Ez-field distribution on the ETPA for deformed TM11 mode. (a) CMA E-field at 5.43 GHz with three pins. (b) HFSS E-field at 5.43 GHz with three pins.

Figure 8. CMA simulated co- and cross-polarization patterns of ETPA with three shorting pins (without probe feed) for the deformed TM11 mode. (a) E-plane patterns with three shorting pins at 5.43 GHz. (b) H-plane patterns with three shorting pins at 5.43 GHz.
Step-2: Converting non-radiating TM11 mode to radiating deformed TM11 mode
At step 1, the deformed TM11 mode ETPA is still non-radiating. To get proper radiation, the symmetry of the aperture Ez-field has to be broken. It is achieved by the probe feed. Figure 7(b) shows that the Ez-field has mostly shifted to the vertical radiating aperture, facing the probe feed. The Ez-field in the vertical aperture is almost uniform without null. Both the slanted apertures have a null, with opposite directed weak Ez-field as obtained from HFSS. Figure 9(a, b) shows the co- and cross-polarized radiation of the pins-loaded ETPA in the E- and H-planes at 5.43 GHz. Using HFSS, the pin location is shifted to d = 25.84 mm, from 22.4 mm, to get the maximum gain at boresight.

Figure 9. HFSS simulated the E- and H-planes co- and cross-polarization levels of the deformed TM11 mode ETPA with three shorting pins. (a) E-plane radiation patterns at 5.43 GHz. (b) H-plane radiation patterns at 5.43 GHz. (c) S11 and gain response of ETPA with three shorting pins.
The gain of the antenna at the boresight is 11.34 dBi with XP levels of −24.81 dB and 13.63 dB in the E-plane and H-plane respectively. The XP null level for H-plane is −38 dB at an angle 7.2°, a little shifted from the boresight location. Figure 9(c) shows the S11-response and gain response of the deformed TM11 mode antenna. It shows resonance frequency with a narrow 5% IMBW. Table 2 compares the performance of the TM10, TM11 modes (without shoring pins) ETPA, and deformed TM11 mode (with three shoring pins) ETPA. The deformed TM11 mode ETPA, with three shorting pins, resonates at 5.43 GHz. So, another fundamental TM10 mode ETPA, resonating at 5.43 GHz, is also designed. It helps to compare, shown in Table 2, the size, and performance of the deformed TM11 mode antenna and TM10 mode antenna at the same resonance frequency. The deformed TM11 mode antenna has 2.54 dB more gain as compared to the ETPA working in TM10 mode at 5.43 GHz. However, the side length “a” is increased by 6.7 mm, i.e. by 17.6%. A larger aperture size results in a higher gain. As compared to the TM10 mode antenna at the same physical size a = 38 mm, the deformed TM11 mode ETPA has 4.33 dB more gain. So, the increased gain of the deformed TM11 mode ETPA is due to the increased size of the aperture in terms of the wavelength, while the physical size of the aperture remains unchanged. The aperture field is almost uniform. It is seen through the almost identical ratio of the resonance frequencies and gains of the unperturbed TM10 and deformed TM11 mode given in Table 2 – f 10/f 11 = 5.43 GHz/3.21 GHz = 1.69; Gain TM11/Gain TM10 = 11.34 dBi/7.01 dBi = 1.62. It is further noted that the increased gain of the deformed TM11 mode ETPA, compared to the gain of usual unperturbed TM11 mode ETPA, without shorting pins, is −10.75 dB. The gain can be further increased by incorporating a triangular SMSH discussed in section V. However, before taking up the use of the short horn, the design process of the high-gain ETPA with three shorting pins is summarized in the next section IV.
Table 2. HFSS simulated the performance of ETPA on a substrate with ![]() ${\varepsilon _{r\,}} = 2.2$, h = 3.175 mm
${\varepsilon _{r\,}} = 2.2$, h = 3.175 mm

Design process of high-gain TM11 mode ETPA with three shorting PINS
The design process suggested in this section to develop a high-gain ETPA, at a specified frequency, on a given substrate could be useful to a designer for faster design. The design steps are based on the investigation discussed in previous sections. Equations (1) and (2) are used to design an ETPA, operating in the fundamental TM10 mode at the frequency f 10. To design an ETPA, operating in the TM11 higher order mode, at a specified frequency f 11, the concept of frequency ratio, FR = f 11/f 10 is used. The FR is used to compute the resonance frequency f 10 of the ETPA from the specified operating frequency f 11. The side length “a” of the ETPA is computed at f 10, and the resulting ETPA supports the TM11 mode at f 11. The expression for the FR is obtained from equations (1) and (2):
 \begin{align}
& {f_{10}} = \frac{{2c}}{{3{a_{eff,10}}\sqrt {{\varepsilon _r}} }}\left( a \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;{f_{11}} = \frac{{2c\sqrt 3 }}{{3{a_{eff,11}}\sqrt {{\varepsilon _r}} }}\,\,\,\,\,\,\,\,\,\,\,\,\left( b \right) \nonumber\\
& FR = \frac{{{f_{11}}}}{{{f_{10}}}} = \sqrt 3 \left( {\frac{{{a_{eff,10}}}}{{{a_{eff,11}}}}} \right),\left( c \right),\;\;\;where\,\,{a_{eff,10}} = a + \frac{{2h}}{{\sqrt {{\varepsilon _r}} }}\,\left( d \right) \nonumber\\
& {a_{eff,11}} = a + \frac{{31.91{h^2}}}{{a{\varepsilon _r}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( e \right) \nonumber\\
& For\,\,{a_{eff,10}} = {a_{eff,11}} = a,\,\,\,FR = \sqrt 3 = 1.732\,\,\,\,\,\,\,\,\,\left( \,f \right)
\end{align}
\begin{align}
& {f_{10}} = \frac{{2c}}{{3{a_{eff,10}}\sqrt {{\varepsilon _r}} }}\left( a \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;{f_{11}} = \frac{{2c\sqrt 3 }}{{3{a_{eff,11}}\sqrt {{\varepsilon _r}} }}\,\,\,\,\,\,\,\,\,\,\,\,\left( b \right) \nonumber\\
& FR = \frac{{{f_{11}}}}{{{f_{10}}}} = \sqrt 3 \left( {\frac{{{a_{eff,10}}}}{{{a_{eff,11}}}}} \right),\left( c \right),\;\;\;where\,\,{a_{eff,10}} = a + \frac{{2h}}{{\sqrt {{\varepsilon _r}} }}\,\left( d \right) \nonumber\\
& {a_{eff,11}} = a + \frac{{31.91{h^2}}}{{a{\varepsilon _r}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( e \right) \nonumber\\
& For\,\,{a_{eff,10}} = {a_{eff,11}} = a,\,\,\,FR = \sqrt 3 = 1.732\,\,\,\,\,\,\,\,\,\left( \,f \right)
\end{align} In the above equation, ![]() ${a_{eff,10}}$ and
${a_{eff,10}}$ and ![]() ${a_{eff,11}}$ are the mode-dependent effective side lengths of ETPA for the TM10 and TM11 modes, respectively. Compared to equation (4f) to compute FR, equation (4c) is more accurate, as it accounts for the effect of the fringe field, dependent on substrate relative permittivity
${a_{eff,11}}$ are the mode-dependent effective side lengths of ETPA for the TM10 and TM11 modes, respectively. Compared to equation (4f) to compute FR, equation (4c) is more accurate, as it accounts for the effect of the fringe field, dependent on substrate relative permittivity ![]() ${\varepsilon _r}$ and thickness h. However, on ignoring the effect of the fringe field on effective side length “a”, a constant value of FR, given by equation (4f), is obtained for an ETPA on any substrate. Seventeen numbers of experimental and theoretical data on f 10 and f 11 are collected from published sources to compute the FR of the ETPA. The minimum, maximum, and average values of FR are 1.72, 1.77, and 1.75, respectively. Table 1 also shows that the average value of FR is 1.77. To maintain the computed value of FR at 1.75, the constant 19.71 used in equation (2) is changed to 31.9 in equation (4e). For
${\varepsilon _r}$ and thickness h. However, on ignoring the effect of the fringe field on effective side length “a”, a constant value of FR, given by equation (4f), is obtained for an ETPA on any substrate. Seventeen numbers of experimental and theoretical data on f 10 and f 11 are collected from published sources to compute the FR of the ETPA. The minimum, maximum, and average values of FR are 1.72, 1.77, and 1.75, respectively. Table 1 also shows that the average value of FR is 1.77. To maintain the computed value of FR at 1.75, the constant 19.71 used in equation (2) is changed to 31.9 in equation (4e). For ![]() ${\varepsilon _r} = 2.2,h = 3.175,a = 38mm$, the computed value of FR using equation (4c) is 1.75. Once f 10 is known for the specified f 11 using the FR, the side length “a” of the ETPA is computed from the following equation:
${\varepsilon _r} = 2.2,h = 3.175,a = 38mm$, the computed value of FR using equation (4c) is 1.75. Once f 10 is known for the specified f 11 using the FR, the side length “a” of the ETPA is computed from the following equation:
 \begin{equation}a = \frac{{2c}}{{3{f_{10}}\sqrt {{\varepsilon _r}} }} - \frac{{2h}}{{\sqrt {{\varepsilon _r}} }}\end{equation}
\begin{equation}a = \frac{{2c}}{{3{f_{10}}\sqrt {{\varepsilon _r}} }} - \frac{{2h}}{{\sqrt {{\varepsilon _r}} }}\end{equation} where c is the velocity of light. No closed-form expression is available to compute the ![]() $50\Omega $ feed location F d from the base of ETPA on the bisector of length D. However, an average normalized value of feed location F d/D could be obtained from the published results on ETPA designed on substrates with
$50\Omega $ feed location F d from the base of ETPA on the bisector of length D. However, an average normalized value of feed location F d/D could be obtained from the published results on ETPA designed on substrates with ![]() ${\varepsilon _r} = 4.4,h = 1.63,$ a = 100 mm, 86.6 mm, 32.04 mm, and our investigations for ETPA on
${\varepsilon _r} = 4.4,h = 1.63,$ a = 100 mm, 86.6 mm, 32.04 mm, and our investigations for ETPA on ![]() ${\varepsilon _r} = 2.2,h = 3.175,$ with a = 38 mm, 21.3 mm. The average value of the normalized feed location is F d/D = 0.52. Thus, the initial approximate feed location of an ETPA can be estimated from F d/D = 0.52. Further, the electric field minimum Ez,min of TM10, and maximum Ez,max of TM11 mode occur at the centroid of the ETPA, i.e. at the normalized pin location d/D = 0.67. Initially, three shorting pins at the three bisectors, shown in Fig. 1(b), are located at d/D = 0.67 to suppress the Ez,max of TM11 mode near the apex. Further, it moves the Ez-field to the center of ETPA. The ETPA with three shorting pins and probe feed is simulated on HFSS. The simulated resonance frequency
${\varepsilon _r} = 2.2,h = 3.175,$ with a = 38 mm, 21.3 mm. The average value of the normalized feed location is F d/D = 0.52. Thus, the initial approximate feed location of an ETPA can be estimated from F d/D = 0.52. Further, the electric field minimum Ez,min of TM10, and maximum Ez,max of TM11 mode occur at the centroid of the ETPA, i.e. at the normalized pin location d/D = 0.67. Initially, three shorting pins at the three bisectors, shown in Fig. 1(b), are located at d/D = 0.67 to suppress the Ez,max of TM11 mode near the apex. Further, it moves the Ez-field to the center of ETPA. The ETPA with three shorting pins and probe feed is simulated on HFSS. The simulated resonance frequency ![]() $f_{11}^s$ of the deformed TM11 mode ETPA is obtained from the S11 response. The
$f_{11}^s$ of the deformed TM11 mode ETPA is obtained from the S11 response. The ![]() $f_{11}^s$ is normally less than the specified resonance frequency f 11 of the ETPA. The presence of the shorting pins and feed probe increases the surface current path to decrease the resonance frequency. The % frequency deviation (FD) in resonance frequency is
$f_{11}^s$ is normally less than the specified resonance frequency f 11 of the ETPA. The presence of the shorting pins and feed probe increases the surface current path to decrease the resonance frequency. The % frequency deviation (FD) in resonance frequency is
 \begin{equation}\% FD = \frac{{\left(\, {{f_{11}} - f_{11}^s} \right)}}{{{f_{11}}}} \times 100\end{equation}
\begin{equation}\% FD = \frac{{\left(\, {{f_{11}} - f_{11}^s} \right)}}{{{f_{11}}}} \times 100\end{equation} It is seen that for an ETPA, ![]() ${f_{11}}\alpha \left( {1/a} \right)$. So, by decreasing the side length with the same % as that of FD, a more accurate value of f 11 could be obtained. The corrected side length is obtained as
${f_{11}}\alpha \left( {1/a} \right)$. So, by decreasing the side length with the same % as that of FD, a more accurate value of f 11 could be obtained. The corrected side length is obtained as
The ETPA could be redesigned with the corrected side length a cor, recalculated feed location F d, and shorting pins location d. The redesigned ETPA is simulated on HFSS to get a more accurate operating resonance frequency showing less deviation from the specified frequency f 11. The feed location F d is optimized for better impedance match. Finally, the shorting pins locations d are optimized for maximum boresight gain.
Design examples of ETPA
The flowchart, shown in Fig. 10, summarizes the design process of the TM11 mode high-gain ETPA, operating at the specified frequency f 11. A few ETPA are designed and EM-simulated using the design process suggested in the flowchart. To validate the design process, three pins loaded ETPA is designed at frequency f 11 = 5.45 GHz on a substrate with ![]() ${\varepsilon _r} = 2.2$, h = 3.175. Following the flowchart, the approximate fundamental mode resonance frequency f 10 = 3.14 GHz, approximate side length a = 38.57 mm, a eff10 = 42.85, and a eff11 = 42.36, giving FR = 1.75, are calculated. Using FR = 1.75, the computed improved f 10 is 3.11 GHz. It helps to get recomputed a = 39.07 mm, F d = 17.59 mm, and d = 22.66 mm. At this stage, approximately designed ETPA is simulated on HFSS. The ETPA resonates at f 11 = 5.52 GHz. However, its gain is only −10.14 dBi. To improve the gain to 11.24 dBi at
${\varepsilon _r} = 2.2$, h = 3.175. Following the flowchart, the approximate fundamental mode resonance frequency f 10 = 3.14 GHz, approximate side length a = 38.57 mm, a eff10 = 42.85, and a eff11 = 42.36, giving FR = 1.75, are calculated. Using FR = 1.75, the computed improved f 10 is 3.11 GHz. It helps to get recomputed a = 39.07 mm, F d = 17.59 mm, and d = 22.66 mm. At this stage, approximately designed ETPA is simulated on HFSS. The ETPA resonates at f 11 = 5.52 GHz. However, its gain is only −10.14 dBi. To improve the gain to 11.24 dBi at ![]() $f_{11}^s$ = 5.34 GHz, the pin position d is tuned to 26.56 mm. Using the FD = 2.02%, the corrected side length a is computed at 38.2 mm. The ETPA with a = 38.2 mm, F d = 17.59 mm, and d = 26.56 mm is again EM-simulated on HFSS. The dimensions are slightly tuned at a = 38.0 mm, F d = 18.0 mm, and d = 25.84 mm to get 11.34 dBi gain at f 11 = 5.43 GHz. The simulated design frequency deviates only by 0.37% from the specified frequency of ETPA. The design process is further validated on HFSS for three pins loaded ETPA at specified frequencies f 11 = 4.5, 5.75, 6.50, 8.50 GHz on a substrate
$f_{11}^s$ = 5.34 GHz, the pin position d is tuned to 26.56 mm. Using the FD = 2.02%, the corrected side length a is computed at 38.2 mm. The ETPA with a = 38.2 mm, F d = 17.59 mm, and d = 26.56 mm is again EM-simulated on HFSS. The dimensions are slightly tuned at a = 38.0 mm, F d = 18.0 mm, and d = 25.84 mm to get 11.34 dBi gain at f 11 = 5.43 GHz. The simulated design frequency deviates only by 0.37% from the specified frequency of ETPA. The design process is further validated on HFSS for three pins loaded ETPA at specified frequencies f 11 = 4.5, 5.75, 6.50, 8.50 GHz on a substrate![]() $\,{\varepsilon _r} = 2.2$, h = 3.175, and at f 11 = 5.45 GHz on FR-4,
$\,{\varepsilon _r} = 2.2$, h = 3.175, and at f 11 = 5.45 GHz on FR-4, ![]() ${\varepsilon _r} = 4.4$, h = 3.2 mm. Table 3 summarizes the dimensions and simulated resonance frequency of ETPA and their gains. The maximum deviation in designed frequency from the specified frequency is 3.88%, and the average deviation is 1.1%. At a low permittivity substrate
${\varepsilon _r} = 4.4$, h = 3.2 mm. Table 3 summarizes the dimensions and simulated resonance frequency of ETPA and their gains. The maximum deviation in designed frequency from the specified frequency is 3.88%, and the average deviation is 1.1%. At a low permittivity substrate ![]() ${\varepsilon _r} = 2.2$, the gain is about 11.0 dBi, whereas it is decreased to 8.54 dBi on high permittivity substrate
${\varepsilon _r} = 2.2$, the gain is about 11.0 dBi, whereas it is decreased to 8.54 dBi on high permittivity substrate ![]() ${\varepsilon _r} = 4.4$.
${\varepsilon _r} = 4.4$.

Figure 10. The flowchart of the design process of TM11 mode high-gain ETPA.
Table 3. Summary of design of ETPA with shoring pins at several frequencies on two substrates

High-gain TM11 mode ETPA with SMSH
The gain of the ETPA could be further increased by suppressing the surface wave on the conductor-backed substrate. It is achieved with the help of a triangular SMSH of height nearly ![]() $\lambda /5$. Figure 11 shows the ETPA with SMSH. The pyramidal and conical SMSH, with patch antennas, have been used to increase the gain of the patch antenna [Reference Nasimuddin and Verma23, Reference Elboushi and Sebak24]. However, the triangular SMSH with ETPA is not reported. To trap the surface wave on the conductor-backed dielectric sheet of substrate, the equilateral triangular SMSH, on the surface of the substrate, is located at the distance S from the edges of the ETPA. The trapped field of the surface wave and radiated field of the ETPA excite the aperture of the SMSH that provides the far-field radiation of the antenna 2. The top arm length M, bottom arm length N, slanted length L s, inclination angle
$\lambda /5$. Figure 11 shows the ETPA with SMSH. The pyramidal and conical SMSH, with patch antennas, have been used to increase the gain of the patch antenna [Reference Nasimuddin and Verma23, Reference Elboushi and Sebak24]. However, the triangular SMSH with ETPA is not reported. To trap the surface wave on the conductor-backed dielectric sheet of substrate, the equilateral triangular SMSH, on the surface of the substrate, is located at the distance S from the edges of the ETPA. The trapped field of the surface wave and radiated field of the ETPA excite the aperture of the SMSH that provides the far-field radiation of the antenna 2. The top arm length M, bottom arm length N, slanted length L s, inclination angle ![]() $\theta $, and height H of SMSH are optimized on HFSS to obtain the maximum gain of antenna 2, i.e. the three shorting pins loaded ETPA with SMSH. The results of detailed numerical experimentation for M = 135 mm, N = 93, and pin radius R = 1.3 mm at 5.52 GHz, are summarized in Fig. 12(a–c). Figure 12(a–c) shows the variation in the gain with three parameters of SMSH, i.e. with spacing S, flared angle
$\theta $, and height H of SMSH are optimized on HFSS to obtain the maximum gain of antenna 2, i.e. the three shorting pins loaded ETPA with SMSH. The results of detailed numerical experimentation for M = 135 mm, N = 93, and pin radius R = 1.3 mm at 5.52 GHz, are summarized in Fig. 12(a–c). Figure 12(a–c) shows the variation in the gain with three parameters of SMSH, i.e. with spacing S, flared angle ![]() $\left( \theta \right)$, and slanted length L. Figure 11 shows the nearly optimized dimensions of antenna 2 at an operating frequency of 5.52 GHz. The presence of SMSH increased the resonance frequency of ETPA with shorting pins, antenna 1, from 5.43 to 5.52 GHz. The SMSH has changed the path of the surface current, increasing the resonance frequency. It is noted that for L s = 19.3 mm
$\left( \theta \right)$, and slanted length L. Figure 11 shows the nearly optimized dimensions of antenna 2 at an operating frequency of 5.52 GHz. The presence of SMSH increased the resonance frequency of ETPA with shorting pins, antenna 1, from 5.43 to 5.52 GHz. The SMSH has changed the path of the surface current, increasing the resonance frequency. It is noted that for L s = 19.3 mm ![]() $\left( { \approx \lambda /3} \right)$, the height of SMSH is only H = 12.4 mm
$\left( { \approx \lambda /3} \right)$, the height of SMSH is only H = 12.4 mm ![]() $\left( { \approx \lambda /5} \right)$. The presence of SMSH has increased the gain of ETPA from 12.1 to 14.2 dBi. Thus, the SMSH has added a 2.1 dB gain to the ETPA. Figure 13(a–b) compares the HFSS simulated co-polarization and XP of antenna 1 and antenna 2 in the E- and H-planes.
$\left( { \approx \lambda /5} \right)$. The presence of SMSH has increased the gain of ETPA from 12.1 to 14.2 dBi. Thus, the SMSH has added a 2.1 dB gain to the ETPA. Figure 13(a–b) compares the HFSS simulated co-polarization and XP of antenna 1 and antenna 2 in the E- and H-planes.

Figure 11. Shorting pins loaded ETPA with SMSH (antenna 2) M = 135 mm, N = 93 mm, L s = 19.3 mm, θ = 40°, S = 15.75 mm, H = 12.4 mm, a = 38 mm, F d = 18 mm, d = 25.84 mm,![]() ${\varepsilon _r}$ = 2.2, h = 3.175 mm. (a) Top view. (b) Bottom view.
${\varepsilon _r}$ = 2.2, h = 3.175 mm. (a) Top view. (b) Bottom view.

Figure 12. Variation in the gain of antenna 2 with three parameters of SMSH. (a) Gain with spacing S (L s = 19.3 mm, ![]() $\theta = 40^\circ $). (b) Gain with flaring angle
$\theta = 40^\circ $). (b) Gain with flaring angle ![]() $\theta $ (L s = 19.3 mm, S = 15.75 mm). (c) Gain with slanted length L s (
$\theta $ (L s = 19.3 mm, S = 15.75 mm). (c) Gain with slanted length L s (![]() $\theta = 40^\circ $, S = 15.75 mm).
$\theta = 40^\circ $, S = 15.75 mm).

Figure 13. Simulated E-plane (EP) and H-plane (HP) co- and cross-polarization (XP) of antenna 1 and antenna 2. (a) E-plane (HP) co- and cross-polarization (XP) of antennas 1 and 2. (b) H-plane (HP) co- and cross-polarization (XP) of antennas 1 and 2.
The SMSH decreases the 3 dB beamwidth of antenna 1 from 31.5° to 31° in the E-plane and from 21.70° to 14.7° in the H-plane. It results in an improvement of 2 dB gain for the antenna 2. At boresight, antenna 1 exhibits XP in the E-plane. The presence of SMSH for antenna 2 improves the XP level in the E-plane to 15.16 dB from −24.81 to −40 dB. However, in H-plane the SMSH improves the XP level only by 29 dB, from −21 to −50 dB at boresight. The SMSH further improves the SLL in E-plane from −13 to −20 dB i.e. by 7 dB, in the H-plane, the improvement in the SLL is 8 dB, i.e. from −20 to −28 dBi.
Experimental validation of high-gain TM11 mode ETPA
To validate the design process of deformed TM11 mode ETPA, both antennae 1 and 2 are fabricated and tested. The performances of both antennas 1 and 2 are further compared for the directive gain against reported results in the open literature. Figure 14(a, b) shows fabricated ETPA i.e. antenna 1, and ETPA with triangular SMSH, i.e. antenna 2 on Rogers 5880 substrate with ![]() ${\varepsilon _r} = 2.2$, h = 3.175 mm. The structural details of ETPA are as follows: side length a = 38 mm, feed location F d = 18 mm, and pin location d = 25.84 mm. Figure 15(a–d) compares the HFSS simulated and measured S11 and gain response of both the antenna 1 and antenna 2 respectively. The simulated and measured resonance frequency and IMBW of antenna 1 are 5.43 GHz, 5.45 GHz; 5.0%, and 5.05% respectively. It is noted that the SMSH has almost negligible influence on resonance frequency and IMBW of the patch antenna 1. At 5.43 GHz, the simulated gain of ETPA i.e. antenna 1 is 11.34 dBi, whereas its measured gain is 12.1 dBi. The use of triangular SHSH improves the simulated gain to 13.4 dBi at 5.52 GHz, while its measured gain is 14.1 dBi.
${\varepsilon _r} = 2.2$, h = 3.175 mm. The structural details of ETPA are as follows: side length a = 38 mm, feed location F d = 18 mm, and pin location d = 25.84 mm. Figure 15(a–d) compares the HFSS simulated and measured S11 and gain response of both the antenna 1 and antenna 2 respectively. The simulated and measured resonance frequency and IMBW of antenna 1 are 5.43 GHz, 5.45 GHz; 5.0%, and 5.05% respectively. It is noted that the SMSH has almost negligible influence on resonance frequency and IMBW of the patch antenna 1. At 5.43 GHz, the simulated gain of ETPA i.e. antenna 1 is 11.34 dBi, whereas its measured gain is 12.1 dBi. The use of triangular SHSH improves the simulated gain to 13.4 dBi at 5.52 GHz, while its measured gain is 14.1 dBi.

Figure 14. Fabricated antenna 1 and antenna 2. (a) Antenna 1, ETPA. (b) Antenna 2 ETPA with SMSH.

Figure 15. Simulated and measured S11 and gain of antenna 1 and antenna 2. (a) Simulated S11, (b) measured S11, (c) simulated gain, and (d) measured gain.
Figure 16(a, b) compares the measured radiation patterns of antenna 1 and antenna 2, at 5.43 GHz and 5.52 GHz, respectively, in both the E- and H-planes. The SMSH improves the gain by narrowing the 3 dB beamwidth. The measured boresight gains of antenna 1 and antenna 2 are 12.1 dBi and 14.2 dBi, respectively. The SMSH further reduces the SLL in the E-plane from −12 to −23 dB, i.e. by 11 dB. However, in the H-plane, using SMSH, the SLL is improved from −18.7 to −30 dB, i.e. only by 11.3 dB. XP level at the boresight in the E-plane from the antenna 1 is −22 dB. The SMSH, for antenna 2, improves it to more than −42 dB due to a boresight null. In the H-plane, both antennas have null in the XP at the boresight. However, the antenna 2 with SMSH has a centrally located deep null.

Figure 16. Measured radiation pattern of E-plane (EP) and H-plane (HP) of antenna 1 at a frequency of 5.43 GHz. (a) E-plane (HP) co- and cross-polarization (XP) of antenna 1 and antenna 2. (b) H-plane (HP) co- and cross-polarization (XP) of antenna 1 and antenna 2.
Finally, Table 4 compares the performance of antenna 1 and antenna 2 against the performance of recently reported planar antennas with gains above 8 dBi. The aperture efficiency can be obtained by using equation (8) as given below [Reference Liu, Chen and Qing46], where “![]() $Dir$” is the directivity,
$Dir$” is the directivity, ![]() ${\lambda _o}\,$ is the free-space wavelength at antenna resonating frequency, and “
${\lambda _o}\,$ is the free-space wavelength at antenna resonating frequency, and “![]() ${A_p}$” is the physical size of the antenna.
${A_p}$” is the physical size of the antenna.
 \begin{equation}{\eta _{aper}} = \frac{{Dir \times \lambda _o^2}}{{4\pi \times {A_p}}}\end{equation}
\begin{equation}{\eta _{aper}} = \frac{{Dir \times \lambda _o^2}}{{4\pi \times {A_p}}}\end{equation}Table 4. Comparative performance of our antennas with earlier published work

In the present design the physical size of the antenna with ground is determined for the maximum realized directivity. Table 4 demonstrates that the present ETPAs, operating in deformed TM11 mode, provide larger gains as compared to gains of the reported high-gain antennas. The aperture efficiency of the standard ETPA, without shorting pins, operating in TM10 mode, at 5.43 GHz, is only 41.4%. The present antennas design 1 and design 2 have aperture efficiencies of 84.2% and 94.2%. These are more than the other reported efficiencies. The simulated IMBW in the present design is 5.0%. It could be increased to 10.13% by inserting the triangular slot in the triangular patch [Reference Row and Liou7]. However, the simulated gain is reduced from 11.34 to 10.2 dBi.
Conclusion
This work suggests a method to convert the non-radiating TM11 mode of an ETPA to a radiating antenna by deforming the TM11 mode. It is achieved by the proper placement of three shorting pins near the apex of three bisectors that move Ez from the apex region to radiating aperture. A systematic design process is presented for faster design of a high-gain antenna, at a specified frequency, on a suitable substrate. The measured gain of the ETPA with shorting pins (antenna 1) is 12.1 dBi at 5.43 GHz. The use of a triangular SMSH further improves the measured gain to 14.2 dBi at 5.42 GHz. The SMSH further improves the XP −47 dB at the boresight and SLL to −22 dB. The aperture efficiency of antenna 1 is 84.2%, and for antenna 2 it is 94.2%.
Acknowledgements
Ashwani Kumar would like to acknowledge with thanks the SERB Government of India for awarding him the startup research grant (Grant No: SRG/2021/001038).
Competing interests
The authors report no conflict of interest.

Ashwani Kumar received his M.Tech degree in Microwave Electronics and Ph.D. degree in Electronics in 2006 and 2014, respectively, from the Department of Electronic Science, University of Delhi, Delhi, India. He was with the Department of Electrical and Computer Engineering, University of Central Florida, Orlando, Florida, USA, for his postdoctoral research from 2016 to 2017. Currently, he is an associate professor in the Department of Electronic Science, University of Delhi South Campus, New Delhi. He served as an assistant professor at the School of Engineering, Jawaharlal Nehru University, New Delhi, India, from December 2019 to September 2023. Earlier, he was with the Department of Electronics, Sri Aurobindo College, University of Delhi, Delhi, India. His current research interests include designing and developing microwave passive components such as microstrip filters, dielectric resonator-based filters, MIMO antennae, UWB antennae, and circularly polarized antennae using metamaterials. He is a member of the IEEE Microwave Theory and Techniques Society. He has published 80 journal and conference technical papers on filters and antennas and has two book chapters. He has one Indian patent.

Shatish K. Gautam is working as a JRF in SERB project. His research interests include designing and developing high-gain antennas.

Maifuz Ali was born in Sabalmara, West-Midnapure, India. He received a Ph.D. degree in Electronics and Electrical Communication Engineering from the Indian Institute of Technology, Kharagpur, India, in 2010. He received the Brain Korea Research Fellowship in 2010 and was a Postdoctoral Researcher at the Korea Advanced Institute of Science and Technology, Daejeon, Korea, until 2012. Since 2012, he has been a Postdoctoral Researcher at the Tokyo Institute of Technology, Tokyo, Japan. He is a senior member of IEEE. His main research interests include high-frequency diffraction theory, such as physical optics and geometrical theory of diffraction. His research also covers the design of reflector antennae, electromagnetic field sensors, wireless channel modeling, and antenna.

Ravi Kumar Arya is a Distinguished Professor at Xiangshan Laboratory (XSL), Zhongshan Institute of Changchun University of Science and Technology (ZICUST), Zhongshan, Guangdong, China. He obtained his Ph.D. degree in Electrical Engineering from the Pennsylvania State University, USA, under the supervision of Prof. Raj Mittra. He received his master’s degree in RF and Microwave Engineering from the Indian Institute of Technology, Kharagpur, India, and a bachelor’s degree from Delhi Technological University, Delhi, India. Before joining ZICUST, he worked for several years in academia and industry. He has published over 70 technical papers in highly ranked journals and refereed conference proceedings, including seven book chapters. His research interests include antenna design, computational electromagnetics, machine learning applications, and 3D modeling.

P. P. Singh is with the Department of Electronics, Sri Aurobindo College, University of Delhi, Delhi, India. His current research interests include designing and developing microwave passive components such as microstrip filters, UWB antenns, and circularly polarized antennas using metamaterials.

A. K. Verma was professor in Department of Electronic Science, University of Delhi, Delhi, India. His current research interests include modeling and designing and developing microwave passive components such as microstrip filters, dielectric resonator-based filters, MIMO antennae, UWB antenns, and circularly polarized antennae using metamaterials. He is a member of the IEEE Microwave Theory and Techniques Society. He has published 200 journal and conference technical papers on filters and antennas and has two book chapters. He has one Indian Patent.

Raj Mittra is currently professor at the Department of Electrical and Computer Engineering, University of Central Florida, Orlando, USA. He is a prominent figure in the field of electrical engineering and computational electromagnetics. Born on April 4, 1934, in India, he pursued his education at esteemed institutions, earning a bachelor's degree in Electrical Engineering from the Indian Institute of Technology (IIT) Kharagpur, followed by a master's degree from the University of Manitoba, Canada, and a Ph.D. from the University of Toronto. Throughout his career, Professor Mittra has made significant contributions to electromagnetics research, focusing on computational techniques for analyzing electromagnetic structures. He is known for developing the Method of Moments (MoM) and Finite Difference Time Domain (FDTD) methods, which have revolutionized electromagnetic simulation and antenna design. Professor Mittra has held academic positions at leading universities including the University of Manitoba, University of Illinois at Urbana-Champaign, and Pennsylvania State University. He has authored numerous research papers and books that are highly regarded in the field. Professor Mittra's achievements have been recognized with prestigious awards such as Fellowship of the IEEE (Institute of Electrical and Electronics Engineers) and the ACES (Applied Computational Electromagnetics Society) Computational Electromagnetics Award. His work continues to shape the landscape of electromagnetics research and inspire future generations of engineers and scientists worldwide.