Published online by Cambridge University Press: 30 August 2017
How do the laws of physics change with changes in spatial dimension? Maybe not at all in some cases, but in important cases, the changes are dramatic. Fluid turbulence – the fluctuating, intermittent and many-degree-of-freedom state of a highly forced fluid – determines the transport of heat, mass and momentum and is ubiquitous in nature, where turbulence is found on spatial scales from microns to millions of kilometres (turbulence in stars) and beyond (galactic events such as supernovae). When the turbulent degrees of freedom are suppressed in one spatial dimension, the resulting turbulent state in two dimensions (2D) is remarkably changed compared with the turbulence in three dimensions (3D) – energy flows to small scales in 3D but towards large scales in 2D. Although this result has been known since the 1960s due to the pioneering work of Kraichnan, Batchelor and Leith, how one transitions between 3D and 2D turbulence has remained remarkably unexplored. For real physical systems, this is a highly significant question with important implications about transport in geophysical systems that determine weather on short time scales and climate on longer scales. Is the transition from 3D to 2D smooth or are there sharp transitions that signal a threshold of the dominance of one type of turbulence over another? Recent results by Benavides & Alexakis (J. Fluid Mech., vol. 822 (2017), pp. 364–385) suggest that the latter may be the case – a surprising and provocative discovery.

Figure 1. Examples of ideal and quasi-2D fluid turbulence that emphasize the role of coherent vortex structures in thin layers: (a) numerical simulation of ideal 2D turbulence (vorticity) (Boffetta & Ecke 2012), (b) laboratory quasi-2D turbulence (vorticity) (Boffetta & Ecke 2012) and (c) Atlantic Gulf Stream eddies (streak image) (Sirah 2012).
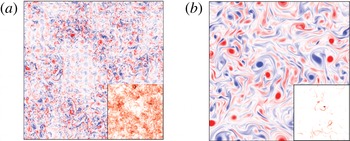
Figure 2. Vertical vorticity and (insets) 3D energy density ${\mathcal{E}}$ for (a)
$\ell _{f}/H\sim 1$, where vortices are weak and
${\mathcal{E}}$ is fairly evenly distributed in space, and (b)
$\ell _{f}/H\sim 10$, where vortices are stronger and more spatially localized and
${\mathcal{E}}$ is more spatially intermittent. After figure 7 in Benavides & Alexakis (2017).
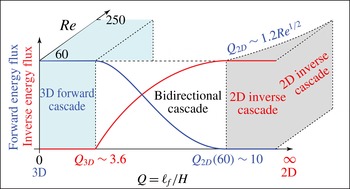
Figure 3. Schematic illustration of the behaviour of the normalized energy fluxes (forward and inverse) as a function of the degree of layer thinness $Q=\ell _{f}/H$, adopted from Benavides & Alexakis (2017, figures 1, 2 and 8). The ideal limits of 3D and 2D correspond to
$Q=0$ and
$Q=\infty$ respectively. The transition to diminished forward energy flux at the expense of growing inverse energy flux occurs at
$Q_{3D}\sim 3.6$, whereas the transition to no forward energy flux occurs at an
$Re$-dependent value where
$Q_{2D}\sim 1.2Re^{1/2}$. In between, energy flows in a bidirectional cascade where there is no inertial regime for either forward or inverse flux.
1 Introduction
We live in a world of three spatial dimensions, and most of the physics we observe reflects that dimensionality. In some circumstances, however, the degrees of freedom in one (or more) dimensions are suppressed, leading to an effectively lower-dimensional system. This change of dimensionality can have profound impact on the physics of such systems. In fluid dynamics, a reduction in dimensionality is important because there are many mechanisms that generate large spatial anisotropy with two spatial dimensions dominant compared with the third: thin fluid layers, stratification, rotation, magnetic field, etc. Here, we consider the dramatic changes that strong dimensional anisotropy imposes on the character of fluid turbulence.
Figure 1. Examples of ideal and quasi-2D fluid turbulence that emphasize the role of coherent vortex structures in thin layers: (a) numerical simulation of ideal 2D turbulence (vorticity) (Boffetta & Ecke Reference Boffetta and Ecke2012), (b) laboratory quasi-2D turbulence (vorticity) (Boffetta & Ecke Reference Boffetta and Ecke2012) and (c) Atlantic Gulf Stream eddies (streak image) (Sirah Reference Sirah2012).
So what is the difference between two-dimensional (2D) turbulence (Boffetta & Ecke Reference Boffetta and Ecke2012) and the more familiar three-dimensional (3D) version (Frisch Reference Frisch1995)? In 3D, when energy is injected at large scales, it is transferred on average to smaller scales in a forward cascade with energy dissipated at the smallest scales by viscous forces. If the spatial scales of forcing and dissipation are widely separated, energy is conserved at intermediate scales, leading to a $-5/3$
power-law relationship between energy and wavenumber. In 2D, this transfer of energy to small scales cannot occur due to an additional conservation law related to the condition in 2D that the vorticity contained within a spatial contour is conserved; the vorticity can only be rearranged in space but not increased or reduced as is possible in 3D. Thus, a characteristic of 2D turbulence is the persistence of vortical structures; see figure 1. The constraint on vorticity implies that the mean-square vorticity is transferred to small scales whereas the energy flow is inverse, i.e. it is transferred to large scales. This leads to a double cascade in 2D, with energy cascading towards scales larger than the forcing scale whereas the mean-square vorticity cascades towards smaller scales. In many circumstances, the ideal limits of 3D or 2D turbulence are not met and there is a bidirectional cascade where different transfer mechanisms dominate at different length scales and no inertial range may exist. The relationship between the ideal limits in 2D and 3D with a bidirectional cascade for thin but 3D layers is what we consider here.
$-5/3$
power-law relationship between energy and wavenumber. In 2D, this transfer of energy to small scales cannot occur due to an additional conservation law related to the condition in 2D that the vorticity contained within a spatial contour is conserved; the vorticity can only be rearranged in space but not increased or reduced as is possible in 3D. Thus, a characteristic of 2D turbulence is the persistence of vortical structures; see figure 1. The constraint on vorticity implies that the mean-square vorticity is transferred to small scales whereas the energy flow is inverse, i.e. it is transferred to large scales. This leads to a double cascade in 2D, with energy cascading towards scales larger than the forcing scale whereas the mean-square vorticity cascades towards smaller scales. In many circumstances, the ideal limits of 3D or 2D turbulence are not met and there is a bidirectional cascade where different transfer mechanisms dominate at different length scales and no inertial range may exist. The relationship between the ideal limits in 2D and 3D with a bidirectional cascade for thin but 3D layers is what we consider here.
2 Overview
Much research on 3D and 2D turbulence has focused on ideal isotropic homogeneous turbulence in the respective spatial dimensions. There is, however, a large amount of interesting physics in the anisotropic regime of 3D turbulence where one direction is suppressed compared with the other two degrees of freedom. This is the regime recently addressed by Benavides & Alexakis (Reference Benavides and Alexakis2017), which significantly extends earlier work exploring the crossover from 3D turbulence to 2D turbulence (Celani, Musacchio & Vincenzi Reference Celani, Musacchio and Vincenzi2010). Benavides and Alexakis numerically compute a model with highly resolved 2D components in the lateral direction coupled to a truncated single-mode vertical component. The system is forced on a lateral scale $\ell _{f}$
that is large compared with the vertical height
$\ell _{f}$
that is large compared with the vertical height
 $H$
. The control parameter is
$H$
. The control parameter is
 $Q=\ell _{f}/H$
, where larger values correspond to thinner, more 2D systems. The energy flux is computed and its behaviour as a function of
$Q=\ell _{f}/H$
, where larger values correspond to thinner, more 2D systems. The energy flux is computed and its behaviour as a function of
 $Q$
is considered. The resulting vorticity field reveals the quantitative feature of dominant vertical vorticity, as seen in figure 2. The insets show the 3D energy density and reflect the trend that as
$Q$
is considered. The resulting vorticity field reveals the quantitative feature of dominant vertical vorticity, as seen in figure 2. The insets show the 3D energy density and reflect the trend that as
 $Q$
is increased, the overall 3D energy density decreases, becoming highly singular in space for higher
$Q$
is increased, the overall 3D energy density decreases, becoming highly singular in space for higher
 $Q$
.
$Q$
.
Figure 2. Vertical vorticity and (insets) 3D energy density ${\mathcal{E}}$
for (a)
${\mathcal{E}}$
for (a)
 $\ell _{f}/H\sim 1$
, where vortices are weak and
$\ell _{f}/H\sim 1$
, where vortices are weak and
 ${\mathcal{E}}$
is fairly evenly distributed in space, and (b)
${\mathcal{E}}$
is fairly evenly distributed in space, and (b)
 $\ell _{f}/H\sim 10$
, where vortices are stronger and more spatially localized and
$\ell _{f}/H\sim 10$
, where vortices are stronger and more spatially localized and
 ${\mathcal{E}}$
is more spatially intermittent. After figure 7 in Benavides & Alexakis (Reference Benavides and Alexakis2017).
${\mathcal{E}}$
is more spatially intermittent. After figure 7 in Benavides & Alexakis (Reference Benavides and Alexakis2017).
Figure 3. Schematic illustration of the behaviour of the normalized energy fluxes (forward and inverse) as a function of the degree of layer thinness $Q=\ell _{f}/H$
, adopted from Benavides & Alexakis (Reference Benavides and Alexakis2017, figures 1, 2 and 8). The ideal limits of 3D and 2D correspond to
$Q=\ell _{f}/H$
, adopted from Benavides & Alexakis (Reference Benavides and Alexakis2017, figures 1, 2 and 8). The ideal limits of 3D and 2D correspond to
 $Q=0$
and
$Q=0$
and
 $Q=\infty$
respectively. The transition to diminished forward energy flux at the expense of growing inverse energy flux occurs at
$Q=\infty$
respectively. The transition to diminished forward energy flux at the expense of growing inverse energy flux occurs at
 $Q_{3D}\sim 3.6$
, whereas the transition to no forward energy flux occurs at an
$Q_{3D}\sim 3.6$
, whereas the transition to no forward energy flux occurs at an
 $Re$
-dependent value where
$Re$
-dependent value where
 $Q_{2D}\sim 1.2Re^{1/2}$
. In between, energy flows in a bidirectional cascade where there is no inertial regime for either forward or inverse flux.
$Q_{2D}\sim 1.2Re^{1/2}$
. In between, energy flows in a bidirectional cascade where there is no inertial regime for either forward or inverse flux.
As $Q$
is varied, the forward energy flux characteristic of 3D turbulence and the 2D inverse energy flux behave in unexpected ways, namely they exhibit sharp transitions at specific values of
$Q$
is varied, the forward energy flux characteristic of 3D turbulence and the 2D inverse energy flux behave in unexpected ways, namely they exhibit sharp transitions at specific values of
 $Q$
. This behaviour is common in bifurcations in low-dimensional dynamical systems and in transitions from laminar to turbulent flow, but sharp transitions in turbulent flows are unusual. Benavides and Alexakis show that there is net inverse energy transfer that increases from zero at a well-defined value
$Q$
. This behaviour is common in bifurcations in low-dimensional dynamical systems and in transitions from laminar to turbulent flow, but sharp transitions in turbulent flows are unusual. Benavides and Alexakis show that there is net inverse energy transfer that increases from zero at a well-defined value
 $Q_{3D}\sim 3.6$
; see figure 3. At higher
$Q_{3D}\sim 3.6$
; see figure 3. At higher
 $Q$
, the 3D energy flux goes to zero sharply at a critical value of
$Q$
, the 3D energy flux goes to zero sharply at a critical value of
 $Q_{2D}$
that depends on the Reynolds number
$Q_{2D}$
that depends on the Reynolds number
 $Re$
of the flow. The empirically observed
$Re$
of the flow. The empirically observed
 $Re^{1/2}$
dependence of
$Re^{1/2}$
dependence of
 $Q_{2D}$
is consistent with scaling arguments by Benavides & Alexakis (Reference Benavides and Alexakis2017) and with a linear stability analysis of 2D flows with respect to 3D perturbations (Gallet & Doering Reference Gallet and Doering2015). Finally, Benavides & Alexakis (Reference Benavides and Alexakis2017) argue that the critical points should persist, as additional vertical modes are included in a fully resolved 3D numerical computation.
$Q_{2D}$
is consistent with scaling arguments by Benavides & Alexakis (Reference Benavides and Alexakis2017) and with a linear stability analysis of 2D flows with respect to 3D perturbations (Gallet & Doering Reference Gallet and Doering2015). Finally, Benavides & Alexakis (Reference Benavides and Alexakis2017) argue that the critical points should persist, as additional vertical modes are included in a fully resolved 3D numerical computation.
3 Future
The exciting results of Benavides & Alexakis (Reference Benavides and Alexakis2017) regarding the existence of sharp critical points in the crossover from 3D to 2D turbulent flows raise a number of questions that will be important in understanding how these results relate to large high- $Re$
turbulent flows in geophysical/astrophysical flows. In particular, the following questions arise. (i) To what degree are the transitions ‘sharp’ as resolution in
$Re$
turbulent flows in geophysical/astrophysical flows. In particular, the following questions arise. (i) To what degree are the transitions ‘sharp’ as resolution in
 $Q$
is increased? Even bifurcations in extremely well-controlled low-dimensional dynamical systems show some rounding due to experimental imperfections. Could the apparent
$Q$
is increased? Even bifurcations in extremely well-controlled low-dimensional dynamical systems show some rounding due to experimental imperfections. Could the apparent
 $(Q_{2D}-Q)^{2}$
dependence near the second critical point be instead rounding due to noise? (ii) What is the nature of the bidirectional cascades in which both forward and inverse energy transfer compete and the forward enstrophy cascade emerges? Can these cascades be inertial for sufficient scale separation between the critical points? (iii) Would a more realistic 3D model of thin layer flows preserve the nature of the critical points, as argued by Benavides & Alexakis (Reference Benavides and Alexakis2017), or would more degrees of freedom broaden the transitions (see also the question of sharpness above). The results of Benavides & Alexakis (Reference Benavides and Alexakis2017) raise numerous exciting questions as scientists attempt to extend idealized fluid experiments in the laboratory or in direct numerical simulations to real physical systems in nature such as the atmosphere and the ocean. The future continues to hold a wide range of challenges in understanding the roles of forcing scale, layer thickness, Reynolds number and body-force constraints such as magnetic field or rotation, to name just a few.
$(Q_{2D}-Q)^{2}$
dependence near the second critical point be instead rounding due to noise? (ii) What is the nature of the bidirectional cascades in which both forward and inverse energy transfer compete and the forward enstrophy cascade emerges? Can these cascades be inertial for sufficient scale separation between the critical points? (iii) Would a more realistic 3D model of thin layer flows preserve the nature of the critical points, as argued by Benavides & Alexakis (Reference Benavides and Alexakis2017), or would more degrees of freedom broaden the transitions (see also the question of sharpness above). The results of Benavides & Alexakis (Reference Benavides and Alexakis2017) raise numerous exciting questions as scientists attempt to extend idealized fluid experiments in the laboratory or in direct numerical simulations to real physical systems in nature such as the atmosphere and the ocean. The future continues to hold a wide range of challenges in understanding the roles of forcing scale, layer thickness, Reynolds number and body-force constraints such as magnetic field or rotation, to name just a few.