No CrossRef data available.
Published online by Cambridge University Press: 13 March 2015
We study the computable structure theory of linear orders of size 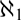 $\aleph _1 $ within the framework of admissible computability theory. In particular, we characterize which of these linear orders are computably categorical.
$\aleph _1 $ within the framework of admissible computability theory. In particular, we characterize which of these linear orders are computably categorical.