We construct a mean-field model that describes the nonlinear dynamics of a spin-polarized electron gas interacting with fixed, positively charged ions possessing a magnetic moment that evolves in time. The mobile electrons are modelled by a four-component distribution function in the two-dimensional phase space $(x,v)$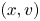 , obeying a Vlasov–Poisson set of equations. The ions are modelled by a Landau–Lifshitz equation for their spin density, which contains ion–ion and electron–ion magnetic exchange terms. We perform a linear response study of the coupled Vlasov–Poisson–Landau–Lifshitz (VPLL) equations for the case of a Maxwell–Boltzmann equilibrium, focussing in particular on the spin dispersion relation. Conditions of stability or instability for the spin modes are identified, which depend essentially on the electron spin polarization rate $\eta$
, obeying a Vlasov–Poisson set of equations. The ions are modelled by a Landau–Lifshitz equation for their spin density, which contains ion–ion and electron–ion magnetic exchange terms. We perform a linear response study of the coupled Vlasov–Poisson–Landau–Lifshitz (VPLL) equations for the case of a Maxwell–Boltzmann equilibrium, focussing in particular on the spin dispersion relation. Conditions of stability or instability for the spin modes are identified, which depend essentially on the electron spin polarization rate $\eta$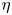 and the electron–ion magnetic coupling constant $K$
and the electron–ion magnetic coupling constant $K$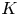 . We also develop an Eulerian grid-based computational code for the fully nonlinear VPLL equations, based on the geometric Hamiltonian method first developed by Crouseilles et al. (J. Plasma Phys., vol. 89, no. 2, 2023, p. 905890215). This technique allows us to achieve great accuracy for the conserved quantities, such as the modulus of the ion spin vector and the total energy. Numerical tests in the linear regime are in accordance with the estimations of the linear response theory. For two-stream equilibria, we study the interplay of instabilities occurring in both the charge and the spin sectors. The set of parameters used in the simulations, with densities close to those of solids (${\approx }10^{29}\ {\rm m}^{-3}$
. We also develop an Eulerian grid-based computational code for the fully nonlinear VPLL equations, based on the geometric Hamiltonian method first developed by Crouseilles et al. (J. Plasma Phys., vol. 89, no. 2, 2023, p. 905890215). This technique allows us to achieve great accuracy for the conserved quantities, such as the modulus of the ion spin vector and the total energy. Numerical tests in the linear regime are in accordance with the estimations of the linear response theory. For two-stream equilibria, we study the interplay of instabilities occurring in both the charge and the spin sectors. The set of parameters used in the simulations, with densities close to those of solids (${\approx }10^{29}\ {\rm m}^{-3}$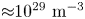 ) and temperatures of the order of 10 eV, may be relevant to the warm dense matter regime appearing in some inertial fusion experiments.
) and temperatures of the order of 10 eV, may be relevant to the warm dense matter regime appearing in some inertial fusion experiments.