Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T21:14:59.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex ring formation coupled with a translating bluff body

Published online by Cambridge University Press:  18 September 2020

Minho Song ,
Hyeonseong Kim  and
Daegyoum Kim Open the ORCID record for Daegyoum Kim [Opens in a new window]
Minho Song
Affiliation:
Department of Mechanical Engineering, KAIST, Daejeon34141, Republic of Korea
Hyeonseong Kim
Affiliation:
Department of Mechanical Engineering, KAIST, Daejeon34141, Republic of Korea
Daegyoum Kim*
Affiliation:
Department of Mechanical Engineering, KAIST, Daejeon34141, Republic of Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

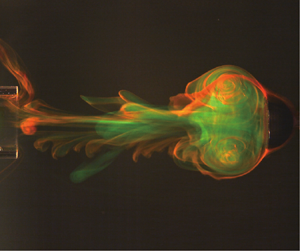
Motivated by the explosive launch of Sphagnum spores, this experimental study investigates how the vortices generated from two different sources, a piston–cylinder apparatus and a translating bluff body, interact with each other. While there have been numerous studies on the formation of a single vortex ring or multiple vortex rings, little is known about the effect of a translating bluff body on the formation of the coupled vortices. By varying the stroke ratio of the piston and the velocity ratio of the body to the piston, three distinct modes are identified for the mutual interaction between the starting jet from the piston and the wake from the cap: spill mode, attached mode and detached mode. The transitions between the vortex modes are predicted with simple analytical models. For the attached mode that appears at a velocity ratio intermediate between those of the spill mode and the detached mode, the merged flow structure becomes similar to a single vortex ring in the absence of the bluff body. By virtue of stable propagation following the cap, the vortex of the attached mode is capable of transporting a significant fluid volume initially inside the cylinder over a long distance, which shows its effectiveness in transport using a ballistic mechanism.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 903 , 25 November 2020 , A8
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arakeri, J. H., Das, D., Krothapalli, A. & Lourenco, L. 2004 Vortex ring formation at the open end of a shock tube: a particle image velocimetry study. Phys. Fluids 16, 1008–1019.CrossRefGoogle Scholar
Bouremel, Y. & Ducci, A. 2017 Scalar mixing and strain dynamics methodologies for PIV/LIF measurements of vortex ring flows. Phys. Fluids 29, 013602.CrossRefGoogle Scholar
Cheng, M., Lou, J. & Lim, T. T. 2015 Leapfrogging of multiple coaxial viscous vortex rings. Phys. Fluids 27, 031702.CrossRefGoogle Scholar
Chu, C., Wang, C. & Chang, C. 1995 A vortex ring impinging on a solid plane surface – vortex structure and surface force. Phys. Fluids 7, 1391–1401.CrossRefGoogle Scholar
Dabiri, J. O. 2005 On the estimation of swimming and flying forces from wake measurements. J. Expl Biol. 208, 3519–3532.CrossRefGoogle ScholarPubMed
Dabiri, J. O., Colin, S. P., Katija, K. & Costello, J. H. 2010 A wake-based correlate of swimming performance and foraging behavior in seven co-occuring jellyfish species. J. Expl Biol. 213, 1217–1225.CrossRefGoogle Scholar
Dabiri, J. O. & Gharib, M. 2004 Fluid entrainment by isolated vortex rings. J. Fluid Mech. 511, 311–331.CrossRefGoogle Scholar
Dabiri, J. O. & Gharib, M. 2005 a The role of optimal vortex formation in biologcal fluid transport. Proc. R. Soc. B 272, 1557–1560.CrossRefGoogle Scholar
Dabiri, J. O. & Gharib, M. 2005 b Starting flow through nozzles with temporally variable exit diameter. J. Fluid Mech. 538, 111–136.CrossRefGoogle Scholar
Das, D., Bansal, M. & Manghnani, A. 2017 Generation and characteristics of vortex rings free of piston vortex and stopping vortex effects. J. Fluid Mech. 811, 138–167.CrossRefGoogle Scholar
Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. Z. Angew. Math. Phys. 30, 101–116.CrossRefGoogle Scholar
Dora, C. L., Saravanan, D., Karunakar, K. & Das, D. 2011 Characteristics of embedded-shock-free compressible vortex rings: a detailed study using PIV. Adv. Mech. Engng 3, 650871.CrossRefGoogle Scholar
Fernando, J. N., Marzanek, M., Bond, C. & Rival, D. E. 2017 On the separation mechanics of accelerating spheres. Phys. Fluids 29, 037102.CrossRefGoogle Scholar
Fernando, J. N. & Rival, D. E. 2016 On vortex evolution in the wake of axisymmetric and non-axisymmetric low-aspect-ratio accelerating plates. Phys. Fluids 28, 017102.CrossRefGoogle Scholar
Fraenkel, L. E. 1972 Examples of steady vortex rings of small cross-section in an ideal fluid. J. Fluid Mech. 51, 119–135.CrossRefGoogle Scholar
Gao, L. & Yu, S. C. M. 2010 A model for the pinch-off process of the leading vortex ring in a starting jet. J. Fluid Mech. 656, 205–222.CrossRefGoogle Scholar
Gao, L., Yu, S. C. M., Ai, J. J. & Law, A. W. K. 2008 Circulation and energy of the leading vortex ring in a gravity-driven starting jet. Phys. Fluids 20, 093604.CrossRefGoogle Scholar
Gharib, M., Rambod, E., Kheradvar, A., Sahn, D. J. & Dabiri, J. O. 2006 Optimal vortex formation as an index of cardiac health. Proc. Natl Acad. Sci. 103, 6305–6308.CrossRefGoogle ScholarPubMed
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Green, S. I. 1995 Fluid Vortices. Springer.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Lim, T. T. 1997 A note on the leapfrogging between two coaxial vortex rings at low Reynolds numbers. Phys. Fluids 9, 239–241.CrossRefGoogle Scholar
Maxworthy, T. 1972 The structure and stability of vortex rings. J. Fluid Mech. 51, 15–32.CrossRefGoogle Scholar
Mohseni, K. & Gharib, M. 1998 A model for universal time scale of vortex ring formation. Phys. Fluids 10, 2436.CrossRefGoogle Scholar
New, T. H. & Long, J. 2015 Dynamics of laminar circular jet impingement upon convex cylinders. Phys. Fluids 27, 024109.CrossRefGoogle Scholar
Olcay, A. B. & Krueger, P. S. 2008 Measurement of ambient fluid entrainment during laminar vortex ring formation. Exp. Fluids 44, 235–247.CrossRefGoogle Scholar
Orlandi, P. & Verzicco, R. 1993 Vortex rings impinging on walls: axisymmetric and three-dimensional simulations. J. Fluid Mech. 256, 615–646.CrossRefGoogle Scholar
Oshima, Y., Noguchi, T. & Oshima, K. 1986 Numerical study of interaction of two vortex rings. Fluid Dyn. Res. 1, 215–227.CrossRefGoogle Scholar
Qin, S., Liu, H. & Xiang, Y. 2018 On the formation modes in vortex interaction for multiple co-axial co-rotating vortex rings. Phys. Fluids 30, 011901.CrossRefGoogle Scholar
Riley, N. & Stevens, D. P. 1993 A note on leapfrogging vortex rings. Fluid Dyn. Res. 11, 235–244.CrossRefGoogle Scholar
Rosenfeld, M., Rambod, E. & Gharib, M. 1998 Circulation and formation number of laminar vortex rings. J. Fluid Mech. 376, 297–318.CrossRefGoogle Scholar
Saffman, P. G. 1970 The velocity of viscous vortex rings. Stud. Appl. Maths 49, 371–380.CrossRefGoogle Scholar
Saffman, P. G. 1993 Vortex Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Satti, J. & Peng, J. 2013 Leapfrogging of two thick-cored vortex rings. Fluid Dyn. Res. 45, 035503.CrossRefGoogle Scholar
Shadden, S. C., Dabiri, J. O. & Marsden, J. E. 2006 Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18, 047105.CrossRefGoogle Scholar
Shadden, S. C., Katija, K., Rosenfeld, M., Marsden, J. E. & Dabiri, J. O. 2007 Transport and stirring induced by vortex formation. J. Fluid Mech. 593, 315–331.CrossRefGoogle Scholar
Shusser, M. & Gharib, M. 2000 Energy and velocity of a forming vortex ring. Phys. Fluids 12, 618.CrossRefGoogle Scholar
Shusser, M., Rosenfeld, M., Dabiri, J. O. & Gharib, M. 2006 Energy of time-dependent piston velocity program on vortex ring formation in a piston/cylinder arrangement. Phys. Fluids 18, 033601.CrossRefGoogle Scholar
Sullivan, I. S., Niemela, J. J., Hershberger, R. E., Bolster, D. & Donnelly, R. J. 2008 Dynamics of thin vortex rings. J. Fluid Mech. 609, 319–347.CrossRefGoogle Scholar
Sundberg, S. 2005 Larger capsules enhance short-range spore dispersal in sphagnum, nut what happens further away? Oikos 108, 115–124.CrossRefGoogle Scholar
Sundberg, S. 2010 Size matters for violent discharge height and settling spped of sphagnum spores: important attributes for dispersal potential. Ann. Bot. 105, 291–300.CrossRefGoogle Scholar
Whitaker, D. L. & Edwards, J. 2010 Sphagnum moss disperses spores with vortex rings. Science 329, 406.CrossRefGoogle ScholarPubMed
Wilke, C. R. & Chang, P. 1955 Correlation of diffusion coefficients in dilute solutions. AIChE J. 1, 264–270.CrossRefGoogle Scholar
Willert, C. E. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10, 181–193.CrossRefGoogle Scholar
Xia, X. & Mohseni, K. 2017 Unsteady aerodynamics and vortex-sheet formation of a two-dimensional airfoil. J. Fluid Mech. 830, 439–478.CrossRefGoogle Scholar

Song et al. supplementary movie 1

Movie 1 for Figure 2

Download Song et al. supplementary movie 1(Video)
Video 1.9 MB

Song et al. supplementary movie 2

Movie 2 for Figure 3

Download Song et al. supplementary movie 2(Video)
Video 3 MB

Song et al. supplementary movie 3

Movie 3 for Figure 4

Download Song et al. supplementary movie 3(Video)
Video 2.6 MB

Song et al. supplementary movie 4

Movie 4 for Figures 6(a,d)

Download Song et al. supplementary movie 4(Video)
Video 10.1 MB