1. Introduction
The structural organisation of wall-bounded turbulent flows has been a topic of great interest for the past several decades and significant development has been achieved during this time. The regions from the wall up to the free stream are shown to be populated with a range of coherent structures. Near the wall, the main building elements are low-speed streamwise streaks in the viscous sublayer, first identified by Kline et al. (Reference Kline, Reynolds, Schraub and Runstadler1967), with a spanwise spacing of 100 wall units (![]() $\nu /u_{\tau }$, where
$\nu /u_{\tau }$, where ![]() $\nu$ is the fluid's kinematic viscosity and
$\nu$ is the fluid's kinematic viscosity and ![]() $u_{\tau }$ the friction velocity), while further away from the wall, hairpin vortices of various scales are prominent, a structural element originally hypothesised by Theodorsen (Reference Theodorsen1952) and later observed experimentally (Offen & Kline Reference Offen and Kline1975; Head & Bandyopadhyay Reference Head and Bandyopadhyay1981; Adrian, Meinhart & Tomkins Reference Adrian, Meinhart and Tomkins2000). More recently, very-large-scale motions (VLSMs) or superstructures (internal or external geometries, respectively) were identified in the logarithmic region, and large-scale motions (LSMs) in the outer region, linked to the formation of downstream-leaning ramp-like bulges at the boundary with the irrotational free stream (see Kim & Adrian Reference Kim and Adrian1999; Zhou et al. Reference Zhou, Adrian, Balachandar and Kendall1999; Guala, Hommema & Adrian Reference Guala, Hommema and Adrian2006; Balakumar & Adrian Reference Balakumar and Adrian2007; Hutchins & Marusic Reference Hutchins and Marusic2007; Monty et al. Reference Monty, Hutchins, Ng, Marusic and Chong2009, among others). Associated with these characteristic elements is another structural feature, observed initially by Meinhart & Adrian (Reference Meinhart and Adrian1995) in the outer region of turbulent boundary layers: the organisation of the streamwise velocity into large zones of uniform momentum (UMZs), separated by internal shear layers of concentrated vorticity.
$u_{\tau }$ the friction velocity), while further away from the wall, hairpin vortices of various scales are prominent, a structural element originally hypothesised by Theodorsen (Reference Theodorsen1952) and later observed experimentally (Offen & Kline Reference Offen and Kline1975; Head & Bandyopadhyay Reference Head and Bandyopadhyay1981; Adrian, Meinhart & Tomkins Reference Adrian, Meinhart and Tomkins2000). More recently, very-large-scale motions (VLSMs) or superstructures (internal or external geometries, respectively) were identified in the logarithmic region, and large-scale motions (LSMs) in the outer region, linked to the formation of downstream-leaning ramp-like bulges at the boundary with the irrotational free stream (see Kim & Adrian Reference Kim and Adrian1999; Zhou et al. Reference Zhou, Adrian, Balachandar and Kendall1999; Guala, Hommema & Adrian Reference Guala, Hommema and Adrian2006; Balakumar & Adrian Reference Balakumar and Adrian2007; Hutchins & Marusic Reference Hutchins and Marusic2007; Monty et al. Reference Monty, Hutchins, Ng, Marusic and Chong2009, among others). Associated with these characteristic elements is another structural feature, observed initially by Meinhart & Adrian (Reference Meinhart and Adrian1995) in the outer region of turbulent boundary layers: the organisation of the streamwise velocity into large zones of uniform momentum (UMZs), separated by internal shear layers of concentrated vorticity.
In the seminal work by Adrian et al. (Reference Adrian, Meinhart and Tomkins2000), the presence of UMZs in turbulent boundary layers was incorporated into the conceptual model of a hairpin packet: the backflow originating from consecutive hairpin vortices forming a packet is responsible for the long regions of low momentum, while the shear layers forming behind the hairpin heads demarcate the limits of these zones. Additionally, the probability density function (p.d.f.) of the streamwise velocity was shown to be a good indicator for the presence of UMZs: each region of almost uniform momentum is associated with a local maximum in the p.d.f. and a narrow distribution around it. Further analysis of the statistical characteristics of these zones for a range of Reynolds numbers was performed by de Silva, Hutchins & Marusic (Reference de Silva, Hutchins and Marusic2016) and of the shear layers demarcating them by Eisma et al. (Reference Eisma, Westerweel, Ooms and Elsinga2015) and de Silva et al. (Reference de Silva, Philip, Hutchins and Marusic2017), among others. Chen, Chung & Wan (Reference Chen, Chung and Wan2020) extended these observations in the case of turbulent pipe flow, while Morris et al. (Reference Morris, Stolpa, Slaboch and Klewicki2007) showed for the first time that this particular flow organisation is also present in atmospheric boundary layers at very high Reynolds number, ![]() $Re$, an observation later supported in much more extensive measurements by Heisel et al. (Reference Heisel, Dasari, Liu, Hong, Coletti and Guala2018). Time-resolved volumetric particle tracking velocimetry measurements from Bross, Fuchs & Kähler (Reference Bross, Fuchs and Kähler2019) indicated the presence of UMZs in adverse pressure gradient boundary layers, while the very high spatial resolution allowed identification of these zones already from the viscous sublayer near the wall, all the way up to the logarithmic region. On average 2–3 UMZs were detected below the log region, linked to near-wall streaks in the buffer layer and viscous sublayer. Including high- and low-speed superstructures in the log region and regions convecting with the mean, a model was proposed by the authors illustrating all possible combinations of UMZs depending on the sign of each of these features across
$Re$, an observation later supported in much more extensive measurements by Heisel et al. (Reference Heisel, Dasari, Liu, Hong, Coletti and Guala2018). Time-resolved volumetric particle tracking velocimetry measurements from Bross, Fuchs & Kähler (Reference Bross, Fuchs and Kähler2019) indicated the presence of UMZs in adverse pressure gradient boundary layers, while the very high spatial resolution allowed identification of these zones already from the viscous sublayer near the wall, all the way up to the logarithmic region. On average 2–3 UMZs were detected below the log region, linked to near-wall streaks in the buffer layer and viscous sublayer. Including high- and low-speed superstructures in the log region and regions convecting with the mean, a model was proposed by the authors illustrating all possible combinations of UMZs depending on the sign of each of these features across ![]() $y$ (Bross et al. Reference Bross, Fuchs and Kähler2019).
$y$ (Bross et al. Reference Bross, Fuchs and Kähler2019).
All the above studies are statistical in nature and UMZs are identified in independent snapshots as instantaneous entities. Laskari et al. (Reference Laskari, de Kat, Hearst and Ganapathisubramani2018) provided some insights into the temporal evolution of these structures, however, a link between time information and the statistical picture is still missing. The first goal of the present work is to highlight such connections, particularly between the time evolution of the number of zones, ![]() $N_{UMZ}$, and the resulting Gaussian distribution of
$N_{UMZ}$, and the resulting Gaussian distribution of ![]() $N_{UMZ}$, when a sufficient number of independent instantaneous realisations is available (see de Silva et al. Reference de Silva, Hutchins and Marusic2016).
$N_{UMZ}$, when a sufficient number of independent instantaneous realisations is available (see de Silva et al. Reference de Silva, Hutchins and Marusic2016).
Together with experimental work, modelling efforts have been able to highlight essential flow features that give rise to the development of UMZs, such that the experimentally observed statistical behaviour is reproduced, without the need for the full velocity fields but with minimal input information. Moreover, the use of well-defined building blocks allows for the investigation of specific velocity and vorticity structures that are linked to the presence and evolution of UMZs, without the additional layer of complexity that is added when the p.d.f. is computed, something that is not possible from experimental data alone. In this context, de Silva et al. (Reference de Silva, Hutchins and Marusic2016) employed the attached eddy model (Marusic & Perry Reference Marusic and Perry1995; Perry & Marusic Reference Perry and Marusic1995) to generate instantaneous velocity fields and showed that it can successfully capture many statistical characteristics of the UMZs. Bautista et al. (Reference Bautista, Ebadi, White, Chini and Klewicki2019) recently developed a model, where the concentrated vorticity in the shear layers separating the UMZs was modelled as vortical fissures, distributed in the inertial and subinertial domains (as defined from the analysis of the mean momentum equation) and adhering to self-similarity scaling arguments and the step-like behaviour of the instantaneous velocity profile. Ensembles of streamwise velocity profiles were subsequently constructed using random displacement of the fissures and were shown to approximately reproduce streamwise velocity statistics up to fourth-order moments. UMZs were also examined from the lens of travelling wave solutions in Saxton-Fox & McKeon (Reference Saxton-Fox and McKeon2017). The authors used a resolvent model of an LSM structure in the outer region of a turbulent boundary layer and were able to recreate many elements of UMZ behaviour.
A particular advantage of models based on travelling wave solutions, such as the resolvent model (McKeon & Sharma Reference McKeon and Sharma2010), in contrast to statistical ones (based on the mean momentum balance or attached eddies) is their inherent temporal continuity that allows them to capture the time evolution of important flow features; as such, they are particularly suitable for the current analysis. The second point of focus of this work is therefore to evaluate how well a simple travelling wave model, based on the resolvent framework and informed by experimental results, can reproduce the experimentally observed temporal evolution of the p.d.f. More importantly, by leveraging its low-order nature, the characteristics of the underlying velocity structures that lead to this behaviour can be identified. Finally, building upon that, a resolvent model of self-similar hierarchies with triadically consistent members is also used to evaluate to which extent the inherent geometric similarity and relative convection speed of the members in each hierarchy can reproduce the observed patterns.
2. Datasets
Throughout this paper, we use the coordinate system ![]() $x$,
$x$, ![]() $y$ and
$y$ and ![]() $z$ to denote the streamwise, wall-normal and spanwise directions, respectively and
$z$ to denote the streamwise, wall-normal and spanwise directions, respectively and ![]() $u$,
$u$, ![]() $v$,
$v$, ![]() $w$ to denote the corresponding velocity components. Lower case letters denote the fluctuating fields and overbars the time-averaged means, following a Reynolds decomposition of the flow:
$w$ to denote the corresponding velocity components. Lower case letters denote the fluctuating fields and overbars the time-averaged means, following a Reynolds decomposition of the flow: ![]() $U = \bar {U}+u$. Vectors are denoted with bold letters. Unless specified otherwise, all velocity components are in outer units, normalised using the free-stream velocity,
$U = \bar {U}+u$. Vectors are denoted with bold letters. Unless specified otherwise, all velocity components are in outer units, normalised using the free-stream velocity, ![]() $U_{\infty }$ (or centreline velocity
$U_{\infty }$ (or centreline velocity ![]() $U_{CL}$ for internal geometries).
$U_{CL}$ for internal geometries).
2.1. Experimental dataset
The experimental database used in the present work is time-resolved, planar particle image velocimetry (PIV) data of a turbulent boundary layer at a friction Reynolds number ![]() $Re_{\tau }=5300$ (Laskari et al. Reference Laskari, de Kat, Hearst and Ganapathisubramani2018), henceforth referred to as E1. The database includes
$Re_{\tau }=5300$ (Laskari et al. Reference Laskari, de Kat, Hearst and Ganapathisubramani2018), henceforth referred to as E1. The database includes ![]() $37$ time-resolved sets (acquisition frequency of
$37$ time-resolved sets (acquisition frequency of ![]() $800$ Hz) of
$800$ Hz) of ![]() $10\,944$ images in streamwise–wall-normal planes and a field of view (FOV) of approximately
$10\,944$ images in streamwise–wall-normal planes and a field of view (FOV) of approximately ![]() $0.5 \delta \times 1.8 \delta$ in
$0.5 \delta \times 1.8 \delta$ in ![]() $x$ and
$x$ and ![]() $y$, respectively. The nominal flow conditions can be found in table 1. The boundary layer thickness was computed based on the Jones integral (Jones, Marusic & Perry Reference Jones, Marusic and Perry2001) and the friction velocity was estimated using the Clauser chart method (Clauser Reference Clauser1954). Filtering in time (effective time step of
$y$, respectively. The nominal flow conditions can be found in table 1. The boundary layer thickness was computed based on the Jones integral (Jones, Marusic & Perry Reference Jones, Marusic and Perry2001) and the friction velocity was estimated using the Clauser chart method (Clauser Reference Clauser1954). Filtering in time (effective time step of ![]() $\textrm {d}t=0.027\delta /U_{\infty }$) and space (two-dimensional Gaussian filter with a
$\textrm {d}t=0.027\delta /U_{\infty }$) and space (two-dimensional Gaussian filter with a ![]() $3\times 3$ point kernel) was performed to minimise pixel-locking effects that can have an effect on UMZ detection (see Kwon et al. Reference Kwon, Philip, de Silva, Hutchins and Monty2014; de Silva et al. Reference de Silva, Hutchins and Marusic2016). More details on the experimental set-up can be found in Laskari et al. (Reference Laskari, de Kat, Hearst and Ganapathisubramani2018).
$3\times 3$ point kernel) was performed to minimise pixel-locking effects that can have an effect on UMZ detection (see Kwon et al. Reference Kwon, Philip, de Silva, Hutchins and Monty2014; de Silva et al. Reference de Silva, Hutchins and Marusic2016). More details on the experimental set-up can be found in Laskari et al. (Reference Laskari, de Kat, Hearst and Ganapathisubramani2018).
Table 1. E1. Nominal flow conditions.

2.2. Model datasets
Alongside experiments, three model datasets are used, based on the resolvent framework (McKeon & Sharma Reference McKeon and Sharma2010), with the focus solely on the streamwise velocity component. For two of them, a mean velocity profile from a channel flow at a ![]() $Re_{\tau }=15\,000$, constant in the wall-parallel directions, is used (turbulent viscosity model as described in Moarref et al. Reference Moarref, Sharma, Tropp and McKeon2013), while only velocity fluctuations within the logarithmic region are considered. For completeness, an additional model dataset with a mean velocity profile from a channel flow at
$Re_{\tau }=15\,000$, constant in the wall-parallel directions, is used (turbulent viscosity model as described in Moarref et al. Reference Moarref, Sharma, Tropp and McKeon2013), while only velocity fluctuations within the logarithmic region are considered. For completeness, an additional model dataset with a mean velocity profile from a channel flow at ![]() $Re_{\tau }=5300$ (equal to the one in E1) was also included. Although there are documented differences between internal (model datasets) and external (experimental dataset) geometries, particularly with respect to the largest energetic scales (Monty et al. Reference Monty, Hutchins, Ng, Marusic and Chong2009), the main structural elements that give rise to the experimental observations discussed here are common in all wall-bounded flows, especially with respect to UMZs: the methodology developed by Adrian et al. (Reference Adrian, Meinhart and Tomkins2000) for identifying these zones in boundary layers, was successfully applied by Kwon et al. (Reference Kwon, Philip, de Silva, Hutchins and Monty2014) in the case of a channel flow while Chen et al. (Reference Chen, Chung and Wan2020) showed very similar behaviours in a pipe flow. Additionally, the velocity fluctuations considered in the modelling databases are localised in the logarithmic region, further minimising such differences.
$Re_{\tau }=5300$ (equal to the one in E1) was also included. Although there are documented differences between internal (model datasets) and external (experimental dataset) geometries, particularly with respect to the largest energetic scales (Monty et al. Reference Monty, Hutchins, Ng, Marusic and Chong2009), the main structural elements that give rise to the experimental observations discussed here are common in all wall-bounded flows, especially with respect to UMZs: the methodology developed by Adrian et al. (Reference Adrian, Meinhart and Tomkins2000) for identifying these zones in boundary layers, was successfully applied by Kwon et al. (Reference Kwon, Philip, de Silva, Hutchins and Monty2014) in the case of a channel flow while Chen et al. (Reference Chen, Chung and Wan2020) showed very similar behaviours in a pipe flow. Additionally, the velocity fluctuations considered in the modelling databases are localised in the logarithmic region, further minimising such differences.
Our goal here is to identify links between velocity structures and patterns observed in the streamwise velocity p.d.f. and highlight the robustness of such analysis without optimising for the best agreement between model and experiments. As such, the focus on the logarithmic region also provides us with model databases consisting of fluctuations localised within a region where their location and geometry is well defined through self-similar relationships, instead of a random placing of space-filling structures throughout ![]() $y$. Self-similarity is then not a requirement as such for recovering the experimentally observed behaviour, but the underlying scaling relationships it provides allow us to remove one layer of empiricism from our modelling assumptions when datasets of increasing complexity are needed. Besides, the importance of the logarithmic region in the formation of UMZs has been extensively documented; although the wake region has also been known to be a contributor, the model datasets allowed us to determine that the particular temporal behaviour analysed here is unaffected by structures located higher than
$y$. Self-similarity is then not a requirement as such for recovering the experimentally observed behaviour, but the underlying scaling relationships it provides allow us to remove one layer of empiricism from our modelling assumptions when datasets of increasing complexity are needed. Besides, the importance of the logarithmic region in the formation of UMZs has been extensively documented; although the wake region has also been known to be a contributor, the model datasets allowed us to determine that the particular temporal behaviour analysed here is unaffected by structures located higher than ![]() $y/\delta >0.25$: due to the mean shear profile and intensity decrease with
$y/\delta >0.25$: due to the mean shear profile and intensity decrease with ![]() $y$, these fluctuations only add to the highest modal velocity peak. Finally, by focusing on the log region we are neglecting 2–3 UMZs that have been observed in the near-wall region (Bross et al. Reference Bross, Fuchs and Kähler2019). As will be discussed later, this has an effect on the modal velocity range and the overall complexity of the p.d.f., without, however, altering the main patterns observed experimentally; besides, resolution effects and difficulty in measuring in the wall vicinity are limiting effects for experimental datasets as well, when near-wall UMZs are concerned. Based on the above, the chosen, well-defined but localised velocity structuring proposed here can provide enough information to represent the key features observed, while minimising the number of assumptions.
$y$, these fluctuations only add to the highest modal velocity peak. Finally, by focusing on the log region we are neglecting 2–3 UMZs that have been observed in the near-wall region (Bross et al. Reference Bross, Fuchs and Kähler2019). As will be discussed later, this has an effect on the modal velocity range and the overall complexity of the p.d.f., without, however, altering the main patterns observed experimentally; besides, resolution effects and difficulty in measuring in the wall vicinity are limiting effects for experimental datasets as well, when near-wall UMZs are concerned. Based on the above, the chosen, well-defined but localised velocity structuring proposed here can provide enough information to represent the key features observed, while minimising the number of assumptions.
Regarding the choice of ![]() $Re$, a logarithmic increase in the average number of zones with increasing
$Re$, a logarithmic increase in the average number of zones with increasing ![]() $Re$ is expected (de Silva et al. Reference de Silva, Hutchins and Marusic2016). Since the fluctuations in the model datasets are centred in the log region, the high
$Re$ is expected (de Silva et al. Reference de Silva, Hutchins and Marusic2016). Since the fluctuations in the model datasets are centred in the log region, the high ![]() $Re$ datasets are chosen to provide a way of relatively balancing out the missing zones in the wake and near-wall region, in a statistical sense, as well as to highlight the robustness of the phenomena observed. The use of the lower
$Re$ datasets are chosen to provide a way of relatively balancing out the missing zones in the wake and near-wall region, in a statistical sense, as well as to highlight the robustness of the phenomena observed. The use of the lower ![]() $Re$ model dataset was to facilitate more direct comparisons with the experimental dataset, E1. We should, however, stress that the goal here is not a complete
$Re$ model dataset was to facilitate more direct comparisons with the experimental dataset, E1. We should, however, stress that the goal here is not a complete ![]() $Re$ dependence study, but rather showcasing the universality of the observed behaviour between datasets that differ both in geometry and
$Re$ dependence study, but rather showcasing the universality of the observed behaviour between datasets that differ both in geometry and ![]() $Re$.
$Re$.
In all model datasets, the fluctuating velocity field consists of downstream propagating travelling waves, periodic in ![]() $x$ and
$x$ and ![]() $z$, each characterised by a wall-normal profile
$z$, each characterised by a wall-normal profile ![]() $u_{\boldsymbol {k}}(y)$, where
$u_{\boldsymbol {k}}(y)$, where ![]() $\boldsymbol {k}$ is the wavenumber triplet,
$\boldsymbol {k}$ is the wavenumber triplet, ![]() $\boldsymbol {k}=(k_x,k_z,\omega )$ consisting of the streamwise, spanwise and temporal wavenumbers, respectively. In the resolvent framework for wall-bounded turbulence, the Navier–Stokes (NS) equations are treated as an input–output system. In that context,
$\boldsymbol {k}=(k_x,k_z,\omega )$ consisting of the streamwise, spanwise and temporal wavenumbers, respectively. In the resolvent framework for wall-bounded turbulence, the Navier–Stokes (NS) equations are treated as an input–output system. In that context, ![]() $u_{\boldsymbol {k}}(y)$ is the streamwise component of the output response
$u_{\boldsymbol {k}}(y)$ is the streamwise component of the output response ![]() $\boldsymbol {u}_{\boldsymbol {k}}$, from the excitation of the linear NS operator (the resolvent,
$\boldsymbol {u}_{\boldsymbol {k}}$, from the excitation of the linear NS operator (the resolvent, ![]() $\boldsymbol {\mathcal {H}}$) by the nonlinear term, which acts as an intrinsic input forcing. Performing a singular value decomposition, the resolvent operator can be written in terms of left and right singular functions and singular values, per wavenumber triplet
$\boldsymbol {\mathcal {H}}$) by the nonlinear term, which acts as an intrinsic input forcing. Performing a singular value decomposition, the resolvent operator can be written in terms of left and right singular functions and singular values, per wavenumber triplet
 \begin{equation} \mathcal{H}_{\boldsymbol{k}} = \sum_{j=1}^{\infty} \psi_{\boldsymbol{k},j}\sigma_{\boldsymbol{k},j}\phi_{\boldsymbol{k},j}^*. \end{equation}
\begin{equation} \mathcal{H}_{\boldsymbol{k}} = \sum_{j=1}^{\infty} \psi_{\boldsymbol{k},j}\sigma_{\boldsymbol{k},j}\phi_{\boldsymbol{k},j}^*. \end{equation}
The required velocity response mode ![]() $\boldsymbol {u}_{\boldsymbol {k}}$ can then be decomposed in terms of the singular functions and appropriate weighting functions (McKeon Reference McKeon2017)
$\boldsymbol {u}_{\boldsymbol {k}}$ can then be decomposed in terms of the singular functions and appropriate weighting functions (McKeon Reference McKeon2017)
 \begin{equation} \boldsymbol{u}_{\boldsymbol{k}} = \sum_{j=1}^{\infty} \sigma_{\boldsymbol{k},j}\psi_{\boldsymbol{k},j}\bar{\chi}_{\boldsymbol{k},j} = \sum_{j=1}^{\infty} \psi_{\boldsymbol{k},j}{\chi}_{\boldsymbol{k},j}. \end{equation}
\begin{equation} \boldsymbol{u}_{\boldsymbol{k}} = \sum_{j=1}^{\infty} \sigma_{\boldsymbol{k},j}\psi_{\boldsymbol{k},j}\bar{\chi}_{\boldsymbol{k},j} = \sum_{j=1}^{\infty} \psi_{\boldsymbol{k},j}{\chi}_{\boldsymbol{k},j}. \end{equation}
Key turbulent structures (specific wavenumber triplets) are captured with a rank-1 approximation (McKeon Reference McKeon2017) and in what follows only the first singular function will be considered and the singular value subscript ![]() $j$ will be dropped for clarity
$j$ will be dropped for clarity
2.2.1. Single response mode
For the first model dataset, referred to as N1M1, a single response mode is considered, localised around a critical layer ![]() $y_c$, where the phase speed of the mode matches the local mean velocity
$y_c$, where the phase speed of the mode matches the local mean velocity ![]() $c=\omega /k_x=\bar {U}(y_c)$. For simplicity and to allow for changes in phase variation across the critical layer, the wall-normal coherence of the mode,
$c=\omega /k_x=\bar {U}(y_c)$. For simplicity and to allow for changes in phase variation across the critical layer, the wall-normal coherence of the mode, ![]() $u_{\boldsymbol {k}}(y)$, is directly estimated using an analytical function for the mode amplitude and imposing a specified phase variation with increasing
$u_{\boldsymbol {k}}(y)$, is directly estimated using an analytical function for the mode amplitude and imposing a specified phase variation with increasing ![]() $y$. Dawson & McKeon (Reference Dawson and McKeon2019) used a wavepacket pseudoeigenmode analysis to approximate the form of the class of leading resolvent modes with footprints not concentrated close to the wall. We exploit the resulting formulation here, isolating the amplitude and phase functions separately. Thus we model the response mode amplitude,
$y$. Dawson & McKeon (Reference Dawson and McKeon2019) used a wavepacket pseudoeigenmode analysis to approximate the form of the class of leading resolvent modes with footprints not concentrated close to the wall. We exploit the resulting formulation here, isolating the amplitude and phase functions separately. Thus we model the response mode amplitude, ![]() $|u_{\boldsymbol {k}}(y)|$, using a Gaussian function given by
$|u_{\boldsymbol {k}}(y)|$, using a Gaussian function given by
where the wall-normal location ![]() $y_c =0.15\delta$, wall-normal extent
$y_c =0.15\delta$, wall-normal extent ![]() $L_y=0.04\delta$ and amplitude
$L_y=0.04\delta$ and amplitude ![]() $\alpha =0.05$, are chosen to best match the experimental results. In terms of the phase variation, real and imaginary parts of
$\alpha =0.05$, are chosen to best match the experimental results. In terms of the phase variation, real and imaginary parts of ![]() $u_{\boldsymbol {k}}(y)$ are tuned such that
$u_{\boldsymbol {k}}(y)$ are tuned such that ![]() $\Delta [\arg ({u_k})] \to -{\rm \pi}$, as
$\Delta [\arg ({u_k})] \to -{\rm \pi}$, as ![]() $y$ increases from the wall (see figure 2e), a phase variation (mode inclination to the downstream direction) observed for wall-parallel modes and consistent with the presence of a viscous critical layer (McKeon & Sharma Reference McKeon and Sharma2010). The effect of both the prescribed phase variation across the critical layer and the mode's maximum amplitude on the resulting temporal patterns of the p.d.f. of
$y$ increases from the wall (see figure 2e), a phase variation (mode inclination to the downstream direction) observed for wall-parallel modes and consistent with the presence of a viscous critical layer (McKeon & Sharma Reference McKeon and Sharma2010). The effect of both the prescribed phase variation across the critical layer and the mode's maximum amplitude on the resulting temporal patterns of the p.d.f. of ![]() $U$, will be discussed in the next section.
$U$, will be discussed in the next section.
We select ![]() $\lambda _x = \lambda _z = h$, where
$\lambda _x = \lambda _z = h$, where ![]() $h$ is the channel half-height, for a streamwise or spanwise vortex representation (table 2 and figure 1a). The streamwise convection velocity (and thus the angular frequency) is prescribed by the chosen critical wall-normal location
$h$ is the channel half-height, for a streamwise or spanwise vortex representation (table 2 and figure 1a). The streamwise convection velocity (and thus the angular frequency) is prescribed by the chosen critical wall-normal location ![]() $y_c$ and the temporal evolution of the constructed response mode is given by
$y_c$ and the temporal evolution of the constructed response mode is given by
The present analysis is performed in streamwise–wall-normal planes to match the experimental dataset; the ![]() $x$–
$x$–![]() $y$ plane at
$y$ plane at ![]() $z=0$ is used for that purpose. For a fluctuating field consisting of a single mode, periodic in
$z=0$ is used for that purpose. For a fluctuating field consisting of a single mode, periodic in ![]() $x$ and
$x$ and ![]() $z$, the choice of the spanwise location will only have an impact on the resulting mode amplitude, the effect of which is discussed in the next section.
$z$, the choice of the spanwise location will only have an impact on the resulting mode amplitude, the effect of which is discussed in the next section.

Figure 1. Instantaneous velocity fields for N1M1 (a) and N2M6 (b).
Table 2. Dataset details. Both ![]() $c$ and
$c$ and ![]() $\max |\boldsymbol {u}_{\boldsymbol {k}}|$ are normalised with
$\max |\boldsymbol {u}_{\boldsymbol {k}}|$ are normalised with ![]() $U_{CL}$ and
$U_{CL}$ and ![]() $\textrm {d}t$ with
$\textrm {d}t$ with ![]() $U_{CL}/h$. For N2M5 and N2M6 only the outmost modes (
$U_{CL}/h$. For N2M5 and N2M6 only the outmost modes (![]() $m=1$) of each hierarchy are included; the rest are found through the appropriate geometric self-similarity arguments.
$m=1$) of each hierarchy are included; the rest are found through the appropriate geometric self-similarity arguments.

As was mentioned above, the use of a single travelling wave, with prescribed amplitude and phase variation across ![]() $y$, allows for the assessment of the effect of these velocity characteristics on the resulting p.d.f. patterns, something an experimental dataset cannot provide. However, the periodic nature of the solution does not allow for proper statistical analysis of the p.d.f. transitions or a significant variation in the number of UMZs in order to compare the trends observed in the experimental dataset. For this reason, two other model datasets of increased complexity are constructed, as outlined in the next paragraph.
$y$, allows for the assessment of the effect of these velocity characteristics on the resulting p.d.f. patterns, something an experimental dataset cannot provide. However, the periodic nature of the solution does not allow for proper statistical analysis of the p.d.f. transitions or a significant variation in the number of UMZs in order to compare the trends observed in the experimental dataset. For this reason, two other model datasets of increased complexity are constructed, as outlined in the next paragraph.
2.2.2. Self-similar hierarchies with triadically consistent members
The other two model datasets are based on a resolvent model consisting of three self-similar hierarchies (![]() $\mathcal {S}_1$,
$\mathcal {S}_1$, ![]() $\mathcal {S}_2$,
$\mathcal {S}_2$, ![]() $\mathcal {S}_3$) with triadically consistent members, henceforth referred to as N2M5 (
$\mathcal {S}_3$) with triadically consistent members, henceforth referred to as N2M5 (![]() $Re_{\tau }=5300$) and N2M6 (
$Re_{\tau }=5300$) and N2M6 (![]() $Re_{\tau }=15\,000$), which allow us to assess the effect of a multiscale input on the resulting temporal behaviour of the p.d.f. Each self-similar hierarchy contains five and six members respectively for each dataset, localised within the logarithmic region and obeys the constraints for geometric self-similarity of its members and self-similar behaviour of the resolvent as discussed by Moarref et al. (Reference Moarref, Sharma, Tropp and McKeon2013). The triadic consistency of the three hierarchies is not a required feature of the model, but is consonant with a self-sustaining resolvent model. The shortest member (
$Re_{\tau }=15\,000$), which allow us to assess the effect of a multiscale input on the resulting temporal behaviour of the p.d.f. Each self-similar hierarchy contains five and six members respectively for each dataset, localised within the logarithmic region and obeys the constraints for geometric self-similarity of its members and self-similar behaviour of the resolvent as discussed by Moarref et al. (Reference Moarref, Sharma, Tropp and McKeon2013). The triadic consistency of the three hierarchies is not a required feature of the model, but is consonant with a self-sustaining resolvent model. The shortest member (![]() $m=6$ for N2M6) of each hierarchy is centred at the start of the inertial region in the mean velocity profile,
$m=6$ for N2M6) of each hierarchy is centred at the start of the inertial region in the mean velocity profile, ![]() $y_{c,6}/h= 3/\sqrt {Re_{\tau }}=0.0245$ (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013), and defines the location of all other members in the hierarchy through:
$y_{c,6}/h= 3/\sqrt {Re_{\tau }}=0.0245$ (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013), and defines the location of all other members in the hierarchy through: ![]() $y_{c,m} = A^{6-m}y_{c,6}$ (see also McKeon Reference McKeon2019). For N2M5,
$y_{c,m} = A^{6-m}y_{c,6}$ (see also McKeon Reference McKeon2019). For N2M5, ![]() $y_{c,5}/h=0.0412$. In the present work the longest member in each hierarchy (
$y_{c,5}/h=0.0412$. In the present work the longest member in each hierarchy (![]() $m=1$) is constrained by
$m=1$) is constrained by ![]() $y_{c,1}/h \leq 0.4$, thus prescribing the total number of members in each hierarchy, while
$y_{c,1}/h \leq 0.4$, thus prescribing the total number of members in each hierarchy, while ![]() $A$ is chosen equal to the golden ratio,
$A$ is chosen equal to the golden ratio, ![]() $\phi =1.6$, leading to a slightly denser hierarchy than the more commonly used factor of 2 (see also Perry & Chong Reference Perry and Chong1982; McKeon Reference McKeon2019). The convection speed of each mode is dictated by its wall-normal location:
$\phi =1.6$, leading to a slightly denser hierarchy than the more commonly used factor of 2 (see also Perry & Chong Reference Perry and Chong1982; McKeon Reference McKeon2019). The convection speed of each mode is dictated by its wall-normal location: ![]() $c_m=\bar {U}(y_{c,m})$ and we further select the wavelength of the largest mode in
$c_m=\bar {U}(y_{c,m})$ and we further select the wavelength of the largest mode in ![]() $\mathcal {S}_3$ to be representative of an LSM, with
$\mathcal {S}_3$ to be representative of an LSM, with ![]() $k_{x1}=2$ for N2M6 and
$k_{x1}=2$ for N2M6 and ![]() $k_{x1}=1.8$ for N2M5. The corresponding spanwise wavenumber of the mode,
$k_{x1}=1.8$ for N2M5. The corresponding spanwise wavenumber of the mode, ![]() $k_{z1}$, is chosen such that, given the scaling relationships
$k_{z1}$, is chosen such that, given the scaling relationships ![]() $\lambda _z\sim y_c$ and
$\lambda _z\sim y_c$ and ![]() $\lambda _x\sim y_c^2$, the aspect ratio condition (
$\lambda _x\sim y_c^2$, the aspect ratio condition (![]() $\gamma = k_z/k_x \gg 1$) is satisfied all the way down to the mode closest to the wall (Moarref et al. Reference Moarref, Sharma, Tropp and McKeon2013). The wavenumbers of the outmost modes in hierarchies
$\gamma = k_z/k_x \gg 1$) is satisfied all the way down to the mode closest to the wall (Moarref et al. Reference Moarref, Sharma, Tropp and McKeon2013). The wavenumbers of the outmost modes in hierarchies ![]() $\mathcal {S}_1$ and
$\mathcal {S}_1$ and ![]() $\mathcal {S}_2$ are subsequently selected to be triadically consistent, while being non-integer multiples of each other (see table 2 and figure 1b). The temporal evolution for each hierarchy is given by
$\mathcal {S}_2$ are subsequently selected to be triadically consistent, while being non-integer multiples of each other (see table 2 and figure 1b). The temporal evolution for each hierarchy is given by
 \begin{align} u_s(x,y,z,t) = \mathrm{Re}\left[\sum_{m=1}^{6}u_{\boldsymbol{k}m}(y)(\exp({\textrm{i}(k_{xm}+k_{zm}-\omega_{m} t)})+\exp({\textrm{i}(k_{xm}-k_{zm}-\omega_{m} t)}))\right]. \end{align}
\begin{align} u_s(x,y,z,t) = \mathrm{Re}\left[\sum_{m=1}^{6}u_{\boldsymbol{k}m}(y)(\exp({\textrm{i}(k_{xm}+k_{zm}-\omega_{m} t)})+\exp({\textrm{i}(k_{xm}-k_{zm}-\omega_{m} t)}))\right]. \end{align}
Unlike the single mode dataset above, where the velocity profile, ![]() $u_{\boldsymbol {k}}(y)$, was estimated directly, here the projection weights
$u_{\boldsymbol {k}}(y)$, was estimated directly, here the projection weights ![]() ${\chi }_{\boldsymbol {k}m}$ (see (2.3)) have to be selected separately from the response modes
${\chi }_{\boldsymbol {k}m}$ (see (2.3)) have to be selected separately from the response modes ![]() ${\psi }_{\boldsymbol {k}m}$. They are chosen such that the resulting fluctuation intensity (
${\psi }_{\boldsymbol {k}m}$. They are chosen such that the resulting fluctuation intensity (![]() $u_{\boldsymbol {k}m}^2$) decreases logarithmically with
$u_{\boldsymbol {k}m}^2$) decreases logarithmically with ![]() $y$, with
$y$, with ![]() $\max |u_{\boldsymbol {k}6}|=0.16U_{CL}$ for the mode closest to the wall (table 2). The fluctuating velocity field is then constructed as a sum of all hierarchies
$\max |u_{\boldsymbol {k}6}|=0.16U_{CL}$ for the mode closest to the wall (table 2). The fluctuating velocity field is then constructed as a sum of all hierarchies
 \begin{equation} u(x,y,z,t) = \sum_{s=1}^{3}u_s(x,y,z,t). \end{equation}
\begin{equation} u(x,y,z,t) = \sum_{s=1}^{3}u_s(x,y,z,t). \end{equation}
The same as in N1M1, the plane ![]() $z=0$ is used for the analysis. Since the three hierarchies are selected such that neither their streamwise nor spanwise wavenumbers are multiple integers of each other, the choice of a different
$z=0$ is used for the analysis. Since the three hierarchies are selected such that neither their streamwise nor spanwise wavenumbers are multiple integers of each other, the choice of a different ![]() $z$ plane in these datasets leads to a different amplitude balance between the hierarchies (similar to the effect of a weighted sum in (2.7)). As such, the selection of the spanwise location dictates the largest scale present in the flow, depending on which hierarchy is the most prominent (see table 2), a topic that will be briefly revisited later on. In general, however, apart from slight changes in the quantification of transition rates, as discussed in the following section, for all different planes tested, the main conclusions presented here remained unaltered.
$z$ plane in these datasets leads to a different amplitude balance between the hierarchies (similar to the effect of a weighted sum in (2.7)). As such, the selection of the spanwise location dictates the largest scale present in the flow, depending on which hierarchy is the most prominent (see table 2), a topic that will be briefly revisited later on. In general, however, apart from slight changes in the quantification of transition rates, as discussed in the following section, for all different planes tested, the main conclusions presented here remained unaltered.
The superposition of three such hierarchies, whose members are triadically consistent but whose wavenumbers are not multiple integers of each other, offers a deviation from the strictly periodic behaviour observed in the single response mode model (N1M1) and increases significantly the complexity of the resulting temporal patterns.
3. Methodology
3.1. The p.d.f. construction
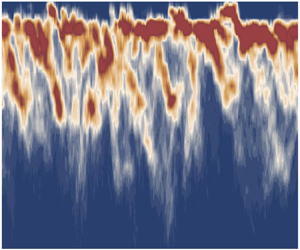
The central focus of the current work is the interpretation of the temporal evolution of the p.d.f. of streamwise velocity, P![]() $(U$). In order to address this, a two-step process is followed. Initially, spatial information from each snapshot is used to construct the corresponding instantaneous p.d.f. (see figures 2a–c and 2g–i). For time-resolved snapshots, a p.d.f. sequence in time can subsequently be plotted (figure 3) where the variation in the location of each peak creates temporal patterns in the contours of P
$(U$). In order to address this, a two-step process is followed. Initially, spatial information from each snapshot is used to construct the corresponding instantaneous p.d.f. (see figures 2a–c and 2g–i). For time-resolved snapshots, a p.d.f. sequence in time can subsequently be plotted (figure 3) where the variation in the location of each peak creates temporal patterns in the contours of P![]() $(U,t$). Details of this process are outlined below; the same approach is used for all datasets, with some minor differences which are highlighted.
$(U,t$). Details of this process are outlined below; the same approach is used for all datasets, with some minor differences which are highlighted.

Figure 2. Instantaneous velocity fields. Data from E1 (a–c), N1M1 (d–f ) and N2M6 (g–i). Panels (a,d,g) and (c,f ,i) show the full and fluctuating velocity fields, ![]() $U$ and
$U$ and ![]() $u$, respectively. Panels (b,h) show the corresponding p.d.f. while the amplitude and phase profile of the individual mode is shown in panel (e). The region of the fluctuating and full fields shown in colour denotes the streamwise extent used for the construction of the p.d.f.,
$u$, respectively. Panels (b,h) show the corresponding p.d.f. while the amplitude and phase profile of the individual mode is shown in panel (e). The region of the fluctuating and full fields shown in colour denotes the streamwise extent used for the construction of the p.d.f., ![]() $\mathcal {L}_x^+=1590$ for all datasets.
$\mathcal {L}_x^+=1590$ for all datasets.

Figure 3. Moving from space to time: each instantaneous p.d.f. is constructed using velocity vectors contained within a certain spatial extent (figure 2a). When plotted in a time sequence, the variation of each peak's location forms repeating temporal patterns in P![]() $(U,t$), which now contains both space and time information (figure 3).
$(U,t$), which now contains both space and time information (figure 3).
For each instantaneous velocity field, P![]() $(U$) includes all vectors located within specified limits in
$(U$) includes all vectors located within specified limits in ![]() $x$ and
$x$ and ![]() $y$. With respect to
$y$. With respect to ![]() $x$, we specify a streamwise limit scaled on viscous units (
$x$, we specify a streamwise limit scaled on viscous units (![]() $\mathcal {L}_x^+=1590$) such that there is consistency across the different
$\mathcal {L}_x^+=1590$) such that there is consistency across the different ![]() $Re$ datasets, following de Silva et al. (Reference de Silva, Hutchins and Marusic2016) (figure 2 and table 2). Sensitivity of the results for
$Re$ datasets, following de Silva et al. (Reference de Silva, Hutchins and Marusic2016) (figure 2 and table 2). Sensitivity of the results for ![]() $\mathcal {L}_x^+=1000\text {--}2500$ will be discussed in the section that follows. In the wall-normal direction, only vectors within the turbulent region are included. The turbulent/non-turbulent interface is identified using a kinetic energy threshold for dataset E1, as described in Chauhan et al. (Reference Chauhan, Philip, de Silva, Hutchins and Marusic2014). For the channel datasets N1M1, N2M5 and N2M6, the quiescent core is identified using the isocontour lines of
$\mathcal {L}_x^+=1000\text {--}2500$ will be discussed in the section that follows. In the wall-normal direction, only vectors within the turbulent region are included. The turbulent/non-turbulent interface is identified using a kinetic energy threshold for dataset E1, as described in Chauhan et al. (Reference Chauhan, Philip, de Silva, Hutchins and Marusic2014). For the channel datasets N1M1, N2M5 and N2M6, the quiescent core is identified using the isocontour lines of ![]() $U=0.95U_{CL}$, following Kwon et al. (Reference Kwon, Philip, de Silva, Hutchins and Monty2014). The velocity vectors contained within these limits are then distributed in 67 bins for
$U=0.95U_{CL}$, following Kwon et al. (Reference Kwon, Philip, de Silva, Hutchins and Monty2014). The velocity vectors contained within these limits are then distributed in 67 bins for ![]() $U/U_{\infty } \in [0,1]$ of size approximately
$U/U_{\infty } \in [0,1]$ of size approximately ![]() $0.4U_{\tau }$ for all datasets (see figure 2b,e,h). Local maxima of P
$0.4U_{\tau }$ for all datasets (see figure 2b,e,h). Local maxima of P![]() $(U$) indicate modal velocities representative of UMZs. More details on the peak detection parameters can be found in Laskari et al. (Reference Laskari, de Kat, Hearst and Ganapathisubramani2018) (it should also be noted here that, given a slight bias of the model datasets towards higher P
$(U$) indicate modal velocities representative of UMZs. More details on the peak detection parameters can be found in Laskari et al. (Reference Laskari, de Kat, Hearst and Ganapathisubramani2018) (it should also be noted here that, given a slight bias of the model datasets towards higher P![]() $(U$) values, the detection thresholds for the model datasets were proportionately adjusted). Apart from the spatial extent for the p.d.f. construction, a comment should also be made here regarding the spatial resolution of the datasets. In order to have an appropriate comparison with E1, both model datasets are interpolated onto an equidistant grid where the grid spacing in wall units is comparable to the experimental one (see table 2). Our choice is based on the fact that a finer resolution close to the wall, common in spectral models, would create a bias towards lower velocities in the p.d.f. when compared with equidistant PIV data, while a much finer resolution throughout would lead to a bias towards the free stream, given the wall-normal variation of the velocity profile.
$(U$) values, the detection thresholds for the model datasets were proportionately adjusted). Apart from the spatial extent for the p.d.f. construction, a comment should also be made here regarding the spatial resolution of the datasets. In order to have an appropriate comparison with E1, both model datasets are interpolated onto an equidistant grid where the grid spacing in wall units is comparable to the experimental one (see table 2). Our choice is based on the fact that a finer resolution close to the wall, common in spectral models, would create a bias towards lower velocities in the p.d.f. when compared with equidistant PIV data, while a much finer resolution throughout would lead to a bias towards the free stream, given the wall-normal variation of the velocity profile.
As was mentioned above, dataset E1 includes 37 temporal records, ![]() $100\delta /U_{\infty }$ long each, with a temporal resolution dictated by the acquisition frequency. For dataset N1M1, a single temporal record is constructed with a length of
$100\delta /U_{\infty }$ long each, with a temporal resolution dictated by the acquisition frequency. For dataset N1M1, a single temporal record is constructed with a length of ![]() $30\delta /U_{CL}$ and a resolution of
$30\delta /U_{CL}$ and a resolution of ![]() $\textrm {d}t=0.02\delta /U_{CL}$. The temporal resolution is chosen according to the experimental dataset E1, and such that the fast transitions towards higher modal peaks in the p.d.f. can be appropriately resolved. For the quantification of p.d.f. transitions in time, a single period would be enough due to the periodicity of the solution; however, we chose a larger record to provide better visual comparison with the experimental dataset. Finally, for datasets N2M5 and N2M6, temporal records distinct from one another can be constructed: for all three hierarchies each mode propagates downstream with a different convection velocity and the streamwise wavenumbers within each triad are non-integer multiples of each other. We construct 21 temporal records, each
$\textrm {d}t=0.02\delta /U_{CL}$. The temporal resolution is chosen according to the experimental dataset E1, and such that the fast transitions towards higher modal peaks in the p.d.f. can be appropriately resolved. For the quantification of p.d.f. transitions in time, a single period would be enough due to the periodicity of the solution; however, we chose a larger record to provide better visual comparison with the experimental dataset. Finally, for datasets N2M5 and N2M6, temporal records distinct from one another can be constructed: for all three hierarchies each mode propagates downstream with a different convection velocity and the streamwise wavenumbers within each triad are non-integer multiples of each other. We construct 21 temporal records, each ![]() $30\delta /U_{CL}$ long with a temporal resolution
$30\delta /U_{CL}$ long with a temporal resolution ![]() $\textrm {d}t=0.027\delta /U_{\infty }$. Four temporal records of P
$\textrm {d}t=0.027\delta /U_{\infty }$. Four temporal records of P![]() $(U,t$), one for each dataset, together with the parameters used for their construction can be found in figure 4 and table 2, respectively.
$(U,t$), one for each dataset, together with the parameters used for their construction can be found in figure 4 and table 2, respectively.

Figure 4. Variation of P![]() $(U,t$) in E1 (a), N1M1 (b), N2M5 (c) and N2M6 (d). Solid black lines denote
$(U,t$) in E1 (a), N1M1 (b), N2M5 (c) and N2M6 (d). Solid black lines denote ![]() $U^*(t)=U|P(U,t)>P_{th}$ with
$U^*(t)=U|P(U,t)>P_{th}$ with ![]() $P_{th}=0.1, 1$ and
$P_{th}=0.1, 1$ and ![]() $2.5$.
$2.5$.
3.2. Pattern identification
When plotted in time, P![]() $(U,t$) exhibits repeated transitions to lower velocities and faster jumps to higher velocities (figure 4). As expected, the experimental dataset leads to much more complex temporal patterns as a result of the different scales involved (figure 4a). A single mode at the outer edge of the logarithmic region (N1M1) leads to a purely periodic variation in P
$(U,t$) exhibits repeated transitions to lower velocities and faster jumps to higher velocities (figure 4). As expected, the experimental dataset leads to much more complex temporal patterns as a result of the different scales involved (figure 4a). A single mode at the outer edge of the logarithmic region (N1M1) leads to a purely periodic variation in P![]() $(U,t$), which, however, follows the main trends observed in the experimental dataset, indicating that even the simplest model can provide valuable insight into the skeleton of this spatio-temporal behaviour (figure 4b). When multiple velocity modes are included throughout the log region (N2M5 and N2M6), the emerging picture is no longer periodic and increases significantly in complexity (figure 4c,d). This highlights how the presence of a range of scales leads to a branching in the clean transitions from N1M1 (with the higher
$(U,t$), which, however, follows the main trends observed in the experimental dataset, indicating that even the simplest model can provide valuable insight into the skeleton of this spatio-temporal behaviour (figure 4b). When multiple velocity modes are included throughout the log region (N2M5 and N2M6), the emerging picture is no longer periodic and increases significantly in complexity (figure 4c,d). This highlights how the presence of a range of scales leads to a branching in the clean transitions from N1M1 (with the higher ![]() $Re$ dataset exhibiting even finer branching) something that, albeit not explicitly compared with the smaller variations in E1 in the present work, shows promise in reproducing the full-scale picture. The goal is to quantify these large-scale transitions, but most importantly identify their potential link to the underlying velocity structures and the change in the number of UMZs in the flow. To this end, we analyse the time history of
$Re$ dataset exhibiting even finer branching) something that, albeit not explicitly compared with the smaller variations in E1 in the present work, shows promise in reproducing the full-scale picture. The goal is to quantify these large-scale transitions, but most importantly identify their potential link to the underlying velocity structures and the change in the number of UMZs in the flow. To this end, we analyse the time history of ![]() $U^*$ defined as the minimum velocity for which the p.d.f. exceeds a certain threshold value:
$U^*$ defined as the minimum velocity for which the p.d.f. exceeds a certain threshold value: ![]() $U^*(t)= \min (U|P(U,t)>P_{th})$ (solid black lines in figure 4). As such,
$U^*(t)= \min (U|P(U,t)>P_{th})$ (solid black lines in figure 4). As such, ![]() $U^*$ traces the lowest velocities for which the p.d.f. exceeds
$U^*$ traces the lowest velocities for which the p.d.f. exceeds ![]() $P_{th}$ and essentially defines the range [
$P_{th}$ and essentially defines the range [![]() $U^*$,
$U^*$, ![]() $U_{\infty }$] within which the p.d.f. might exhibit peaks. For high
$U_{\infty }$] within which the p.d.f. might exhibit peaks. For high ![]() $U^*$ values it is then expected that the number of peaks will be small. When
$U^*$ values it is then expected that the number of peaks will be small. When ![]() $U^*$ values are low, the chances are higher that multiple peaks could exist within [
$U^*$ values are low, the chances are higher that multiple peaks could exist within [![]() $U^*$,
$U^*$, ![]() $U_{\infty }$] although not a priori true; given the Gaussian distribution of
$U_{\infty }$] although not a priori true; given the Gaussian distribution of ![]() $N_{UMZ}$, however, it should be expected (and will be discussed later) that
$N_{UMZ}$, however, it should be expected (and will be discussed later) that ![]() $N_{UMZ}$ will increase in these instances. A moving average (kernel size of
$N_{UMZ}$ will increase in these instances. A moving average (kernel size of ![]() $0.1\delta /U_{\infty }$) is used to filter out noisy transitions in the
$0.1\delta /U_{\infty }$) is used to filter out noisy transitions in the ![]() $U^*(t)$ signal and its effects on the qualitative trends discussed here are found to be minimal. Different threshold values can be used and the effect of varying
$U^*(t)$ signal and its effects on the qualitative trends discussed here are found to be minimal. Different threshold values can be used and the effect of varying ![]() $P_{th}$ will be discussed in the following sections. It should be noted here that an upper limit for this threshold is dictated by requiring
$P_{th}$ will be discussed in the following sections. It should be noted here that an upper limit for this threshold is dictated by requiring ![]() $U^*$ to be continuous in all snapshots, while a lower limit is imposed by requiring non-negligible correlation between the resulting time signals of
$U^*$ to be continuous in all snapshots, while a lower limit is imposed by requiring non-negligible correlation between the resulting time signals of ![]() $U^*$ across all threshold values. A more detailed discussion on the selection of these limits for both numerical and experimental datasets can be found in appendix A.
$U^*$ across all threshold values. A more detailed discussion on the selection of these limits for both numerical and experimental datasets can be found in appendix A.
Using the time evolution of ![]() $U^*$, we identify regions where the gradient
$U^*$, we identify regions where the gradient ![]() $\textrm {d}U^*/\textrm {d}t$ is continuously positive (negative) and exceeds a minimum value (
$\textrm {d}U^*/\textrm {d}t$ is continuously positive (negative) and exceeds a minimum value (![]() $|\textrm {d}U^*/\textrm {d}t|>0.1$) throughout each transition (figure 5a). The absolute rate of transitions is then defined as:
$|\textrm {d}U^*/\textrm {d}t|>0.1$) throughout each transition (figure 5a). The absolute rate of transitions is then defined as: ![]() $|\tan \phi |=|\overline {\delta U^*/\delta t}|$ (where
$|\tan \phi |=|\overline {\delta U^*/\delta t}|$ (where ![]() $\delta U^*$ and
$\delta U^*$ and ![]() $\delta t$ are estimated by linearly interpolating
$\delta t$ are estimated by linearly interpolating ![]() $U^*$ in each segment), while
$U^*$ in each segment), while ![]() $T$ denotes the total time elapsed between two pairs of opposite sign transitions (figure 5b). Transitions to higher velocities (
$T$ denotes the total time elapsed between two pairs of opposite sign transitions (figure 5b). Transitions to higher velocities (![]() $|\tan \phi |>0$) will be denoted with
$|\tan \phi |>0$) will be denoted with ![]() $\phi _+$ and those to lower (
$\phi _+$ and those to lower (![]() $|\tan \phi |<0$) with
$|\tan \phi |<0$) with ![]() $\phi _-$. For the remainder of the analysis we will focus on these transitions in
$\phi _-$. For the remainder of the analysis we will focus on these transitions in ![]() $U^*$ in order to characterise the temporal evolution of P
$U^*$ in order to characterise the temporal evolution of P![]() $(U,t$), so it is important to further clarify the connection between them. High
$(U,t$), so it is important to further clarify the connection between them. High ![]() $U^*$ values (see
$U^*$ values (see ![]() $U^*_{M1}$ in figure 5b) indicate a prominence of high-speed events in the instantaneous fields leading to p.d.f. peaks clustered around
$U^*_{M1}$ in figure 5b) indicate a prominence of high-speed events in the instantaneous fields leading to p.d.f. peaks clustered around ![]() $U_{\infty }$. Low
$U_{\infty }$. Low ![]() $U^*$ values (see
$U^*$ values (see ![]() $U^*_{M2}$ in figure 5b) on the other hand indicate that vectors with lower velocities are becoming more numerous, thus high values of the p.d.f. (including local peaks) appear at lower velocities. From figure 4 (and especially figure 4b) it is also clear that
$U^*_{M2}$ in figure 5b) on the other hand indicate that vectors with lower velocities are becoming more numerous, thus high values of the p.d.f. (including local peaks) appear at lower velocities. From figure 4 (and especially figure 4b) it is also clear that ![]() $\phi _-$ transitions in
$\phi _-$ transitions in ![]() $U^*$ mark a continuous migration of high P
$U^*$ mark a continuous migration of high P![]() $(U,t$) values (and therefore modal peaks) to lower velocities. The positive transitions in
$(U,t$) values (and therefore modal peaks) to lower velocities. The positive transitions in ![]() $U^*$, however, are faster and indicate a more abrupt jump from a peak at a low velocity to a peak close to
$U^*$, however, are faster and indicate a more abrupt jump from a peak at a low velocity to a peak close to ![]() $U_{\infty }$. In other words, a velocity
$U_{\infty }$. In other words, a velocity ![]() $U^*_{M2} < U^* < U^*_{M1}$ would correspond to a high P
$U^*_{M2} < U^* < U^*_{M1}$ would correspond to a high P![]() $(U,t$) value (and perhaps a modal peak) in the case of a
$(U,t$) value (and perhaps a modal peak) in the case of a ![]() $\phi _-$ transition, while the same velocity would be associated with a low P
$\phi _-$ transition, while the same velocity would be associated with a low P![]() $(U,t$) value in the case of a
$(U,t$) value in the case of a ![]() $\phi _+$ transition.
$\phi _+$ transition.

Figure 5. Transitions in P![]() $(U,t$) from E1. (a) Identified
$(U,t$) from E1. (a) Identified ![]() $\phi _+$ (light colours) and
$\phi _+$ (light colours) and ![]() $\phi _-$ (dark colours) transitions in
$\phi _-$ (dark colours) transitions in ![]() $U^*$ (
$U^*$ (![]() $P_{th}=2$), overlaid on top of the corresponding P
$P_{th}=2$), overlaid on top of the corresponding P![]() $(U,t$) contours (grey scale). (b) Definition of rate,
$(U,t$) contours (grey scale). (b) Definition of rate, ![]() $\tan \phi$, and period,
$\tan \phi$, and period, ![]() $T$, of transitions.
$T$, of transitions.
Finally, in order to link these transitions in ![]() $U^*$ with the variation in the number of UMZs and the underlying velocity structures, we conditionally average
$U^*$ with the variation in the number of UMZs and the underlying velocity structures, we conditionally average ![]() $N_{UMZ}$ and
$N_{UMZ}$ and ![]() $u$ on
$u$ on ![]() $\phi _+$ (
$\phi _+$ (![]() $\phi _-$) transitions, using the same velocity bins for
$\phi _-$) transitions, using the same velocity bins for ![]() $U^*$ as those used for the construction of the instantaneous p.d.f. Then the variation of both
$U^*$ as those used for the construction of the instantaneous p.d.f. Then the variation of both ![]() $N_{UMZ}|{\phi }$ and
$N_{UMZ}|{\phi }$ and ![]() $u|{\phi }$ across the different
$u|{\phi }$ across the different ![]() $U^*$ bins can be represented as a time dependence using
$U^*$ bins can be represented as a time dependence using ![]() $|\overline {\tan \phi }|=|\overline {\delta U^*/\delta t}|$.
$|\overline {\tan \phi }|=|\overline {\delta U^*/\delta t}|$.
4. Results
Following the procedure outlined above, the rates and periods of transitions in P![]() $(U,t$) are estimated for all datasets (see figure 6). The effect of both
$(U,t$) are estimated for all datasets (see figure 6). The effect of both ![]() $\mathcal {L}_x$ and
$\mathcal {L}_x$ and ![]() $P_{th}$ on these estimates – used for the construction of the p.d.f. and the estimation of
$P_{th}$ on these estimates – used for the construction of the p.d.f. and the estimation of ![]() $U^*$, respectively – is assessed using dataset E1.
$U^*$, respectively – is assessed using dataset E1.

Figure 6. Quantification of transitions in P![]() $(U,t$). Mean period between two pairs of transitions,
$(U,t$). Mean period between two pairs of transitions, ![]() $\bar {T}$ (a) and rate of transition
$\bar {T}$ (a) and rate of transition ![]() $|\overline {\tan \phi }|$ (b), for different
$|\overline {\tan \phi }|$ (b), for different ![]() $P_{th}$ and
$P_{th}$ and ![]() $\mathcal {L}_x$ values (
$\mathcal {L}_x$ values (![]() $\mathcal {L}_x^+=1060,1590,2120,2550$). Colours as in figure 5. Solid, dash, dot and dot-dash lines denote E1, N1M1, N2M5, N2M6, respectively. Appropriate parameter selection in the modelling datasets allows for sufficient agreement with experiments.
$\mathcal {L}_x^+=1060,1590,2120,2550$). Colours as in figure 5. Solid, dash, dot and dot-dash lines denote E1, N1M1, N2M5, N2M6, respectively. Appropriate parameter selection in the modelling datasets allows for sufficient agreement with experiments.
Results indicate that ![]() $\bar {T}\sim \delta /U_{\infty }$ and there is general agreement between all three datasets, with both N2M5 and N2M6 sets slightly under-predicting the average period (figure 6a). This value increases with increasing
$\bar {T}\sim \delta /U_{\infty }$ and there is general agreement between all three datasets, with both N2M5 and N2M6 sets slightly under-predicting the average period (figure 6a). This value increases with increasing ![]() $\mathcal {L}_x$. The streamwise extent
$\mathcal {L}_x$. The streamwise extent ![]() $\mathcal {L}_x$ has to be large enough to include a sufficient number of vectors for the p.d.f. to exhibit well-converged peaks, since UMZs have a non-negligible streamwise extent by definition, but also short enough to allow identification of the smallest zones, which would otherwise be averaged out. Therefore, lower values of
$\mathcal {L}_x$ has to be large enough to include a sufficient number of vectors for the p.d.f. to exhibit well-converged peaks, since UMZs have a non-negligible streamwise extent by definition, but also short enough to allow identification of the smallest zones, which would otherwise be averaged out. Therefore, lower values of ![]() $\mathcal {L}_x$ lead to slightly noisier
$\mathcal {L}_x$ lead to slightly noisier ![]() $U^*$ signals and a higher number of short-lived transitions, thus resulting in lower values for
$U^*$ signals and a higher number of short-lived transitions, thus resulting in lower values for ![]() $\bar {T}$. With respect to the threshold used for
$\bar {T}$. With respect to the threshold used for ![]() $U^*$, there is an increasing trend in
$U^*$, there is an increasing trend in ![]() $\bar {T}$ with increasing
$\bar {T}$ with increasing ![]() $P_{th}$ for
$P_{th}$ for ![]() $P_{th}<0.5$, while for higher threshold values tracing stronger p.d.f. peaks, the resulting period becomes almost independent of
$P_{th}<0.5$, while for higher threshold values tracing stronger p.d.f. peaks, the resulting period becomes almost independent of ![]() $P_{th}$. It should be noted that, although a proportionality with outer scaling parameters is observed here and outer scaling is chosen in what follows, informed by the large-scale nature of UMZs in general, that does not necessarily establish a conclusive argument on the relevant temporal scaling for log region structures, a topic which would require further analysis and/or datasets.
$P_{th}$. It should be noted that, although a proportionality with outer scaling parameters is observed here and outer scaling is chosen in what follows, informed by the large-scale nature of UMZs in general, that does not necessarily establish a conclusive argument on the relevant temporal scaling for log region structures, a topic which would require further analysis and/or datasets.
With respect to the rate of transitions, ![]() $|\overline {\tan \phi }|$, the first thing to note is that,
$|\overline {\tan \phi }|$, the first thing to note is that, ![]() $\phi _+$ transitions are shown to be relatively faster than
$\phi _+$ transitions are shown to be relatively faster than ![]() $\phi _-$ ones (i.e.
$\phi _-$ ones (i.e. ![]() $|\overline {\tan \phi }|$ is larger), especially in the simplest model dataset N1M1 (see figures 4b and 6b). For the experimental dataset E1, where multiple scales are present, this difference becomes more prominent for higher values of
$|\overline {\tan \phi }|$ is larger), especially in the simplest model dataset N1M1 (see figures 4b and 6b). For the experimental dataset E1, where multiple scales are present, this difference becomes more prominent for higher values of ![]() $P_{th}$ and therefore when tracking higher
$P_{th}$ and therefore when tracking higher ![]() $U^*$ values. Sharper transitions towards both higher and lower velocities are observed for an increase in
$U^*$ values. Sharper transitions towards both higher and lower velocities are observed for an increase in ![]() $\mathcal {L}_x$. This can be understood when considering the effect of using larger streamwise extents in the p.d.f. construction: short-lived transitions which act as small-scale variations superimposed on longer and more uniform transitions (a branching that can be seen in figure 4c as opposed to figure 4b) are filtered out. As such, the detected transitions are less noisy and their estimated rates increase. General agreement can be observed across datasets, especially between E1 and N2M5 and for lower
$\mathcal {L}_x$. This can be understood when considering the effect of using larger streamwise extents in the p.d.f. construction: short-lived transitions which act as small-scale variations superimposed on longer and more uniform transitions (a branching that can be seen in figure 4c as opposed to figure 4b) are filtered out. As such, the detected transitions are less noisy and their estimated rates increase. General agreement can be observed across datasets, especially between E1 and N2M5 and for lower ![]() $P_{th}$ values. Further fine tuning of the modelling parameters can provide improved agreement with experiments for both
$P_{th}$ values. Further fine tuning of the modelling parameters can provide improved agreement with experiments for both ![]() $T$ and
$T$ and ![]() $|\overline {\tan \phi }|$. This, however, is not the primary goal here; due to the various thresholds and modelling parameters used, we do not seek accurate quantification of these transitions. Rather, we want to showcase that experimentally informed modelling parameters and consistency in the process followed for the p.d.f. construction can generally provide temporal patterns that compare well with the experimental ones but most importantly are associated with the same underlying velocity structures.
$|\overline {\tan \phi }|$. This, however, is not the primary goal here; due to the various thresholds and modelling parameters used, we do not seek accurate quantification of these transitions. Rather, we want to showcase that experimentally informed modelling parameters and consistency in the process followed for the p.d.f. construction can generally provide temporal patterns that compare well with the experimental ones but most importantly are associated with the same underlying velocity structures.
The dataset E1 was selected for the assessment of the effect of both ![]() $P_{th}$ and
$P_{th}$ and ![]() $\mathcal {L}_x$ on the rate of transitions, since it contains all experimentally resolved scales, making it the optimal choice for such a parameter study. However, for the sensitivity of the results on velocity amplitude and phase variation, some manipulation of the scales present in the flow would be required that is not possible in either E1 or N2M5 and N2M6 (since the projection weights are chosen a priori, the relative amplitude of the modes could be tuned, however the phase variation across
$\mathcal {L}_x$ on the rate of transitions, since it contains all experimentally resolved scales, making it the optimal choice for such a parameter study. However, for the sensitivity of the results on velocity amplitude and phase variation, some manipulation of the scales present in the flow would be required that is not possible in either E1 or N2M5 and N2M6 (since the projection weights are chosen a priori, the relative amplitude of the modes could be tuned, however the phase variation across ![]() $y$ is prescribed). The dataset N1M1 in contrast is constructed such that these manipulations are possible. Increase of the maximum mode amplitude relative to the mean velocity value at the critical layer of the mode,
$y$ is prescribed). The dataset N1M1 in contrast is constructed such that these manipulations are possible. Increase of the maximum mode amplitude relative to the mean velocity value at the critical layer of the mode, ![]() $\max [|u_k|/\bar {U}_{y_c}]$, leads to an increase in the rate of both type of transitions in
$\max [|u_k|/\bar {U}_{y_c}]$, leads to an increase in the rate of both type of transitions in ![]() $U^*$ and is monotonic in the case of
$U^*$ and is monotonic in the case of ![]() $\phi _-$ transitions (figure 7a). Values of
$\phi _-$ transitions (figure 7a). Values of ![]() $\max [|u_k|/\bar {U}_{y_c}]>0.1$, lead to a drop in the rate of positive transitions, as the temporal pattern in P
$\max [|u_k|/\bar {U}_{y_c}]>0.1$, lead to a drop in the rate of positive transitions, as the temporal pattern in P![]() $(U,t$) starts to break down (rightmost panel in figure 7a).
$(U,t$) starts to break down (rightmost panel in figure 7a).

Figure 7. N1M1. Variation of ![]() $|\tan \phi |$ with the maximum amplitude at
$|\tan \phi |$ with the maximum amplitude at ![]() $y_c$,
$y_c$, ![]() $\max [|u_k|/\bar {U}_{y_c}]$ in (a,c) and the phase change,
$\max [|u_k|/\bar {U}_{y_c}]$ in (a,c) and the phase change, ![]() $\Delta [\arg ({u_k})]$ in (b,d). Contour plots at (a,b) show the evolution of P
$\Delta [\arg ({u_k})]$ in (b,d). Contour plots at (a,b) show the evolution of P![]() $(U,t$) for five representative cases, which are indicated with dashed black lines in (c,d). An increase in amplitude of a single velocity mode leads to an increase in the rate of transitions of either sign, while the phase jump across the critical layer of the mode influences uniquely the orientation of the patterns observed in the p.d.f.
$(U,t$) for five representative cases, which are indicated with dashed black lines in (c,d). An increase in amplitude of a single velocity mode leads to an increase in the rate of transitions of either sign, while the phase jump across the critical layer of the mode influences uniquely the orientation of the patterns observed in the p.d.f.
More interestingly, the trend of a slow ![]() $\phi _-$ transition followed by a faster jump to
$\phi _-$ transition followed by a faster jump to ![]() $U_{\infty }$, observed in both experiments and modelling results, is directly coupled with the phase change across
$U_{\infty }$, observed in both experiments and modelling results, is directly coupled with the phase change across ![]() $y_c$ moving from the wall up. As was mentioned above, wall-parallel modes are shown to have a phase variation across
$y_c$ moving from the wall up. As was mentioned above, wall-parallel modes are shown to have a phase variation across ![]() $y$,
$y$, ![]() $\Delta [\arg ({u_k})] \to -{\rm \pi}$, consistent with the presence of a viscous critical layer (McKeon & Sharma Reference McKeon and Sharma2010). This phase variation is equivalent to ramp-like velocity modes and is key to the temporal patterns observed in P
$\Delta [\arg ({u_k})] \to -{\rm \pi}$, consistent with the presence of a viscous critical layer (McKeon & Sharma Reference McKeon and Sharma2010). This phase variation is equivalent to ramp-like velocity modes and is key to the temporal patterns observed in P![]() $(U,t$). Results indicate that, for a constant phase across
$(U,t$). Results indicate that, for a constant phase across ![]() $y$ (
$y$ (![]() $\Delta [\arg ({u_k})]=0$, modes are vertical with respect to
$\Delta [\arg ({u_k})]=0$, modes are vertical with respect to ![]() $x$), the rates of transitions of either sign in the p.d.f. are equal but not as pronounced as in cases where the modes are inclined in either direction with respect to the horizontal (middle panel in figure 7b). On the contrary, if modes are inclined upstream,
$x$), the rates of transitions of either sign in the p.d.f. are equal but not as pronounced as in cases where the modes are inclined in either direction with respect to the horizontal (middle panel in figure 7b). On the contrary, if modes are inclined upstream, ![]() $\Delta [\arg ({u_k})]\to {\rm \pi}$, the p.d.f. exhibits a reversal in the temporal patterns from the experimentally observed ones: transitions in
$\Delta [\arg ({u_k})]\to {\rm \pi}$, the p.d.f. exhibits a reversal in the temporal patterns from the experimentally observed ones: transitions in ![]() $U^*$ towards higher velocities are now slower while those to lower velocities are faster. This means that, for an increase in the phase variation from
$U^*$ towards higher velocities are now slower while those to lower velocities are faster. This means that, for an increase in the phase variation from ![]() $-{\rm \pi}$ to
$-{\rm \pi}$ to ![]() ${\rm \pi}$,
${\rm \pi}$, ![]() $\phi _+$ transitions will initially be significantly faster than
$\phi _+$ transitions will initially be significantly faster than ![]() $\phi _-$, they will equalise for a zero phase jump and eventually become much slower. In order to analyse these observations further, knowledge of the underlying velocity structures associated with such transitions is required, prompting us to consider conditionally averaged velocity fields, which follows next. Generally though, large, ramp-like structures are well documented in wall turbulence, so it comes as no surprise that the experimentally and mathematically consistent phase variation would provide the desired temporal pattern; however, identifying which characteristics of P
$\phi _-$, they will equalise for a zero phase jump and eventually become much slower. In order to analyse these observations further, knowledge of the underlying velocity structures associated with such transitions is required, prompting us to consider conditionally averaged velocity fields, which follows next. Generally though, large, ramp-like structures are well documented in wall turbulence, so it comes as no surprise that the experimentally and mathematically consistent phase variation would provide the desired temporal pattern; however, identifying which characteristics of P![]() $(U,t$) are a direct consequence of this geometry, is not trivial.
$(U,t$) are a direct consequence of this geometry, is not trivial.
Fluctuating velocity fields are conditionally averaged on each type of transition in ![]() $U^*$. The streamwise extent of interest is
$U^*$. The streamwise extent of interest is ![]() $\mathcal {L}_x$, since only the vectors used for the p.d.f. construction are responsible for the patterns observed in P
$\mathcal {L}_x$, since only the vectors used for the p.d.f. construction are responsible for the patterns observed in P![]() $(U,t$). For a time continuous
$(U,t$). For a time continuous ![]() $\phi _-$ or
$\phi _-$ or ![]() $\phi _+$ transition in
$\phi _+$ transition in ![]() $U^*$ (symbols in left and right of figures 8, respectively), the corresponding
$U^*$ (symbols in left and right of figures 8, respectively), the corresponding ![]() $u$ fields are estimated (
$u$ fields are estimated (![]() $u|{\phi }$, contour plots in figure 8), together with the locations of the maximum absolute amplitude
$u|{\phi }$, contour plots in figure 8), together with the locations of the maximum absolute amplitude ![]() $y_c^*=\mathrm {argmax}|u|\phi |$ for increasing
$y_c^*=\mathrm {argmax}|u|\phi |$ for increasing ![]() $P_{th}$ (line plots in figures 8(a) and 8(c) – the dataset N1M1 is excluded from this analysis since the presence of a single mode dictates a constant
$P_{th}$ (line plots in figures 8(a) and 8(c) – the dataset N1M1 is excluded from this analysis since the presence of a single mode dictates a constant ![]() $y_c^*=y_c$). As was mentioned above, the average transition rates for each dataset,
$y_c^*=y_c$). As was mentioned above, the average transition rates for each dataset, ![]() $|\overline {\tan \phi }|=|\overline {\delta U^*/\delta t}|$ are used to translate the transitions in
$|\overline {\tan \phi }|=|\overline {\delta U^*/\delta t}|$ are used to translate the transitions in ![]() $U^*$ into temporal ones.
$U^*$ into temporal ones.

Figure 8. Conditionally averaged streamwise velocity fluctuations for each type of transition, ![]() $u|\phi _+$ (left) and
$u|\phi _+$ (left) and ![]() $u|\phi _-$ (right), from E1 (a), N1M1 (b), N2M5 (c) and N2M6 (d).
$u|\phi _-$ (right), from E1 (a), N1M1 (b), N2M5 (c) and N2M6 (d). ![]() $P_{th}=(1,3,3,3)$ for (a), (b), (c) and (d), respectively. Top panels indicate the variation of
$P_{th}=(1,3,3,3)$ for (a), (b), (c) and (d), respectively. Top panels indicate the variation of ![]() $U^*$ during each transition. Dashed lines in (a) indicate the location of the maximum absolute amplitude,
$U^*$ during each transition. Dashed lines in (a) indicate the location of the maximum absolute amplitude, ![]() $y_c^*$. Bottom panel in (a,c,d) indicate the variation of
$y_c^*$. Bottom panel in (a,c,d) indicate the variation of ![]() $y_c^*$ for an increase in
$y_c^*$ for an increase in ![]() $P_{th}$ (from dark to light colours) from
$P_{th}$ (from dark to light colours) from ![]() $P_{th}=0.1$ to 2.5 in (a) and from
$P_{th}=0.1$ to 2.5 in (a) and from ![]() $P_{th}=2$ to 5 in (c,d). In order to provide spatially continuous structures from left to right, time increases from right to left.
$P_{th}=2$ to 5 in (c,d). In order to provide spatially continuous structures from left to right, time increases from right to left.
The first thing to note is that, for all datasets, the resulting velocity structures are similar, in that both transitions in ![]() $U^*$ are associated with the passage of downstream inclined structures with a high(low)-speed event followed in time by a low(high)-speed one in the case of a
$U^*$ are associated with the passage of downstream inclined structures with a high(low)-speed event followed in time by a low(high)-speed one in the case of a ![]() $\phi _-$ (
$\phi _-$ (![]() $\phi _+$) transition in
$\phi _+$) transition in ![]() $U^*$ (contour plots in figures 8). The actual angle with respect to the horizontal, directly equivalent to the phase change across
$U^*$ (contour plots in figures 8). The actual angle with respect to the horizontal, directly equivalent to the phase change across ![]() $y_c$ for N1M1, is shown to be lower compared to E1; a much better agreement is observed for N2M6, where the large-scale ramp is now linked to the presence and relative location of the different scales across
$y_c$ for N1M1, is shown to be lower compared to E1; a much better agreement is observed for N2M6, where the large-scale ramp is now linked to the presence and relative location of the different scales across ![]() $y$, rather than their individual phase variation. For N2M5, the conditional velocity structure exhibits a similar behaviour, however, the resulting prominent scale is shorter when compared to
$y$, rather than their individual phase variation. For N2M5, the conditional velocity structure exhibits a similar behaviour, however, the resulting prominent scale is shorter when compared to ![]() $\mathcal {L}_x$. This is an indication of the importance of choosing the appropriate large scales in the flow with respect to the streamwise extent used for the p.d.f. construction, a topic which we will also revisit later. For dataset N1M1, where
$\mathcal {L}_x$. This is an indication of the importance of choosing the appropriate large scales in the flow with respect to the streamwise extent used for the p.d.f. construction, a topic which we will also revisit later. For dataset N1M1, where ![]() $u$ consists of a single travelling wave, the
$u$ consists of a single travelling wave, the ![]() $u|\phi$ fields indicate that the same part of the wave passes through the FOV during each transition (as expected for a periodic solution) and that it agrees with the experimental results at the region where N1M1 has spatial support. The similar conditional structures in N2M5 and N2M6, for which the velocity fields show a much more complex structure instantaneously (see figure 2g–i), further indicate that, even when multiple scales are involved in the model, most of them are averaged out in
$u|\phi$ fields indicate that the same part of the wave passes through the FOV during each transition (as expected for a periodic solution) and that it agrees with the experimental results at the region where N1M1 has spatial support. The similar conditional structures in N2M5 and N2M6, for which the velocity fields show a much more complex structure instantaneously (see figure 2g–i), further indicate that, even when multiple scales are involved in the model, most of them are averaged out in ![]() $u|\phi$ and only the ones directly linked to the temporal patterns in the p.d.f. are highlighted.
$u|\phi$ and only the ones directly linked to the temporal patterns in the p.d.f. are highlighted.
The wall-normal location of maximum amplitude (line plots in figures 8a and 8c) indicates another effect of ![]() $P_{th}$ on the results, namely, that by choosing a higher threshold when identifying
$P_{th}$ on the results, namely, that by choosing a higher threshold when identifying ![]() $U^*$ in P
$U^*$ in P![]() $(U,t$), the identified transitions are due to the passage of structures that sit at higher wall-normal locations. It is encouraging that this trend is also present in both N2M5 and N2M6, where the superposition of three self-similar hierarchies with multiple members each, provides enough scale separation in
$(U,t$), the identified transitions are due to the passage of structures that sit at higher wall-normal locations. It is encouraging that this trend is also present in both N2M5 and N2M6, where the superposition of three self-similar hierarchies with multiple members each, provides enough scale separation in ![]() $y$ to make this distinction possible. In particular, although the ramp angle is more pronounced for lower thresholds, the same large-scale trends are recovered for all threshold values, with structures localised at higher wall-normal locations with increasing
$y$ to make this distinction possible. In particular, although the ramp angle is more pronounced for lower thresholds, the same large-scale trends are recovered for all threshold values, with structures localised at higher wall-normal locations with increasing ![]() $P_{th}$.
$P_{th}$.
Based on these results we can now revisit the link between the spatial orientation of velocity structures with respect to the horizontal (associated with the phase change across ![]() $y_c$) and the temporal patterns observed in P
$y_c$) and the temporal patterns observed in P![]() $(U,t$) (as was depicted in figure 7b). In the simplest case (dataset N1M1, see figure 4b), identified transitions in the p.d.f. are between a high velocity, denoted
$(U,t$) (as was depicted in figure 7b). In the simplest case (dataset N1M1, see figure 4b), identified transitions in the p.d.f. are between a high velocity, denoted ![]() $U^*_{M1}$, and the lowest velocity for which
$U^*_{M1}$, and the lowest velocity for which ![]() $P>P_{th}$,
$P>P_{th}$, ![]() $U^*_{M2}$ (see figure 5). It is then the mean gradient,
$U^*_{M2}$ (see figure 5). It is then the mean gradient, ![]() $\textrm {d}U/{\textrm {d}y}>0$, and the geometry of the velocity structure in space (defining
$\textrm {d}U/{\textrm {d}y}>0$, and the geometry of the velocity structure in space (defining ![]() $\partial u/ \partial y$) that dictate the rate of each type of transition between these two velocities. Since UMZs are discussed in terms of the full velocity, it is instructive to think of full velocity contours and how their corrugation depends on the sign of
$\partial u/ \partial y$) that dictate the rate of each type of transition between these two velocities. Since UMZs are discussed in terms of the full velocity, it is instructive to think of full velocity contours and how their corrugation depends on the sign of ![]() $u$ and
$u$ and ![]() $\partial u/ \partial y$. For
$\partial u/ \partial y$. For ![]() $u<0$ (equivalent to
$u<0$ (equivalent to ![]() $U^*_{M1}$ in our scenario), there would be an upwards corrugation of the
$U^*_{M1}$ in our scenario), there would be an upwards corrugation of the ![]() $U$ isocontours (McKeon Reference McKeon2017; Saxton-Fox & McKeon Reference Saxton-Fox and McKeon2017), forming a bulge-like structure (see also figure 2 and the top schematic in figure 10). Assuming alternating positive and negative fluctuation events in
$U$ isocontours (McKeon Reference McKeon2017; Saxton-Fox & McKeon Reference Saxton-Fox and McKeon2017), forming a bulge-like structure (see also figure 2 and the top schematic in figure 10). Assuming alternating positive and negative fluctuation events in ![]() $x$, this
$x$, this ![]() $u<0$ event would be preceded and followed in space by opposite sign fluctuations (
$u<0$ event would be preceded and followed in space by opposite sign fluctuations (![]() $u>0$, equivalent to
$u>0$, equivalent to ![]() $U^*_{M2}$ in the p.d.f.). Even assuming complete symmetry for these structures in the fluctuating field (as is the case in the travelling-wave models), their ramp-like geometry creates an asymmetry in the full velocity field due to constructive or destructive interference of the instantaneous shear with the mean shear (as discussed in detail by McKeon Reference McKeon2017). It is this geometric asymmetry that leads to the difference in transition rates between
$U^*_{M2}$ in the p.d.f.). Even assuming complete symmetry for these structures in the fluctuating field (as is the case in the travelling-wave models), their ramp-like geometry creates an asymmetry in the full velocity field due to constructive or destructive interference of the instantaneous shear with the mean shear (as discussed in detail by McKeon Reference McKeon2017). It is this geometric asymmetry that leads to the difference in transition rates between ![]() $\phi _+$ and
$\phi _+$ and ![]() $\phi _-$. In particular, at the back of this bulge, upstream of which
$\phi _-$. In particular, at the back of this bulge, upstream of which ![]() $u>0$, the geometry dictates that
$u>0$, the geometry dictates that ![]() $\partial u/ \partial y >0$, adding to the mean shear and creating a very strong local shear layer: closely packed isocontours in
$\partial u/ \partial y >0$, adding to the mean shear and creating a very strong local shear layer: closely packed isocontours in ![]() $U$ indicate very rapid change in values, inhibiting the formation of UMZs. As such, as the back of the bulge crosses the FOV, a fast transition to high velocity values is observed (contour plots on the left in figure 8,
$U$ indicate very rapid change in values, inhibiting the formation of UMZs. As such, as the back of the bulge crosses the FOV, a fast transition to high velocity values is observed (contour plots on the left in figure 8, ![]() $\phi _+$ transition). On the other hand,
$\phi _+$ transition). On the other hand, ![]() $\partial u/ \partial y <0$ at the front of the bulge, thus creating a destructive interference with the mean shear, loosely packed isocontours in
$\partial u/ \partial y <0$ at the front of the bulge, thus creating a destructive interference with the mean shear, loosely packed isocontours in ![]() $U$, and the formation of UMZs: as the front of the bulge crosses the FOV,
$U$, and the formation of UMZs: as the front of the bulge crosses the FOV, ![]() $U$ gradually decreases (contour plots on the right in figure 8,
$U$ gradually decreases (contour plots on the right in figure 8, ![]() $\phi _-$ transition). Similar reasoning explains why the opposite result for the transition rates in the p.d.f. is observed in the case of upstream-leaning velocity structures (see figure 7b).
$\phi _-$ transition). Similar reasoning explains why the opposite result for the transition rates in the p.d.f. is observed in the case of upstream-leaning velocity structures (see figure 7b).
Another important point highlighted from these conditional fields is that a certain velocity value ![]() $U^*$ in the p.d.f. is associated with a different flow field (mainly with respect to the wall-normal gradient) depending on whether it is part of a
$U^*$ in the p.d.f. is associated with a different flow field (mainly with respect to the wall-normal gradient) depending on whether it is part of a ![]() $\phi _+$ or
$\phi _+$ or ![]() $\phi _-$ transition in time, a distinction that would not be possible without the full temporal information. As was mentioned earlier, a velocity in the middle of a
$\phi _-$ transition in time, a distinction that would not be possible without the full temporal information. As was mentioned earlier, a velocity in the middle of a ![]() $\phi _-$ transition would indicate a peak in P
$\phi _-$ transition would indicate a peak in P![]() $(U,t$) at that velocity and would be associated with a negative wall-normal gradient in
$(U,t$) at that velocity and would be associated with a negative wall-normal gradient in ![]() $u$ (contour plots on the right of figure 8). On the other hand, the same velocity in the middle of a
$u$ (contour plots on the right of figure 8). On the other hand, the same velocity in the middle of a ![]() $\phi _+$ transition would be represented by a very small number of vectors spatially and would be associated with a velocity snapshot where
$\phi _+$ transition would be represented by a very small number of vectors spatially and would be associated with a velocity snapshot where ![]() $\partial u/ \partial y>0$ (see also contour panels on the left in figure 8).
$\partial u/ \partial y>0$ (see also contour panels on the left in figure 8).
It should be noted that, for N1M1, placing the mode closer to the wall, such that there are non-zero velocity fluctuations in the region close to the wall (i.e. if near-wall streak structures are present), can lead to better agreement in both P![]() $(U,t$) and
$(U,t$) and ![]() $u|\phi$ (not shown here). Specifically, the velocity range of the p.d.f. peaks increases, such that there are peaks for
$u|\phi$ (not shown here). Specifically, the velocity range of the p.d.f. peaks increases, such that there are peaks for ![]() $U<0.7U_{\infty }$, in agreement with the experimental dataset (see figure 4), allowing also better comparisons for the rest of the metrics discussed here. Although the main focus in UMZ studies has predominantly been in the log and wake regions, this indicates that the near-wall region has a significant imprint on the resulting p.d.f. However, it is stressed here again that since the goal of the present work is not a data-driven search for the perfect agreement between modelling and experiments but rather establishing a connection between spatial structuring, temporal evolution and statistical behaviour using as simple an input as possible, we focused on structures contained in the inertial region for all model datasets.
$U<0.7U_{\infty }$, in agreement with the experimental dataset (see figure 4), allowing also better comparisons for the rest of the metrics discussed here. Although the main focus in UMZ studies has predominantly been in the log and wake regions, this indicates that the near-wall region has a significant imprint on the resulting p.d.f. However, it is stressed here again that since the goal of the present work is not a data-driven search for the perfect agreement between modelling and experiments but rather establishing a connection between spatial structuring, temporal evolution and statistical behaviour using as simple an input as possible, we focused on structures contained in the inertial region for all model datasets.
Until this point, we have mostly focused our attention on the temporal characteristics of P![]() $(U,t$) and their link to the spatial signature of the underlying velocity structures. The peaks of this p.d.f., however, have also been shown to be an important indication of UMZs in the flow, the average number of which,
$(U,t$) and their link to the spatial signature of the underlying velocity structures. The peaks of this p.d.f., however, have also been shown to be an important indication of UMZs in the flow, the average number of which, ![]() $\overline {N_{UMZ}}$, follows a Gaussian distribution in wall-bounded flows (de Silva et al. Reference de Silva, Hutchins and Marusic2016). It is therefore natural to ask whether the previously analysed temporal patterns in P
$\overline {N_{UMZ}}$, follows a Gaussian distribution in wall-bounded flows (de Silva et al. Reference de Silva, Hutchins and Marusic2016). It is therefore natural to ask whether the previously analysed temporal patterns in P![]() $(U,t$) are also associated with a repeatable transition in
$(U,t$) are also associated with a repeatable transition in ![]() $N_{UMZ}$, leading to the observed statistical behaviour. To this end, the number of identified peaks for datasets E1, N2M5 and N2M6 is conditionally averaged on
$N_{UMZ}$, leading to the observed statistical behaviour. To this end, the number of identified peaks for datasets E1, N2M5 and N2M6 is conditionally averaged on ![]() $\phi _+$ and
$\phi _+$ and ![]() $\phi _-$ transitions of
$\phi _-$ transitions of ![]() $U^*$. Dataset N1M1 is excluded from this analysis, since the use of a single velocity scale does not allow for a significant variation in the number of UMZs or for a sensitivity analysis with respect to
$U^*$. Dataset N1M1 is excluded from this analysis, since the use of a single velocity scale does not allow for a significant variation in the number of UMZs or for a sensitivity analysis with respect to ![]() $P_{th}$. Results for the multiscale datasets (for which inclusion of more scales provides better statistical representation) show that the average number of UMZs for N2M6 (
$P_{th}$. Results for the multiscale datasets (for which inclusion of more scales provides better statistical representation) show that the average number of UMZs for N2M6 (![]() $\overline {N_{UMZ}}|_{N2M6}=3.2$) is comparable to the E1 dataset (
$\overline {N_{UMZ}}|_{N2M6}=3.2$) is comparable to the E1 dataset (![]() $\overline {N_{UMZ}}|_{E1}=3.2$) and higher than N2M5 (
$\overline {N_{UMZ}}|_{E1}=3.2$) and higher than N2M5 (![]() $\overline {N_{UMZ}}|_{N2M5}=2.2$). As was mentioned earlier, the limited number of modes in the model datasets leads to a lower
$\overline {N_{UMZ}}|_{N2M5}=2.2$). As was mentioned earlier, the limited number of modes in the model datasets leads to a lower ![]() $N_{UMZ}$ for N2M5, while the increase in
$N_{UMZ}$ for N2M5, while the increase in ![]() $Re$ partly compensates for that in N2M6. This allows comparison of the relative trends between the datasets, further facilitated by subtracting the mean in each case. The repeating temporal transitions in
$Re$ partly compensates for that in N2M6. This allows comparison of the relative trends between the datasets, further facilitated by subtracting the mean in each case. The repeating temporal transitions in ![]() $U^*$ are shown to be associated with clearly defined transitions in the number of UMZs, similar for all datasets (figure 9). In particular,
$U^*$ are shown to be associated with clearly defined transitions in the number of UMZs, similar for all datasets (figure 9). In particular, ![]() $\phi _+$ (
$\phi _+$ (![]() $\phi _-$) transitions in the p.d.f. are linked to a monotonic decrease (increase) in
$\phi _-$) transitions in the p.d.f. are linked to a monotonic decrease (increase) in ![]() $N_{UMZ}$ compared to the average. For dataset E1, different values of
$N_{UMZ}$ compared to the average. For dataset E1, different values of ![]() $P_{th}$ show a marginal effect on the observed trends. For N2M5, this effect is more pronounced (figure 9a), while for N2M6 it is the lowest values of
$P_{th}$ show a marginal effect on the observed trends. For N2M5, this effect is more pronounced (figure 9a), while for N2M6 it is the lowest values of ![]() $P_{th}$ that provide the most well-defined patterns an effect of the discrete nature of the model (figure 9b). Taking into account the corresponding conditional velocity fields
$P_{th}$ that provide the most well-defined patterns an effect of the discrete nature of the model (figure 9b). Taking into account the corresponding conditional velocity fields ![]() $u|\phi$ (figure 8), these trends are also in line with the correlations found by Laskari et al. (Reference Laskari, de Kat, Hearst and Ganapathisubramani2018) between the number of UMZs and large-scale sweep and ejection events in the log region. For the temporal patterns analysed here, the focus is solely on the
$u|\phi$ (figure 8), these trends are also in line with the correlations found by Laskari et al. (Reference Laskari, de Kat, Hearst and Ganapathisubramani2018) between the number of UMZs and large-scale sweep and ejection events in the log region. For the temporal patterns analysed here, the focus is solely on the ![]() $u$ fluctuations since it is their geometry together with the mean shear profile that are of importance for the observed behaviour. Generally though, given the prominence of sweep and ejection events throughout the boundary layer, a joint
$u$ fluctuations since it is their geometry together with the mean shear profile that are of importance for the observed behaviour. Generally though, given the prominence of sweep and ejection events throughout the boundary layer, a joint ![]() $u$–
$u$–![]() $v$ analysis could provide further insight, particularly in a statistical sense, based on the observations from Laskari et al. (Reference Laskari, de Kat, Hearst and Ganapathisubramani2018). In that respect, the resolvent analysis providing the travelling wave models is particularly advantageous since it gives specific information about the relationship between
$v$ analysis could provide further insight, particularly in a statistical sense, based on the observations from Laskari et al. (Reference Laskari, de Kat, Hearst and Ganapathisubramani2018). In that respect, the resolvent analysis providing the travelling wave models is particularly advantageous since it gives specific information about the relationship between ![]() $u$ and
$u$ and ![]() $v$ at the critical layer. In the same context, the corresponding behaviour of the spanwise velocity component
$v$ at the critical layer. In the same context, the corresponding behaviour of the spanwise velocity component ![]() $w$, would also be an interesting point for future work, since it is not measured or analysed as often.
$w$, would also be an interesting point for future work, since it is not measured or analysed as often.

Figure 9. Conditionally averaged number of UMZs, ![]() $\tilde {N}_{UMZ}|_{U^{*}}$ in each type of transition, where (
$\tilde {N}_{UMZ}|_{U^{*}}$ in each type of transition, where (![]() $\tilde {\cdot }$) denotes that the mean
$\tilde {\cdot }$) denotes that the mean ![]() $\overline {N_{UMZ}}$ has been subtracted for better comparison between datasets. (a) E1 and N2M5 for different
$\overline {N_{UMZ}}$ has been subtracted for better comparison between datasets. (a) E1 and N2M5 for different ![]() $P_{th}$ values, denoted with solid and dot lines, respectively. (b) E1 and N2M6 for different
$P_{th}$ values, denoted with solid and dot lines, respectively. (b) E1 and N2M6 for different ![]() $P_{th}$ values, denoted with solid and dot-dash lines, respectively. For E1 the
$P_{th}$ values, denoted with solid and dot-dash lines, respectively. For E1 the ![]() $P_{th}$ values used are
$P_{th}$ values used are ![]() $P_{th}=[0.1, 0.2, 0.5, 1, 1.5, 2, 2.5]$ and for N2M5 and N2M6
$P_{th}=[0.1, 0.2, 0.5, 1, 1.5, 2, 2.5]$ and for N2M5 and N2M6 ![]() $P_{th}=[2, 3, 4, 5]$. Colours as in figure 5.
$P_{th}=[2, 3, 4, 5]$. Colours as in figure 5.
All the above results and procedure followed for the analysis are summarised in a conceptual sketch (figure 10): the asymmetry in the full velocity contours (denoted with black lines at the top) leads to (faster) ![]() $\phi _+$ and (slower)
$\phi _+$ and (slower) ![]() $\phi _-$ transitions in P
$\phi _-$ transitions in P![]() $(U,t$) (denoted with light and dark colours, respectively). Three representative spatial extents for the velocity fluctuations (following the conditional fields from figure 8) during such transitions are highlighted and the resulting variations of
$(U,t$) (denoted with light and dark colours, respectively). Three representative spatial extents for the velocity fluctuations (following the conditional fields from figure 8) during such transitions are highlighted and the resulting variations of ![]() $U^*$ and
$U^*$ and ![]() $N_{UMZ}$, conditioned on such transitions, are depicted as insets to the full P
$N_{UMZ}$, conditioned on such transitions, are depicted as insets to the full P![]() $(U,t$) field. The process of constructing P
$(U,t$) field. The process of constructing P![]() $(U,t$) is described on the right of figure 10, while the progressive increase in scale representation for each dataset used is schematically shown on the left.
$(U,t$) is described on the right of figure 10, while the progressive increase in scale representation for each dataset used is schematically shown on the left.

Figure 10. Conceptual sketch: two-mode representation of velocity fluctuations ![]() $u$, with full velocity contours superimposed (black lines), highlighting the asymmetry induced due to the mean shear profile (top). Coloured boxes indicate three representative spatial extents of the convecting structures, as identified in the conditional velocity fields in figure 8, with dark and light colours denoting
$u$, with full velocity contours superimposed (black lines), highlighting the asymmetry induced due to the mean shear profile (top). Coloured boxes indicate three representative spatial extents of the convecting structures, as identified in the conditional velocity fields in figure 8, with dark and light colours denoting ![]() $\phi _-$ and
$\phi _-$ and ![]() $\phi _+$ transitions, respectively (as in figures 5–9). The resulting temporal variations in
$\phi _+$ transitions, respectively (as in figures 5–9). The resulting temporal variations in ![]() $U^*$ and
$U^*$ and ![]() $N_{UMZ}$ during each transition are shown in the two circular insets of P
$N_{UMZ}$ during each transition are shown in the two circular insets of P![]() $(U,t$), the construction of which is depicted on the left. Increasing scale representation from N1M1 to the experimental dataset E1, is shown on the right.
$(U,t$), the construction of which is depicted on the left. Increasing scale representation from N1M1 to the experimental dataset E1, is shown on the right.
5. Discussion
There are several thresholding parameters used throughout the analysis presented here. However, the effect of most was limited to the quantification of the p.d.f. characteristics (figure 6), without altering any of the main conclusions. Instead, the parameter study provided some coarse guidelines for data acquisition and processing while some of the observed trends contributed to our physical understanding of the flow. Both of these were further enhanced with the use of the model datasets: knowledge of the exact velocity scales present in the flow significantly improved spatial and temporal resolution considerations, while the manipulation of geometrical characteristics of the velocity field in a controlled manner allowed us to isolate the spatial characteristics of ![]() $u$ responsible for the temporal patterns in P
$u$ responsible for the temporal patterns in P![]() $(U,t$).
$(U,t$).
Starting at the instantaneous p.d.f. construction, P![]() $(U$), the choice of velocity vectors within the turbulent region should be appropriately limited in both
$(U$), the choice of velocity vectors within the turbulent region should be appropriately limited in both ![]() $x$ and
$x$ and ![]() $y$ such that the p.d.f. is sufficiently converged without averaging out modal peaks from smaller UMZs. The choice of the limit in
$y$ such that the p.d.f. is sufficiently converged without averaging out modal peaks from smaller UMZs. The choice of the limit in ![]() $x$ was found to have an effect only on the estimated rates of transitions in P
$x$ was found to have an effect only on the estimated rates of transitions in P![]() $(U,t$) due to increased filtering with increasing
$(U,t$) due to increased filtering with increasing ![]() $\mathcal {L}_x$ (figure 6). A similar parameter study also showed that
$\mathcal {L}_x$ (figure 6). A similar parameter study also showed that ![]() $\mathcal {L}_x$ has a negligible effect on the average number of peaks detected in the p.d.f. (for
$\mathcal {L}_x$ has a negligible effect on the average number of peaks detected in the p.d.f. (for ![]() $250< \mathcal {L}_x^+<2500$, de Silva et al. Reference de Silva, Hutchins and Marusic2016). These authors further concluded that, for consistency between different
$250< \mathcal {L}_x^+<2500$, de Silva et al. Reference de Silva, Hutchins and Marusic2016). These authors further concluded that, for consistency between different ![]() $Re$ datasets, a viscous scaling of
$Re$ datasets, a viscous scaling of ![]() $\mathcal {L}_x$ is appropriate. The multiscale numerical datasets employed here allow us to specify which scales from a self-similar log-region hierarchy are represented in the p.d.f. (not filtered out), when the largest scale in the hierarchy is fixed with respect to
$\mathcal {L}_x$ is appropriate. The multiscale numerical datasets employed here allow us to specify which scales from a self-similar log-region hierarchy are represented in the p.d.f. (not filtered out), when the largest scale in the hierarchy is fixed with respect to ![]() $\mathcal {L}_x$. In particular, for both N2M5 and N2M6, the two smallest modes have a negligible effect on the p.d.f. evolution while for the latter, the third mode from the wall, although leading to a more observable change in the p.d.f., still does not alter the metrics discussed. In other words, it is the three larger modes within the logarithmic region that are relevant to the temporal behaviour of the p.d.f. which is of interest here. Aside from the ratio between the streamwise extent and the smallest scales in the flow, which has been sufficiently explored in the literature, including a range of velocity modes in the flow while exactly controlling their scales (as was the case in datasets N2M5 and N2M6) allowed us to also explore the relationship between outer scaling and the largest modes present in the flow. The choice of a constant
$\mathcal {L}_x$. In particular, for both N2M5 and N2M6, the two smallest modes have a negligible effect on the p.d.f. evolution while for the latter, the third mode from the wall, although leading to a more observable change in the p.d.f., still does not alter the metrics discussed. In other words, it is the three larger modes within the logarithmic region that are relevant to the temporal behaviour of the p.d.f. which is of interest here. Aside from the ratio between the streamwise extent and the smallest scales in the flow, which has been sufficiently explored in the literature, including a range of velocity modes in the flow while exactly controlling their scales (as was the case in datasets N2M5 and N2M6) allowed us to also explore the relationship between outer scaling and the largest modes present in the flow. The choice of a constant ![]() $\mathcal {L}_x^+$ for different
$\mathcal {L}_x^+$ for different ![]() $Re$ datasets ensures that small UMZs can still be recovered in high-
$Re$ datasets ensures that small UMZs can still be recovered in high-![]() $Re$ flows; typically then, even in low-
$Re$ flows; typically then, even in low-![]() $Re$ datasets, the resulting outer-normalised extent will not exceed
$Re$ datasets, the resulting outer-normalised extent will not exceed ![]() $\mathcal {L}_x=1\text {--}2\delta$ (de Silva et al. Reference de Silva, Hutchins and Marusic2016). Given the well-known presence of LSMs (
$\mathcal {L}_x=1\text {--}2\delta$ (de Silva et al. Reference de Silva, Hutchins and Marusic2016). Given the well-known presence of LSMs (![]() ${\sim }2\text {--}3\delta$) and VLSMs (
${\sim }2\text {--}3\delta$) and VLSMs (![]() ${\sim }6\delta$) in wall-bounded flows, such a choice of experimental datasets or broadband models also ensures that scales a few times larger than
${\sim }6\delta$) in wall-bounded flows, such a choice of experimental datasets or broadband models also ensures that scales a few times larger than ![]() $\mathcal {L}_x$ will be present in the flow; this is critical for the temporal p.d.f. patterns discussed in the previous sections. The models analysed here, however, require an a priori choice of all velocity scales introduced in the flow: following self-similar scaling, the largest scale in the flow has then to be carefully selected. Specifically, in order to achieve good agreement between experiments and modelling (
$\mathcal {L}_x$ will be present in the flow; this is critical for the temporal p.d.f. patterns discussed in the previous sections. The models analysed here, however, require an a priori choice of all velocity scales introduced in the flow: following self-similar scaling, the largest scale in the flow has then to be carefully selected. Specifically, in order to achieve good agreement between experiments and modelling (![]() $\mathcal {L}_x=1590^+$ for both), the largest velocity scale in the flow had to comply with
$\mathcal {L}_x=1590^+$ for both), the largest velocity scale in the flow had to comply with ![]() $\delta < {\lambda }_{x1} < 6\delta$; when the largest mode was closer to the lower limit, temporal patterns in P
$\delta < {\lambda }_{x1} < 6\delta$; when the largest mode was closer to the lower limit, temporal patterns in P![]() $(U,t$) were limited to the main branching structure observed in the single mode dataset (N1M1, figure 4b). This was particularly pronounced for N2M5 as was seen both in the p.d.f. patterns (figure 4c) and the conditional velocity structures (figure 8c). For larger
$(U,t$) were limited to the main branching structure observed in the single mode dataset (N1M1, figure 4b). This was particularly pronounced for N2M5 as was seen both in the p.d.f. patterns (figure 4c) and the conditional velocity structures (figure 8c). For larger ![]() ${\lambda }_{x1}$, complexity increased with smaller-scale branching in P
${\lambda }_{x1}$, complexity increased with smaller-scale branching in P![]() $(U,t$) providing better agreement with the experimental results, however, closer to the higher limit (
$(U,t$) providing better agreement with the experimental results, however, closer to the higher limit (![]() ${\lambda }_{x1} = 6\delta$), not enough periods of the largest-scale transitions were present leading to a significant decrease in the estimated average transition rates (for the same temporal extent in outer units). Based on the previous, we chose an intermediate value of
${\lambda }_{x1} = 6\delta$), not enough periods of the largest-scale transitions were present leading to a significant decrease in the estimated average transition rates (for the same temporal extent in outer units). Based on the previous, we chose an intermediate value of ![]() ${\lambda }_{x1} = 3\delta$ (
${\lambda }_{x1} = 3\delta$ (![]() $k_{x1}=2$) for the largest scale in the flow, which resulted in the most favourable comparison with experiments. The limit in
$k_{x1}=2$) for the largest scale in the flow, which resulted in the most favourable comparison with experiments. The limit in ![]() $y$ is selected such that vectors from the irrotational free-stream region are removed. Although this boundary is necessary in order to allow p.d.f. peaks below
$y$ is selected such that vectors from the irrotational free-stream region are removed. Although this boundary is necessary in order to allow p.d.f. peaks below ![]() $U_{\infty }$ to be identifiable, a rough detection of the turbulent/non-turbulent interface (quiescent core region in channel flows) is sufficient (such as the use of a velocity threshold), while more detailed identification schemes (kinetic energy, vorticity or scalar thresholds) further improve the temporal pattern identification in the p.d.f.
$U_{\infty }$ to be identifiable, a rough detection of the turbulent/non-turbulent interface (quiescent core region in channel flows) is sufficient (such as the use of a velocity threshold), while more detailed identification schemes (kinetic energy, vorticity or scalar thresholds) further improve the temporal pattern identification in the p.d.f.
In order to construct P![]() $(U,t$), sufficient temporal resolution is important, however, given the estimated periods of the p.d.f. transitions (figure 5a), time steps
$(U,t$), sufficient temporal resolution is important, however, given the estimated periods of the p.d.f. transitions (figure 5a), time steps ![]() $\textrm {d}T<0.5\delta /U_{\infty }$ are still expected to provide enough resolution for a coarse representation of the temporal patterns discussed here. The length of each temporal record is also of importance for statistical convergence, although, depending on the dataset and/or measurement limitations, multiple records of shorter lengths can also be used.
$\textrm {d}T<0.5\delta /U_{\infty }$ are still expected to provide enough resolution for a coarse representation of the temporal patterns discussed here. The length of each temporal record is also of importance for statistical convergence, although, depending on the dataset and/or measurement limitations, multiple records of shorter lengths can also be used.
With respect to pattern identification, the parameter found to have the largest effect on the results was the threshold on ![]() $\textrm {d}U^*/\textrm {d}t$ used to identify continuous transitions in time. Not surprisingly higher (lower) thresholds resulted in faster (slower) transitions on average; however, exact quantitative description of these patterns was not the main goal here. Rather, highlighting their connection with the underlying velocity structures was of importance and for that the use of higher (lower) thresholds for
$\textrm {d}U^*/\textrm {d}t$ used to identify continuous transitions in time. Not surprisingly higher (lower) thresholds resulted in faster (slower) transitions on average; however, exact quantitative description of these patterns was not the main goal here. Rather, highlighting their connection with the underlying velocity structures was of importance and for that the use of higher (lower) thresholds for ![]() $\phi _+$ (
$\phi _+$ (![]() $\phi _-$) transitions in
$\phi _-$) transitions in ![]() $U^*$ led to much more well-defined conditionally averaged velocity fields. This choice was more crucial in datasets E1 and N2M6, where more scales were involved and various rates of transitions in
$U^*$ led to much more well-defined conditionally averaged velocity fields. This choice was more crucial in datasets E1 and N2M6, where more scales were involved and various rates of transitions in ![]() $U^*$ were present. For consistency, the same threshold for both
$U^*$ were present. For consistency, the same threshold for both ![]() $\phi _+$ and
$\phi _+$ and ![]() $\phi _-$ transitions was used in all datasets for the results presented, however, this observation indicates that the ramp-like velocity structures depicted in figure 8 are indeed linked with the slowest
$\phi _-$ transitions was used in all datasets for the results presented, however, this observation indicates that the ramp-like velocity structures depicted in figure 8 are indeed linked with the slowest ![]() $\phi _-$ and fastest
$\phi _-$ and fastest ![]() $\phi _+$ transitions. The values of
$\phi _+$ transitions. The values of ![]() $P_{th}$ were shown to have minimal influence on the estimated rate of transitions, however, lower thresholds were associated with structures which were located closer to the wall and whose downstream angle was much more well defined. This variation in the wall-normal location with
$P_{th}$ were shown to have minimal influence on the estimated rate of transitions, however, lower thresholds were associated with structures which were located closer to the wall and whose downstream angle was much more well defined. This variation in the wall-normal location with ![]() $P_{th}$, was also observed in the second model dataset and thus allows us to view the experimental dataset from an ideal structural perspective: starting with an instantaneous velocity field consisting of a superposition of structures of increasing size with increasing distance from the wall and convecting in time, each mode will be associated with distinct temporal patterns in the resulting p.d.f., appearing as branching of the large-scale transition (see figure 4c) and as such, each will be identified by a different
$P_{th}$, was also observed in the second model dataset and thus allows us to view the experimental dataset from an ideal structural perspective: starting with an instantaneous velocity field consisting of a superposition of structures of increasing size with increasing distance from the wall and convecting in time, each mode will be associated with distinct temporal patterns in the resulting p.d.f., appearing as branching of the large-scale transition (see figure 4c) and as such, each will be identified by a different ![]() $P_{th}$ value. In reality, the temporal patterns in P
$P_{th}$ value. In reality, the temporal patterns in P![]() $(U,t$) are much more complicated than that (figure 4a) and each
$(U,t$) are much more complicated than that (figure 4a) and each ![]() $P_{th}$ value outlines transitions due to a multitude of scales; besides, our analysis mainly deals with the large-scale component of these temporal patterns and therefore a more focused approach would be needed to identify further similarities between the full-scale dataset and the multiscale model. However, we still find it instructive in its simplicity, allowing us to understand the main connections between the spatial structure and temporal behaviour reflected in the p.d.f., as more scales are added in the flow.
$P_{th}$ value outlines transitions due to a multitude of scales; besides, our analysis mainly deals with the large-scale component of these temporal patterns and therefore a more focused approach would be needed to identify further similarities between the full-scale dataset and the multiscale model. However, we still find it instructive in its simplicity, allowing us to understand the main connections between the spatial structure and temporal behaviour reflected in the p.d.f., as more scales are added in the flow.
The above discussions on scale selection for the model datasets highlight how this freedom benefits the UMZ analysis, particularly with respect to understanding the links between the geometry and size of ![]() $u$ structures and the p.d.f. temporal patterns. On the other hand, unless many different scales are added to the flow, statistical convergence is much harder to attain and that can be seen in the
$u$ structures and the p.d.f. temporal patterns. On the other hand, unless many different scales are added to the flow, statistical convergence is much harder to attain and that can be seen in the ![]() $N_{UMZ}$ variation (figure 9), where the choice of threshold affects the model datasets significantly more than E1. This greater difficulty in predicting trends in
$N_{UMZ}$ variation (figure 9), where the choice of threshold affects the model datasets significantly more than E1. This greater difficulty in predicting trends in ![]() $N_{UMZ}$, as well as the sensitivity of the model to the selected input scales, as discussed above, can be more pronounced in comparison to other models which employ a broader scale representation (albeit without temporal information, see for example de Silva et al. Reference de Silva, Hutchins and Marusic2016). In that aspect, the underlying periodicity and limit of the velocity fluctuations within the logarithmic region chosen here, although particularly suited for the analysis of the temporal behaviour of the p.d.f., can further hinder statistical predictions relying on broadband velocity input. Given these limitations, however, the agreement achieved in the patterns observed, between datasets representing a full-scale boundary layer (E1) and a low-order model of both a comparable and high-
$N_{UMZ}$, as well as the sensitivity of the model to the selected input scales, as discussed above, can be more pronounced in comparison to other models which employ a broader scale representation (albeit without temporal information, see for example de Silva et al. Reference de Silva, Hutchins and Marusic2016). In that aspect, the underlying periodicity and limit of the velocity fluctuations within the logarithmic region chosen here, although particularly suited for the analysis of the temporal behaviour of the p.d.f., can further hinder statistical predictions relying on broadband velocity input. Given these limitations, however, the agreement achieved in the patterns observed, between datasets representing a full-scale boundary layer (E1) and a low-order model of both a comparable and high-![]() $Re$ channel flow of increasing scale representation (N1M1, N2M5 and N2M6) underscores the robustness of the behaviour discussed here, regardless of flow geometry and Reynolds number.
$Re$ channel flow of increasing scale representation (N1M1, N2M5 and N2M6) underscores the robustness of the behaviour discussed here, regardless of flow geometry and Reynolds number.
Overall, we can say that the time-resolved velocity data (E1) allowed the observation of temporal patterns in P![]() $(U,t$) in their full complexity, and informed the parameter choice in the model datasets. The purpose of the first model dataset (N1M1) was to indicate the simplest model able to reproduce the core characteristics of the observed temporal behaviour. The use of multiscale model datasets (N2M5 and N2M6) yielded more complex p.d.f. patterns, the finer scales of which, although not analysed here, show promise in reproducing full-scale datasets. We particularly consider the comparison between small-scale branching in the model p.d.f. with that of the experimental p.d.f. as a quite relevant topic for future work. With respect to the large-scale temporal variations of the p.d.f., which are the focus of the present analysis, the multiscale datasets supported the observations from the single-scale model, indicating that the geometric similarity of the members of each hierarchy, as well as their relative evolution in time (dictated by their wall-normal varying wave speed), both inherent to the resolvent framework, can reproduce these key experimental observations. Further, comparisons between N2M5 and N2M6 indicate that the behaviour observed is likely independent of
$(U,t$) in their full complexity, and informed the parameter choice in the model datasets. The purpose of the first model dataset (N1M1) was to indicate the simplest model able to reproduce the core characteristics of the observed temporal behaviour. The use of multiscale model datasets (N2M5 and N2M6) yielded more complex p.d.f. patterns, the finer scales of which, although not analysed here, show promise in reproducing full-scale datasets. We particularly consider the comparison between small-scale branching in the model p.d.f. with that of the experimental p.d.f. as a quite relevant topic for future work. With respect to the large-scale temporal variations of the p.d.f., which are the focus of the present analysis, the multiscale datasets supported the observations from the single-scale model, indicating that the geometric similarity of the members of each hierarchy, as well as their relative evolution in time (dictated by their wall-normal varying wave speed), both inherent to the resolvent framework, can reproduce these key experimental observations. Further, comparisons between N2M5 and N2M6 indicate that the behaviour observed is likely independent of ![]() $Re$, although a more extensive analysis would be needed to confirm this trend, preferably including a range of
$Re$, although a more extensive analysis would be needed to confirm this trend, preferably including a range of ![]() $Re$ in full-scale experimental datasets. Conversely, all model datasets offered a much deeper understanding of the experimental observations: complete control over the geometric characteristics of a single velocity mode (N1M1) and user-defined scale separation in multiscale models (N2M5, N2M6) highlighted structural characteristics and scale relationships responsible for the experimental patterns, that could not be identified from the experimental dataset alone.
$Re$ in full-scale experimental datasets. Conversely, all model datasets offered a much deeper understanding of the experimental observations: complete control over the geometric characteristics of a single velocity mode (N1M1) and user-defined scale separation in multiscale models (N2M5, N2M6) highlighted structural characteristics and scale relationships responsible for the experimental patterns, that could not be identified from the experimental dataset alone.
6. Conclusions
A novel way of examining the probability density function of the streamwise velocity using both experimental and numerical data is presented. This p.d.f. has commonly been analysed instantaneously; we show how temporal information allows the observation of repeating patterns in P![]() $(U,t$). In particular p.d.f. peaks are observed to migrate slowly to lower velocities and subsequently faster towards
$(U,t$). In particular p.d.f. peaks are observed to migrate slowly to lower velocities and subsequently faster towards ![]() $U_{\infty }$, linked with a corresponding monotonic increase and decrease of the average number of UMZs. The main skeleton of these patterns is reproduced by considering the convection of a single velocity structure modelled as a travelling wave. Much more complex temporal patterns are observed when multiple velocity scales are included in two additional model datasets of self-similar resolvent hierarchies, which are promising for comparisons with full-scale datasets, although further analysis would be needed to establish similarities. For all datasets, the large-scale temporal patterns are shown to be linked to the convection of downstream-leaning velocity fluctuations of alternating sign in space. Manipulation of the geometrical characteristics of the velocity structures in the model datasets further demonstrates that it is their ramp-like nature that is mainly responsible for the observed temporal behaviour. Next to the physical understanding, the achieved temporal and statistical agreement between datasets is particularly hopeful from a modelling perspective regarding the capability of capturing key turbulence features and statistics through low-order models.
$U_{\infty }$, linked with a corresponding monotonic increase and decrease of the average number of UMZs. The main skeleton of these patterns is reproduced by considering the convection of a single velocity structure modelled as a travelling wave. Much more complex temporal patterns are observed when multiple velocity scales are included in two additional model datasets of self-similar resolvent hierarchies, which are promising for comparisons with full-scale datasets, although further analysis would be needed to establish similarities. For all datasets, the large-scale temporal patterns are shown to be linked to the convection of downstream-leaning velocity fluctuations of alternating sign in space. Manipulation of the geometrical characteristics of the velocity structures in the model datasets further demonstrates that it is their ramp-like nature that is mainly responsible for the observed temporal behaviour. Next to the physical understanding, the achieved temporal and statistical agreement between datasets is particularly hopeful from a modelling perspective regarding the capability of capturing key turbulence features and statistics through low-order models.
Acknowledgements
The experimental dataset used in this study was acquired by the corresponding author as part of her doctoral degree in the University of Southampton, under the supervision of Professor B. Ganapathisubramani and Professor R. de Kat, both of whom are gratefully acknowledged.
Funding
The support of the Office of Naval Research under award N00014-17-1-3022 is gratefully acknowledged.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Choice of  $P_{th}$
$P_{th}$
The choice of ![]() $P_{th}$ is bound by an upper limit,
$P_{th}$ is bound by an upper limit, ![]() $P_{th,u}$, set by requiring the resulting
$P_{th,u}$, set by requiring the resulting ![]() $U^*_u$ signal to be continuous in all snapshots, and a lower limit,
$U^*_u$ signal to be continuous in all snapshots, and a lower limit, ![]() $P_{th,l}$, set by requiring the resulting
$P_{th,l}$, set by requiring the resulting ![]() $U^*_l$ signals to be sufficiently correlated for
$U^*_l$ signals to be sufficiently correlated for ![]() $P_{th,l} < P_{th} < P_{th,u}$. The upper limit values for the three datasets E1, N2M5 and N2M6 are
$P_{th,l} < P_{th} < P_{th,u}$. The upper limit values for the three datasets E1, N2M5 and N2M6 are ![]() $P_{th,u}=2.8, 7.3$ and
$P_{th,u}=2.8, 7.3$ and ![]() $8.1$, respectively. Regarding the lower limit, for the experimental dataset E1 we can use a threshold as low as
$8.1$, respectively. Regarding the lower limit, for the experimental dataset E1 we can use a threshold as low as ![]() $P_{th,l}=0.1$, which results in non-zero correlation for
$P_{th,l}=0.1$, which results in non-zero correlation for ![]() $P_{th,l} < P_{th} < P_{th,u}$ (see solid line in figure 11). The Pearson correlation coefficient used here is based on the
$P_{th,l} < P_{th} < P_{th,u}$ (see solid line in figure 11). The Pearson correlation coefficient used here is based on the ![]() $U^*$ signals, for different threshold values
$U^*$ signals, for different threshold values
where ![]() $U^*_l = \min (U|P(U,t)>P_{th,l})$ is constant for each dataset, and
$U^*_l = \min (U|P(U,t)>P_{th,l})$ is constant for each dataset, and ![]() $U^* = \min (U|P (U,t)>P_{th})$ varies with
$U^* = \min (U|P (U,t)>P_{th})$ varies with ![]() $P_{th}$. For the numerical datasets, the situation is slightly more complicated. A significantly higher value of
$P_{th}$. For the numerical datasets, the situation is slightly more complicated. A significantly higher value of ![]() $P_{th,l}=2$ has to be used in order to get a
$P_{th,l}=2$ has to be used in order to get a ![]() $U^*_l$ signal for which
$U^*_l$ signal for which ![]() $R_{{U^*_l}U^*}>0$, although, even then, this holds true for
$R_{{U^*_l}U^*}>0$, although, even then, this holds true for ![]() $P_{th,l} < P_{th} < 5$ (dashed and dotted lines in figure 11). However, for
$P_{th,l} < P_{th} < 5$ (dashed and dotted lines in figure 11). However, for ![]() $P_{th}=5$ the resulting
$P_{th}=5$ the resulting ![]() $U^*$ still outlines the appropriate temporal patterns at the highest velocities (figure 12), while the largest mode from the numerical datasets is already identified in the conditionally averaged fields (figure 13d). Thus, given that increasing values of
$U^*$ still outlines the appropriate temporal patterns at the highest velocities (figure 12), while the largest mode from the numerical datasets is already identified in the conditionally averaged fields (figure 13d). Thus, given that increasing values of ![]() $P_{th}$ identify structures centred higher from the wall, a further increase of the threshold would not provide any meaningful results. In fact, for values of
$P_{th}$ identify structures centred higher from the wall, a further increase of the threshold would not provide any meaningful results. In fact, for values of ![]() $P_{th}>6$, the resulting
$P_{th}>6$, the resulting ![]() $U^*$ signal reaches values close to 0.9, where the p.d.f. values are almost constant over time, and as such no longer appropriately delineates the repeating patterns in the p.d.f. that are of interest here. Subsequently, the resulting conditional velocities also deviate from the patterns observed when intermediate and low threshold values of
$U^*$ signal reaches values close to 0.9, where the p.d.f. values are almost constant over time, and as such no longer appropriately delineates the repeating patterns in the p.d.f. that are of interest here. Subsequently, the resulting conditional velocities also deviate from the patterns observed when intermediate and low threshold values of ![]() $P_{th}$ are used (see figures 8 and 13c). It is apparent that, for the numerical datasets, the choice of an appropriate threshold range is more constrained than in the experimental one, which should be expected given the difference in scales involved.
$P_{th}$ are used (see figures 8 and 13c). It is apparent that, for the numerical datasets, the choice of an appropriate threshold range is more constrained than in the experimental one, which should be expected given the difference in scales involved.

Figure 11. Correlation coefficient ![]() $R_{{U^*_l} U^*}$ for E1 (
$R_{{U^*_l} U^*}$ for E1 (![]() $P_{th,l}=0.1$, solid line), N2M5 (
$P_{th,l}=0.1$, solid line), N2M5 (![]() $P_{th,l}=2$, dashed line) and N2M6 (
$P_{th,l}=2$, dashed line) and N2M6 (![]() $P_{th,l}=2$, dotted line).
$P_{th,l}=2$, dotted line).

Figure 12. Variation of P![]() $(U,t$) for N2M5 (a), and N2M6 (b) as in figure 4. Solid black lines denote
$(U,t$) for N2M5 (a), and N2M6 (b) as in figure 4. Solid black lines denote ![]() $U^*(t)=U|P(U,t)>P_{th}$ with
$U^*(t)=U|P(U,t)>P_{th}$ with ![]() $P_{th}=2$ and
$P_{th}=2$ and ![]() $5$.
$5$.

Figure 13. Conditionally averaged streamwise velocity fluctuations for each type of transition, ![]() $u|\phi _+$ (left) and
$u|\phi _+$ (left) and ![]() $u|\phi _-$ (right) as in figure 8. (a) E1 for
$u|\phi _-$ (right) as in figure 8. (a) E1 for ![]() $P_{th}=0.1$, (b) E1 for
$P_{th}=0.1$, (b) E1 for ![]() $P_{th}=2.5$, (c) N2M5 for
$P_{th}=2.5$, (c) N2M5 for ![]() $P_{th}=2$, (d) N2M5 for
$P_{th}=2$, (d) N2M5 for ![]() $P_{th}=5$.
$P_{th}=5$.
Based on the above restrictions, the range of ![]() $P_{th}$ for E1 was chosen as
$P_{th}$ for E1 was chosen as ![]() $0.1 < P_{th} < 2.5$ and for both numerical datasets (including more than a single velocity scale) as
$0.1 < P_{th} < 2.5$ and for both numerical datasets (including more than a single velocity scale) as ![]() $2 < P_{th} < 5$. These limits indicate that there is a bias of the numerical datasets towards higher p.d.f. values clustered closer to higher velocities when compared to the experimental database (illustrated clearly by the
$2 < P_{th} < 5$. These limits indicate that there is a bias of the numerical datasets towards higher p.d.f. values clustered closer to higher velocities when compared to the experimental database (illustrated clearly by the ![]() $U^*$ signals for the minimum and maximum
$U^*$ signals for the minimum and maximum ![]() $P_{th}$ values in figures 4a and 12). For the conditionally averaged velocity fields, two intermediate values within those ranges (
$P_{th}$ values in figures 4a and 12). For the conditionally averaged velocity fields, two intermediate values within those ranges (![]() $P_{th}=1$ for E1 and
$P_{th}=1$ for E1 and ![]() $P_{th}=3$ for all three numerical datasets) were chosen (figure 8). For completeness, we also present here the conditional fields for E1 and N2M5 when the extreme values of the threshold are used (see figure 13). The structures retain a similar character as the ones for intermediate
$P_{th}=3$ for all three numerical datasets) were chosen (figure 8). For completeness, we also present here the conditional fields for E1 and N2M5 when the extreme values of the threshold are used (see figure 13). The structures retain a similar character as the ones for intermediate ![]() $P_{th}$ values, albeit less clearly formed, especially for the
$P_{th}$ values, albeit less clearly formed, especially for the ![]() $\phi _+$ transitions using high threshold values in the experimental dataset (figure 13b).
$\phi _+$ transitions using high threshold values in the experimental dataset (figure 13b).
Overall, we can say that the full-scale database (E1) allows the use of very low threshold values ![]() $P_{th}$ for the detection of the temporal transitions in P
$P_{th}$ for the detection of the temporal transitions in P![]() $(U,t$). These threshold values, although far from the peak values of the p.d.f., still detect the appropriate temporal patterns. In fact, the use of lower threshold values leads to better formed conditionally averaged velocity structures and clearer trends for the variation in
$(U,t$). These threshold values, although far from the peak values of the p.d.f., still detect the appropriate temporal patterns. In fact, the use of lower threshold values leads to better formed conditionally averaged velocity structures and clearer trends for the variation in ![]() $N_{UMZ}$ during each type of transition, indicating that it is the upper limit for
$N_{UMZ}$ during each type of transition, indicating that it is the upper limit for ![]() $P_{th}$ that needs to be more carefully selected. In particular, it seems that it is the
$P_{th}$ that needs to be more carefully selected. In particular, it seems that it is the ![]() $\phi _+$ transitions which are less robust for increasing
$\phi _+$ transitions which are less robust for increasing ![]() $P_{th}$, while the opposite is true for the
$P_{th}$, while the opposite is true for the ![]() $\phi _-$ ones for which the associated ramp-like nature of the conditionally averaged velocities becomes more pronounced as
$\phi _-$ ones for which the associated ramp-like nature of the conditionally averaged velocities becomes more pronounced as ![]() $P_{th}$ increases (figure 13b, left). For the numerical datasets, on the other hand, the limited number of scales present in the flow limits the choice of
$P_{th}$ increases (figure 13b, left). For the numerical datasets, on the other hand, the limited number of scales present in the flow limits the choice of ![]() $P_{th}$ on both ends: below a certain velocity value, P
$P_{th}$ on both ends: below a certain velocity value, P![]() $(U,t$) is close or equal to zero and above a certain threshold P
$(U,t$) is close or equal to zero and above a certain threshold P![]() $(U,t$) is close to its maximum value: in either case there is little or no variation over time and as such the selection of
$(U,t$) is close to its maximum value: in either case there is little or no variation over time and as such the selection of ![]() $P_{th}$ has to be in between those limits in order to capture the temporal patterns of interest.
$P_{th}$ has to be in between those limits in order to capture the temporal patterns of interest.