Published online by Cambridge University Press: 17 September 2020
We study concentration-driven natural convection boundary layers on horizontal surfaces, subjected to a weak, surface normal, uniform blowing velocity  $V_i$ for three orders of range of the dimensionless blowing parameter
$V_i$ for three orders of range of the dimensionless blowing parameter  $10^{-8}\le J=Re_x^3/Gr_x\le 10^{-5}$, where
$10^{-8}\le J=Re_x^3/Gr_x\le 10^{-5}$, where  $Re_x$ and
$Re_x$ and  $Gr_x$ are the local Reynolds and Grashof numbers at the horizontal location
$Gr_x$ are the local Reynolds and Grashof numbers at the horizontal location  $x$, based respectively on
$x$, based respectively on  $V_i$ and
$V_i$ and  ${\rm \Delta} C$, the concentration difference across the boundary layer. We formulate the integral boundary layer equations, with the assumption of no concentration drop within the species boundary layer, which is valid for weak blowing into the thin species boundary layers that occur at the high Schmidt number (
${\rm \Delta} C$, the concentration difference across the boundary layer. We formulate the integral boundary layer equations, with the assumption of no concentration drop within the species boundary layer, which is valid for weak blowing into the thin species boundary layers that occur at the high Schmidt number ( $Sc \simeq 600$) of concentration-driven convection. The equations are then numerically solved to show that the species boundary layer thickness
$Sc \simeq 600$) of concentration-driven convection. The equations are then numerically solved to show that the species boundary layer thickness  $\delta _d = 1.6\,x(Re_x/Gr_x)^{1/4}$, the velocity boundary layer thickness
$\delta _d = 1.6\,x(Re_x/Gr_x)^{1/4}$, the velocity boundary layer thickness  $\delta _v=\delta _d Sc^{1/5}$, the horizontal velocity
$\delta _v=\delta _d Sc^{1/5}$, the horizontal velocity  $u = V_i(Gr_x/Re_x)^{1/4}f(\eta )$, where
$u = V_i(Gr_x/Re_x)^{1/4}f(\eta )$, where  $\eta =y/\delta _v$, and the drag coefficient based on
$\eta =y/\delta _v$, and the drag coefficient based on  $V_i$,
$V_i$,  $C_D = 2.32/\sqrt {J}$. We find that the vertical profile of the horizontally averaged dimensionless concentration across the boundary layer becomes, surprisingly, independent of the blowing and the species diffusion effects to follow a
$C_D = 2.32/\sqrt {J}$. We find that the vertical profile of the horizontally averaged dimensionless concentration across the boundary layer becomes, surprisingly, independent of the blowing and the species diffusion effects to follow a  $Gr_y^{2/3}$ scaling, where
$Gr_y^{2/3}$ scaling, where  $Gr_y$ is the Grashof number based on the vertical location
$Gr_y$ is the Grashof number based on the vertical location  $y$ within the boundary layer. We then show that the above profile matches the experimentally observed mean concentration profile within the boundary layers that form on the top surface of a membrane, when a weak flow is forced gravitationally from below the horizontal membrane that has brine above it and water below it. A similar match between the theoretical scaling of the species boundary layer thickness and its experimentally observed variation is also shown to occur.
$y$ within the boundary layer. We then show that the above profile matches the experimentally observed mean concentration profile within the boundary layers that form on the top surface of a membrane, when a weak flow is forced gravitationally from below the horizontal membrane that has brine above it and water below it. A similar match between the theoretical scaling of the species boundary layer thickness and its experimentally observed variation is also shown to occur.
Now independent researcher.
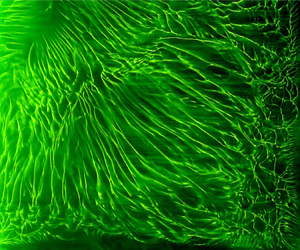
Front view of the spatial and temporal evolution of near-membrane sheet plumes when water with a constant, uniform velocity of 0.002 cm/s is forced through the membrane from below, with the membrane separating brine above it from water below it. The membrane is 150 mm wide, of which a region of 20 mm width is shown in the movie. The red regions at the bottom of the movie, of approximately up to 0.3 mm height, are the boundary layers, while the swaying near-vertical red streaks are the sheet plumes, with the yellow background being the bulk fluid. The Rayleigh number, based on the density difference and the height of the liquid layer above the membrane, of the first frame of the movie = 8.4*10^11. The movie plays with the same frame rate (14 Hz) as it was acquired.