Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T14:30:30.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Scale invariance in finite Reynolds number homogeneous isotropic turbulence

Published online by Cambridge University Press:  07 February 2019

L. Djenidi Open the ORCID record for L. Djenidi [Opens in a new window] ,
R. A. Antonia  and
S. L. Tang Open the ORCID record for S. L. Tang [Opens in a new window]
L. Djenidi
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
R. A. Antonia
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
S. L. Tang*
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen518055, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The problem of homogeneous isotropic turbulence (HIT) is revisited within the analytical framework of the Navier–Stokes equations, with a view to assessing rigorously the consequences of the scale invariance (an exact property of the Navier–Stokes equations) for any Reynolds number. The analytical development, which is independent of the 1941 (K41) and 1962 (K62) theories of Kolmogorov for HIT for infinitely large Reynolds number, is applied to the transport equations for the second- and third-order moments of the longitudinal velocity increment, 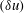$(\unicode[STIX]{x1D6FF}u)$. Once the normalised equations and the constraints required for complying with the scale-invariance property of the equations are presented, results derived from these equations and constraints are discussed and compared with measurements. It is found that the fluid viscosity, $\unicode[STIX]{x1D708}$, and the mean kinetic energy dissipation rate, $\overline{\unicode[STIX]{x1D716}}$ (the overbar denotes spatial and/or temporal averaging), are the only scaling parameters that make the equations scale-invariant. The analysis further leads to expressions for the distributions of the skewness and the flatness factor of 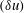$(\unicode[STIX]{x1D6FF}u)$ and shows that these distributions must exhibit plateaus (of different magnitudes) in the dissipative and inertial ranges, as the Taylor microscale Reynolds number 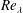$Re_{\unicode[STIX]{x1D706}}$ increases indefinitely. Also, the skewness and flatness factor of the longitudinal velocity derivative become constant as 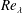$Re_{\unicode[STIX]{x1D706}}$ increases; this is supported by experimental data. Further, the analysis, backed up by experimental evidence, shows that, beyond the dissipative range, the behaviour of 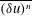$\overline{(\unicode[STIX]{x1D6FF}u)^{n}}$ with 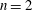$n=2$, 3 and 4 cannot be represented by a power law of the form 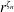$r^{\unicode[STIX]{x1D701}_{n}}$ when the Reynolds number is finite. It is shown that only when 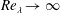$Re_{\unicode[STIX]{x1D706}}\rightarrow \infty$ can an $n$-thirds law (i.e. $\overline{(\unicode[STIX]{x1D6FF}u)^{n}}\sim r^{\unicode[STIX]{x1D701}_{n}}$, with 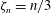$\unicode[STIX]{x1D701}_{n}=n/3$) emerge, which is consistent with the onset of a scaling range.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 244 - 272
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Anselmet, F. & Chambers, A. J. 1986 Assessment of local isotropy using measurements in a turbulent plane jet. J. Fluid Mech. 163, 365–391.Google Scholar
Antonia, R. A. & Burattini, P. 2006 Approach to the 4/5 law in homogeneous isotropic turbulence. J. Fluid Mech. 550, 175–184.Google Scholar
Antonia, R. A., Djenidi, L. & Danaila, L. 2014 Collapse of the turbulent dissipation range on Kolmogorov scales. Phys. Fluids 26, 045105.Google Scholar
Antonia, R. A., Djenidi, L., Danaila, L. & Tang, S. L. 2017 Small scale turbulence and the finite Reynolds number effect. Phys. Fluids 29 (2), 020715.Google Scholar
Antonia, R. A., Tang, S. L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.Google Scholar
Antonia, R. A., Zhou, T. & Romano, G. P. 2002 Small-scale turbulence characteristics of two-dimensional bluff body wakes. J. Fluid Mech. 459, 67–92.Google Scholar
Barenblatt, G. I. 1996 Scaling, Self-Similarity, and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics, vol. 14. Cambridge University Press.Google Scholar
Batchelor, G. K. 1947 Kolmogoroff’s theory of locally isotropic turbulence. Math. Proc. Camb. Phil. Soc. 43, 533–559.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1947 Decay of vorticity in isotropic turbulence. Proc. R. Soc. Lond. Ser. A 190, 534–550.Google Scholar
de Bruyn Kops, S. M. 2015 Classical scaling and intermittency in strongly stratified Boussinesq turbulence. J. Fluid Mech. 775, 436–463.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005 Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 025101.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 1999 A generalization of Yaglom’s equation which accounts for the large-scale forcing in heated decaying turbulence. J. Fluid Mech. 391, 359–372.Google Scholar
Davidson, P. 2015 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Djenidi, L. & Antonia, R. A. 2015 A general self-preservation analysis for decaying homogeneous isotropic turbulence. J. Fluid Mech. 773, 345–365.Google Scholar
Djenidi, L., Antonia, R. A. & Danaila, L. 2017a Self-preservation relation to the Kolmogorov similarity hypotheses. Phys. Rev. Fluids 2 (5), 054606.Google Scholar
Djenidi, L., Antonia, R. A., Lefeuvre, N. & Lemay, J. 2015 Complete self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 790, 57–70.Google Scholar
Djenidi, L., Danaila, L., Antonia, R. A. & Tang, S. 2017b A note on the velocity derivative flatness factor in decaying hit. Phys. Fluids 29 (5), 051702.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press.Google Scholar
Gagne, Y., Castaing, B., Baudet, C. & Malecot, Y. 2004 Reynolds dependence of third-order velocity structure functions. Phys. Fluids 16 (2), 482–485.Google Scholar
Gamard, S. & George, W. K. 2000 Reynolds number dependence of energy spectra in the overlap region of isotropic turbulence. Flow Turbul. Combust. 63 (1–4), 443–477.Google Scholar
Gotoh, T. & Nakano, T. 2003 Role of pressure in turbulence. J. Stat. Phys. 113 (5), 855–874.Google Scholar
Henriksen, R. N. 2015 Scale Invariance: Self-Similarity of the Physical World. Wiley.Google Scholar
Hill, R. J. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434, 379–388.Google Scholar
Hill, R. J. & Boratav, O. N. 2001 Next-order structure-function equations. Phys. Fluids 13, 276–283.Google Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.Google Scholar
Kármán, T. V. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164, 192–215.Google Scholar
Kolmogorov, A. N. 1941a The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Dokl. Akad. Nauk SSSR 30, (see also Proc. R. Soc. Lond. A (1991), 434, 9–13).Google Scholar
Kolmogorov, A. N. 1941b Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, (see also Proc. R. Soc. Lond. A (1991), 434, 15–17).Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics: Vol 6 of Course of Theoretical Physics, 2nd edn. Pergamon Press.Google Scholar
Lundgren, T. S. 2002 Kolmogorov two-thirds law by matched asymptotic expansion. Phys. Fluids 14 (2), 638–642.Google Scholar
Meldi, M., Djenidi, L. & Antonia, R. 2018 Reynolds number effect on the velocity derivative flatness factor. J. Fluid Mech. 856, 426–443.Google Scholar
Novikov, E. A 1965 Functionals and the random-force method in turbulence theory. Sov. Phys. JETP 20 (5), 1290–1294.Google Scholar
Oberlack, M. 1997 Invariant modeling in large-eddy simulation of turbulence. In Annu. Res. Briefs, pp. 3–22. Center for Turbulence Research, Stanford University.Google Scholar
Oboukhov, A. M. 1962 Some specific features of atmospheric turbulence. J. Fluid Mech. 13 (1), 77–81.Google Scholar
Saffman, P. G. 1968 Lectures on homogeneous turbulence. In Top. Nonlinear Phys. (ed. Zabusky, N.), pp. 485–614. Springer.Google Scholar
Sreenivasan, K. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L., Abe, H., Zhou., T., Danaila, L. & Zhou, Y. 2015a Transport equation for the meant turbulent energy dissipation rate on the centreline of a fully developed channel flow. J. Fluid Mech. 777, 151–177.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L., Danaila, L. & Zhou, Y. 2017 Finite Reynolds number effect on the scaling range behavior of turbulent longitudinal velocity structure functions. J. Fluid Mech. 820, 341–369.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y. 2015b Complete self-preservation along the axis of a circular cylinder far wake. J. Fluid Mech. 786, 253–274.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y. 2015c Transport equation for the meant turbulent energy dissipation rate in the far-wake of a circular cylinder. J. Fluid Mech. 784, 109–129.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y. 2018 Reappraisal of the velocity derivative flatness factor in various turbulent flows. J. Fluid Mech. 847, 244–265.Google Scholar
Tchoufag, J., Sagaut, P. & Cambon, C. 2012 Spectral approach to finite Reynolds number effects on Kolmogorovs 4/5 law in isotropic turbulence. Phys. Fluids 24 (1), 015107.Google Scholar
Tennekes, I. & Lumley, J. 1975 A First Course in Turbulence. MIT Press, Cambridge, MA.Google Scholar
Thiesset, F., Antonia, R. A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, R2.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence, vol. 483. Springer.Google Scholar
Xu, G., Antonia, R. A. & Rajagopalan, S. 2001 Sweeping decorrelation hypothesis in a turbulent round jet. Fluid Dyn. Res. 28 (5), 311–321.Google Scholar
Yaglom, A. M. 1994 A. N. Kolmogorov as a fluid mechanician and founder of a school in turbulence research. Annu. Rev. Fluid Mech. 26 (1), 1–23.Google Scholar
Yakhot, V. 2001 Mean-field approximation and a small parameter in turbulence theory. Phys. Rev. E 63 (2), 026307.Google Scholar
Zhou, T. & Antonia, R. A. 2000 Reynolds number dependence of the small-scale structure of grid turbulence. J. Fluid Mech. 406, 81–107.Google Scholar