Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-13T22:02:56.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Role of internal structures within a vortex in helicity dynamics

Published online by Cambridge University Press:  04 September 2023

Weiyu Shen Open the ORCID record for Weiyu Shen [Opens in a new window] ,
Jie Yao Open the ORCID record for Jie Yao [Opens in a new window] ,
Fazle Hussain Open the ORCID record for Fazle Hussain [Opens in a new window]  and
Yue Yang Open the ORCID record for Yue Yang [Opens in a new window]
Weiyu Shen
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing 100871, PR China
Jie Yao
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
Fazle Hussain
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
Yue Yang*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing 100871, PR China HEDPS-CAPT and BIC-ESAT, Peking University, Beijing 100871, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

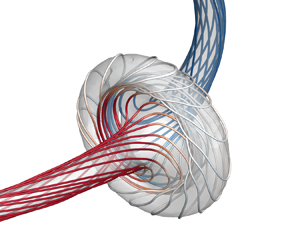
Helicity, an invariant under ideal-fluid (Euler) evolution, has a topological interpretation in terms of writhe and twist for a closed vortex tube, but accurately quantifying twist is challenging in viscous flows. With a novel helicity decomposition, we present a framework to construct the differential twist that establishes the theoretical relation between the total twisting number and the local twist rate of each vortex surface. This framework can characterize coiling vortex lines and internal structures within a vortex – important in laminar–turbulence transition, and in vortex instability, reconnection and breakdown. As a typical example, we explore the dynamics of vortex rings with differential twist via direct numerical simulation (DNS) of the Navier–Stokes equations. Two twist waves with opposite chiralities propagate towards each other along the ring and then collide whence the local twist rate rapidly surges. Local vortex surfaces are squeezed into a disk-like dipole structure containing coiled vortex lines, leading to vortex bursting. We derive a Burgers-equation-like model to quantify this process, which predicts a bursting time that agrees well with DNS.

JFM classification

Mathematical Foundations: Topological fluid dynamics Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 970 , 10 September 2023 , A26
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angriman, S., Cobelli, P.J., Bourgoin, M., Huisman, S.G., Volk, R. & Mininni, P.D. 2021 Broken mirror symmetry of tracer's trajectories in turbulence. Phys. Rev. Lett. 127 (25), 254502.CrossRefGoogle ScholarPubMed
Arendt, S., Fritts, D.C. & Andreassen, Ø. 1997 The initial value problem for Kelvin vortex waves. J. Fluid Mech. 344, 181–212.CrossRefGoogle Scholar
Buaria, D. & Pumir, A. 2022 Vorticity-strain rate dynamics and the smallest scales of turbulence. Phys. Rev. Lett. 128 (9), 094501.CrossRefGoogle ScholarPubMed
Chui, A.Y.K. & Moffatt, H.K. 1995 The energy and helicity of knotted magnetic flux tubes. Proc. R. Soc. Lond. A 451, 609–629.Google Scholar
Cirtain, J.W., et al. 2013 Energy release in the solar corona from spatially resolved magnetic braids. Nature 493, 501–503.CrossRefGoogle ScholarPubMed
Cuypers, Y., Maurel, A. & Petitjeans, P. 2003 Vortex burst as a source of turbulence. Phys. Rev. Lett. 91 (19), 194502.CrossRefGoogle ScholarPubMed
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.CrossRefGoogle Scholar
Fritts, D.C., Arendt, S. & Andreassen, Ø. 1998 Vorticity dynamics in a breaking internal gravity wave. Part 2. Vortex interactions and transition to turbulence. J. Fluid Mech. 367, 47–65.CrossRefGoogle Scholar
Fuller, F.B. 1971 The writhing number of a space curve. Proc. Natl Acad. Sci. USA 68, 815–819.CrossRefGoogle ScholarPubMed
Hussain, A.K.M.F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.CrossRefGoogle Scholar
Hussain, F. & Stout, E. 2013 Self-limiting and regenerative dynamics of perturbation growth on a vortex column. J. Fluid Mech. 718, 39–88.CrossRefGoogle Scholar
Ji, L. & van Rees, W.M. 2022 Bursting on a vortex tube with initial axial core-size perturbations. Phys. Rev. Fluids 7, 044704.CrossRefGoogle Scholar
Kerr, R.M. 2018 a Topology of interacting coiled vortex rings. J. Fluid Mech. 854, R2.CrossRefGoogle Scholar
Kerr, R.M. 2018 b Enstrophy and circulation scaling for Navier–Stokes reconnection. J. Fluid Mech. 839, R2.CrossRefGoogle Scholar
Kleckner, D. & Irvine, W.T.M. 2013 Creation and dynamics of knotted vortices. Nat. Phys. 9 (4), 253–258.CrossRefGoogle Scholar
Kleckner, D., Kauffman, L.H. & Irvine, W.T.M. 2016 How superfluid vortex knots untie. Nat. Phys. 12, 650–655.CrossRefGoogle Scholar
Koplik, J. & Levine, H. 1996 Scattering of superfluid vortex rings. Phys. Rev. Lett. 76 (25), 4745.CrossRefGoogle ScholarPubMed
Leibovich, S. 1978 The structure of vortex breakdown. Annu. Rev. Fluid Mech. 10 (1), 221–246.CrossRefGoogle Scholar
Mayer, E.W. & Powell, K.G. 1992 Viscous and inviscid instabilities of a trailing vortex. J. Fluid Mech. 245, 91–114.CrossRefGoogle Scholar
Melander, M.V. & Hussain, F. 1994 Core dynamics on a vortex column. Fluid Dyn. Res. 13 (1), 1–37.CrossRefGoogle Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43, 219–245.CrossRefGoogle Scholar
Meng, Z., Shen, W. & Yang, Y. 2023 Evolution of dissipative fluid flows with imposed helicity conservation. J. Fluid Mech. 954, A36.CrossRefGoogle Scholar
Moffatt, H.K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.CrossRefGoogle Scholar
Moffatt, H.K. 2021 Extreme events in turbulent flow. J. Fluid Mech. 914, F1.CrossRefGoogle Scholar
Moffatt, H.K., Kida, S. & Ohkitani, K. 1994 Stretched vortices – the sinews of turbulence; large-Reynolds-number asymptotics. J. Fluid Mech. 259, 241–264.CrossRefGoogle Scholar
Moffatt, H.K. & Ricca, R.L. 1992 Helicity and the Călugăreanu invariant. Proc. R. Soc. Lond. A 439, 411–429.Google Scholar
Moffatt, H.K. & Tsinober, A. 1992 Helicity in laminar and turbulent flow. Annu. Rev. Fluid Mech. 24, 281–312.CrossRefGoogle Scholar
Moreau, J.J. 1961 Constantes d'un îlot tourbillonnaire en fluide parfait barotrope. C. R. Hebd. Seances Acad. Sci. 252, 2810–2812.Google Scholar
Pradeep, D.S. & Hussain, F. 2001 Core dynamics of a strained vortex: instability and transition. J. Fluid Mech. 447, 247–285.CrossRefGoogle Scholar
Pullin, D.I. & Saffman, P.G. 1998 Vortex dynamics in turbulence. Annu. Rev. Fluid Mech. 30, 31–51.CrossRefGoogle Scholar
van Rees, W.M. 2020 Vortex bursting. Phys. Rev. Fluids 5 (11), 110504.CrossRefGoogle Scholar
Ricca, R.L., Samuels, D.C. & Barenghi, C.F. 1999 Evolution of vortex knots. J. Fluid Mech. 391, 29–44.CrossRefGoogle Scholar
Robinson, S.K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.CrossRefGoogle Scholar
Ruan, S., Xiong, S., You, J. & Yang, Y. 2022 Generation of streamwise helical vortex loops via successive reconnections in early pipe transition. Phys. Fluids 34 (5), 054112.CrossRefGoogle Scholar
Scheeler, M.W., van Rees, W.M., Kedia, H., Kleckner, D. & Irvine, W.T.M. 2017 Complete measurement of helicity and its dynamics in vortex tubes. Science 357, 487–491.CrossRefGoogle ScholarPubMed
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24 (1), 235–279.CrossRefGoogle Scholar
Shen, W., Yao, J., Hussain, F. & Yang, Y. 2022 Topological transition and helicity conversion of vortex knots and links. J. Fluid Mech. 943, A41.CrossRefGoogle Scholar
Stout, E. 2021 Genesis and evolution of vortex bursting. PhD thesis, Texas Tech University.Google Scholar
Tombach, I. 1973 Observations of atmospheric effects on vortex wake behavior. J. Aircraft 10 (11), 641–647.CrossRefGoogle Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2015 Vortical Flows, vol. 28. Springer.CrossRefGoogle Scholar
Xiong, S. & Yang, Y. 2019 Construction of knotted vortex tubes with the writhe-dependent helicity. Phys. Fluids 31, 047101.CrossRefGoogle Scholar
Xiong, S. & Yang, Y. 2020 Effects of twist on the evolution of knotted magnetic flux tubes. J. Fluid Mech. 895, A28.CrossRefGoogle Scholar
Yang, Y. & Pullin, D.I. 2010 On Lagrangian and vortex-surface fields for flows with Taylor–Green and Kida–Pelz initial conditions. J. Fluid Mech. 661, 446–481.CrossRefGoogle Scholar
Yang, Y. & Pullin, D.I. 2011 Evolution of vortex-surface fields in viscous Taylor–Green and Kida–Pelz flows. J. Fluid Mech. 685, 146–164.CrossRefGoogle Scholar
Yao, J. & Hussain, F. 2022 Vortex reconnection and turbulence cascade. Annu. Rev. Fluid Mech. 54, 317–347.CrossRefGoogle Scholar
Yao, J., Shen, W., Yang, Y. & Hussain, F. 2022 Helicity dynamics of viscous vortex links. J. Fluid Mech. 944, A41.CrossRefGoogle Scholar
Yao, J., Yang, Y. & Hussain, F. 2021 Dynamics of a trefoil knotted vortex. J. Fluid Mech. 923, A19.CrossRefGoogle Scholar
Zhao, X., Yu, Z., Chapelier, J.-B. & Scalo, C. 2021 Direct numerical and large-eddy simulation of trefoil knotted vortices. J. Fluid Mech. 910, A31.CrossRefGoogle Scholar
Zheng, W., Yang, Y. & Chen, S. 2016 Evolutionary geometry of Lagrangian structures in a transitional boundary layer. Phys. Fluids 28, 035110.CrossRefGoogle Scholar