Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T12:46:13.950Z Has data issue: false hasContentIssue false
  • English
  • Français

Resonant three-dimensional nonlinear sloshing in a square-base basin. Part 4. Oblique forcing and linear viscous damping

Published online by Cambridge University Press:  02 June 2017

Odd M. Faltinsen  and
Alexander N. Timokha Open the ORCID record for Alexander N. Timokha [Opens in a new window]
Odd M. Faltinsen*
Affiliation:
Centre for Autonomous Marine Operations and Systems and Department of Marine Technology, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway
Alexander N. Timokha
Affiliation:
Centre for Autonomous Marine Operations and Systems and Department of Marine Technology, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway Institute of Mathematics, National Academy of Sciences of Ukraine, 01601 Kiev, Ukraine
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Faltinsen et al. (J. Fluid Mech., vol. 487, 2003, pp. 1–42) (henceforth, Part 1) examined an undamped nonlinear resonant steady-state sloshing in a square-base tank by developing an approximate (asymptotic) Narimanov–Moiseev-type multimodal theory. The focus was on longitudinal and diagonal harmonic tank excitations. Neglecting the linear viscous boundary-layer damping was justified for model tanks with breadths of the order of metres. However, nonlinear sloshing in clean tanks of smaller size (count in centimetres) may be affected by damping in finite depth conditions. Qualitative and quantitative properties of the damped resonant steady-state sloshing in a square-base tank are now studied by using the modal theory from Part 1 equipped with the linear damping terms. The tank harmonically oscillates along an arbitrary horizontal (oblique) direction. An analytical asymptotic steady-state undamped solution is derived and the corresponding response curves are analysed versus the forcing direction. When the tank width $=$ breadth $=$ $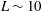L\sim 10$  cm, the surface tension effect on the free-surface dynamics can be neglected but the linear viscous damping should be included into the Narimanov–Moiseev nonlinear asymptotic modal theory. We analytically show that the steady-state damped sloshing possesses a series of distinguishing features so that, e.g. the square-like standing wave regime fully disappears and becomes replaced by swirling. Typical response curves of the damped steady-state resonant sloshing are studied for the liquid depth-to-width ratio exceeding 0.5. The computational results of the steady-state resonant response amplitudes are in a satisfactory agreement with observations and measurements by Ikeda et al. (J. Fluid Mech., vol. 700, 2012, pp. 304–328), which were conducted with a relatively small laboratory container.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
Papers
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , pp. 139 - 169
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ducci, A. & Weheliye, W. H. 2014 Orbitally shaken bioreactors-viscosity effects on flow characteristics. AIChE J. 60 (11), 3951–3968.Google Scholar
Faltinsen, O. M., Rognebakke, O. F. & Timokha, A. N. 2003 Resonant three-dimensional nonlinear sloshing in a square-base basin. J. Fluid Mech. 487, 1–42.Google Scholar
Faltinsen, O. M., Rognebakke, O. F. & Timokha, A. N. 2005a Classification of three-dimensional nonlinear sloshing in a square-base tank with finite depth. J. Fluids Struct. 20 (1), 81–103.Google Scholar
Faltinsen, O. M., Rognebakke, O. F. & Timokha, A. N. 2005b Resonant three-dimensional nonlinear sloshing in a square-base basin. Part 2. Effect of higher modes. J. Fluid Mech. 523, 199–218.CrossRefGoogle Scholar
Faltinsen, O. M., Rognebakke, O. F. & Timokha, A. N. 2006a Resonant three-dimensional nonlinear sloshing in a square-base basin. Part 3. Base ratio perturbation. J. Fluid Mech. 551, 93–116.CrossRefGoogle Scholar
Faltinsen, O. M., Rognebakke, O. F. & Timokha, A. N. 2006b Transient and steady-state amplitudes of resonant three-dimensional sloshing in a square base tank with a finite fluid depth. Phys. Fluids 18, 012103.Google Scholar
Faltinsen, O. M. & Timokha, A. N. 2009 Sloshing. Cambridge University Press.Google Scholar
Grundelius, M.2001 Methods for control of liquid slosh. PhD thesis, Department of Automatic Control, Lund Institute of Technology, Sweden.Google Scholar
Henderson, D. M. & Miles, J. W. 1994 Surface-wave damping in a circular cylinder with a fixed contact line. J. Fluid Mech. 275, 285–299.CrossRefGoogle Scholar
Ikeda, T., Harata, Y. & Osasa, T. 2016 Internal resonance of nonlinear sloshing in rectangular liquid tanks subjected to obliquely horizontal excitation. J. Sound Vib. 361, 210–225.Google Scholar
Ikeda, T., Ibrahim, R. A., Harata, Y. & Kuriyama, T. 2012 Nonlinear liquid sloshing in a square tank subjected to obliquely horizontal excitation. J. Fluid Mech. 700, 304–328.CrossRefGoogle Scholar
Keulegan, G. 1959 Energy dissipation in standing waves in rectangular basins. J. Fluid Mech. 6 (1), 33–50.Google Scholar
Pilipchuk, V. N. 2013 Nonlinear interactions and energy exchange between liquid sloshing modes. Physica D 263, 21–40.Google Scholar
Royon-Lebeaud, A., Hopfinger, E. J. & Cartellier, A. 2007 Liquid sloshing and wave breaking in circular and square-base cylindrical containers. J. Fluid Mech. 577, 467–494.Google Scholar
Shukhmurzaev, Yu. D. 1997 Moving contact lines in liquid/liquid/solid systems. J. Fluid Mech. 334, 211–249.Google Scholar
Wu, C.-H. & Chen, B.-F. 2009 Sloshing waves and resonance modes of fluid in a 3D tank by a time-independent finite difference method. Ocean Engng 36, 500–510.CrossRefGoogle Scholar
Wu, C.-H., Chen, B.-F. & Hung, T.-K. 2013a Hydrodynamic forces induced by transient sloshing in a 3D rectangular tank due to oblique horizontal excitation. Comput. Math. Appl. 65, 1163–1186.Google Scholar
Wu, C.-H., Faltinsen, O. M. & Chen, B.-F. 2013b Analysis on shift of nature modes of liquid sloshing in a 3D tank subjected to oblique horizontal ground motions with damping devices. Adv. Mech. Engng 627124.Google Scholar
Zhang, H.-S., Wu, P.-F. & Liu, W.-B. 2014 The analysis of second-order sloshing resonance in a 3-D tank. J. Hydrodyn. 26 (2), 309–315.Google Scholar
Supplementary material: File

Faltinsen and Timokha supplementary material

Faltinsen and Timokha supplementary material 1

Download Faltinsen and Timokha supplementary material(File)
File 2.5 KB