Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T14:54:31.607Z Has data issue: false hasContentIssue false
  • English
  • Français

On drag reduction scaling and sustainability bounds of superhydrophobic surfaces in high Reynolds number turbulent flows

Published online by Cambridge University Press:  07 February 2019

Amirreza Rastegari Open the ORCID record for Amirreza Rastegari [Opens in a new window]  and
Rayhaneh Akhavan Open the ORCID record for Rayhaneh Akhavan [Opens in a new window]
Amirreza Rastegari
Affiliation:
Department of Mechanical Engineering, The University of Michigan, Ann Arbor, MI 48109-2125, USA
Rayhaneh Akhavan*
Affiliation:
Department of Mechanical Engineering, The University of Michigan, Ann Arbor, MI 48109-2125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The drag reduction characteristics and sustainability bounds of superhydrophobic (SH) surfaces in high Reynolds number turbulent flows are investigated using results from direct numerical simulation (DNS) and scaling-law analysis. The DNS studies were performed, using lattice Boltzmann methods, in turbulent channel flows at bulk Reynolds numbers of 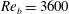$Re_{b}=3600$ (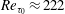$Re_{\unicode[STIX]{x1D70F}_{0}}\approx 222$) and 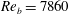$Re_{b}=7860$ (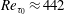$Re_{\unicode[STIX]{x1D70F}_{0}}\approx 442$) with SH longitudinal microgrooves or SH aligned microposts on the walls. Surface microtexture geometrical parameters corresponding to microgroove widths or micropost spacings of 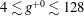$4\lesssim g^{+0}\lesssim 128$ in base flow wall units and solid fractions of 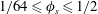$1/64\leqslant \unicode[STIX]{x1D719}_{s}\leqslant 1/2$ were investigated at interface protrusion angles of 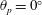$\unicode[STIX]{x1D703}_{p}=0^{\circ }$ and 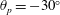$\unicode[STIX]{x1D703}_{p}=-30^{\circ }$. Analysis of the governing equations and DNS results shows that the magnitude of drag reduction is not only a function of the geometry and size of the surface microtexture in wall units, but also the Reynolds number of the base flow. A Reynolds number independent measure of drag reduction can be constructed by parameterizing the magnitude of drag reduction in terms of the friction coefficient of the base flow and the shift, 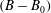$(B-B_{0})$, in the intercept of a logarithmic law representation of the mean velocity profile in the flow with SH walls compared to the base flow, where 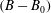$(B-B_{0})$ is Reynolds number independent. The scaling laws for 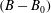$(B-B_{0})$, in terms of the geometrical parameters of the surface microtexture in wall units, are presented for SH longitudinal microgrooves and aligned microposts. The same scaling laws are found to also apply to liquid-infused (LI) surfaces as long as the viscosity ratios are large, 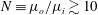$N\equiv \unicode[STIX]{x1D707}_{o}/\unicode[STIX]{x1D707}_{i}\gtrsim 10$. These scaling laws, in conjunction with the parametrization of drag reduction in terms of 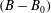$(B-B_{0})$, allow for a priori prediction of the magnitude of drag reduction with SH or LI surfaces in turbulent flow at any Reynolds number. For the most stable of these SH surface microtextures, namely, longitudinal microgrooves, the pressure stability bounds of the SH surface under the pressure loads of turbulent flow are investigated. It is shown that the pressure stability bounds of SH surfaces are also significantly curtailed with increasing Reynolds number of the flow. Using these scaling laws, the narrow range of SH surface geometrical parameters which can yield large drag reduction as well as sustainability in high Reynolds number turbulent flows is identified.

JFM classification

Flow Control: Drag reduction Turbulent Flows: Turbulence control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 327 - 347
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aljallis, E., Sarshar, M. A., Datla, R., Sikka, V., Jones, A. & Choi, C. H. 2013 Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 25 (2), 025103.Google Scholar
Arenas-Navarro, I.2017 Numerical simulations for turbulent drag reduction using liquid infused surfaces. PhD thesis, The University of Texas at Dallas.Google Scholar
Bechert, D. W., Bruse, M., Hage, W., Van Der Hoeven, J. G. T. & Hoppe, G. 1997 Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech. 338, 59–87.10.1017/S0022112096004673Google Scholar
Bidkar, R. A., Leblanc, L., Kulkarni, A. J., Bahadur, V., Ceccio, S. L. & Perlin, M. 2014 Skin-friction drag reduction in the turbulent regime using random-textured hydrophobic surfaces. Phys. Fluids 26 (8), 085108.10.1063/1.4892902Google Scholar
Checco, A., Ocko, B. M., Rahman, A., Black, C. T., Tasinkevych, M., Giacomello, A. & Dietrich, S. 2014 Collapse and reversibility of the superhydrophobic state on nanotextured surfaces. Phys. Rev. Lett. 112 (21), 216101.Google Scholar
Daniello, R. J., Waterhouse, N. E. & Rothstein, J. P. 2009 Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids 21 (8), 085103.Google Scholar
Dean, R. B. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. Trans. ASME J. Fluids Engng 100 (2), 215–223.10.1115/1.3448633Google Scholar
Fu, M. K., Arenas, I., Leonardi, S. & Hultmark, M. 2017 Liquid-infused surfaces as a passive method of turbulent drag reduction. J. Fluid Mech. 824, 688–700.10.1017/jfm.2017.360Google Scholar
García-Mayoral, R. & Jiménez, J. 2012 Scaling of turbulent structures in riblet channels up to Re 𝜏 ≈ 550. Phys. Fluids 24 (10), 105101.Google Scholar
Gose, J., Golovin, K., Boban, M., Mabry, J., Tuteja, A., Perlin, M. & Ceccio, S. 2018 Characterization of superhydrophobic surfaces for drag reduction in turbulent flow. J. Fluid Mech. 845, 560–580.10.1017/jfm.2018.210Google Scholar
Karatay, E., Tsai, P. A. & Lammertink, R. G. H. 2013 Rate of gas absorption on a slippery bubble mattress. Soft Matt. 9 (46), 11098–11106.10.1039/c3sm51928gGoogle Scholar
Lagrava, D., Malaspinas, O., Latt, J. & Chopard, B. 2012 Advances in multi-domain lattice Boltzmann grid refinement. J. Comput. Phys. 231 (14), 4808–4822.Google Scholar
Ling, H., Katz, J., Fu, M. & Hultmark, M. 2017 Effect of Reynolds number and saturation level on gas diffusion in and out of a superhydrophobic surface. Phys. Rev. Fluids 2 (12), 124005.10.1103/PhysRevFluids.2.124005Google Scholar
Ling, H., Srinivasan, S., Golovin, K., McKinley, G. H., Tuteja, A. & Katz, J. 2016 High-resolution velocity measurement in the inner part of turbulent boundary layers over super-hydrophobic surfaces. J. Fluid Mech. 801, 670–703.10.1017/jfm.2016.450Google Scholar
Min, T. & Kim, J. 2004 Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 16 (7), L55.Google Scholar
Nishino, T., Meguro, T., Nakamae, K., Matsushita, M. & Ueda, Y. 1999 The lowest surface free energy based on -CF3 alignment. Langmuir 15, 4321–4323.10.1021/la981727sGoogle Scholar
Park, H., Park, H. & Kim, J. 2013 A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25 (11), 110815.Google Scholar
Park, H., Sun, G. & Kim, C.-J. 2014 Superhydrophobic turbulent drag reduction as a function of surface grating parameters. J. Fluid Mech. 747, 722–734.10.1017/jfm.2014.151Google Scholar
Philip, J. R. 1972 Flows satisfying mixed no-slip and no-shear conditions. Z. Angew. Math. Phys. 23 (3), 353–372.Google Scholar
Rastegari, A. & Akhavan, R. 2015 On the mechanism of turbulent drag reduction with super-hydrophobic surfaces. J. Fluid Mech. 773, R4.Google Scholar
Rastegari, A. & Akhavan, R. 2018a The common mechanism of turbulent skin-friction drag reduction with super-hydrophobic longitudinal microgrooves and riblets. J. Fluid Mech. 838, 68–104.10.1017/jfm.2017.865Google Scholar
Rastegari, A. & Akhavan, R. 2018b Effect of interface dynamics on drag reduction and sustainability of superhydrophobic and liquid-infused surfaces in turbulent flow. Bull. Am. Phys. Soc. 63 (13), 143.Google Scholar
Reholon, D. & Ghaemi, S. 2018 Plastron morphology and drag of a superhydrophobic surface in turbulent regime. Phys. Rev. Fluids 3, 104003.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.10.1146/annurev-fluid-121108-145558Google Scholar
Samaha, M. A., Tafreshi, H. V. & Gad-el Hak, M. 2012 Influence of flow on longevity of superhydrophobic coatings. Langmuir 28 (25), 9759–9766.10.1021/la301299eGoogle Scholar
Schellenberger, F., Encinas, N., Vollmer, D. & Butt, H.-J. 2016 How water advances on superhydrophobic surfaces. Phys. Rev. Lett. 116 (9), 096101.Google Scholar
Schewe, G. 1983 On the structure and resolution of wall-pressure fluctuations associated with turbulent boundary-layer flow. J. Fluid Mech. 134, 311–328.10.1017/S0022112083003389Google Scholar
Schönecker, C., Baier, T. & Hardt, S. 2014 Influence of the enclosed fluid on the flow over a microstructured surface in the Cassie state. J. Fluid Mech. 740, 168–195.10.1017/jfm.2013.647Google Scholar
Seo, J., García-Mayoral, R. & Mani, A. 2015 Pressure fluctuations and interfacial robustness in turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 783, 448–473.10.1017/jfm.2015.573Google Scholar
Seo, J. & Mani, A. 2016 On the scaling of the slip velocity in turbulent flows over superhydrophobic surfaces. Phys. Fluids 28, 025110.10.1063/1.4941769Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.Google Scholar
Spalart, P. R. & McLean, D. 2011 Drag reduction: enticing turbulence, and then an industry. Phil. Trans. R. Soc. Lond. A 369, 1556–1569.Google Scholar
Srinivasan, S., Kleingartner, J. A., Gilbert, J. B., Cohen, R. E., Milne, A. J. B. & McKinley, G. H. 2015 Sustainable drag reduction in turbulent Taylor–Couette flows by depositing sprayable superhydrophobic surfaces. Phys. Rev. Lett. 114 (1), 014501.10.1103/PhysRevLett.114.014501Google Scholar
Succi, S. 2001 The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond. Oxford University Press.Google Scholar
Tsuji, Y., Fransson, J. H. M., Alfredsson, P. H. & Johansson, A. V. 2007 Pressure statistics and their scaling in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 585, 1–40.Google Scholar
Van Buren, T. & Smits, A. J. 2017 Substantial drag reduction in turbulent flow using liquid-infused surfaces. J. Fluid Mech. 827, 448–456.10.1017/jfm.2017.503Google Scholar
Wexler, J. S., Jacobi, I. & Stone, H. A. 2015 Shear-driven failure of liquid-infused surfaces. Phys. Rev. Lett. 114 (16), 168301.10.1103/PhysRevLett.114.168301Google Scholar
Ybert, C., Barentin, C., Cottin-Bizonne, C., Joseph, P. & Bocquet, L. 2007 Achieving large slip with superhydrophobic surfaces: scaling laws for generic geometries. Phys. Fluids 19 (12), 123601.10.1063/1.2815730Google Scholar
Zanoun, E.-S., Nagib, H. & Durst, F. 2009 Refined c f relation for turbulent channels and consequences for high-re experiments. Fluid Dyn. Res. 41 (2), 021405.Google Scholar
Zhang, J., Tian, H., Yao, Z., Hao, P. & Jiang, N. 2015 Mechanisms of drag reduction of superhydrophobic surfaces in a turbulent boundary layer flow. Exp. Fluids 56 (9), 179.Google Scholar
Zheng, Q.-S., Yu, Y. & Zhao, Z.-H. 2005 Effects of hydraulic pressure on the stability and transition of wetting modes of superhydrophobic surfaces. Langmuir 21 (26), 12207–12212.10.1021/la052054yGoogle Scholar