Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Desai, Nikhil
and
Ardekani, Arezoo M.
2017.
Modeling of active swimmer suspensions and their interactions with the environment.
Soft Matter,
Vol. 13,
Issue. 36,
p.
6033.
Desai, Nikhil
Shaik, Vaseem A.
and
Ardekani, Arezoo M.
2018.
Hydrodynamics-mediated trapping of micro-swimmers near drops.
Soft Matter,
Vol. 14,
Issue. 2,
p.
264.
Jabbarzadeh, Mehdi
and
Fu, Henry Chien
2018.
Viscous constraints on microorganism approach and interaction.
Journal of Fluid Mechanics,
Vol. 851,
Issue. ,
p.
715.
Shaik, Vaseem A.
Vasani, Vishwa
and
Ardekani, Arezoo M.
2018.
Locomotion inside a surfactant-laden drop at low surface Péclet numbers.
Journal of Fluid Mechanics,
Vol. 851,
Issue. ,
p.
187.
Desai, Nikhil
and
Ardekani, Arezoo M.
2018.
Combined influence of hydrodynamics and chemotaxis in the distribution of microorganisms around spherical nutrient sources.
Physical Review E,
Vol. 98,
Issue. 1,
Shaik, Vaseem A.
and
Ardekani, Arezoo M.
2019.
Swimming sheet near a plane surfactant-laden interface.
Physical Review E,
Vol. 99,
Issue. 3,
K V S, Chaithanya
and
Thampi, Sumesh P
2020.
Deformation dynamics of an active compound particle in an imposed shear flow—a theoretical study.
Journal of Physics D: Applied Physics,
Vol. 53,
Issue. 31,
p.
314001.
Dalal, Swapnil
Farutin, Alexander
and
Misbah, Chaouqi
2020.
Amoeboid swimming in a compliant channel.
Soft Matter,
Vol. 16,
Issue. 6,
p.
1599.
Poddar, Antarip
Bandopadhyay, Aditya
and
Chakraborty, Suman
2020.
Near-wall hydrodynamic slip triggers swimming state transition of micro-organisms.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Sprenger, Alexander R.
Shaik, Vaseem A.
Ardekani, Arezoo M.
Lisicki, Maciej
Mathijssen, Arnold J. T. M.
Guzmán-Lastra, Francisca
Löwen, Hartmut
Menzel, Andreas M.
and
Daddi-Moussa-Ider, Abdallah
2020.
Towards an analytical description of active microswimmers in clean and in surfactant-covered drops.
The European Physical Journal E,
Vol. 43,
Issue. 9,
Desai, Nikhil
and
Ardekani, Arezoo M.
2020.
Biofilms at interfaces: microbial distribution in floating films.
Soft Matter,
Vol. 16,
Issue. 7,
p.
1731.
Chisholm, Nicholas G.
and
Stebe, Kathleen J.
2021.
Driven and active colloids at fluid interfaces.
Journal of Fluid Mechanics,
Vol. 914,
Issue. ,
Faltas, M.S.
Sherief, H.H.
Allam, Allam A.
and
Ahmed, Baraa A.
2021.
Axisymmetric motion of a slip spherical particle in the presence of a Brinkman interface with stress jump.
European Journal of Mechanics - B/Fluids,
Vol. 90,
Issue. ,
p.
73.
Sherief, H. H.
Faltas, M. S.
and
Ragab, Kareem E.
2021.
Exact solution for the slow motion of a spherical particle in the presence of an interface with slip regime.
The European Physical Journal Plus,
Vol. 136,
Issue. 4,
Kurzthaler, Christina
and
Stone, Howard A.
2021.
Microswimmers near corrugated, periodic surfaces.
Soft Matter,
Vol. 17,
Issue. 12,
p.
3322.
Pourali, Meisam
Jaensson, Nick O.
and
Kröger, Martin
2021.
Drag on a spheroidal particle at clean and surfactant-laden interfaces: effects of particle aspect ratio, contact angle and surface viscosities.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Nezamipour, Shima
and
Najafi, Ali
2021.
Flow pumping by external periodic shear applied to a soft interface.
Scientific Reports,
Vol. 11,
Issue. 1,
Sherief, H.H.
Faltas, M.S.
and
Ragab, Kareem E.
2021.
Motion of a slip spherical particle near a planar micropolar-viscous interface.
European Journal of Mechanics - B/Fluids,
Vol. 89,
Issue. ,
p.
274.
Ruiz-Martín, Désirée
Rivero-Rodriguez, Javier
and
Sánchez-Sanz, Mario
2022.
Solid particles moving parallel to a deformable liquid–liquid interface in a micro-channel: migration forces.
Journal of Fluid Mechanics,
Vol. 948,
Issue. ,
Gidituri, Harinadha
Shen, Zaiyi
Würger, Alois
and
Lintuvuori, Juho S.
2022.
Reorientation dynamics of microswimmers at fluid-fluid interfaces.
Physical Review Fluids,
Vol. 7,
Issue. 4,
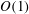 $O(1)$ distances of the swimmer from the interface.
$O(1)$ distances of the swimmer from the interface.