Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T20:07:20.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Interferometric detection of hydrodynamic bubble–bubble interactions

Published online by Cambridge University Press:  17 May 2022

D. Raciti Open the ORCID record for D. Raciti [Opens in a new window] ,
P. Brocca Open the ORCID record for P. Brocca [Opens in a new window] ,
A. Raudino  and
M. Corti
D. Raciti*
Affiliation:
CNR-IMM, Zona Industriale, VIII Strada 5, 95121 Catania, Italy
P. Brocca
Affiliation:
Department of Biotechnologies and Translational Medicine, University of Milan, LITA, via Fratelli Cervi 93, 20090 Segrate, Italy
A. Raudino
Affiliation:
Department of Chemical Sciences, University of Catania, Viale A. Doria 6, 95125 Catania, Italy
M. Corti
Affiliation:
CNR-IPCF, Viale Ferdinando Stagno d'Alcontres 37, 98158 Messina, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

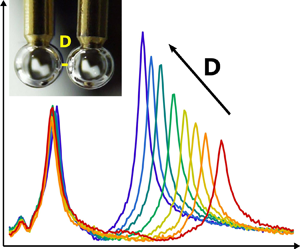
We report a new interferometric method to study the interactions between two gas bubbles undergoing small-amplitude oscillations in a liquid, based on the extension of a previously developed one-bubble set-up. Nanometric oscillations of millimetre-sized supported bubbles are excited acoustically; the response of each bubble is recorded interferometrically, as a function of the mutual distance (from quasi-contact to greater than the bubbles radii). The interferometric nature of the technique and the resonant nature of the vibration modes enable the accurate measurement of the amplitude (with sub-nanometric sensitivity), frequency and mutual phase of oscillation, whose variations over the bubble–bubble distance range allow the interactions to be probed. The bubbles oscillate at the same frequencies, exhibiting a low-frequency, in-phase and a high-frequency, out-of-phase resonance peak, whose separation is a function of distance, in good agreement with the theory for free interacting bubbles. The technique, here demonstrated for the volume modes of air bubbles in water, can be extended to other gas–liquid and liquid–liquid interfaces, bare or adsorbate-covered, as well as to shape oscillations.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Multiphase flow
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 942 , 10 July 2022 , R1
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bjerknes, C.A. 1915 Hydrodynamische Fernkräfte: fünf Abhandlungen über die Bewegung kugelförmiger Körper in einer inkompressiblen Flüssigkeit (1863–1880). W. Engelmann.Google Scholar
Bjerknes, V. 1906 Fields of Force: Supplementary Lectures, Applications to Meteorology; A Course of Lectures in Mathematical Physics Delivered December 1 to 23, 1905. Columbia University Press.Google Scholar
Bjerknes, V. 1909 Die Kraftfelder, vol. 28. F. Vieweg.Google Scholar
Blue, J.E. 1967 Resonance of a bubble on an infinite rigid boundary. J. Acoust. Soc. Am. 41 (2), 369–372.CrossRefGoogle Scholar
Boughzala, M., Stephan, O., Bossy, E., Dollet, B. & Marmottant, P. 2021 Polyhedral bubble vibrations. Phys. Rev. Lett. 126 (5), 054502.CrossRefGoogle ScholarPubMed
Bremond, N., Arora, M., Ohl, C.D. & Lohse, D. 2005 Cavitating bubbles on patterned surfaces. Phys. Fluids 17 (9), 091111.CrossRefGoogle Scholar
Bremond, N., Arora, M., Ohl, C.D. & Lohse, D. 2006 Controlled multibubble surface cavitation. Phys. Rev. Lett. 96 (22), 224501.CrossRefGoogle ScholarPubMed
Brocca, P., Saponaro, A., Introini, B., Rondelli, V., Pannuzzo, M., Raciti, D., Corti, M. & Raudino, A. 2019 Protein adsorption at the air–water interface by a charge sensing interferometric technique. Langmuir 35 (49), 16087–16100.CrossRefGoogle ScholarPubMed
Cantu’, L., Raudino, A. & Corti, M. 2017 An interferometric technique to study capillary waves. Adv. Colloid Interface Sci. 247, 23–32.CrossRefGoogle ScholarPubMed
Chew, L.W., Klaseboer, E., Ohl, S.W. & Khoo, B.C. 2011 Interaction of two differently sized oscillating bubbles in a free field. Phys. Rev. E 84 (6), 066307.CrossRefGoogle Scholar
Combriat, T., Rouby-Poizat, P., Doinikov, A.A., Stephan, O. & Marmottant, P. 2020 Acoustic interaction between 3d-fabricated cubic bubbles. Soft Matt. 16 (11), 2829–2835.CrossRefGoogle ScholarPubMed
Corti, M., Bonomo, M. & Raudino, A. 2012 New interferometric technique to evaluate the electric charge of gas bubbles in liquids. Langmuir 28 (14), 6060–6066.CrossRefGoogle ScholarPubMed
Corti, M., Pannuzzo, M. & Raudino, A. 2014 Out of equilibrium divergence of dissipation in an oscillating bubble coated by surfactants. Langmuir 30 (2), 477–487.CrossRefGoogle Scholar
Corti, M., Pannuzzo, M. & Raudino, A. 2015 Trapping of sodium dodecyl sulfate at the air–water interface of oscillating bubbles. Langmuir 31 (23), 6277–6281.CrossRefGoogle ScholarPubMed
Corti, M., Raudino, A., Cantu’, L., Theisen, J., Pleines, M. & Zemb, T. 2018 Nanometric surface oscillation spectroscopy of water-poor microemulsions. Langmuir 34 (28), 8154–8162.CrossRefGoogle ScholarPubMed
Deane, G.B. & Stokes, M.D. 2008 The acoustic excitation of air bubbles fragmenting in sheared flow. J. Acoust. Soc. Am. 124 (6), 3450–3463.CrossRefGoogle ScholarPubMed
Doinikov, A.A., Bienaimé, D., Gonzalez-Avila, S.R., Ohl, C.D. & Marmottant, P. 2019 Nonlinear dynamics of two coupled bubbles oscillating inside a liquid-filled cavity surrounded by an elastic medium. Phys. Rev. E 99 (5), 053106.CrossRefGoogle ScholarPubMed
Doinikov, A.A. & Bouakaz, A. 2015 Theoretical model for coupled radial and translational motion of two bubbles at arbitrary separation distances. Phys. Rev. E 92 (4), 043001.CrossRefGoogle ScholarPubMed
Foldy, L.L. 1945 The multiple scattering of waves. I. General theory of isotropic scattering by randomly distributed scatterers. Phys. Rev. 67 (3–4), 107–119.CrossRefGoogle Scholar
Fong, S.W., Adhikari, D., Klaseboer, E. & Khoo, B.C. 2009 Interactions of multiple spark-generated bubbles with phase differences. Exp. Fluids 46 (4), 705–724.CrossRefGoogle Scholar
Garbin, V., Dollet, B., Overvelde, M.L.J., De Jong, N., Lohse, D., Versluis, M., Cojoc, D., Ferrari, E. & Di Fabrizio, E. 2007 9B-1 coupled dynamics of an isolated UCA microbubble pair. In 2007 IEEE Ultrasonics Symposium Proceedings, pp. 757–760. IEEE.CrossRefGoogle Scholar
Guédra, M., Inserra, C., Mauger, C. & Gilles, B. 2016 Experimental evidence of nonlinear mode coupling between spherical and nonspherical oscillations of microbubbles. Phys. Rev. E 94 (5), 053115.CrossRefGoogle ScholarPubMed
Hsiao, P.Y., Devaud, M. & Bacri, J.C. 2001 Acoustic coupling between two air bubbles in water. Eur. Phys. J. E 4 (1), 5–10.CrossRefGoogle Scholar
Ida, M. 2002 A characteristic frequency of two mutually interacting gas bubbles in an acoustic field. Phys. Lett. A 297 (3–4), 210–217.CrossRefGoogle Scholar
Kapodistrias, G. & Dahl, P.H. 2000 Effects of interaction between two bubble scatterers. J. Acoust. Soc. Am. 107 (6), 3006–3017.CrossRefGoogle ScholarPubMed
Kuramoto, Y. 2003 Chemical Oscillations, Waves, and Turbulence. Courier Corporation.Google Scholar
Lauterborn, W. & Kurz, T. 2010 Physics of bubble oscillations. Rep. Prog. Phys. 73 (10), 106501.CrossRefGoogle Scholar
Leighton, T.G. 2004 From seas to surgeries, from babbling brooks to baby scans: the acoustics of gas bubbles in liquids. Intl J. Mod. Phys. B 18 (25), 3267–3314.CrossRefGoogle Scholar
Leighton, T.G. 2012 The Acoustic Bubble. Academic Press.Google Scholar
Ma, Y. & Zhao, F. 2021 Nonlinear oscillation and acoustic scattering of bubbles. Ultrason. Sonochem. 74, 105573.CrossRefGoogle ScholarPubMed
Maksimov, A.O. 2005 On the volume oscillations of a tethered bubble. J. Sound Vib. 283 (3–5), 915–926.CrossRefGoogle Scholar
Maksimov, A.O. 2018 Symmetry approach in the evaluation of the effect of boundary proximity on oscillation of gas bubbles. Fluids 3 (4), 90–106.CrossRefGoogle Scholar
Maksimov, A.O. & Polovinka, Y.A. 2018 Scattering from a pair of closely spaced bubbles. J. Acoust. Soc. Am. 144 (1), 104–114.CrossRefGoogle ScholarPubMed
Maksimov, A.O. & Yusupov, V.I. 2016 Coupled oscillations of a pair of closely spaced bubbles. Eur. J. Mech. B/Fluids 60, 164–174.CrossRefGoogle Scholar
Manasseh, R., Riboux, G. & Risso, F. 2008 Sound generation on bubble coalescence following detachment. Intl J. Multiphase Flow 34 (10), 938–949.CrossRefGoogle Scholar
Mathijssen, A.J.T.M., Culver, J., Bhamla, M.S. & Prakash, M. 2019 Collective intercellular communication through ultra-fast hydrodynamic trigger waves. Nature 571 (7766), 560–564.CrossRefGoogle ScholarPubMed
Mettin, R. 2005 Bubble structures in acoustic cavitation. In Bubble and Particle Dynamics in Acoustic Fields: Modern Trends and Applications (ed. A.A. Doinikov), pp. 1–36. Research Signpost, Kerala.Google Scholar
Minnaert, M. 1933 XVI. On musical air-bubbles and the sounds of running water. Lond. Edinb. Dublin Philos. Mag. J. Sci. 16 (104), 235–248.CrossRefGoogle Scholar
Oguz, H.N. & Prosperetti, A. 1990 Bubble oscillations in the vicinity of a nearly plane free surface. J. Acoust. Soc. Am. 87 (5), 2085–2092.CrossRefGoogle Scholar
Oguz, H.N. & Prosperetti, A. 1998 The natural frequency of oscillation of gas bubbles in tubes. J. Acoust. Soc. Am. 103 (6), 3301–3308.CrossRefGoogle Scholar
Pandey, V. 2019 Asymmetricity and sign reversal of secondary Bjerknes force from strong nonlinear coupling in cavitation bubble pairs. Phys. Rev. E 99 (4), 042209.CrossRefGoogle ScholarPubMed
Pelekasis, N.A., Gaki, A., Doinikov, A.A. & Tsamopoulos, J.A. 2004 Secondary Bjerknes forces between two bubbles and the phenomenon of acoustic streamers. J. Fluid Mech. 500, 313–347.CrossRefGoogle Scholar
Raudino, A., Raciti, D. & Corti, M. 2017 Anomalous behavior of ultra-low-amplitude capillary waves. A glimpse of the viscoelastic properties of interfacial water? Langmuir 33 (25), 6439–6448.CrossRefGoogle ScholarPubMed
Robinson, P.B., Blake, J.R., Kodama, T., Shima, A. & Tomita, Y. 2001 Interaction of cavitation bubbles with a free surface. J. Appl. Phys. 89 (12), 8225–8237.CrossRefGoogle Scholar
Van der Meer, S.M., Dollet, B., Voormolen, M.M., Chin, C.T., Bouakaz, A., de Jong, N., Versluis, M. & Lohse, D. 2007 Microbubble spectroscopy of ultrasound contrast agents. J. Acoust. Soc. Am. 121 (1), 648–656.CrossRefGoogle ScholarPubMed
Versluis, M., Goertz, D.E., Palanchon, P., Heitman, I.L., van der Meer, S.M., Dollet, B., de Jong, N. & Lohse, D. 2010 Microbubble shape oscillations excited through ultrasonic parametric driving. Phys. Rev. E 82 (2), 026321.CrossRefGoogle ScholarPubMed
Wiedemair, W., Tukovic, Z., Jasak, H., Poulikakos, D. & Kurtcuoglu, V. 2014 Modeling the interaction of microbubbles: effects of proximity, confinement, and excitation amplitude. Phys. Fluids 26 (6), 062106.CrossRefGoogle Scholar
Zeravcic, Z., Lohse, D. & Van Saarloos, W. 2011 Collective oscillations in bubble clouds. J. Fluid Mech. 680, 114–149.CrossRefGoogle Scholar
Supplementary material: File

Raciti et al. supplementary material

Raciti et al. supplementary material

Download Raciti et al. supplementary material(File)
File 425.6 KB