Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jepson, Alys
Martinez, Vincent A.
Schwarz-Linek, Jana
Morozov, Alexander
and
Poon, Wilson C. K.
2013.
Enhanced diffusion of nonswimmers in a three-dimensional bath of motile bacteria.
Physical Review E,
Vol. 88,
Issue. 4,
Kasyap, T. V.
Koch, Donald L.
and
Wu, Mingming
2014.
Hydrodynamic tracer diffusion in suspensions of swimming bacteria.
Physics of Fluids,
Vol. 26,
Issue. 8,
Balk, Andrew L.
Mair, Lamar O.
Mathai, Pramod P.
Patrone, Paul N.
Wang, Wei
Ahmed, Suzanne
Mallouk, Thomas E.
Liddle, J. Alexander
and
Stavis, Samuel M.
2014.
Kilohertz Rotation of Nanorods Propelled by Ultrasound, Traced by Microvortex Advection of Nanoparticles.
ACS Nano,
Vol. 8,
Issue. 8,
p.
8300.
Kaiser, A.
and
Löwen, H.
2014.
Unusual swelling of a polymer in a bacterial bath.
The Journal of Chemical Physics,
Vol. 141,
Issue. 4,
Clarke, R. J.
Finn, M. D.
and
MacDonald, M.
2014.
Hydrodynamic persistence within very dilute two-dimensional suspensions of squirmers.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 470,
Issue. 2167,
p.
20130508.
Morozov, Alexander
and
Marenduzzo, Davide
2014.
Enhanced diffusion of tracer particles in dilute bacterial suspensions.
Soft Matter,
Vol. 10,
Issue. 16,
p.
2748.
Molina, John J.
and
Yamamoto, Ryoichi
2014.
Diffusion of colloidal particles in swimming suspensions.
Molecular Physics,
Vol. 112,
Issue. 9-10,
p.
1389.
Pushkin, Dmitri O
and
Yeomans, Julia M
2014.
Stirring by swimmers in confined microenvironments.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2014,
Issue. 4,
p.
P04030.
Frenkel, Gad
2015.
Droplet shape fluctuations in agitated emulsions—Beyond the dilute limit.
Physica A: Statistical Mechanics and its Applications,
Vol. 427,
Issue. ,
p.
251.
Stenhammar, Joakim
Wittkowski, Raphael
Marenduzzo, Davide
and
Cates, Michael E.
2015.
Activity-Induced Phase Separation and Self-Assembly in Mixtures of Active and Passive Particles.
Physical Review Letters,
Vol. 114,
Issue. 1,
Saintillan, David
and
Shelley, Michael J.
2015.
Complex Fluids in Biological Systems.
p.
319.
Kaiser, A.
Sokolov, A.
Aranson, I. S.
and
Löwen, H.
2015.
Motion of two micro-wedges in a turbulent bacterial bath.
The European Physical Journal Special Topics,
Vol. 224,
Issue. 7,
p.
1275.
Krishnamurthy, Deepak
and
Subramanian, Ganesh
2015.
Collective motion in a suspension of micro-swimmers that run-and-tumble and rotary diffuse.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
p.
422.
Mallory, S. A.
Valeriani, C.
and
Cacciuto, A.
2015.
Anomalous dynamics of an elastic membrane in an active fluid.
Physical Review E,
Vol. 92,
Issue. 1,
Kaiser, Andreas
Sokolov, Andrey
Aranson, Igor S.
and
Lowen, Hartmut
2015.
Mechanisms of Carrier Transport Induced by a Microswimmer Bath.
IEEE Transactions on NanoBioscience,
Vol. 14,
Issue. 3,
p.
260.
Thiffeault, Jean-Luc
2015.
Distribution of particle displacements due to swimming microorganisms.
Physical Review E,
Vol. 92,
Issue. 2,
Mathijssen, A. J. T. M.
Pushkin, D. O.
and
Yeomans, J. M.
2015.
Tracer trajectories and displacement due to a micro-swimmer near a surface.
Journal of Fluid Mechanics,
Vol. 773,
Issue. ,
p.
498.
Dey, Krishna Kanti
Pong, Frances Ying
Breffke, Jens
Pavlick, Ryan
Hatzakis, Emmanuel
Pacheco, Carlos
and
Sen, Ayusman
2016.
Dynamic Coupling at the Ångström Scale.
Angewandte Chemie International Edition,
Vol. 55,
Issue. 3,
p.
1113.
Lauga, Eric
2016.
Bacterial Hydrodynamics.
Annual Review of Fluid Mechanics,
Vol. 48,
Issue. 1,
p.
105.
Peng, Yi
Lai, Lipeng
Tai, Yi-Shu
Zhang, Kechun
Xu, Xinliang
and
Cheng, Xiang
2016.
Diffusion of Ellipsoids in Bacterial Suspensions.
Physical Review Letters,
Vol. 116,
Issue. 6,
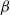 $\beta $, as observed experimentally. This paper shows that
$\beta $, as observed experimentally. This paper shows that 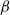 $\beta $ increases as a result of the interaction with solid surfaces. The coefficient
$\beta $ increases as a result of the interaction with solid surfaces. The coefficient 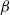 $\beta $ scales as the tracer–swimmer cross-section times the mean square displacement produced by single scattering events, which depends on the swimmer propulsion forces. Considering simple swimmer models (acting on the fluid as two monopoles or as a force dipole), it is shown that
$\beta $ scales as the tracer–swimmer cross-section times the mean square displacement produced by single scattering events, which depends on the swimmer propulsion forces. Considering simple swimmer models (acting on the fluid as two monopoles or as a force dipole), it is shown that 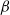 $\beta $ increases for decreasing swimming efficiencies. Close to solid surfaces, the swimming efficiency degrades and, consequently, the induced diffusion increases. Experiments on wild-type Escherichia coli in a Hele-Shaw cell, under buoyant conditions, are performed to measure the induced diffusion on tracers near surfaces. The modification of the suspension pH varies the swimmers’ velocity over a wide range, allowing the
$\beta $ increases for decreasing swimming efficiencies. Close to solid surfaces, the swimming efficiency degrades and, consequently, the induced diffusion increases. Experiments on wild-type Escherichia coli in a Hele-Shaw cell, under buoyant conditions, are performed to measure the induced diffusion on tracers near surfaces. The modification of the suspension pH varies the swimmers’ velocity over a wide range, allowing the 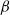 $\beta $ coefficient to be extracted with precision. It is found that solid surfaces modify the induced diffusion: decreasing the confinement height of the cell,
$\beta $ coefficient to be extracted with precision. It is found that solid surfaces modify the induced diffusion: decreasing the confinement height of the cell, 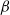 $\beta $ increases by a factor of 4. The theoretical model reproduces this increase, although there are quantitative differences, probably attributed to the simplicity of the swimmer models and to the estimates for the parameters that model E. coli.
$\beta $ increases by a factor of 4. The theoretical model reproduces this increase, although there are quantitative differences, probably attributed to the simplicity of the swimmer models and to the estimates for the parameters that model E. coli.