Published online by Cambridge University Press: 22 March 2017
We present a model for ice formation in a thin, viscous liquid film driven by a Blasius boundary layer after heating is switched off along part of the flat plate. The flow is assumed to initially be in the Nelson et al. (J. Fluid Mech., vol. 284, 1995, pp. 159–169) steady-state configuration with a constant flux of liquid supplied at the tip of the plate, so that the film thickness grows like 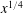 $x^{1/4}$ in distance along the plate. Plate cooling is applied downstream of a point,
$x^{1/4}$ in distance along the plate. Plate cooling is applied downstream of a point, 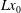 $Lx_{0}$, an
$Lx_{0}$, an 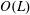 $O(L)$-distance from the tip of the plate, where
$O(L)$-distance from the tip of the plate, where 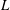 $L$ is much larger than the film thickness. The cooling is assumed to be slow enough that the flow is quasi-steady. We present a thorough asymptotic derivation of the governing equations from the incompressible Navier–Stokes equations in each fluid and the corresponding Stefan problem for ice growth. The problem breaks down into two temporal regimes corresponding to the relative size of the temperature difference across the ice, which are analysed in detail asymptotically and numerically. In each regime, two distinct spatial regions arise, an outer region of the length scale of the plate, and an inner region close to
$L$ is much larger than the film thickness. The cooling is assumed to be slow enough that the flow is quasi-steady. We present a thorough asymptotic derivation of the governing equations from the incompressible Navier–Stokes equations in each fluid and the corresponding Stefan problem for ice growth. The problem breaks down into two temporal regimes corresponding to the relative size of the temperature difference across the ice, which are analysed in detail asymptotically and numerically. In each regime, two distinct spatial regions arise, an outer region of the length scale of the plate, and an inner region close to 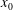 $x_{0}$ in which the film and air are driven over the growing ice layer. Moreover, in the early time regime, there is an additional intermediate region in which the air–water interface propagates a slope discontinuity downstream due to the sudden onset of the ice at the switch-off point. For each regime, we present ice profiles and growth rates, and show that for large times, the film is predicted to rupture in the outer region when the slope discontinuity becomes sufficiently enhanced.
$x_{0}$ in which the film and air are driven over the growing ice layer. Moreover, in the early time regime, there is an additional intermediate region in which the air–water interface propagates a slope discontinuity downstream due to the sudden onset of the ice at the switch-off point. For each regime, we present ice profiles and growth rates, and show that for large times, the film is predicted to rupture in the outer region when the slope discontinuity becomes sufficiently enhanced.
Article last updated 07 March 2023