Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-11T18:23:53.015Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized slip condition over rough surfaces

Published online by Cambridge University Press:  06 November 2018

Giuseppe A. Zampogna Open the ORCID record for Giuseppe A. Zampogna [Opens in a new window] ,
Jacques Magnaudet Open the ORCID record for Jacques Magnaudet [Opens in a new window]  and
Alessandro Bottaro Open the ORCID record for Alessandro Bottaro [Opens in a new window]
Giuseppe A. Zampogna
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, INPT, UPS, 31400 Toulouse, France
Jacques Magnaudet
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, INPT, UPS, 31400 Toulouse, France
Alessandro Bottaro*
Affiliation:
Dipartimento di Ingegneria Civile, Chimica e Ambientale, Università di Genova, Via Montallegro 1, 16145 Genova, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

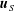A macroscopic boundary condition to be used when a fluid flows over a rough surface is derived. It provides the slip velocity $\boldsymbol{u}_{S}$ on an equivalent (smooth) surface in the form 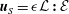$\boldsymbol{u}_{S}=\unicode[STIX]{x1D716}{\mathcal{L}}\boldsymbol{ : }{\mathcal{E}}$, where the dimensionless parameter $\unicode[STIX]{x1D716}$ is a measure of the roughness amplitude, 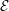${\mathcal{E}}$ denotes the strain-rate tensor associated with the outer flow in the vicinity of the surface and 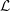${\mathcal{L}}$ is a third-order slip tensor arising from the microscopic geometry characterizing the rough surface. This boundary condition represents the tensorial generalization of the classical Navier slip condition. We derive this condition, in the limit of small microscopic Reynolds numbers, using a multi-scale technique that yields a closed system of equations, the solution of which allows the slip tensor to be univocally calculated, once the roughness geometry is specified. We validate this generalized slip condition by considering the flow about a rough sphere, the surface of which is covered with a hexagonal lattice of cylindrical protrusions. Comparisons with direct numerical simulations performed in both laminar and turbulent regimes allow us to assess the validity and limitations of this condition and of the mathematical model underlying the determination of the slip tensor 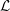${\mathcal{L}}$.

JFM classification

Boundary Layers: Boundary Layers Flow Control: Drag reduction Flow Control: Flow Control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 407 - 436
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allaire, G. 1989 Homogenization of Stokes flow in a connected porous medium. Asymp. Anal. 2, 203–222.Google Scholar
Amirat, Y., Bresch, D., Lemoine, J. & Simon, J. 2001 Effect of rugosity on a flow governed by stationary Navier–Stokes equations. Q. J. Appl. Maths 59, 769–785.Google Scholar
Barenblatt, G. I., Zheltov, I. P. & Kochina, I. N. 1960 Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. Z. Angew. Math. Mech. J. Appl. Math. Mech. 24, 1286–1303.Google Scholar
Bazant, M. Z. & Vinogradova, O. I. 2008 Tensorial hydrodynamic slip. J. Fluid Mech. 613, 125–134.Google Scholar
Bechert, D. W. & Bartenwerfer, M. 1989 The viscous flow on surfaces with longitudinal ribs. J. Fluid Mech. 206, 105–129.Google Scholar
Bella, P., Ferhman, B., Fischer, J. & Otto, F. 2016 Stochastic homogenization of linear elliptic equations: higher-order error estimates in weak norms via second-order correctors. SIAM J. Math. Anal. 49, 4658–4703.Google Scholar
Bhirde, A. A., Patel, V., Gavard, J., Zhang, G., Sousa, A. A., Masedunskas, R., Leapman, D., Weigert, R., Gutkind, J. S. & Rusling, J. F. 2009 Targeted killing of cancer cells in vivo and in vitro with EGF-directed nanotube-based drug delivery. ACS Nano 3, 307–316.Google Scholar
Bhushan, B. & Jung, Y. C. 2011 Natural and biomimetic artificial surfaces for superhydrophobicity, self-cleaning, low adhesion, and drug reduction. Prog. Mater. Sci. 56, 1–108.Google Scholar
Bradshaw, P. 2000 Note on critical roughness height and transitional roughness. Phys. Fluids 12, 1611–1614.Google Scholar
Cottereau, R. 2012 A stochastic-deterministic coupling method for multiscale problems. Application to numerical homogenization of random materials. Proc. IUTAM 6, 35–43.Google Scholar
Cottin-Bizonne, C., Barentin, C. & Bocquet, L. 2012 Scaling laws for slippage on superhydrophobic fractal surfaces. Phys. Fluids 24, 012001.Google Scholar
Davis, A. M. J. & Lauga, E. 2010 Hydrodynamic friction of fakir-like superhydrophobic surfaces. J. Fluid Mech. 661, 402–411.Google Scholar
De Gennes, P. G., Brochart-Wyart, F. & Quéré, D. 2003 Capillary and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
De Nicola, F., Castrucci, P., Scarselli, M., Nanni, F., Cacciotti, I. & De Crescenzi, M. 2015 Multi-fractal hierarchy of single-walled carbon nanotube hydrophobic coatings. Sci. Rep. 5, 8583.Google Scholar
García-Mayoral, R. & Jiménez, J. 2011 Drag reduction by riblets. Phil. Trans. R. Soc. Lond. A 369, 1412–1427.Google Scholar
Goh, P. S., Ismail, A. F. & Ng, B. C. 2009 Carbon nanotubes for desalination: performance evaluation and current hurdles. Desalination 308, 2–14.Google Scholar
Guo, J., Veran-Tissoires, S. & Quintard, M. 2016 Effective surface and boundary conditions for heterogeneous surfaces with mixed boundary conditions. J. Comput. Phys. 305, 942–963.Google Scholar
Introïni, C., Quintard, M. & Duval, F. 2011 Effective surface modeling for momentum and heat transfer over rough surfaces: application to a natural convection problem. Intl J. Heat Mass Transfer 54, 3622–3641.Google Scholar
Jiménez Bolaños, S. & Vernescu, B. 2017 Derivation of the Navier slip and slip length for viscous flows over a rough boundary. Phys. Fluids 29, 057103.Google Scholar
Kamrin, K., Bazant, M. & Stone, H. A. 2010 Effective slip boundary conditions for arbitrary periodic surfaces: the surface mobility tensor. J. Fluid Mech. 658, 409–437.Google Scholar
Lācis, U. & Bagheri, S. 2017 A framework for computing effective boundary conditions at the interface between free fluid and a porous medium. J. Fluid Mech. 812, 866–889.Google Scholar
Lācis, U., Zampogna, G. A. & Bagheri, S. 2017 A computational continuum model of poroelastic beds. Proc. R. Soc. Lond. A 473, 20160932.Google Scholar
Lauga, E., Brenner, M. P. & Stone, H. A. 2005 Microfluidics: the no-slip boundary condition. In Handbook of Experimental Fluid Dynamics (ed. Foss, J., Tropea, C. & Yarin, A.), chap. 15, Springer.Google Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.Google Scholar
Legendre, D., Lauga, E. & Magnaudet, J. 2009 Influence of slip on the dynamics of two-dimensional wakes. J. Fluid Mech. 633, 437–447.Google Scholar
Lilley, G. M. 1998 A study of the silent flight of the owl. AIAA J. 2340, 1–6.Google Scholar
Luchini, P. 1992 Effects of riblets on the growth of laminar and turbulent boundary. In Emerging Techniques in Drag Reduction (ed. Choi, K. S., Prasad, K. K. & Truong, T. V.), pp. 101–116. Wiley.Google Scholar
Luchini, P. 2013 Linearized no-slip boundary conditions at a rough surface. J. Fluid Mech. 737, 349–367.Google Scholar
Luchini, P., Manzo, D. & Pozzi, A. 1991 Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 228, 87–109.Google Scholar
Magnaudet, J. & Mougin, G. 2007 Wake instability of a fixed spheroidal bubble. J. Fluid Mech. 572, 311–337.Google Scholar
Majumder, M., Chopra, N., Andrews, R. & Hinds, B. J. 2005 Nanoscale hydrodynamics: enhanced flow in carbon nanotubes. Nature 438, 44–44.Google Scholar
Mei, C. C. & Vernescu, B. 2010 Homogenization Methods for Multiscale Mechanics. World Scientific.Google Scholar
Navier, C. L. M. H. 1823 Mémoires sur les lois du mouvement des fluides. Mém. Acad. Sci. Inst. France 6, 389–416.Google Scholar
Oeffner, J. & Lauder, G. V. 2012 The hydrodynamic function of shark skin and two biomimetic applications. J. Expl Biol. 215, 785–795.Google Scholar
Onda, T., Shibuichi, S., Satoh, N. & Tsujii, K. 1996 Super-water-repellent fractal surfaces. Langmuir 12, 2125–2127.Google Scholar
Orr, T. S., Domaradzki, J. A., Spedding, G. R. & Constantinescu, G. S. 2015 Numerical simulations of the near wake of a sphere moving in a steady, horizontal motion through a linearly stratified fluid at Re = 1000. Phys. Fluids 27, 035113.Google Scholar
Pasquier, S., Quintard, M. & Davit, Y. 2017 Modeling flow in porous media with rough surfaces: effective slip boundary conditions and application to structured packings. Chem. Engng Sci. 165, 131–146.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Sarkar, K. & Prosperetti, A. 1996 Effective boundary conditions for Stokes flow over a rough surface. J. Fluid Mech. 316, 223–240.Google Scholar
Schlichting, H. 1979 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Slegers, N., Heilman, M., Cranford, J., Lang, A., Yoder, J. & Hebegger, M. L. 2017 Beneficial aerodynamic effect of wing scales on the climbing flight of butterflies. Bioinspir. Biomim. 12, 016013.Google Scholar
Thakkar, M., Busse, A. & Sandham, N. D. 2018 Direct numerical simulation of turbulent channel flow over a surrogate for Nikuradse-type roughness. J. Fluid Mech. 837, R1.Google Scholar
Tricinci, O., Terencio, T., Mazzolai, B., Pugno, N., Greco, F. & Mattoli, V. 2015 3D micropatterned surface inspired by Salvinia molesta via direct laser lithography. ACS J. Appl. Mater. Interfaces 7, 2556–25567.Google Scholar
Veran, S., Aspa, Y. & Quintard, M. 2009 Effective boundary conditions for rough reactive walls in laminar boundary layers. Intl J. Heat Mass Transfer 52, 3712–3725.Google Scholar
Versteeg, H. K. & Malalasekera, W. 2007 An Introduction to Computational Fluid Dynamics. The Finite Volume Method. Pearson Education.Google Scholar
Walsh, M. J. 1983 Riblets as a viscous drag reduction technique. AIAA J. 21, 485–486.Google Scholar
Ybert, C., Barentin, C. & Cottin-Bizonne, C. 2007 Achieving large slip with superhydrophobic surfaces: scaling laws for generic geometries. Phys. Fluids 19, 123601.Google Scholar
Zampogna, G. A. & Bottaro, A. 2016 Fluid flow over and through a regular bundle of rigid fibres. J. Fluid Mech. 792, 1–31.Google Scholar